Development of Psi Factors for Thermal Bypass Due to Insulation Gaps in Low-Slope Roofing Assemblies
Abstract
:1. Introduction
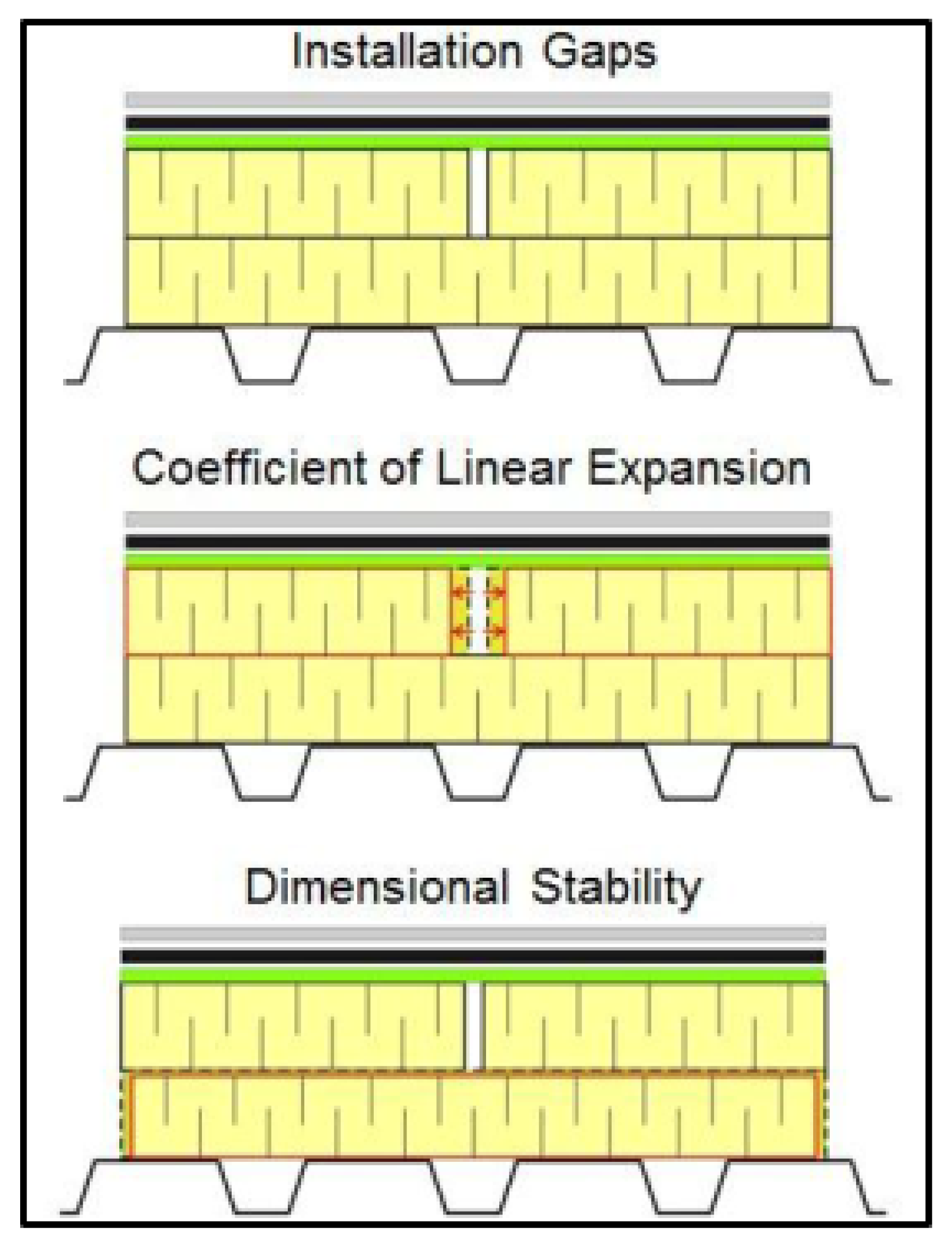
- When the insulation is installed during the roof assembly construction, it is not uncommon to see between 1.6 mm (1/16 in) and 3.2 mm (1/8 in) gaps between the insulation boards. These gaps can be further compounded by the deficiencies in the manufactured boards;
- The daily and seasonal temperature variations in the life cycle of the roof assemblies can cause the insulation boards to expand or contract depending on their coefficient of expansion. These changes in the board dimensions might not be permanent, and the boards could return to their original dimensions. However, this expansion and contraction leads to gap formation and transfers stresses to the attached components within the roof assembly;
- The dimensional stability of the insulation boards could also lead to gaps between the boards. In simple terms, dimensional stability is the material’s permanent change in dimensions (length, width, and thickness) in response to the changes in temperature and humidity conditions to which it is exposed;
- Gaps in the range of an inch or greater at the insulation joints may seem far-fetched, but the reality is that these gaps exist. Figure 2 shows the field examples of the magnitude of gap formation in commercial roofs that further emphasizes the importance of considering gaps in the thermal design of roofs.
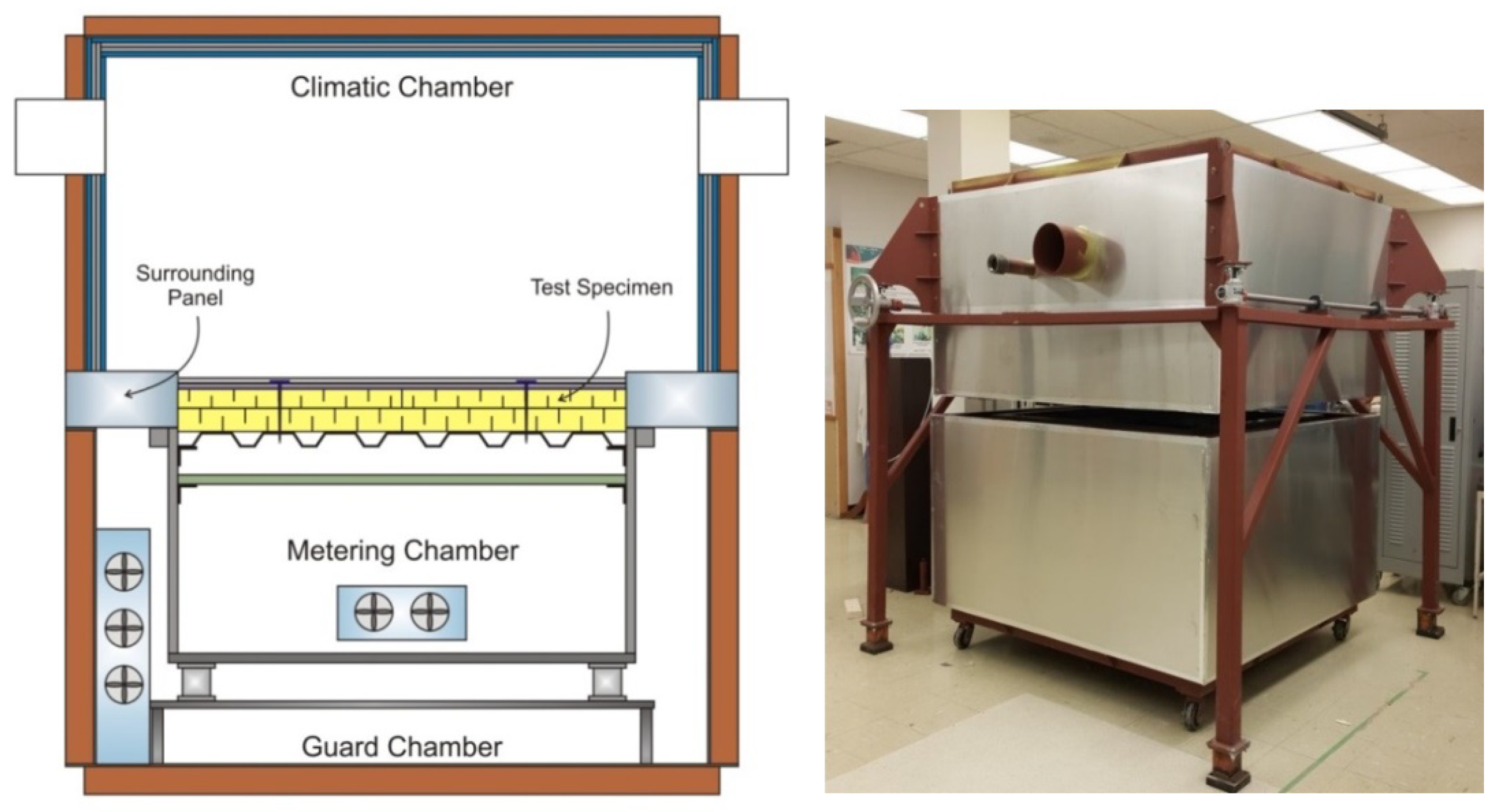
2. Part 1: Experimental Approach
3. Part 2: Numerical Analysis—Psi Factor Approach
4. Results and Discussion
4.1. Part 1: Experimental Approach
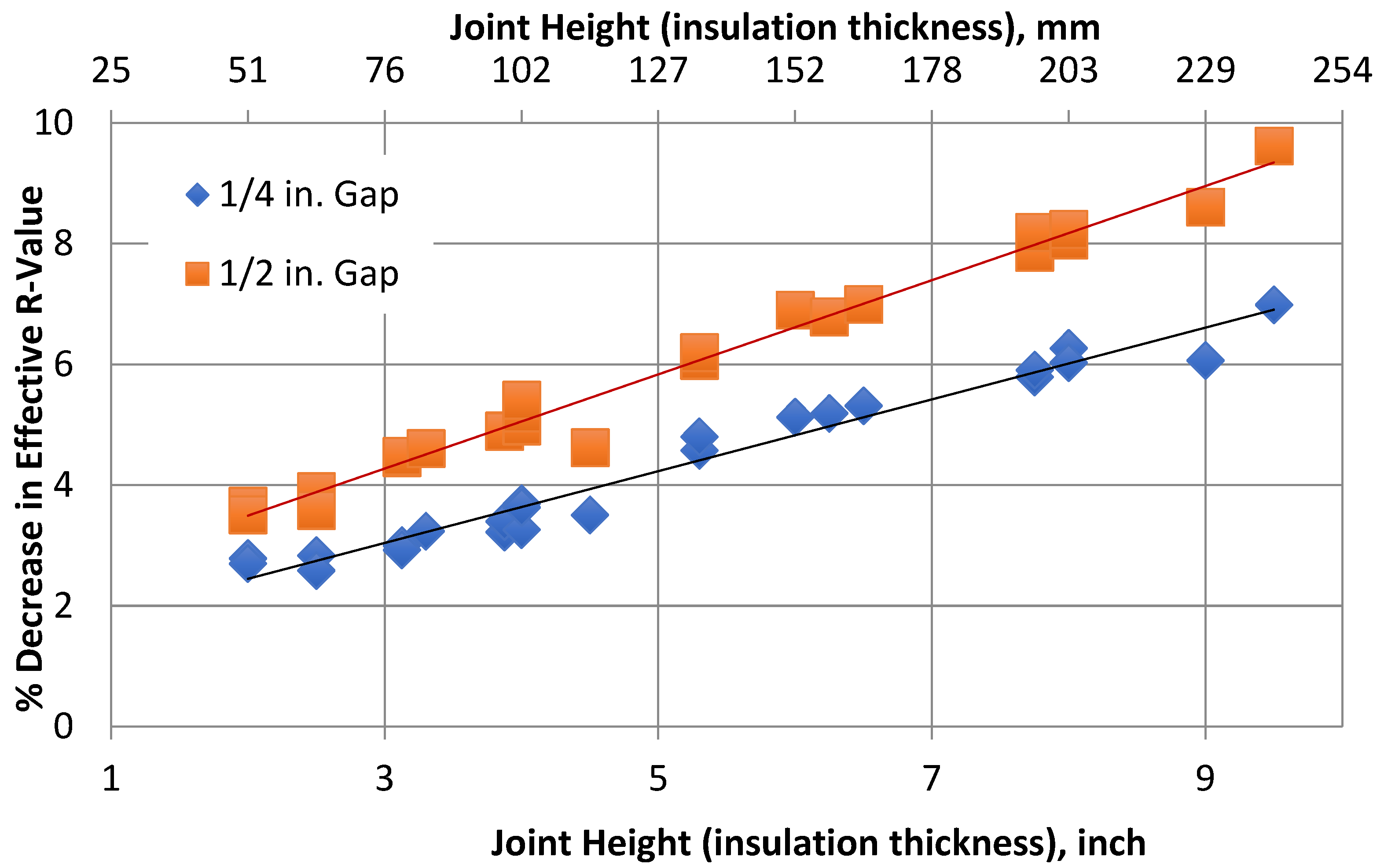
4.1.1. Gap Impact Factor
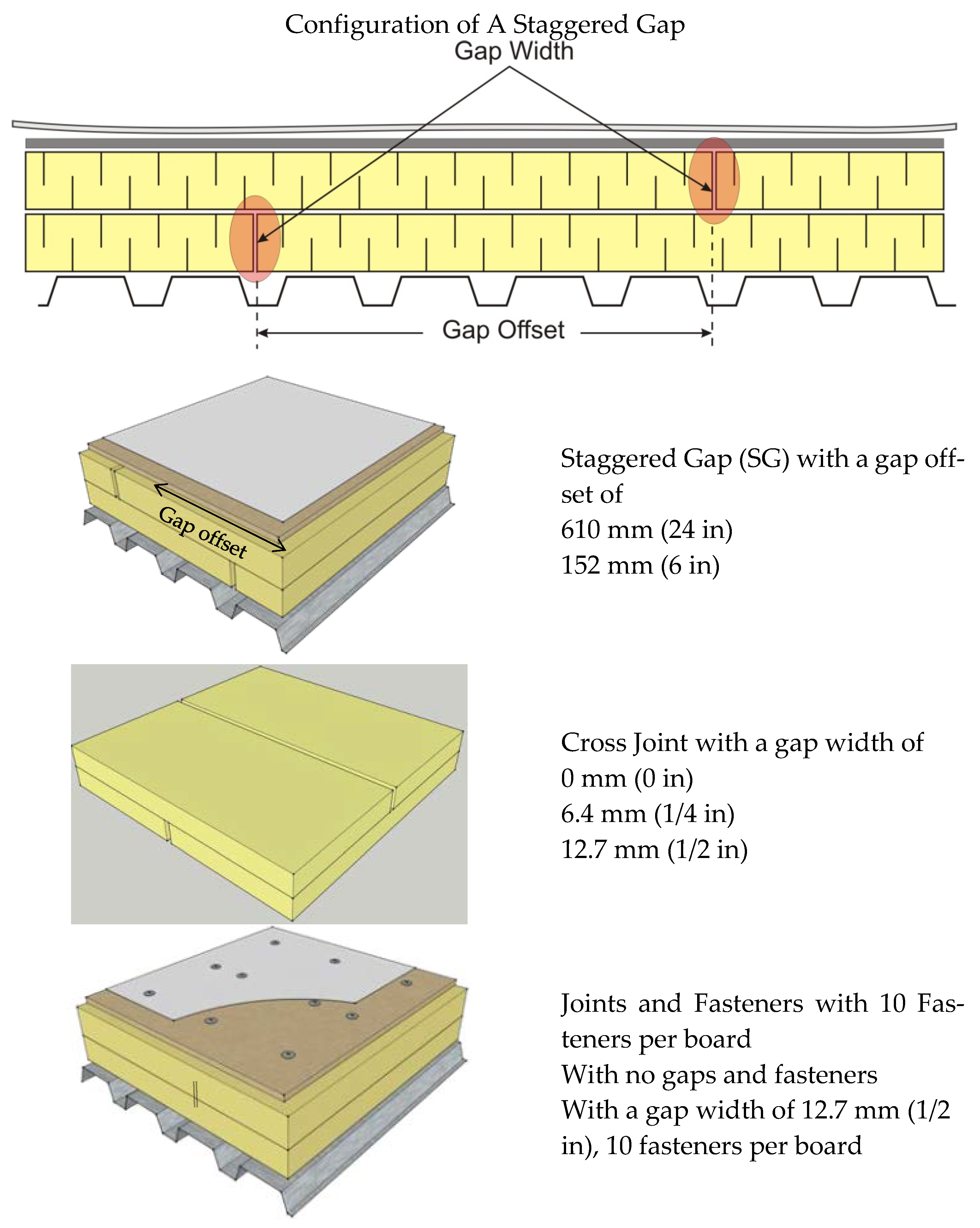
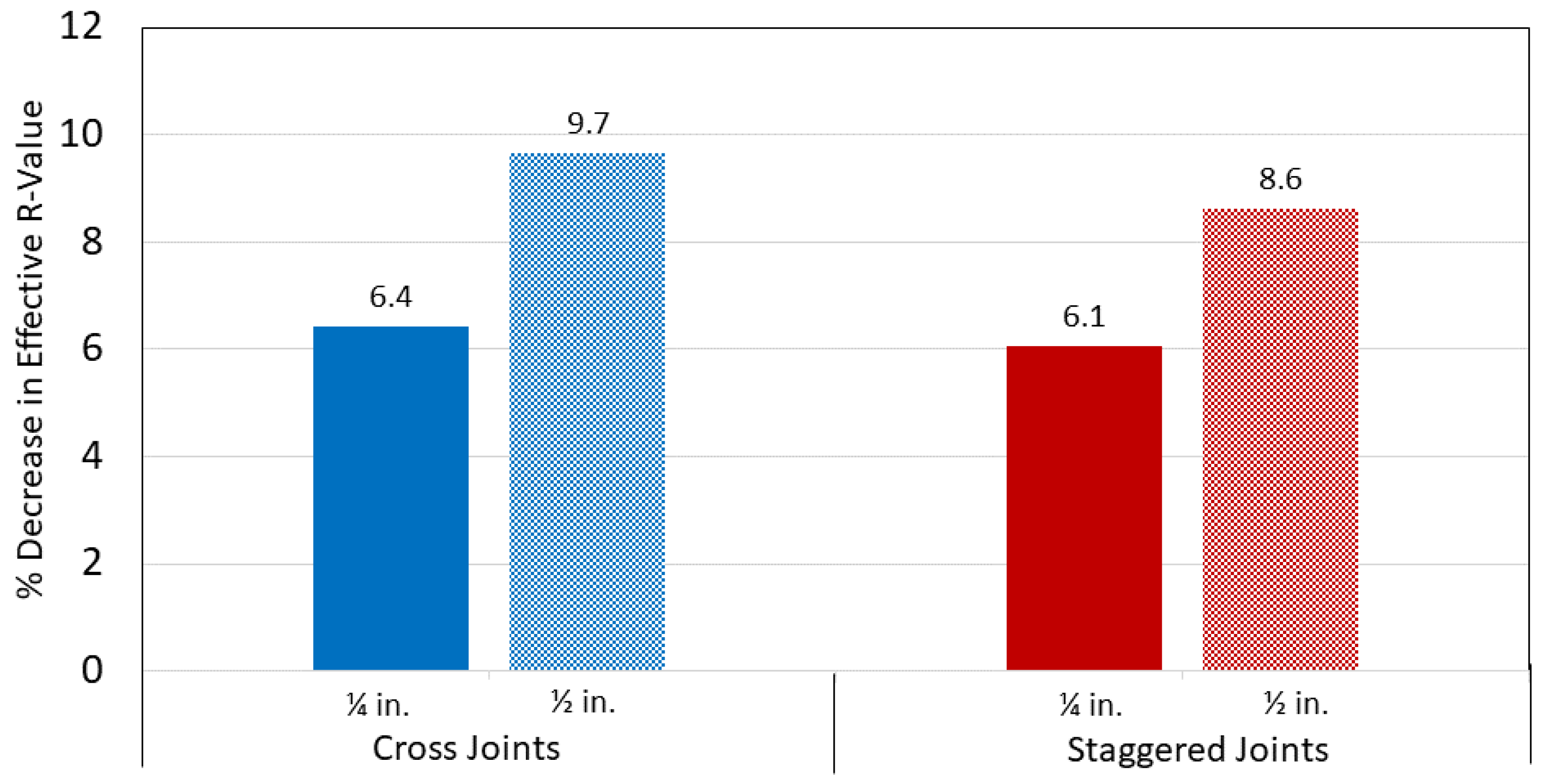
4.1.2. Impact of Joint Offset in Staggered Insulation
4.1.3. Cross Joint
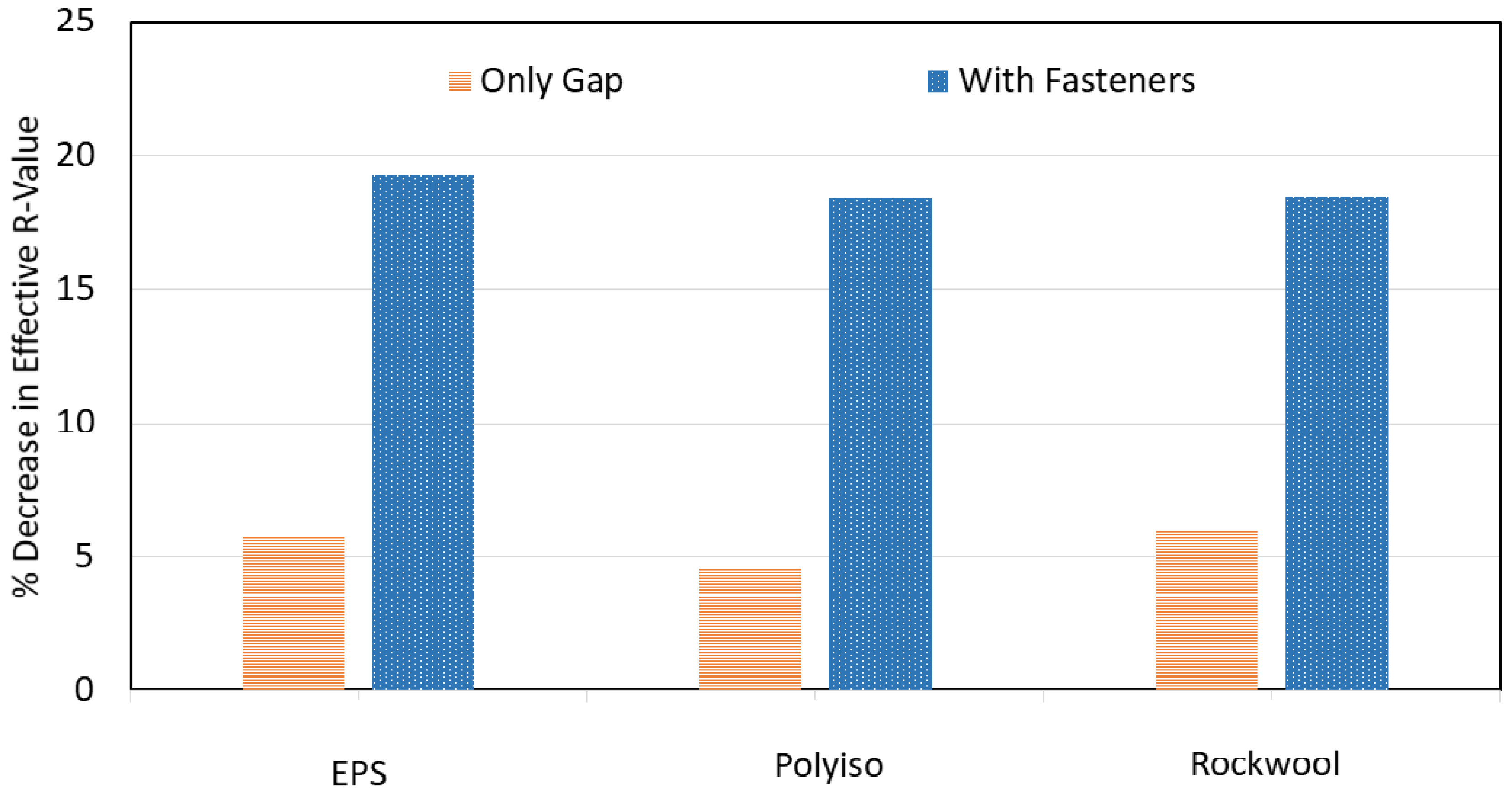
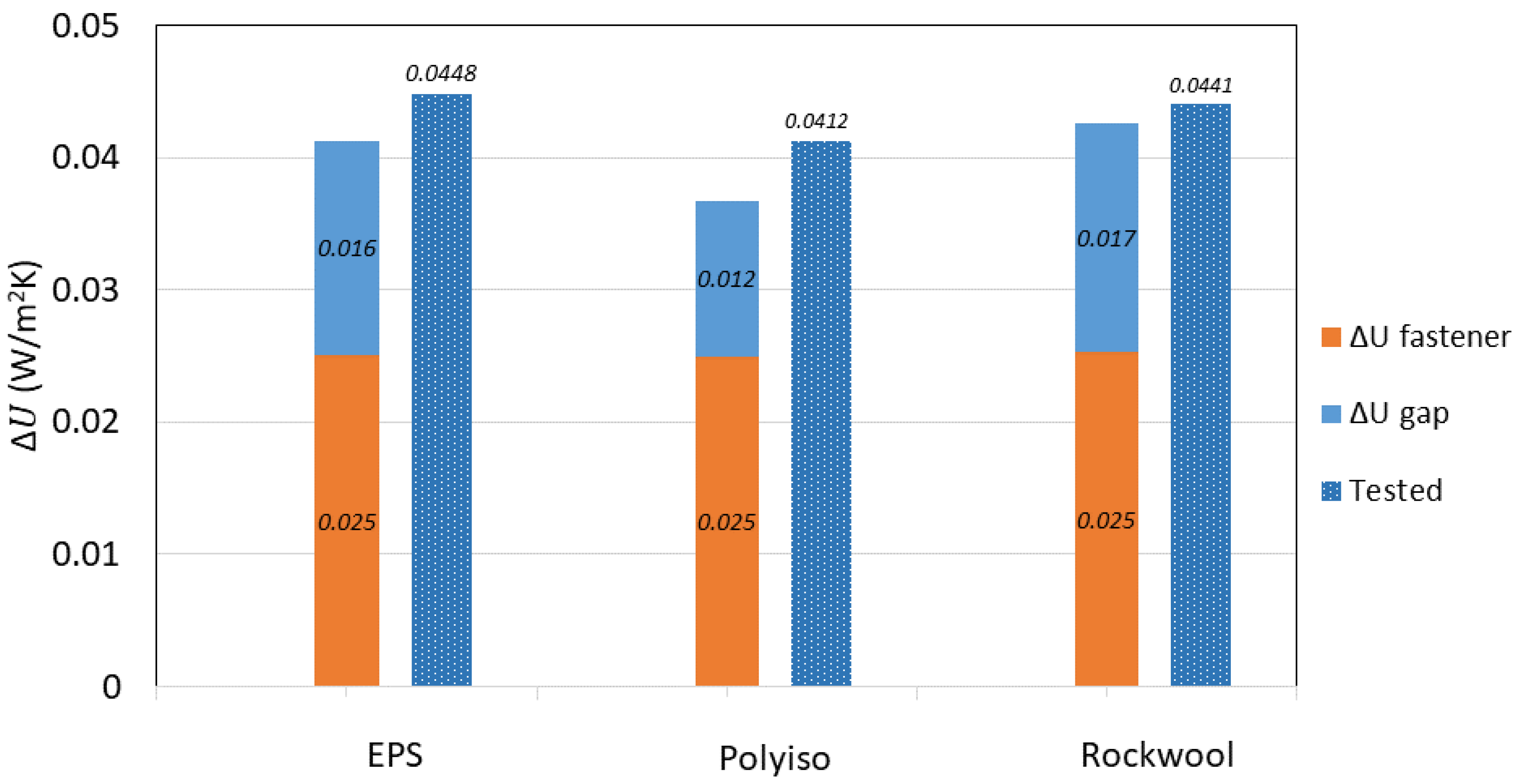
4.1.4. Joints and Fasteners
4.2. Part 2: Numerical Approach
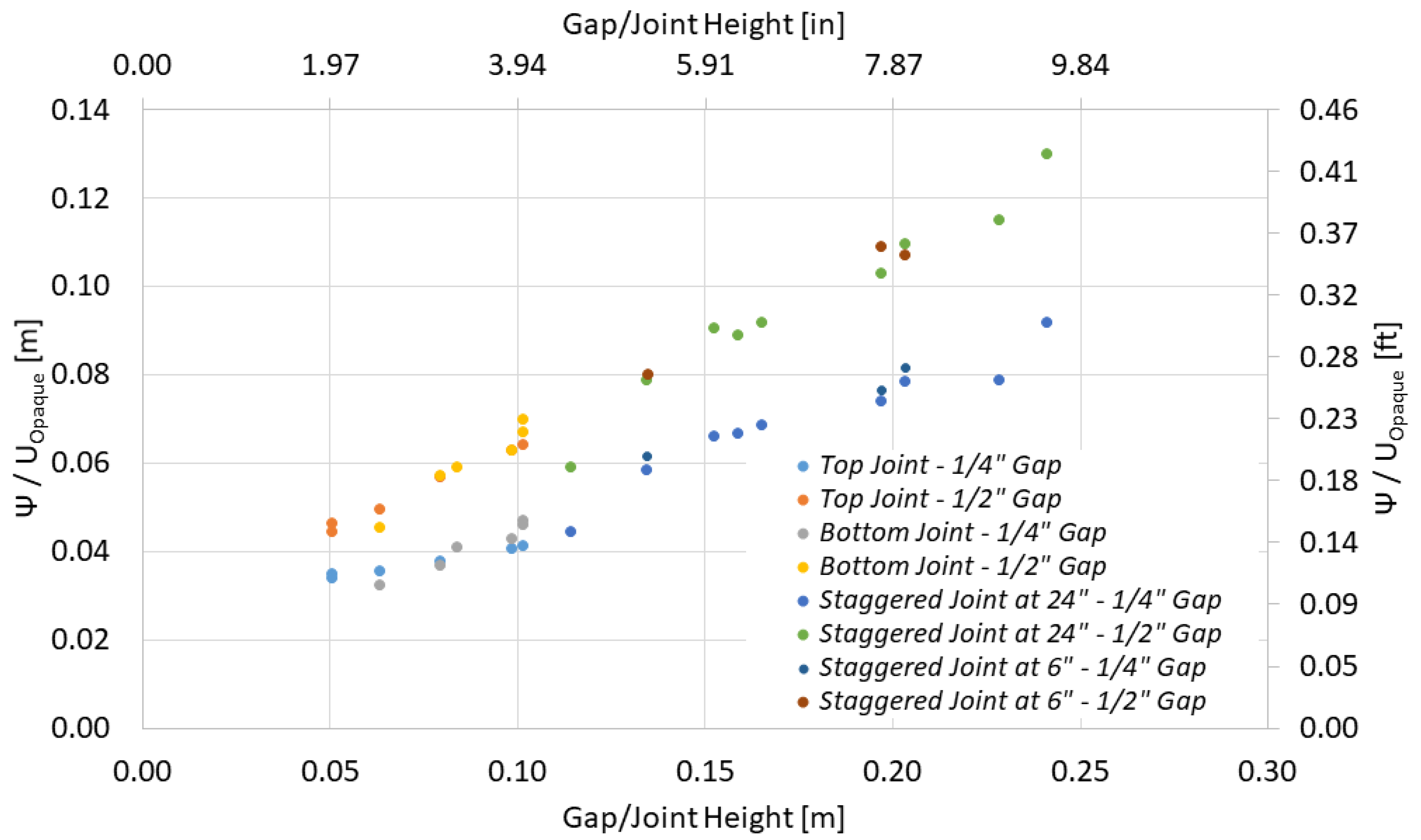
4.2.1. Psi Factor Approach
4.2.2. Application of Psi Factors
5. Summary and Conclusions
- Thermal bypass increases with the gap width between insulation boards. The relative (percentage) thermal bypass also increases as the gap height increases. Overall, the average loss in effective R-value ranged from 2% to 7% and 4% to 9% for 6.4 mm (1/4 in) and 12.7 mm (1/2 in), respectively, for gap height ranging from 51 mm (2 in) to 241 mm (9.5 in). Generalized gap impact curves applicable for all three design categories-R26, R31 and R36 were developed;
- Testing on cross joints on the EPS R-36 system having 229 mm (9 in) of insulation showed a 6% and 12% increase in the percentage loss in effective R-Value for the 6.4 mm (1/4 in) and 12.7 mm (1/2 in) gaps, respectively. This indicates an increase in the thermal losses due to the cross joints. However, to further quantify this phenomenon, further investigation is required;
- A psi factor relationship was developed from the experimental data to support the calculation of linear thermal bypass effects on the thermal performance of the commercial roofs. These relationships provide a basis for determining the impact of gaps by using the Psi factor approach. This will allow users to assess the thermal bypass of staggered gaps and top and bottom gaps in roofing systems with two insulation layers. This testing was conducted over a range of R-values from R-26 to R-36 with 6.4 mm (1/4 in) and 12.7 mm (1/2 in) insulation gaps;
- The psi and chi factors developed from the experimental testing were used to determine the anticipated thermal bridging and thermal bypass due to the combined fasteners and gaps and calculate the total transmittance. When comparing the test with combined fasteners and gaps, it was found that there was a higher thermal transmittance with the fasteners and gaps compared to the calculations. This could be due to thermal interactions between the fasteners and the gaps. However, further investigation is required to quantify this interaction further;
- Based on the developed psi factors, a procedure was developed for determining the thermal transmittance due to 6.4 mm (1/4 in) and 12.7 mm (1/2 in) gaps within insulation boards in roofing systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mukhopadhyaya, P.; Kumaran, M.K.; Ping, F.; Normandin, N. Use of vacuum insulation panel in building envelope construction: Advantages and challenges. In Proceedings of the 13th Canadian Conference on Building Science and Technology, Winnipeg, MB, Canada, 10–13 May 2011. [Google Scholar]
- ASHRAE 90.1; Energy Standard for Building Except Low-Rise Residential Buildings (ANSI/ASHRAE/IES Standarad 90.1). ASHRAE: Atlanta, GA, USA, 2019.
- ASTM Standard C518-17; Steady-State Thermal Transmission by Heat Flow Meter Apparatus. ASTM International: West Conshohocken, PA, USA, 2017.
- Harrje, D.T.; Dutt, G.S.; Gadsby, K.J. Convective Loop Heat Losses in Buildings. ASHRAE Trans. 1985, 91, 751–760. [Google Scholar]
- Chebil, S.; Galanis, N.; Zmeureanu, R. Computer Simulation of Thermal Impact of Air infiltration through Multi-layered Exterior Walls. In Proceedings of the Eighth International IBPSA Conference, Eindhoven, The Netherlands, 11–14 August 2003; pp. 155–162. [Google Scholar]
- Bankvall, C.; Sikander, E. Air Transport in Building Envelope and Construction Process. In Proceedings of the 8th Symposium on Building Physics in the Nordic Countries, Copenhagen, Denmark, 16–18 June 2008; Volume 3, pp. 1389–1396. [Google Scholar]
- Qin, M.; Belarbi, R.; Aït-Mokhtar, A.; Nilsson, L.O. Coupled heat and moisture transfer in multi-layer building materials. Constr. Build. Mater. 2009, 23, 967–975. [Google Scholar] [CrossRef]
- Šeduikytė, L.; Paukštys, V. Evaluation of indoor environmental conditions in offices located in buildings with large glazed areas. J. Civ. Eng. Manag. 2008, 14, 39–44. [Google Scholar] [CrossRef] [Green Version]
- Šadauskienė, J.; Stankevičius, V.; Bliūdžius, R.; Gailius, A. The impact of the exterior painted thin-layer render’s water va[our and liquid water permeability on the moisture state of the wall insulating system. Constr. Build. Mater. 2009, 23, 2788–2794. [Google Scholar] [CrossRef]
- Kosinski, P. Air thermal bridges. Tech. Trans. 2014, 3-B, 221–228. [Google Scholar]
- Kosinski, P. Thermal Bridge Effect of Air Gaps in Wall Construction. Tech. Sci. 2015, 18, 159–169. [Google Scholar]
- Lewis, J.E. Thermal Evaluation of the Effects of Gaps Between Adjacent Roof Insulation Panels. J. Therm. Insul. 1979, 3, 80–103. [Google Scholar] [CrossRef]
- Hedlin, C.P. Effect of insulation joints on heat loss through flat roofs. ASHRAE Trans. 1985, 91, 608–622. [Google Scholar]
- Petrie, T.W.; Atchley, J.A.; Desjarlais, A.O.; Christian, J.E. Effects of Mechanical Fasteners and Gaps between Insulation Boards on Thermal Performance of Low-Slope Roofs. J. Therm. Envel. Build. Sci. 2000, 23, 292–317. [Google Scholar] [CrossRef]
- ASTM Standard C1363-19; Standard Test Method for Thermal Performance of Building Materials and Envelop Assemblies by Means of Hot Box Apparatus. ASTM International: West Conshohocken, PA, USA, 2019.
- Šadauskiene, J.; Buska, A.; Burlingis, A.; Bliūdžius, R.; Gailius, A. The effect of vertical air gaps to thermal transmittance of horizontal thermal insulating layer. J. Civ. Eng. Manag. 2009, 15, 309–315. [Google Scholar] [CrossRef] [Green Version]
- ISO 14683:2007; Thermal Bridges in Building Construction—Linear Thermal Transmittance—Simplified Methods and Default Values. ISO: Geneva, Switzerland, 2007.
- International Code Council. Internation Energy Conservation Code (IECC); International Code Council: Country Club Hills, IL, USA, 2018. [Google Scholar]
- Canadian Commission on Building and Fire Codes. National Energy Code of Canada for Buildings; National Research Council of Canada: Ottawa, ON, Canada, 2015. [Google Scholar]
- Molleti, S.; Baskaran, A. Energy Resistance of Commercial Roofs; ASTM International: West Conshohocken, PA, USA, 2020; pp. 161–185. [Google Scholar] [CrossRef]
- Molleti, S.; van Reenen, D.; Baskaran, A. Development of chi-factors towards codification of the thermal bridging in low slope roofing assemblies. Energy Build. 2021, 231, 110559. [Google Scholar] [CrossRef]
- Molleti, S. Mind the gap: Thermal bypass occurs through gaps between insulation boards in low-slope roof assemblies. NRCA Prof. Roof. 2020, 50. [Google Scholar]
- ISO 6946:2007; Building Components and Building Elements—Thermal RESISTANCE and Thermal Transmittance—Calculation Method. ISO: Geneva, Switzerland, 2007.




| Board Thickness | R-25.21 | R-30.21 | R-35.21 |
|---|---|---|---|
| Polyisocyanurate (polyiso) | [2 in + 2.5 in] | [2 in + 3 1/3 in] | [2 in + 4 in] |
| Expanded Polystyrene (EPS) | [3 1/8 in + 3 1/8 in] | [3 7/8 in + 3 7/8 in] | [4.625 in + 4.625 in] |
| Rockwool | [2.5 in + 4 in] | [4 in + 4 in] | [5.5 in + 4 in] |
| System | Staggered Joints (610 mm [24”] OC) | Staggered Joints (152 mm [6”] OC) | Joints and Fasteners | ||||||
|---|---|---|---|---|---|---|---|---|---|
| mm [in] | mm [in] | mm [in] | |||||||
| 0.0 [0] | 6.4 [0.25] | 12.7 [0.50] | 0.0 [0] | 6.4 [0.25] | 12.7 [0.50] | 0 [0] | 12.7 [0.50] | ||
| EPS | R-26 | √ | √ | √ | |||||
| R-31 | √ | √ | √ | √ | √ | √ | √ | √ | |
| R-36 | √ | √ | √ | ||||||
| ISO | R-26 | √ | √ | √ | |||||
| R-31 | √ | √ | √ | √ | √ | √ | √ | √ | |
| R-36 | √ | √ | √ | ||||||
| SW | R-26 | √ | √ | √ | |||||
| R-31 | √ | √ | √ | √ | √ | √ | √ | √ | |
| R-36 | √ | √ | √ | ||||||
| Additional Tests | |||||||||
| Cross Joints—EPS R-26 System for 0, 6.4, 12.7 mm (0, 1/4 and 1/2 in) | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molleti, S.; van Reenen, D. Development of Psi Factors for Thermal Bypass Due to Insulation Gaps in Low-Slope Roofing Assemblies. Buildings 2022, 12, 68. https://doi.org/10.3390/buildings12010068
Molleti S, van Reenen D. Development of Psi Factors for Thermal Bypass Due to Insulation Gaps in Low-Slope Roofing Assemblies. Buildings. 2022; 12(1):68. https://doi.org/10.3390/buildings12010068
Chicago/Turabian StyleMolleti, Sudhakar, and David van Reenen. 2022. "Development of Psi Factors for Thermal Bypass Due to Insulation Gaps in Low-Slope Roofing Assemblies" Buildings 12, no. 1: 68. https://doi.org/10.3390/buildings12010068
APA StyleMolleti, S., & van Reenen, D. (2022). Development of Psi Factors for Thermal Bypass Due to Insulation Gaps in Low-Slope Roofing Assemblies. Buildings, 12(1), 68. https://doi.org/10.3390/buildings12010068






