Python-LMDI: A Tool for Index Decomposition Analysis of Building Carbon Emissions
Abstract
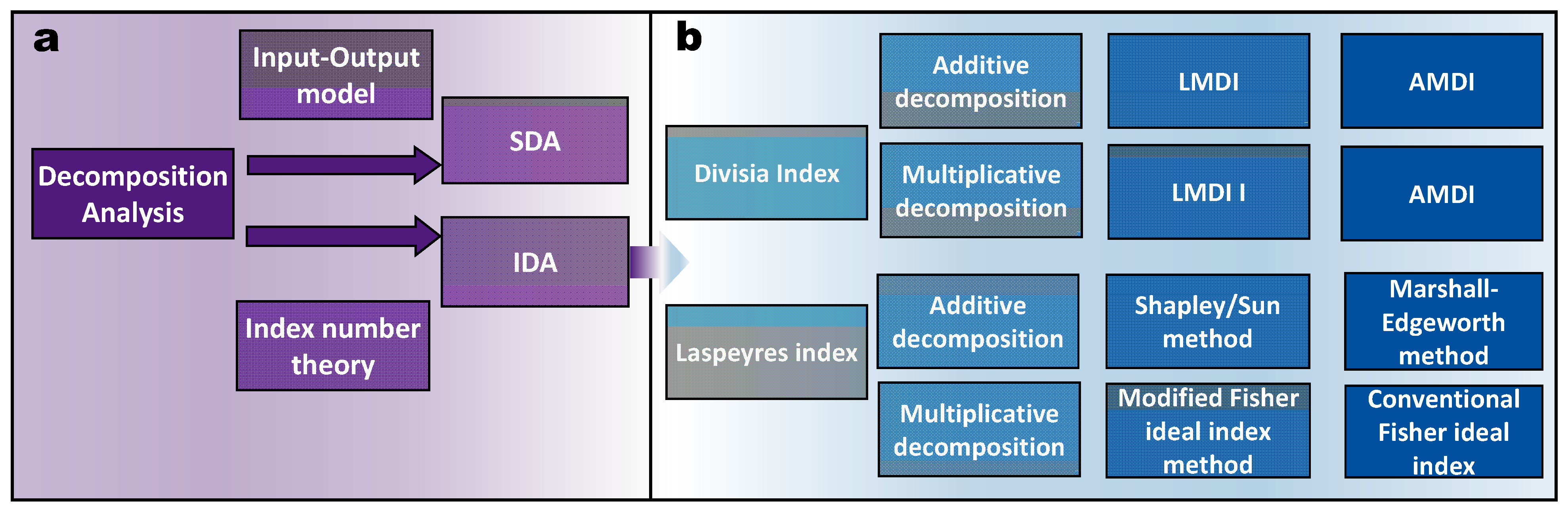
:1. Introduction
- How to develop a simple and convenient tool for LMDI decomposition analysis;
- How to use this tool to analyze carbon emissions from commercial buildings, using China and the US as examples.
2. Literature Review
3. PyLMDI: A Python Tool for LMDI Decomposition Analysis
3.1. The LMDI Decomposition Analysis
3.2. The PyLMDI Open-Source Tool
4. The Numerical Example and Discussion
4.1. Historical Carbon Abatement in the Commercial Building Operation: China versus the US
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, N.; Khanna, N.; Feng, W.; Ke, J.; Levine, M. Scenarios of energy efficiency and CO2 emissions reduction potential in the buildings sector in China to year 2050. Nat. Energy 2018, 3, 978–984. [Google Scholar] [CrossRef]
- UNEP. 2021 Global Status Report for Buildings and Construction. Available online: https://globalabc.org/sites/default/files/2021-10/GABC_Buildings-GSR-2021_BOOK.pdf (accessed on 10 December 2021).
- Xiang, X.; Ma, X.; Ma, Z.; Ma, M. Operational Carbon Change in Commercial Buildings under the Carbon Neutral Goal: A LASSO-WOA Approach. Buildings 2022, 12, 54. [Google Scholar] [CrossRef]
- Yang, L.; Ma, Z.; Ma, M.; Xu, Y. Decarbonization, Environmental Regulation, and Economic Boom: An Indicator Assessment Based on the Industrial Waste. Front. Energy Res. 2022, 9, 838852. [Google Scholar]
- Lou, Y.; Ye, Y.; Yang, Y.; Zuo, W. Long-term carbon emission reduction potential of building retrofits with dynamically changing electricity emission factors. Build. Environ. 2021, 210, 108683. [Google Scholar] [CrossRef]
- Wu, W.; Ma, X.; Zhang, Y.; Li, W.; Wang, Y. A novel conformable fractional non-homogeneous grey model for forecasting carbon dioxide emissions of BRICS countries. Sci. Total Environ. 2020, 707, 135447. [Google Scholar] [CrossRef]
- Dong, K.; Hochman, G.; Timilsina, G.R. Do drivers of CO2 emission growth alter overtime and by the stage of economic development? Energy Policy 2020, 140, 111420. [Google Scholar] [CrossRef]
- Ang, B.W.Z.; Fang, Q. A survey of index decomposition analysis in energy and environmental studies. Energy 2000, 25, 1149–1176. [Google Scholar] [CrossRef]
- Ang, B.W. Decomposition analysis for policymaking in energy: Which is the preferred method? Energy Policy 2004, 32, 1131–1139. [Google Scholar] [CrossRef]
- Ang, B.W. The LMDI approach to decomposition analysis: A practical guide. Energy Policy 2005, 33, 867–871. [Google Scholar] [CrossRef]
- Xu, X.; Ang, B.W. Index decomposition analysis applied to CO2 emission studies. Ecol. Econ. 2013, 93, 313–329. [Google Scholar] [CrossRef]
- Ang, B.W. LMDI decomposition approach: A guide for implementation. Energy Policy 2015, 86, 233–238. [Google Scholar] [CrossRef]
- Ma, M.; Ma, X.; Cai, W.; Cai, W. Low carbon roadmap of residential building sector in China: Historical mitigation and prospective peak. Appl. Energy 2020, 273, 115247. [Google Scholar] [CrossRef]
- Li, K.; Ma, M.; Xiang, X.; Feng, W.; Ma, Z.; Cai, W.; Ma, X. Carbon reduction in commercial building operations: A provincial retrospection in China. Appl. Energy 2022, 306, 118098. [Google Scholar] [CrossRef]
- Kaltenegger, O. What drives total real unit energy costs globally? A novel LMDI decomposition approach. Appl. Energy 2020, 261, 114340. [Google Scholar] [CrossRef] [Green Version]
- Ang, B.W. Decomposition methodology in industrial energy demand analysis. Energy 1995, 20, 1081–1095. [Google Scholar] [CrossRef]
- Su, B.; Ang, B.W. Structural decomposition analysis applied to energy and emissions: Some methodological developments. Energy Econ. 2012, 34, 177–188. [Google Scholar] [CrossRef]
- Liu, N.; Ang, B.W. Factors shaping aggregate energy intensity trend for industry: Energy intensity versus product mix. Energy Econ. 2007, 29, 609–635. [Google Scholar] [CrossRef]
- Su, B.; Ang, B.W. Multiplicative decomposition of aggregate carbon intensity change using input–output analysis. Appl. Energy 2015, 154, 13–20. [Google Scholar] [CrossRef]
- Wang, H.; Ang, B.; Su, B. Assessing drivers of economy-wide energy use and emissions: IDA versus SDA. Energy Policy 2017, 107, 585–599. [Google Scholar] [CrossRef]
- Choi, K.-H.; Ang, B. Measuring thermal efficiency improvement in power generation: The Divisia decomposition approach. Energy 2002, 27, 447–455. [Google Scholar] [CrossRef]
- Boyd, G.A.; Hanson, D.A.; Sterner, T. Decomposition of changes in energy intensity: A comparison of the Divisia index and other methods. Energy Econ. 1988, 10, 309–312. [Google Scholar] [CrossRef]
- Ang, B.W.; Liu, N. Negative-value problems of the logarithmic mean Divisia index decomposition approach. Energy Policy 2007, 35, 739–742. [Google Scholar] [CrossRef]
- Jiang, R.; Li, R.; Wu, Q. Investigation for the decomposition of carbon emissions in the USA with CD function and LMDI methods. Sustainability 2019, 11, 334. [Google Scholar] [CrossRef] [Green Version]
- Alajmi, R.G. Factors that impact greenhouse gas emissions in Saudi Arabia: Decomposition analysis using LMDI. Energy Policy 2021, 156, 112454. [Google Scholar] [CrossRef]
- Gong, Y.; Song, D. Life cycle building carbon emissions assessment and driving factors decomposition analysis based on LMDI—A case study of Wuhan City in China. Sustainability 2015, 7, 16670–16686. [Google Scholar] [CrossRef] [Green Version]
- Lin, B.; Liu, H. CO2 emissions of China’s commercial and residential buildings: Evidence and reduction policy. Build. Environ. 2015, 92, 418–431. [Google Scholar] [CrossRef]
- Lin, B.; Liu, H. CO2 mitigation potential in China’s building construction industry: A comparison of energy performance. Build. Environ. 2015, 94, 239–251. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, S.; Liu, J.; Liu, F.; Fu, X. Analysis of factors affecting CO2 emissions by civil buildings in China’s urban areas. Int. J. Low-Carbon Technol. 2015, 10, 460–463. [Google Scholar] [CrossRef] [Green Version]
- Yuan, B.; Ren, S.; Chen, X. The effects of urbanization, consumption ratio and consumption structure on residential indirect CO2 emissions in China: A regional comparative analysis. Appl. Energy 2015, 140, 94–106. [Google Scholar] [CrossRef]
- Lu, Y.; Cui, P.; Li, D. Carbon emissions and policies in China’s building and construction industry: Evidence from 1994 to 2012. Build. Environ. 2016, 95, 94–103. [Google Scholar] [CrossRef]
- Jiang, R.; Li, R. Decomposition and decoupling analysis of life-cycle carbon emission in China’s building sector. Sustainability 2017, 9, 793. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Chau, K.; Lu, W.; Shen, L.; Shuai, C.; Chen, J. Decoupling relationship between economic output and carbon emission in the Chinese construction industry. Environ. Impact Assess. Rev. 2018, 71, 60–69. [Google Scholar] [CrossRef]
- Wang, M.; Feng, C. Exploring the driving forces of energy-related CO2 emissions in China’s construction industry by utilizing production-theoretical decomposition analysis. J. Clean. Prod. 2018, 202, 710–719. [Google Scholar] [CrossRef]
- Lai, X.; Lu, C.; Liu, J. A synthesized factor analysis on energy consumption, economy growth, and carbon emission of construction industry in China. Environ. Sci. Pollut. Res. 2019, 26, 13896–13905. [Google Scholar] [CrossRef]
- Wu, P.; Song, Y.; Zhu, J.; Chang, R. Analyzing the influence factors of the carbon emissions from China’s building and construction industry from 2000 to 2015. J. Clean. Prod. 2019, 221, 552–566. [Google Scholar] [CrossRef]
- Wang, C.; Wu, K.; Zhang, X.; Wang, F.; Zhang, H.; Ye, Y.; Wu, Q.; Huang, G.; Wang, Y.; Wen, B. Features and drivers for energy-related carbon emissions in mega city: The case of Guangzhou, China based on an extended LMDI model. PloS ONE 2019, 14, e0210430. [Google Scholar] [CrossRef] [Green Version]
- Du, Q.; Lu, X.; Li, Y.; Wu, M.; Bai, L.; Yu, M. Carbon emissions in China’s construction industry: Calculations, factors and regions. Int. J. Environ. Res. Public Health 2018, 15, 1220. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Yue, Q.; Li, Y.; Zhao, F.; Wang, H. Driving force analysis of carbon emissions in China’s building industry: 2000–2015. Sustain. Cities Soc. 2020, 60, 102268. [Google Scholar] [CrossRef]
- Liu, Z.; Yin, Y. LMDI model-based analysis of direct carbon emission accounting and influencing factors of China’s building industry. Proc. IOP Conf. Ser. Mater. Sci. Eng. 2020, 768, 052096. [Google Scholar] [CrossRef]
- Chen, X.; Shuai, C.; Wu, Y.; Zhang, Y. Analysis on the carbon emission peaks of China’s industrial, building, transport, and agricultural sectors. Sci. Total Environ. 2020, 709, 135768. [Google Scholar] [CrossRef]
- Li, D.; Huang, G.; Zhang, G.; Wang, J. Driving factors of total carbon emissions from the construction industry in Jiangsu Province, China. J. Clean. Prod. 2020, 276, 123179. [Google Scholar] [CrossRef]
- Sihui, Y.; Jing, L.; Mengjie, W. Study on Influencing Factors of Carbon Emission of Civil Buildings Based on Regional Differences. Proc. IOP Conf. Ser. Earth Environ. Sci. 2021, 647, 012194. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Q. Examining the Driving Factors of Urban Residential Carbon Intensity Using the LMDI Method: Evidence from China’s County-Level Cities. Int. J. Environ. Res. Public Health 2021, 18, 3929. [Google Scholar] [CrossRef]
- Milano, F. A Python-based software tool for power system analysis. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, USA, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Langtangen, H.P.; Barth, T.J.; Griebel, M. Python Scripting for Computational Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 3. [Google Scholar]
- Sánchez-Pérez, P.A.; Kurtz, S. California’s vision for reaching zero-carbon emissions. In Proceedings of the 2020 47th IEEE Photovoltaic Specialists Conference (PVSC), Calgary, AB, Canada, 15 June–21 August 2020; pp. 2570–2573. [Google Scholar]
- Milano, F. An open source power system analysis toolbox. IEEE Trans. Power Syst. 2005, 20, 1199–1206. [Google Scholar] [CrossRef]
- Murillo-Sánchez, C.E.; Zimmerman, R.D.; Anderson, C.L.; Thomas, R.J. Secure planning and operations of systems with stochastic sources, energy storage, and active demand. IEEE Trans. Smart Grid 2013, 4, 2220–2229. [Google Scholar] [CrossRef]
- Cole, S.; Belmans, R.J. Matdyn, a new matlab-based toolbox for power system dynamic simulation. IEEE Trans. Power Syst. 2010, 26, 1129–1136. [Google Scholar] [CrossRef]
- Langiu, M.; Shu, D.Y.; Baader, F.J.; Hering, D.; Bau, U.; Xhonneux, A.; Müller, D.; Bardow, A.; Mitsos, A.; Dahmen, M.J.C.; et al. COMANDO: A Next-Generation Open-Source Framework for Energy Systems Optimization; Elsevier: Amsterdam, The Netherlands, 2021; Volume 152, p. 107366. [Google Scholar]
- Schwarz, S.; Uerlich, S.A.; Monti, A. Pycity_Scheduling—A Python framework for the development and assessment of optimisation-based power scheduling algorithms for multi-energy systems in city districts. SoftwareX 2021, 16, 100839. [Google Scholar] [CrossRef]
- Maryasin, O.Y.; Lukashov, A.I. A python application for hourly electricity prices forecasting using neural networks. In Proceedings of the 2020 International Russian Automation Conference (RusAutoCon), Sochi, Russia, 6–12 September 2020; pp. 138–143. [Google Scholar]
- Thurner, L.; Scheidler, A.; Schäfer, F.; Menke, J.-H.; Dollichon, J.; Meier, F.; Meinecke, S.; Braun, M. Pandapower—An open-source python tool for convenient modeling, analysis, and optimization of electric power systems. IEEE Trans. Power Syst. 2018, 33, 6510–6521. [Google Scholar] [CrossRef] [Green Version]
- Boyd, G.; McDonald, J.F.; Ross, M.; Hansont, D.A. Separating the changing composition of US manufacturing production from energy efficiency improvements: A Divisia index approach. Energy J. 1987, 8, 77–96. [Google Scholar] [CrossRef]
- Xiang, X.; Ma, X.; Ma, M.; Wu, W.; Yu, L. Research and application of novel Euler polynomial-driven grey model for short-term PM10 forecasting. Grey Syst. Theory Appl. 2020, 11, 498–517. [Google Scholar] [CrossRef]
- Xiang, X.; Ma, X.; Fang, Y.; Wu, W.; Zhang, G. A novel hyperbolic time-delayed grey model with Grasshopper Optimization Algorithm and its applications. Ain Shams Eng. J. 2021, 12, 865–874. [Google Scholar] [CrossRef]
- Hörning, S.; Haese, B. RMWSPy (v 1.1): A Python code for spatial simulation and inversion for environmental applications. Environ. Model. Softw. 2021, 138, 104970. [Google Scholar] [CrossRef]
- Oliphant, T.E. Python for scientific computing. Comput. Sci. Eng. 2007, 9, 10–20. [Google Scholar] [CrossRef] [Green Version]
- Lu, H.; Ma, X.; Huang, K.; Azimi, M. Prediction of offshore wind farm power using a novel two-stage model combining kernel-based nonlinear extension of the Arps decline model with a multi-objective grey wolf optimizer. Renew. Sustain. Energy Rev. 2020, 127, 109856. [Google Scholar] [CrossRef]
- Ma, X.; Xie, M.; Suykens, J.A. A novel neural grey system model with Bayesian regularization and its applications. Neurocomputing 2021, 456, 61–75. [Google Scholar] [CrossRef]
- Yu, L.; Ma, X.; Wu, W.; Xiang, X.; Wang, Y.; Zeng, B. Application of a novel time-delayed power-driven grey model to forecast photovoltaic power generation in the Asia-Pacific region. Sustain. Energy Technol. Assess. 2021, 44, 100968. [Google Scholar] [CrossRef]
- Jing, R.; Xie, M.N.; Wang, F.X.; Chen, L.X. Fair P2P energy trading between residential and commercial multi-energy systems enabling integrated demand-side management. Appl. Energy 2020, 262, 114551. [Google Scholar] [CrossRef]
- Lu, M.; Lai, J. Review on carbon emissions of commercial buildings. Renew. Sustain. Energy Rev. 2020, 119, 109545. [Google Scholar] [CrossRef]
- Ma, M.; Pan, T.; Ma, Z. Examining the Driving Factors of Chinese Commercial Building Energy Consumption from 2000 to 2015: A STIRPAT Model Approach. J. Eng. Sci. Technol. Rev. 2017, 10, 28–38. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, S.; Zhang, Z.; Liu, Y.; Ahmad, A. Driving factors of carbon emissions embodied in China-US trade: A structural decomposition analysis. J. Clean. Prod. 2016, 131, 678–689. [Google Scholar] [CrossRef]
- Chen, M.; Ma, M.; Lin, Y.; Ma, Z.; Li, K. Carbon Kuznets curve in China’s building operations: Retrospective and prospective trajectories. Sci. Total Environ. 2022, 803, 150104. [Google Scholar] [CrossRef]
- Cai, W.; Wu, Y.; Zhong, Y.; Ren, H. China building energy consumption: Situation, challenges and corresponding measures. Energy Policy 2009, 37, 2054–2059. [Google Scholar] [CrossRef]
- Zhang, S.; Ma, M.; Li, K.; Ma, Z.; Feng, W.; Cai, W. Historical carbon abatement in the commercial building operation: China versus the US. Energy Econ. 2021, 105, 105712. [Google Scholar] [CrossRef]
- York, R.; Rosa, E.A.; Dietz, T. STIRPAT, IPAT and ImPACT: Analytic tools for unpacking the driving forces of environmental impacts. Ecol. Econ. 2003, 46, 351–365. [Google Scholar] [CrossRef]
- Ehrlich, P.R.; Holdren, J.P. Impact of population growth. Science 1971, 171, 1212–1217. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Xing, Y.; Zeng, X.; Ji, Y.; Hou, H.; Zhang, Y.; Zhu, Z.J. Factors influencing carbon emissions from China’s electricity industry: Analysis using the combination of LMDI and K-means clustering. Environ. Impact Assess. Rev. 2022, 93, 106724. [Google Scholar] [CrossRef]
- Vaninsky, A. Factorial decomposition of CO2 emissions: A generalized Divisia index approach. Energy Econ. 2014, 45, 389–400. [Google Scholar] [CrossRef]
- Shao, S.; Liu, J.; Geng, Y.; Miao, Z.; Yang, Y. Uncovering driving factors of carbon emissions from China’s mining sector. Appl. Energy 2016, 166, 220–238. [Google Scholar] [CrossRef]




| Source | Year | Location | Scope | Major Driver Forces |
|---|---|---|---|---|
| Gong et al. [26] | 2015 | Wuhan City in China | Life cycle building carbon emissions | Increasing building area |
| Lin et al. [27] | 2015 | China | Commercial and residential buildings | Residents’ income |
| Lin et al. [28] | 2015 | China | Building construction industry | Energy intensity decline |
| Liu et al. [29] | 2015 | China’s urban areas | Civil buildings | Urban population and per capita floor space |
| Yuan et al. [30] | 2015 | China | Residential building operation | Population, energy intensity, consumption factors, urbanization effect |
| Lu et al. [31] | 2016 | China | Material consumption and on-site construction activities | Emission factor, energy structure, energy intensity |
| Jiang et al. [32] | 2017 | China | Life-cycle carbon emissions in China’s building sector | Indirect emission intensity effect and economic output effects |
| Wu et al. [33] | 2018 | 30 provinces in China | Construction industry | Economic growth in most provinces of China |
| Wang et al. [34] | 2018 | China | Direct and indirect CO2 emissions in construction industry | Industrial activity |
| Lai et al. [35] | 2019 | China | Construction industry | Energy consumption |
| Wu et al. [36] | 2019 | China | construction stage | unit cost constructed floor area |
| Building operation | Urban development, floor space effect, and energy demand from appliance effect | |||
| Wang et al. [37] | 2019 | Guangzhou, China | Residential sector | Affluence effect of urban development |
| Du et al. [38] | 2020 | 30 provinces in China | Construction industry | Different in different provinces |
| Ma et al. [13] | 2020 | China | Residential building | Per capita income |
| He et al. [39] | 2020 | China | Rural residential buildings, urban residential buildings and public buildings | Economic output effect and per capita iron and steel accumulation effect |
| Lin et al. [40] | 2020 | China | Direct carbon emissions of buildings | Energy intensity, energy structure, economic output |
| Chen et al. [41] | 2020 | China | Building sector | Economic output |
| Li et al. [42] | 2020 | Jiangsu province in China | Construction industry | Area factor and the output value intensity factor |
| Yang et al. [43] | 2021 | China | Civil buildings | Per capita building area effect |
| Zhao et al. [44] | 2021 | 620 county-level cities in 30 Chinese provinces | Residential sector | Energy consumption per capita, urban sprawl, and land demand |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, X.; Ma, X.; Ma, Z.; Ma, M.; Cai, W. Python-LMDI: A Tool for Index Decomposition Analysis of Building Carbon Emissions. Buildings 2022, 12, 83. https://doi.org/10.3390/buildings12010083
Xiang X, Ma X, Ma Z, Ma M, Cai W. Python-LMDI: A Tool for Index Decomposition Analysis of Building Carbon Emissions. Buildings. 2022; 12(1):83. https://doi.org/10.3390/buildings12010083
Chicago/Turabian StyleXiang, Xiwang, Xin Ma, Zhili Ma, Minda Ma, and Weiguang Cai. 2022. "Python-LMDI: A Tool for Index Decomposition Analysis of Building Carbon Emissions" Buildings 12, no. 1: 83. https://doi.org/10.3390/buildings12010083
APA StyleXiang, X., Ma, X., Ma, Z., Ma, M., & Cai, W. (2022). Python-LMDI: A Tool for Index Decomposition Analysis of Building Carbon Emissions. Buildings, 12(1), 83. https://doi.org/10.3390/buildings12010083









