Performance-Based Bi-Objective Retrofit Optimization of Building Portfolios Considering Uncertainties and Environmental Impacts
Abstract
:1. Introduction
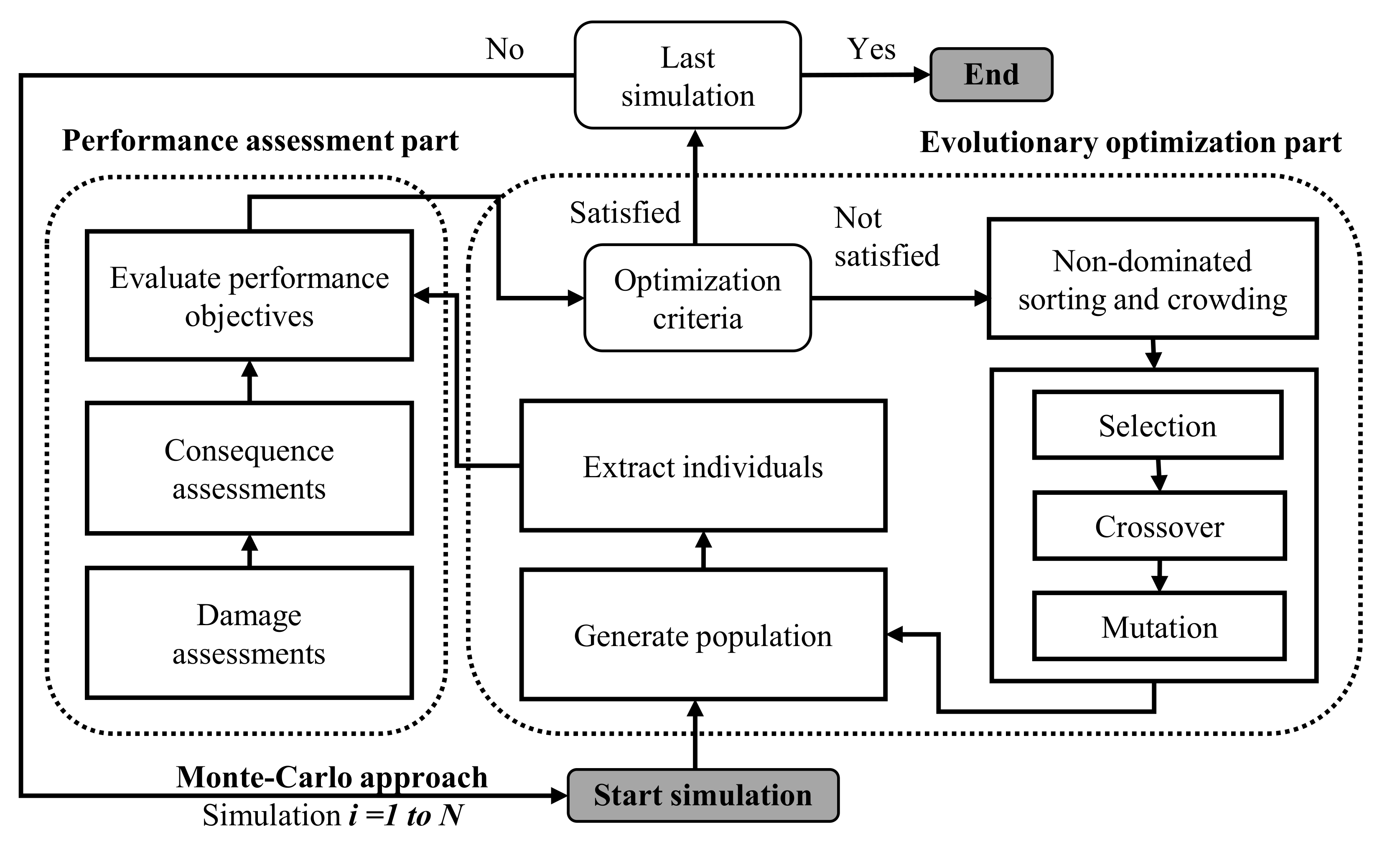
2. Proposed Optimization Framework for Community Building Portfolios
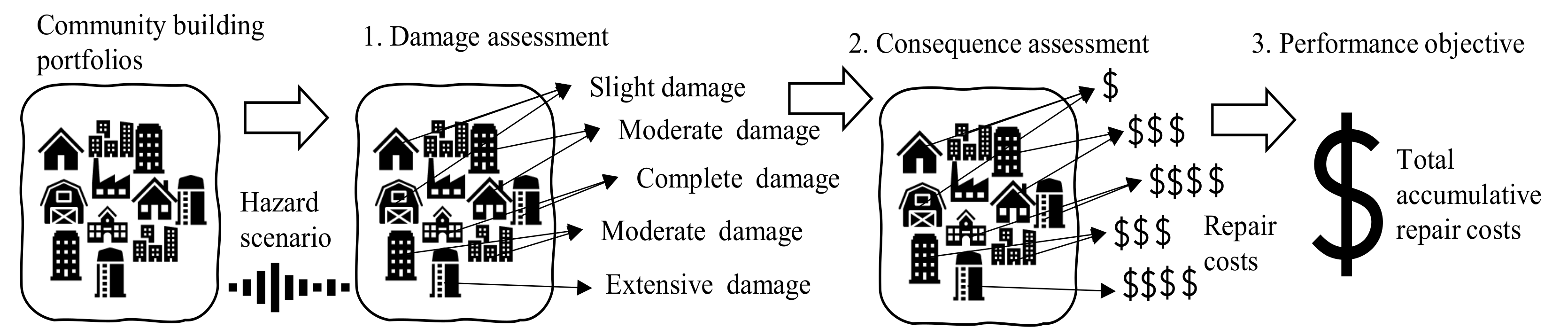
3. Performance-Based Community Objectives Assessment
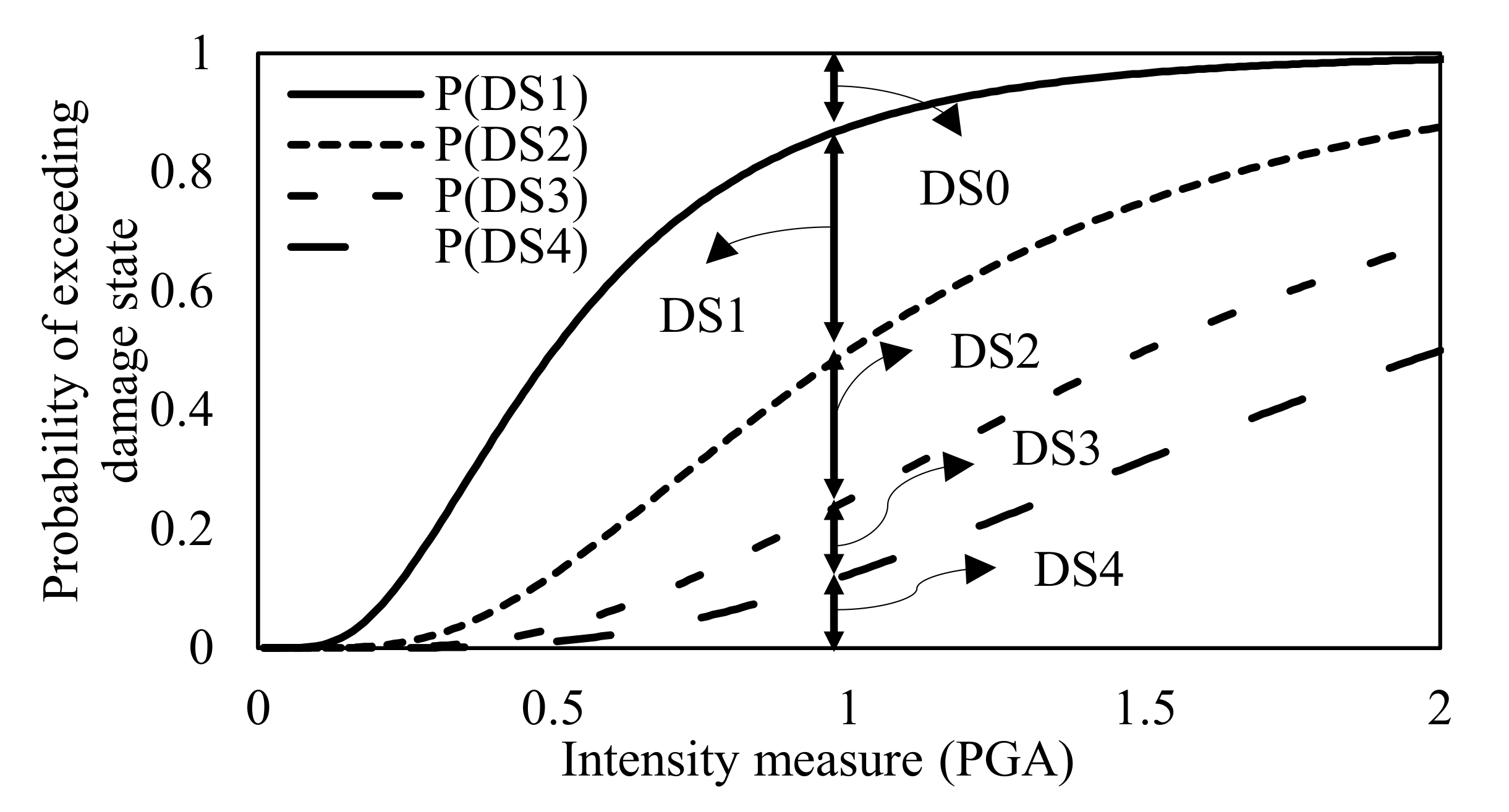
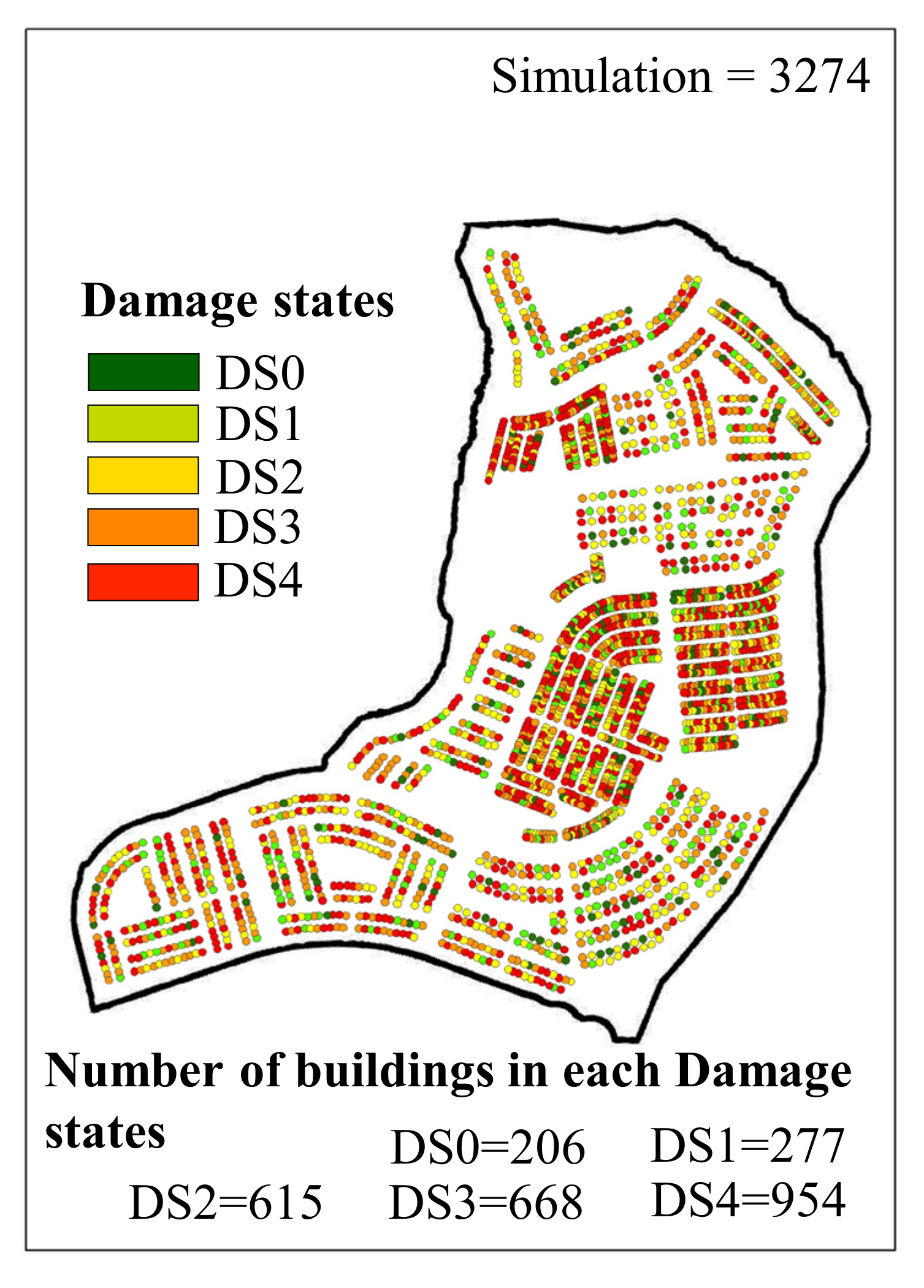
3.1. Building-Level Damage Assessments
3.2. Building-Level Consequence Assessments
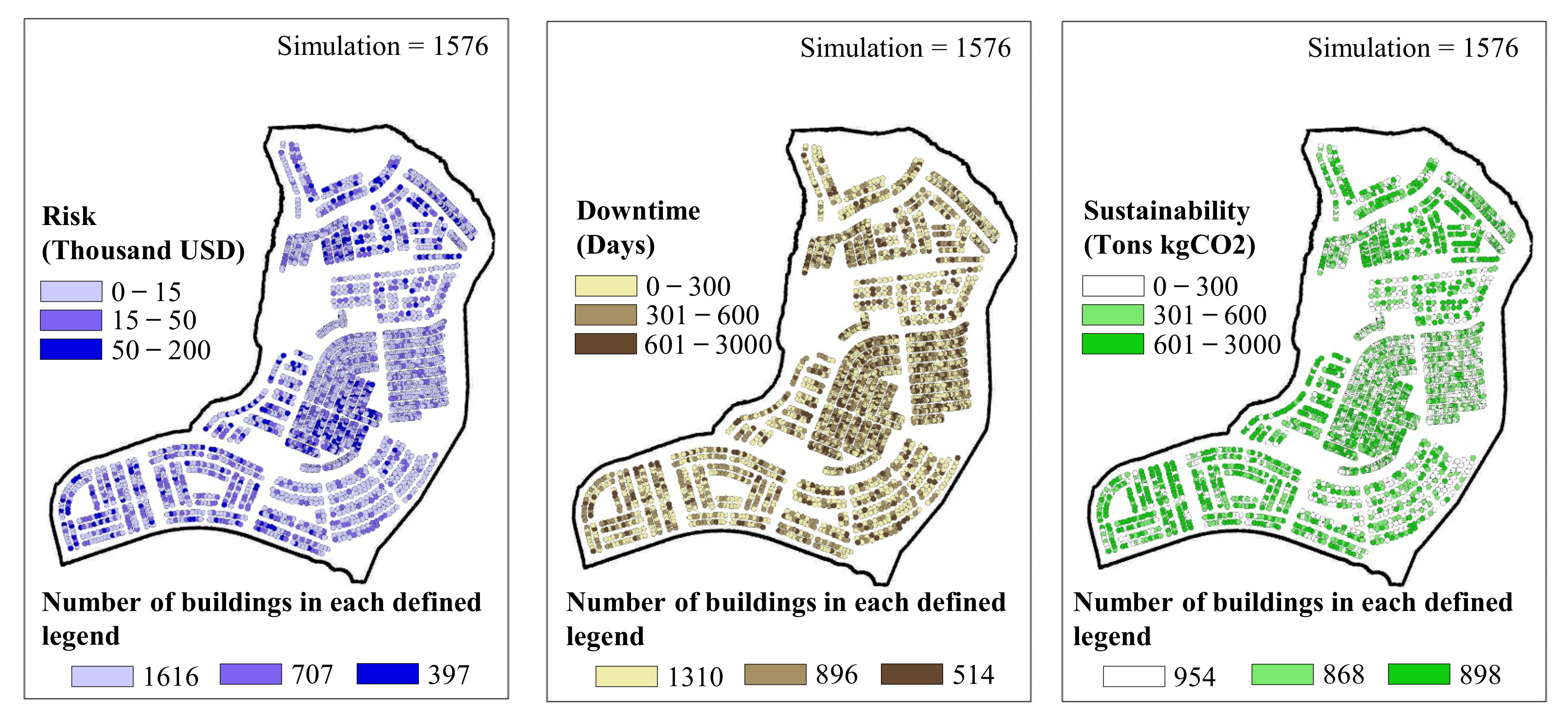
3.3. Portfolio-Level Performance Objectives Assessment
4. Bi-Objective Evolutionary Optimization
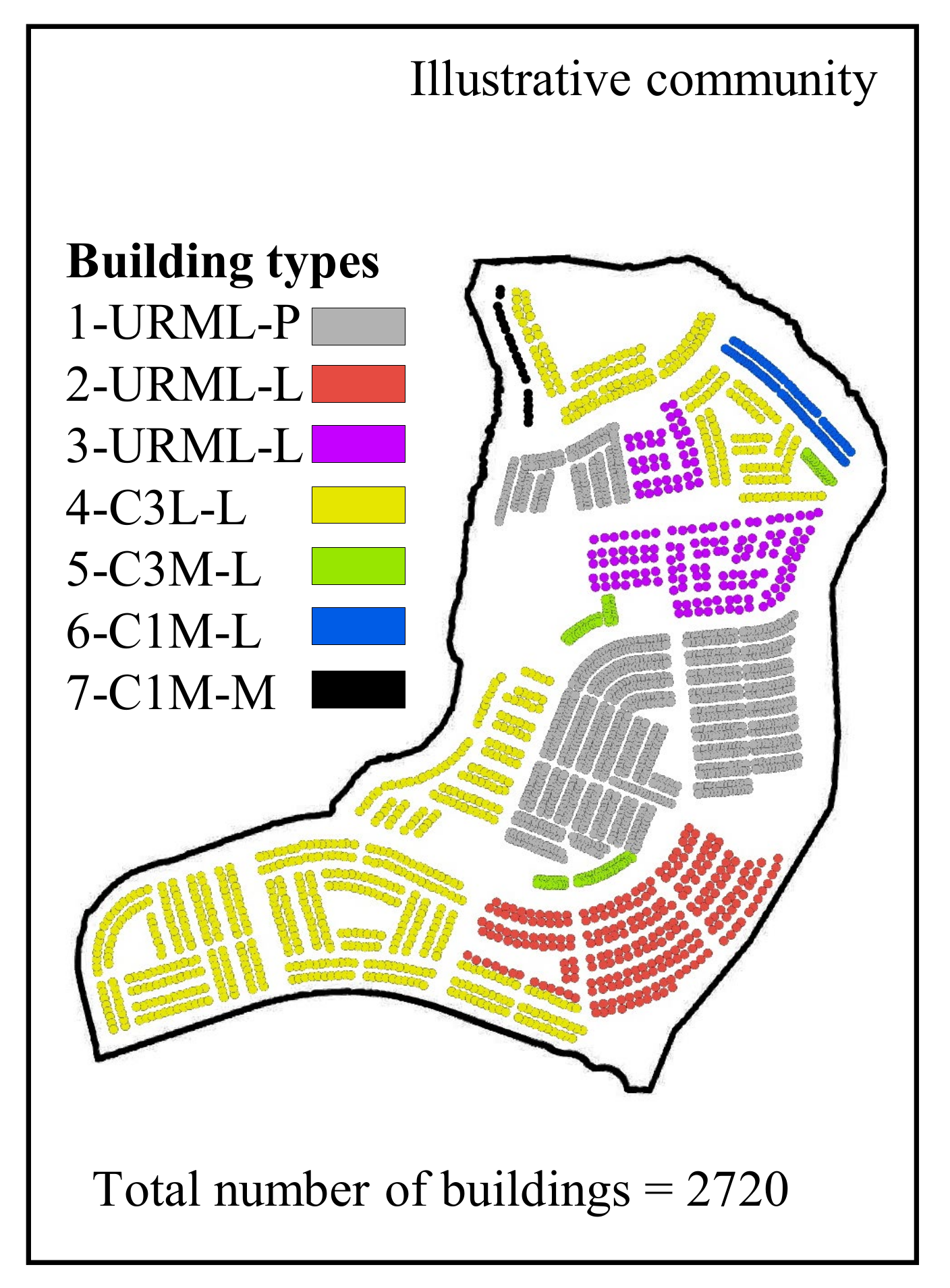
- The community building portfolio with different structural systems, code-conformance, building heights, fragility, and consequence functions, among others;
- Intensity measure at building locations under a given hazard scenario;
- Probabilistic damage assessment of community building portfolio;
- Consequences of all the buildings in a community building portfolio;
- The damage and consequences of buildings for different retrofit-levels.
- The retrofit actions for all the buildings in a community building portfolio.
- The retrofit costs associated with the retrofit levels is minimized;
- The performance of a community associated with the retrofit-level is maximized.
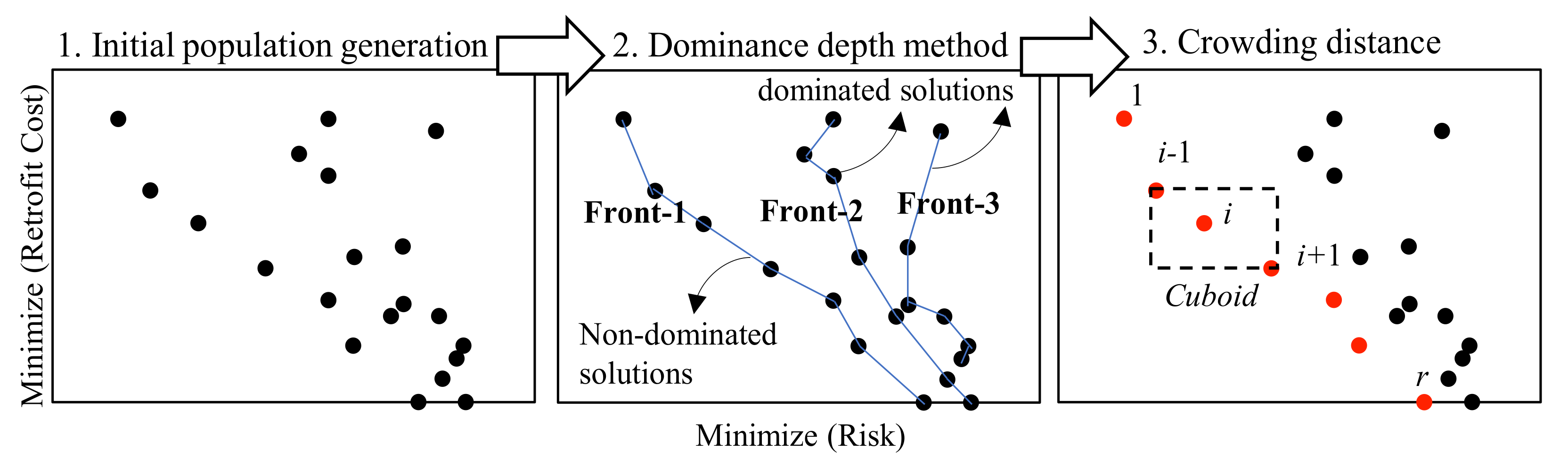
4.1. Fast Non-Dominated Sorting and Crowding Distances
4.2. Selection, Crossover, and Mutation
4.3. New Population Generation
5. Illustrative Example
5.1. Performance-Based Assessment
5.2. Bi-Objective Evolutionary Optimization
6. Conclusions
- The proposed bi-objective retrofit optimization framework considered risk, downtime, and sustainability performance indicators for assessment and enhancement of community performance under a designed seismic hazard scenario. The proposed framework optimized the performance objectives for given pre-hazard mitigation alternatives considering uncertainties and provided the decision-makers with retrofit programs to enhance community performance for given retrofit costs.
- The distributions of discrete damage states and the performance indicators showed negligible skewness with kurtosis values close to three. This showed the distributions were almost normally distributed. The normal distributions were also observed for the retrofit programs extracted after performing performance-based evolutionary optimization.
- Pareto-optimal solutions were determined by utilizing bi-objective optimization which provided optimal solutions for the considered performance indicators against the retrofit cost. The number of buildings required to be retrofitted at different retrofit levels to achieve performance enhancements for given retrofit costs were also determined. For instance, in a random simulation, to achieve risk, downtime, and sustainability performance of US$35.8 million, 0.727 million days, and 1.2 million tons of kgCO2 emissions, a retrofit cost of US$17.5 million is required. To achieve this level of performance, the number of buildings needed to be retrofitted in the five retrofit levels ranging from 1–5 were 518, 583, 536, 553, and 530.
- For an illustration of the proposed framework, four retrofit programs were extracted ranging from US$5–20 million and the resulting performance enhancements along with the number of buildings required to be retrofitted at different retrofit levels were determined. For instance, by applying a retrofit program of US$20 million, the mean risk, downtime, and sustainability performance values were reduced to 48.91%, 32.59%, and 50%. Furthermore, to achieve this level of performance enhancement, the mean number of buildings required to be retrofitted ranging from retrofit levels 1–5 were 105, 721, 799, 834, and 261.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Inputs Related to the Fragility and Consequence Functions Utilized in the Illustrative Example
| ID | Building Type | Code Level | Damage State | Fragility Function (g) |
|---|---|---|---|---|
| URML-P | Low-Rise Unreinforced Masonry Bearing Walls | Pre-code | Slight Moderate Extensive Complete | 0.13 0.17 0.26 0.37 |
| URML-L | Low-Rise Unreinforced Masonry Bearing Walls | Low code | Slight Moderate Extensive Complete | 0.14 0.20 0.32 0.46 |
| URMM-L | Mid-Rise Unreinforced Masonry Bearing Walls | Low code | Slight Moderate Extensive Complete | 0.10 0.16 0.27 0.46 |
| C3L-L | Low-Rise Concrete Frame with Unreinforced Masonry Infill Walls | Low code | Slight Moderate Extensive Complete | 0.12 0.17 0.26 0.44 |
| C3M-L | Mid-Rise Concrete Frame with Unreinforced Masonry Infill Walls | Low code | Slight Moderate Extensive Complete | 0.11 0.17 0.32 0.51 |
| C1M-L | Mid-Rise Concrete Moment Frame | Low code | Slight Moderate Extensive Complete | 0.12 0.17 0.32 0.54 |
| C1M-M | Mid-Rise Concrete Moment Frame | Moderate code | Slight Moderate Extensive Complete | 0.13 0.21 0.49 0.89 |
| ID | Construction Materials | Tons kg/Thousand Sft |
|---|---|---|
| URML-P, URML-L, URMM-L | Brick Wood Concrete Steel | 35 10.5 41 4 |
| C3L-L, C3M-L, C1M-L, C1M-M | Brick Wood Concrete Steel | 20 5.3 90 4 |
| Construction Materials | Cost in USD per kg Tons | Tons kgCO2 Emissions per kg Tons |
|---|---|---|
| Brick Wood Concrete Steel | 28 140 20 650 | 0.2–0.6 0.75–1.35 0.05–5.15 1.72–2.82 |
| ID | Damage State | Percentage of Total Material Damaged | |||
|---|---|---|---|---|---|
| Brick | Wood | Concrete | Steel | ||
| URML-P, URML-L, URMM-L | Slight Moderate Extensive Complete | 3.5 18.5 50 100 | 3.5 18.5 50 100 | 0 6 27 100 | 0 6 27 100 |
| C3L-L, C3M-L | Slight Moderate Extensive Complete | 3 16 47.5 100 | 3 16 47.5 100 | 0.05 7 31 100 | 0.05 7 31 100 |
| C1M-L, C1M-M | Slight Moderate Extensive Complete | 0.5 3.5 17.5 100 | 0.5 3.5 17.5 100 | 0.05 6.5 30.5 100 | 0.05 6.5 30.5 100 |
| ID | Damage State | Repair Time in Days |
|---|---|---|
| URML-P, URML-L, URMM-L C3L-L | Slight Moderate Extensive Complete | 2 30 90 180 |
| C3M-L, C1M-L C1M-M | Slight Moderate Extensive Complete | 5 30 120 240 |
| Component | Building Condition | Delay Time in Days | Coefficient of Variation |
|---|---|---|---|
| Inspection | Slight other | 0 5 | 0 0.54 |
| Engineering mobilization | Slight Moderate Extensive Complete | 6 12 12 50 | 0.4 0.4 0.4 0.32 |
| Financing | Insurance Private loans SBA-backed loans Not covered | 6 15 48 48 | 1.11 0.68 0.57 0.65 |
| Contractor mobilization | Slight other | 7 19 | 0.6 0.38 |
| Permitting | Slight other | 1 8 | 0.86 0.32 |
References
- Godschalk, D.R. Urban hazard mitigation: Creating resilient cities. Nat. Hazards Rev. 2003, 4, 136–143. [Google Scholar] [CrossRef]
- McAllister, T.P. Community Resilience Planning Guide for Buildings and Infrastructure Systems; NIST: Gaithersburg, MD, USA, 2015; Volume I. [Google Scholar]
- Koliou, M.; van de Lindt, J.W.; McAllister, T.P.; Ellingwood, B.R.; Dillard, M.; Cutler, H. State of the research in community resilience: Progress and challenges. Sustain. Resilient Infrastruct. 2017, 5, 131–151. [Google Scholar] [CrossRef]
- Huang, Y.-N.; Whittaker, A.S.; Hamburger, R.O. A simplified analysis procedure for performance-based earthquake engineering of buildings. Eng. Struct. 2017, 150, 719–735. [Google Scholar] [CrossRef]
- Fajfar, P. A nonlinear analysis method for performance-based seismic design. Earthq. Spectra 2000, 16, 573–592. [Google Scholar] [CrossRef]
- Ghobarah, A. Performance-based design in earthquake engineering: State of development. Eng. Struct. 2001, 23, 878–884. [Google Scholar] [CrossRef]
- Guo, H.; Dong, Y.; Bastidas-Arteaga, E.; Gu, X.-L. Probabilistic failure analysis, performance assessment, and sensitivity analysis of corroded reinforced concrete structures. Eng. Fail. Anal. 2021, 124, 105328. [Google Scholar] [CrossRef]
- Moehle, J.P. Seismic analysis, design, and review for tall buildings. Struct. Des. Tall Spec. Build. 2006, 15, 495–513. [Google Scholar] [CrossRef]
- Jeong, S.-H.; Mwafy, A.M.; Elnashai, A.S. Probabilistic seismic performance assessment of code-compliant multi-story RC buildings. Eng. Struct. 2012, 34, 527–537. [Google Scholar] [CrossRef]
- Qian, J.; Dong, Y. Uncertainty and multi-criteria global sensitivity analysis of structural systems using acceleration algorithm and sparse polynomial chaos expansion. Mech. Syst. Signal Processing 2022, 163, 108120. [Google Scholar] [CrossRef]
- Lemma, M.; Rebelo, C.; Silva, L. Seismic Design and Performance Assessment of Steel Frames Considering Joints’Behaviour. ce/papers 2021, 4, 1965–1973. [Google Scholar] [CrossRef]
- FEMA 440. Improvement of Nonlinear Static Seismic Analysis Procedures; FEMA 440: Redwood City, CA, USA, 2005. [Google Scholar]
- Jalayer, F.; Ebrahimian, H.; Miano, A. Record-to-record variability and code-compatible seismic safety-checking with limited number of records. Bull. Earthq. Eng. 2021, 19, 6361–6396. [Google Scholar] [CrossRef]
- Guan, M.; EERI, X.; Burton, M.; EERI, H.; Shokrabadi, M. A database of seismic designs, nonlinear models, and seismic responses for steel moment-resisting frame buildings. Earthq. Spectra 2021, 37, 1199–1222. [Google Scholar] [CrossRef]
- Zheng, Y.; Dong, Y.; Chen, B.; Anwar, G.A. Seismic damage mitigation of bridges with self-adaptive SMA-cable-based bearings. Smart Struct. Syst. 2019, 24, 127–139. [Google Scholar]
- Chen, L.; Qian, J.; Tu, B.; Frangopol, D.M.; Dong, Y. Performance-based risk assessment of reinforced concrete bridge piers subjected to vehicle collision. Eng. Struct. 2021, 229, 111640. [Google Scholar] [CrossRef]
- Giouvanidis, A.I.; Dong, Y. Seismic loss and resilience assessment of single-column rocking bridges. Bull. Earthq. Eng. 2020, 4481–4513. [Google Scholar] [CrossRef]
- Anwar, G.A.; Dong, Y.; Zhai, C. Performance-based probabilistic framework for seismic risk, resilience, and sustainability assessment of reinforced concrete structures. Adv. Struct. Eng. 2020, 23, 1454–1472. [Google Scholar] [CrossRef]
- Anwar, G.A.; Dong, Y.; Li, Y. Performance-based decision-making of buildings under seismic hazard considering long-term loss, sustainability, and resilience. Struct. Infrastruct. Eng. 2020, 17, 454–470. [Google Scholar] [CrossRef]
- Hashemi, M.J.; Al-Attraqchi, A.Y.; Kalfat, R.; Al-Mahaidi, R. Linking seismic resilience into sustainability assessment of limited-ductility RC buildings. Eng. Struct. 2019, 188, 121–136. [Google Scholar] [CrossRef]
- Dong, Y.; Frangopol, D.M. Performance-based seismic assessment of conventional and base-isolated steel buildings including environmental impact and resilience. Earthq. Eng. Struct. Dyn. 2016, 45, 739–756. [Google Scholar] [CrossRef]
- Vettore, M.; Donà, M.; Carpanese, P.; Follador, V.; da Porto, F.; Valluzzi, M.R. A multilevel procedure at urban scale to assess the vulnerability and the exposure of residential masonry buildings: The case study of Pordenone, Northeast Italy. Heritage 2020, 3, 80. [Google Scholar] [CrossRef]
- HAZUS. Multi-Hazard Loss Estimation Methodology, Earthquake Model; FEMA: Washington, DC, USA, 2003. [Google Scholar]
- FEMA-P-58. Seismic Performance Assessment of Buildings: Volume 1–Methodology; ATC: Camarillo, CA, USA, 2012. [Google Scholar]
- Yang, D.Y.; Frangopol, D.M. Chapter 23 in Routledge Handbook of Sustainable and Resilient Infrastructure. In Bridging the Gap between Sustainability and Resilience of Civil Infrastructure Using Lifetime Resilience; Routledge: Abingdon-on-Thames, UK, 2018; pp. 419–442. [Google Scholar]
- McAllister, T.P.; Moddemeyer, S. Aligning community resilience and sustainability. In Routledge Handbook of Sustainable and Resilient Infrastructure; Routledge: Abingdon-on-Thames, UK, 2018; pp. 15–27. [Google Scholar]
- Rodriguez-Nikl, T. Linking disaster resilience and sustainability. Civ. Eng. Environ. Syst. 2015, 32, 157–169. [Google Scholar] [CrossRef]
- Erdik, M. Earthquake risk assessment. Bull. Earthq. Eng. 2017, 15, 5055–5092. [Google Scholar] [CrossRef]
- Battarra, M.; Balcik, B.; Xu, H. Disaster preparedness using risk-assessment methods from earthquake engineering. Eur. J. Oper. Res. 2018, 269, 423–435. [Google Scholar] [CrossRef] [Green Version]
- Barbat, A.H.; Carreño, M.L.; Pujades, L.G.; Lantada, N.; Cardona, O.D.; Marulanda, M.C. Seismic vulnerability and risk evaluation methods for urban areas. A review with application to a pilot area. Struct. Infrastruct. Eng. 2010, 6, 17–38. [Google Scholar] [CrossRef]
- Miles, S.B.; Burton, H.V.; Kang, H. Community of Practice for Modeling Disaster Recovery. Nat. Hazards Rev. 2018, 20, 04018023. [Google Scholar] [CrossRef]
- Miles, S.B.; Chang, S.E. Modeling community recovery from earthquakes. Earthq. Spectra 2006, 22, 439–458. [Google Scholar] [CrossRef]
- Donà, M.; Bizzaro, L.; Carturan, F.; da Porto, F. Effects of business recovery strategies on seismic risk and cost-effectiveness of structural retrofitting for business enterprises. Earthq. Spectra 2019, 35, 1795–1819. [Google Scholar] [CrossRef]
- Sen, M.K.; Dutta, S.; Kabir, G.; Pujari, N.N.; Laskar, S.A. An integrated approach for modelling and quantifying housing infrastructure resilience against flood hazard. J. Clean. Prod. 2021, 288, 125526. [Google Scholar] [CrossRef]
- Masoomi, H.; van de Lindt, J.W. Community-Resilience-Based Design of the Built Environment. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2018, 5, 04018044. [Google Scholar] [CrossRef]
- Feng, K.; Wang, N.; Li, Q.; Lin, P. Measuring and enhancing resilience of building portfolios considering the functional interdependence among community sectors. Struct. Saf. 2017, 66, 118–126. [Google Scholar] [CrossRef]
- Burton, H.V.; Deierlein, G.; Lallemant, D.; Singh, Y. Measuring the Impact of Enhanced Building Performance on the Seismic Resilience of a Residential Community. Earthq. Spectra 2017, 33, 1347–1367. [Google Scholar] [CrossRef]
- Lin, P.; Wang, N. Stochastic post-disaster functionality recovery of community building portfolios I: Modeling. Struct. Saf. 2017, 69, 96–105. [Google Scholar] [CrossRef]
- Hassan, E.M.; Mahmoud, H. An integrated socio-technical approach for post-earthquake recovery of interdependent healthcare system. Reliab. Eng. Syst. Saf. 2020, 201, 106953. [Google Scholar] [CrossRef]
- Zinke, T.; Bocchini, P.; Frangopol, D.; Ummenhofer, T. Combining resilience and sustainability in infrastructure projects. In Life-Cycle and Sustainability of Civil Infrastructure Systems; Taylor & Francis Group: London, UK, 2013; p. 473. [Google Scholar]
- Asprone, D.; Manfredi, G. Linking disaster resilience and urban sustainability: A glocal approach for future cities. Disasters 2015, 39, s96–s111. [Google Scholar] [CrossRef] [Green Version]
- Dong, Y.; Frangopol, D.M.; Saydam, D. Pre-earthquake multi-objective probabilistic retrofit optimization of bridge networks based on sustainability. J. Bridge Eng. 2014, 19, 04014018. [Google Scholar] [CrossRef]
- Dong, Y.; Frangopol, D.M. Adaptation optimization of residential buildings under hurricane threat considering climate change in a lifecycle context. J. Perform. Constr. Facil. 2017, 31, 04017099. [Google Scholar] [CrossRef]
- Holland, J. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Schaffer, J.D. Multiple objective optimization with vector evaluated genetic algorithms. In Proceedings of the first International Conference on Genetic Algorithms and Their Applications, Pittsburg, PA, USA, 24–26 July 1985. [Google Scholar]
- Horn, J.; Nafpliotis, N.; Goldberg, D.E. A niched Pareto genetic algorithm for multiobjective optimization. In Proceedings of the first IEEE conference on evolutionary computation, IEEE world congress on computational intelligence, Orlando, FL, USA, 27–29 June 1994; pp. 82–87. [Google Scholar]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength Pareto evolutionary algorithm. TIK-Report 2001, 1–13. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Nicholson, C. A multi-objective optimization model for retrofit strategies to mitigate direct economic loss and population dislocation. Sustain. Resilient Infrastruct. 2016, 1, 123–136. [Google Scholar] [CrossRef]
- Sutley, E.J.; van de Lindt, J.W.; Peek, L. Multihazard analysis: Integrated engineering and social science approach. J. Struct. Eng. 2017, 143, 04017107. [Google Scholar] [CrossRef]
- Hammersley, J. Monte Carlo Methods; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Donà, M.; Carpanese, P.; Follador, V.; Sbrogiò, L.; da Porto, F. Mechanics-based fragility curves for Italian residential URM buildings. Bull. Earthq. Eng. 2021, 19, 3099–3127. [Google Scholar] [CrossRef]
- Šipoš, T.K.; Hadzima-Nyarko, M. Rapid seismic risk assessment. Int. J. Disaster Risk Reduct. 2017, 24, 348–360. [Google Scholar] [CrossRef]
- Carreño, M.L.; Cardona, O.D.; Barbat, A.H. New methodology for urban seismic risk assessment from a holistic perspective. Bull. Earthq. Eng. 2012, 10, 547–565. [Google Scholar] [CrossRef]
- Zentner, I.; Gündel, M.; Bonfils, N. Fragility analysis methods: Review of existing approaches and application. Nucl. Eng. Des. 2017, 323, 245–258. [Google Scholar] [CrossRef] [Green Version]
- Crowley, H.; Pinho, R.; van Elk, J.; Uilenreef, J. Probabilistic damage assessment of buildings due to induced seismicity. Bull. Earthq. Eng. 2019, 17, 4495–4516. [Google Scholar] [CrossRef]
- Da Porto, F.; Donà, M.; Rosti, A.; Rota, M.; Lagomarsino, S.; Cattari, S.; Borzi, B.; Onida, M.; De Gregorio, D.; Perelli, F.L. Comparative analysis of the fragility curves for Italian residential masonry and RC buildings. Bull. Earthq. Eng. 2021, 19, 3209–3252. [Google Scholar] [CrossRef]
- Park, J.; Towashiraporn, P.; Craig, J.I.; Goodno, B.J. Seismic fragility analysis of low-rise unreinforced masonry structures. Eng. Struct. 2009, 31, 125–137. [Google Scholar] [CrossRef]
- Farhan, M.; Bousias, S. Seismic fragility analysis of LNG sub-plant accounting for component dynamic interaction. Bull. Earthq. Eng. 2020, 18, 5063–5085. [Google Scholar] [CrossRef]
- Qian, J.; Dong, Y. Multi-criteria decision making for seismic intensity measure selection considering uncertainty. Earthq. Eng. Struct. Dyn. 2020, 49, 1095–1114. [Google Scholar] [CrossRef]
- Wang, X.; Shahzad, M.M.; Wang, T. Research on dynamic response characteristics and control effect of mega-sub controlled structural system under long-period ground motions. In Structures; Elsevier: Amsterdam, The Netherlands, 2021; Volume 29, pp. 225–234. [Google Scholar]
- Zhang, N.; Gu, Q.; Dong, Y.; Qian, J.; Zheng, Y. Seismic performance of bridges with ECC-reinforced piers. Soil Dyn. Earthq. Eng. 2021, 146, 106753. [Google Scholar] [CrossRef]
- Li, Y.; Dong, Y.; Frangopol, D.M.; Gautam, D. Long-term resilience and loss assessment of highway bridges under multiple natural hazards. Struct. Infrastruct. Eng. 2020, 16, 626–641. [Google Scholar] [CrossRef]
- Silva, V. Critical issues on probabilistic earthquake loss assessment. J. Earthq. Eng. 2018, 22, 1683–1709. [Google Scholar] [CrossRef]
- Stojadinović, Z.; Kovačević, M.; Marinković, D.; Stojadinović, B. Rapid earthquake loss assessment based on machine learning and representative sampling. Earthq. Spectra 2021. [Google Scholar] [CrossRef]
- Erdik, M.; Şeşetyan, K.; Demircioğlu, M.; Hancılar, U.; Zülfikar, C. Rapid earthquake loss assessment after damaging earthquakes. Soil Dyn. Earthq. Eng. 2011, 31, 247–266. [Google Scholar] [CrossRef]
- Kircher, C.A.; Whitman, R.V.; Holmes, W.T. HAZUS earthquake loss estimation methods. Nat. Hazards Rev. 2006, 7, 45–59. [Google Scholar] [CrossRef]
- Cardone, D.; Perrone, G. Damage and loss assessment of pre-70 RC frame buildings with FEMA P-58. J. Earthq. Eng. 2017, 21, 23–61. [Google Scholar] [CrossRef]
- Molina Hutt, C.; Almufti, I.; Willford, M.; Deierlein, G. Seismic loss and downtime assessment of existing tall steel-framed buildings and strategies for increased resilience. J. Struct. Eng. 2016, 142, C4015005. [Google Scholar] [CrossRef]
- Mitrani-Reiser, J. An ounce of prevention: Probabilistic Loss Estimation for Performance-Based Earthquake Engineering. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2007. [Google Scholar]
- Almufti, I.; Willford, M. REDi™ Rating System: Resilience Based Earthquake Design Initiative for the Next Generation of Buildings. Version 1.0; Arup: London, UK, 2013; pp. 1–68. [Google Scholar]
- Asadi, E.; Salman, A.M.; Li, Y. Multi-criteria decision-making for seismic resilience and sustainability assessment of diagrid buildings. Eng. Struct. 2019, 191, 229–246. [Google Scholar] [CrossRef]
- FEMA-547. Techniques for the Seismic Rehabilitation of Existing Buildings; Building Seismic Safety Council for the Federal Emergency Management Agency: Washington, DC, USA, 2006. [Google Scholar]
- FEMA-P695. Quantification of Building Seismic Performance Factors; US Department of Homeland Security, FEMA: Washington, DC, USA, 2009. [Google Scholar]
- Anwar, G.A.; Dong, Y. Seismic resilience of retrofitted RC buildings. Earthq. Eng. Eng. Vib. 2020, 19, 561–571. [Google Scholar] [CrossRef]

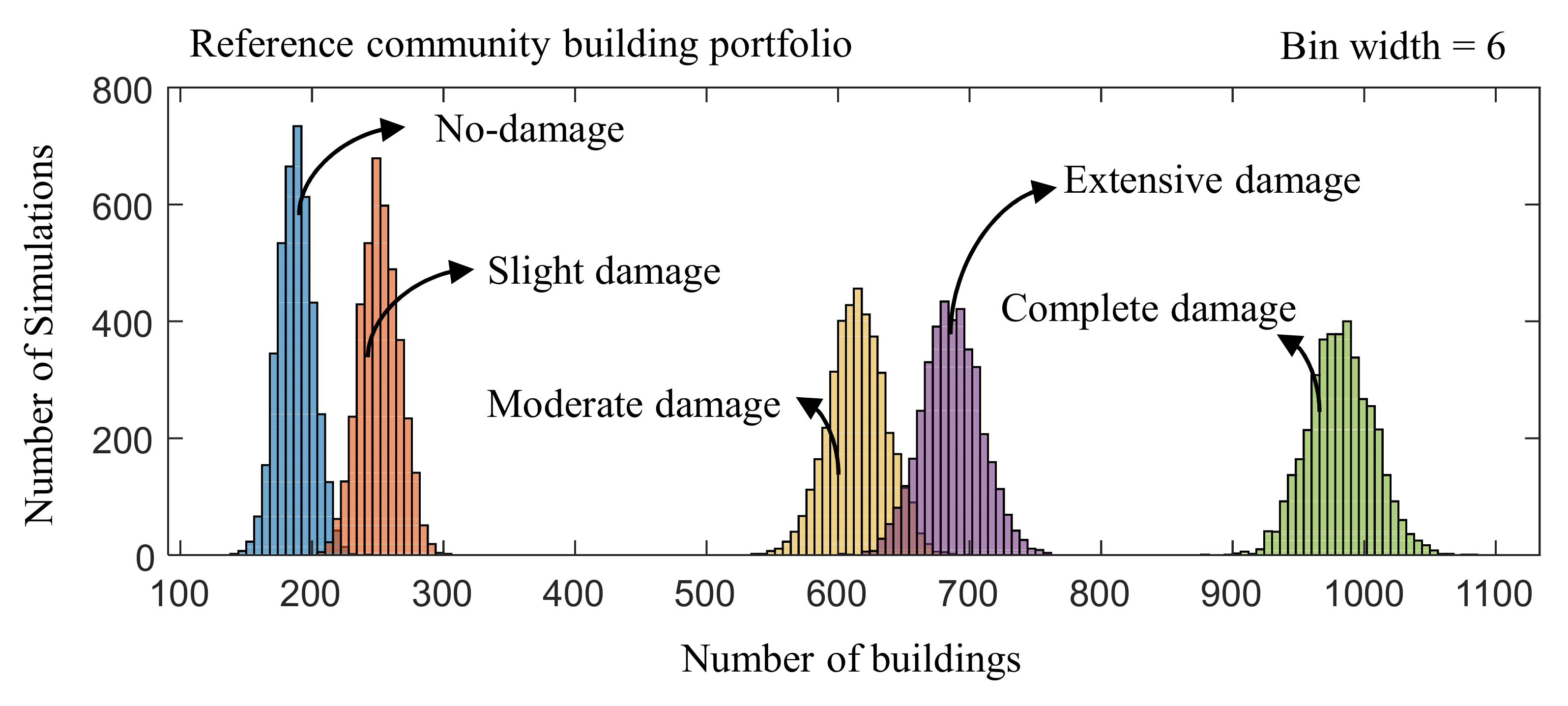
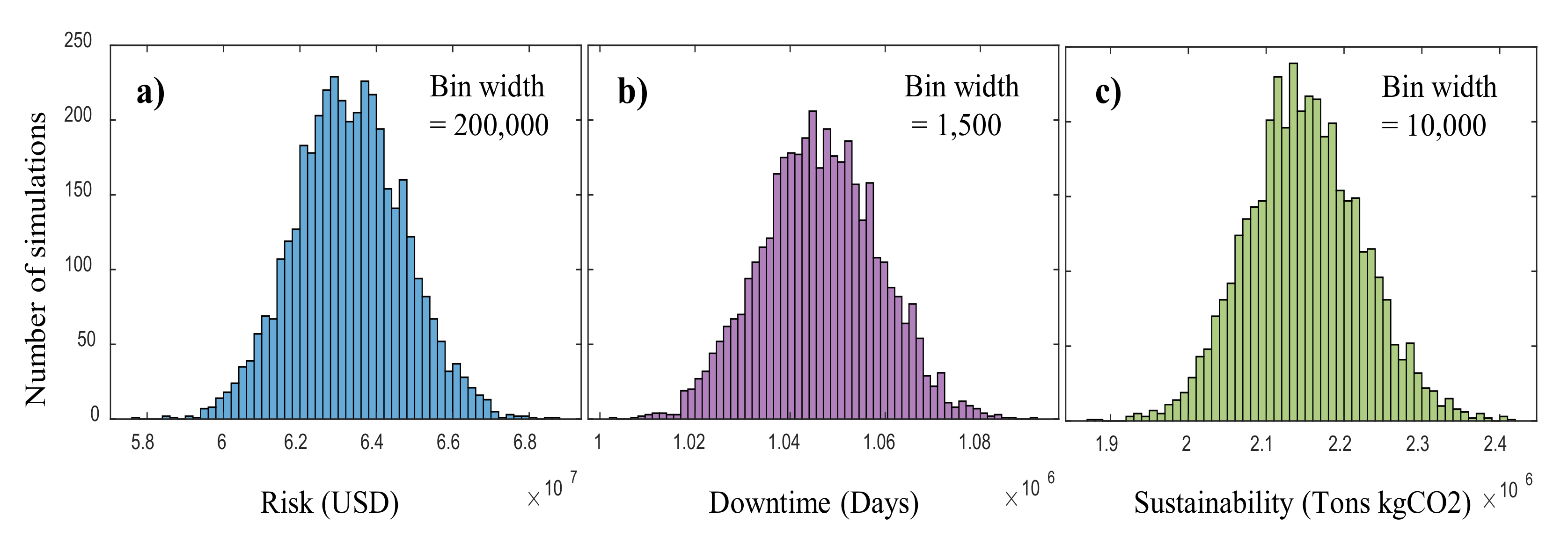
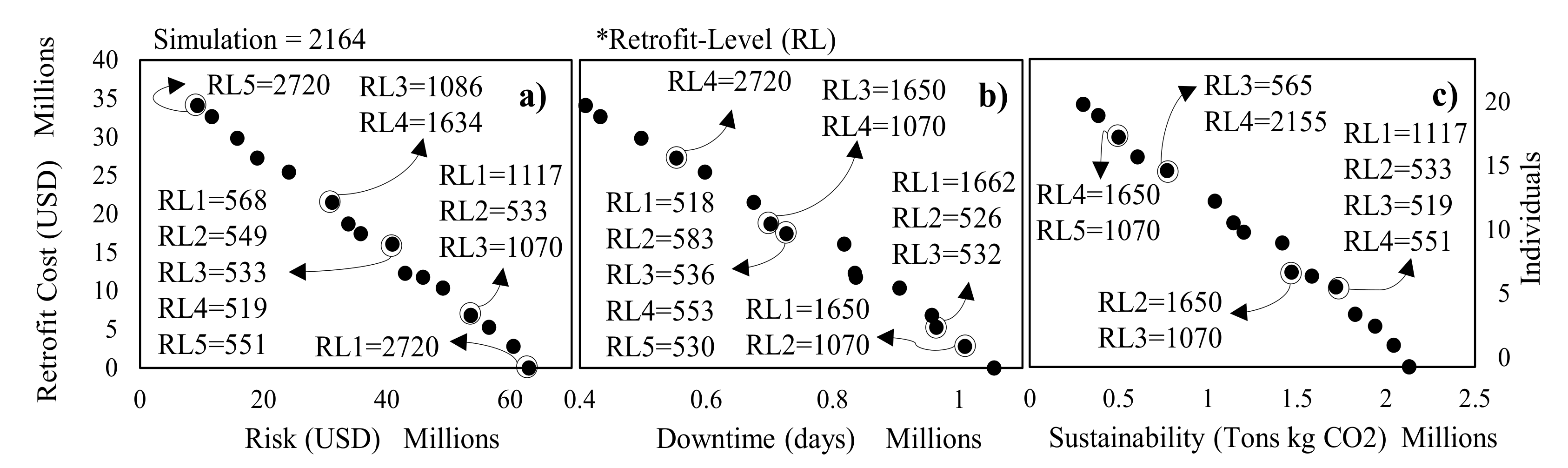
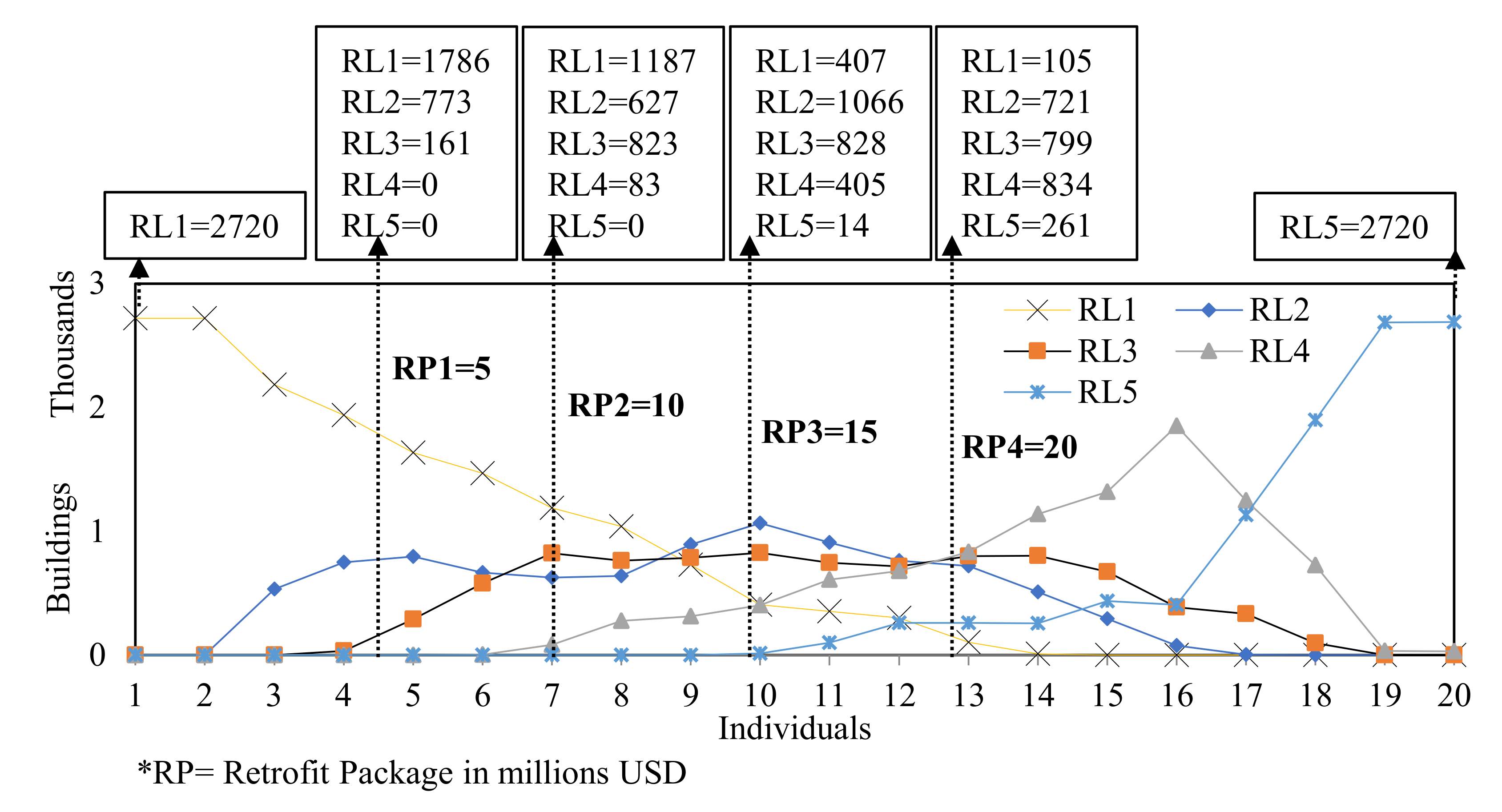
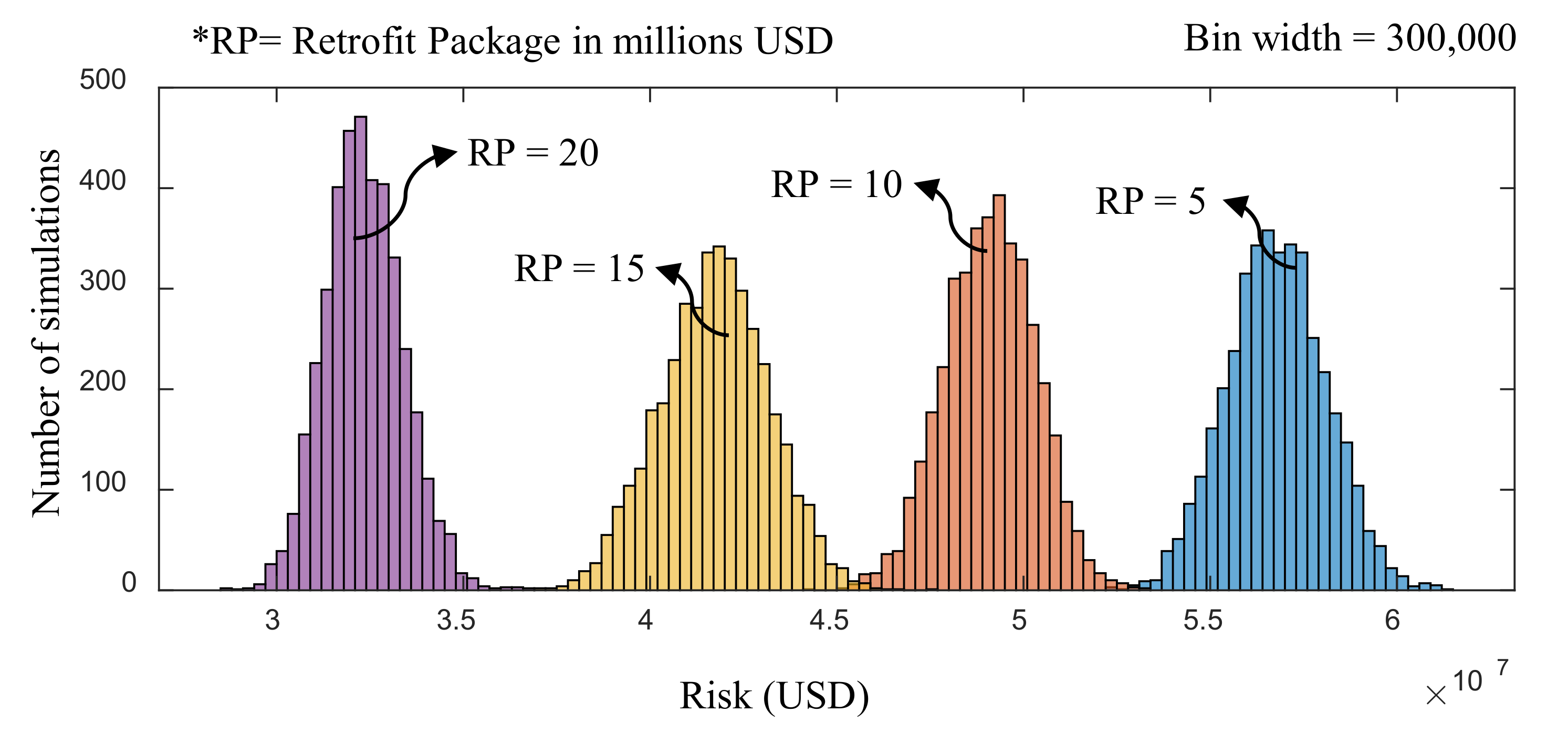
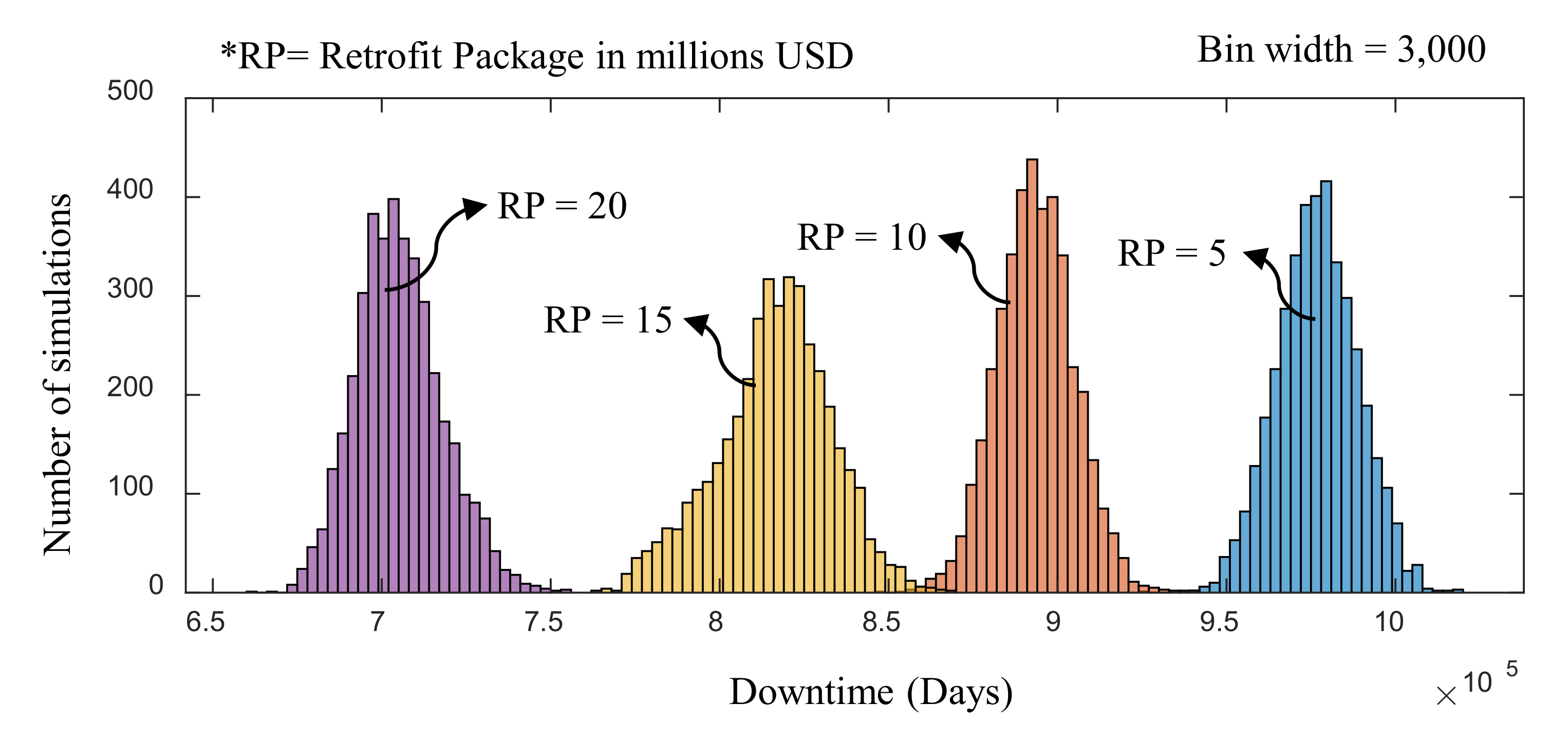
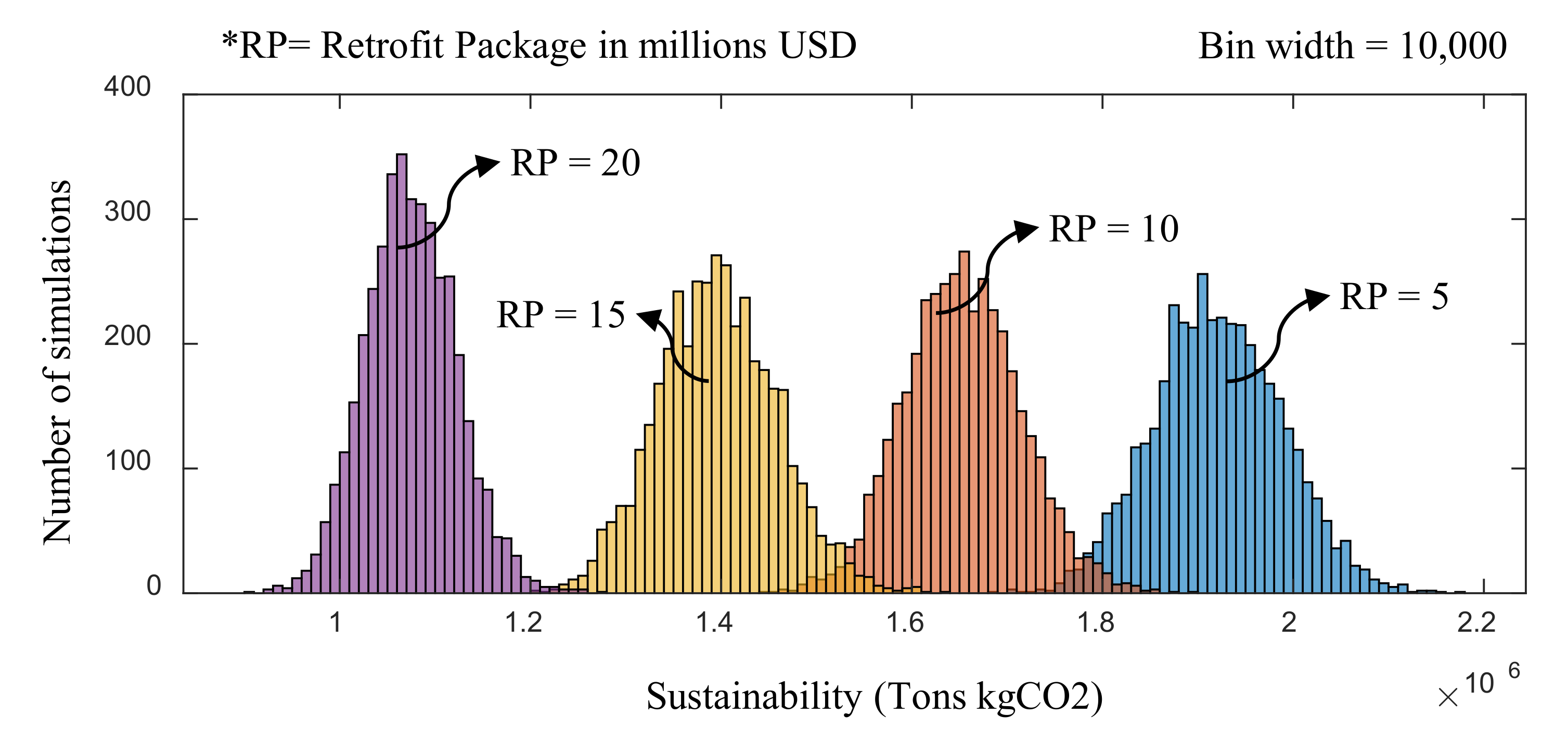
| Damage States | Mean (Buildings) | Standard Deviation | Skewness | Kurtosis |
|---|---|---|---|---|
| No-damage | 187.13 | 13.11 | 0.023 | 2.996 |
| Slight damage | 251.05 | 14.79 | 0.051 | 2.877 |
| Moderate damage | 614.41 | 21.84 | −0.012 | 3.058 |
| Extensive damage | 685.84 | 22.36 | 0.046 | 3.045 |
| Complete damage | 981.57 | 24.53 | 0.078 | 3.126 |
| Risk Performance Indicator | Mean (Million USD) | Standard Deviation (Million USD) | Skewness | Kurtosis |
|---|---|---|---|---|
| Without a retrofit program | 63.30 | 1.42 | 0.057 | 3.03 |
| Retrofit of 5 million USD | 56.78 | 1.33 | 0.043 | 2.93 |
| Retrofit of 10 million USD | 49.10 | 1.22 | −0.065 | 2.98 |
| Retrofit of 15 million USD | 41.74 | 1.44 | −0.026 | 2.86 |
| Retrofit of 20 million USD | 32.34 | 1.04 | 0.211 | 3.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Anwar, G.A.; Dong, Y. Performance-Based Bi-Objective Retrofit Optimization of Building Portfolios Considering Uncertainties and Environmental Impacts. Buildings 2022, 12, 85. https://doi.org/10.3390/buildings12010085
Zhou Z, Anwar GA, Dong Y. Performance-Based Bi-Objective Retrofit Optimization of Building Portfolios Considering Uncertainties and Environmental Impacts. Buildings. 2022; 12(1):85. https://doi.org/10.3390/buildings12010085
Chicago/Turabian StyleZhou, Ziyi, Ghazanfar Ali Anwar, and You Dong. 2022. "Performance-Based Bi-Objective Retrofit Optimization of Building Portfolios Considering Uncertainties and Environmental Impacts" Buildings 12, no. 1: 85. https://doi.org/10.3390/buildings12010085
APA StyleZhou, Z., Anwar, G. A., & Dong, Y. (2022). Performance-Based Bi-Objective Retrofit Optimization of Building Portfolios Considering Uncertainties and Environmental Impacts. Buildings, 12(1), 85. https://doi.org/10.3390/buildings12010085








