A New General Formulation for the PMV Thermal Comfort Index

Abstract

The PMV index forms the basis of international thermal comfort standards. PMV was developed based on empirical relationships between the metabolic rate of activity and the body mean skin temperature and evaporative heat loss under the comfort conditions. However, many recent studies have questioned the accuracy and reliability of the PMV predictions, particularly for the discomfort range. This paper develops a general formulation of PMV that does not involve the mean skin temperature and evaporative heat loss. The new metabolic-based predicted mean vote (MPMV) index is expressed as the difference between the metabolic rate of activity and the metabolic rate required to achieve a comfort state under the imposed environment conditions. The comfort metabolic rate is found to vary linearly with the metabolic rate required to maintain the body core and mean skin temperatures at the resting thermo-neutral state. The model constants are determined using public experimental data on thermal sensation votes of young and older people. The new formulation accounts for body core cooling to achieve comfort under hot exposures; it also addresses the overlooked non-shivering thermogenesis in the body heat balance at the comfort state and covers comfort requirements for young and older people in wakeful and sleep states.

1. Introduction

The predicted mean vote index (PMV) is the most popular deterministic index to evaluate thermal comfort requirement in built environments. PMV is adopted in many international thermal comfort standards [1,2], and implemented in many comfort design tools [3]. PMV was developed by Fanger [4] to study indoor thermal comfort in buildings with HVAC systems under temperate climates, but it has been used, and often abused (extending its use outside the validity ranges of its parameters), in many other applications including outdoor environments and various types of climates and buildings without HVAC systems [5,6,7]. However, with the surge of many experimental studies covering different applications during this long period of time, the accuracy and reliability of PMV has been questioned for all building applications [8,9,10,11,12,13]. The PMV has consequently gone through many studies to improve its accuracy, but none of them have been successful in replacing it or gaining a widespread application in air-conditioned buildings [7]. This indicates that further research is needed.

Fanger [4] developed PMV for thermal comfort of whole body based on subjective studies of a large pool of college-aged (male and female) subjects in controlled climatic chambers. PMV relates the physiological thermal response of people to their psychological thermal sensation votes (TSV) under steady state conditions using the ASHRAE’s seven-point thermal sensation scale: (cold (−3); cool (−2); slightly cool (−1); neutral (0); slightly warm (+1); warm (+2); and hot (+3)). The human body thermal response is expressed in terms of the heat load, which is the difference between the internal metabolic rate of activity and the total body heat loss to the surrounding environment if the body is at a state of thermal comfort. Fanger determined the state of comfort when the body is under heat balance, and the mean skin temperature and skin evaporative heat loss are within narrow ranges around the neutral thermal state. The comfort mean skin temperature was determined for four activity levels (sedentary, low, medium and high) using experiments on 20 male and female college students in climatic chambers, with the environmental conditions set to the neutral conditions (TSV = 0). A linear correlation was established between the mean skin temperature and metabolic rate at these comfort environmental conditions. A similar approach was used to compute the evaporative heat loss at the comfort environmental conditions covering additional data from McNall et al. [14] Fanger did not, however, provide any relationship for the metabolic rate of activity required to maintain a comfort state as a function of the environment conditions and subject clothing insulation so that the equations of the mean skin temperature and evaporative heat loss at the comfort state can be evaluated. The actual metabolic rate of activity is instead used in these equations. It is therefore expected that the PMV model would yield inaccurate results for cases where the metabolic rate of activity significantly deviates from the metabolic rate required to maintain a comfort state at the imposed environment conditions. In other words, PMV predictions would not be accurate for the discomfort range. ISO 7730 [2] recommends the use of PMV in the cool/warm thermal sensation range (−2 ≤ PMV ≤ 2). Humphreys and Nicol [8] found that the more thermal conditions moved away from neutral, the larger the bias became. PMV is only reliable within the range of ±0.5.

Since its release in 1970, PMV has gone through many studies to evaluate its accuracy in various building applications and climates. These studies found that PMV consistently overestimates TSV for both the cold and warm sides, particularly in the discomfort range (PMV > 0.5 or PMV < −0.5) [8,12,13]. Overestimation of thermal comfort may lead to thermal discomfort in actual spaces and more energy use to operate buildings [8,13,15]. The main causes of such inaccuracies are attributed to four main sources directly or indirectly related to the PMV model: (1) PMV model assumptions and theory; (2) uncertainties in the input parameter values; (3) individual (as opposed to group) differences for perception of thermal sensation; and (4) people thermal adaptation to local climates and in actual indoor spaces, which were not initially covered in the PMV model development. Research by van Hoof [8] presented a comprehensive review of literature on PMV improvement studies, covering thermal comfort in air-conditioned and free running buildings. This paper focuses on the error sources arising from the PMV model theory as outlined in [8,16,17].

As previously mentioned, the main theoretical error sources of the PMV model are related to the formulations of the mean skin temperature and evaporative heat loss at the comfort state. Furthermore, and to a lesser extent, the errors due to the estimation of the scaling factor (α; Equation (7)) relating PMV to TSV could be significant at high activity levels (Metabolic rate > 2.5 met). The latter error source is rarely addressed in literature. Doherty and Arens [18] compared PMV predictions with the measured TSV of subjects under various activity levels in controlled climatic chambers, and their study found that PMV overestimated TSV by an average value of 1.26 units. Mochida and Soiko [9] experimentally proved that PMV is weekly correlated with the heat load (more likely due to inaccurate determination of heat load). Holmer [17] found out that the formulations of the mean skin temperature and evaporative heat loss at the comfort state are problematic, as they depend not only on the metabolic rate of activity, but also on the environmental conditions and clothing insulation of subjects. Compared to the measurement data of Gavhed [19], Fanger’s formulations yielded higher mean skin temperature by a few degrees Celsius for standing and walking activities in cold environment conditions (−6 to −22 °C). Yeo et al. [20] found that PMV failed to predict TSV in climatic chambers with air temperature from 21 to 29 °C. The authors attributed this difference to individual differences in the limited number of subjects. However, when the mean skin temperature was replaced by its measured values at the actual environmental conditions, the PMV predictions were improved. The study also found that the measurement method of the mean skin temperature may result in differences of up to 1.5 °C, particularly under cold exposure conditions. Omidvar and Kim [21] identified that the PMV sweating model does not account for sweating that occurs at a low metabolic rate (around 1 met) at the comfort state. Therefore, they modified the PMV sweating model by adding a basal sweating component. The added term was calculated using a piece-wise fuzzy regression model and validated using public experimental data. Zhang and Lin [16] replaced the PMV evaporative heat loss at the comfort state with the one calculated at the actual environmental conditions, using the two-node model of Gagge et al. [22]. Similarly, Xu and An [23] replaced the PMV mean skin temperature by the one calculated at the actual activity level and environment conditions, using the two-node model of Gagge et al. ASHRAE 55 [1] does not recommend the use of PMV for metabolic rates higher than 2 met for the reason that PMV does not properly account for the evaporative sweating heat to achieve a comfort state.

The goal of this paper is to develop a new alternative formulation of the PMV index that does not involve the controversial mean skin temperature and evaporative heat loss, but does extend its applicability to older people and people in a sleeping state. The paper is structured as follows: Section 1 reviews prior work dealing with the PMV model improvement; Section 2 presents a brief description of the PMV model with its limitations; Section 3 elaborates on the proposed model and its application to older people and people in a sleep state; Section 4 presents the model results, followed by Section 5 and Section 6 on results discussion and conclusions.

2. Fanger’s PMV Model

The PMV index is expressed in terms of the body heat load imposed by the surrounding environment under steady state conditions. The body heat load is given as the difference between the net internal heat generation and the body heat loss to the surrounding environment of persons in a state of comfort. PMV is expressed by the following equation:

$$\mathrm{PMV}=\mathsf{\alpha }\left(\mathrm{M}\right)·\left\{{(\mathrm{M}-\mathrm{W})-(\mathrm{Q}}_{\mathrm{resC}}+{\mathrm{E}}_{\mathrm{skC}}+{\mathrm{D}}_{\mathrm{skC}})\right\}$$

(1)

where (α) is a scaling factor, M is the metabolic rate of person activity (W/m²), W is the effective mechanical power (W/m²), D_skC is the skin dry (convective + radiative) heat exchange (W/m²) of a person in a state of comfort to its surrounding environment, E_skC is the skin evaporative heat loss (W/m²) due to the regulatory sweating and skin water vapour diffusion of a person under a state of comfort, and Q_resC is the respiration heat loss (convective and latent) (W/m²) of a person in a state of comfort to the surrounding environment.

Fanger [4] defines the comfort state for a whole body as:

• The body is in a heat balance with the environment;
• The mean skin temperature is within the comfort limits;
• The sweating is within the comfort limits.

Fanger used an experimental approach to determine the comfort state (items 2 and 3). A significant number of experiments were carried out on college students in controlled climatic chambers to determine the mean skin temperature and sweating evaporative heat loss at the comfort environmental conditions under which subjects were exposed for three hours. The mean skin temperature at the comfort environmental conditions (T_skC) was determined using experiments on 20 young male and female subjects wearing standard clothing (0.6 clo) under four activity levels with measured metabolic rates of 1, 1.56, 2.08, and 2.64 met. The comfort environmental conditions (with TSV = 0) at each activity level were taken from the experiments of McNall et al. [14]. The mean skin temperature (in °C) was obtained by curve fitting of the measured data using the following linear regression equation:

$${\mathrm{T}}_{\mathrm{skC}}=35.7-0.0275·\left(\mathrm{M}-\mathrm{W}\right)$$

(2)

The measured mean skin temperature shows a high scatter (standard error of the mean is 0.69 °C [24]), particularly at high activity levels (M > 1.5 met).

Equation (2) can be interpreted as the relationship between the mean skin temperature at the comfort state and the activity level of subjects required to achieve the comfort state under the imposed environmental conditions. As the comfort mean skin temperature depends also on the environmental conditions and subject clothing insulation [17], Equation (2) is limited to the conditions of the experiments. Furthermore, Equation (2) cannot be applied for deep body core cooling situations for which the net internal heat generation (M minus any external heat removal) is lower than 1 met.

For the determination of the evaporative heat loss of a person under the comfort environmental conditions, Fanger assumed that the evaporative heat loss is composed of two components: (1) the evaporative heat loss due to water vapour diffusion through the skin (E_difC); and (2) evaporative heat loss due to the regulatory sweating (E_swC). These are linked to the skin wettedness as follows:

$${\mathrm{E}}_{\mathrm{skC}}={\mathrm{E}}_{\mathrm{difC}}+{\mathrm{E}}_{\mathrm{swC}}={\mathrm{w}}_{\mathrm{C}}·{\mathrm{E}}_{\mathrm{maxC}}$$

(3)

with:

$${\mathrm{E}}_{\mathrm{difC}}=0.00305·\left[5733-6.99·\left(\mathrm{M}-\mathrm{W}\right)-{\mathrm{P}}_{\mathrm{a}}\right]$$

(4)

where E_maxC is the maximum skin evaporative heat loss of a person under the comfort environmental conditions, P_a is the vapour pressure (Pa) at the environment temperature, and w_C is the skin wettedness evaluated at the comfort conditions.

Fanger [24] used his own measurement data and those of McNall et al. [14] to develop a regression-based formulation for E_swC as a function of subject activity level at the comfort state. In experiments by McNall et al., young college subjects (n = 183) wore standard clothing uniforms and were exposed to different environmental conditions to perform three (low, medium and high) activity levels for three hours of exposure. At the end of the exposure time, subjects voted on their thermal sensation using the seven-point ASHRAE thermal sensation scale. Measurement data for which subjects voted thermally comfortable were used to develop the following regression relationships:

$${\mathrm{E}}_{\mathrm{swC}}=0.42·\left(\mathrm{M}-\mathrm{W}-58.15\right)$$

(5)

Equation (5) is as well subject to a high scatter (standard error of the mean is 0.25 met [24]), particularly for non-sedentary activities (metabolic rates > 1.2 met).

The regulatory sweating in Equation (5) was determined from the experiments as the average value over the exposure time (3 h), by accounting for the subject weight loss between the start and end times. It is therefore expected that the steady state evaporative heat at the end of the exposure time will be higher than the average value, and thus Equation (5) underestimates the evaporative heat loss. Furthermore, Equation (5) stipulates that sweating is suppressed when body core cooling is used to achieve a comfort state under hot exposure conditions for which the net heat production (M minus any external heat removal) is lower than 1 met. This may not be correct. Under such core cooling situations where the body gains dry heat from the environment (T_a > T_sk) the core temperature should therefore be lower than its neutral value at rest (due to the heat removal), but the mean skin temperature should be higher than its neutral value at rest to achieve a comfort state under such hot environments [25]. Sweating will thus be activated due to the positive signals of the peripheral (skin) temperature sensors (no positive signal from the central core sensor).

The total heat loss by respiration of a person at a comfort state to the actual environment is given by the following equation:

$${\mathrm{Q}}_{\mathrm{resC}}=\left(\mathrm{M}+{\mathrm{M}}_{\mathrm{nstC}}\right)·{10}^{-3}\left\{1.4·\left(34-{\mathrm{T}}_{\mathrm{a}}\right)+0.017·\left(5867-{\mathrm{P}}_{\mathrm{a}}\right)\right\}$$

(6)

where T_a is the ambient temperature (°C) and M_nstC is the metabolic rate produced by non-shivering thermogenesis (NST) (W/m²) at the comfort state.

The new in Equation (6) is the inclusion of the NST heat production at the comfort state (M_nstC), which is not accounted for in the PMV formulation (Equation (1)). More details to justify this inclusion are given in the Discussion Section 5.

Finally, the scaling factor (α) was graphically determined from the experiments on thermal sensation votes at the comfort conditions of Fanger [4], Nevins et al. [26] and McNall et al. [14], covering 1396 subjects and four activity levels (1, 1.56, 2.08, and 2.64 met). Four data points of (α) at each activity level were obtained and fitted using the following relationship:

$$\mathsf{\alpha }\left(\mathrm{M}\right)=0.303·{\mathrm{e}}^{-0.036·\mathrm{M}}+0.028$$

(7)

Equation (7) converges to an asymptotic value of 0.028 at M > 2.5 met. Therefore, Equation (7), among other factors, might be responsible for the over-estimation of the PMV index for high activity levels (M > 2.5 met) in air-conditioned indoor environments of sport centers as reported in many studies [27,28].

Equations (2)–(7) are substituted into Equation (1) to calculate the PMV index at any given environmental conditions. These equations constitute then the main sources of error in the PMV calculation.

Limitations of the PMV Index

The limitations of the PMV formulation can be attributed to two sources: (1) theory of the model development; and (2) experimental conditions. From the theory perspective, the limitations include:

• Equation (1) is developed for young and healthy adults under an active (wakeful) state. Older people, who experience age-related physiological changes, and may therefore need different comfort conditions, are not covered;
• The comfort conditions do not cover people in a sleep state (M = 0.7 met);
• The PMV accounts only for external body skin cooling for which the mean skin temperature at the comfort state is lower than its neutral value at rest to trigger blood vasoconstriction for active people with M ≥ 1 met. For internal body core cooling (e.g., infusion of intravenous cold fluids, or ingesting cold commodities to drop the core temperature), which is required to achieve comfort under hot exposure conditions, the PMV index is not applicable as Equation (2) cannot be evaluated or extrapolated (net internal heat generation < 1 met);
• The body heat load of Equation (1) does not include heat generated by NST under cold exposure conditions, resulting therefore in over/under-estimation of comfort levels;
• Experiments for the derivation of Equations (2), (5) and (7) covered only one value of the clothing insulation (0.6 clo). Extension of the formulations to other clothing insulations is therefore unknown.

The limitations from the experimental conditions include the PMV parameter ranges. These are well identified in applicable comfort standards such as ISO 7730 [2] and ASHRAE 55 [1]. For ISO 7730 the ranges are as follows: subject clothing within 0 to 2 clo; metabolic rate within 0.8 to 4 met (this excludes people in a sleep state); ambient temperature within 10 to 30 °C; ambient mean radiant temperature within 10 to 40 °C; ambient relative humidity in terms of vapour pressure within 0 to 2700 Pa; and relative air velocity within 0 to 1 m/s. ASHRAE 55 and Humphreys and Nicole [8] identified, however, narrower parameter ranges for valid predictions of PMV in air-conditioned built environments. Furthermore, PMV is a continuous index, developed as a statistical average of discrete TSV of a large pool of young people; therefore, individual differences are not accounted for and differences with single (individualised) TSV are expected.

3. New Formulation of PMV

A new alternative and general formulation of the PMV index is proposed to address the aforementioned limitations and extend its predictability to wide ranges of parameter values, including comfort requirement for older people and sleep.

3.1. Definition of Thermo-Neutral and Comfort States

The states of thermal neutrality and comfort, as expressed by a person exposed to environmental conditions, are worth elucidating as these vary with the person parameters and exposure conditions [25,29,30]. These two states are sometimes used interchangeably, but in this paper a clear distinction is made. From the psychological perspective, a thermal neutral state corresponds to a person’s thermal preference of neither warm nor cold with a thermal sensation vote equal to zero [31]. The state of thermal comfort is defined as a state of mind for which a person reports a thermal sensation vote within ±0.5 units according to ASHRAE-55 [1], or within ±0.7 units according to ISO 7730 [2] when exposed to a range of environmental conditions. The range of the thermal neutrality conditions is therefore a subset of that of the comfort state conditions. A thermal sensation vote can only be determined by direct interrogation of people through experimentation or surveys. From the physiological perspective, thermal neutrality corresponds to the minimum metabolic energy production of the body under the imposed environmental conditions [29]. For an average adult person in a wakeful state, the lowest metabolic energy production corresponds to a nude person in supine posture and postabsorptive resting state with a basal metabolic rate of around 0.77 met with no active thermoregulation for vasomotor, sweat and thermogenesis [32,33]. The reported body core and mean skin temperatures at this neutral state are 36.8 °C and 33.7 °C, respectively. These neutral temperature values are as well the threshold values for the central and peripheral (skin) control systems, respectively, to effect thermoregulatory actions of an average adult person [22,31]. For other people’s clothing, posture and/or activity, the neutral state will be different and will involve the thermoregulatory system to dissipate or produce energy to minimize the deviations of the body core and mean skin temperatures from their neutral values at the resting state. Vasodilation for the skin blood flow control and regulatory sweating are used to slow the increase in the core temperature by increasing the heat loss to the environment, whereas vasoconstriction and non-shivering thermogenesis (NST) are used to reduce the drop in the core temperature by producing metabolic energy and reducing the heat loss to the environment. The conditions of the comfort state will accordingly vary around the neutral state conditions within the aforementioned TSV limits. It follows from this analysis that for skin cooling cases (requiring cold environmental conditions to dissipate high internal heat), the neutral (or comfort) core temperature (which is directly affected by internal heat) should be higher than its neutral value at the resting state, whereas the neutral (comfort) mean skin temperature (which is directly affected by the environment conditions) should be lower than its neutral value at the resting state. This is consistent with the measurements of Olesen et al. [34]. It follows as well that under skin cooling cases, the comfort state will require high metabolic energy production (e.g., exercising in cold environments) to compensate for the high heat loss. The situation is, however, inversed for body core cooling cases (requiring the reduction or removal of internal heat under hot exposures). The neutral (comfort) core temperature should be lower than its neutral value at the resting state, whereas the neutral (comfort) mean skin temperature should be higher than its neutral value at the resting state. This is consistent with the analysis of Kingma et al. [25]). Under this situation, the comfort state will require low net internal heat production to reduce the core temperature.

It should be noted that the aforementioned requirements for the comfort conditions are consistent with those established by Fanger (Section 2), except that NST is not accounted for. Therefore, a fourth condition could be added to the whole body thermal comfort as “metabolic energy production by NST is within the comfort range.”

3.2. Body Heat Balance

The heat balance of the human body under steady state conditions is given by the following equation:

$$\mathrm{M}+{\mathrm{M}}_{\mathrm{sh}}-\mathrm{W}+{\mathrm{Q}}_{\mathrm{ex}}={\mathrm{Q}}_{\mathrm{res}}+{\mathrm{E}}_{\mathrm{sk}}+{\mathrm{D}}_{\mathrm{sk}}$$

(8)

where M_sh is the metabolic energy produced by non-shivering and muscular shivering thermogenesis (W/m²), Q_ex is the external heat intervention to cool or heat the body core section (W/m²), Q_res is the respiratory heat exchange with the environment (W/m²), and E_sk and D_sk are, respectively, the body skin evaporative and dry heat exchanges with the environment (W/m²).

The instantaneous external heat intervention flux (Q_ex) may take positive values (for internal core heating) or negative values (for internal core cooling) and may therefore depend on the body core temperature. The effective mechanical power (W) depends on the metabolic rate of activity (M) and is usually significant at high activity levels (M > 1.6 met; [35]). For normal activities, including stepping and cycling, Fiala [35] proposed the following regression-based relationship for the mechanical efficiency:

$$\mathsf{\eta }\left(\mathrm{M}\right)=\frac{\mathrm{W}}{\mathrm{M}}=0.2·\mathrm{TAN}\mathrm{H}\left(6.7·{10}^{-3}\mathrm{M}-0.6\right)$$

(9)

The required heat flux (Q_C) to be added to or subtracted from the internal metabolic rate (M) to achieve a thermal comfort state under the imposed environment conditions is expressed as follows:

$${\mathrm{Q}}_{\mathrm{C}}=\mathrm{M}-{\mathrm{M}}_{\mathrm{C}}=\left(\mathrm{M}+{\mathrm{M}}_{\mathrm{nstC}}-{\mathrm{W}}_{\mathrm{C}}+{\mathrm{Q}}_{\mathrm{exC}}\right)-\left\{{\mathrm{Q}}_{\mathrm{resC}}+{\mathrm{E}}_{\mathrm{skC}}+{\mathrm{D}}_{\mathrm{skC}}\right\}$$

(10)

where M_C is the internal heat (or metabolic rate) required to achieve a comfort state under the imposed environmental conditions, W_C is the effective mechanical power at the comfort state, and Q_exC is the external heat supplied to, stored in (from transitioning between environments) or extracted from the body core section at the comfort state.

As was previously pointed out, the new feature in the comfort Equation (10) is the inclusion of the metabolic rate produced by NST alongside the regulatory sweating. The legitimate question in this new treatment is whether NST is indeed present when the body is in the neutral or comfort state, and if so, how significant is it to induce any change in the body thermal response. Evidence to answer these questions is provided under the Discussion Section 5.

3.3. New Comfort Index

The new metabolic-based predicted mean vote index (MPMV) index is defined as follows [36]:

$$\mathrm{MPMV}=\mathsf{\beta }\left(\mathrm{M}\right)·{\mathrm{Q}}_{\mathrm{C}}=\mathsf{\beta }\left(\mathrm{M}\right)·\left(\mathrm{M}-{\mathrm{M}}_{\mathrm{C}}\right)$$

(11)

where (β) is a scaling factor to be determined experimentally.

When the body is at the comfort state under the imposed environment conditions (Q_C = 0), the required internal heat generation (or metabolic rate) (M_C) to achieve such comfort state is deduced from Equation (10) as follows:

$${\mathrm{M}}_{\mathrm{C}}=\frac{{\mathrm{E}}_{\mathrm{skC}}+{\mathrm{D}}_{\mathrm{skC}}-{\mathrm{Q}}_{\mathrm{exC}}-\left(1-{\mathrm{Q}}_{\mathrm{r}}\right)·{\mathrm{M}}_{\mathrm{nstC}}}{1-\mathsf{\eta }\left({\mathrm{M}}_{\mathrm{C}}\right)-\mathsf{\gamma }·{\mathrm{Q}}_{\mathrm{r}}}$$

(12)

where Q_r is the ratio of the respiratory heat exchange to the total metabolic rate, γ is a coefficient equal to one if the internal heat generation (M_C) is provided by the body metabolism (M_C > 0) or zero if the internal heat is provided by an external source (M_C ≤ 0). Similarly, the mechanical efficiency (η) will be zero if M_C ≤ 0. The NST heat at the comfort state (M_nstC) is calculated as a function of the deviations of the core and mean skin temperatures at the comfort state from their neutral values at the resting state using a suitable shivering model (e.g., model of Ji et al. [37]; or Tikuisis and Giesbrecht [38]). The ratio Q_r is derived from Equation (6) as follows:

$${\mathrm{Q}}_{\mathrm{r}}=\frac{{\mathrm{Q}}_{\mathrm{resC}}}{{\mathrm{M}}_{\mathrm{C}}+{\mathrm{M}}_{\mathrm{nstC}}}=1.7·{10}^{-5}\left(5867-{\mathrm{P}}_{\mathrm{v}}\right)+14·{10}^{-3}\left(34-{\mathrm{T}}_{\mathrm{a}}\right)$$

(13)

In most cases (with M_C > 0), the required net internal heat (M_C) to achieve a comfort state under the imposed environmental conditions comes from the metabolic rate of activity performed under such comfort conditions. However, in some cases under hot exposure conditions (M_C ≤ 0), the body metabolism cannot theoretically be further reduced (by reducing activity level) to achieve a comfort state, and therefore the required net internal heat has to be extracted from the body core section using an external source. Throughout this paper, M_C will be called the comfort metabolic rate irrespective of its heat source.

The required comfort metabolic rate (M_C) will vary as a function of the environmental exposure conditions and subject parameters (i.e., clothing insulation). Under cold exposure conditions (or body skin cooling), the required M_C will take high values (>1 met) to maintain the comfort state with a corresponding mean skin temperature (which is closely related to the environment conditions) lower than its neutral value at the resting state, but with a core temperature (which is closely related to the internal heat production) higher than its neutral value at the resting state. Therefore, the regulatory sweating at the comfort state is activated by the central sensor system, which uses the warm core temperature control signal. NST at the comfort state may as well be induced by the peripheral sensor system, which uses the cold mean skin temperature control signal. However, under hot exposure conditions, the required M_C will take lower values towards zero or negative values. This case corresponds to deep body core cooling (e.g., infusion of intravenous cold fluids, or inhalation of cold gas or ingestion of cold commodities; for example gradually drinking one kg of ice cubes or slurries per hour can remove about 1.2 met of internal heat) to reduce the internal metabolic rate generation. Under this situation, achieving a comfort state is not possible unless the body metabolism of activity is reduced and/or an external cooling source is used. The mean skin temperature at the comfort state will be higher than its neutral value at the resting state (due to the dry heat gain from the environment), but with a core temperature lower than its neutral value at the resting state (due to heat removal). Regulatory sweating at the comfort state is therefore activated by the peripheral warm mean skin temperature control signal. NST may as well be induced by the central cold core temperature control signal. This is consistent with publicly reported measurement data of shivering thermogenesis due to body core cooling, for which the mean skin temperature is at or higher than its neutral value but the core temperature is below its neutral value [38,39]. This case of core cooling is not covered under the formulation of the PMV index (where M ≥ 1 met).

Equation (12) represents the link between the required metabolic rate (M_C) to achieve a comfort state under the imposed environment conditions and the corresponding mean skin temperature and evaporative heat loss at the comfort state. If M_C is known, the mean skin temperature and evaporative heat loss can thus be determined. However, an additional equation for the core temperature (heat transfer between the core and skin layers) at the comfort state is needed to solve for the sweating and NST heat production. Three comfort equations will thus be deduced for the core and mean skin temperatures and evaporative heat loss. The profile of the core temperature at the comfort state versus M_C will represent a new addition to the field (according to the author’s knowledge); it is particularly important for thermal safety to limit any health injury from hyper or hypothermia for people exposed to hot or cold conditions. Further details on this topic will be a subject of another technical paper.

Equation (11) looks similar to the PMV Equation (1), but it is fundamentally different as it is given in terms of the metabolic rate required to achieve a comfort state under the imposed environment conditions. The environment conditions in the PMV Equation (1) are not necessarily the comfort conditions for which the relationships between the metabolic rate and mean skin temperature and evaporative heat loss were developed from the measurement data. Furthermore, the NST heat at the comfort state (M_nstC) is included in the definition of the new MPMV index, but not in PMV. In addition, the case of deep body cooling (M_C < M_basal = 0.77 met) is not represented in the PMV index (M ≥ 1 met) and therefore the results of the PMV index are just extrapolations of the curve with no regulatory sweating. The scaling constant (β) may as well be different than the scaling constant (α) of PMV (Equation (7)).

3.4. Determination of the Comfort Metabolic Rate

Evaluation of Equation (11) will require the calculation of the comfort metabolic rate (M_C). As mentioned before, the comfort conditions vary around the neutral conditions within the limits of TSV = ±1 units. M_C is also directly related to the core and mean skin temperatures at the comfort state. M_C may therefore be expressed as a perturbation around the resting neutral state (T_c = T_cN, and T_sk = T_skN,) using one of the following Taylor expansion series:

$${\mathrm{M}}_{\mathrm{C}}={\mathrm{M}}_{\mathrm{N}}+\left({\mathrm{T}}_{\mathrm{skC}}-{\mathrm{T}}_{\mathrm{skN}}\right)·\frac{{\mathrm{dM}}_{\mathrm{C}}}{{\mathrm{dT}}_{\mathrm{skC}}}{\rfloor }_{\left({\mathrm{T}}_{\mathrm{cN}},{\mathrm{T}}_{\mathrm{skN}}\right)}+\cdots$$

(14)

$${\mathrm{M}}_{\mathrm{C}}={\mathrm{M}}_{\mathrm{N}}+\left({\mathrm{T}}_{\mathrm{cC}}-{\mathrm{T}}_{\mathrm{cN}}\right)·\frac{{\mathrm{dM}}_{\mathrm{C}}}{{\mathrm{dT}}_{\mathrm{cC}}}{\rfloor }_{({\mathrm{T}}_{\mathrm{cN}},{\mathrm{T}}_{\mathrm{skN}})}+\cdots$$

(15)

M_N is the metabolic rate to maintain the body at the neutral core and mean skin temperatures at resting state, calculated from Equation (12) by substituting T_cC = T_cN, and T_skC = T_skN, where T_cC and T_skC are, respectively, the core and mean skin temperatures at the comfort state, and T_cN and T_skN are their neutral values at the resting state.

A heat balance around the body core section under steady state conditions stipulates that the core temperature at the comfort state (T_cC) is proportional to the comfort metabolic rate in a linear fashion (as it is weakly altered by the environment conditions). However, the mean skin temperature can be influenced by the environment conditions and subject characteristics and may therefore take a nonlinear relationship with the comfort metabolic rate. The following profiles are assumed for the core and mean skin temperatures:

$${\mathrm{T}}_{\mathrm{cC}}-{\mathrm{T}}_{\mathrm{cN}}={\mathrm{a}}_{\mathrm{c}}·\left({\mathrm{M}}_{\mathrm{C}}-{\mathrm{M}}_{\mathrm{basal}}\right)$$

(16)

$${\mathrm{T}}_{\mathrm{skC}}-{\mathrm{T}}_{\mathrm{skN}}={\mathrm{a}}_{\mathrm{s}}·\left({\mathrm{M}}_{\mathrm{C}}-{\mathrm{M}}_{\mathrm{basal}}\right)+{\mathrm{b}}_{\mathrm{s}}·{\left({\mathrm{M}}_{\mathrm{C}}-{\mathrm{M}}_{\mathrm{basal}}\right)}^2+\cdots$$

(17)

where a_c, a_s, and b_s are constants and M_basal is the basal metabolic rate at the resting state, given by:

$${\mathrm{M}}_{\mathrm{basal}}=12.6·\left({\mathrm{T}}_{\mathrm{cN}}-{\mathrm{T}}_{\mathrm{skN}}\right)/\left(1-{\mathrm{Q}}_{\mathrm{r}}\right)$$

(18)

Equations (14) or (15) is evaluated for two body cooling situations, core and skin cooling.

3.4.1. Body Core Cooling (M_C < M_basal)

Body core cooling occurs when the body gains dry heat from the environment and the evaporative sweating is not capable to achieve a comfort state (this situation may ultimately lead to non-steady state conditions and failure of thermoregulation). The only option to achieve a comfort state under the steady state conditions is to cool the body core section. Under this situation, the required comfort metabolic (or internal) heat is lower than the minimum basal metabolic rate (M_basal). The corresponding mean skin temperature (closely related to the environment conditions) will be higher than its neutral value at the resting state, but the core temperature (directly affected by internal heat) will be lower than its neutral value at the resting state. Consequently, the skin blood vasodilation is suppressed, and vasoconstriction is only activated by the cold core temperature control signal. NST heat production can be significant as it is activated by the cold core temperature control signal as mentioned before. Sweating does occur, but it is significantly reduced as it is activated by the warm mean skin temperature control signal. Similarly, the external heat (Q_exC) supplied to, or extracted from, the body may be independent (constant) or linearly proportional to the core temperature to be able to remove a portion of the internal metabolic rate generation. Since the core and mean skin temperatures under the core cooling situation vary within narrow ranges around the neutral values at the resting state, the external heat Q_exC may be considered as constant, and the profile of the mean skin temperature (Equation (17)) may take a linear relationship with the comfort metabolic rate. Equation (14) is then used to determine the comfort metabolic rate.

Differentiating Equation (12) with respect to the mean skin temperature at the comfort state, one obtains the following equation:

$$\left[1-\mathsf{\eta }\left({\mathrm{M}}_{\mathrm{C}}\right)-\mathsf{\gamma }·{\mathrm{Q}}_{\mathrm{r}}\right]\frac{{\mathrm{dM}}_{\mathrm{C}}}{{\mathrm{dT}}_{\mathrm{skC}}}=-\left(1-{\mathrm{Q}}_{\mathrm{r}}\right)·\frac{{\mathrm{dM}}_{\mathrm{nstC}}}{{\mathrm{dT}}_{\mathrm{cC}}}·\frac{{\mathrm{dT}}_{\mathrm{cC}}}{{\mathrm{dT}}_{\mathrm{skC}}}+\frac{{\mathrm{dE}}_{\mathrm{skC}}}{{\mathrm{dT}}_{\mathrm{skC}}}+\frac{{\mathrm{dD}}_{\mathrm{skC}}}{{\mathrm{dT}}_{\mathrm{skC}}}$$

(19)

Adopting the two-node physiological models for young and older people of Ji et al. [37,40], and neglecting the rate of change in the skin evaporative diffusion and dry heat compared to the NST heat and evaporative sweating, Equation (19) reduces to:

$$\left(1-\mathsf{\eta }\left({\mathrm{M}}_{\mathrm{C}}\right)-\mathsf{\gamma }·{\mathrm{Q}}_{\mathrm{r}}\right)\frac{{\mathrm{dM}}_{\mathrm{C}}}{{\mathrm{dT}}_{\mathrm{sk}}}=\left(1-{\mathrm{Q}}_{\mathrm{r}}\right)·\left(50·\mathrm{CSHs}\right)·\frac{{\mathrm{dT}}_{\mathrm{cC}}}{{\mathrm{dT}}_{\mathrm{skC}}}+40.46·\mathsf{\epsilon }·\mathrm{CSWs}$$

(20)

where CSHs is a non-shivering coefficient for sleeping subjects (equal to 0.3875; otherwise to 1 for wakeful subjects), CSWs is a sweating coefficient for sleeping subjects (equal to 0.5875; otherwise to 1 for wakeful subjects); and (ε) is the sweating evaporative efficiency.

Substituting Equations (17) and (20) in Equation (14), one obtains:

$$\left({\mathrm{M}}_{\mathrm{C}}-{\mathrm{M}}_{\mathrm{basal}}\right)\left[1-\frac{{\mathrm{a}}_{\mathrm{s}}}{\left(1-\mathsf{\eta }\left({\mathrm{M}}_{\mathrm{C}}\right)-\mathsf{\gamma }·{\mathrm{Q}}_{\mathrm{r}}\right)}·\left\{\left(1-{\mathrm{Q}}_{\mathrm{r}}\right)·\left(50·\mathrm{CSHs}\right)·\frac{{\mathrm{dT}}_{\mathrm{cC}}}{{\mathrm{dT}}_{\mathrm{skC}}}+40.46·\mathsf{\epsilon }·\mathrm{CSWs}\right\}\right]=\left({\mathrm{M}}_{\mathrm{N}}-{\mathrm{M}}_{\mathrm{basal}}\right)$$

(21)

Given the fact that the actual sweating of subjects may be different from the modelled data, sweating efficiency is close to one (due to low sweating under core cooling) and the derivative dT_cC/dT_skC is around −1.55 (taken from simulation data), Equation (21) may be further reduced to:

$${\mathrm{M}}_{\mathrm{C}}={\mathrm{M}}_{\mathrm{basal}}+\frac{{\mathrm{M}}_{\mathrm{N}}-{\mathrm{M}}_{\mathrm{basal}}}{1-\mathrm{A}·\left(\mathrm{CSHs}-0.58·\mathrm{CSWs}\right)}$$

(22)

where A is an average positive constant to be determined experimentally.

3.4.2. Body Skin Cooling (M_C ≥ M_basal)

Body skin cooling occurs when the internal heat generation can be dissipated to a cooler surrounding environment through evaporative sweating and dry heat loss to achieve a comfort state. Under this situation, the core temperature is higher than its neutral value at the resting state, and the mean skin temperature is lower than its neutral value at the resting state. Consequently, the blood flow from the core to the skin layer is controlled by a combined effect of vasoconstriction and vasodilation. Regulatory sweating is controlled by the core temperature and can be significant, particularly at high activity levels. NST heat is only controlled by the cold mean skin temperature. Contrary to the core temperature, which follows a linear profile with the comfort metabolic rate, the mean skin temperature is highly altered by the environment conditions and can become nonlinear. Equation (15) is therefore retained to determine the comfort metabolic rate. Since the evaporative sweating dominates the body heat transfer to the environment, the rate of change in the skin dry heat loss and NST can be neglected.

Differentiating Equation (12) with respect to the core temperature, one obtains the following equation:

$$\left[1-\mathsf{\eta }\left({\mathrm{M}}_{\mathrm{C}}\right)-{\mathrm{Q}}_{\mathrm{r}}\right]\frac{{\mathrm{dM}}_{\mathrm{C}}}{{\mathrm{dT}}_{\mathrm{cC}}}=\frac{{\mathrm{dE}}_{\mathrm{skC}}}{{\mathrm{dT}}_{\mathrm{cC}}}=115.6·\mathsf{\epsilon }·\left(1-\mathsf{\mu }\right)·\mathrm{CSWs}$$

(23)

where (µ) is the ratio of the core body mass to the total body mass (varies with the skin blood flow).

By substituting Equations (16) and (23) in Equation (15), one obtains:

$$\left({\mathrm{M}}_{\mathrm{C}}-{\mathrm{M}}_{\mathrm{basal}}\right)\left[1-\frac{115.6}{\left(1-\mathsf{\eta }\left({\mathrm{M}}_{\mathrm{C}}\right)-{\mathrm{Q}}_{\mathrm{r}}\right)}·{\mathrm{a}}_{\mathrm{c}}·\mathsf{\epsilon }·\left(1-\mathsf{\mu }\right)·\mathrm{CSWs}\right]=\left({\mathrm{M}}_{\mathrm{N}}-{\mathrm{M}}_{\mathrm{basal}}\right)$$

(24)

Which can be reduced to:

$${\mathrm{M}}_{\mathrm{C}}={\mathrm{M}}_{\mathrm{basal}}+\frac{{\mathrm{M}}_{\mathrm{N}}-{\mathrm{M}}_{\mathrm{basal}}}{1-\mathrm{B}·\mathrm{CSWs}}$$

(25)

With B is an average positive constant to be determined experimentally.

Evaluating the comfort metabolic rate M_C from Equation (22) or (25) will require first to determine the average constants A and B, and then calculating the metabolic rate at the resting neutral conditions (M_N). The latter is deduced from Equation (12) as follows:

$${\mathrm{M}}_{\mathrm{N}}=\frac{{\mathrm{E}}_{\mathrm{skN}}+{\mathrm{D}}_{\mathrm{skN}}-{\mathrm{Q}}_{\mathrm{exN}}}{1-\mathsf{\eta }\left({\mathrm{M}}_{\mathrm{N}}\right)-\mathsf{\gamma }·{\mathrm{Q}}_{\mathrm{r}}}$$

(26)

where E_skN and D_skN are the skin evaporative and dry heat losses at the resting neutral state, respectively, Q_exN is the external heat supplied to the core section at the resting neutral state, and γ is set to one if M_N is positive otherwise set to zero. Equation (26) is solved iteratively if the mechanical efficiency η(M_N) is not zero.

As mentioned before, the regulatory sweating and NST are not active when the body is at the resting neutral state. The corresponding neutral values of the core and mean skin temperatures are, respectively, T_cN = 36.8 °C and T_skN = 33.7 °C for a wakeful average person (Parsons, 2014); and T_cN = 36.4 °C (average over a seven-hour sleep period) and T_skN = 34.6 °C for a sleeping person [41,42]. The skin evaporative and dry heat losses at the neutral conditions are therefore given by:

$${\mathrm{E}}_{\mathrm{skN}}={\mathrm{w}}_{\mathrm{dif}}·{\mathrm{H}}_{\mathrm{eN}}·\left({\mathrm{P}}_{\mathrm{satN}}-{\mathrm{P}}_{\mathrm{v}}\right)$$

(27)

$${\mathrm{D}}_{\mathrm{skN}}={\mathrm{H}}_{\mathrm{dN}}·\left({\mathrm{T}}_{\mathrm{skN}}-{\mathrm{T}}_{\mathrm{op}}\right)$$

(28)

where H_dN is the total dry heat transfer coefficient from the skin surface at the neutral temperature to the environment (inverse of the total thermal resistance; W/m² °C), H_eN is the total coefficient of the evaporative heat transfer from the skin surface at the neutral temperature to the environment (inverse of the total evaporative heat resistance; W/m²·Pa), P_satN is the saturated water vapour pressure at the neutral skin temperature (Pa), T_op is the operative temperature of the surrounding environment, and w_dif is the diffuse skin wettedness in the absence of the regulatory sweating. Gagge et al. [22] assumed w_dif = 0.06, but a more accurate formula is given by Kubota et al. [43] as follows:

$${\mathrm{w}}_{\mathrm{dif}}=\frac{1}{2+328·{\mathrm{H}}_{\mathrm{eN}}}$$

(29)

It should be noted that the direct evaluation of the skin evaporative heat loss (Equation (27)) involves the evaporative heat resistance of clothing (included in the definition of 1/H_eN), which is not accounted for in the PMV model. The evaporative heat resistance of clothing is very important to study special clothing equipment (e.g., personal protective clothing) to control moisture transfer from the skin surface to the environment. The new MPMV is thus a function of seven parameters.

Finally, to be able to evaluate MPMV from Equation (11), the scaling factor (β) needs to be determined; β is similar to α of PMV (Equation (7)), and therefore β is a function of the metabolic rate of activity (M). The value of β can be assumed to vary according to the following power law relationship:

$$\mathsf{\beta }\left(\mathrm{M}\right)=\mathrm{C}·{\mathrm{M}}^{-\mathrm{D}}$$

(30)

where C and D are constants to be determined experimentally.

3.5. MPMV for Older People

Older people (above the age of 65 years) experience age-related physiological changes such as lower metabolic rate up to 30% than young adults [44]), and delayed threshold temperatures to trigger thermoregulatory actions for vasodilation, vasoconstriction, sweating and shivering [45,46,47]. Consequently, older people respond differently to hot or cold exposure, and may require different environmental conditions for their thermal comfort. Experimental studies in controlled climatic chambers found that older people with lower metabolic rates may require warmer conditions [47,48]. However, older people have the same neutral values at a resting position for the core and skin temperatures as young adults [49,50]. Equations (22) and (25) can therefore be applied to older people, but with different values for the constants A, B, C and D, which will need to be determined experimentally.

3.6. MPMV for Sleep

The thermal comfort requirement for sleeping environments is different than for workplaces [51]. Sleeping people have lower (30%) metabolic rates than wakeful people in a sedentary position. Sleep also reduces sweat secretion and skin blood flow under vasodilation and vasoconstriction [41]. Furthermore, sleeping people cover their bodies while sleeping on a mattress, resulting in higher total clothing insulation values. In addition, the neutral values of the core and skin temperatures under a sleep state are different than the wakeful resting state [41]. Due to the lower metabolic rate, sleeping people prefer mild to warm environments compared to wakeful people [51,52]. Equations (22) and (25) account for sleep (through NST and sweating coefficients CSHs and CSWs) and may therefore be applied to people in a sleep state by accounting for the neutral temperatures for sleep. However, the model constants A, B, C and D will need to be determined experimentally for sleeping environments. Due to the limited high quality of experimental studies on sleep comfort compared to comfort of wakeful people, the constants A, B, C and D determined for wakeful people may be used for sleep comfort, but further research is needed (further details on sleep comfort and comparison with measured data may be found in [53]).

3.7. Procedure to Determine the Model Constants

The model constants (A, B, C, and D) are determined based on public measurement data of steady state thermal sensation votes (TSV) reported by un-acclimatized people in controlled climatic chambers with measured environment conditions (T_op, RH, V_air) and subject parameters (M, I_cl). For young adults, the measurement data used for the Fanger’s PMV formulation plus newer data are used in this study (

Table 1. Input data of the selected experiments.

Experiment	No. of Subjects	No. Points	Ta = Tmrt (°C)	RH (%)	Vair (m/s)	Icl (clo)	M (met)
McNall et al. [14]	420	33	12.2–29.4	25–65	0.2, 0.25, 0.32	0.6	1.58, 2.10, 2.63
Nevins et al. [26]	720	72	18.9–27.8	15–85	0.23	0.6	1
Rohles [55]	1600	160	15.6–36.7	15–85	0.23	0.6	1
Rohles et al. [56]	9	33	22.2–29.6	50	0.4	0.6	1
Tsuzuki and Ohfuko [44]	100 Young; 109 Older	5	23, 25, 27, 29, 31	60	0.20	0.63	1 (Young); 0.7 (Older)
Fanger [4]	128	8	21, 23, 26, 28	30, 50	0.1	0.6	0.95 (Older)
Stapleton et al. [54]	12	1	36.5	20	0.25	0.1	0.95 (Older)

). However, for older people, there are very limited high-quality data (large number of subjects and long exposure times higher than two hours) on TSV in controlled climatic chambers. In this study only the data of [4,44,54] fulfilled these screening criteria. Therefore, the derived constants (A and B) for older people will need further improvement upon the availability of newer data sets covering larger ranges of environment and subject parameter values. Table 1 lists the ranges of the input data of the selected experiments. All the input data were measured during the experiments.

The aforementioned measurement data of TSV are fitted with the predictions of Equation (11) using Equations (22), (25) and (30), and an optimisation procedure is used to select the best fit by maximizing the regression coefficient of determination (R²). To this end, the optimisation algorithm of Simulated Annealing [57] is selected for the study. The function to be maximized is given below:

$${\mathrm{R}}^2=1-\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\left({\mathrm{TSV}}_{\mathrm{i}}-{\mathrm{MPMV}}_{\mathrm{i}}\right)}^2}{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\left({\mathrm{TSV}}_{\mathrm{i}}-\mathrm{MTSV}\right)}^2}$$

(31)

where MTSV is the mean of the measured TSV points of all experiments, i the index of a measurement point, and N is the total number of measurement points of all experiments.

4. Results

The results for the model constants, comparison between MPMV and PMV, and comfort requirement of older people are presented below.

4.1. Model Constants

Table 2. Optimised values of the MPMV model constants.

Constant	A	B	C	D
Young adults	0.62	0.35	0.3	0.53
Older adults	0.64	0.41	0.3	0.53

lists the optimized values of the constants (A, B, C and D) of the new MPMV model for young and older people. Since the scaling factor (β) is a function of the metabolic rate of activity, and no experimental data are available for older people at high activity levels (M > 1 met), the constants C and D for older people are assumed equal to the young adults.

Figure 1 compares the values of the new MPMV and Fanger’s PMV (denoted by PMVF) indices with the measured TSV of the selected experiments (Table 1). The results of the new MPMV index fit very well with the measured TSV data, with a correlation coefficient R² of 0.97 and a slope of 0.99 (or 1% error). Similarly, Fanger’s PMVF index fits linearly very well with the measured TSV data, but with a higher slope resulting in an overestimation of 36% (or error within ±0.33 units).

Figure 2 compares the MPMV and PMVF with the measured TSV for older people. The MPMV predictions are well aligned with the measured TSV data (R² = 0.97 and slope = 0.94). The predictions of the PMVF are, however, not well aligned with the measured data (R² = 0.85), resulting in an overestimation of TSV, particularly for older people having significantly lower metabolic rate (data of [44]).

4.2. MPMV vs. PMV

Figure 3 shows the relationship between MPMV and Fanger’s PMV as obtained by simulation. The simulation data cover the following parameter ranges: 14 °C ≤ T_op ≤ 37 °C; 20% ≤ RH ≤ 70%; 0.1 m/s ≤ V_air ≤ 0.5 m/s; 0.2 ≤ CLO ≤ 3 clo; 0.8 met ≤ M ≤ 3 met. TSV vs. PMV data from published studies (which were not part of Figure 1) are also included in the comparison. PMV is calculated according to the algorithm of ISO 7730, whereas MPMV is calculated using the formulation of the heat transfer coefficients (H_dN and H_eN, used in Equations (27) and (28)) of the SET computer code of ASHRAE 55-2020 [1]. MPMV varies in a linear fashion with PMV, except at PMV > 2 met where its increase becomes slower than PMV. On average (blue is the best curve-fit line), PMV overestimates TSV compared to MPMV, particularly when body core cooling is required to achieve thermal comfort in warm or hot environments (PMV > 1.5), and when skin cooling is needed under high activity levels in cold environments (PMV < 0). This is consistent with the experimental observations in climatic chambers [20,58,59,60] and air-conditioned office buildings [12]. This overestimation of thermal comfort is more likely due to the underestimation of the evaporative heat loss, and overestimation of the mean skin temperature at the comfort state, beside not accounting for the induced NST metabolic rate under cold exposure conditions in the PMV model. The skin evaporative heat loss depends not on the comfort metabolic rate, but also on the environment conditions and clothing insulation and vapor permeance characteristics [17]. Indeed, PMV assumes no regulatory sweating under hot exposure conditions requiring core cooling (Equation (5) cannot be evaluated when M_C < 1 met). Under skin cooling situations, the regulatory sweating becomes significant with activity levels, and it is influenced by the environment relative humidity among other factors. Furthermore, overestimation of the mean skin temperature will result in the over-estimation of the skin dry heat loss.

4.3. Comfort Requirement of Older People

Figure 4 shows the relationship between the comfort requirements of older people versus young adults as predicted by MPMV. The calculations are done for typical indoor conditions covering the following ranges: 18 °C ≤ T_op ≤ 40 °C; 30% ≤ RH ≤ 70%; 0.1 m/s ≤ V_air ≤ 0.5 m/s; 0.5 ≤ CLO ≤ 1 clo; 1 met ≤ M (of young adults) ≤ 1.5 met. Two metabolic reduction factors are used for older people: no reduction (MF = 1), and 20% reduction (MF = 0.8). Experimental data on TSV from published studies are also shown in the figure for comparison. Older people with lower metabolic rates perceive the indoor conditions as slightly cool (−0.6 TSV units) compared to young adults, and therefore warmer temperatures are required to be in thermal comfort. This is consistent with the results of [44,48] with MF = 0.7. To achieve such comfort requirement in real spaces, older people will need to raise the heating or cooling setpoint temperatures (by up to 2 °C), or otherwise wear additional clothing garments to achieve the same comfort level as young adults in mixed occupancy spaces. However, for older people experiencing non-significant age-related metabolic rate reduction (MF ≈ 1), their comfort requirement is not different from young adults (as noted by Fanger [4]). These results may explain the conflicting findings reported in public literature that older people require no change, cooler comfort temperatures, or warmer comfort temperatures [47]. Most studies that reported older people needing cooler comfort temperatures than young adults were conducted in field studies (e.g., [61,62]), indicating the effects of behavioral adaptation of older people in real spaces.

5. Discussion

The new general formulation of the MPMV index (Equation (12)) represents a significant departure from the Fanger’s PMV formulation, in that it does not involve the mean skin temperature and evaporative heat loss at the comfort state. The pivot in this new formulation is the linear relationship between the comfort metabolic (or internal) heat (M_C) with the metabolic (or internal) heat at the resting neutral conditions (M_N, Equation (26)). M_N is directly calculated from the body heat balance and is a function of seven parameters related to the environment and subjects (air temperature, relative humidity, air velocity, mean radian temperature, clothing thermal resistance, and clothing evaporative resistance). Parameters that account for the thermoregulatory system (vasomotor, sweating, and non-shivering thermogenesis) of people are reflected in the experimental model constants A, B, C and D. The new formulation thus represents the foundation to develop other variant formulations of PMV to address other types of people (e.g., children) and environments (e.g., outdoor, vehicle cabins, etc.), personal comfort to account for individual differences, and adaptive thermal comfort in various types of climates and built environments.

The inclusion of the overlooked non-shivering thermogenesis (NST) heat production in the body heat balance at the comfort state (Equation (10)), and as a fourth condition for whole body thermal comfort, represents something new. NST is activated by the autonomic system when the body skin and/or core temperature are lower than their neutral values [38]. Given the fact that the thermal comfort state is achieved at either colder skin or core temperature, NST is therefore present in the body heat balance. In the past, NST in adult humans was believed not to exist or to contribute little to the body energy balance [65,66,67,68]. In recent years, however, NST is well recognized in human thermoregulation and has been extensively studied in cold acclimatization and metabolic studies to induce weight loss in obese or overweight individuals [29,68,69,70,71]. NST thermoregulation occurs before the muscular shivering (which is associated with discomfort), and its intensity is highly variable among individuals and can reach up to 30% of the resting metabolic rate in young adults [72]. The core-to-skin temperature contribution to NST is about 3.6:1 [69]; therefore, NST is more significant in body core cooling situations. For example, using the shivering model of [38], an independent drop of 0.1 °C in the core temperature from its neutral value at the resting state results in heat production of 4.1 W/m², whereas the same drop in the mean skin temperature results in 1 W/m². Kingma et al. [25] included NST in the body heat balance for the thermo-neutral zone. Likewise, DeGroot and Kenney [49] noticed the presence of NST in the thermo-neutral conditions in their mild cold experiments. In cold acclimatization studies, NST is used to shift cold sensation before acclimatization to comfortable sensation after acclimatization [71]. Warwick and Busby [73] found that when subjects were free to choose their own clothing to maintain thermal comfort in environments of 28 °C and 20 °C for a 24 h exposure, the average energy expenditure was increased by 5% at 20 °C compared to 28 °C. Celi et al. [74] found similar results, an increase of 6% in NST for subjects dressed in hospital uniforms exposed to 19 °C as compared to 24 °C. These findings show that NST is significant and should be part of the energy balance of a human body at the comfort state. In this paper, the indirect effect of NST on MPMV is reflected in the model constants (A and B). However, the direct effect of NST is present in the heat balance to determine the core and mean skin temperatures and evaporate heat loss sat the comfort state using Equation (12). For the PMV formulation, NST should be included in Equation (1).

Similar to PMV, the new formulation of MPMV is developed for indoor thermal comfort in buildings where behavioral (excluding thermal) adaptation is well known (in terms of activity level of people, clothing insulation, space ventilation). However, the new MPMV index has the following advantages not covered in Fanger’s PMV:

• MPMV Equation (12) can handle the two types of body cooling methods to achieve a state of comfort: (1) Skin cooling method where the skin evaporative sweating is the dominant factor to achieve a comfort state. Practically, this case corresponds to working or exercising in cool or cold environments; (2) Deep core cooling method where a comfort state cannot be achieved unless the internal metabolic rate is reduced, or an external cooling source is introduced in the body. Practical cases of internal heat removal include infusion of intravenous cold fluids, inhaling cold gases (e.g., Heliox), or ingesting cold modalities in situations of exercising in the heat, or long exposure under extreme heat events.
• Equation (12) can be evaluated by simply calculating the metabolic rate M_C to maintain a comfort state under the imposed environment conditions for any physiological state (wake or sleep) of young or older people who are not acclimatized to heat;
• The comfort metabolic rate, Equations (22) and (25), has no limitations on the environmental and subject parameters (operative temperature, air velocity, relative humidity, metabolic rate of activity, clothing insulation level, posture) to evaluate the comfort level, as long as the steady state conditions under the imposed environmental conditions can be reached (under non steady state conditions, MPMV Equation (11) can still be evaluated, but the results will have no physical meaning with very high MPMV values).

Beside the better accuracy for the evaluation of thermal comfort using the MPMV index, the comfort metabolic rate (M_C) and its relationship with the mean skin and core temperatures have many practical applications. First, M_C Equations (22) and (25) may be used to compute the corresponding core and mean skin temperatures (using Equation (12)) and set limits on people activities to avoid any heat-related health injury such as limiting the core temperature to avoid hyperthermia (Tc > 38 °C) or hypothermia (Tc < 36 °C). More details on this topic will be presented in another related paper. Second, M_C equations may be used directly to designate suitable activity levels of people in sport centers, which are maintained at given environmental conditions, or to evaluate strategies for deep body cooling (such as inhalation of cold air or Heliox gas, or drinking ice slurries; [75,76]) to maintain a comfort state of people engaged in high activity levels for a limited exposure time under warm or hot environmental conditions. Third, the equation of the comfort metabolic rate can be used as a reverse engineering method to estimate the metabolic rate of people in real spaces after knowing their thermal sensation votes in these spaces (i.e., using field surveys). The metabolic rate is an important input for thermal comfort and heat stress models of people in workplaces [77]. Fourth, the reverse engineering method may be used to calculate the clothing insulation required (IREQ) for the neutral comfort conditions (MPMV = 0) and minimum conditions (MPMV = −1) for people working in cold environments to prevent cooling of the body core and avoid any cold-related health injury such as hypothermia [19]. The MPMV method to calculate IREQ is different than the ISO 11,079 method in that it does require any empirical formulation for the mean skin temperature and evaporation heat loss. IREQ is obtained by using Equation (11) to get M_C (with MPMV and M as inputs), then Equation (25) to get M_N, which is related to the clothing thermal resistance through Equations (26) to (28). Equations (25) and (26) are then solved iteratively to get the clothing thermal resistance and IREQ. Figure 5 compares preliminary results of IREQ_neutral as obtained using the MPMV model, Fanger’s PMV and ISO/TR 11,079 (data taken from [17]). MPMV predictions of IREQ_neutral are close to ISO/TR 11,079 [78], particularly at higher activity levels than sedentary. It should be noted that further validation work is needed to apply the MPMV method to the IREQ calculation using the heat transfer algorithms of the current ISO 11079:2007 standard suitable for cold environments, and the correction factors for clothing thermal insulation values to account for the effects of wind speed and body movement.

Limitations

The following model limitations are noted:

• MPMV is developed based on TSV data in controlled climatic chambers, and therefore it should be used to evaluate thermal comfort in built environments where occupants are not adapted to heat or cold;
• MPMV should be used with caution in sub-zero environments (air temperature < 0 °C), as this case may require a different value of the model constant (B) to account for the cold-induced vasodilation when the local skin temperatures are lower than 15 °C [19];
• MPMV for older people was developed based on very limited data of TSV in climate chambers, and therefore it should be used with caution. The model constants A and B will have to be improved upon the availability of newer and larger TSV data for older people;
• MPMV for sleep comfort will need further testing and evaluation and possibly fine-tuning of model constants.

6. Conclusions

This paper presented an alternative general formulation of the predicted mean vote (PMV) index that does not involve the mean skin temperature and evaporative heat loss at the comfort state. The new metabolic-based predicted mean vote index (MPMV) is expressed as the difference between the metabolic rate of person activity, and the metabolic rate (or net internal heat) required to achieve a comfort state under the imposed environment conditions. It was demonstrated that the comfort metabolic rate follows a linear relationship with the metabolic rate required to maintain the body at the resting neutral core and mean skin temperatures under the imposed environment conditions. The model constants were determined using public experimental data on thermal sensation votes of young and older people obtained from studies in controlled climatic chambers. MPMV accounts for two methods of body core and skin cooling to achieve thermal comfort under steady state conditions and extends the (original) Fanger’s PMV formulation to cover thermal comfort of young and older (above 65 years old) adults in wakeful and sleep states, and larger input ranges of seven parameters (air temperature, relative humidity, air velocity, mean radiant temperature, clothing insulation resistance, clothing evaporative resistance, metabolic rate of activity). The new formulation represents the foundation to develop other variant formulations of PMV to address special types of people and environments, personal comfort to account for individual differences, and adaptive thermal comfort in various types of climates and built environments.

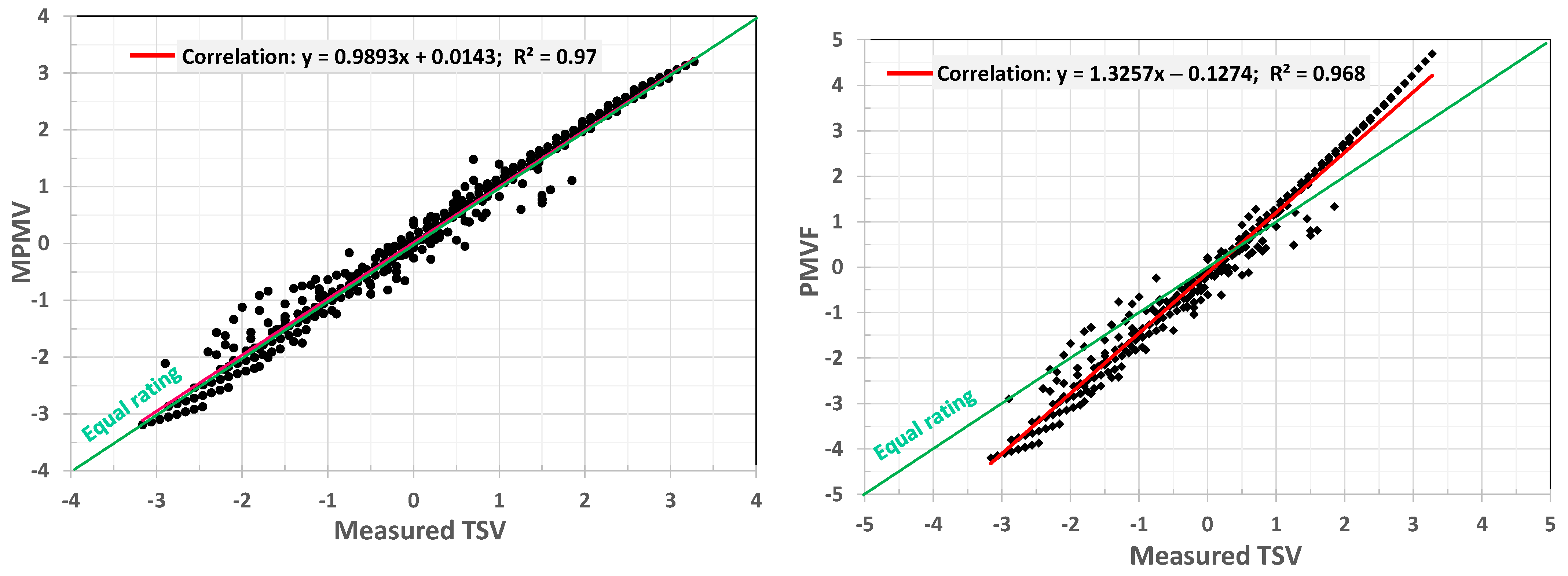
Comparison of the new model with Fanger’s PMV showed that PMV overestimates TSV at both the warm and cold sides, more likely due to the underestimation of the evaporative heat loss, overestimation of the mean skin temperature and ignoring the NST heat production at the comfort state. This observation is consistent with findings from public experimental studies [8,12].

Application of the new model to older people revealed that older people experiencing significant age-related reduction in metabolic rate require up to 2 °C warmer temperatures (or +0.5 TSV units) than young adults. However, older people with insignificant age-related reduction in their metabolic rate perceive thermal comfort similar to young adults. These results clarify the conflicting findings in public literature on older people requiring warmer or cooler temperatures, often reported in climatic chambers and field studies, respectively [47].

Future Work

The immediate envisioned work should include:

• Establish relationships between the comfort metabolic rate and the core and mean skin temperatures and evaporative heat loss at the comfort state by evaluating Equation (12) for typical indoor conditions. This is very important as such relationships may be used to set limits of activity levels to avoid any heat or cold-related health injury of people working or exercising in warm or cold environments;
• Test and validate the model predictions for various cases of thermal comfort requirement for active people under low, medium or high activity levels, and for sleeping environments;
• Explore the applicability and possibly fine-tuning of the model to thermal comfort of people acclimatized to warm temperatures;
• Explore the applicability of the model to thermal comfort in transitioning environments by properly accounting for the heat stored in the body core section (Q_exC of Equation (12));
• Revisit the old models derived from the concept of equivalent temperature and standard person, particularly the standard effective temperature (SET) [22]. PMV and SET are both adopted in ASHRAE-55 [1]. It is well known that the neutral value of SET corresponding to PMV = TSV = 0 (fixed at 24 °C) is not constant and varies with the environment conditions and person parameters [79]. This is more likely due to the definition of the standard conditions and standard person, which will need to be revisited. The developed model of MPMV can be used for this purpose.