Identifying Potential Indicators of Neighbourhood Solar Access in Urban Planning
Abstract
:1. Introduction
2. Methods
2.1. Neighbourhood Design Iterations
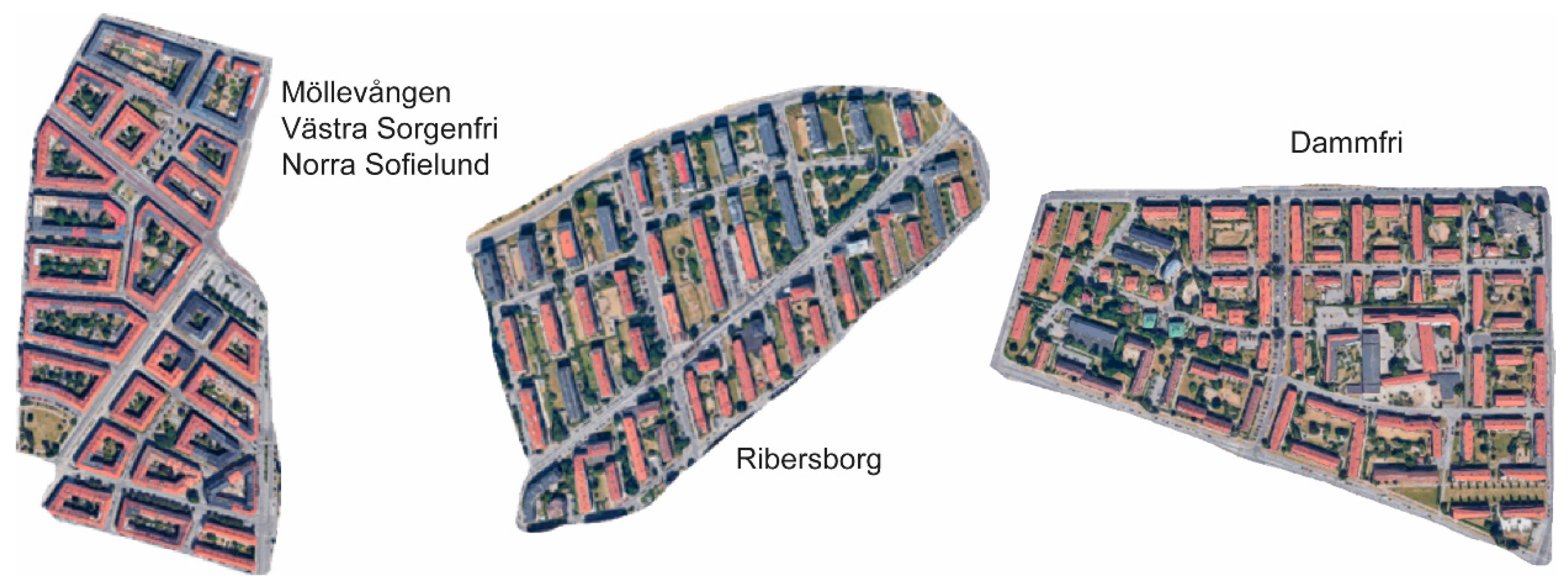
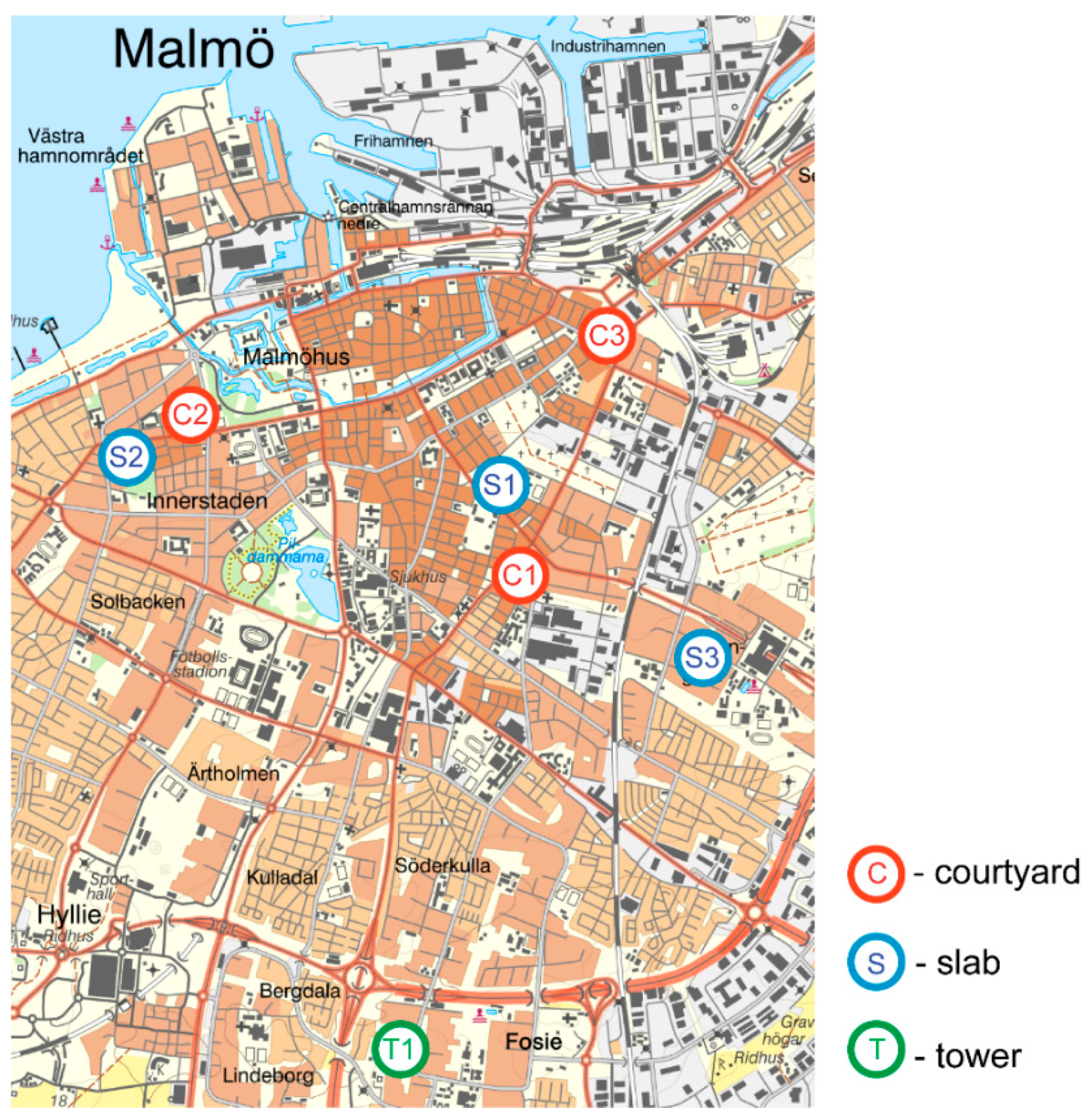
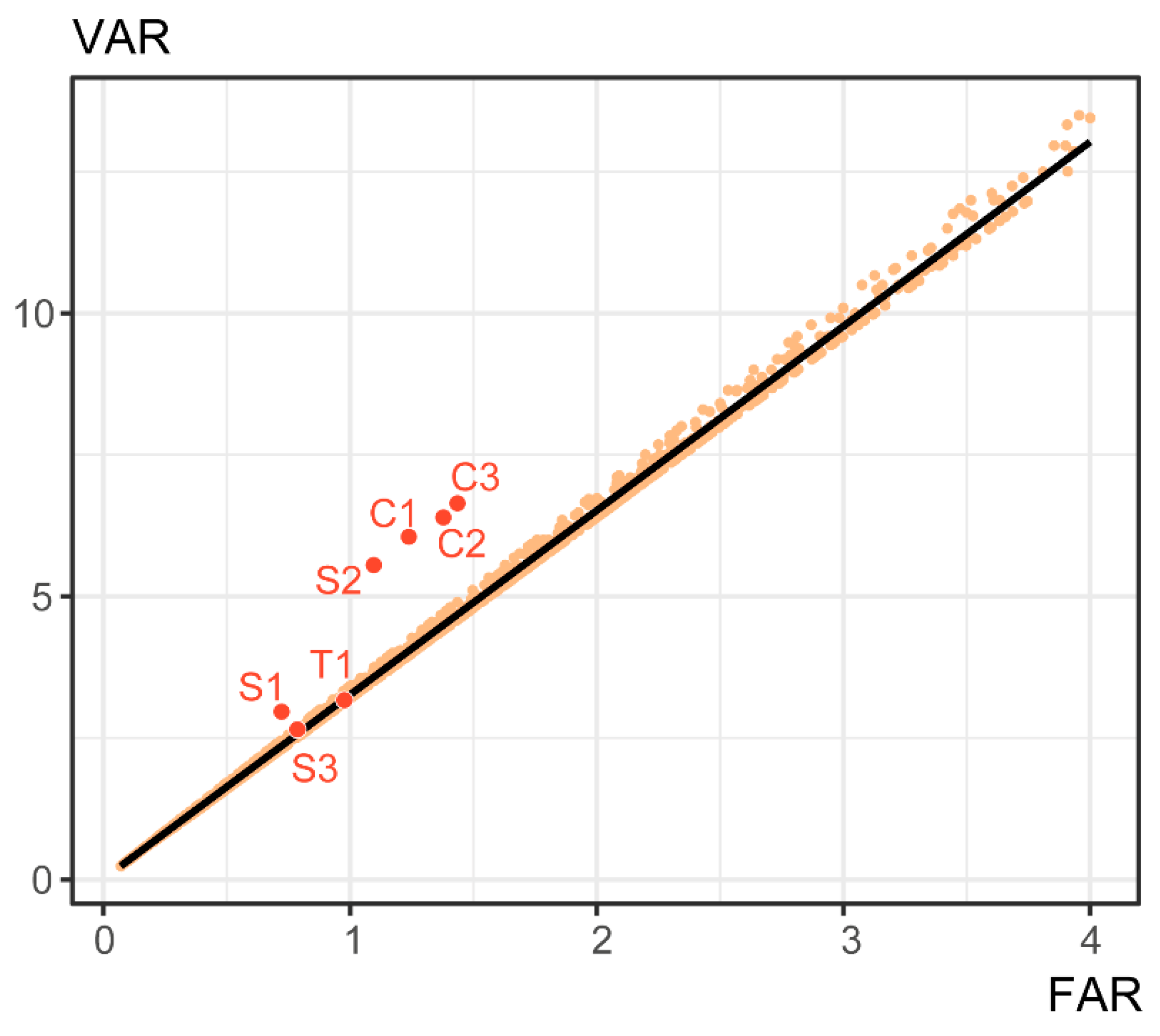
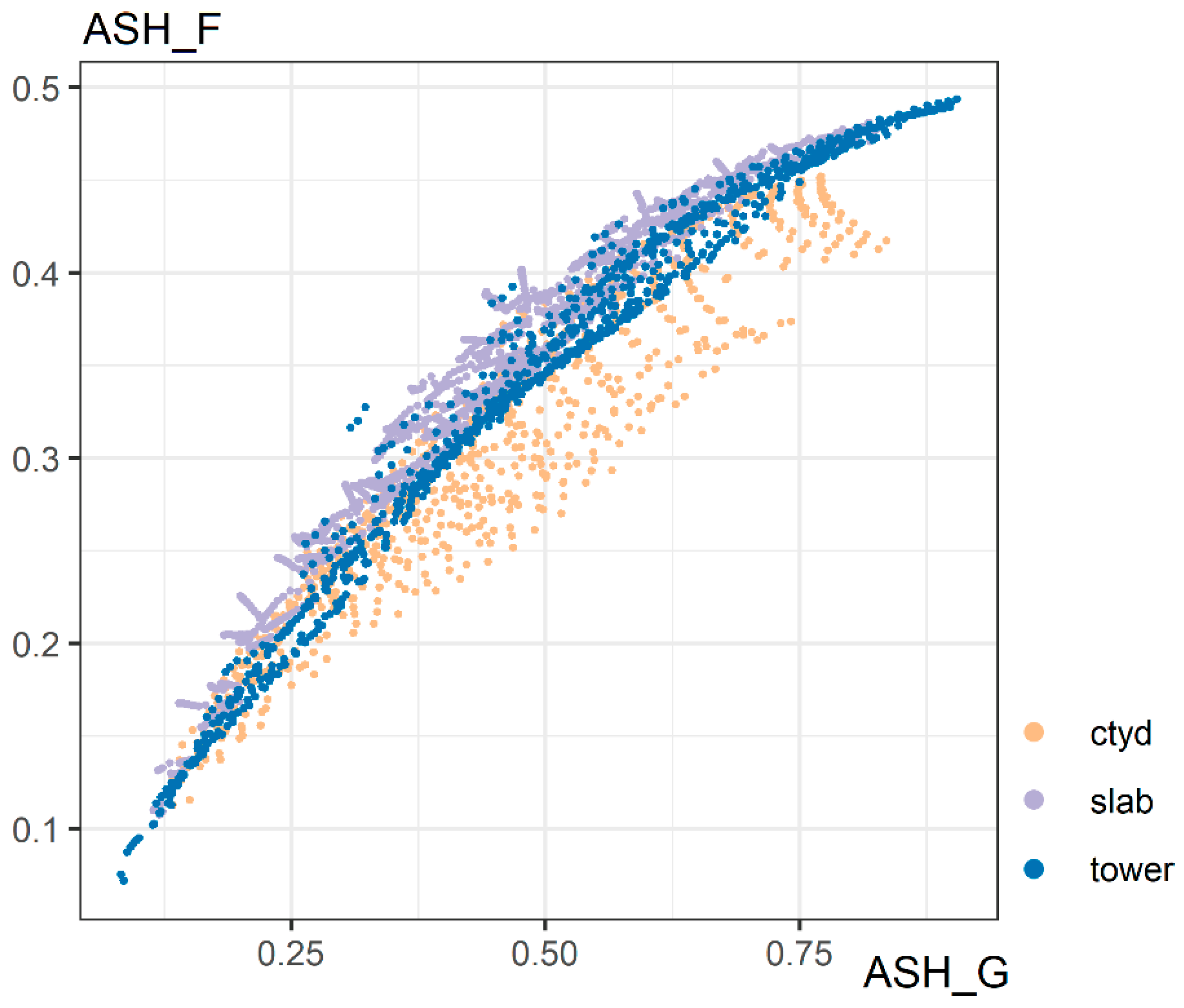
2.2. Case Studies
- The neighbourhood shall not be intersected by large traffic roads,
- The neighbourhood must be comprised of residential multi-storey buildings and include one of the three analysed typologies (courtyard, slab, tower),
- The neighbourhood shall be nearly homogenous (composed of the same typology),
- The neighbourhood shall be surrounded by built context of similar height,
- The case studies shall come from different administrative districts (sv: delområde).
2.3. Solar Performance Metrics
2.4. Data Analysis
3. Results
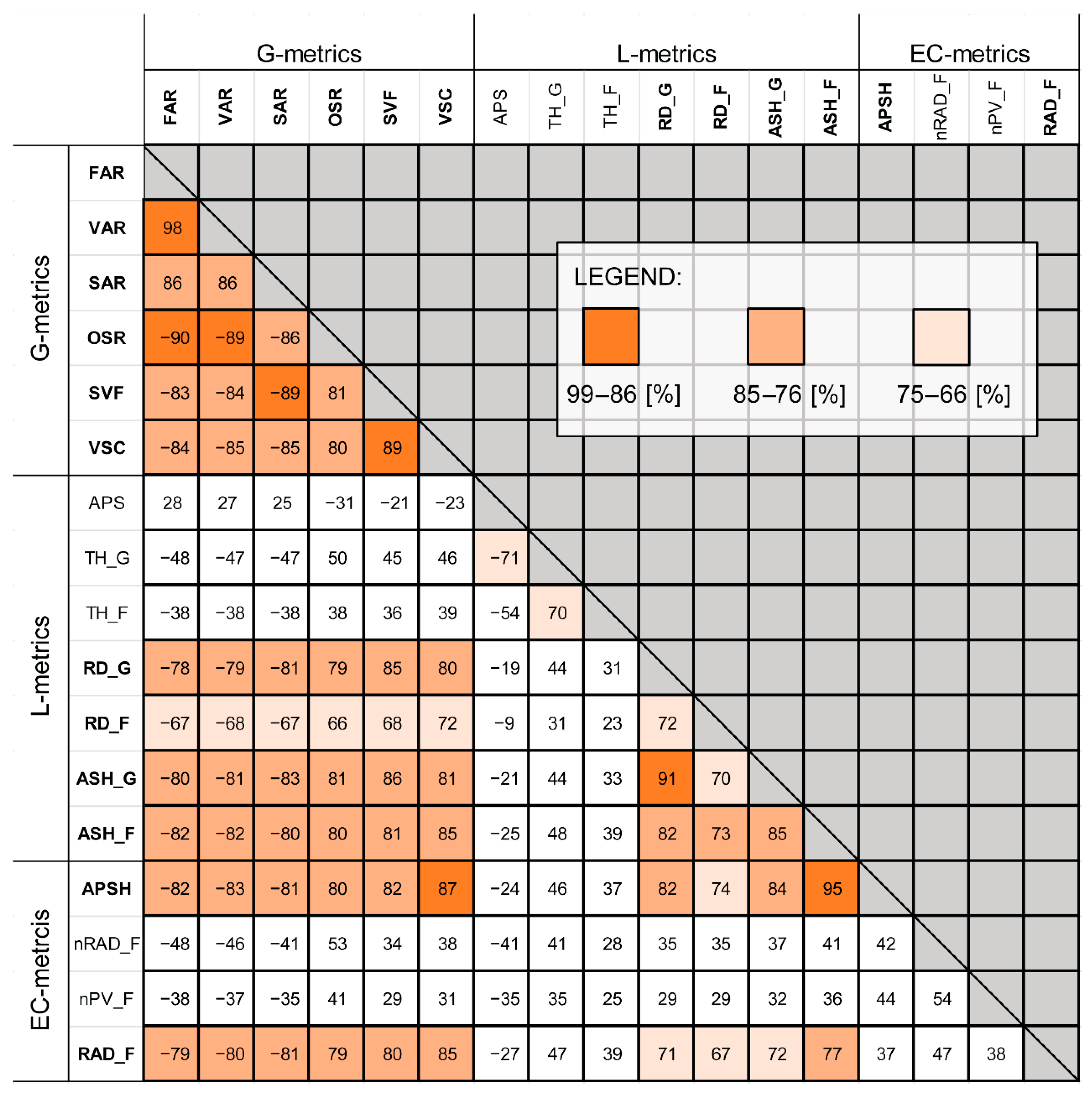
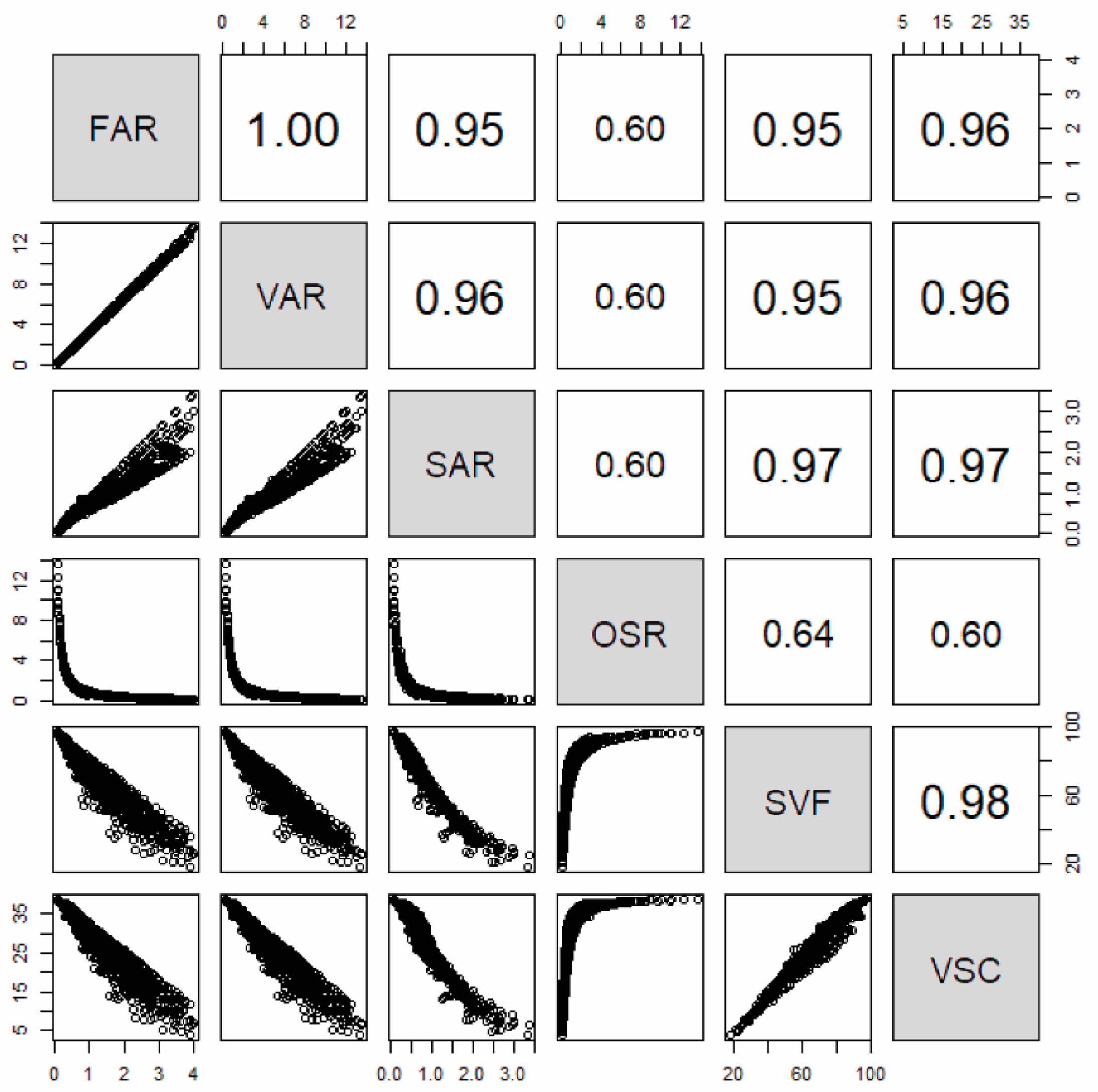
3.1. Metric Correlation
3.2. Urban Density
3.3. G-Metrics
3.4. L-Metrics
3.5. EC-Metrics
4. Discussion
4.1. Solar Access Indoors
4.1.1. Daylight
4.1.2. Sunlight
4.2. Solar Access Outdoors
4.3. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Littlefair, P. Passive Solar Urban Design: Ensuring the Penetration of Solar Energy into the City. Renew. Sustain. Energy Rev. 1998, 2, 303–326. [Google Scholar] [CrossRef]
- Beckers, B. Solar Energy at Urban Scale; John Wiley and Sons: Hoboken, NJ, USA, 2013; ISBN 9781848213562. [Google Scholar]
- Knowles, R.L. The Solar Envelope: Its Meaning for Energy and Buildings. Energy Build. 2003, 35, 15–25. [Google Scholar] [CrossRef]
- IEA SHC. Task 51 Solar Energy in Urban Planning. In Approaches, Methods and Tools for Solar Energy in Urban Planning; IEA SHC: Cedar, MI, USA, 2018. [Google Scholar]
- Peronato, G.; Rastogi, P.; Rey, E.; Andersen, M. A Toolkit for Multi-Scale Mapping of the Solar Energy-Generation Potential of Buildings in Urban Environments under Uncertainty. Sol. Energy 2018, 173, 861–874. [Google Scholar] [CrossRef]
- Sarralde, J.J.; Quinn, D.J.; Wiesmann, D.; Steemers, K. Solar Energy and Urban Morphology: Scenarios for Increasing the Renewable Energy Potential of Neighbourhoods in London. Renew. Energy 2015, 73, 10–17. [Google Scholar] [CrossRef]
- Bilu, C.; Einat, H.; Zimmet, P.; Vishnevskia-Dai, V.; Kronfeld-Schor, N. Beneficial Effects of Daytime High-Intensity Light Exposure on Daily Rhythms, Metabolic State and Affect. Sci. Rep. 2020, 10, 19782. [Google Scholar] [CrossRef] [PubMed]
- Knoop, M.; Stefani, O.; Bueno, B.; Matusiak, B.; Hobday, R.; Wirz-Justice, A.; Martiny, K.; Kantermann, T.; Aarts, M.P.J.; Zemmouri, N.; et al. Daylight: What Makes the Difference? Light. Res. Technol. 2020, 52, 423–442. [Google Scholar] [CrossRef]
- Holick, M.F. Sunlight and Vitamin D for Bone Health and Prevention of Autoimmune Diseases, Cancers, and Cardiovascular Disease. Am. J. Clin. Nutr. 2004, 80, 1678S–1688S. [Google Scholar] [CrossRef] [PubMed]
- Fahimipour, A.K.; Hartmann, E.M.; Siemens, A.; Kline, J.; Levin, D.A.; Wilson, H.; Betancourt-Román, C.M.; Brown, G.; Fretz, M.; Northcutt, D.; et al. Daylight Exposure Modulates Bacterial Communities Associated with Household Dust. Microbiome 2018, 6, 175. [Google Scholar] [CrossRef]
- United Nations-Department of Economic and Social Affairs-Population Division. World Urbanization Prospects. The 2018 Revision; United Nations: New York, NY, USA, 2019. [Google Scholar]
- Angel, S.; Lamson-Hall, P.; Blei, A.; Shingade, S.; Kumar, S. Densify and Expand: A Global Analysis of Recent Urban Growth. Sustainability 2021, 13, 3835. [Google Scholar] [CrossRef]
- Bournas, I.; Dubois, M.-C. Daylight Regulation Compliance of Existing Multi-Family Apartment Blocks in Sweden. Build. Environ. 2019, 150, 254–265. [Google Scholar] [CrossRef]
- Kanters, J.; Wall, M. Experiences from the Urban Planning Process of a Solar Neighbourhood in Malmö, Sweden. Urban Plan. Transp. Res. 2018, 6, 54–80. [Google Scholar] [CrossRef]
- Lobaccaro, G.; Croce, S.; Lindkvist, C.; Munari Probst, M.C.; Scognamiglio, A.; Dahlberg, J.; Lundgren, M.; Wall, M. A Cross-Country Perspective on Solar Energy in Urban Planning: Lessons Learned from International Case Studies. Renew. Sustain. Energy Rev. 2019, 108, 209–237. [Google Scholar] [CrossRef]
- Kanters, J.; Gentile, N.; Bernardo, R. Planning for Solar Access in Sweden: Routines, Metrics, and Tools. Urban Plan. Transp. Res. 2021, 9, 348–368. [Google Scholar] [CrossRef]
- Nault, E.; Peronato, G.; Rey, E.; Andersen, M. Review and Critical Analysis of Early-Design Phase Evaluation Metrics for the Solar Potential of Neighborhood Designs. Build. Environ. 2015, 92, 679–691. [Google Scholar] [CrossRef]
- Czachura, A.; Kanters, J.; Gentile, N.; Wall, M. Solar Performance Metrics in Urban Planning: A Review and Taxonomy. Buildings 2022, 12, 393. [Google Scholar] [CrossRef]
- Morganti, M.; Salvati, A.; Coch, H.; Cecere, C. Urban Morphology Indicators for Solar Energy Analysis. Energy Procedia 2017, 134, 807–814. [Google Scholar] [CrossRef]
- Shi, Z.; Fonseca, J.A.; Schlueter, A. A Parametric Method Using Vernacular Urban Block Typologies for Investigating Interactions between Solar Energy Use and Urban Design. Renew. Energy 2021, 165, 823–841. [Google Scholar] [CrossRef]
- Zhang, J.; Heng, C.K.; Malone-Lee, L.C.; Hii, D.J.C.; Janssen, P.; Leung, K.S.; Tan, B.K. Evaluating Environmental Implications of Density: A Comparative Case Study on the Relationship between Density, Urban Block Typology and Sky Exposure. Autom. Constr. 2012, 22, 90–101. [Google Scholar] [CrossRef]
- Chen, K.W.; Norford, L. Evaluating Urban Forms for Comparison Studies in the Massing Design Stage. Sustainability 2017, 9, 987. [Google Scholar] [CrossRef]
- Statistics Sweden (SCB) Nearly 5.1 Million Dwellings in Sweden. Available online: https://www.scb.se/en/finding-statistics/statistics-by-subject-area/housing-construction-and-building/housing-construction-and-conversion/dwelling-stock/pong/statistical-news/dwelling-stock-december-31-2021/ (accessed on 10 May 2022).
- Rådberg, J.; Friberg, A. Svenska Stadstyper: Historik, Exempel, Klassificering; Kungliga tekniska högskolan, Institutionen för arkitektur och stadsbyggnad: Stockholm, Sweden, 1996; ISBN 9171706992. [Google Scholar]
- Nouvel, R.; Schulte, C.; Eicker, U.; Pietruschka, D.; Coors, V. CityGML-Based 3D City Model for Energy Diagnostics and Urban Energy Policy Support. In Proceedings of the BS2013: 13th Conference of International Building Performance Simulation Association, Chambéry, France, 26–28 August 2013; pp. 218–225. [Google Scholar]
- McNeel, R. Associates Rhinoceros 3D, Version 7. Available online: https://www.rhino3d.com/ (accessed on 6 December 2021).
- McNeel, R. Associates Grasshopper—Algorithmic Modeling for Rhino. 2022. Available online: https://www.grasshopper3d.com/?overrideMobileRedirect=1 (accessed on 6 December 2021).
- American Society of Planning Officials. Information Report No. 111: Floor Area Ratio; American Society of Planning Officials: Chicago, IL, USA, 1958. [Google Scholar]
- Krehl, A.; Siedentop, S.; Taubenböck, H.; Wurm, M.; Behnisch, M.; Meinel, G.; Kainz, W. A Comprehensive View on Urban Spatial Structure: Urban Density Patterns of German City Regions. ISPRS Int. J. Geo-Inf. 2016, 5, 76. [Google Scholar] [CrossRef] [Green Version]
- Moon, B. The Effect of FAR (Floor Area Ratio) Regulations on Land Values: The Case of New York. Pap. Reg. Sci. 2019, 98, 2343–2354. [Google Scholar] [CrossRef]
- Perry, C. The Neighborhood Unit: A Scheme of Arrangement for the Family-Life Community. In The Regional Plan of New York and Its Environs; Russell Sage Foundation: New York, NY, USA, 1929; Volume VII, ISBN 9781136205668. [Google Scholar]
- Mumford, L. The Neighborhood and the Neighborhood Unit. Town Plan. Rev. 1954, 24, 256–270. [Google Scholar] [CrossRef]
- Mehaffy, M.W.; Porta, S.; Romice, O. The “Neighborhood Unit” on Trial: A Case Study in the Impacts of Urban Morphology. J. Urban 2015, 8, 199–217. [Google Scholar] [CrossRef]
- Byun, N.; Choi, Y.; Choi, J. Neighborhood Unit: Effective or Obsolete? J. Asian Archit. Build. Eng. 2014, 13, 617–624. [Google Scholar] [CrossRef]
- Olson, P. Urban Neighborhood Research: Its Development and Current Focus. Urban Aff. Rev. 1982, 17, 491–518. [Google Scholar] [CrossRef]
- Gallion, A.B.; Eisner, S. The Urban Pattern: City Planning and Design, 5th ed.; Van Nostrand Reinhold: New York, NY, USA, 1985; ISBN 0442227310. [Google Scholar]
- Dahlberg, G.-B.; Ödmann, E. Stadsutveckling Och Planering i Sverige; Läromedelsförl. i samverkan med Byggforskningen; T/Statens råd för byggnadsforskning: Stockholm, Sweden, 1969. [Google Scholar]
- Lantmäteriet Geodataportalen. Available online: https://www.lantmateriet.se/sv/geodata/Geodataportalen/ (accessed on 30 August 2022).
- Ladybug Tools Ladybug Tools|Home Page. Available online: https://www.ladybug.tools/ (accessed on 11 October 2021).
- European Environment Agency (EEA). Main Climates of Europe. Available online: https://www.eea.europa.eu/data-and-maps/figures/climate (accessed on 30 August 2022).
- ASHRAE. International Weather for Energy Calculations (IWEC Weather Files) Users Manual and CD-ROM; ASHRAE: Atlanta, GA, USA, 2001. [Google Scholar]
- RStudio Team. RStudio: Integrated Development Environment for R; RStudio, PBC: Boston, MA, USA, 2021. [Google Scholar]
- Joshi, K.K.; Kono, T. Optimization of Floor Area Ratio Regulation in a Growing City. Reg. Sci. Urban Econ. 2009, 39, 502–511. [Google Scholar] [CrossRef]
- Kono, T.; Kusum Joshi, K. A New Interpretation on the Optimal Density Regulations: Closed and Open City. J. Hous. Econ. 2012, 21, 223–234. [Google Scholar] [CrossRef]
- SSI. CEN SS-EN 17037:2018+A1:2021; Daylight in Buildings. Swedish Standards Institute: Stockholm, Sweden, 2021.
- Lobaccaro, G.; Lisowska, M.M.; Saretta, E.; Bonomo, P.; Frontini, F. A Methodological Analysis Approach to Assess Solar Energy Potential at the Neighborhood Scale. Energies 2019, 12, 3554. [Google Scholar] [CrossRef]
- Littlefair, P.J.; King, S.; Howlett, G.; Ticleanu, C.; Longfield, A. Site Layout Planning for Daylight and Sunlight (BR 209), 3rd ed.; S&P Global: New York, NY, USA, 2022; ISBN 978-1-84806-483-6. [Google Scholar]
- Boverket. Boverkets Byggregler (BFS 2019:2)—Föreskrifter Och Allmänna Råd; Boverket: Karlskrona, Sweden, 2011. [Google Scholar]
- Oke, T.R. Canyon Geometry and the Nocturnal Urban Heat Island: Comparison of Scale Model and Field Observations. J. Climatol. 1981, 1, 237–254. [Google Scholar] [CrossRef]
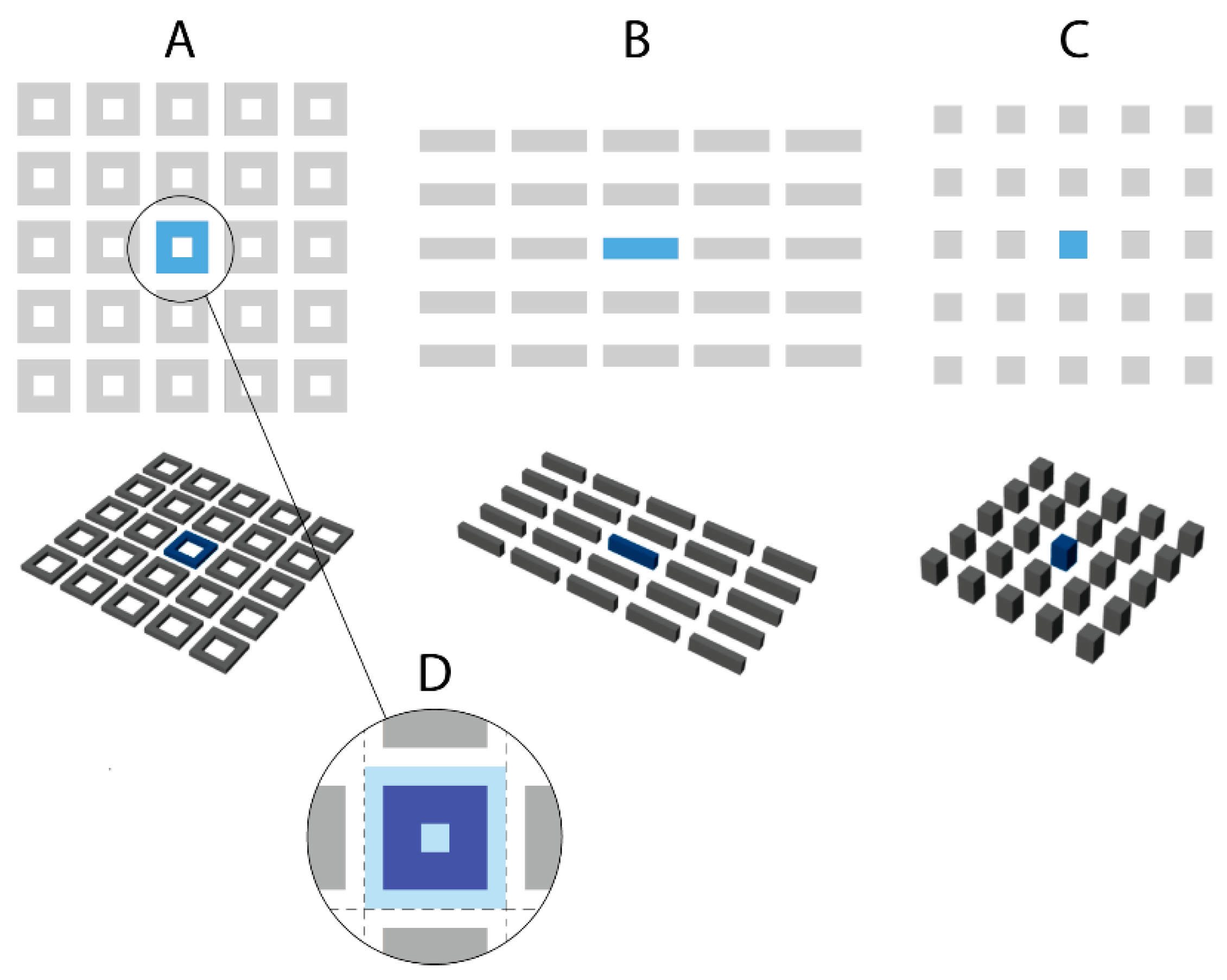



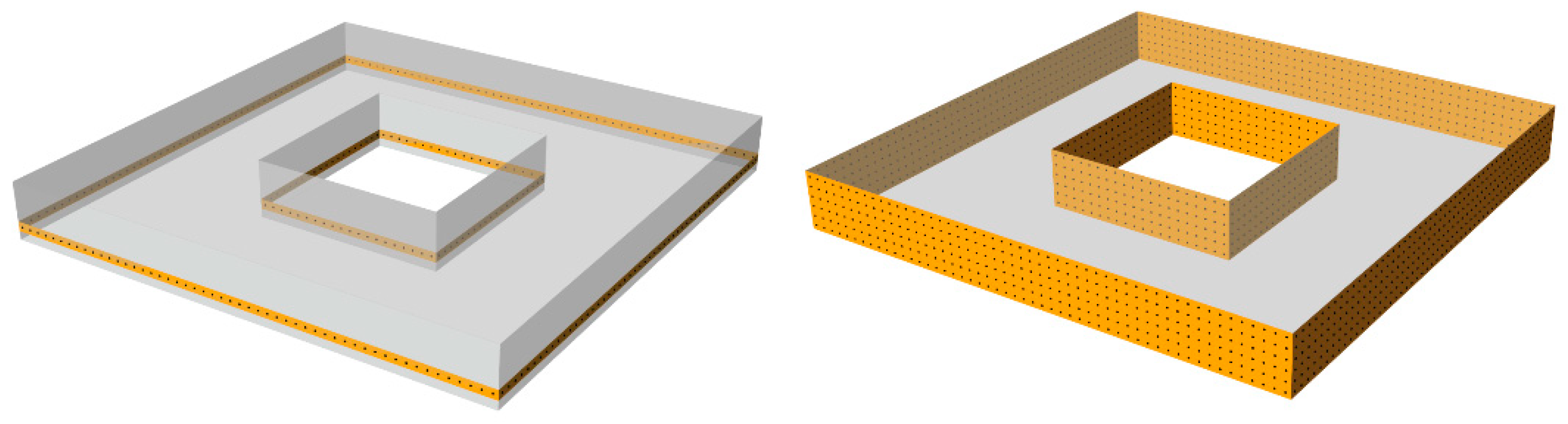








| Typology | Variables | Total No. of Design Iterations [G-Metrics/Other Metrics] | ||||
|---|---|---|---|---|---|---|
| Dimension, B [m] | Plot Offset [m] | Building Depth, D [m] | Storeys | Rotations [°] | ||
| Courtyard | 12–92 (11) | 8–32 (7) | 16 (1) | 2–10 (5) | 0–45 (2) | 385/770 |
| Slab | 32–128 (13) | 8–32 (7) | 16 (1) | 2–10 (5) | 0–90 (3) | 455/1365 |
| Tower | 16–20 (3) | 4–32 (15) | =B | 2–20 (10) | 0–45 (2) | 450/900 |
| Acronym | Name | Subject | Calculation or Simulation Method [Unit] | |
|---|---|---|---|---|
| G-metrics | FAR | Floor Area Ratio | whole | Ratio of gross floor area to plot area [m2/m2; used as unitless] |
| VAR | Volume Area Ratio | whole | Ratio of gross building volume to plot area [m3/m2; used as unitless] | |
| SAR * | Surface Area Ratio | whole | Ratio of gross external building surface area to plot area [m2/m2] | |
| OSR | Open Space Ratio | whole | Ratio of open space area to gross floor area [m2/m2] | |
| SVF | Sky View Factor | ground | Grid-based (1 m), 145 sky patches, cosine-weighted sky dome [%] | |
| VSC | Vertical Sky Component | façade (string) | At 1.4 m height, 1024 sky patches, CIE overcast sky [%] | |
| L-metrics | APS | Area of Permanent Shadow | ground | Grid-based (1 m), ray intersection, fraction of the grid open to no direct sunshine on 21 March |
| TH_G | Two-Hour area | ground | Grid-based (1 m), ray intersection, fraction of the grid open to 2 or more hours of direct sunshine on 21 March | |
| TH_F * | Two-Hour area | façade (string) | Grid-based (1 m), ray intersection, fraction of the grid open to 2 or more hours of direct sunshine on 21 March | |
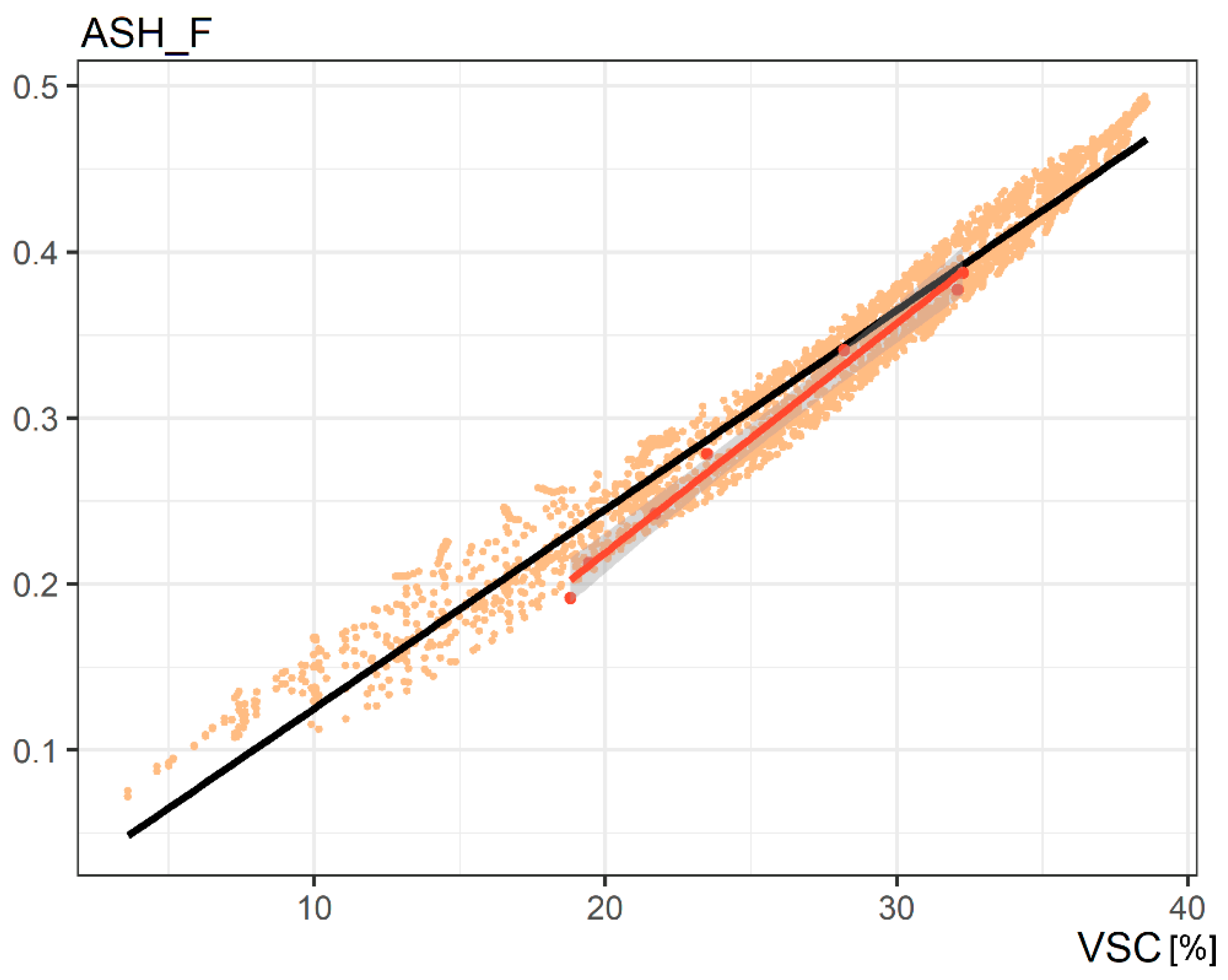
| ASH_G * | Annual Sunlight Hours | ground | Grid-based (1 m), average direct solar access as fraction of all annual hourly sun vectors | |
| ASH_F * | Annual Sunlight Hours | façade (string) | Grid-based (1 m), average direct solar access as fraction of all annual hourly sun vectors | |
| RD_G * | Reference Day (Sunlight Hours) | ground | Grid-based (1 m), ray intersection, average hours of direct sunshine on 21 March [h] | |
| RD_F * | Reference Day (Sunlight Hours) | façade (string) | Grid-based (1 m), ray intersection, average hours of direct sunshine on 21 March [h] | |
| EC-metrics | APSH | Annual Probable Sunlight Hours | façade (string) | Grid-based (1 m), average direct solar access as fraction of all annual hourly sun vectors (relative to cloud coverage: e.g., 40% cloudiness for a given hour gives 0.6 h of direct sun) |
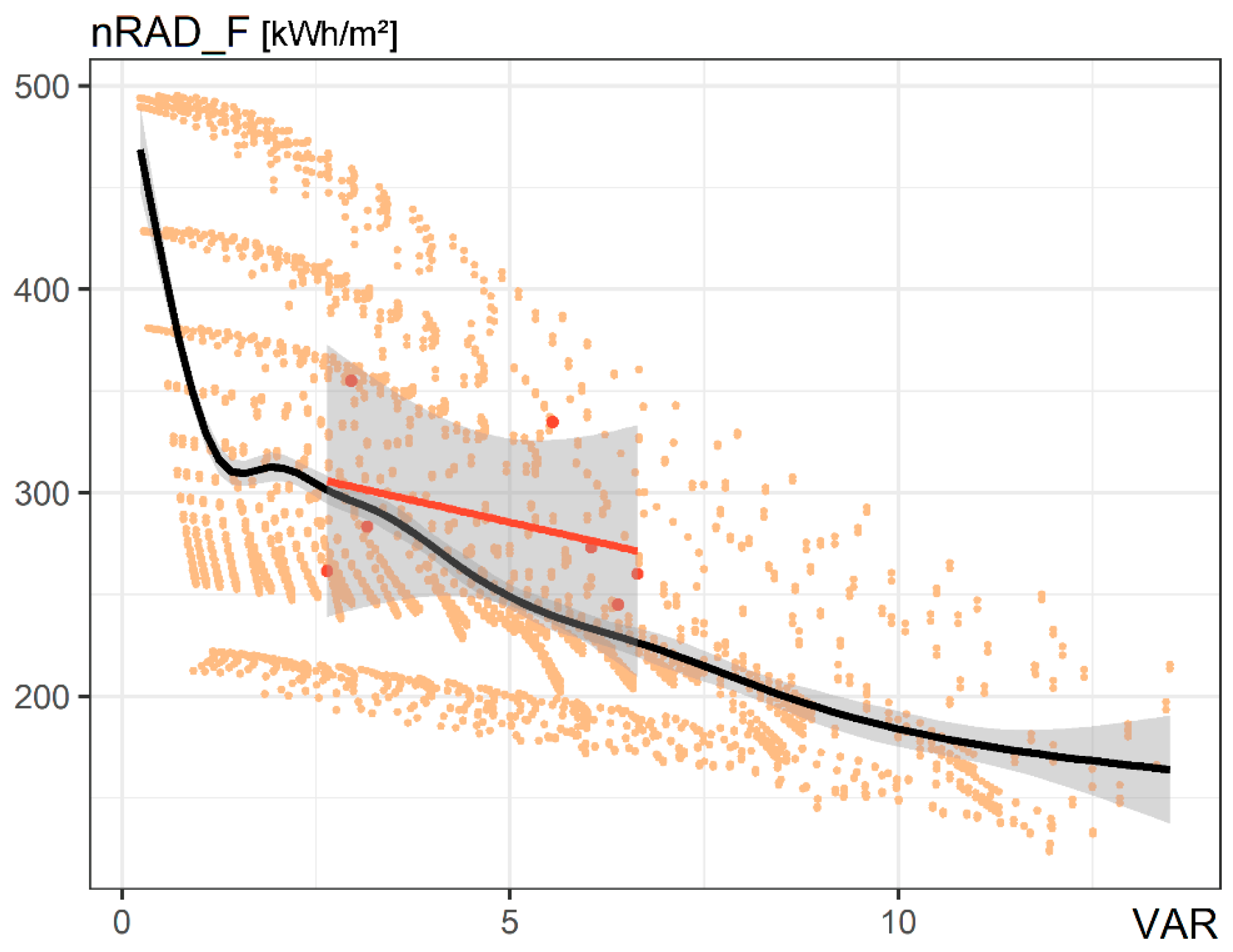
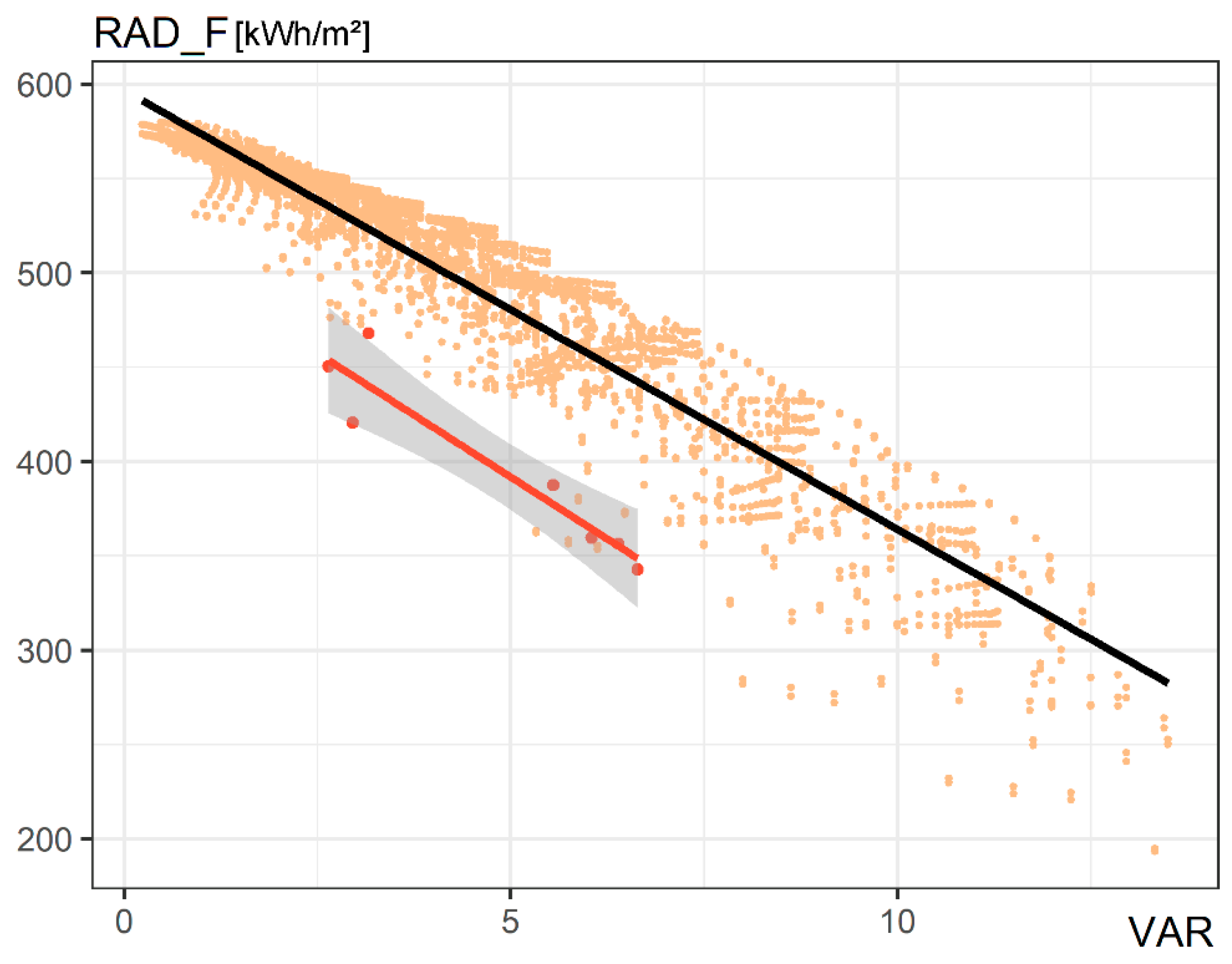
| RAD_F | Solar radiation (mean) | façade | Grid-based (1 m), annual solar radiation mean per façade area [kWh/m2] | |
| nRAD_F | Solar radiation (norm.) | façade | Grid-based (1 m), total annual radiation normalized by gross floor area [kWh/m2] | |
| nPV_F | PV potential | façade | Grid-based (1 m), surface area with solar radiation above 600 kWh/m2 normalised by floor area [m2/m2] |
| G-Metrics | L-Metrics | EC-Metrics |
|---|---|---|
| geometrical dimensions | geometrical dimensions latitude orientation | geometrical dimensions latitude orientation insolation (climate) |
| Metric Pair | Data | Intercept | Slope | ||
|---|---|---|---|---|---|
| Lower CI | Higher CI | Lower CI | Higher CI | ||
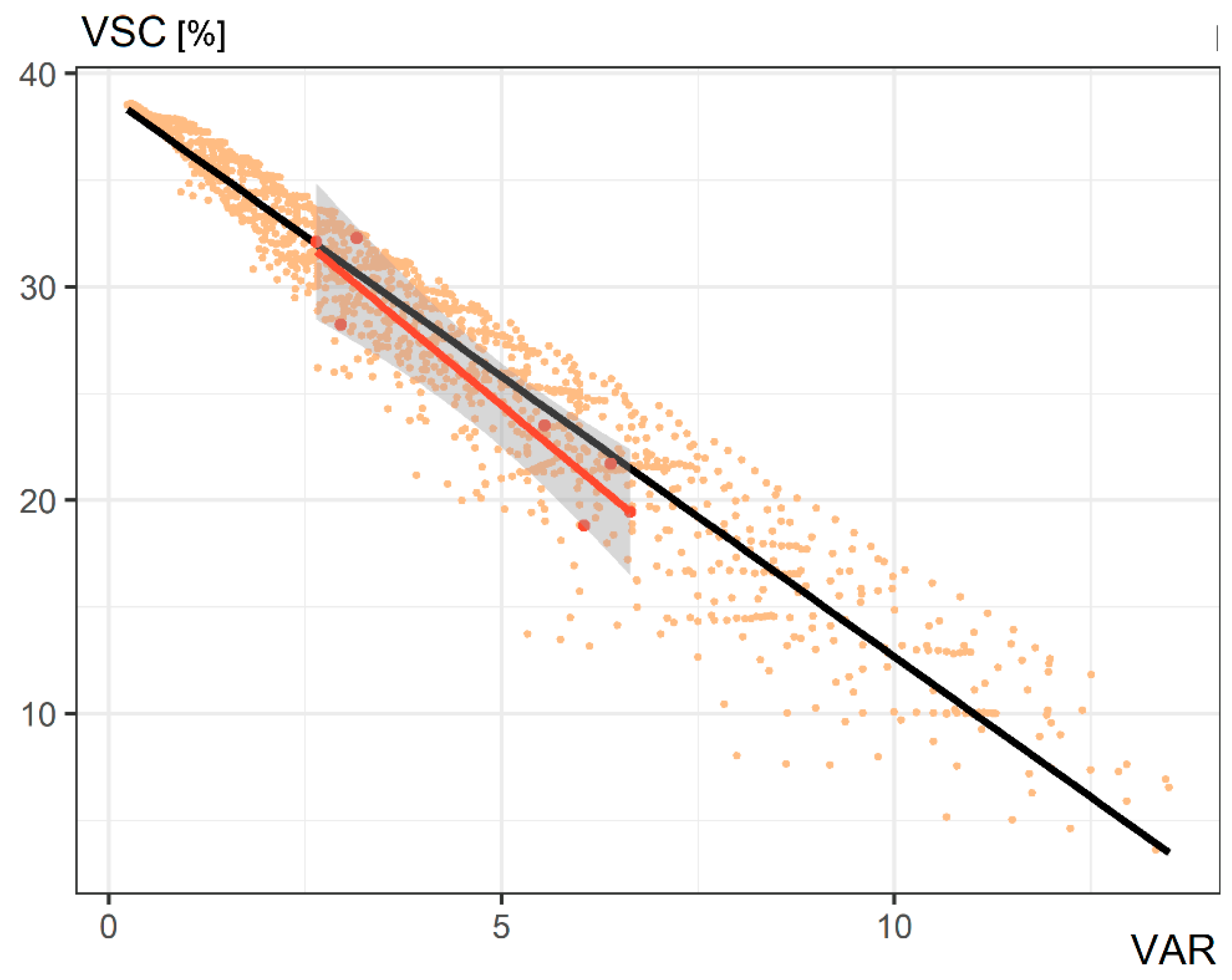
| SVF-VAR | I | 92.4 | 92.9 | −5.65 | −5.56 |
| CS | 76.3 | 110.8 | −10.08 | −3.24 | |
| VSC-VAR | I | 38.8 | 39.0 | −2.65 | −2.61 |
| CS | 33.8 | 45.8 | −4.25 | −1.87 | |
| SVF-VSC | I | 9.84 | 10.4 | 2.10 | 2.12 |
| CS | −13.1 | 29.0 | 1.32 | 2.96 | |
| ASH_G-VAR | I | 0.731 | 0.740 | −0.061 | −0.059 |
| CS | 0.548 | 1.013 | −0.121 | −0.029 | |
| RD_G-VAR | I | 9.36 | 9.49 | −0.84 | −0.81 |
| CS | 7.41 | 12.6 | −1.54 | −0.52 | |
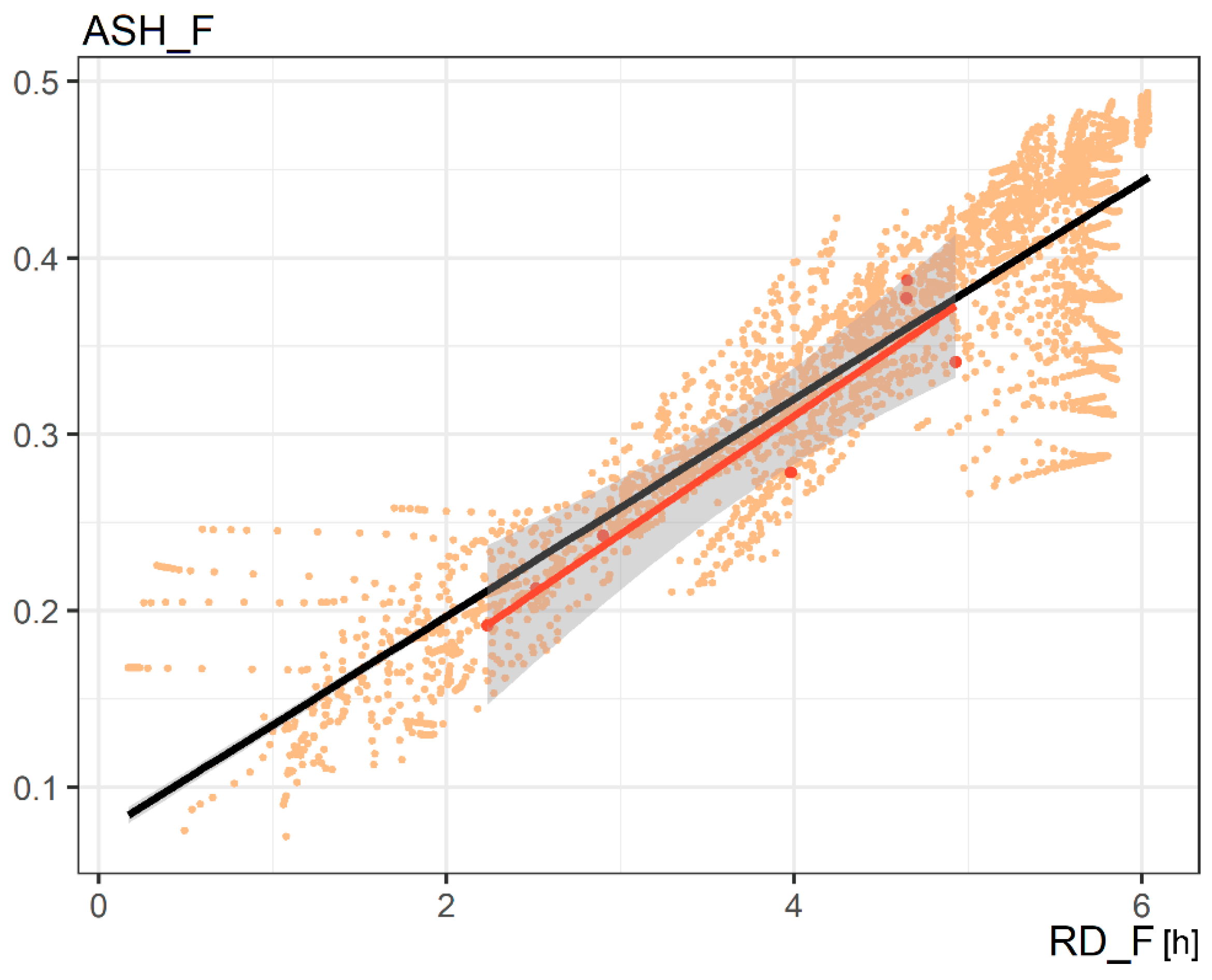
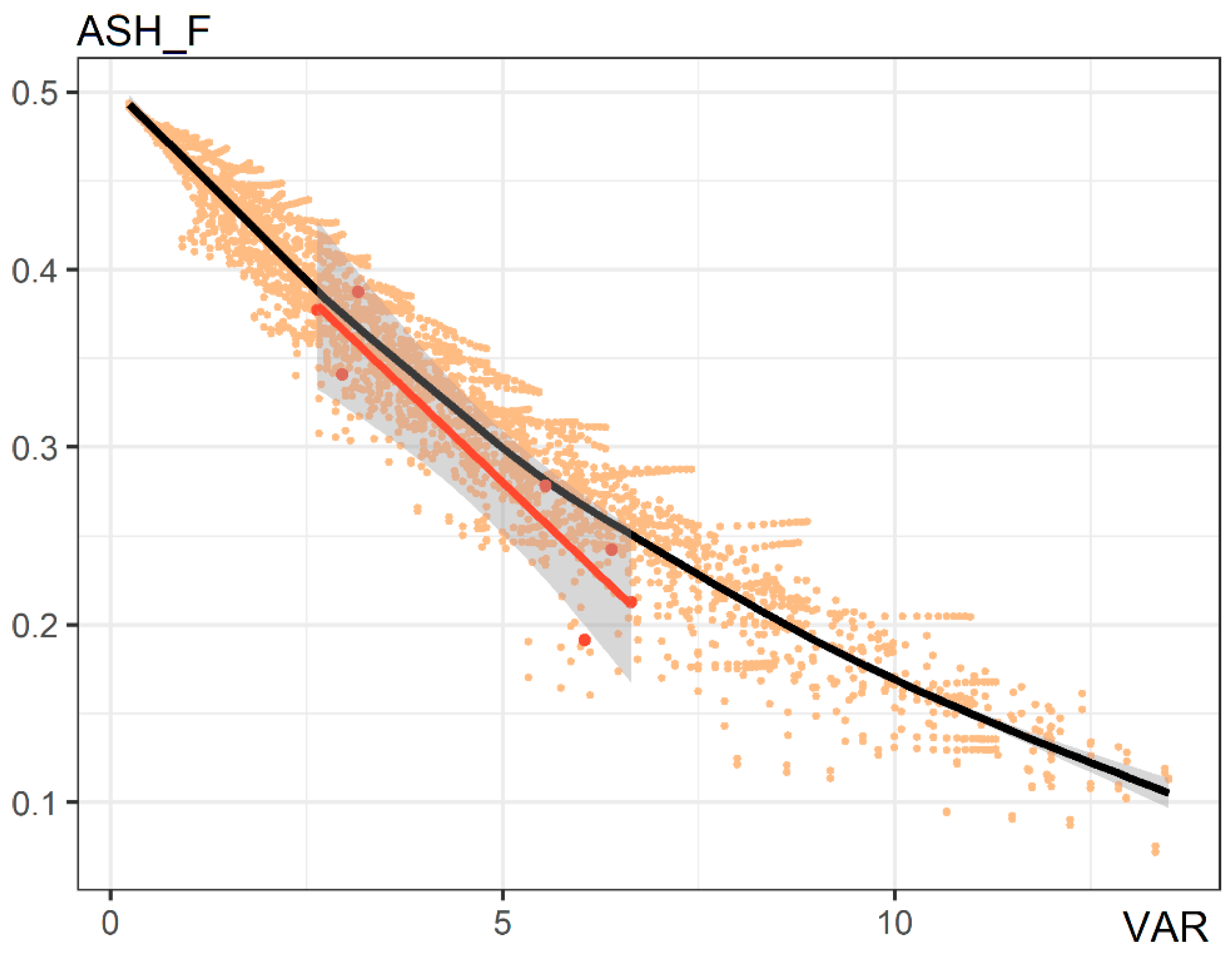
| ASH_F-VAR | I | 0.472 | 0.476 | −0.032 | −0.032 |
| CS | 0.402 | 0.580 | −0.060 | −0.025 | |
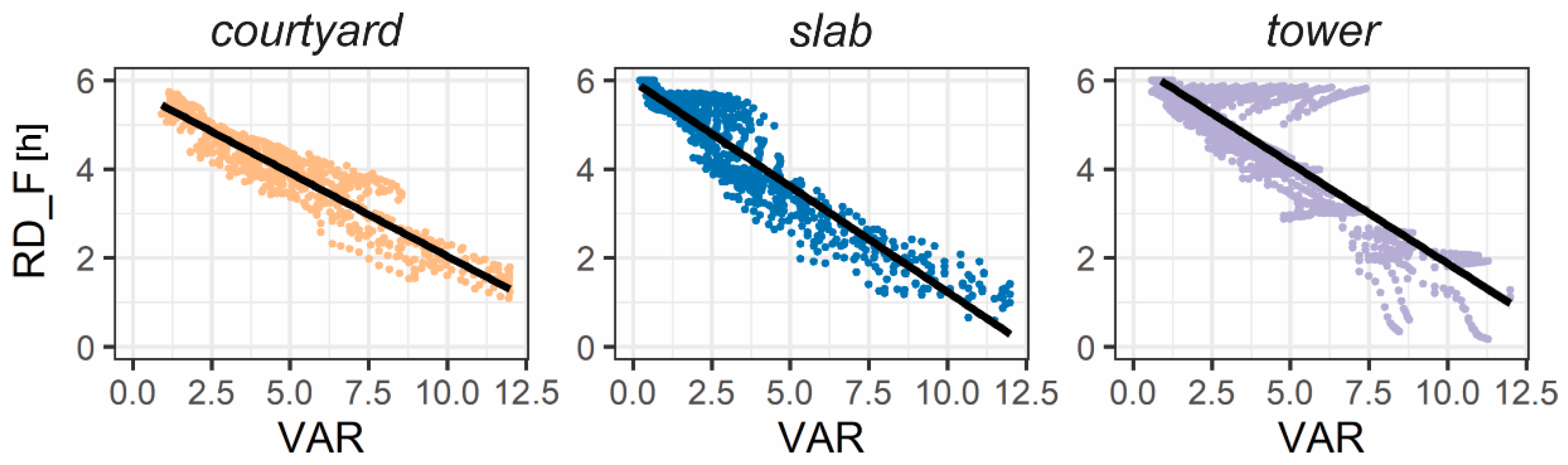
| RD_F-VAR | I | 6.06 | 6.14 | −0.44 | −0.42 |
| CS | 5.00 | 7.94 | −0.87 | −0.29 | |
| RAD_F-VAR | I | 595.3 | 598.3 | −23.6 | −23.0 |
| CS | 470.1 | 576.2 | −36.8 | −15.8 | |
| ASH_G-RD_G | I | 0.058 | 0.063 | 0.071 | 0.071 |
| CS | −0.017 | 0.101 | 0.064 | 0.086 | |
| RAD_F-VSC | I | 252.0 | 256.0 | 8.71 | 8.85 |
| CS | 134.1 | 237.0 | 6.43 | 10.44 | |
| Indoors | Outdoors | |
|---|---|---|
| Daylighting | VSC | SVF |
| Sunlighting | ASH_F | RD_G |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czachura, A.; Gentile, N.; Kanters, J.; Wall, M. Identifying Potential Indicators of Neighbourhood Solar Access in Urban Planning. Buildings 2022, 12, 1575. https://doi.org/10.3390/buildings12101575
Czachura A, Gentile N, Kanters J, Wall M. Identifying Potential Indicators of Neighbourhood Solar Access in Urban Planning. Buildings. 2022; 12(10):1575. https://doi.org/10.3390/buildings12101575
Chicago/Turabian StyleCzachura, Agnieszka, Niko Gentile, Jouri Kanters, and Maria Wall. 2022. "Identifying Potential Indicators of Neighbourhood Solar Access in Urban Planning" Buildings 12, no. 10: 1575. https://doi.org/10.3390/buildings12101575
APA StyleCzachura, A., Gentile, N., Kanters, J., & Wall, M. (2022). Identifying Potential Indicators of Neighbourhood Solar Access in Urban Planning. Buildings, 12(10), 1575. https://doi.org/10.3390/buildings12101575











