A Generalized Framework for the Alternate Load Path Redundancy Analysis of Steel Truss Bridges Subjected to Sudden Member Loss Scenarios
Abstract
:1. Introduction
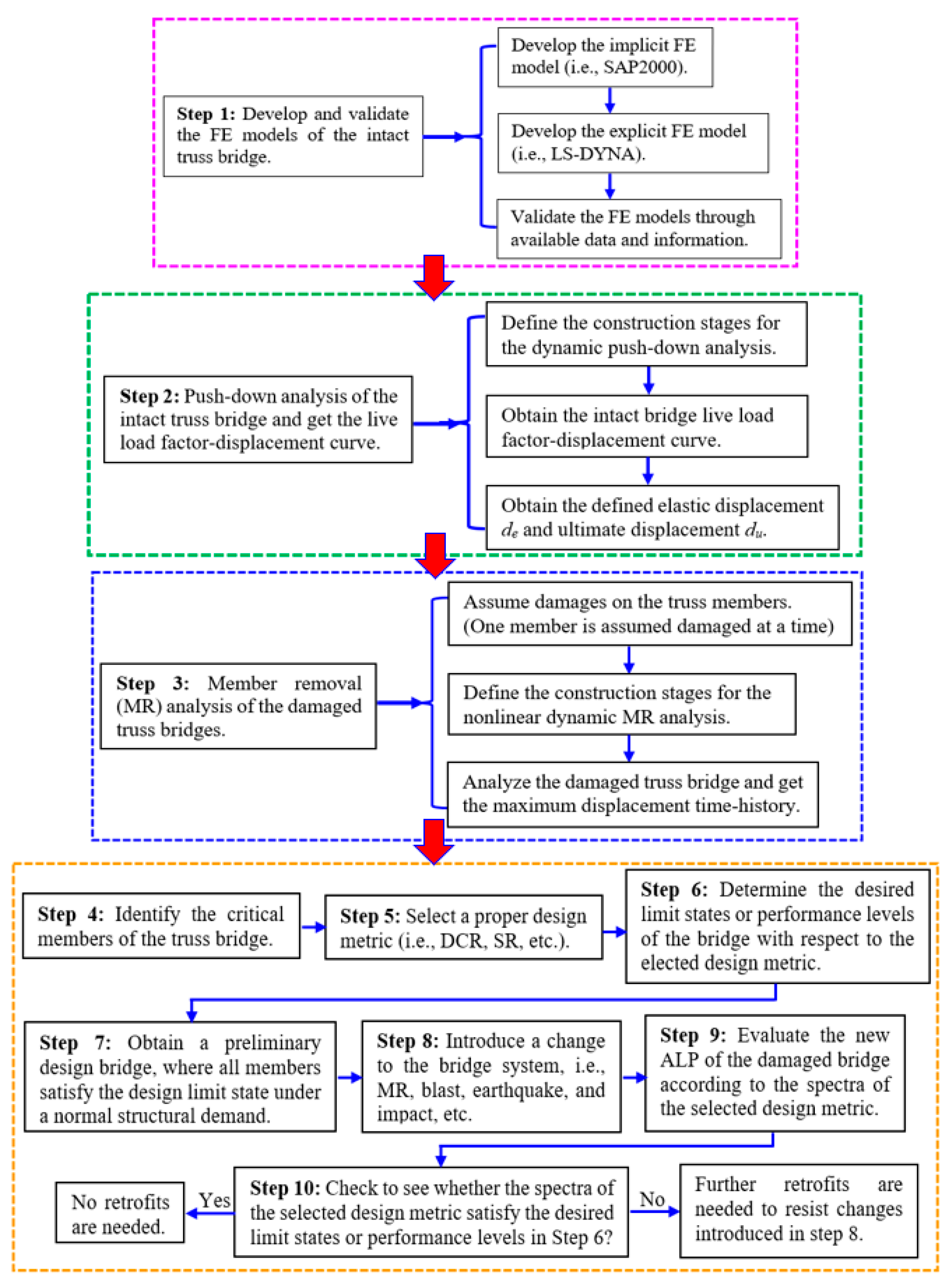
2. The Proposed Framework
2.1. Load Factors and Load Combinations
2.2. DCR Using Linear Static Analysis
2.3. SR Using Nonlinear Dynamic Analysis
3. Case-Study Analysis: The I-35W Truss Bridge
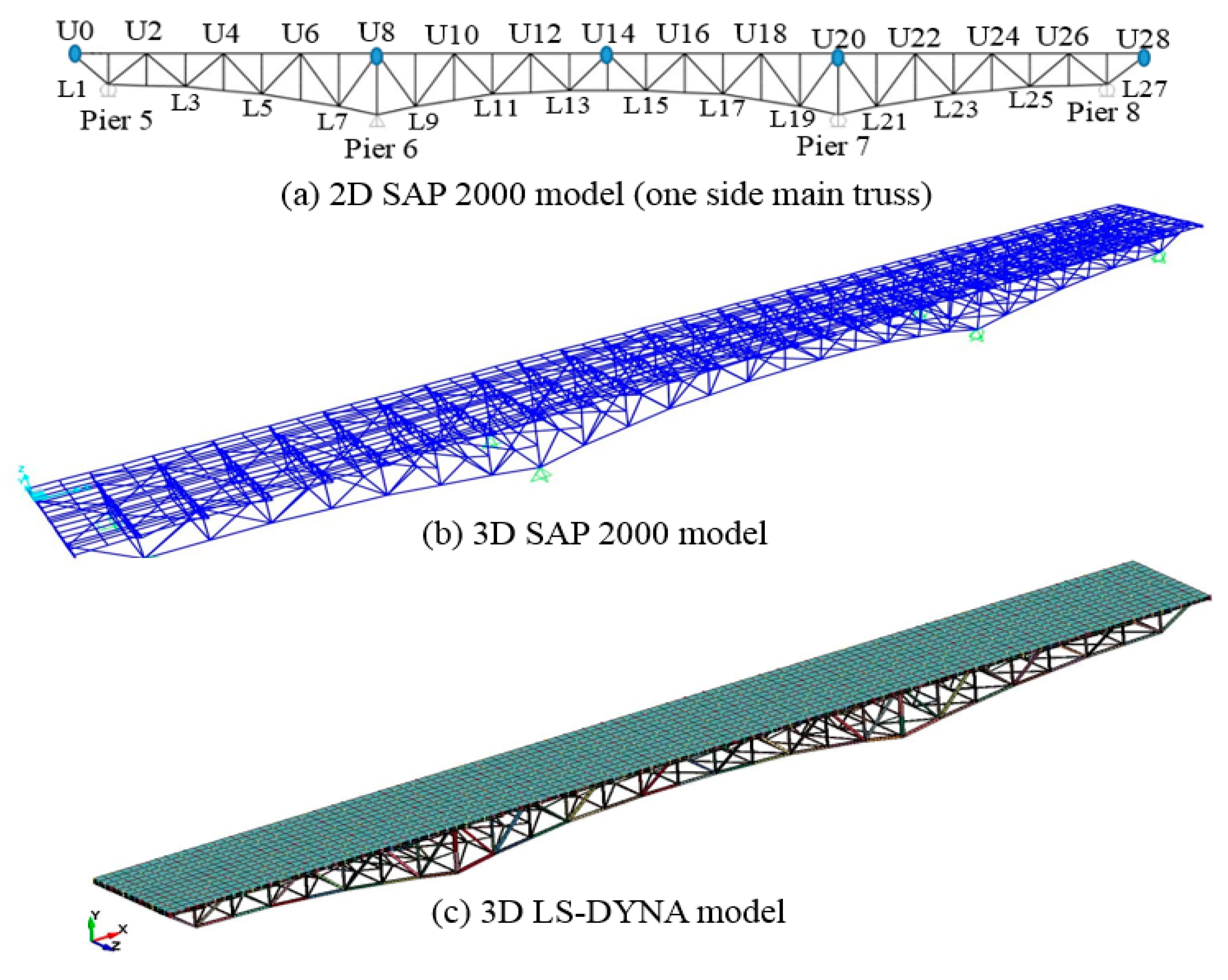
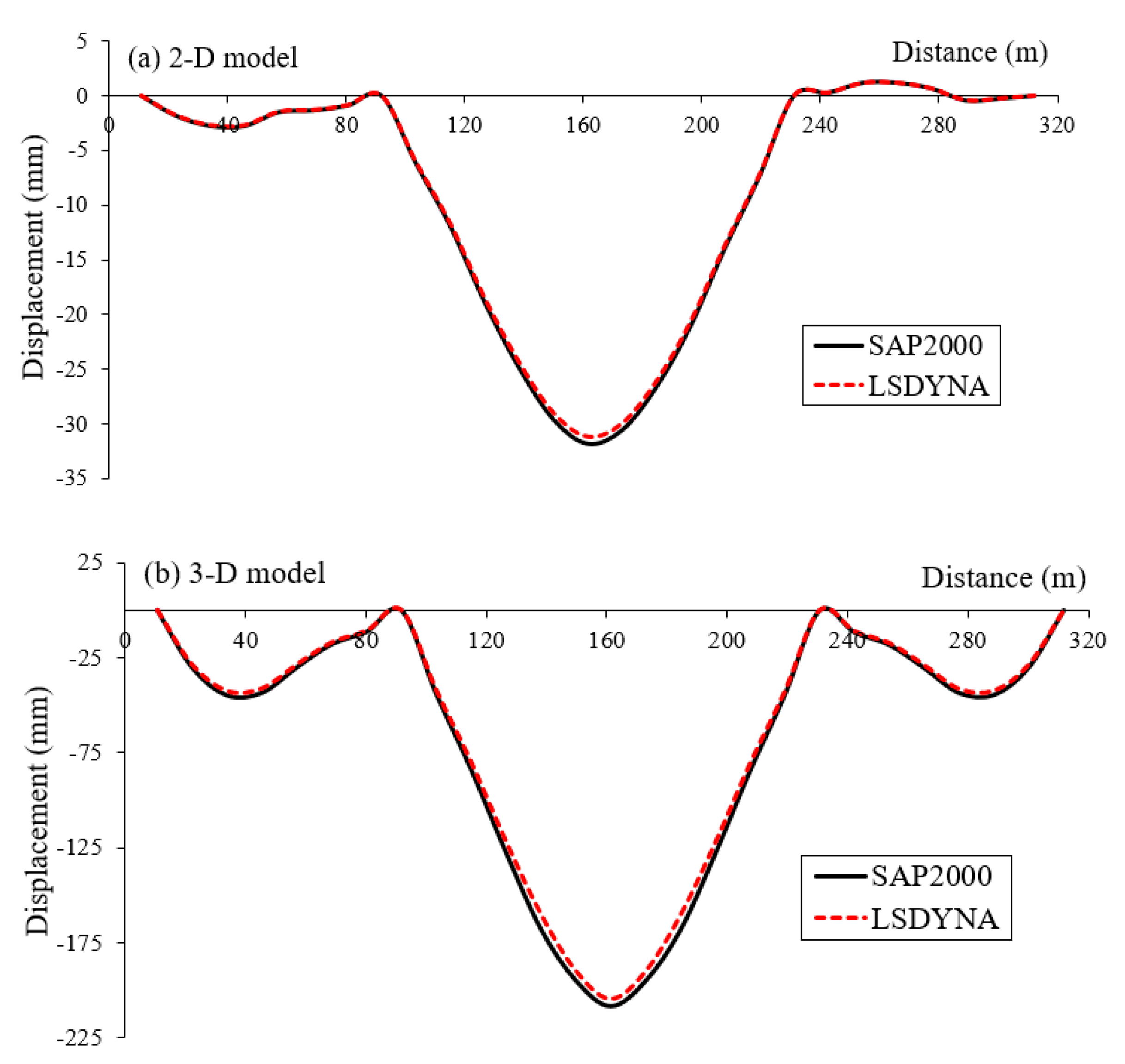
3.1. Bridge Description, Modeling, and Validation of FE Models
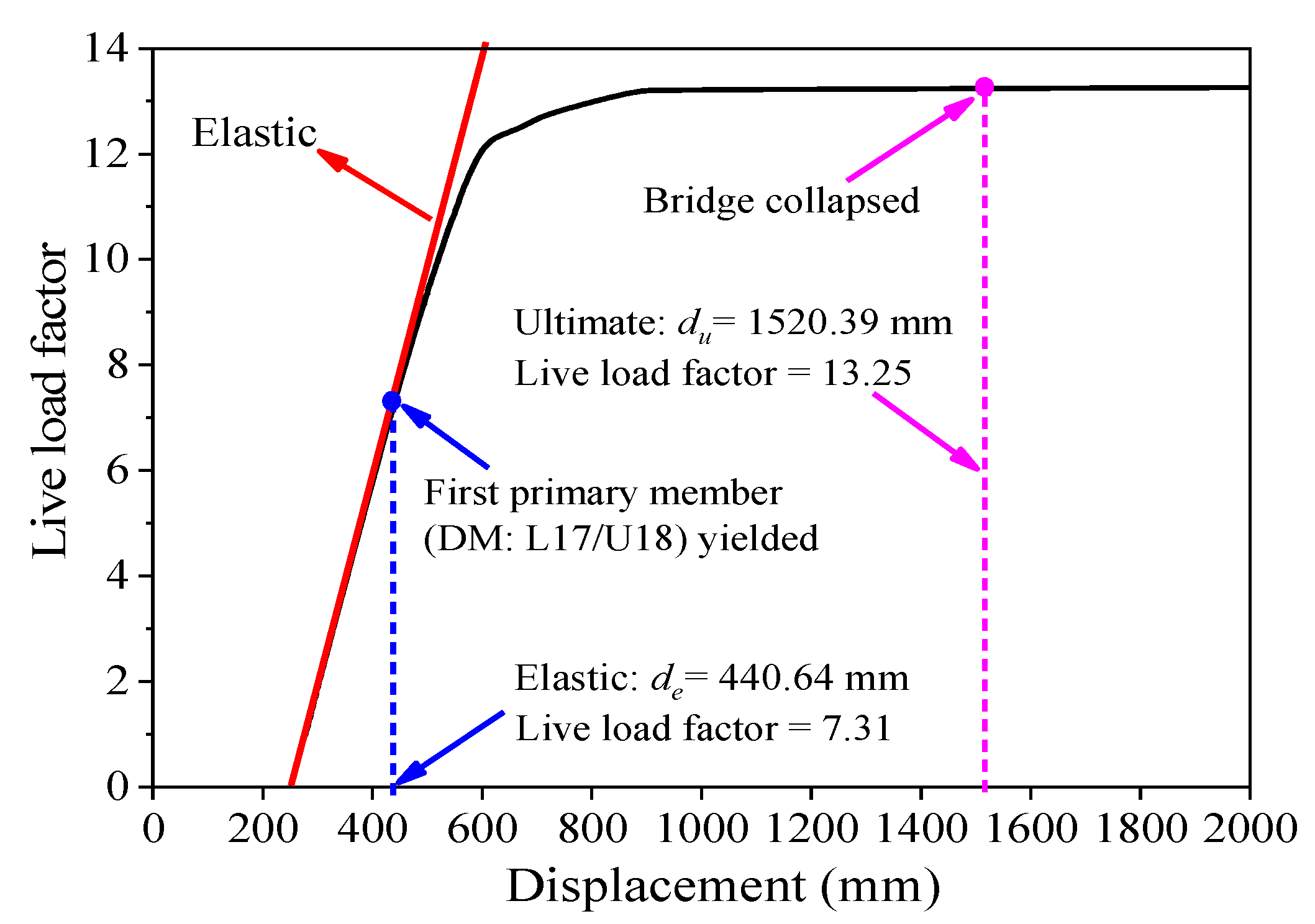
3.2. Push-Down Analysis of the Intact I-35W Truss Bridge
3.3. MR Analysis of the Damaged I-35W Truss Bridge
3.4. Identification of the Critical Members
4. ALP Analysis of the I-35W Truss Bridge
4.1. As-Built Bridge and Design Bridge
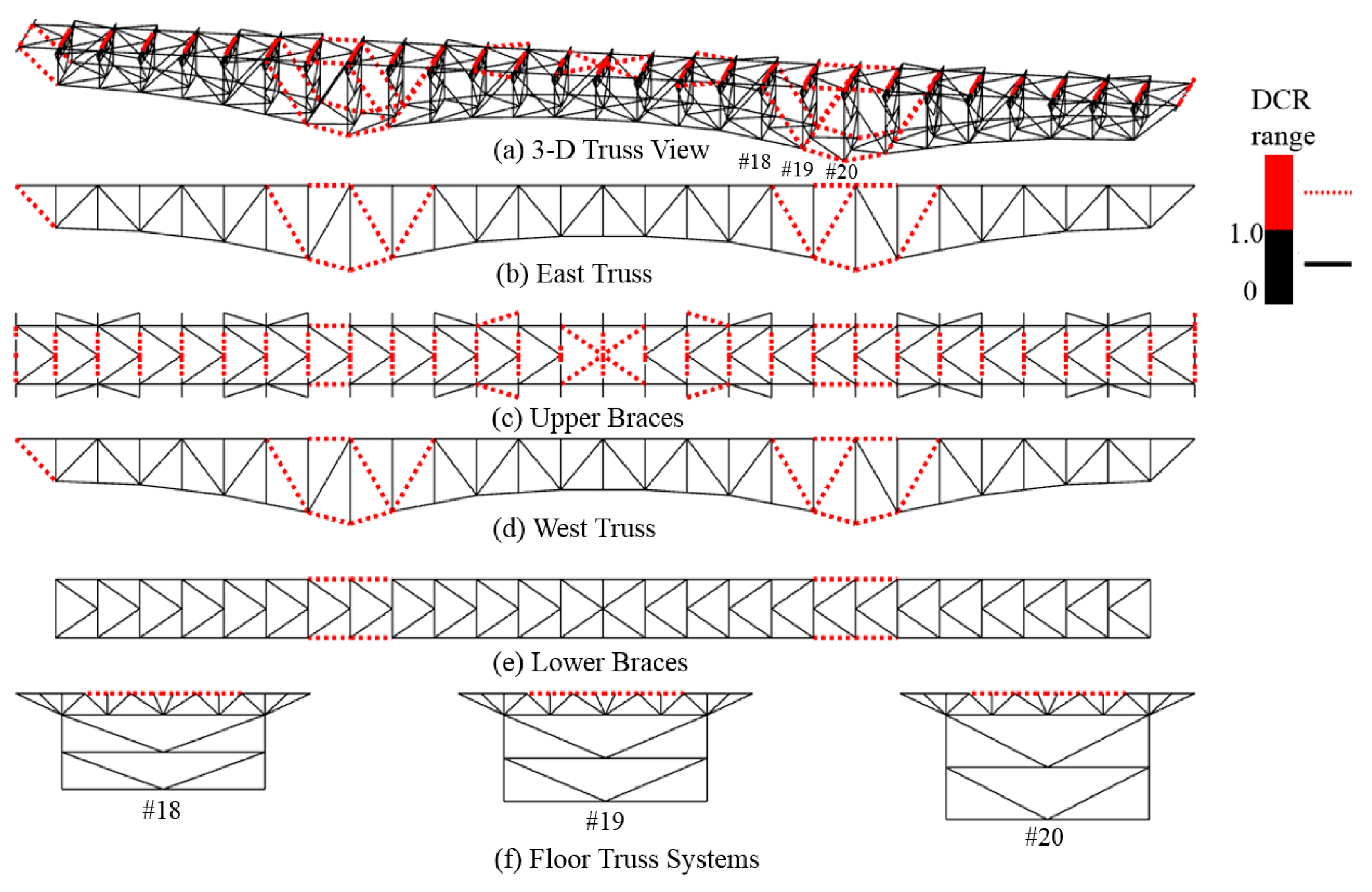
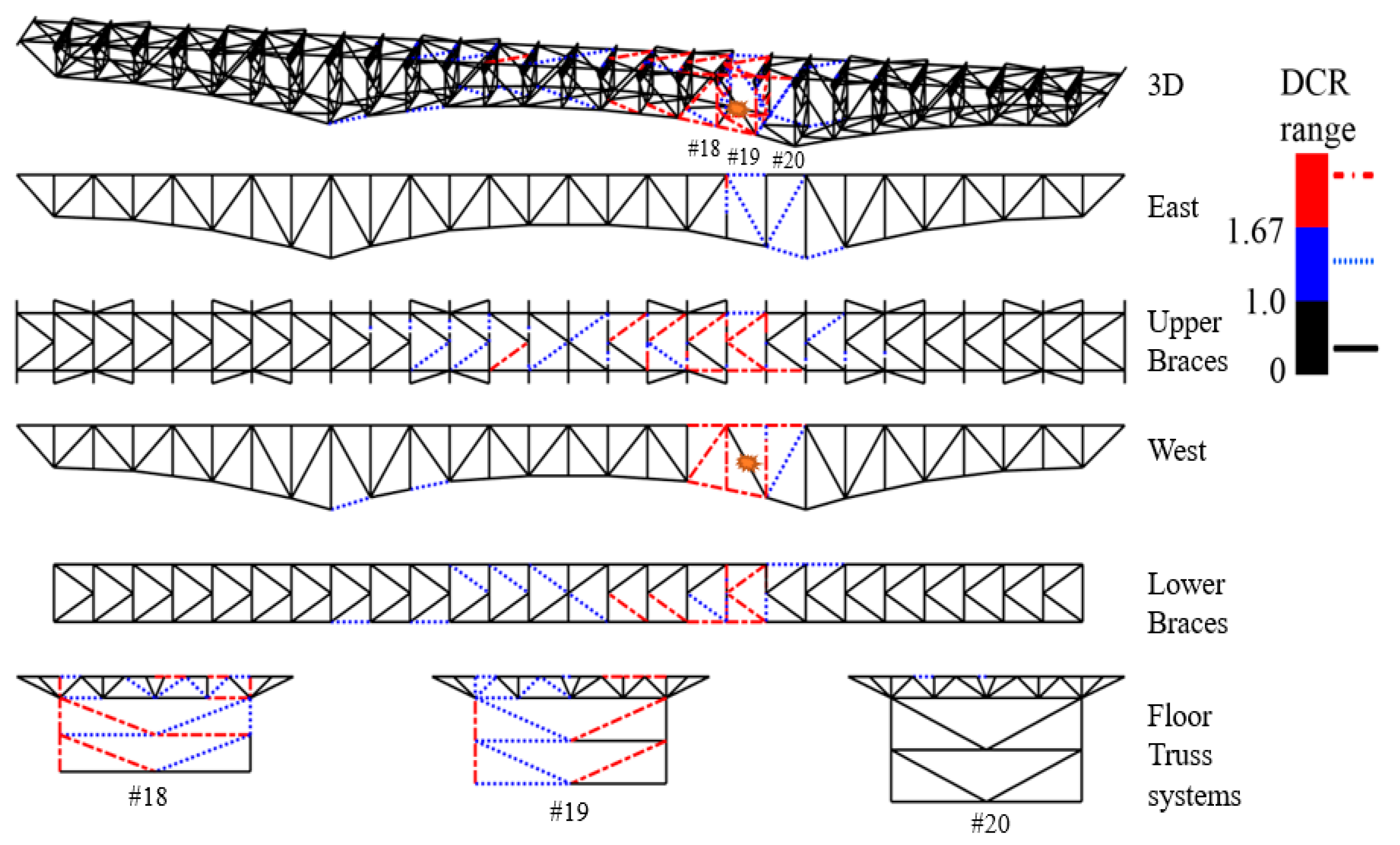
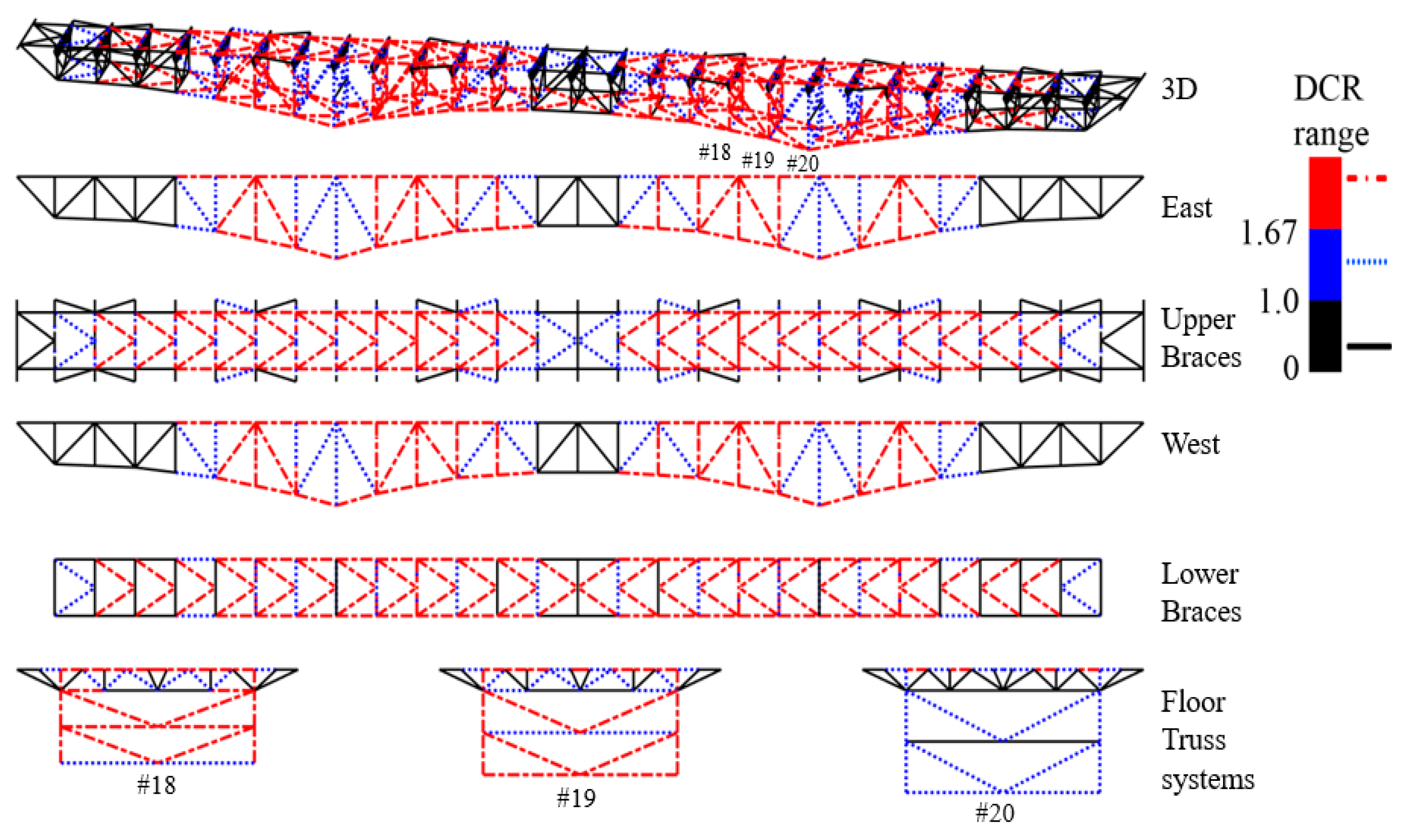
4.2. Linear Static Analysis: DCR-Based Metric
4.3. Nonlinear Dynamic Analysis: SR-Based Metric
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ellingwood, B.R. Mitigating risk from abnormal loads and progressive collapse. J. Perform. Constr. Facil. 2006, 20, 315–323. [Google Scholar] [CrossRef]
- Naji, A.; Ghiasi, M.R. Progressive collapse analysis of cable-stayed bridges. J. Fail. Anal. Prev. 2019, 19, 698–708. [Google Scholar] [CrossRef]
- Agrawal, A.K.; Mohammed, E.; Chen, X.; Li, H.H.; Wang, H.F. Steel Truss Retrofits to Provide Alternate Load Paths for Cut or Blast-Damaged or Destroyed Members; Rep. No. FHWA-HRT-20-055; FHWA: McLean, VA, USA, 2020. [Google Scholar]
- Li, H.H. Alternate Load Paths and Retrofits for Long-Span Truss Bridges under Sudden Member Loss and Blast Loads. Ph.D. Thesis, Department of Civil Engineering, City College of New York, City University of New York, New York, NY, USA, 2021. [Google Scholar]
- Kiakojouri, F.; De Biagi, V.; Chiaia, B.; Sheidaii, M.R. Progressive collapse of framed building structures: Current knowledge and future prospects. Eng. Struct. 2020, 206, 110061. [Google Scholar] [CrossRef]
- El-Tawil, S.; Khandelwal, K.; Kunnath, S.; Lew, H.S. Macro models for progressive collapse analysis of steel moment frame buildings. In Structural Engineering Research Frontiers; ASCE: Long Beach, CA, USA, 2007. [Google Scholar]
- EI-Tawil, S.; Li, H.H.; Kunnath, S. Computational simulation of gravity-induced progressive collapse of steel-frame buildings: Current trends and future research needs. J. Struct. Eng. 2014, 140, A2513001. [Google Scholar] [CrossRef]
- Byfield, M.; Mudalige, W.; Morison, C.; Stoddart, E. A review of progressive collapse research and regulations. Proc. Inst. Civ.-Eng.-Struct. Build. 2014, 167, 447–456. [Google Scholar]
- Qian, K.; Li, B. Research advances in design of structures to resist progressive collapse. J. Perform. Constr. Facil. 2015, 29, B4014007. [Google Scholar] [CrossRef]
- Adam, J.M.; Parisi, F.; Sagaseta, J.; Lu, X.Z. Research and practice on progressive collapse and robustness of building structures in the 21st century. Eng. Struct. 2018, 173, 122–149. [Google Scholar] [CrossRef]
- Stochino, F.; Bedon, C.; Sagaseta, J.; Honfi, D. Robustness and resilience of structures under extreme loads. Adv. Civ. Eng. 2019, 4291703. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q. Structural Robustness of Long-Span Cable-Supported Bridges. Ph.D. Thesis, Department of Civil Engineering, City College of New York, City University of New York, New York, NY, USA, 2021. [Google Scholar]
- GSA (General Services Administration). Progressive Collapse Analysis and Design Guidelines for New Federal Office Buildings and Major Modernization Projects; GSA: Washington, DC, USA, 2003. [Google Scholar]
- GSA (General Services Administration). Progressive Collapse Analysis and Design Guidelines for Progressive Collapse Resistance; GSA: Washington, DC, USA, 2016. [Google Scholar]
- DOD. Unified Facilities Criteria: Design of Buildings to Resist Progressive Collapse; Rep. No. UFC4-023-03; United States Department of Defense: Washington, DC, USA, 2009. [Google Scholar]
- Lee, G.C.; Mohan, S.; Huang, C.; Fard, B.N. A Study of US Bridge Failures (1980–2012); Technical Report 13-0008; MCEER: Buffalo, NY, USA, 2013. [Google Scholar]
- Fisher, J.W.; Roberts, R.; Pense, A.W. Evaluation of fracture of Lafayette Street bridge. J. Struct. Div. 1977, 103, 1339–1357. [Google Scholar] [CrossRef]
- Beauchamp, J.C.; Chan, M.Y.T.; Pion, R.H. Repair and evaluation of a damaged truss bridge—Lewes, Yukon River. Can. J. Civ. Eng. 1984, 11, 494–504. [Google Scholar] [CrossRef]
- Jelinek, J.J.; Bartlett, F.M. Material properties of historical bridge steel. In Proceedings of the 30th Annual Conference of the Canadian Society of Civil Engineering, Canadian Society for Civil Engineering, Montreal, QC, Canada, 5–8 June 2002. [Google Scholar]
- Diggelmann, L.M.; Connor, R.J.; Sherman, R.J.; Beshah, F. Evaluation of Member and Load-Path Redundancy on the US-421 Bridge over the Ohio River; Rep. No. FHWA-HRT-13-105; FHWA: McLean, VA, USA, 2013. [Google Scholar]
- Cha, H.; Lyrenmann, L.; Connor, R.J.; Varma, A.H. Experimental and Numerical Evaluation of the Postfracture Redundancy of a Simple Span Truss Bridge. J. Bridge. Eng. 2014, 19, 04014048. [Google Scholar] [CrossRef]
- Connor, R.J.; Bonachera Martín, F.J.; Varma, A.; Lai, Z.; Korkmaz, C. Fracture-Critical System Analysis for Steel Bridges; (No. Project 12-87A); FHWA: McLean, VA, USA, 2018. [Google Scholar]
- Lin, C.S. Deterioration Effects on Progressive Collapse of Bridges. Ph.D. Thesis, Department of Civil Engineering, Columbia University, New York, NY, USA, 2019. [Google Scholar]
- Lichtenstein, A.G. The silver bridge collapse recounted. J. Perform. Constr. Facil. 1993, 7, 249–261. [Google Scholar] [CrossRef]
- Cho, H.N.; Lim, J.K.; Choi, H.H. Reliability-based fatigue failure analysis for causes assessment of a collapsed steel truss bridge. Eng. Fail. Anal. 2001, 8, 311–324. [Google Scholar] [CrossRef]
- Hao, S. I-35W bridge collapse. J. Bridge Eng. 2010, 15, 608–614. [Google Scholar] [CrossRef]
- Grub, M.A.; Wilson, K.E.; White, C.D.; Nickas, W.N. Load and Resistance Factor Design (LRFD) for Highway Bridge Superstructures–Reference Manual; Rep. No. FHWA-NHI-15-047; FHWA: Washington, DC, USA, 2015. [Google Scholar]
- AASHTO. AASHTO LRFD Bridge Design Specifications, 8th ed.; AASHTO: Washington, DC, USA, 2017. [Google Scholar]
- AASHTO. AASHTO LRFD Bridge Design Specifications, 9th ed.; AASHTO: Washington, DC, USA, 2020. [Google Scholar]
- Lwin, M. Clarification of Requirements for Fracture Critical Members, FHWA Memorandum HIBT 10; Federal Highway Administration: Washington, DC, USA, 2012. [Google Scholar]
- AASHTO. Analysis and Identification of Fracture Critical Members and System Redundant Members; AASHTO: Washington, DC, USA, 2018. [Google Scholar]
- AASHTO. Guide Specifications for Internal Redundancy of Mechanically-Fastened Built-Up Steel Members; AASHTO: Washington, DC, USA, 2018. [Google Scholar]
- ASCE (American Society of Civil Engineers). Minimum Design Loads for Buildings and Other Structures; American Society of Civil Engineers: Reston, VA, USA, 2013. [Google Scholar]
- AISC. Specifications for Structural Steel Buildings; AISC: Chicago, IL, USA, 2016. [Google Scholar]
- Ocel, J.M.; Wright, W.J. Finite Element Modeling of I-35W Bridge Collapse-Final Report; Turner-Fairbank Highway Research Center, Federal Highway Administration: Washington, DC, USA, 2008. [Google Scholar]
- Astaneh-Asl, A. Progressive collapse of steel truss bridges, the case of I-35W collapse. In Proceedings of the 7th International Conference on Steel Bridges, Guimarăes, Portugal, 4–6 June 2008. [Google Scholar]
- Liao, M.; Okazaki, T.; Ballarini, R.; Schultz, A.E.; Galambos, T.V. Nonlinear finite-element analysis of critical gusset plates in the I-35W Bridge in Minnesota. J. Struct. Eng. 2011, 137, 59–68. [Google Scholar] [CrossRef]
- Higgins, C.; Dusicka, P.; Scott, M. Experimental Tests and Numerical Analyses of Steel Truss Bridge Gusset Connections; Rep. No. OTREC-RR-12-03; OTREC: Portland, OR, USA, 2012. [Google Scholar]
- Hallquist, J.O. LS-DYNA Keyword User’s Manual, Version 971; Livermore Software Technology Corporation: Livermore, CA, USA, 2014. [Google Scholar]
- Chang, K.-C.; Kim, C.-W. Modal-parameter identification and vibration-based damage detection of a damaged steel truss bridge. Eng. Struct. 2016, 122, 156–173. [Google Scholar] [CrossRef]
- Bonopera, M.; Chang, K.-C.; Chen, C.-C.; Lin, T.-K.; Tullini, N. Bending tests for the structural safety assessment of space truss members. Int. J. Space Struct. 2018, 33, 138–149. [Google Scholar] [CrossRef]

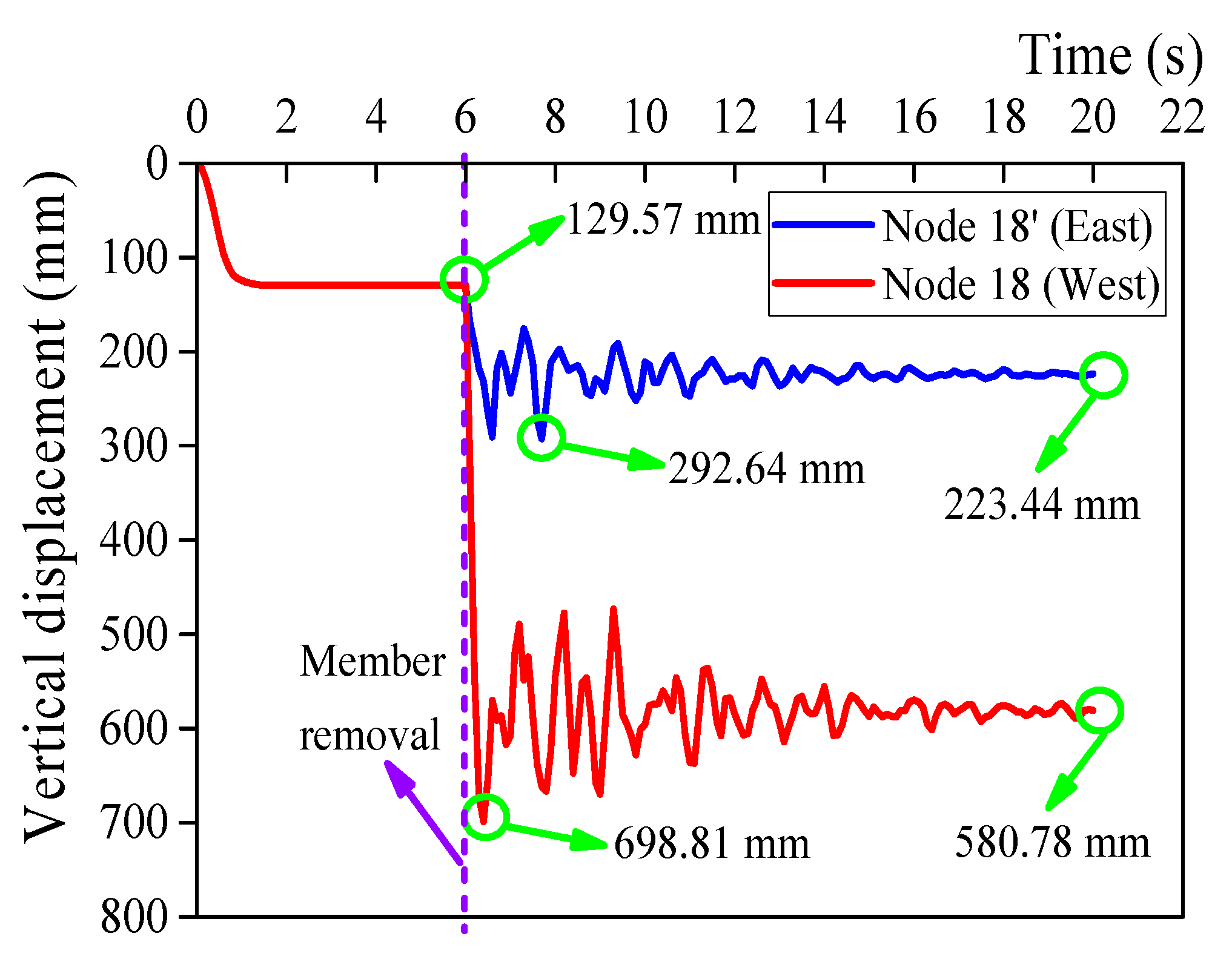
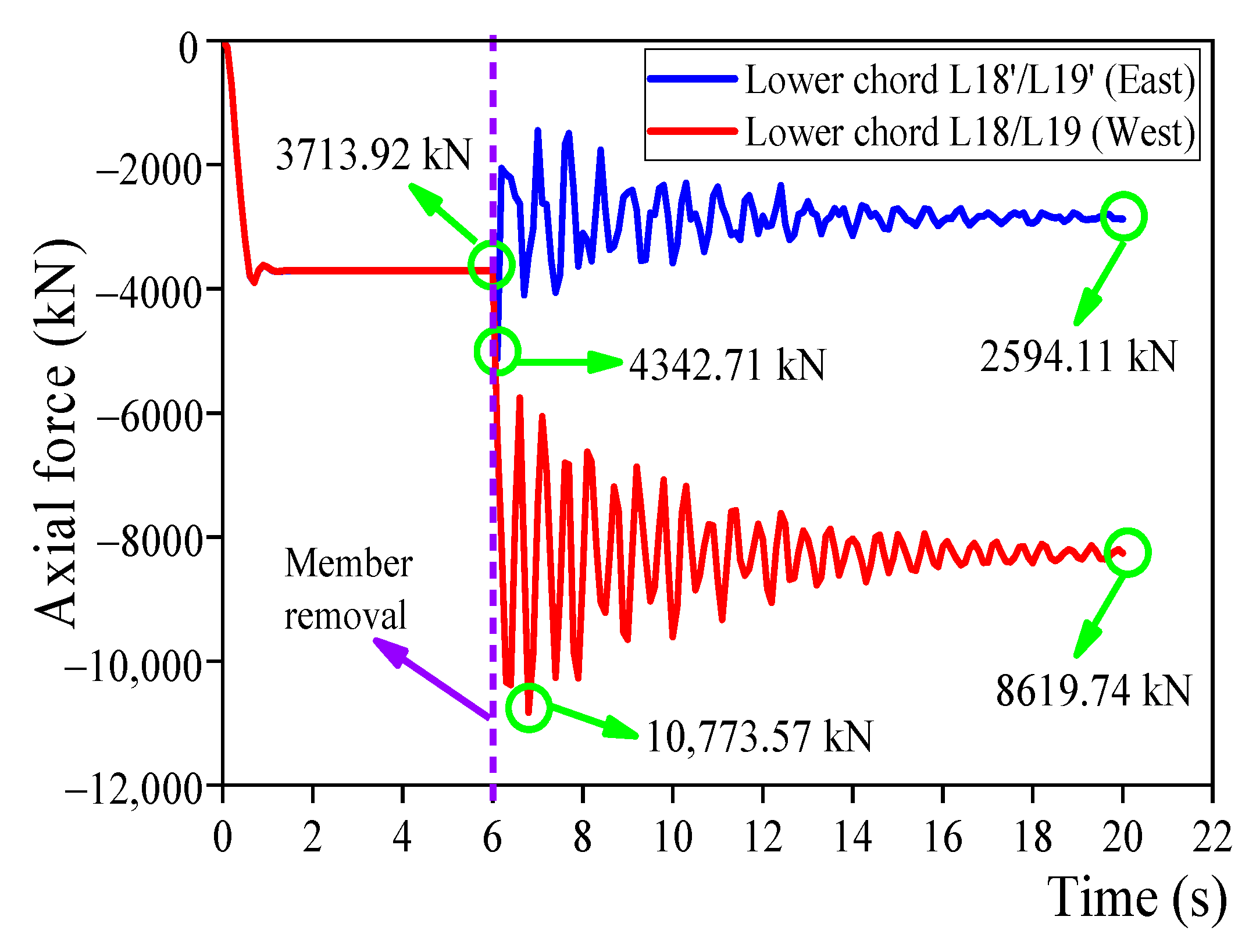
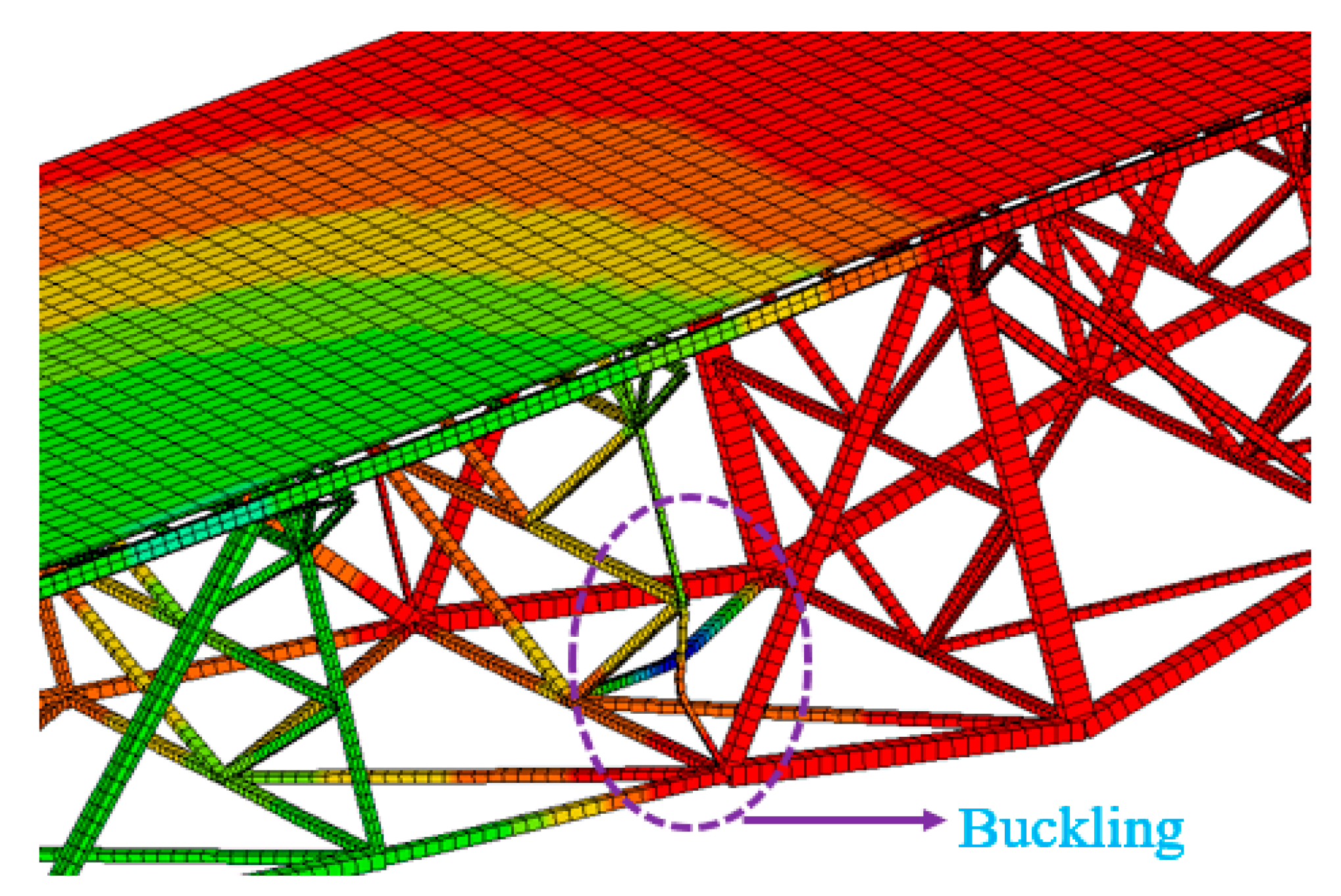
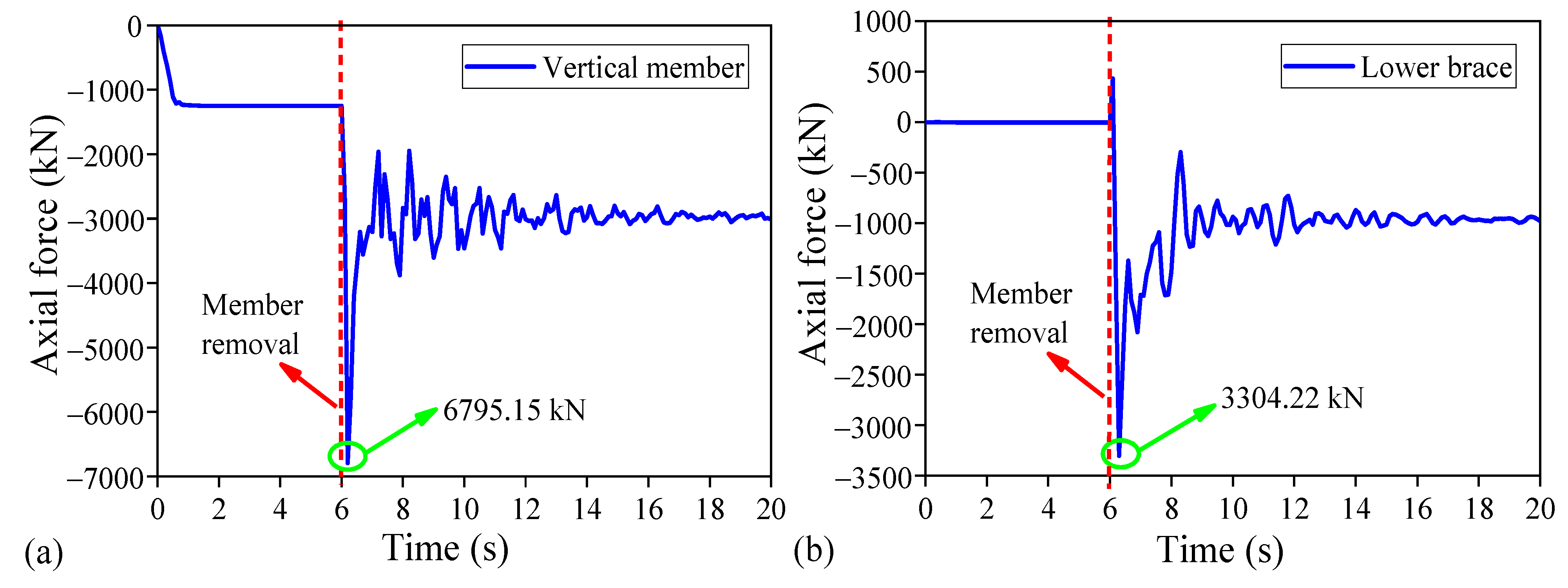

| Limit State | Metric Range |
|---|---|
| Design limit | DCR ≤ 1.0 |
| Elastic limit | 1.0 < DCR ≤ 1.67 |
| Beyond elastic limit | DCR > 1.67 |
| Limit State | Metric Range |
|---|---|
| Elastic limit | SR ≤ 1.0 |
| Limited ductility | 1.0 < SR ≤ 2.0 |
| Medium ductility | 1.0 < SR ≤ 4.0 |
| High ductility | SR > 4.0 |
| Structural Component | DL_1965 (kN) | DL_2007 (kN) |
|---|---|---|
| Steel members | 28,364 | 28,364 |
| Concrete members | 53,248 | 72,889 |
| Approach span | 5585 | 6989 |
| Sum | 87,197 | 108,239 |
| Pier | FHWA’s as-Built Model [35] (D) | SAP2000 Model (S) | LS-DYNA Model (L) | Difference (S-D)/D (%) | Difference (L-D)/D (%) | Difference (L-S)/S (%) |
|---|---|---|---|---|---|---|
| Pier 5 (East) | 4408 | 4600 | 4650 | 4.36% | 5.49% | 1.09% |
| Pier 6 (East) | 16,605 | 16,595 | 16,645 | −0.06% | 0.24% | 0.30% |
| Pier 7 (East) | 16,298 | 16,354 | 16,404 | 0.34% | 0.65% | 0.31% |
| Pier 8 (East) | 6023 | 5975 | 6025 | −0.80% | 0.03% | 0.84% |
| Pier 5 (West) | 4577 | 4783 | 4833 | 4.50% | 5.59% | 1.05% |
| Pier 6 (West) | 16,632 | 16,572 | 16,622 | −0.36% | −0.06% | 0.30% |
| Pier 7 (West) | 16,338 | 16,352 | 16,402 | 0.09% | 0.39% | 0.31% |
| Pier 8 (West) | 5996 | 6000 | 6025 | 0.07% | 0.48% | 0.42% |
| Sum | 86,877 | 87,231 | 87,606 | 0.41% | 0.84% | 0.43% |
| Construction Stage # | Time (s) | Description | Mass Proportional Damping (Rayleigh Damping) |
|---|---|---|---|
| Stage 1 | 0~4 | Apply the self-weight of the steel structural system (elastic material) | 80% |
| Stage 2 | 4~8 | Increase the stiffness of the deck to the normal value (elastic material) | 80% |
| Stage 3 | 8~10 | Change the deck and steel members’ material into nonlinear material models (*MAT_172 and *MAT_98) | 80% |
| 10~12 | Apply the live load on the deck | 80% | |
| 12~13 | Continue construction stage 3 | 80% | |
| 13~15 | Change the damping to the actual level | 2% | |
| Stage 4 | 15~20 | Continue construction stage 3 | 2% |
| 20~200 | Apply the Push-down analysis (increase the live load factor by 0.1/s) | 2% |
| Construction Stage # | Time (s) | Description | Mass Proportional Damping (Rayleigh Damping) |
|---|---|---|---|
| Stage 1 | 0~4 | Apply the self-weight of the steel structural system (elastic material) | 80% |
| Stage 2 | 4~8 | Increase the stiffness of the deck to the normal value (elastic material) | 80% |
| Stage 3 | 8~10 | Change the deck and steel members’ material into nonlinear material models (*MAT_172 and *MAT_98) | 80% |
| 10~12 | Apply the live load on the deck | 80% | |
| 12~15 | Continue construction stage 3 | 80% | |
| Stage 4 | 15~20 | Change the damping to the actual level | 2% |
| 20~40 | Member removal (MR) analysis | 2% |
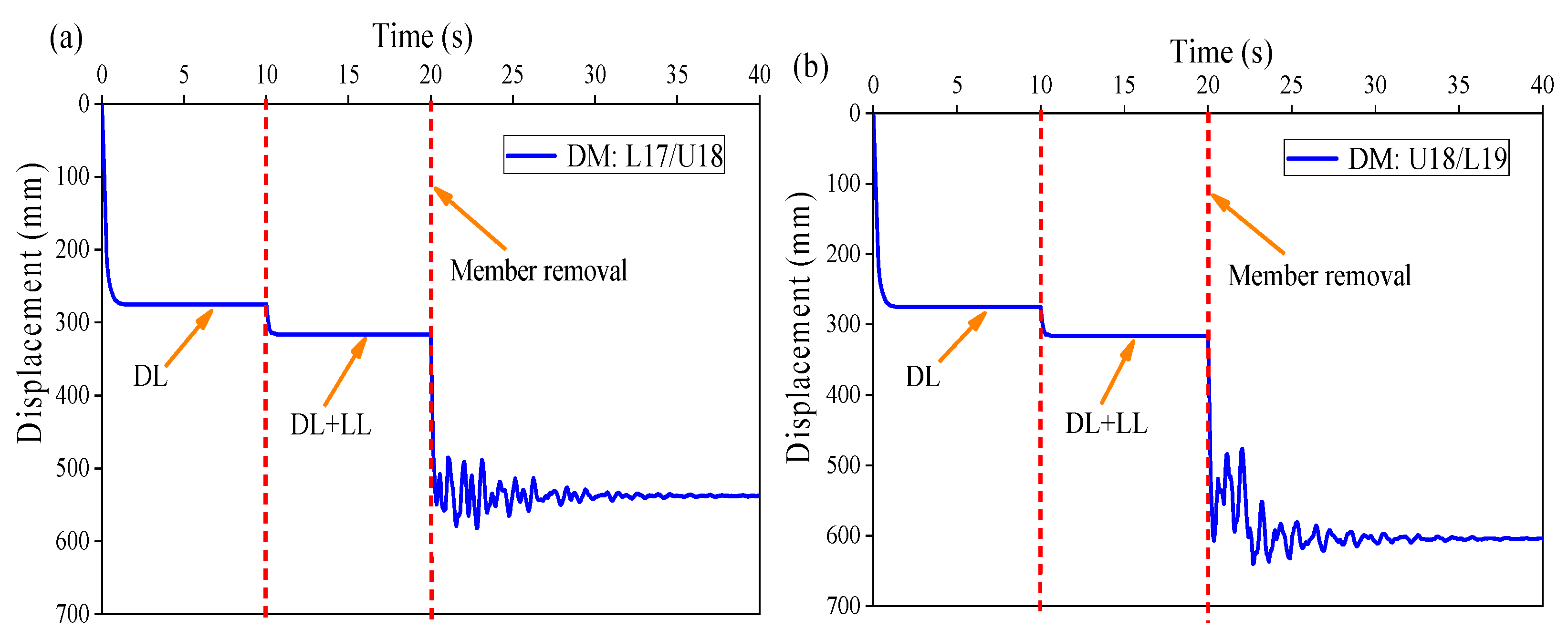
| MR Case # | Member Location | Member Type | Peak Displacement (mm) | Steady-State Displacement (mm) | Peak Displacement Ratio | Steady-State Displacement Ratio | Dynamic Factor |
|---|---|---|---|---|---|---|---|
| 1 | U16/L17 | DM | 472.67 | 424.44 | 1.07 | 0.96 | 1.11 |
| 2 | L17/U18 | DM | 582.46 | 537.55 | 1.32 | 1.22 | 1.08 |
| 3 | U18/L19 | DM | 640.34 | 603.95 | 1.45 | 1.37 | 1.06 |
| 4 | L19/U20 | DM | 485.28 | 440.9 | 1.1 | 1.00 | 1.10 |
| 5 | U20/L21 | DM | 456.91 | 408.15 | 1.04 | 0.93 | 1.12 |
| 6 | L21/U22 | DM | 509.46 | 434.46 | 1.16 | 0.99 | 1.17 |
| 7 | U22/L23 | DM | 461.98 | 400.83 | 1.05 | 0.91 | 1.15 |
| 8 | L19/L20 | LC | 438.35 | 398.83 | 1.00 | 0.91 | 1.11 |
| 9 | L20/L21 | LC | 429.96 | 396.63 | 0.98 | 0.90 | 1.11 |
| 10 | U19/U20 | UC | 440.87 | 398.84 | 1.00 | 0.91 | 1.11 |
| 11 | U20/U21 | UC | 424.77 | 396.69 | 0.96 | 0.90 | 1.07 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Shen, L.; Deng, S. A Generalized Framework for the Alternate Load Path Redundancy Analysis of Steel Truss Bridges Subjected to Sudden Member Loss Scenarios. Buildings 2022, 12, 1597. https://doi.org/10.3390/buildings12101597
Li H, Shen L, Deng S. A Generalized Framework for the Alternate Load Path Redundancy Analysis of Steel Truss Bridges Subjected to Sudden Member Loss Scenarios. Buildings. 2022; 12(10):1597. https://doi.org/10.3390/buildings12101597
Chicago/Turabian StyleLi, Huihui, Lian Shen, and Shuwen Deng. 2022. "A Generalized Framework for the Alternate Load Path Redundancy Analysis of Steel Truss Bridges Subjected to Sudden Member Loss Scenarios" Buildings 12, no. 10: 1597. https://doi.org/10.3390/buildings12101597
APA StyleLi, H., Shen, L., & Deng, S. (2022). A Generalized Framework for the Alternate Load Path Redundancy Analysis of Steel Truss Bridges Subjected to Sudden Member Loss Scenarios. Buildings, 12(10), 1597. https://doi.org/10.3390/buildings12101597






