Wind-Induced Response Characteristics and Equivalent Static Wind-Resistant Design Method of Spherical Inflatable Membrane Structures
Abstract
1. Introduction
2. Wind Tunnel Experiment
2.1. Summarization of Engineering Configurations
2.2. Experimental Apparatus and Procedure
2.3. Results of Wind Pressure Coefficients
3. Wind-Induced Response Analysis
3.1. Nonlinear Dynamic Time–History Analysis Method
3.2. Finite Element Model and Analysis Cases
3.3. Data Processing of Wind-Induced Responses
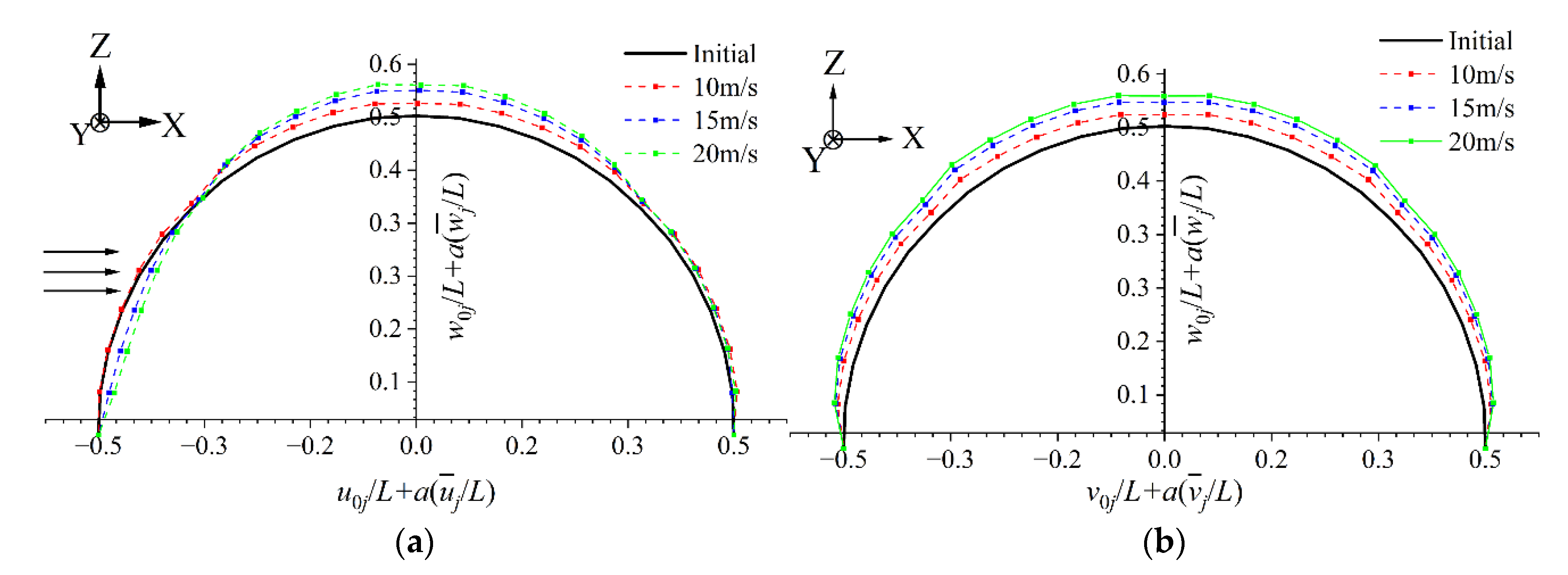
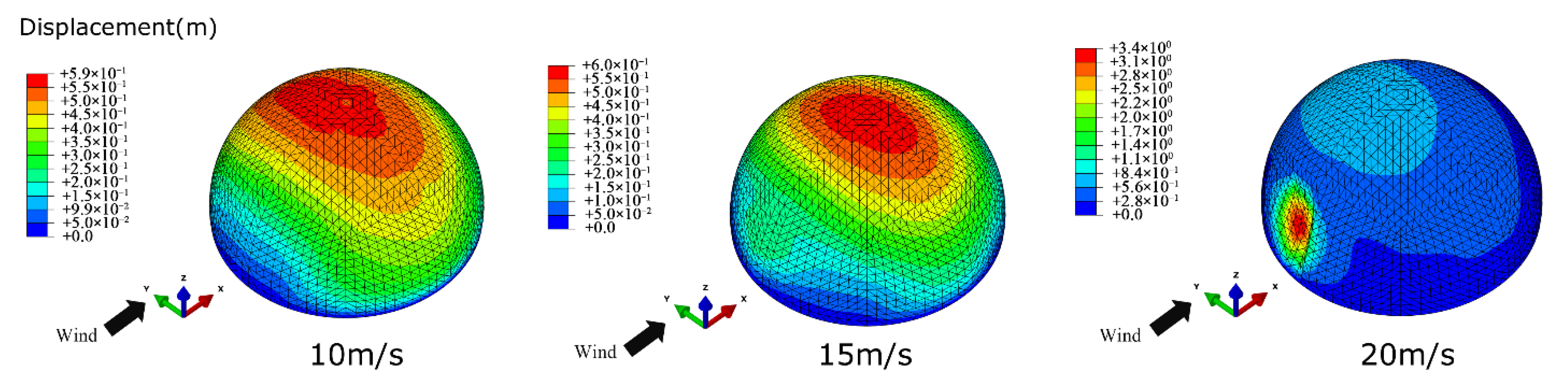
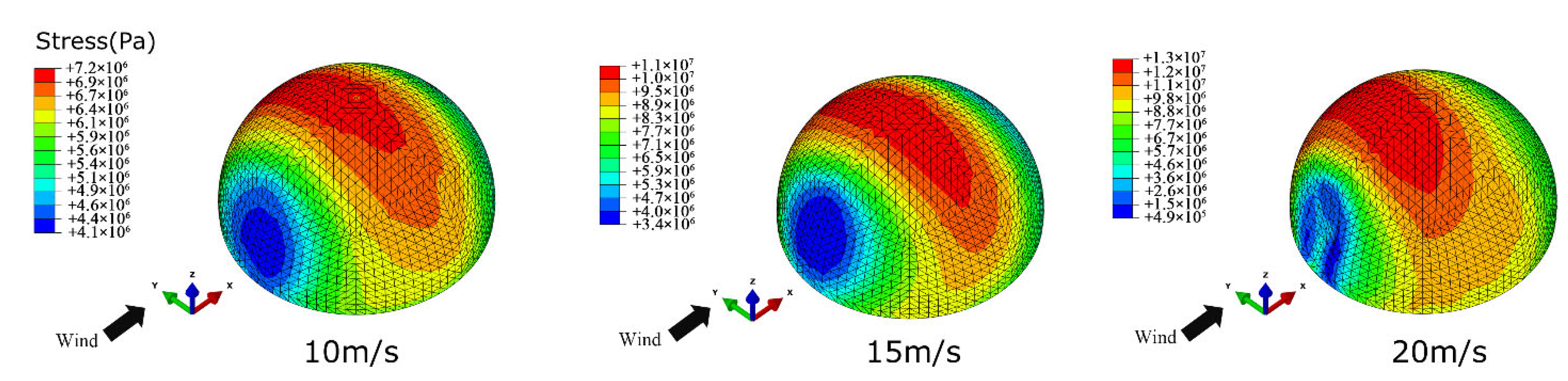
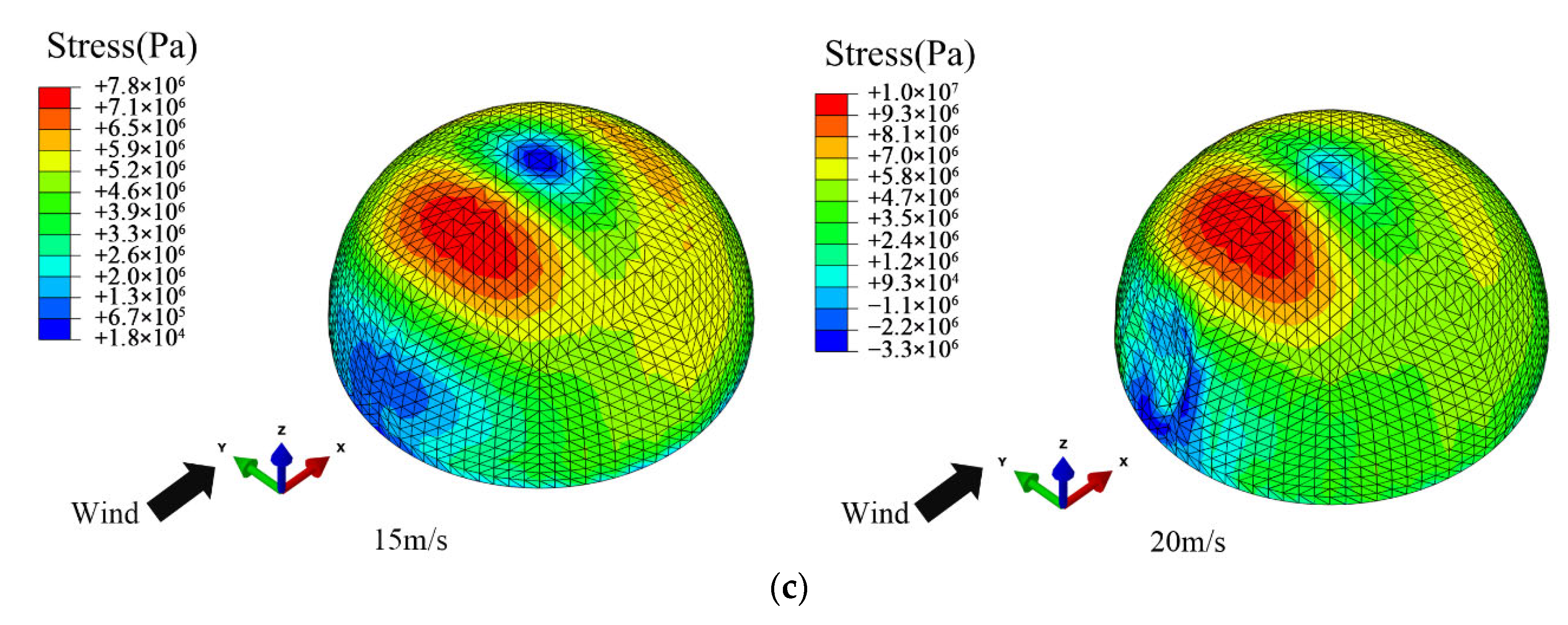
4. Wind-Induced Response Characteristics
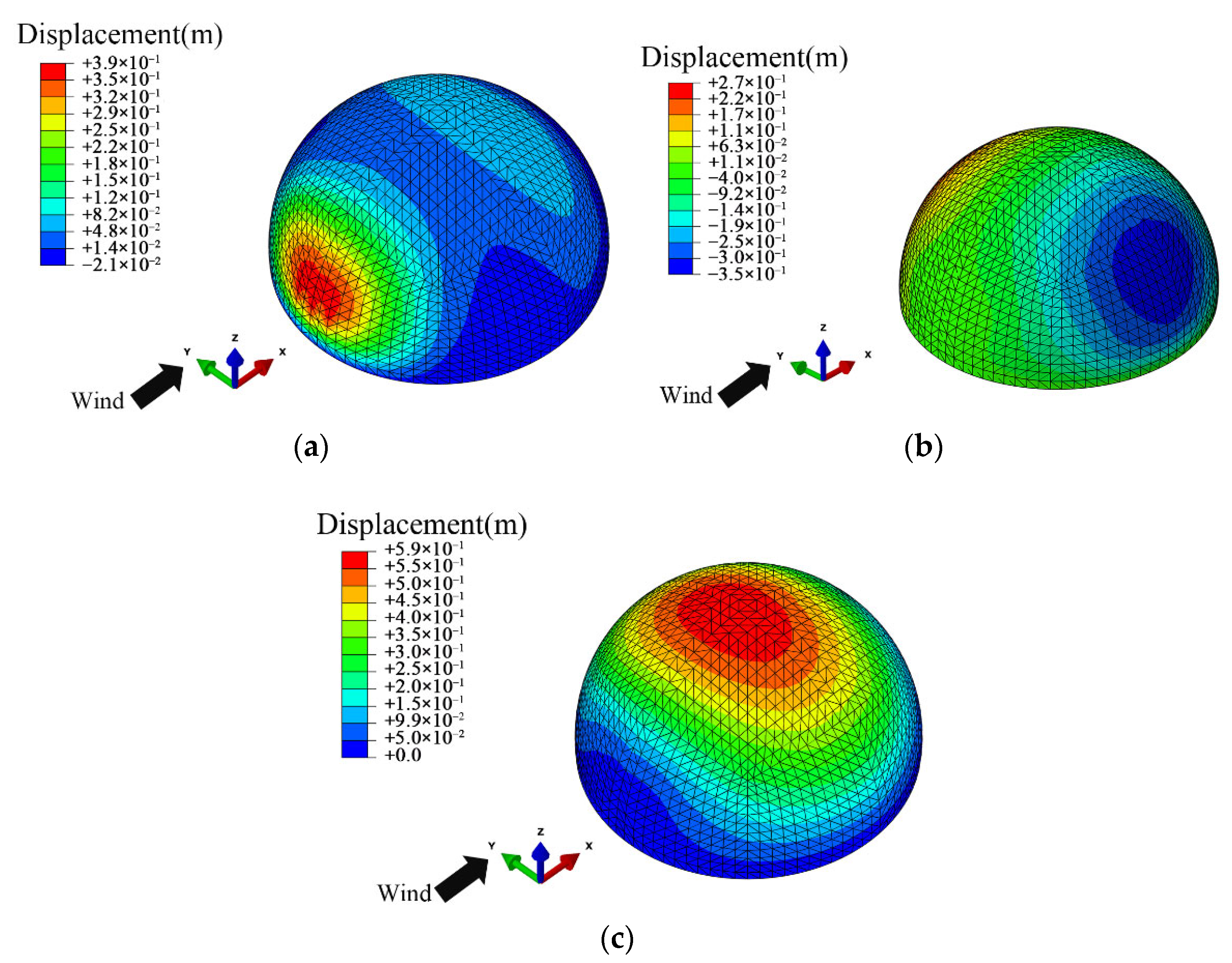
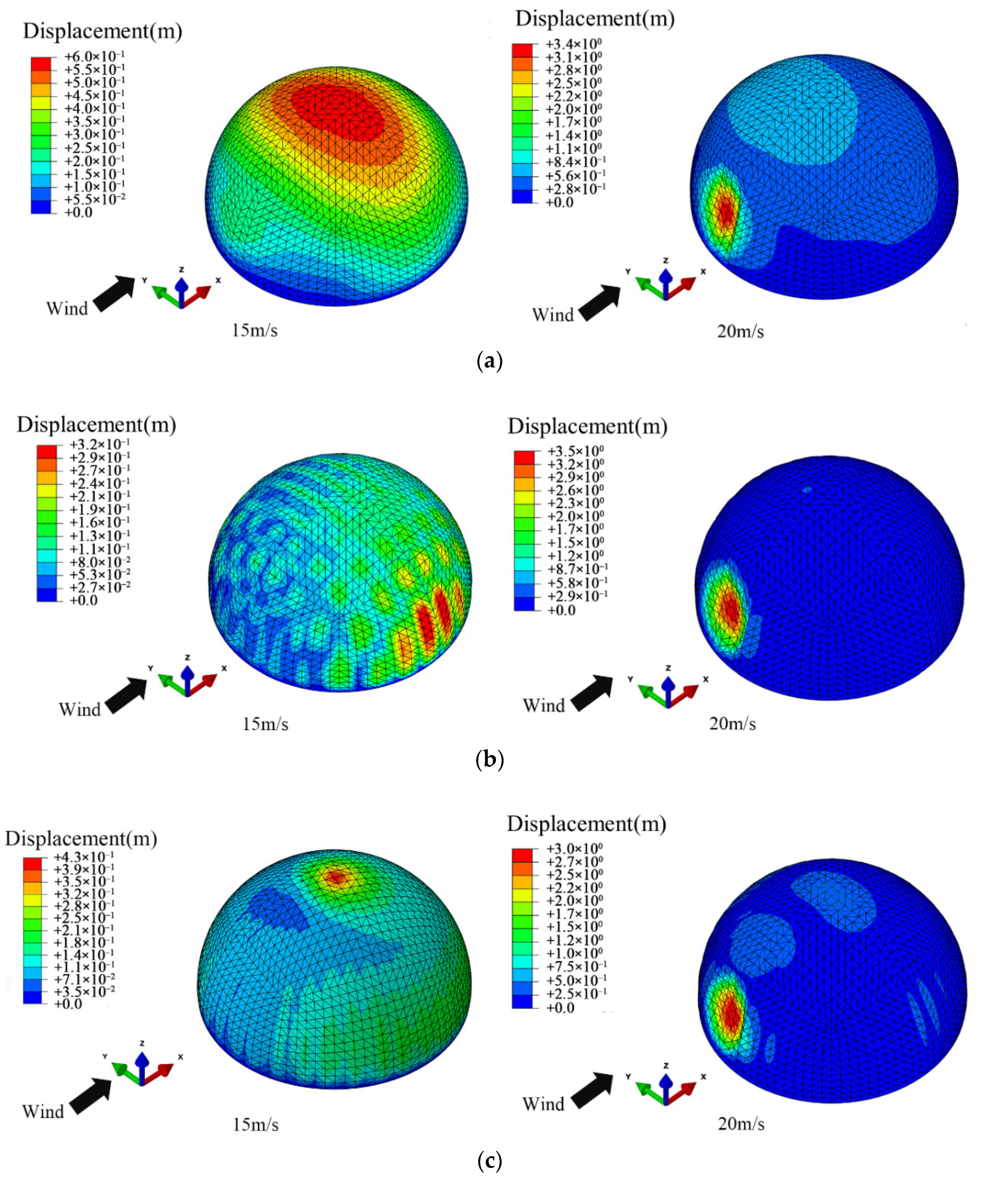
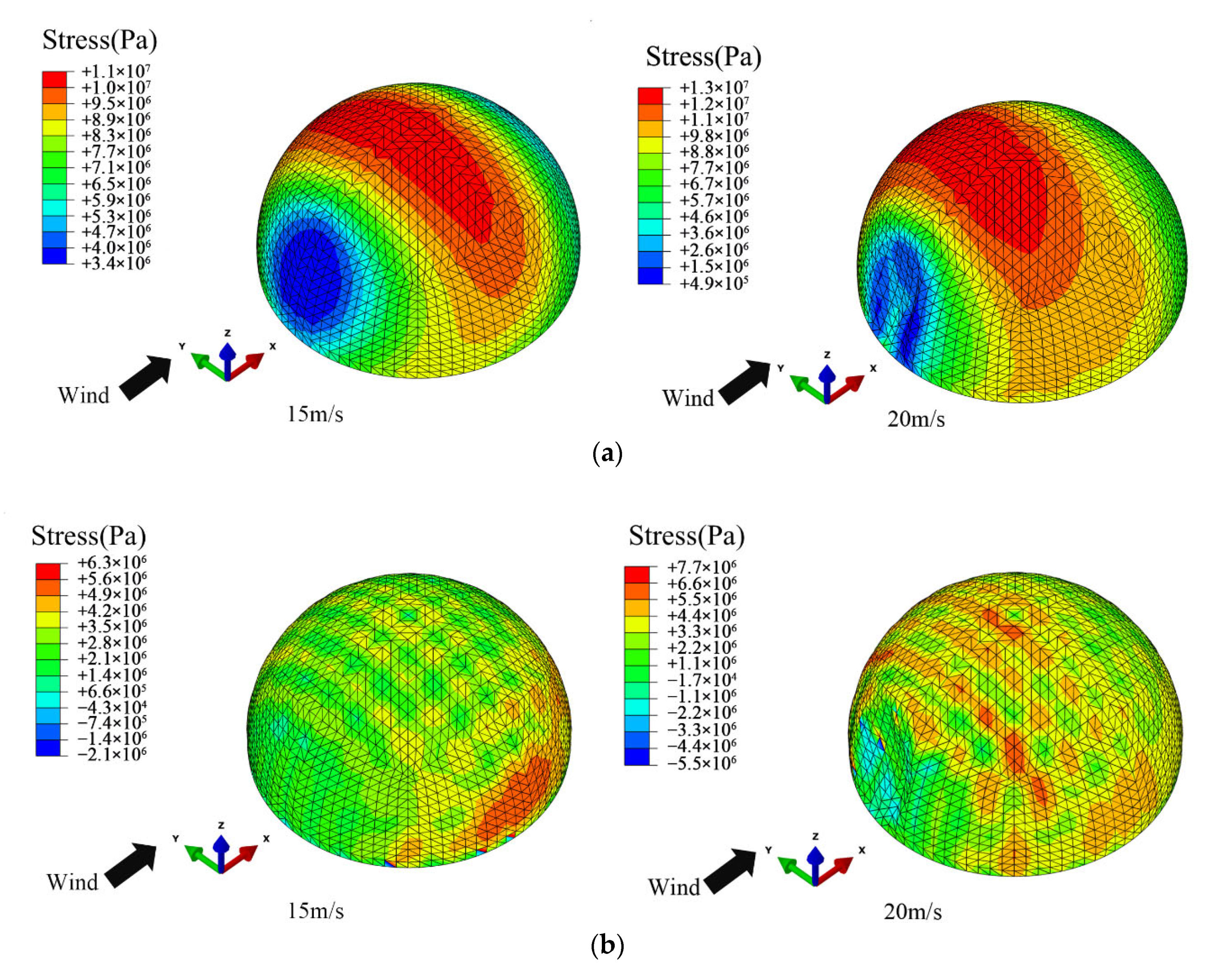
4.1. Wind-Induced Deformation
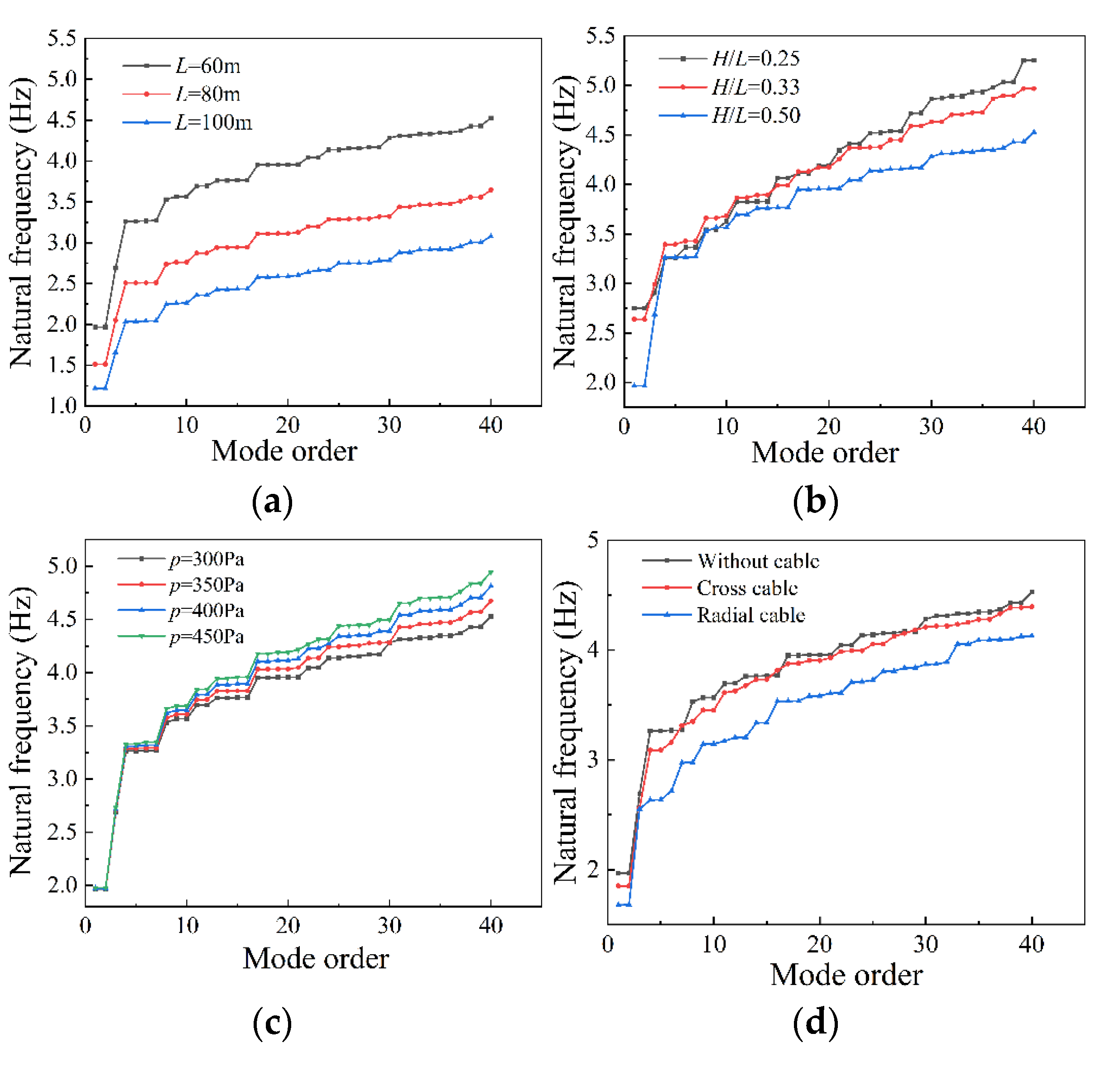
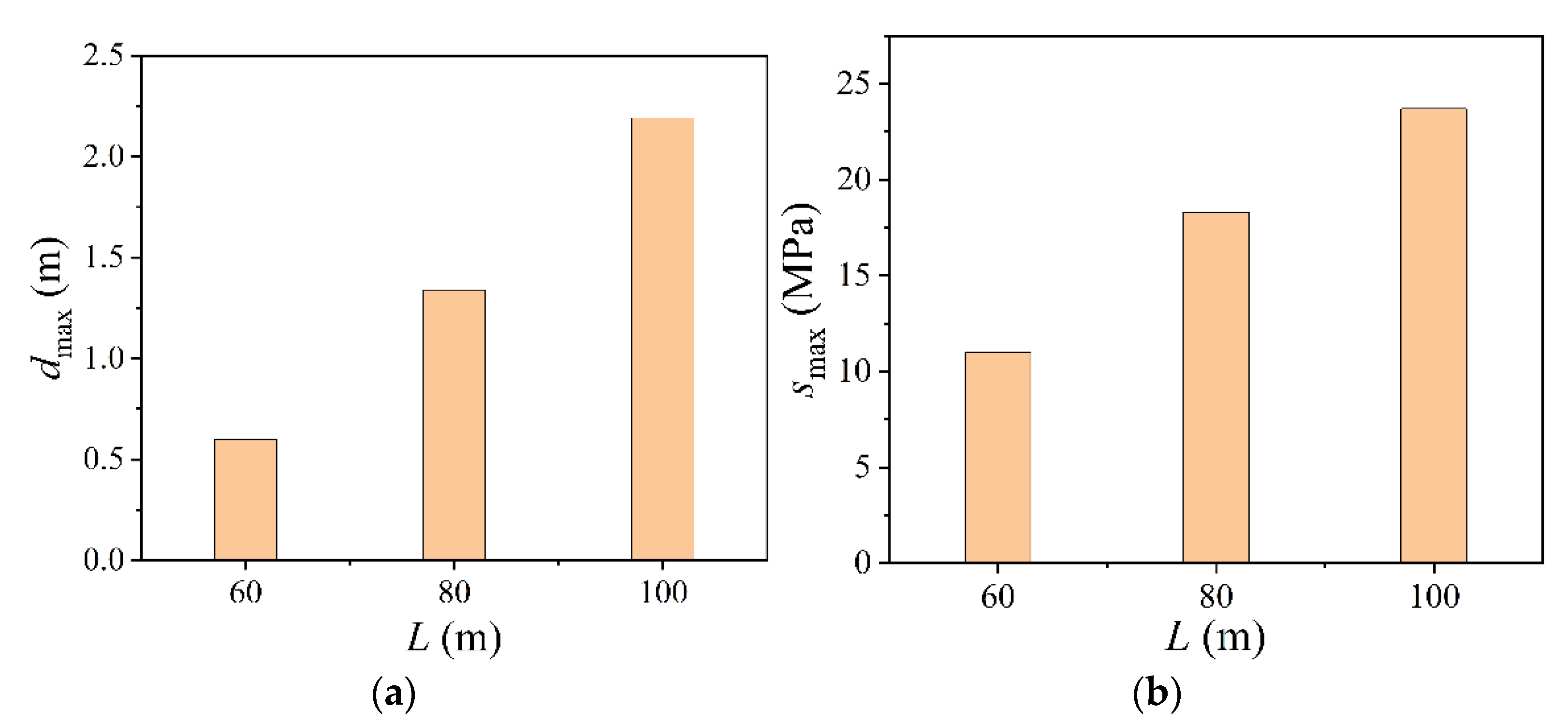
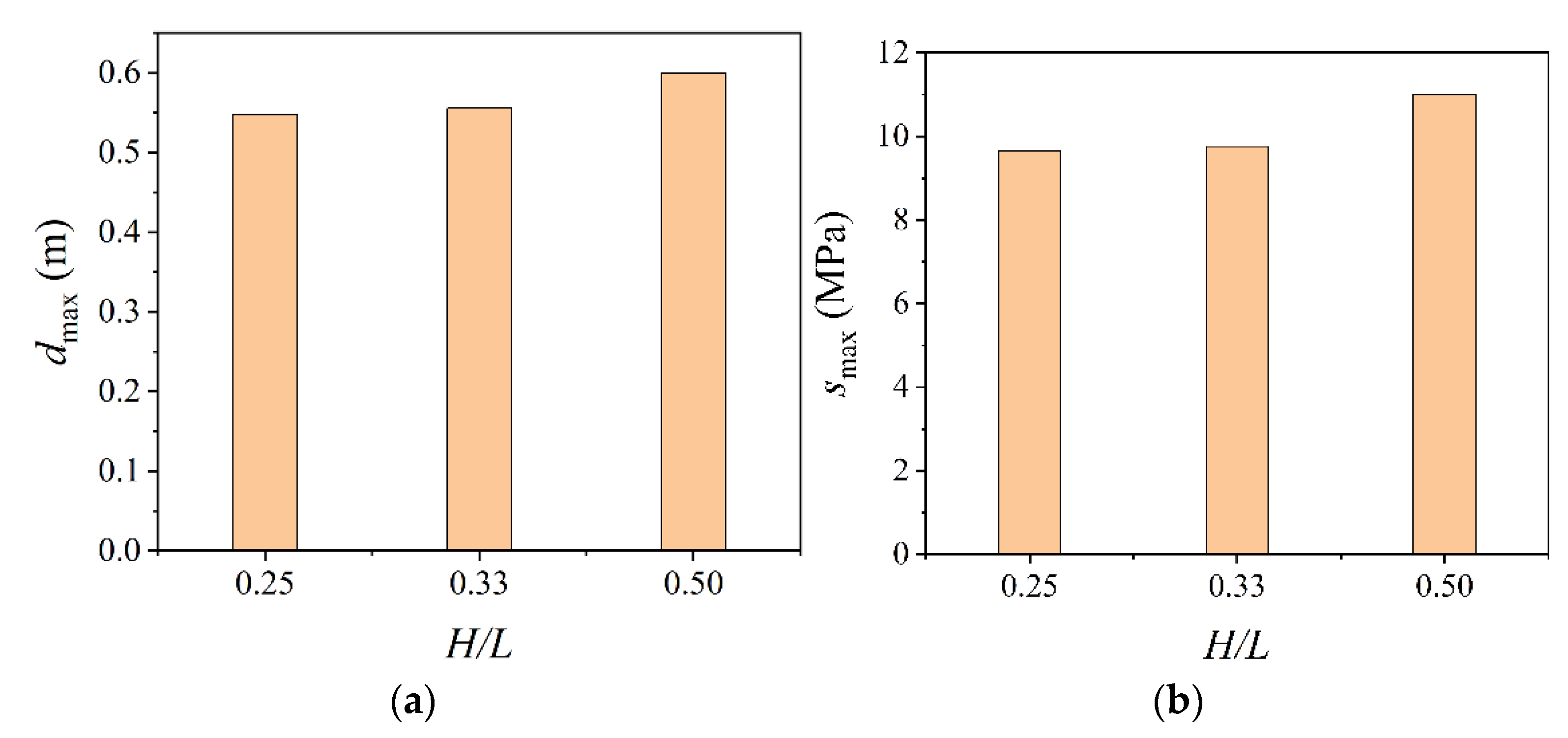
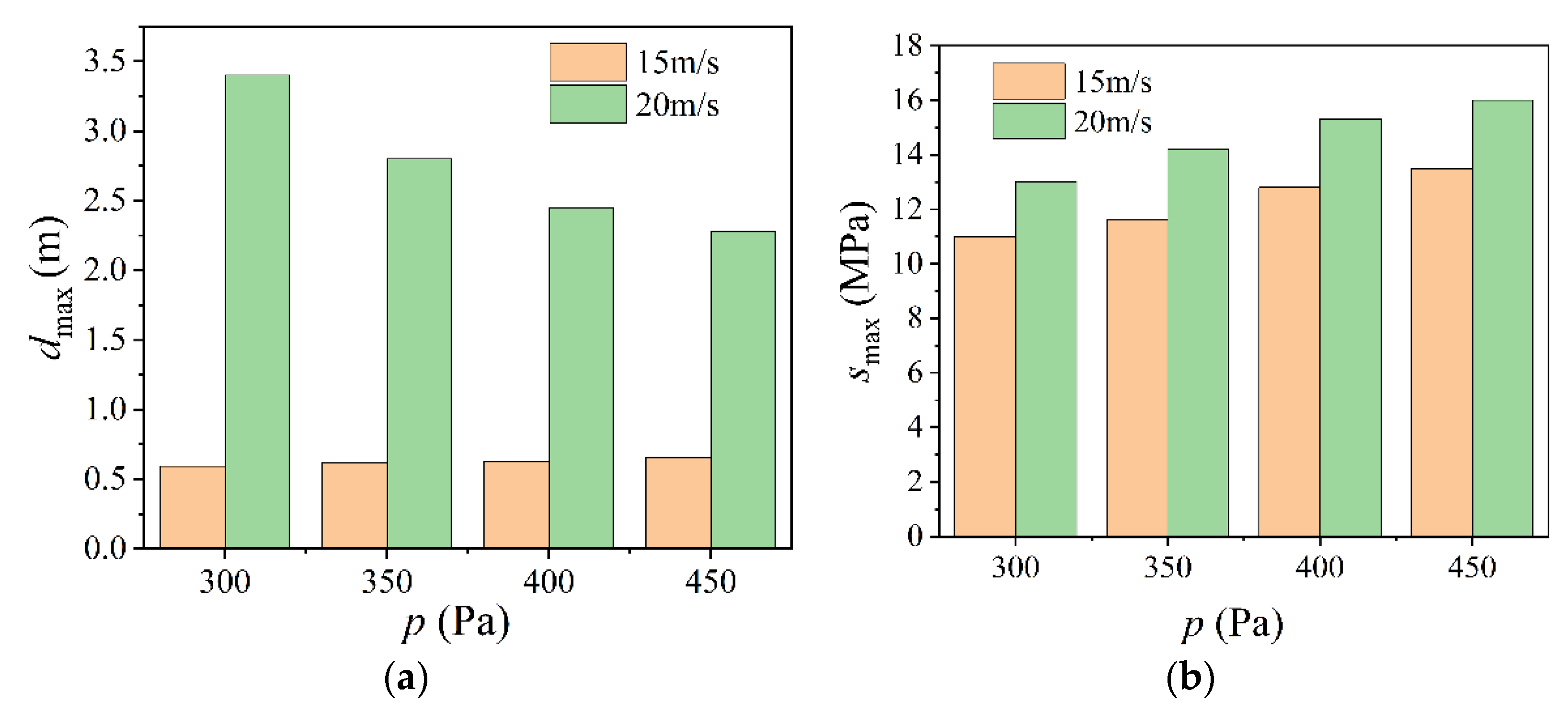
4.2. Parametric Analysis
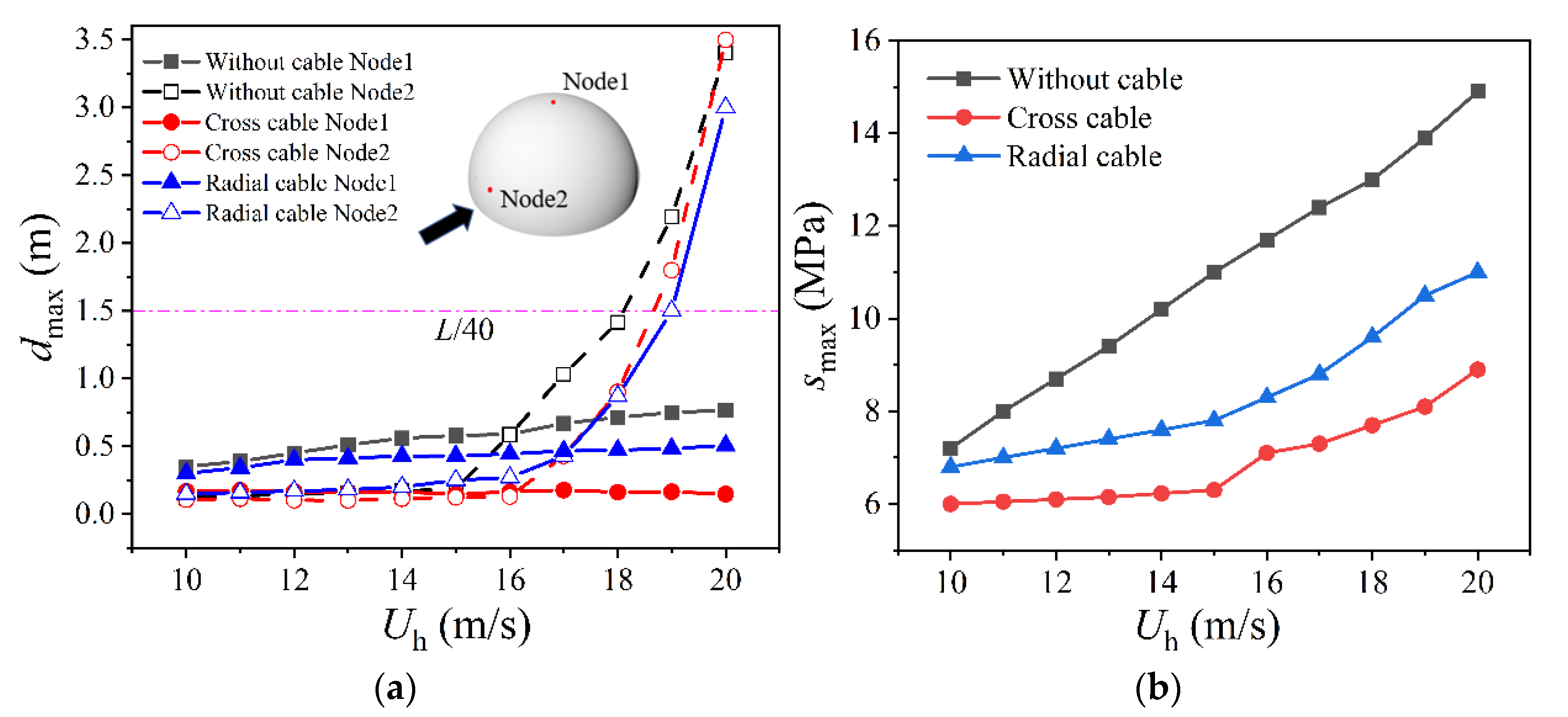
4.3. Influence of Cable Configurations
5. Equivalent Static Wind-Resistant Design Method
5.1. Basic Framework of the Method
5.2. Recommendations of the Factors
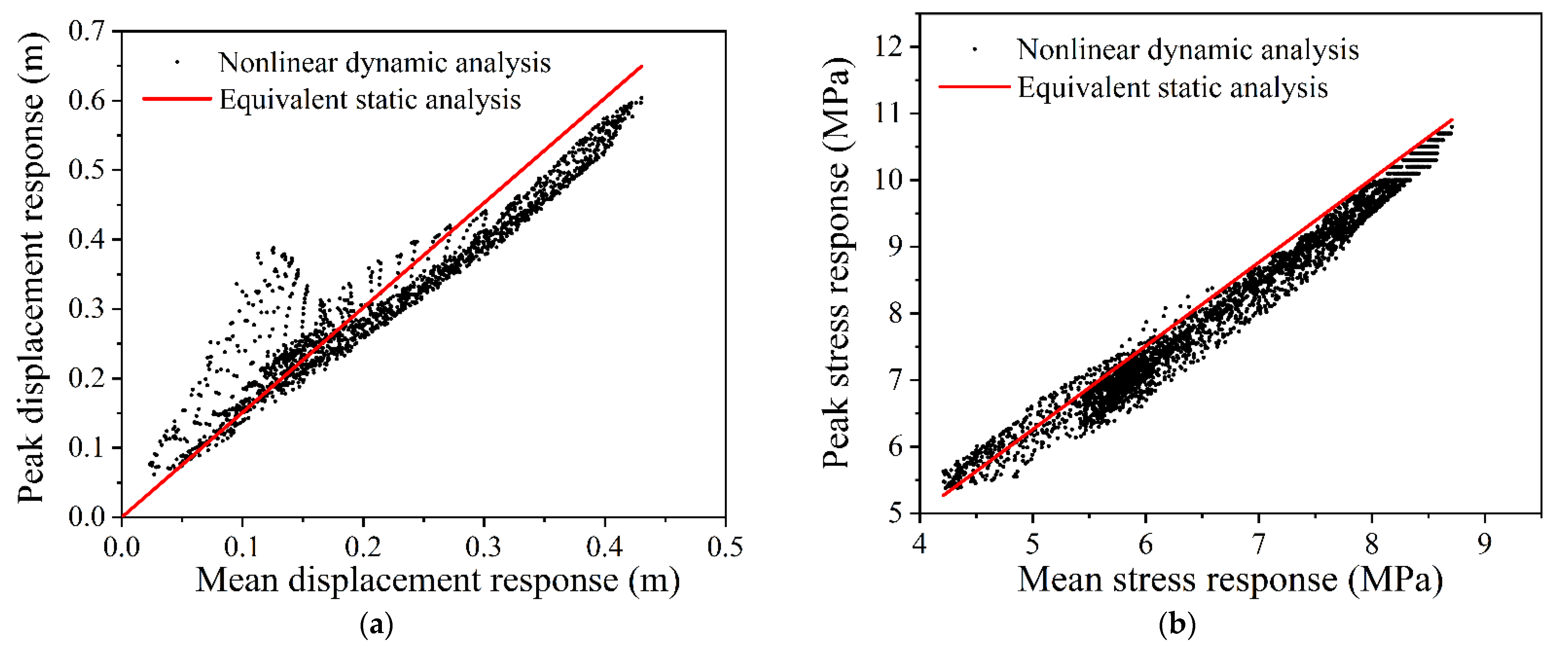
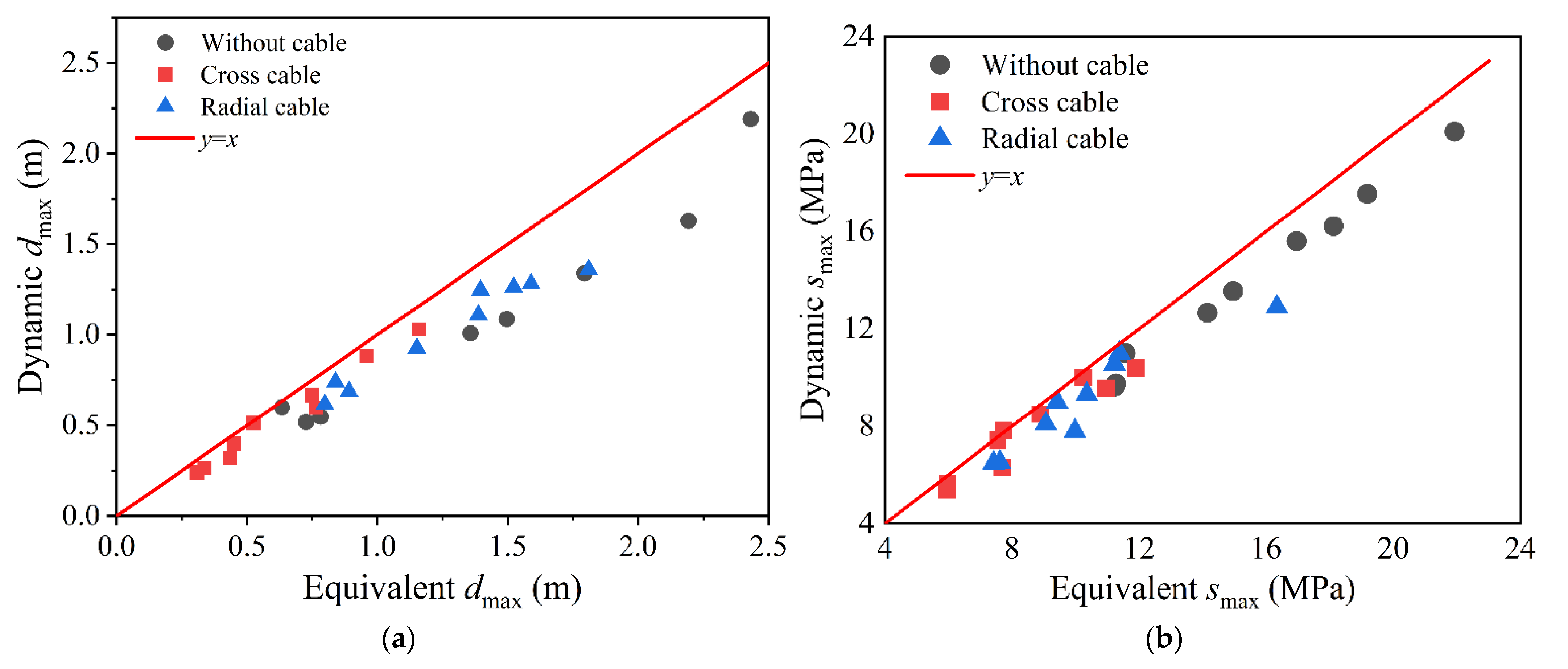
5.3. Result Verification
6. Conclusions
- (1)
- The raised wind-induced deflection at the top is dominant at low wind velocity. At high wind velocity, the concave wind-induced deflection on the windward region becomes dominant, which is prone to exceed the deflection limitation. In this case, the wind resistance of the structural windward region should be improved.
- (2)
- With the increment of span and rise–span ratio, the wind-induced responses of spherical inflatable membrane structures will be increased. However, the influence of the rise–span ratio is less significant than that of span. At high wind velocity, enhancing the internal pressure can effectively reduce deflection, but it also results in the increment of membrane stress. Particular attention should be paid to checking the strength.
- (3)
- Installing cables could effectively control the overall wind-induced deflection and stress. The control effect of cross cables proved to be better than radial cables. The reduction effect on the stress response improved with the increment of wind velocity. However, the effect on the displacement of the windward region is limited, particularly when it exceeds the deflection limitation.
- (4)
- An equivalent static analysis method for the wind-resistant design of spherical inflatable membrane structures based on gust response factors and nonlinear adjustment factors is developed. The empirical formulas of gust response factors and recommendation values of nonlinear adjustment factors for spherical inflatable membrane structures are provided for engineering reference. The equivalent static analysis results well envelope the nonlinear dynamic analysis results, and the coefficients of determination reach 0.98. The method proved to be feasible.
- (5)
- The gust response and nonlinear adjustment factors given in this paper are only applicable to the spherical inflatable membrane structures under given conditions. For other conditions, the factors need to be further calculated. In addition, it is found in this study that the spherical inflatable membrane structures are subject to buckling instability at a certain wind velocity. The critical wind velocities at which this instability occurs need to be further investigated.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Torsing, R.; Oosterman, K.; Bakker, J.; Hinssen, M.; Bosveld, I.; Huijsmans, T. The Shaded Dome™: A Smart, Cool & Adaptable Facility for Sport Venues. Procedia Eng. 2016, 147, 848–853. [Google Scholar] [CrossRef][Green Version]
- Gosling, P.; Bridgens, B.; Zhang, L. Adoption of a reliability approach for membrane structure analysis. Struct. Saf. 2013, 40, 39–50. [Google Scholar] [CrossRef]
- Pauletti, R.M.D.O. Some issues on the design and analysis of pneumatic structures. Int. J. Struct. Eng. 2010, 1, 217–240. [Google Scholar] [CrossRef]
- Kromoser, B.; Huber, P. Pneumatic Formwork Systems in Structural Engineering. Adv. Mater. Sci. Eng. 2016, 2016, 4724036. [Google Scholar] [CrossRef]
- Uematsu, Y.; Yamamura, R. Experimental Study of Wind Loads on Domed Free Roofs. In Proceedings of the XV Conference of the Italian Association for Wind Engineering, Naples, Italy, 9–12 September 2018; pp. 716–729. [Google Scholar] [CrossRef]
- Cheon, D.J.; Kim, Y.C.; Lee, J.H.; Yoon, S.W. Experimental Investigation of Wind Pressure Characteristics for Cladding of Dome Roofs. Materials 2021, 14, 5266. [Google Scholar] [CrossRef] [PubMed]
- Park, M.J.; Yoon, S.W.; Kim, Y.C.; Cheon, D.J. Wind Pressure Characteristics Based on the Rise-Span Ratio of Spherical Domes with Openings on the Roof. Buildings 2022, 12, 576. [Google Scholar] [CrossRef]
- Taylor, T. Wind pressures on a hemispherical dome. J. Wind Eng. Ind. Aerodyn. 1992, 40, 199–213. [Google Scholar] [CrossRef]
- Cheng, C.; Fu, C. Characteristic of wind loads on a hemispherical dome in smooth flow and turbulent boundary layer flow. J. Wind Eng. Ind. Aerodyn. 2010, 98, 328–344. [Google Scholar] [CrossRef]
- Srivastava, N.K.; Turkkan, N. Experimental determination of wind pressure distribution for cylindrical and spherical flexible membrane structures. Can. J. Civil Eng. 1995, 22, 23–31. [Google Scholar] [CrossRef]
- Turkkan, N.; Srivastava, N.K. Prediction of wind load distribution for air-supported structures using neural networks. Can. J. Civil Eng. 1995, 22, 453–461. [Google Scholar] [CrossRef]
- Uematsu, Y.; Tsuruishi, R. Wind load evaluation system for the design of roof cladding of spherical domes. J. Wind Eng. Ind. Aerodyn. 2008, 96, 2054–2066. [Google Scholar] [CrossRef]
- Irwin, H.P.A.H.; Wardlaw, R. A wind tunnel investigation of a retractable fabric roof for the Montreal Olympic stadium. In Proceedings of the Fifth International Conference on Wind Engineering, Fort Collins, CO, USA, 8–14 July 1979; pp. 925–938. [Google Scholar] [CrossRef]
- Kassem, M.; Novak, M. Experiments with Free Vibration of Light Roofs Backed by Cavities. J. Eng. Mech. 1990, 116, 1750–1763. [Google Scholar] [CrossRef]
- Kim, J.Y.; Yu, E.; Kim, D.Y.; Tamura, Y. Long-term monitoring of wind-induced responses of a large-span roof structure. J. Wind Eng. Ind. Aerodyn. 2011, 99, 955–963. [Google Scholar] [CrossRef]
- Wood, J.N.; Breuer, M.; De Nayer, G. Experimental studies on the instantaneous fluid–structure interaction of an air-inflated flexible membrane in turbulent flow. J. Fluid. Struct. 2018, 80, 405–440. [Google Scholar] [CrossRef]
- He, Y.; Shen, J. The Wind Response of Double Layer Membrane Gas Holders When Considering the Effect of FSI. J. Int. Assoc. Shell SP. 2017, 58, 125–135. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, T.; Yan, B.; Li, T.; Liu, M. Nonlinear motion-induced aerodynamic forces on large hyperbolic paraboloid roofs using LES. J. Wind Eng. Ind. Aerodyn. 2021, 216, 104703. [Google Scholar] [CrossRef]
- Kassem, M.; Novak, M. Response of hemispherical, air-supported structures to wind. J. Eng. Mech. 1991, 117, 1718–1737. [Google Scholar] [CrossRef]
- Rizzo, F.; Kopp, G.A.; Giaccu, G.F. Investigation of wind-induced dynamics of a cable net roof with aeroelastic wind tunnel tests. Eng. Struct. 2021, 229, 111569. [Google Scholar] [CrossRef]
- Yin, Y.; Chen, W.; Hu, J.; Zhao, B.; Wang, Q. In-situ measurement of structural performance of large-span air-supported dome under wind loads. Thin-Walled Struct. 2021, 169, 108476. [Google Scholar] [CrossRef]
- Takadate, Y.; Uematsu, Y. Steady and unsteady aerodynamic forces on a long-span membrane structure. J. Wind Eng. Ind. Aerodyn. 2019, 193, 103946. [Google Scholar] [CrossRef]
- Michalski, A.; Gawenat, B.; Gelenne, P.; Haug, E. Computational wind engineering of large umbrella structures. J. Wind Eng. Ind. Aerodyn. 2015, 144, 96–107. [Google Scholar] [CrossRef]
- Huang, H.; Xian, Y.; Zhang, W.; Guo, M.; Yang, K.; Xi, K. Analysis of Wind-Induced Vibration of a Spoke-Wise Cable–Membrane Structure. J. Mar. Sci. Eng. 2020, 8, 603. [Google Scholar] [CrossRef]
- Kandel, A.; Sun, X.; Wu, Y. Wind-induced responses and equivalent static design method of oval-shaped arch-supported membrane structure. J. Wind Eng. Ind. Aerodyn. 2021, 213, 104620. [Google Scholar] [CrossRef]
- Colliers, J.; Degroote, J.; Mollaert, M.; De Laet, L. Mean pressure coefficient distributions over hyperbolic paraboloid roof and canopy structures with different shape parameters in a uniform flow with very small turbulence. Eng. Struct. 2020, 205, 110043. [Google Scholar] [CrossRef]
- Irwin, H.P.A.H. The design of spires for wind simulation. J. Wind Eng. Ind. Aerodyn. 1981, 7, 361–366. [Google Scholar] [CrossRef]
- GB50009-2012; Load Code for the Design of Building Structures. China Architecture and Building Press: Beijing, China, 2012. (In Chinese)
- Qiu, Y.; He, H.; Xu, C.; San, B. Aerodynamic optimization design of single-layer spherical domes using kriging surrogate model. Adv. Struct. Eng. 2021, 24, 2105–2118. [Google Scholar] [CrossRef]
- Opatowicz, D.; Radoń, U.; Zabojszcza, P. Assessment of the Effect of Wind Load on the Load Capacity of a Single-Layer Bar Dome. Buildings 2020, 10, 179. [Google Scholar] [CrossRef]
- Riches, C.; Gosling, P. Pneumatic structures: A review of concepts, applications and analytical methods. In Proceedings of the IASS International Congress, Sydney, Australia, 5–9 October 1998; pp. 874–882. [Google Scholar]
- Picozzi, V.; Malasomma, A.; Avossa, A.M.; Ricciardelli, F. The Relationship between Wind Pressure and Pressure Coefficients for the Definition of Wind Loads on Buildings. Buildings 2022, 12, 225. [Google Scholar] [CrossRef]
- Holmes, J.D.; Allsop, A.C.; Ginger, J.D. Gust durations, gust factors and gust response factors in wind codes and standards. Wind Struct. 2014, 19, 339–352. [Google Scholar] [CrossRef]
- Ding, W.; Uematsu, Y. Discussion of Design Wind Loads on a Vaulted Free Roof. Wind 2022, 2, 479–494. [Google Scholar] [CrossRef]

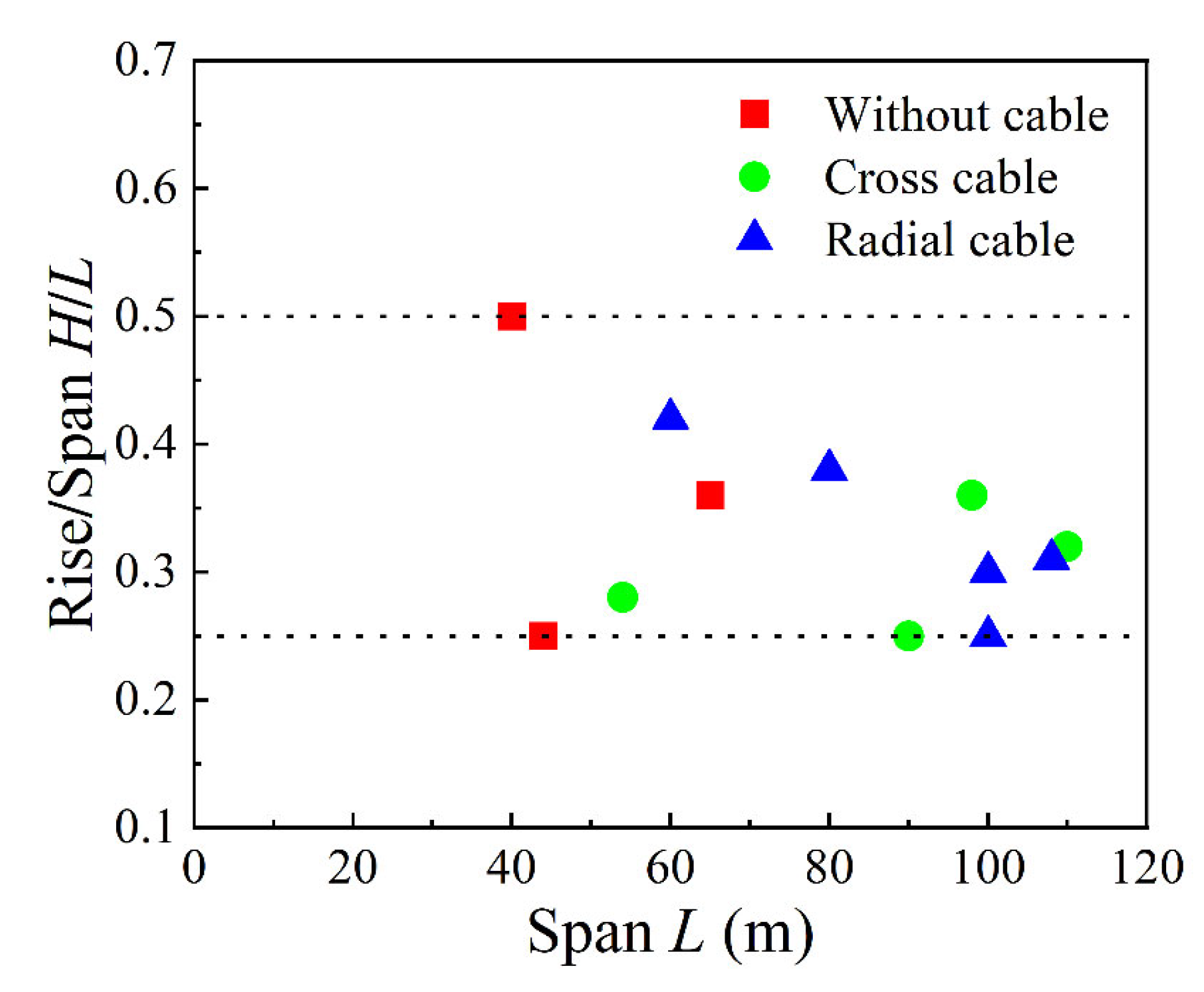
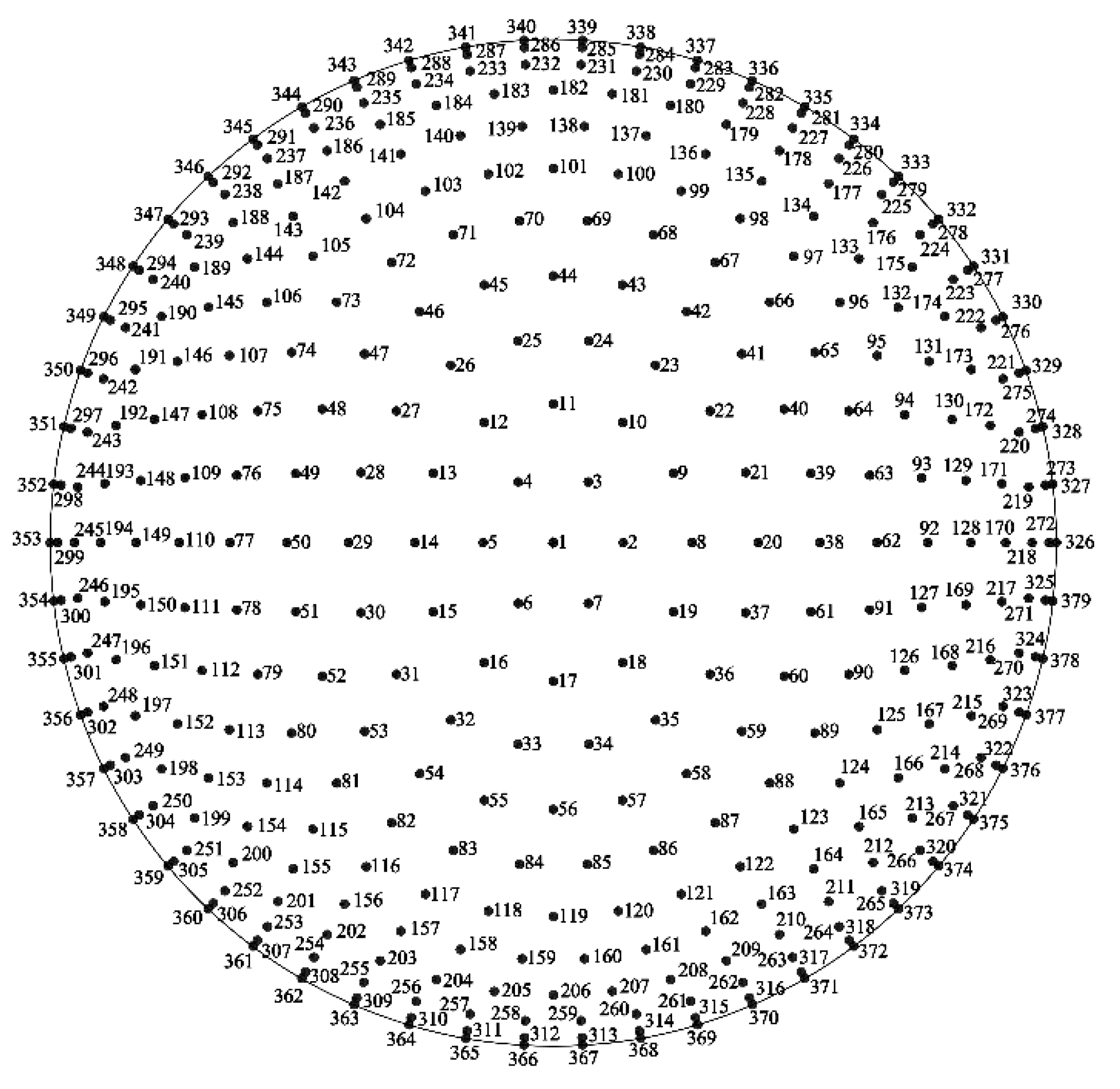


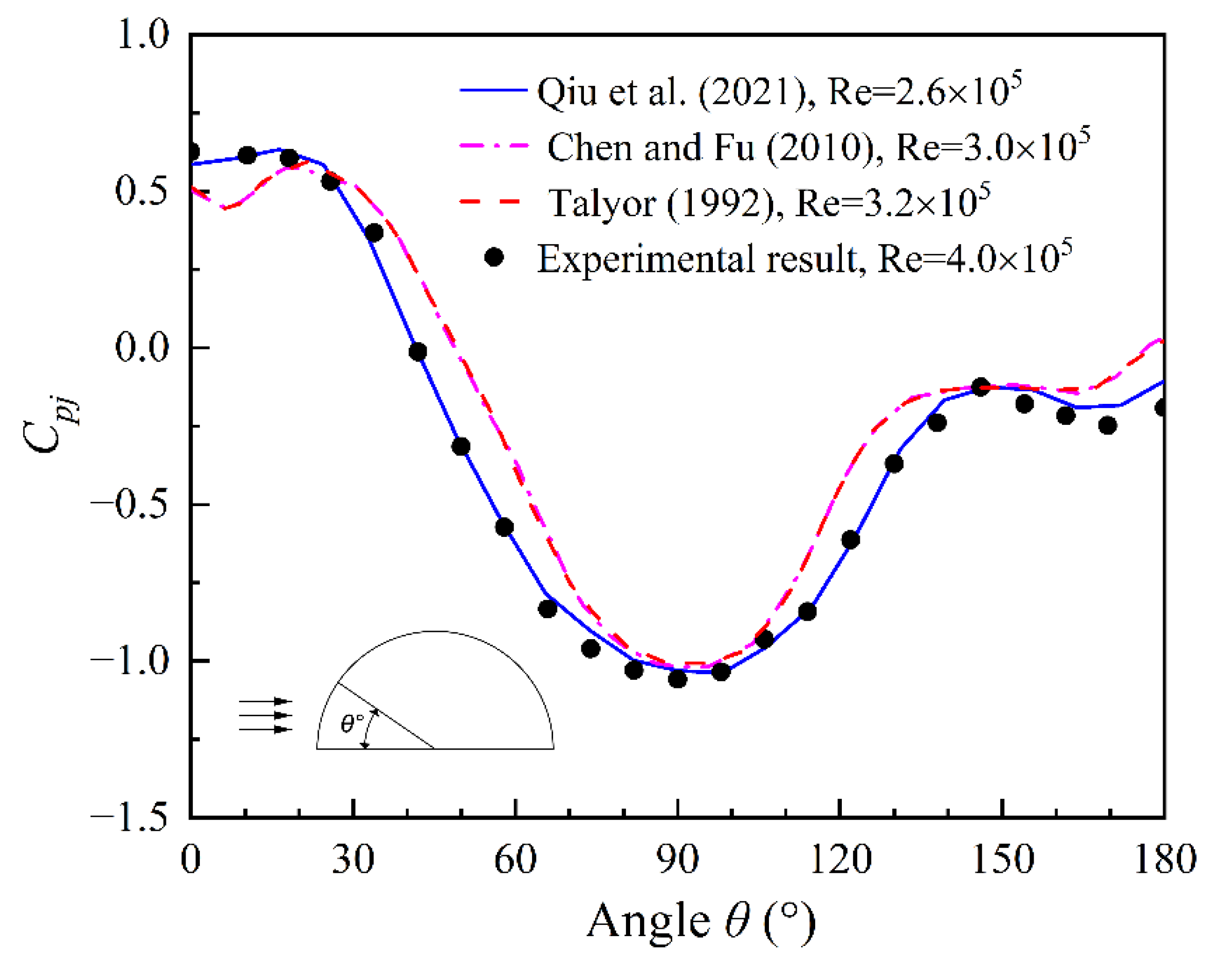

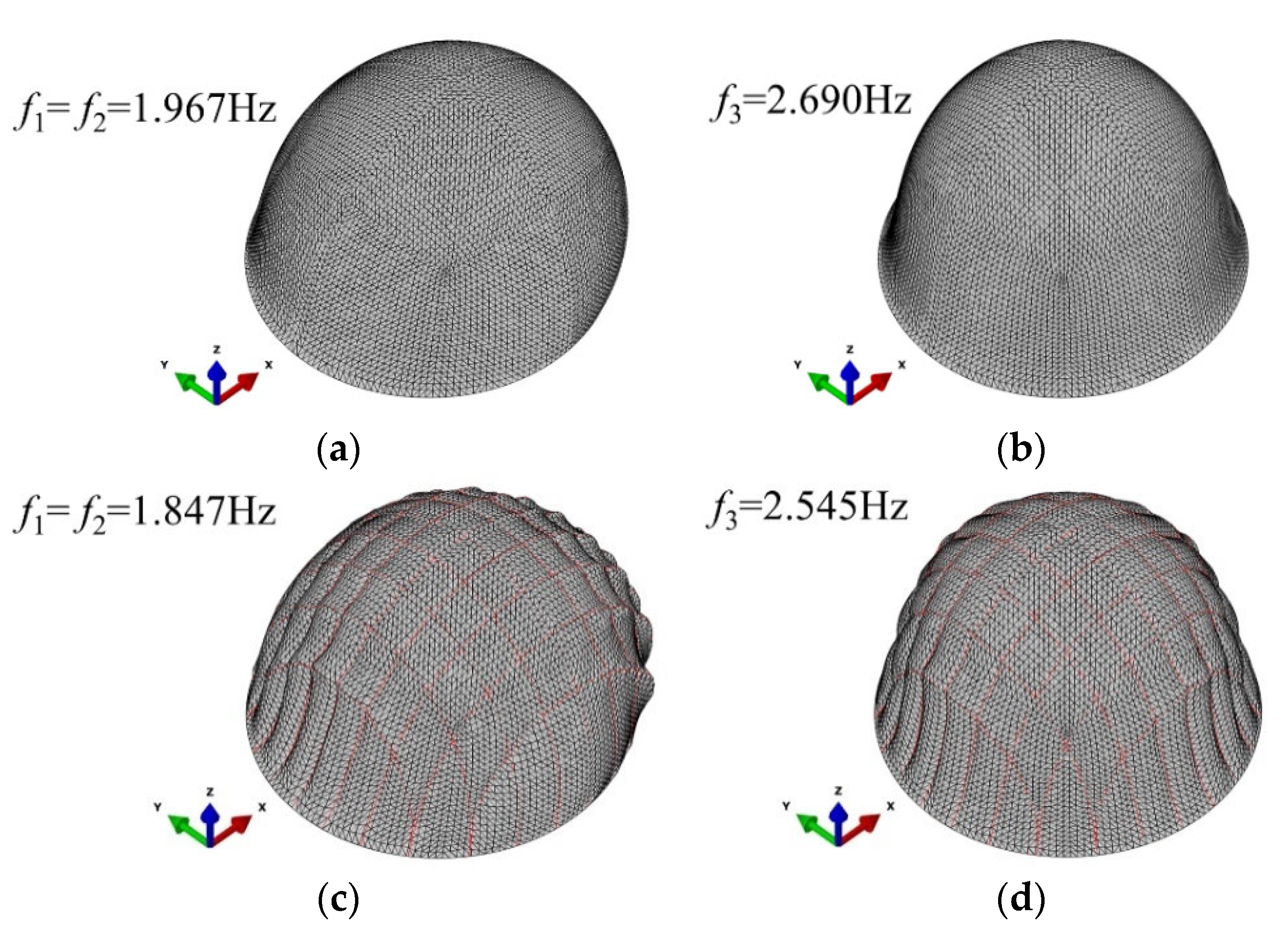
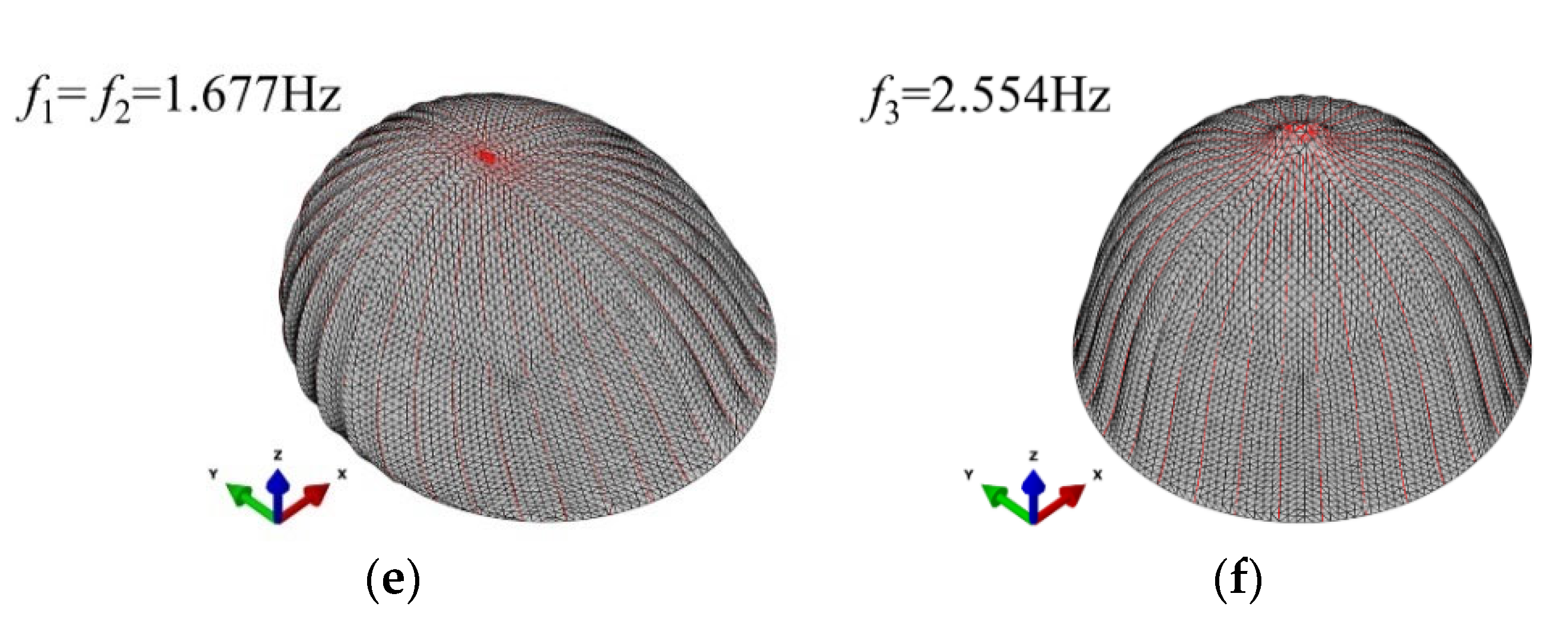


| Engineering Project | Span L (m) | Rise H (m) | Rise/Span H/L | Cable Configuration |
|---|---|---|---|---|
| Nalati Horse Dance Performance Hall | 80 | 30 | 0.38 | Radial cable |
| SOCT Children’s Paradise | 54 | 15 | 0.28 | Cross cable |
| Jinxiu Water Sports Carnival | 100 | 25 | 0.25 | Radial cable |
| Yanjing Shenmuyuan Water Park | 110 | 35 | 0.32 | Cross cable |
| Jiaozhou Sports Center | 108 | 33 | 0.31 | Radial cable |
| Junmei Gymnasium | 90 | 23 | 0.25 | Cross cable |
| Zibo International Convention and Exhibition Center | 98 | 35 | 0.36 | Cross cable |
| Xiangshawan Desert Art Museum | 100 | 30 | 0.30 | Radial cable |
| Large granary in Liaoning | 40 | 20 | 0.50 | Without cable |
| Zhongwei Starry Sky Theater | 60 | 25 | 0.42 | Radial cable |
| Inflated Airform for Pabco Gypsum near Las Vegas | 65 | 23.5 | 0.36 | Without cable |
| The Double Membrane cover in Exeter Maine | 44 | 11 | 0.25 | Without cable |
| No. | Span L (m) | Rise H (m) | Rise/Span H/L | Number of Taps |
|---|---|---|---|---|
| 1 | 0.6 | 0.30 | 0.50 | 379 |
| 2 | 0.6 | 0.20 | 0.33 | 217 |
| 3 | 0.6 | 0.15 | 0.25 | 217 |
| Membrane | Cable | ||
|---|---|---|---|
| Thickness | 1 × 10−3 m | Sectional area | 2 × 10−4 m2 |
| Elastic modulus | 600 MPa | Elastic modulus | 1.5 × 105 MPa |
| Poisson ratio | 0.32 | Poisson ratio | 0.3 |
| Density | 1.38 kg/m2 | Density | 7850 kg/m2 |
| Parameters | Range |
|---|---|
| Span L (m) | 60, 80, 100 |
| Rise–span H/L | 0.50, 0.33, 0.25 |
| Internal pressure p (Pa) | 300, 350, 400, 450 |
| Cable configuration | Without cables, cross cables, radial cables |
| Wind velocity Uh (m/s) | 10–20 (Interval of 1) |
| Response | Internal Pressure | H/L = 0.25 | H/L = 0.33 | H/L = 0.50 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| L = 60 m | L = 80 m | L = 100 m | L = 60 m | L = 80 m | L = 100 m | L = 60 m | L = 80 m | L = 100 m | ||
| Displacement | 300 Pa | 1.26 | 1.27 | 1.28 | 1.30 | 1.35 | 1.35 | 1.41 | 1.50 | 1.52 |
| 350 Pa | 1.24 | 1.25 | 1.26 | 1.25 | 1.32 | 1.32 | 1.40 | 1.50 | 1.50 | |
| 400 Pa | 1.22 | 1.23 | 1.23 | 1.23 | 1.30 | 1.30 | 1.40 | 1.48 | 1.50 | |
| 450 Pa | 1.20 | 1.21 | 1.21 | 1.21 | 1.28 | 1.28 | 1.40 | 1.48 | 1.50 | |
| Stress | 300 Pa | 1.19 | 1.20 | 1.20 | 1.21 | 1.22 | 1.23 | 1.24 | 1.24 | 1.24 |
| 350 Pa | 1.18 | 1.18 | 1.19 | 1.20 | 1.20 | 1.20 | 1.23 | 1.23 | 1.23 | |
| 400 Pa | 1.16 | 1.15 | 1.17 | 1.18 | 1.19 | 1.20 | 1.23 | 1.23 | 1.23 | |
| 450 Pa | 1.15 | 1.12 | 1.16 | 1.17 | 1.18 | 1.18 | 1.23 | 1.22 | 1.23 | |
| Response | Cable Configuration | Gust Response Factor | Nonlinear Adjustment Factor |
|---|---|---|---|
| Displacement | Without cable | 1.03 | |
| Cross cable | 1.04 | ||
| Radial cable | 1.07 | ||
| Stress | Without cable | 1.03 | |
| Cross cable | 1.02 | ||
| Radial cable | 1.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Wei, C.; Li, Z.; Zeng, C.; Zhao, J.; Hong, N.; Su, N. Wind-Induced Response Characteristics and Equivalent Static Wind-Resistant Design Method of Spherical Inflatable Membrane Structures. Buildings 2022, 12, 1611. https://doi.org/10.3390/buildings12101611
Chen Z, Wei C, Li Z, Zeng C, Zhao J, Hong N, Su N. Wind-Induced Response Characteristics and Equivalent Static Wind-Resistant Design Method of Spherical Inflatable Membrane Structures. Buildings. 2022; 12(10):1611. https://doi.org/10.3390/buildings12101611
Chicago/Turabian StyleChen, Zhaoqing, Chao Wei, Zhenmin Li, Cong Zeng, Junbin Zhao, Ningning Hong, and Ning Su. 2022. "Wind-Induced Response Characteristics and Equivalent Static Wind-Resistant Design Method of Spherical Inflatable Membrane Structures" Buildings 12, no. 10: 1611. https://doi.org/10.3390/buildings12101611
APA StyleChen, Z., Wei, C., Li, Z., Zeng, C., Zhao, J., Hong, N., & Su, N. (2022). Wind-Induced Response Characteristics and Equivalent Static Wind-Resistant Design Method of Spherical Inflatable Membrane Structures. Buildings, 12(10), 1611. https://doi.org/10.3390/buildings12101611






