Development of a Mix Design Method for Multiplexed Powder Self-Compacting Concrete Based on the Multiscale Rheological Threshold Theory
Abstract
1. Introduction
2. SCC Mix Design Method Based on Multiscale Rheological Threshold Theory
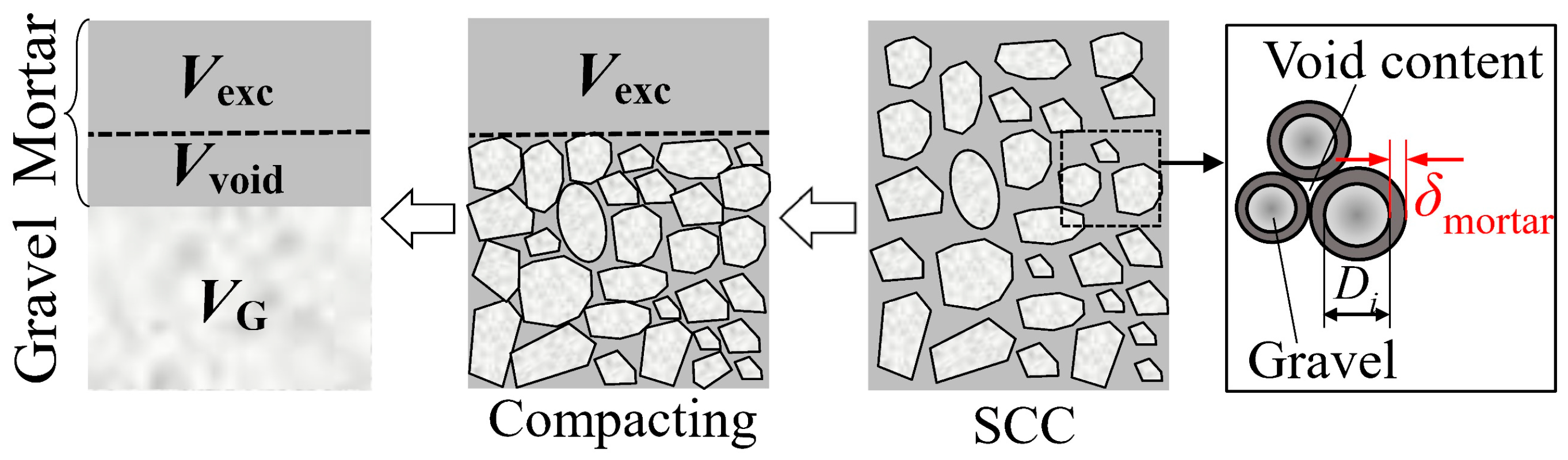
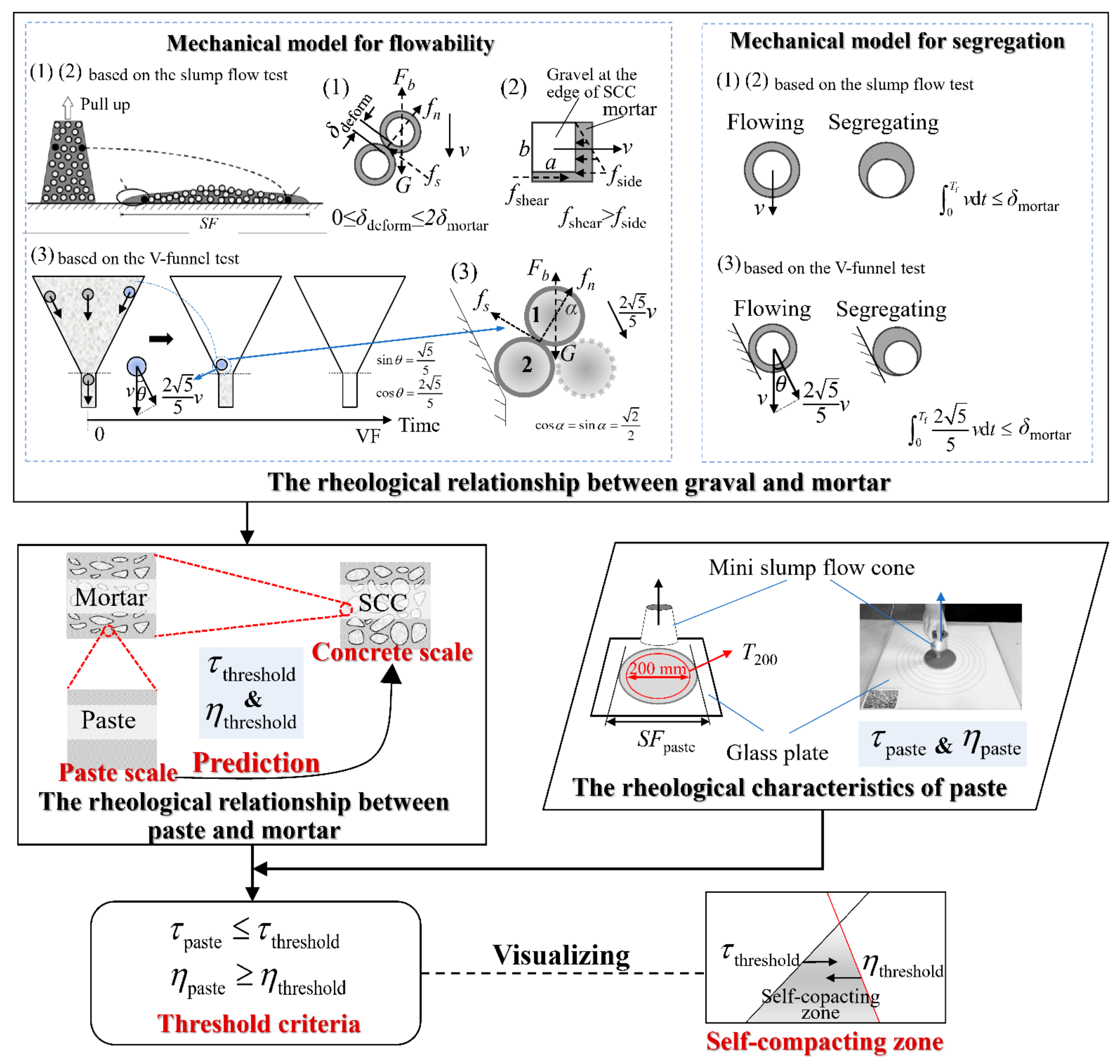
2.1. Multiscale Rheological Threshold Theory
2.2. Self-Compacting Zones
2.3. Limitation of Existing Research
3. Modification of Multi-Scale Threshold Theory
3.1. Materials, Test Design, and Test Method
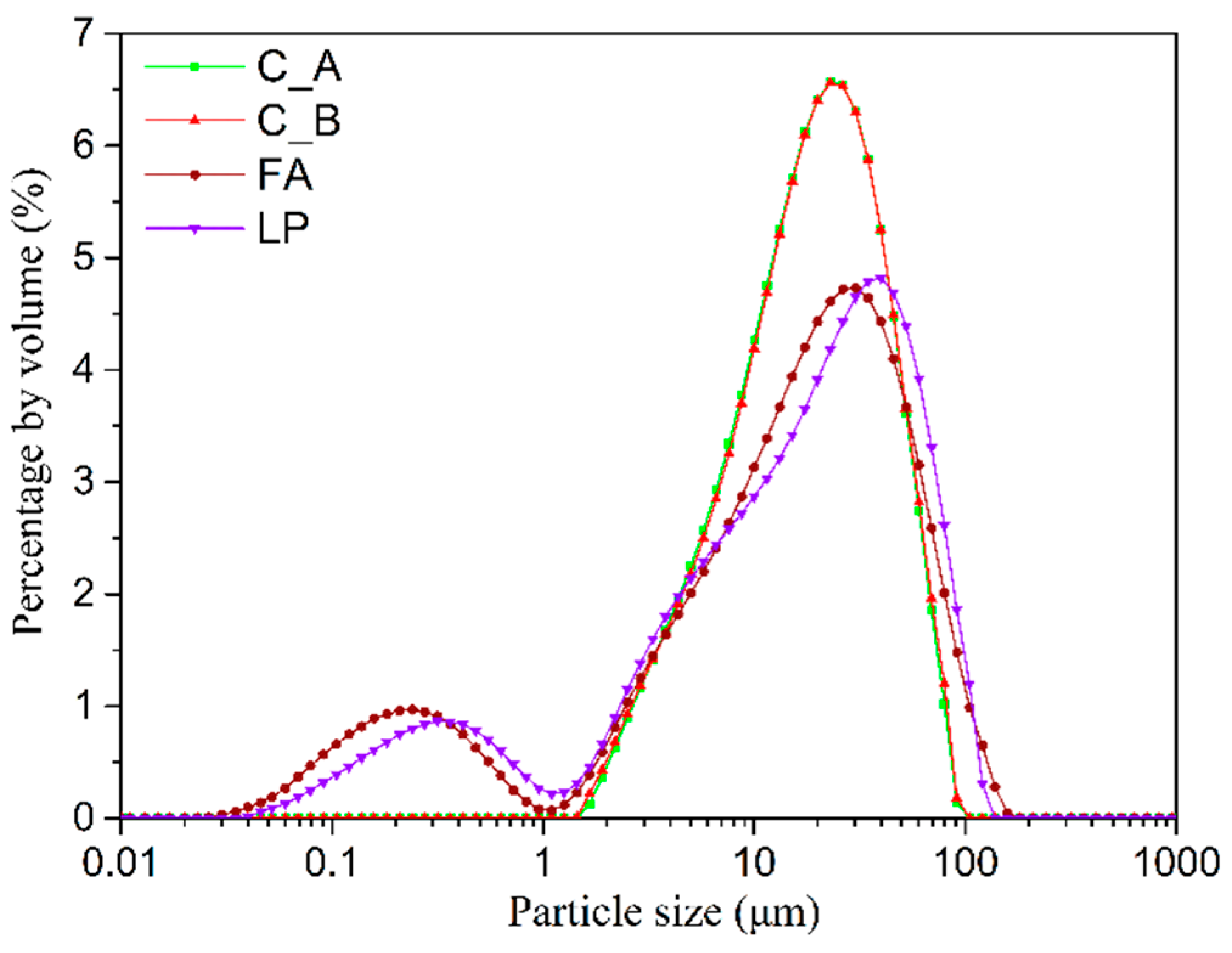
3.2. Modification of Powder Parameters
3.2.1. D50 and Span
3.2.2. Modification of the Powder Fitting Coefficient n
- On the occasion that D50 was similar, the bigger span, τthreshold was calculated to be lower than its real value. The powder fitting coefficient n seemed smaller.
- On the occasion that the span was similar, the bigger D50, τthreshold was calculated to be lower than its real value. The powder fitting coefficient n seemed smaller.
3.2.3. Modification of the Intrinsic Viscosity [η]
- The smaller D50 was, ηthreshold calculated was lesser than its real value. The intrinsic viscosity [η] seemed bigger.
- The bigger D50 was, ηthreshold calculated was bigger than its real value. The intrinsic viscosity [η] seemed smaller.
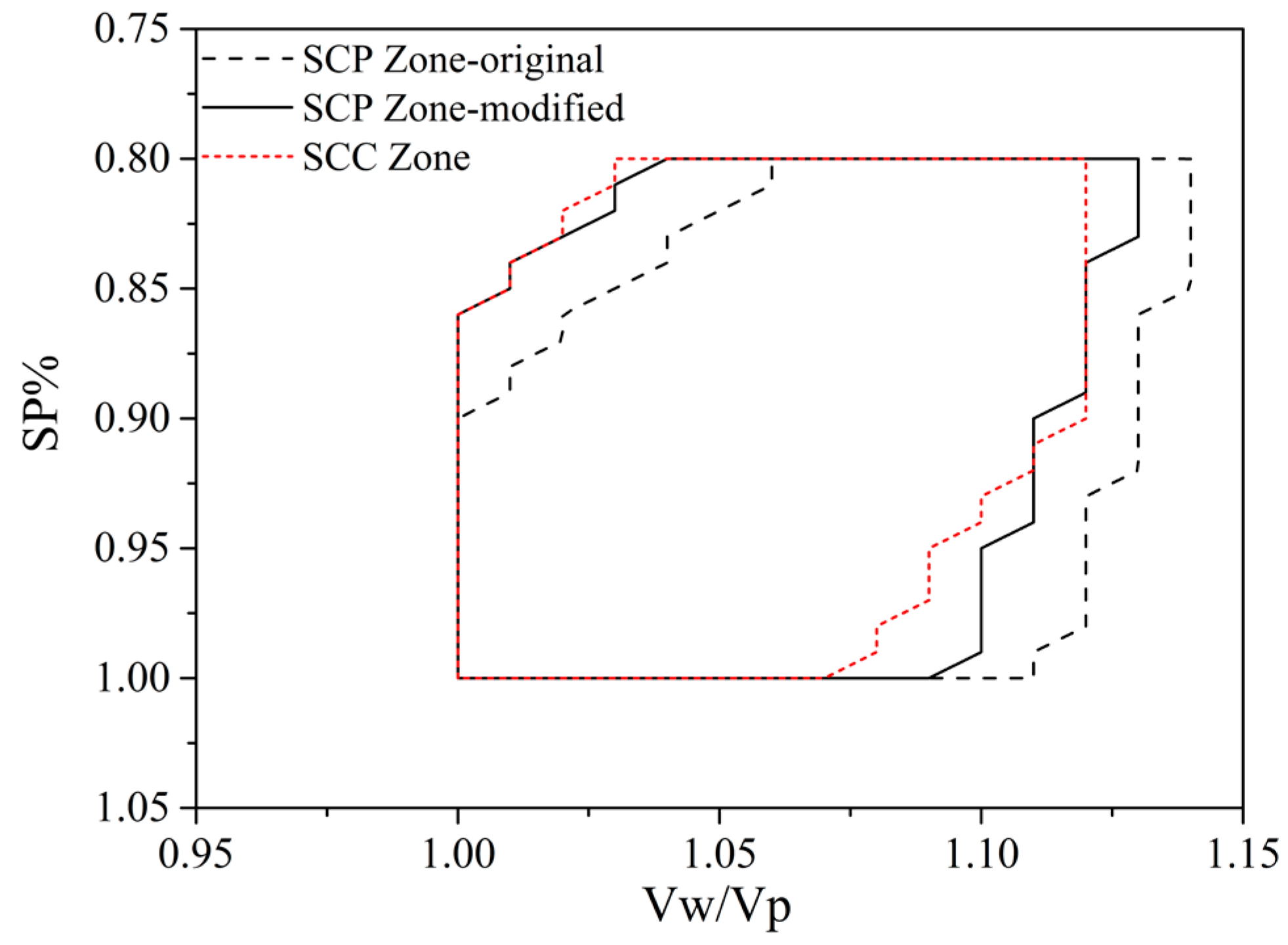
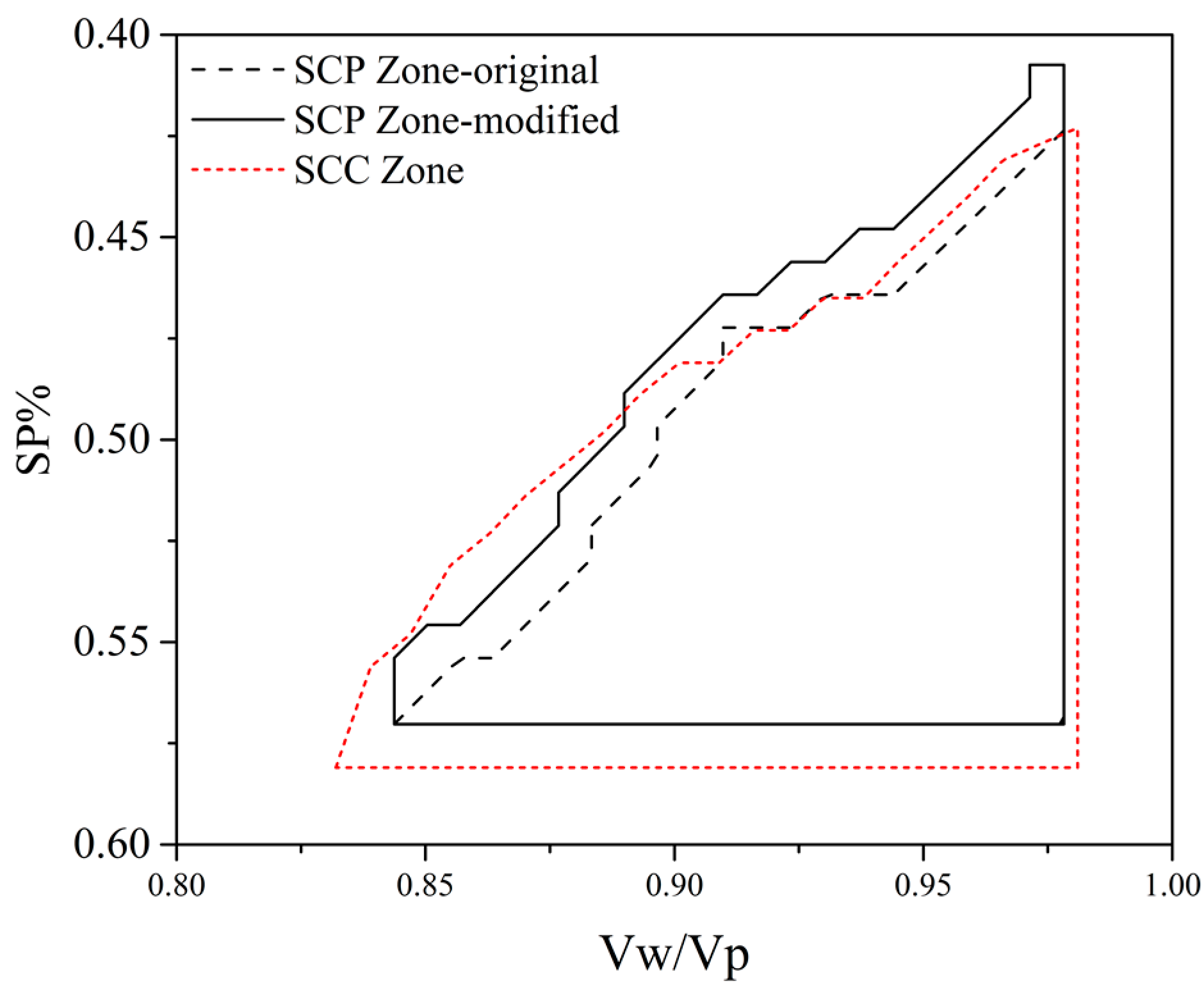
3.3. Applicability of Modified Multiscale Thresholds and Verification
3.3.1. Verification with Single Powder, Cement
3.3.2. Verification with Binary Powder, Cement Substituted by 20% FA
3.3.3. Verification with Binary Powder, Cement Substituted by 30% FA
3.3.4. Verification with Binary Powder, Cement Substituted by 20% LP
3.3.5. Verification with Ternary Powder, Cement Substituted by 16% FA and 21% LP
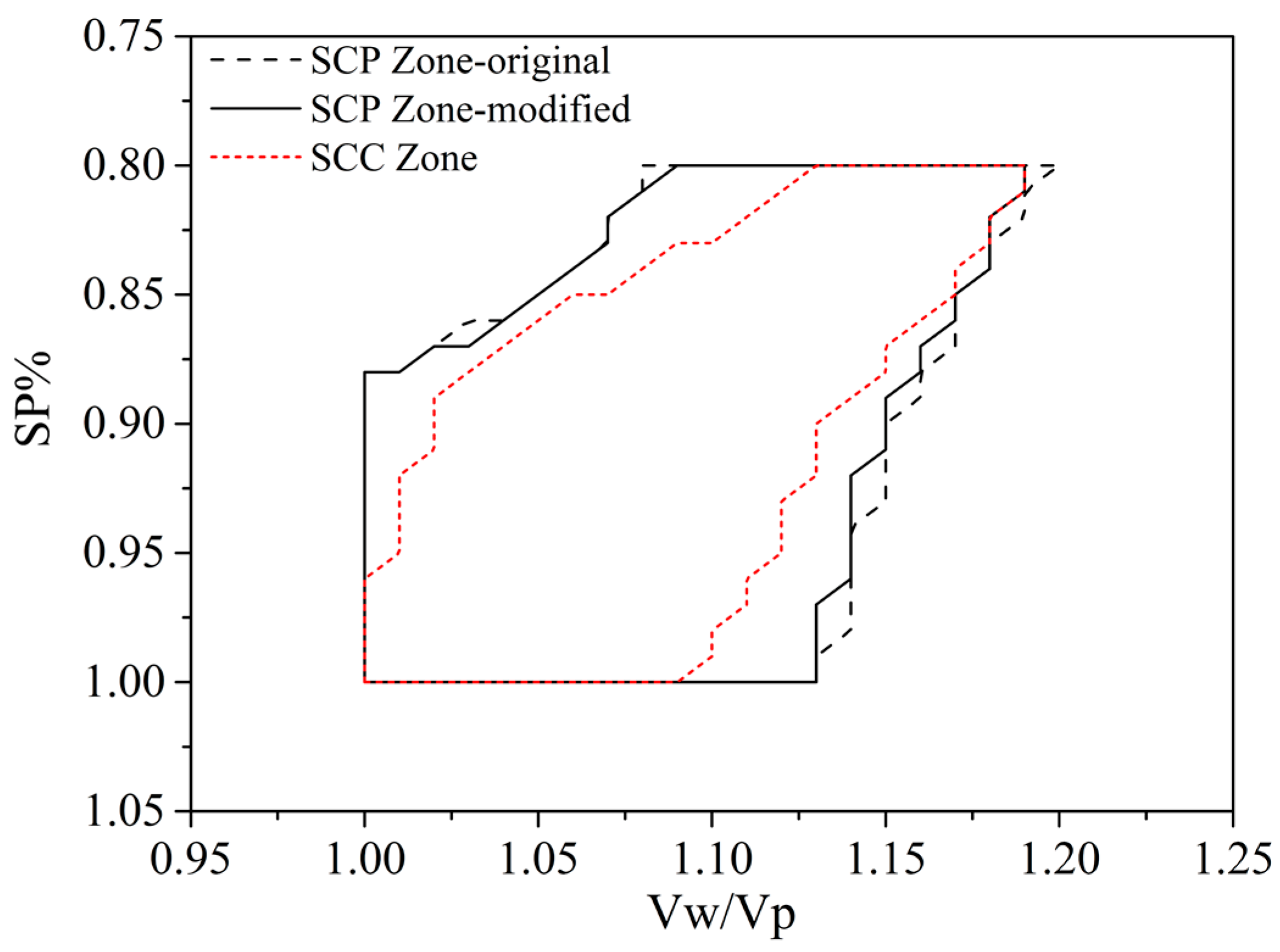
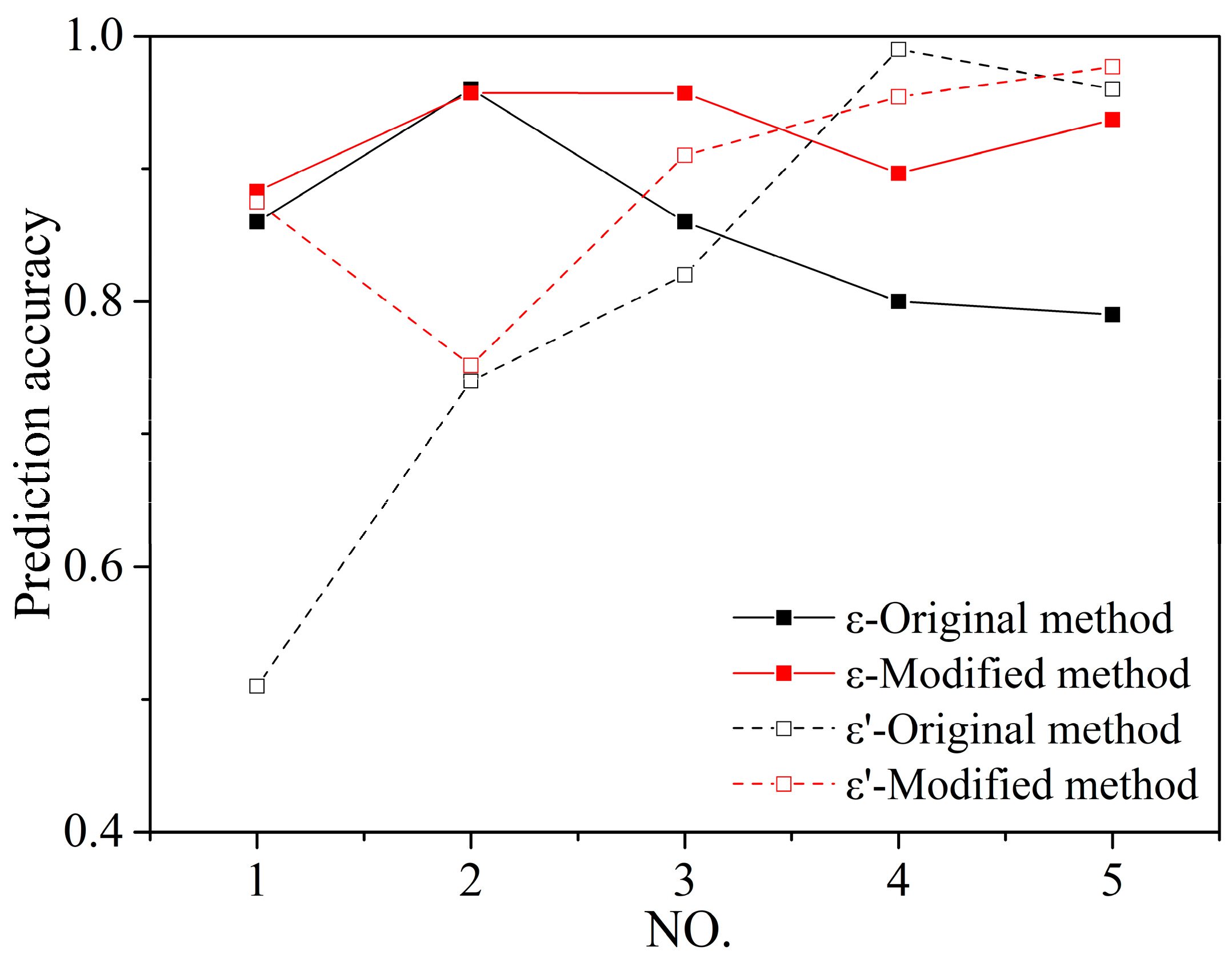
3.4. Prediction Accuracy Evaluation
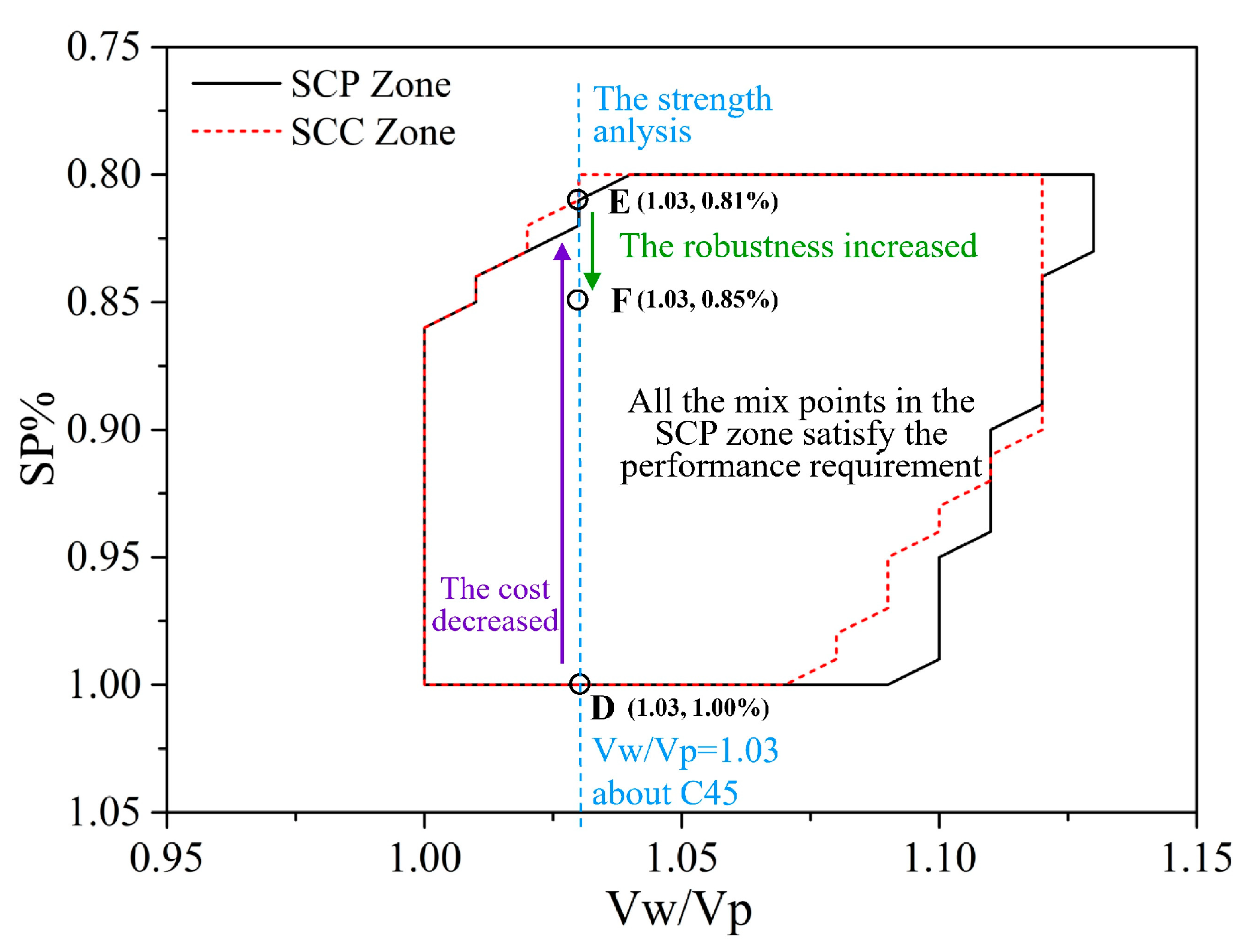
- When ε′ < 1, the partial SCP zone is consistent with the SCC zone, and shows excessive prediction.
- When ε′ = 1, the predicted zone is the same as the real zone, and the SCP and SCC zones are exactly equal to the SCC zone.
- When ε′ > 1, the predicted zone is conservative, and the SCC zone contains the SCP zone.
4. The Mix Design Method for Multiplexed Powder SCC
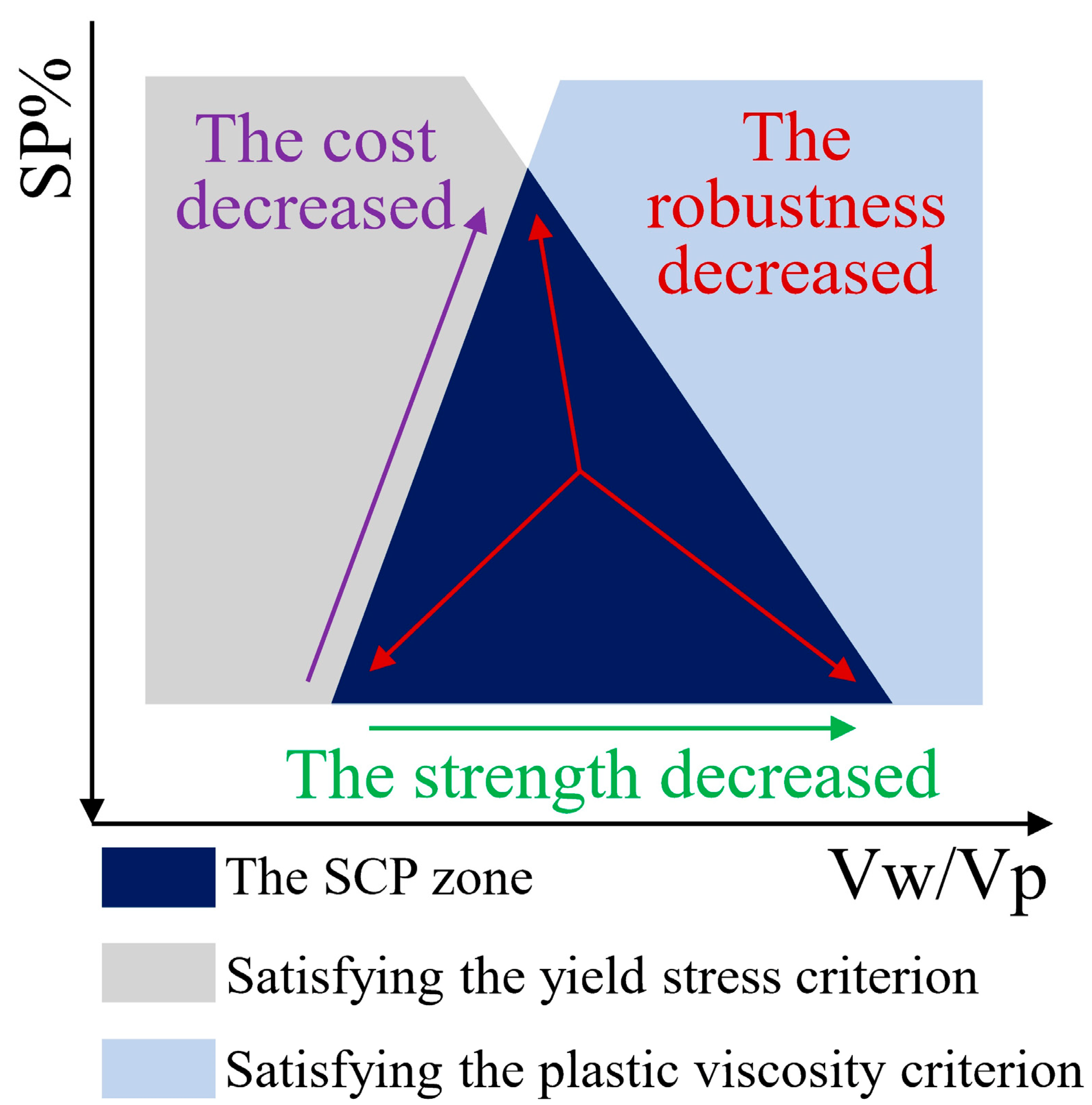
4.1. The Definition and Basic Steps
- In the SCP zone, the mix point with lower Vw/Vp uses more powder and has higher compressive strength, but the economic cost increases.
- For the mix points with the same Vw/Vp in the SCP zone, the smaller the SP% is, the lower the economic cost.
- It also should be noted that the mix points near the boundaries have less robustness in prediction than those far from the boundaries.
- The material properties tests. The required parameters include the densities of all the materials and the size and distribution of the powder particles.
- The mixes of the tests are preset. Vw/Vp is determined by the compressive strength requirement, while SP%, G%, and S% refer to the empirical dosage and can be adjusted if the flowability is insufficient.
- The paste mini-SF tests are proposed. There are a total of nine tests, with three levels at SP% and Vw/Vp, respectively. The relevant rheological properties from Equations (5) and (6) are calculated.
- The threshold calculations are performed with Equations (9) and (10).
- Through the threshold criteria, the SCP zone is obtained by the bilinear interpolation method.
- The compressive strength, robustness, and cost analysis can be evaluated by the SCP zone. Thus, the mix proportion of SCC is confirmed.
4.2. Application Cases
4.2.1. Performance-Based Mix Design
4.2.2. Strength-Based Mix Design
5. Conclusions
- The existing threshold theory lacks consideration of the characteristics of the specific powder. It was found that D50 and Span can describe the properties of the powder. The powder parameters in the threshold formula, the powder fitting coefficient n, and the intrinsic viscosity [η], were modified by the impacts that the powder properties caused.
- There were 90 groups of self-compacting performance tests in total, including 45 groups of pastes and 45 groups of SCCs. Based on the test results, self-compacting zones were obtained. Through the comparison of the predicted zone, the SCP zone, the real zone, and the SCC zone, the prediction accuracies were evaluated. It was confirmed that this improved method is applicable to the multipowder SCC with cement, FA, and LP.
- The modified method increased the prediction accuracy of the threshold theory. According to the increment of ε, up to 20.78%, the overlapping area of the modified SCP zone and SCC zone becomes larger. In the case of ε′, its increment reaches 62.96%, and the relative position of the predicted and real zones increases noticeably through the modified method. Overall, the holistic prediction accuracy of the modified method increases.
- A mix design method for SCC with multiplexed powder was proposed, considering the flowability, economic cost, and strength comprehensively. Through this method, the performance of SCC can be predicted based on the test results of the pastes and the properties of the materials. Thus, the mix design of SCC can be conducted without SCC tests, which is much easier than previous methods.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Okamura, H.; Ouchi, M. Self-compacting concrete. J. Adv. Concr. Technol. 2003, 1, 5–15. [Google Scholar] [CrossRef]
- An, X.; Wu, Q.; Jin, F.; Huang, M.; Zhou, H.; Chen, C.; Liu, C. Rock-filled concrete, the new norm of SCC in hydraulic engineering in China. Cem. Concr. Compos. 2014, 54, 89–99. [Google Scholar] [CrossRef]
- An, X.; Huang, M.; Ouchi, M.; Jin, F. Technical Manual of Self-Compacting Concrete; China Water & Power Press: Beijing, China, 2008. [Google Scholar]
- Shi, C.; Wu, Z.; Lv, K.; Wu, L. A review on mixture design methods for self-compacting concrete. Constr. Build. Mater. 2015, 84, 387–398. [Google Scholar] [CrossRef]
- Okamura, H.; Ozawa, K. Mix design for self-compacting concrete. Concr. Lib. Jpn. Soc. Civ. Eng. 1995, 25, 107–120. [Google Scholar]
- Su, N.; Hsu, K.; Chai, H. A simple mix design method for self-compacting concrete. Cem. Concr. Res. 2001, 31, 1799–1807. [Google Scholar] [CrossRef]
- Su, N.; Miao, B. A new method for the mix design of medium strength flowing concrete with low cement content. Cem. Concr. Compos. 2003, 25, 215–222. [Google Scholar] [CrossRef]
- Domone, P. Mortar tests for material selection and mix design of SCC. Concr. Int. 2006, 28, 39–45. [Google Scholar]
- Bouziani, T. Assessment of fresh properties and compressive strength of self-compacting concrete made with different sand types by mixture design modelling approach. Constr. Build. Mater. 2013, 49, 308–314. [Google Scholar] [CrossRef]
- Saak, A.; Jennings, H.; Shah, S. New methodology for designing self-compacting concrete. ACI Mater. J. 2001, 98, 429–439. [Google Scholar]
- Saak, A.; Jennings, H.; Shah, S. A generalized approach for the determination of yield stress by slump and slump flow. Cem. Concr. Res. 2004, 34, 363–371. [Google Scholar] [CrossRef]
- Bui, V.; Akkaya, Y.; Shah, S. Rheological model for self-consolidating concrete. ACI Mater. J. 2002, 99, 549–559. [Google Scholar]
- Wu, Q.; An, X. Development of a mix design method for SCC based on the rheological characteristics of paste. Constr. Build. Mater. 2014, 53, 642–651. [Google Scholar] [CrossRef]
- Nie, D.; An, X. Optimization of SCC mix at paste level by using numerical method based on a paste rheological threshold theory. Constr. Build. Mater. 2016, 102, 428–434. [Google Scholar] [CrossRef]
- Zhang, J.; An, X.; Yu, Y.; Nie, D. Effects of coarse aggregate content on the paste rheological thresholds of fresh self-compacting concrete. Constr. Build. Mater. 2019, 208, 564–576. [Google Scholar] [CrossRef]
- Zhang, J.; An, X.; Nie, D. Effect of fine aggregate characteristics on the thresholds of self-compacting paste rheological properties. Constr. Build. Mater. 2016, 116, 355–365. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, P.; Gao, X. Multi-scale particles optimization for some rheological properties of Eco-SCC: Modelling and experimental study. Constr. Build. Mater. 2021, 308, 125151. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, J.; An, X.; Qi, B.; Li, W.; Shen, D.; Li, P.; Lv, M. The effect of sand type on the rheological properties of self-compacting mortar. Buildings 2021, 11, 441. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, J.; An, X.; Qi, B.; Shen, D.; Lv, M. Effects of fly ash and limestone powder on the paste rheological thresholds of self-compacting concrete. Constr. Build. Mater. 2021, 281, 122560. [Google Scholar] [CrossRef]
- Zhang, J.; Lv, M.; An, X.; Shen, D.; He, X.; Nie, D. Improved powder equivalence model for the mix design of self-compacting concrete with fly ash and limestone powder. Adv. Mater. Sci. Eng. 2021, 2021, 4966062. [Google Scholar] [CrossRef]
- Li, P.; Zhang, T.; An, X.; Zhang, J. An enhanced mix design method of self-compacting concrete with fly ash content based on paste rheological threshold theory and material packing characteristics. Constr. Build. Mater. 2020, 234, 117380. [Google Scholar] [CrossRef]
- Li, P.; Ran, J.; Nie, D.; Zhang, W. Improvement of mix design method based on paste rheological threshold theory for self-compacting concrete using different mineral additions in ternary blends of powders. Constr. Build. Mater. 2021, 276, 122194. [Google Scholar] [CrossRef]
- Li, P.; Ran, J.; An, X.; Bai, H.; Nie, D.; Zhang, J.; Shao, K. An enhanced mix-design method for self-compacting concrete based on paste rheological threshold theory and equivalent mortar film thickness theories. Constr. Build. Mater. 2022, 347, 128573. [Google Scholar] [CrossRef]
- Toutou, Z.; Roussel, N. Multi scale experimental study of concrete rheology: From water scale to gravel scale. Mater. Struct. 2006, 39, 189–199. [Google Scholar] [CrossRef]
- Banfill, P. The rheology of fresh cement and concrete-a review. In Proceedings of the 11th International Cement Chemistry Congress, Durban, South Africa, 11–16 May 2003. [Google Scholar]
- Türkel, S.; Kandemir, A. Fresh and hardened properties of SCC made with different aggregate and mineral admixtures. J. Mater Civ. Eng. 2010, 22, 1025–1032. [Google Scholar] [CrossRef]
- Sahmaran, M.; Yaman, O.; Tokyay, M. Development of high-volume low-lime and high-lime fly ash incorporated self-consolidating concrete. Cem. Concr. Compos. 2007, 31, 97–106. [Google Scholar] [CrossRef]
- Promsawat, P.; Chatveera, B.; Sua-iam, G.; Makul, N. Properties of self-compacting concrete prepared with ternary Portland cement-high volume fly ash-calcium carbonate blends. Case Stud. Constr. Mater. 2020, 13, e00426. [Google Scholar] [CrossRef]
- Gritsada, S.; Prakasit, S.; Natt, M. Novel ternary blends of Type 1 Portland cement, residual rice husk ash, and limestone powder to improve the properties of self-compacting concrete. Constr. Build. Mater. 2016, 125, 1028–1034. [Google Scholar] [CrossRef]
- Zhu, W.; Gibbs, J. Use of different limestone and chalk powders in self-compacting concrete. Cem. Con. Res. 2005, 35, 1457–1462. [Google Scholar] [CrossRef]
- Miyake, J.; Matsushita, H. Evaluation method for consistencies of mortars with various mixture proportions. J. Adv. Concr. Technol. 2007, 5, 87–97. [Google Scholar] [CrossRef]
- Roussel, N.; Stefani, C.; Leroy, R. From mini-cone test to Abrams cone test: Measurement of cement-based materials yield stress using slump tests. Cem. Concr. Res. 2005, 35, 817–822. [Google Scholar] [CrossRef]
- Chidiac, S.; Maadani, O.; Razaqpur, A.; Mailvaganam, N. Controlling the quality of fresh concrete-a new approach. Mag. Concr. Res. 2000, 52, 353–363. [Google Scholar] [CrossRef]
- GB/T 208-2014; Test Method for Determining Cement Density. Standards Press of China: Beijing, China, 2006.
- JGJ 52-2006; Standard for Technical Requirements and Test Method of Sand and Crushed Stone (or Gravel) for Ordinary Concrete. China Architecture & Building Press: Beijing, China, 2006.
- CECS 203-2006; Technical Specifications for Self-Compacting Concrete Application. China Plan Press: Beijing, China, 2006.
- JGJ 55-2011; Specification for Mix Proportion Design of Ordinary Concrete. China Architecture & Building Press: Beijing, China, 2011.





| Serial No. | C% | FA% | LP% | Cement Type | Gravel Type | Sand Type | G% | S% |
|---|---|---|---|---|---|---|---|---|
| 1 | 100% | - | - | C_A | G_A | S_A | 30% | 45.0% |
| 2 | 80% | 20% | - | |||||
| 3 | 70% | 30% | - | |||||
| 4 | 80% | - | 20% | C_B | G_B | S_B | 27% | 38.5% |
| 5 | 63% | 16% | 21% |
| Serial No. | D50 (μm) | Span (μm) | nexp | τthreshold,o (Pa) | np | τthreshold,m (Pa) |
|---|---|---|---|---|---|---|
| 1 | 20.30 | 2.26 | 4.20 | 0.83 | 4.39 | 0.76 |
| 2 | 19.80 | 2.51 | 4.20 | 0.82 | 4.21 | 0.82 |
| 3 | 19.56 | 2.64 | 4.20 | 0.82 | 4.13 | 0.85 |
| 4 | 20.07 | 2.53 | 4.20 | 0.89 | 4.16 | 0.90 |
| 5 | 19.68 | 2.73 | 4.20 | 0.90 | 4.04 | 0.97 |
| Serial No. | D50 (μm) | [η]exp | ηthreshold,o (Pa·s) | [η]p | ηthreshold,m (Pa·s) |
|---|---|---|---|---|---|
| 1 | 20.30 | 2.5 | 10.76 | 2.72 | 13.63 |
| 2 | 19.80 | 2.5 | 10.90 | 2.44 | 9.27 |
| 3 | 19.56 | 2.5 | 11.82 | 2.29 | 11.35 |
| 4 | 20.07 | 2.5 | 10.76 | 2.59 | 11.06 |
| 5 | 19.68 | 2.5 | 10.80 | 2.36 | 11.90 |
| Vw/Vp | SP% | Mix Proportion (kg/m3) | SFpaste (mm) | T200 (s) | τpaste (Pa) | ηpaste (Pa·s) | ||
|---|---|---|---|---|---|---|---|---|
| C | W | SP | ||||||
| 1.00 | 0.80 | 1536.2 | 488.9 | 12.29 | 237 | 4.30 | 1.89 | 53.81 |
| 1.00 | 0.90 | 1535.7 | 487.6 | 13.82 | 255 | 3.87 | 1.29 | 48.41 |
| 1.00 | 1.00 | 1535.3 | 486.2 | 15.35 | 259 | 3.25 | 1.20 | 40.67 |
| 1.10 | 0.80 | 1463.2 | 513.2 | 11.71 | 261 | 2.15 | 1.12 | 26.18 |
| 1.10 | 0.90 | 1462.8 | 511.9 | 13.17 | 276 | 1.89 | 0.85 | 23.07 |
| 1.10 | 1.00 | 1462.4 | 510.6 | 14.62 | 285 | 1.70 | 0.73 | 20.80 |
| 1.20 | 0.80 | 1396.9 | 535.3 | 11.18 | 284 | 1.03 | 0.71 | 12.24 |
| 1.20 | 0.90 | 1396.5 | 534.0 | 12.57 | 309 | 1.02 | 0.46 | 12.01 |
| 1.20 | 1.00 | 1396.1 | 532.8 | 13.96 | 313 | 0.85 | 0.43 | 10.13 |
| Vw/Vp | SP% | Mix Proportion (kg/m3) | SF (mm) | VF (s) | ||||
|---|---|---|---|---|---|---|---|---|
| C | S | G | W | SP | ||||
| 1.00 | 0.80 | 576.0 | 808 | 810 | 183.3 | 4.61 | 237 | 4.30 |
| 1.00 | 0.90 | 576.0 | 808 | 810 | 182.9 | 5.18 | 255 | 3.87 |
| 1.00 | 1.00 | 576.0 | 808 | 810 | 182.4 | 5.76 | 259 | 3.25 |
| 1.10 | 0.80 | 548.5 | 808 | 810 | 192.4 | 4.39 | 261 | 2.15 |
| 1.10 | 0.90 | 548.5 | 808 | 810 | 192.0 | 4.94 | 276 | 1.89 |
| 1.10 | 1.00 | 548.5 | 808 | 810 | 191.5 | 5.49 | 285 | 1.70 |
| 1.20 | 0.80 | 523.6 | 808 | 810 | 200.7 | 4.19 | 284 | 1.03 |
| 1.20 | 0.90 | 523.6 | 808 | 810 | 200.2 | 4.71 | 309 | 1.02 |
| 1.20 | 1.00 | 523.6 | 808 | 810 | 199.8 | 5.24 | 313 | 0.85 |
| Vw/Vp | SP% | Mix Proportion (kg/m3) | SFpaste (mm) | T200 (s) | τpaste (Pa) | ηpaste (Pa·s) | |||
|---|---|---|---|---|---|---|---|---|---|
| C | FA | W | SP | ||||||
| 1.00 | 0.80 | 1229.1 | 249.4 | 489.4 | 11.83 | 258 | 2.47 | 1.18 | 30.03 |
| 1.00 | 0.90 | 1228.7 | 249.3 | 488.0 | 13.30 | 285 | 2.38 | 0.72 | 28.89 |
| 1.00 | 1.00 | 1228.4 | 249.3 | 486.7 | 14.78 | 315 | 1.67 | 0.43 | 20.34 |
| 1.10 | 0.80 | 1170.7 | 237.6 | 513.6 | 11.27 | 284 | 2.08 | 0.72 | 24.69 |
| 1.10 | 0.90 | 1170.4 | 237.5 | 512.4 | 12.67 | 299 | 1.53 | 0.55 | 18.18 |
| 1.10 | 1.00 | 1170.0 | 237.4 | 511.1 | 14.07 | 330 | 1.21 | 0.33 | 14.32 |
| 1.20 | 0.80 | 1117.6 | 226.8 | 535.7 | 10.76 | 325 | 1.00 | 0.35 | 11.64 |
| 1.20 | 0.90 | 1117.3 | 226.7 | 534.5 | 12.10 | 350 | 0.50 | 0.23 | 5.76 |
| 1.20 | 1.00 | 1117.0 | 226.7 | 533.2 | 13.44 | 363 | 0.47 | 0.19 | 5.10 |
| Vw/Vp | SP% | Mix Proportion (kg/m3) | SF (mm) | VF (s) | |||||
|---|---|---|---|---|---|---|---|---|---|
| C | FA | S | G | W | SP | ||||
| 1.00 | 0.80 | 460.8 | 95.4 | 808 | 810 | 183.4 | 4.45 | 555 | 8.00 |
| 1.00 | 0.90 | 460.8 | 95.4 | 808 | 810 | 183.0 | 5.00 | 590 | 7.86 |
| 1.00 | 1.00 | 460.8 | 95.4 | 808 | 810 | 182.6 | 5.56 | 610 | 9.06 |
| 1.10 | 0.80 | 438.8 | 90.8 | 808 | 810 | 192.5 | 4.24 | 580 | 5.51 |
| 1.10 | 0.90 | 438.8 | 90.8 | 808 | 810 | 192.1 | 4.77 | 663 | 5.20 |
| 1.10 | 1.00 | 438.8 | 90.8 | 808 | 810 | 191.7 | 5.30 | 670 | 5.00 |
| 1.20 | 0.80 | 418.9 | 86.7 | 808 | 810 | 200.8 | 4.04 | 665 | 5.00 |
| 1.20 | 0.90 | 418.9 | 86.7 | 808 | 810 | 200.4 | 4.55 | 670 | 4.70 |
| 1.20 | 1.00 | 418.9 | 86.7 | 808 | 810 | 200.0 | 5.06 | 685 | 4.60 |
| Vw/Vp | SP% | Mix Proportion (kg/m3) | SFpaste (mm) | T200 (s) | τpaste (Pa) | ηpaste (Pa·s) | |||
|---|---|---|---|---|---|---|---|---|---|
| C | FA | W | SP | ||||||
| 1.00 | 0.80 | 1075.5 | 374.1 | 489.6 | 11.60 | 269 | 2.44 | 0.95 | 29.26 |
| 1.00 | 0.90 | 1075.2 | 374.0 | 488.3 | 13.04 | 277 | 2.52 | 0.81 | 30.13 |
| 1.00 | 1.00 | 1074.9 | 373.9 | 487.0 | 14.49 | 292 | 1.79 | 0.62 | 21.48 |
| 1.10 | 0.80 | 1024.4 | 356.4 | 513.8 | 11.05 | 283 | 1.53 | 0.71 | 17.91 |
| 1.10 | 0.90 | 1024.1 | 356.3 | 512.5 | 12.42 | 303 | 1.31 | 0.51 | 15.36 |
| 1.10 | 1.00 | 1023.8 | 356.3 | 511.3 | 13.80 | 323 | 1.09 | 0.36 | 12.77 |
| 1.20 | 0.80 | 977.9 | 340.3 | 535.9 | 10.54 | 314 | 0.36 | 0.41 | 4.09 |
| 1.20 | 0.90 | 977.7 | 340.1 | 534.7 | 11.86 | 327 | 0.37 | 0.33 | 3.85 |
| 1.20 | 1.00 | 977.4 | 340.0 | 533.5 | 13.17 | 338 | 0.34 | 0.28 | 3.93 |
| Vw/Vp | SP% | Mix Proportion (kg/m3) | SF (mm) | VF (s) | |||||
|---|---|---|---|---|---|---|---|---|---|
| C | FA | S | G | W | SP | ||||
| 1.00 | 0.80 | 403.2 | 140.3 | 808 | 810 | 183.3 | 4.35 | 560 | 7.01 |
| 1.00 | 0.90 | 403.2 | 140.3 | 808 | 810 | 183.1 | 4.89 | 640 | 6.30 |
| 1.00 | 1.00 | 403.2 | 140.3 | 808 | 810 | 182.7 | 5.43 | 700 | 5.35 |
| 1.10 | 0.80 | 384.0 | 133.6 | 808 | 810 | 192.6 | 4.14 | 700 | 5.20 |
| 1.10 | 0.90 | 384.0 | 133.6 | 808 | 810 | 192.2 | 4.66 | 715 | 5.10 |
| 1.10 | 1.00 | 384.0 | 133.6 | 808 | 810 | 191.8 | 5.18 | 718 | 4.90 |
| 1.20 | 0.80 | 366.5 | 127.5 | 808 | 810 | 200.8 | 3.95 | 700 | 4.22 |
| 1.20 | 0.90 | 366.5 | 127.5 | 808 | 810 | 200.4 | 4.45 | 710 | 4.63 |
| 1.20 | 1.00 | 366.5 | 127.5 | 808 | 810 | 200.1 | 4.94 | 730 | 4.46 |
| Vw/Vp | SP% | Mix Proportion (kg/m3) | SFpaste (mm) | T200 (s) | τpaste (Pa) | ηpaste (Pa·s) | |||
|---|---|---|---|---|---|---|---|---|---|
| C | LP | W | SP | ||||||
| 0.85 | 0.41 | 1316.5 | 312.1 | 450.6 | 6.68 | 205 | 4.24 | 3.96 | 54.24 |
| 0.85 | 0.49 | 1316.1 | 312.0 | 449.4 | 7.98 | 269 | 3.10 | 1.01 | 39.68 |
| 0.85 | 0.57 | 1315.8 | 311.9 | 448.3 | 9.28 | 283 | 2.90 | 0.78 | 37.14 |
| 0.92 | 0.41 | 1268.3 | 300.7 | 470.7 | 6.43 | 260 | 2.88 | 1.18 | 36.16 |
| 0.92 | 0.49 | 1267.9 | 300.6 | 469.6 | 7.69 | 274 | 2.15 | 0.90 | 27.01 |
| 0.92 | 0.57 | 1267.6 | 300.5 | 468.4 | 8.94 | 305 | 1.22 | 0.52 | 15.33 |
| 0.99 | 0.41 | 1223.6 | 290.0 | 489.4 | 6.21 | 275 | 2.06 | 0.87 | 25.42 |
| 0.99 | 0.49 | 1223.3 | 289.9 | 488.3 | 7.41 | 287 | 1.74 | 0.70 | 21.48 |
| 0.99 | 0.57 | 1222.9 | 289.8 | 487.2 | 8.62 | 310 | 0.88 | 0.47 | 10.87 |
| Vw/Vp | SP% | Mix Proportion (kg/m3) | SF (mm) | VF (s) | |||||
|---|---|---|---|---|---|---|---|---|---|
| C | LP | S | G | W | SP | ||||
| 0.85 | 0.41 | 579.0 | 131.9 | 687 | 776 | 199.4 | 2.89 | 455 | 38.12 |
| 0.85 | 0.49 | 579.0 | 131.9 | 687 | 776 | 198.9 | 3.47 | 610 | 22.43 |
| 0.85 | 0.57 | 579.0 | 131.9 | 687 | 776 | 198.4 | 4.05 | 670 | 16.69 |
| 0.92 | 0.40 | 552.6 | 131.9 | 687 | 776 | 207.8 | 2.76 | 550 | 21.40 |
| 0.92 | 0.48 | 552.6 | 131.9 | 687 | 776 | 207.4 | 3.31 | 700 | 9.75 |
| 0.91 | 0.57 | 552.6 | 131.9 | 687 | 776 | 206.9 | 3.87 | 700 | 10.46 |
| 0.99 | 0.40 | 528.6 | 131.9 | 687 | 776 | 215.5 | 2.64 | 650 | 15.76 |
| 0.98 | 0.48 | 528.6 | 131.9 | 687 | 776 | 215.1 | 3.17 | 700 | 8.12 |
| 0.98 | 0.57 | 528.6 | 131.9 | 687 | 776 | 214.7 | 3.70 | 730 | 45.50 |
| Vw/Vp | SP% | Mix Proportion (kg/m3) | SFpaste (mm) | T200 (s) | τpaste (Pa) | ηpaste (Pa·s) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| C | FA | LP | W | SP | ||||||
| 0.79 | 0.41 | 449.1 | 92.4 | 121.2 | 175.6 | 2.70 | 215 | 3.72 | 3.04 | 46.37 |
| 0.78 | 0.49 | 449.1 | 92.4 | 121.2 | 175.2 | 3.25 | 247 | 2.84 | 1.51 | 35.42 |
| 0.78 | 0.57 | 449.1 | 92.4 | 121.2 | 174.7 | 3.79 | 278 | 1.75 | 0.83 | 21.84 |
| 0.85 | 0.40 | 427.7 | 88.0 | 121.2 | 184.2 | 2.56 | 248 | 2.34 | 1.46 | 28.64 |
| 0.85 | 0.48 | 427.7 | 88.0 | 121.2 | 183.8 | 3.08 | 285 | 1.71 | 0.73 | 20.94 |
| 0.85 | 0.56 | 427.7 | 88.0 | 121.2 | 183.3 | 3.58 | 307 | 1.24 | 0.50 | 15.19 |
| 0.92 | 0.40 | 408.3 | 84.0 | 121.2 | 192.0 | 2.44 | 272 | 1.96 | 0.91 | 23.59 |
| 0.92 | 0.48 | 408.3 | 84.0 | 121.2 | 191.6 | 2.93 | 290 | 1.34 | 0.65 | 16.14 |
| 0.92 | 0.56 | 408.3 | 84.0 | 121.2 | 191.2 | 3.42 | 313 | 1.08 | 0.45 | 13.01 |
| Vw/Vp | SP% | Mix Proportion (kg/m3) | SF (mm) | VF (s) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| C | FA | LP | S | G | W | SP | ||||
| 0.78 | 0.41 | 486.3 | 96.7 | 131.9 | 687 | 776 | 190.2 | 2.91 | 465 | 45.25 |
| 0.78 | 0.49 | 486.3 | 96.7 | 131.9 | 687 | 776 | 189.7 | 3.49 | 550 | 28.78 |
| 0.78 | 0.57 | 486.3 | 96.7 | 131.9 | 687 | 776 | 189.2 | 4.08 | 630 | 10.22 |
| 0.85 | 0.40 | 463.2 | 92.1 | 131.9 | 687 | 776 | 199.5 | 2.78 | 525 | 29.12 |
| 0.85 | 0.48 | 463.2 | 92.1 | 131.9 | 687 | 776 | 199.0 | 3.33 | 630 | 8.27 |
| 0.85 | 0.57 | 463.2 | 92.1 | 131.9 | 687 | 776 | 198.6 | 3.89 | 695 | 5.57 |
| 0.92 | 0.40 | 442.1 | 87.9 | 131.9 | 687 | 776 | 207.9 | 2.65 | 605 | 11.45 |
| 0.92 | 0.48 | 442.1 | 87.9 | 131.9 | 687 | 776 | 207.5 | 3.18 | 660 | 4.79 |
| 0.92 | 0.56 | 442.1 | 87.9 | 131.9 | 687 | 776 | 207.0 | 3.71 | 725 | 3.82 |
| No. | Graphic Presentation | ε | SA∩B/SB | SA/SB | ε′ |
|---|---|---|---|---|---|
| (1) |  | ≤1 | <1 | uncertain | <1 |
| (2) | 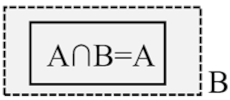 | <1 | <1 | ||
| (3) |  | =1 | =1 | =1 | |
| (4) | 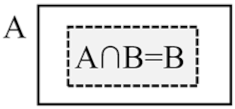 | =1 | >1 | >1 |
| Serial No. | Method | SA | SB | SA∩B | SA∩B/SB |
|---|---|---|---|---|---|
| 1 | Original method | 111 | 112 | 98 | 0.88 |
| Modified method | 111 | 181 | 97 | 0.54 | |
| 2 | Original method | 234 | 298 | 224 | 0.75 |
| Modified method | 234 | 308 | 225 | 0.73 | |
| 3 | Original method | 233 | 245 | 223 | 0.91 |
| Modified method | 233 | 256 | 210 | 0.82 | |
| 4 | Original method | 232 | 218 | 208 | 0.95 |
| Modified method | 232 | 199 | 196 | 0.98 | |
| 5 | Original method | 270 | 259 | 253 | 0.98 |
| Modified method | 270 | 220 | 209 | 0.95 |
| Original Method | Modified Method | Δ | Original Method | Modified Method | Δ |
|---|---|---|---|---|---|
| 0.87 | 0.88 | 1.15% | 0.54 | 0.88 | 62.96% |
| 0.96 | 0.96 | 0.00% | 0.73 | 0.75 | 2.74% |
| 0.90 | 0.96 | 6.67% | 0.82 | 0.91 | 10.98% |
| 0.84 | 0.90 | 5.95% | 0.98 | 0.95 | −3.06% |
| 0.77 | 0.94 | 20.78% | 0.95 | 0.98 | 3.16% |
| Mix No. | Mix Proportion (kg/m3) | Cost (CNY/m3) | |||||
|---|---|---|---|---|---|---|---|
| C | FA | S | G | W | SP | ||
| Mix A | 378.6 | 131.7 | 808 | 810 | 195.1 | 4.08 | 379.96 |
| Mix B | 403.2 | 140.3 | 808 | 810 | 182.7 | 5.43 | 397.12 |
| Mix C | 382.2 | 132.9 | 808 | 810 | 193.4 | 4.22 | 382.28 |
| Mix No. | Mix Proportion (kg/m3) | Cost (CNY/m3) | |||||
|---|---|---|---|---|---|---|---|
| C | FA | S | G | W | SP | ||
| Mix A | 378.6 | 131.7 | 808 | 810 | 195.1 | 4.08 | 379.96 |
| Mix B | 403.2 | 140.3 | 808 | 810 | 182.7 | 5.43 | 397.12 |
| Mix C | 382.2 | 132.9 | 808 | 810 | 193.4 | 4.22 | 382.28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, M.; Jiao, A.; An, X.; Bai, H.; Zhang, J.; Shao, K. Development of a Mix Design Method for Multiplexed Powder Self-Compacting Concrete Based on the Multiscale Rheological Threshold Theory. Buildings 2022, 12, 1663. https://doi.org/10.3390/buildings12101663
Lv M, Jiao A, An X, Bai H, Zhang J, Shao K. Development of a Mix Design Method for Multiplexed Powder Self-Compacting Concrete Based on the Multiscale Rheological Threshold Theory. Buildings. 2022; 12(10):1663. https://doi.org/10.3390/buildings12101663
Chicago/Turabian StyleLv, Miao, Anjia Jiao, Xuehui An, Hao Bai, Jingbin Zhang, and Kun Shao. 2022. "Development of a Mix Design Method for Multiplexed Powder Self-Compacting Concrete Based on the Multiscale Rheological Threshold Theory" Buildings 12, no. 10: 1663. https://doi.org/10.3390/buildings12101663
APA StyleLv, M., Jiao, A., An, X., Bai, H., Zhang, J., & Shao, K. (2022). Development of a Mix Design Method for Multiplexed Powder Self-Compacting Concrete Based on the Multiscale Rheological Threshold Theory. Buildings, 12(10), 1663. https://doi.org/10.3390/buildings12101663








