Variable Factors Affecting Progressive Destruction of Composite Steel Tall Building
Abstract
:1. Introduction
2. Methodology
2.1. Material Models
2.1.1. Material Model of Steel and Reinforcement
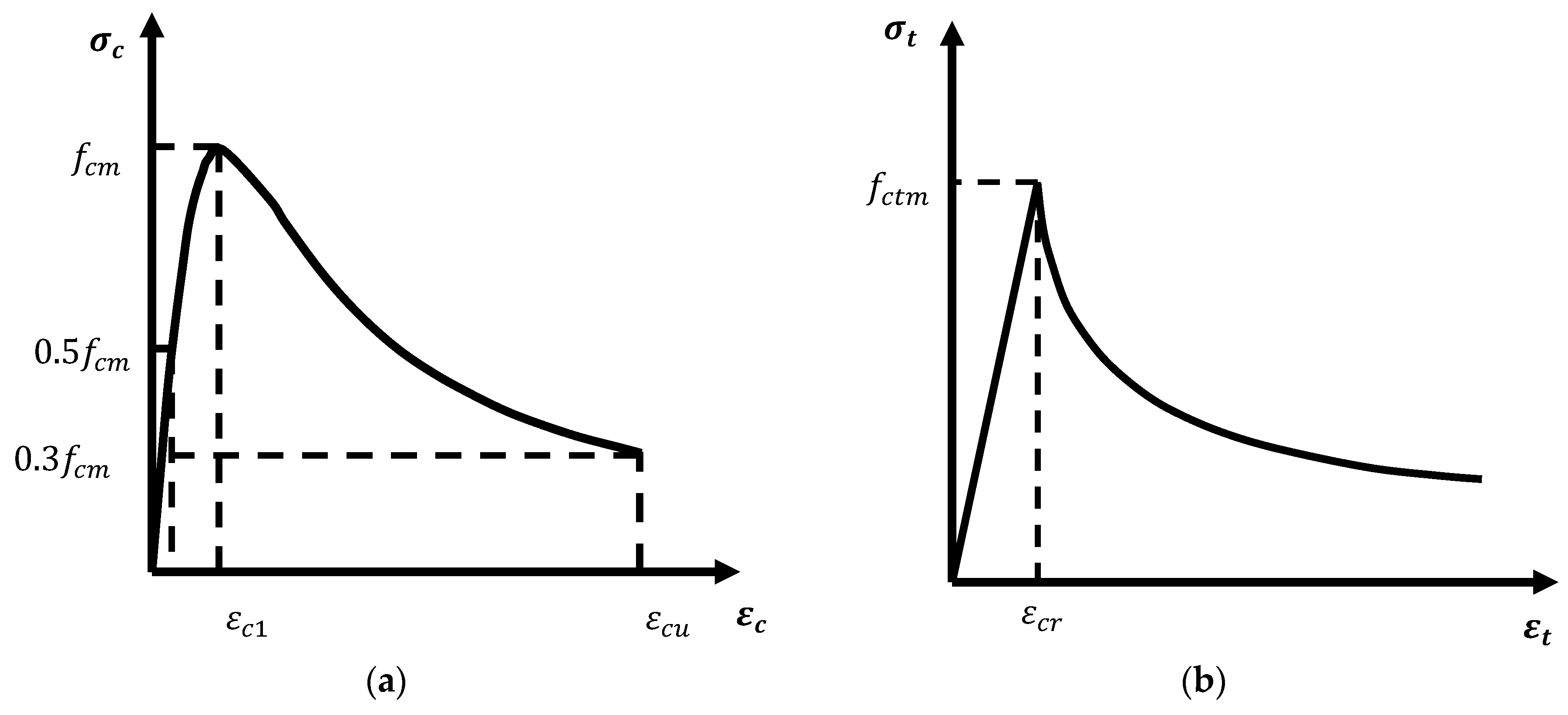
2.1.2. Material Model of Concrete
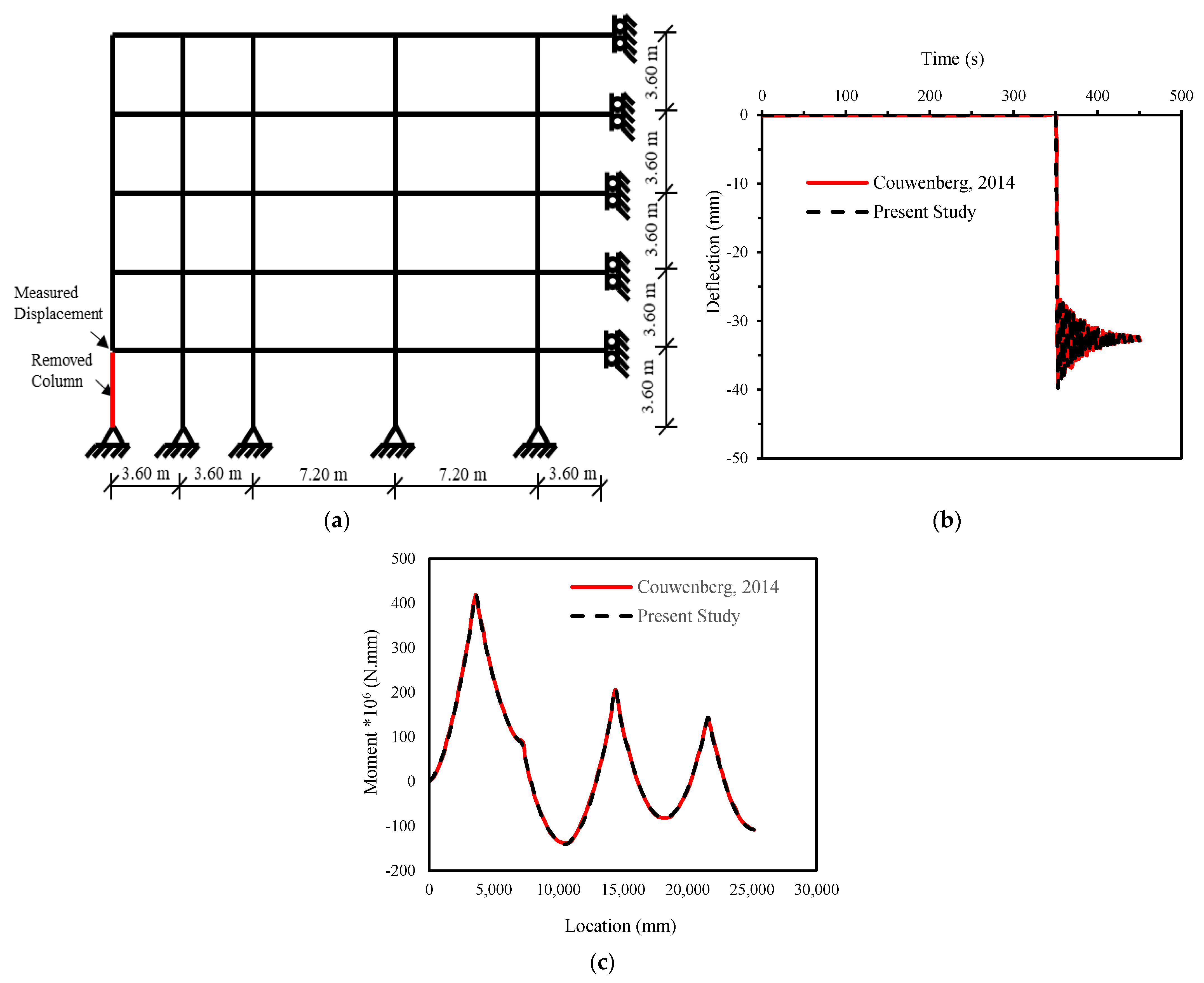
2.2. Validation of Numerical Models and the Composite Action
2.3. Verification of Progressive Collapse
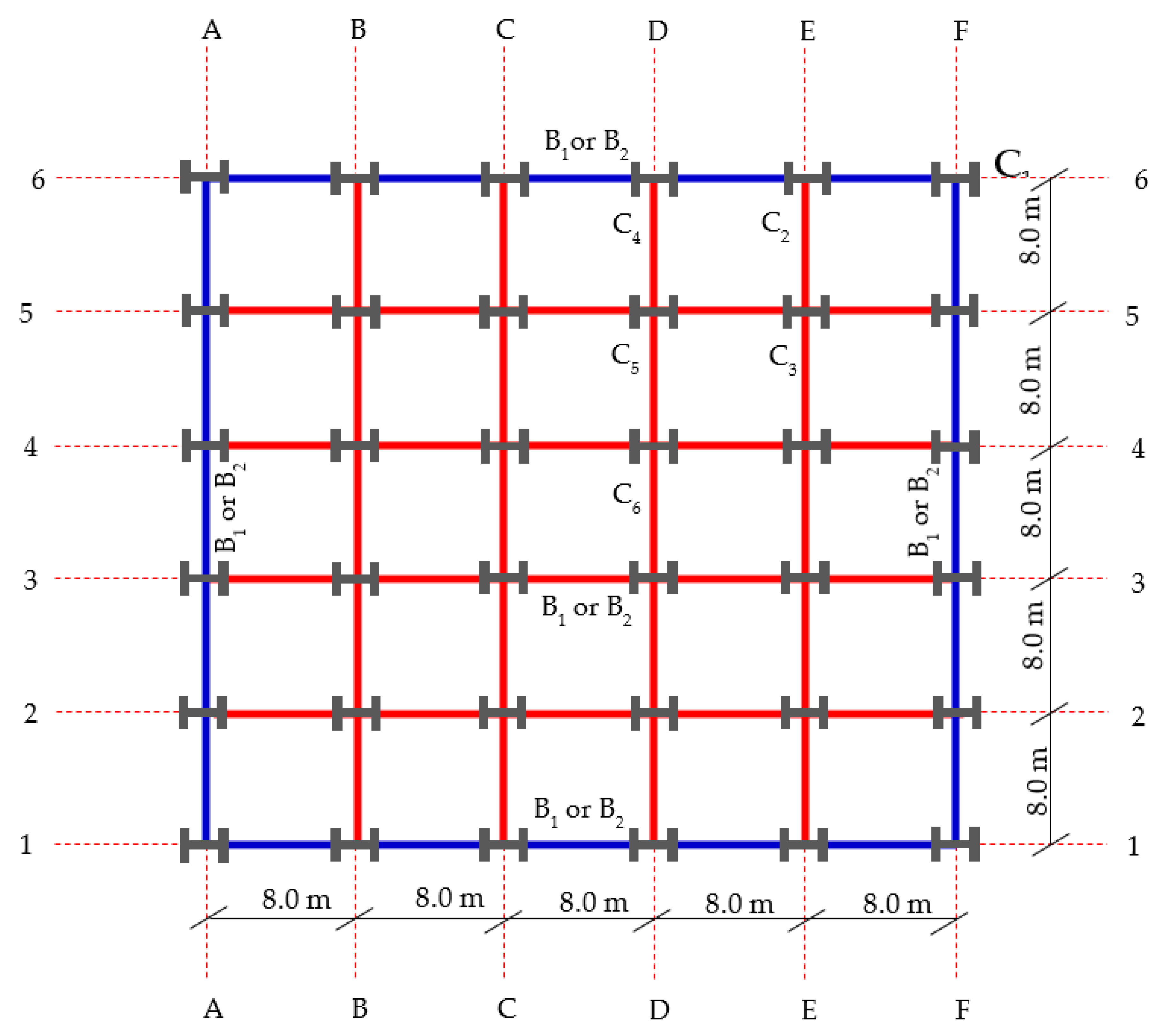
3. Case Study
Three Dimensions Modelling
4. Results and Discussions
4.1. The Steel Grade for Columns and Beams
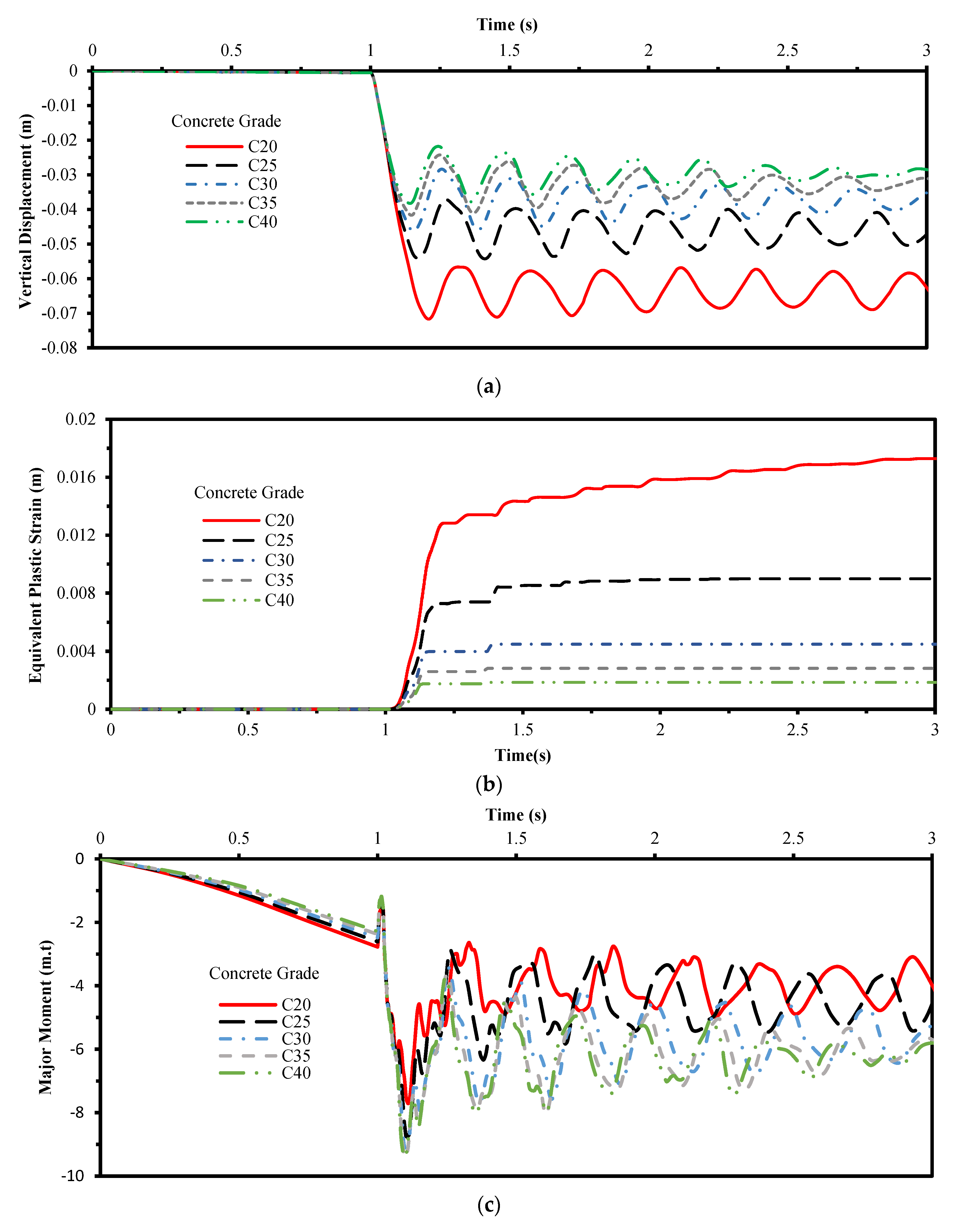
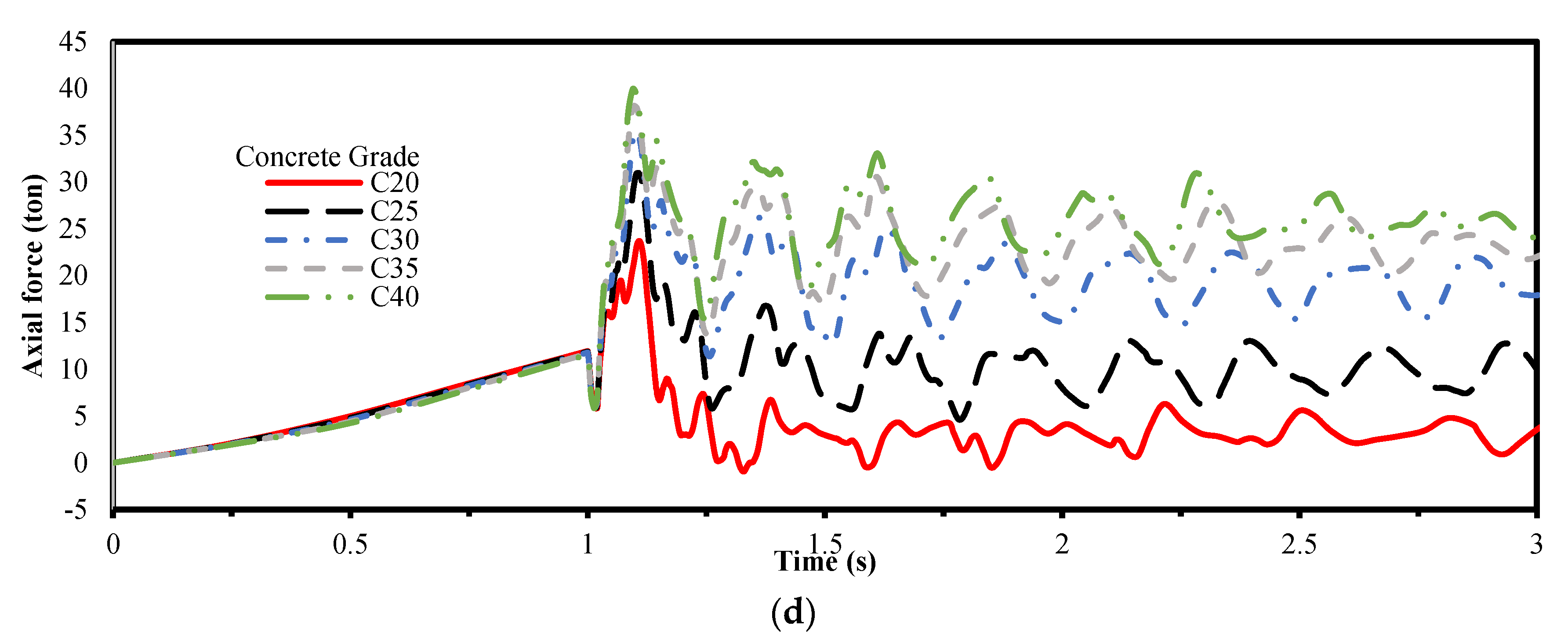
4.2. The Concrete Grade for Slab
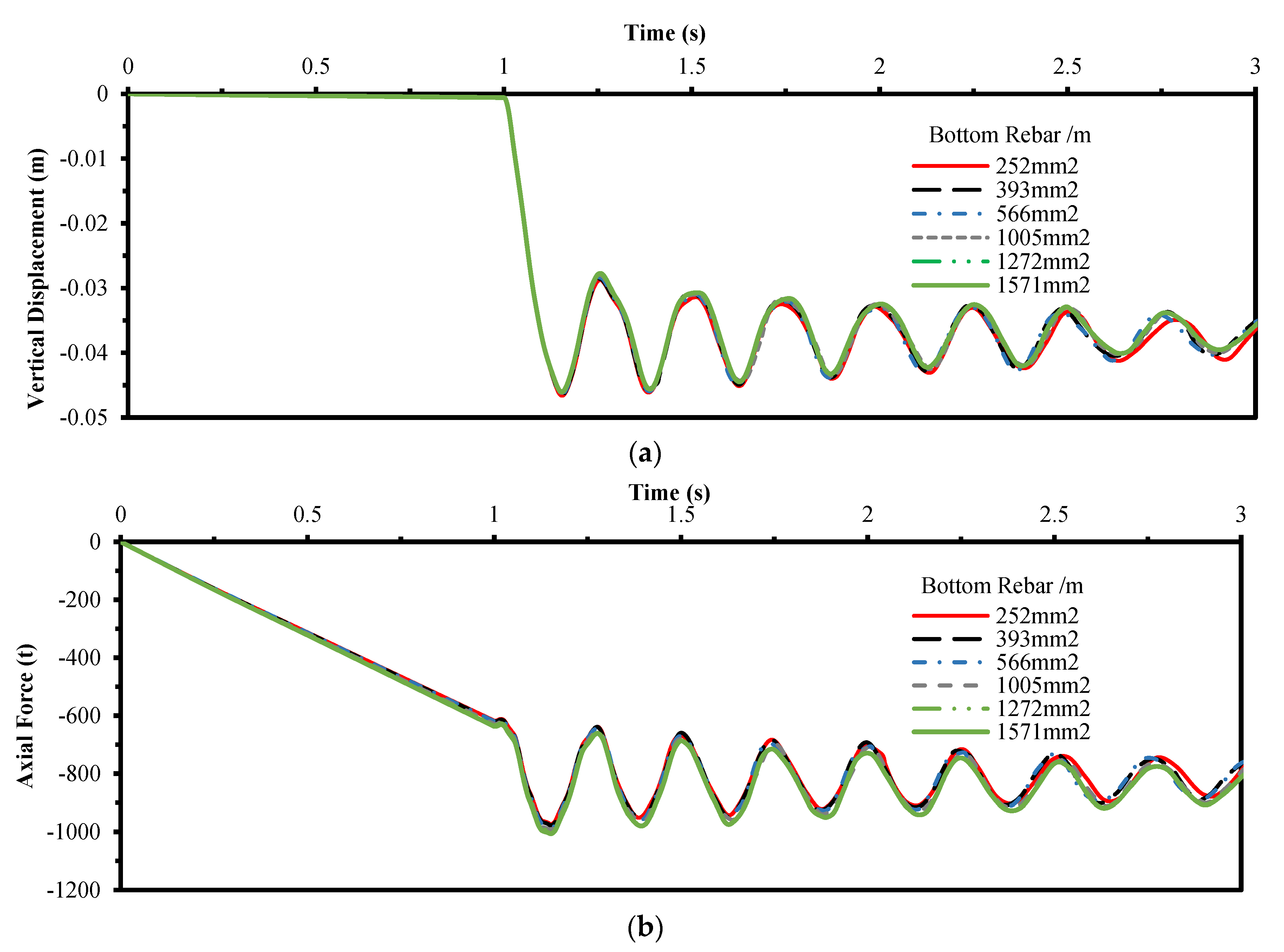
4.3. Bottom Reinforcement Density of Slab
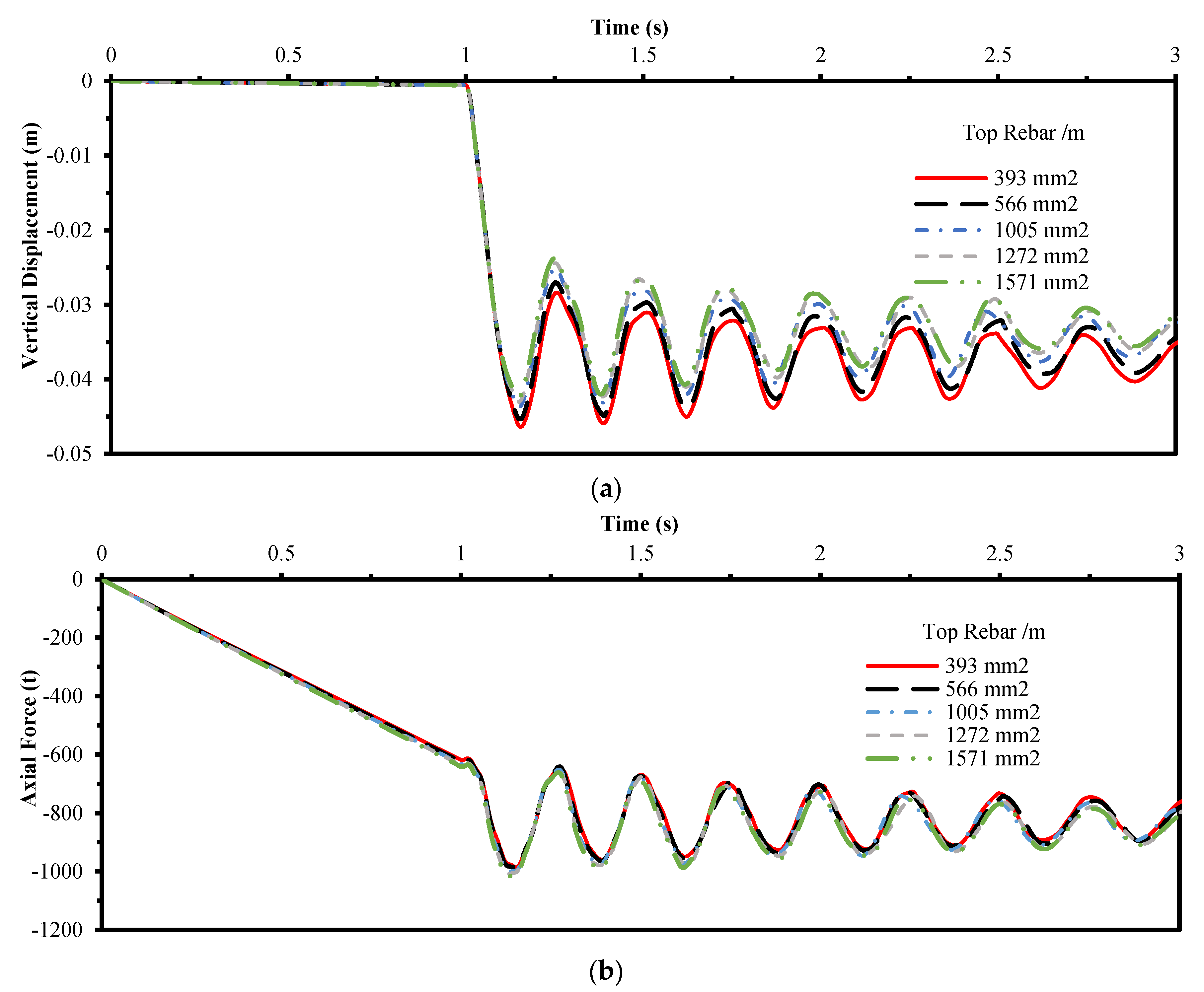
4.4. Top Reinforcement Density of Slab
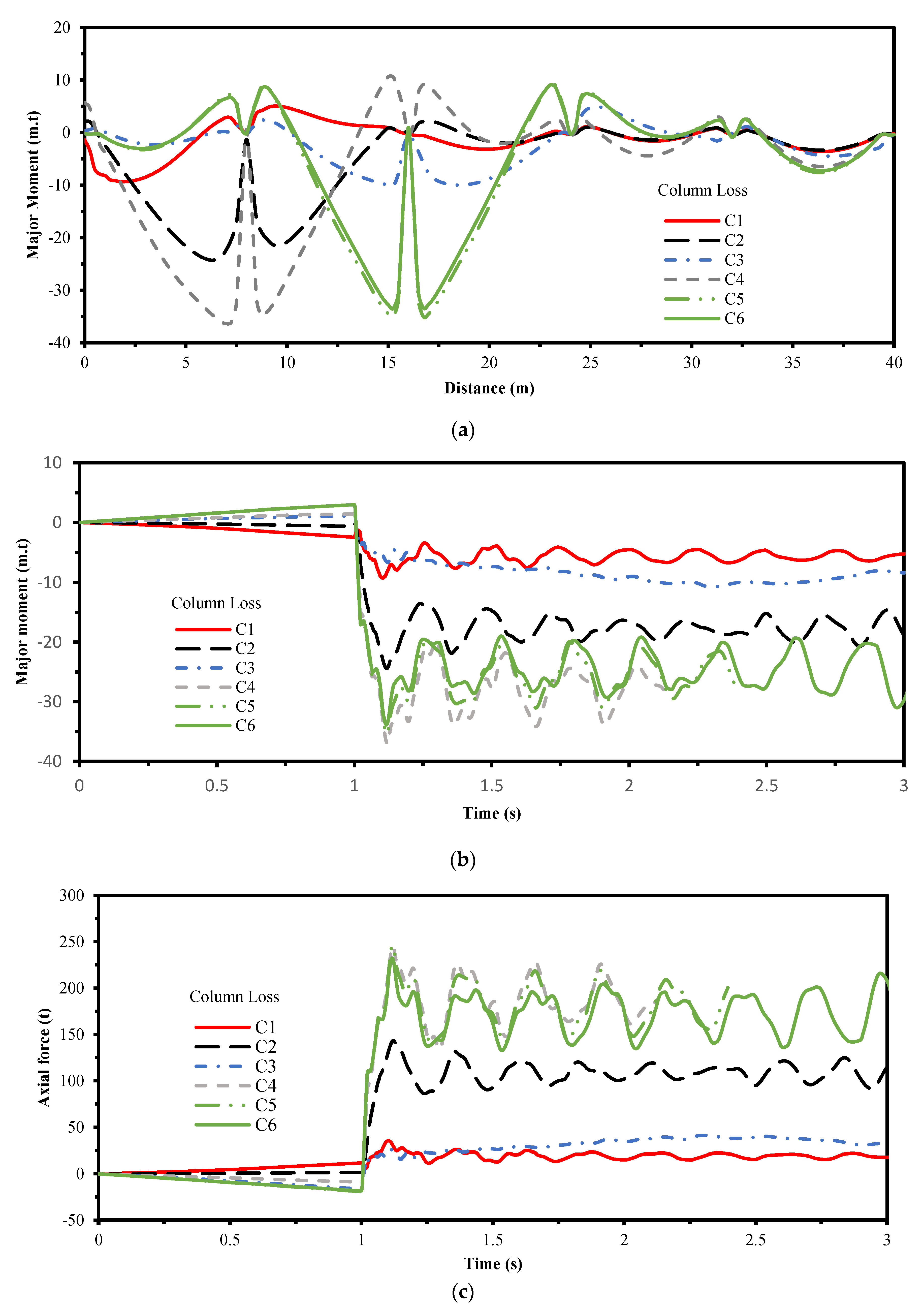
4.5. Position of the Column Loss
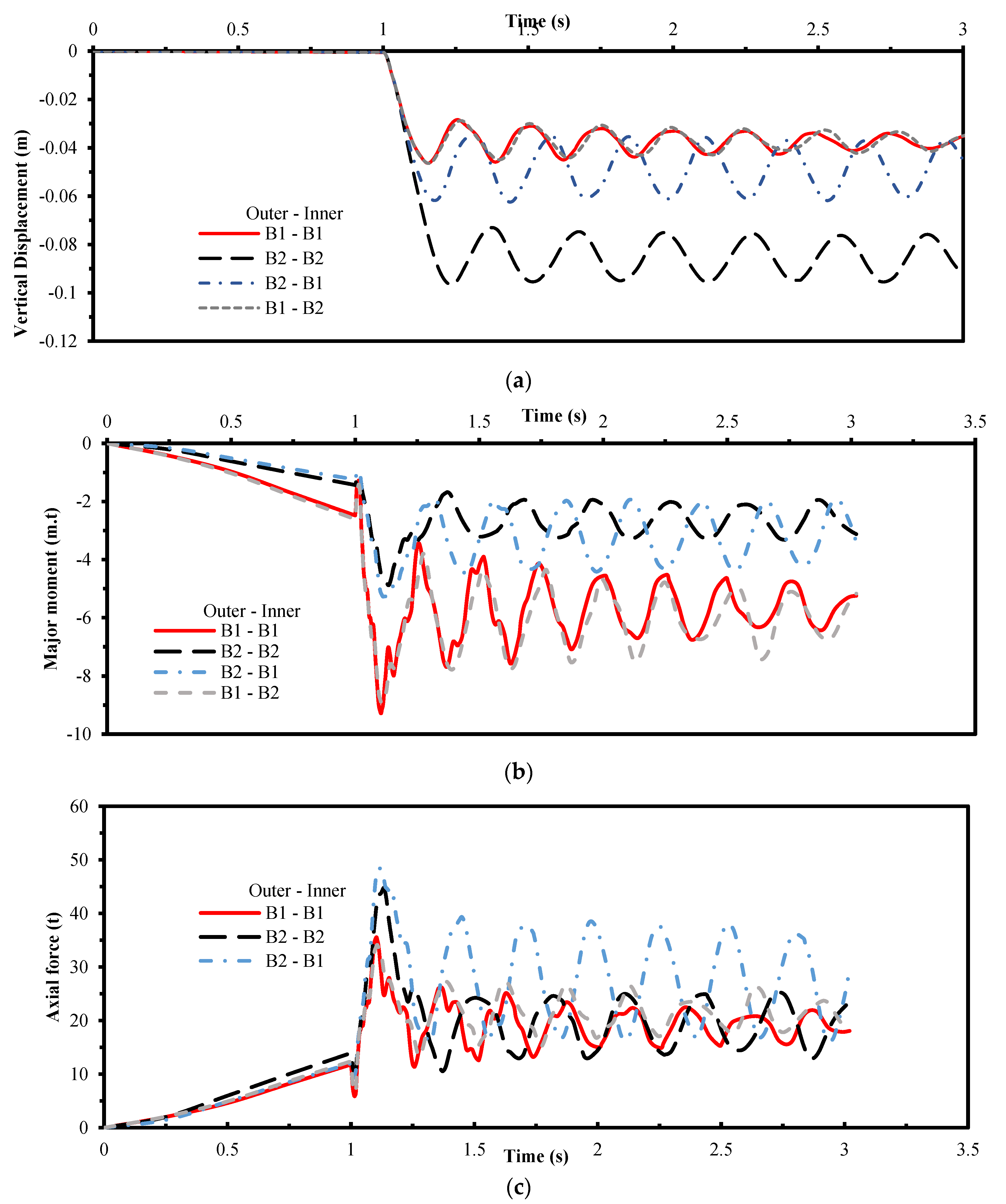
4.6. Beams Cross-Section
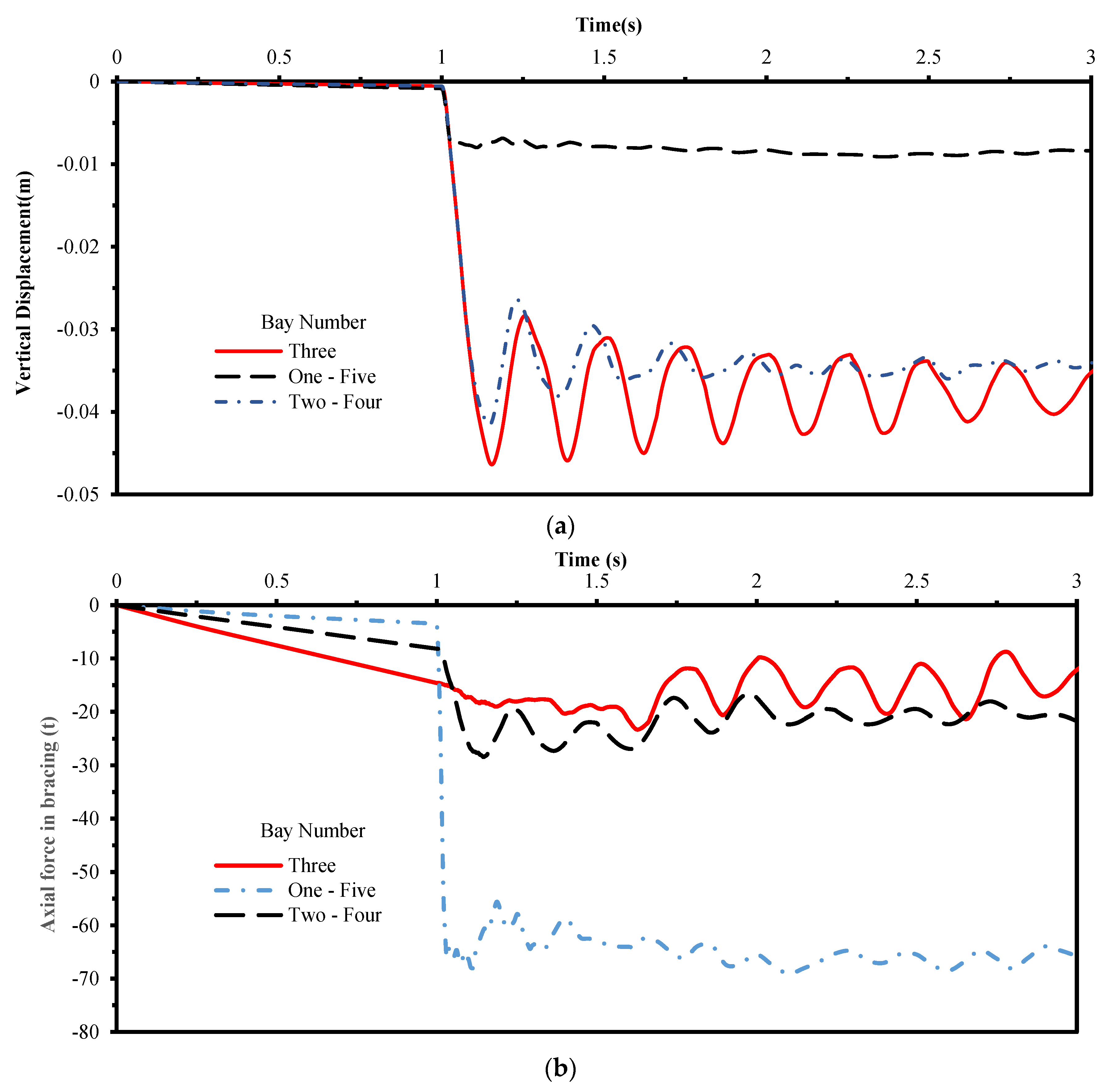
4.7. Bracing Locations
5. Uncertainty Treatment in Finite Element Modelling
5.1. Input Parameter Selection and Experimental Design Strategy
5.2. Probabilistic Progressive Collapse Analysis
6. Conclusions
- The maximum plastic strain occurs in the slab for the case of corner column loss with a value of 0.00449.
- The sudden removal of the exterior column induces the maximum excessive percentage 111.4% of the axial force in the corner column.
- The concrete strength of slabs has a crucial impact on the response rather than the steel strength of columns and beams.
- The density of the bottom and upper reinforcement has no impact on the response rather than the upper reinforcement may affect the deflection with a minor value.
- The removal of inner columns has a much significant effect on the beam major moment and tying forces
- For corner column removal, the cross-section of outer beams has a significant role in the response and the redistribution of the excessive forces.
- The present study recommends an exhaustive consideration of uncertainty for progressive collapse analysis, especially considering uncertainty in position of the removed column, the outer and inner beams cross-section, and position of the vertical bracing on the façade. For other parameters, such as the density of slab top and bottom reinforcements, consideration of mean parameters is sufficient.
- Future avenues of research on this topic will include more discussions on probabilistic models and uncertainty and state the weight of each variable.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Notations
| E | Modulus of Elasticity | the compressive stress | |
| fy | Yield stress of steel | strain corresponding to tensile stress | |
| fu | Ultimate stress of steel | the total strain | |
| Yield strain of steel | plastic strain with stiffness degradation | ||
| Ultimate strain of steel | the damage factor | ||
| ultimate tensile stress of concrete | the tension or compression stress | ||
| strain at peak stress | the tensile or compressive strength of concrete | ||
| average compressive strength of concrete | The dilation angle | ||
| ultimate compressive strain for concrete | Eccentricity | ||
| initial tangent stiffness modulus | Ratio of initial equivalent biaxial compressive yield stress to initial uniaxial compressive yield stress | ||
| strain corresponding to compressive stress | Stress invariant ratio |
Appendix A
| Case | Steel (fy) MPa | Concrete (fcm) MPa | Rebar (fy) MPa | Bottom Rebar mm2/m | Top rebar mm2/m | Collapse Column | Beams | Bracing Location | |
|---|---|---|---|---|---|---|---|---|---|
| Outer | Inner | ||||||||
| 1 | 235 | 30 | 235 | 566 | 393 | C1 | B1 | B1 | Bay 3 |
| 2 | 275 | 30 | 235 | 566 | 393 | C1 | B1 | B1 | Bay 3 |
| 3 | 355 | 30 | 235 | 566 | 393 | C1 | B1 | B1 | Bay 3 |
| 4 | 440 | 30 | 235 | 566 | 393 | C1 | B1 | B1 | Bay 3 |
| Case | Steel (fy) MPa | Concrete (fcm) MPa | Rebar (fy) MPa | Bottom Rebar mm2/m | Top Rebar mm2/m | Collapse Column | Beams | Bracing Location | |
|---|---|---|---|---|---|---|---|---|---|
| Outer | Inner | ||||||||
| 1 | 355 | 20 | 235 | 566 | 393 | C1 | B1 | B1 | Bay 3 |
| 2 | 355 | 25 | 235 | 566 | 393 | C1 | B1 | B1 | Bay 3 |
| 3 | 355 | 30 | 235 | 566 | 393 | C1 | B1 | B1 | Bay 3 |
| 4 | 355 | 35 | 235 | 566 | 393 | C1 | B1 | B1 | Bay 3 |
| 5 | 355 | 40 | 235 | 566 | 393 | C1 | B1 | B1 | Bay 3 |
| Case | Steel (fy) MPa | Concrete (fcm) MPa | Rebar (fy) MPa | Bottom Rebar mm2/m | Top rebar mm2/m | Collapse Column | Beams | Bracing Location | |
|---|---|---|---|---|---|---|---|---|---|
| Outer | Inner | ||||||||
| 1 | 355 | 30 | 235 | 252 | 393 | C1 | B1 | B1 | Bay 3 |
| 2 | 355 | 30 | 235 | 393 | 393 | C1 | B1 | B1 | Bay 3 |
| 3 | 355 | 30 | 235 | 566 | 393 | C1 | B1 | B1 | Bay 3 |
| 4 | 355 | 30 | 235 | 1005 | 393 | C1 | B1 | B1 | Bay 3 |
| 5 | 355 | 30 | 235 | 1272 | 393 | C1 | B1 | B1 | Bay 3 |
| 6 | 355 | 30 | 235 | 1571 | 393 | C1 | B1 | B1 | Bay 3 |
| Case | Steel (fy) MPa | Concrete (fcm) MPa | Rebar (fy) MPa | Bottom Rebar mm2/m | Top Rebar mm2/m | Collapse Column | Beams | Bracing Location | |
|---|---|---|---|---|---|---|---|---|---|
| Outer | Inner | ||||||||
| 1 | 355 | 30 | 235 | 566 | 393 | C1 | B1 | B1 | Bay 3 |
| 2 | 355 | 30 | 235 | 566 | 566 | C1 | B1 | B1 | Bay 3 |
| 3 | 355 | 30 | 235 | 566 | 1005 | C1 | B1 | B1 | Bay 3 |
| 4 | 355 | 30 | 235 | 566 | 1272 | C1 | B1 | B1 | Bay 3 |
| 5 | 355 | 30 | 235 | 566 | 1571 | C1 | B1 | B1 | Bay 3 |
| Case | Steel (fy) MPa | Concrete (fcm) MPa | Rebar (fy) MPa | Bottom Rebar mm2/m | Top Rebar mm2/m | Collapse Column | Beams | Bracing Location | |
|---|---|---|---|---|---|---|---|---|---|
| Outer | Inner | ||||||||
| 1 | 355 | 30 | 235 | 566 | 393 | C1 | B1 | B1 | Bay 3 |
| 2 | 355 | 30 | 235 | 566 | 393 | C2 | B1 | B1 | Bay 3 |
| 3 | 355 | 30 | 235 | 566 | 393 | C3 | B1 | B1 | Bay 3 |
| 4 | 355 | 30 | 235 | 566 | 393 | C4 | B1 | B1 | Bay 3 |
| 5 | 355 | 30 | 235 | 566 | 393 | C5 | B1 | B1 | Bay 3 |
| 6 | 355 | 30 | 235 | 566 | 393 | C6 | B1 | B1 | Bay 3 |
| Case | Steel (fy) MPa | Concrete (fcm) MPa | Rebar (fy) MPa | Bottom Rebar mm2/m | Top Rebar mm2/m | Collapse Column | Beams | Bracing Location | |
|---|---|---|---|---|---|---|---|---|---|
| Outer | Inner | ||||||||
| 1 | 355 | 30 | 235 | 566 | 393 | C1 | B1 | B1 | Bay 3 |
| 2 | 355 | 30 | 235 | 566 | 393 | C1 | B2 | B2 | Bay 3 |
| 3 | 355 | 30 | 235 | 566 | 393 | C1 | B2 | B1 | Bay 3 |
| 4 | 355 | 30 | 235 | 566 | 393 | C1 | B1 | B2 | Bay 3 |
| Case | Steel (fy) MPa | Concrete (fcm) MPa | Rebar (fy) MPa | Bottom Rebar mm2/m | Top Rebar mm2/m | Collapse Column | Beams | Bracing Location | |
|---|---|---|---|---|---|---|---|---|---|
| Outer | Inner | ||||||||
| 1 | 355 | 30 | 235 | 566 | 393 | C1 | B1 | B1 | Bay 3 |
| 2 | 355 | 30 | 235 | 566 | 393 | C1 | B1 | B1 | Bays 1, 5 |
| 3 | 355 | 30 | 235 | 566 | 393 | C1 | B1 | B1 | Bays 2, 4 |
References
- Pugsley, A.; Saunders, S.O. Report of the Inquiry into the Collapse of Flats at Ronan Point, Canning Town; HM Stationery Office: Richmond, UK, 1968.
- Federal Emergency Management Agency (FEMA). The Oklahoma City Bombing: Improving Building Performance through Multi-Hazard Mitigation; Federal Emergency Management Agency: Washington, DC, USA, 1996.
- NCSTAR; NIST. Final Report on the Collapse of the World Trade Center Towers; National Construction Safety Team for the Federal Building Fire Safety: Gaithersburg, MD, USA, 2005.
- Kiakojouri, F.; De Biagi, V.; Chiaia, B.; Sheidaii, M.R. Progressive collapse of framed building structures: Current knowledge and future prospects. Eng. Struct. 2020, 206, 110061. [Google Scholar] [CrossRef]
- Leyendecker, E.V.; Ellingwood, B.R. Design Methods for Reducing the Risk of Progressive Collapse in Building; U.S. Government Printing Office: Washington, DC, USA, 1977. [CrossRef] [Green Version]
- ACI 318-11; Building Code Requirements for Structural Concrete (ACI 318-11). American Concrete Institute: Farmington Hills, MI, USA, 2011.
- ASCE 7-10; Minimum Design Loads for Buildings and Other Structures. American Society for Civil Engineers: Reston, VA, USA, 2000.
- Izzuddin, B.; Vlassis, A.; Elghazouli, A.; Nethercot, D. Progressive collapse of multi-storey buildings due to sudden column loss—Part I: Simplified assessment framework. Eng. Struct. 2008, 30, 1308–1318. [Google Scholar] [CrossRef] [Green Version]
- Vlassis, A.; Izzuddin, B.; Elghazouli, A.; Nethercot, D. Progressive collapse of multi-storey buildings due to sudden column loss—Part II: Application. Eng. Struct. 2008, 30, 1424–1438. [Google Scholar] [CrossRef] [Green Version]
- Izzuddin, B. Mitigation of progressive collapse in multi-storey buildings. Adv. Struct. Eng. 2012, 15, 1505–1520. [Google Scholar] [CrossRef]
- Guo, L.; Gao, S.; Fu, F.; Wang, Y. Experimental study and numerical analysis of progressive collapse resistance of composite frames. J. Constr. Steel Res. 2013, 89, 236–251. [Google Scholar] [CrossRef]
- Song, B.I.; Giriunas, K.A.; Sezen, H. Progressive collapse testing and analysis of a steel frame building. J. Constr. Steel Res. 2014, 94, 76–83. [Google Scholar] [CrossRef]
- Kim, J.; Lee, Y.H. Progressive collapse resisting capacity of tube-type structures. Struct. Des. Tall Spec. Build. 2010, 19, 761–777. [Google Scholar] [CrossRef]
- Kim, J.; Lee, Y.; Choi, H. Progressive collapse resisting capacity of braced frames. Struct. Des. Tall Spec. Build. 2011, 20, 257–270. [Google Scholar] [CrossRef]
- Kim, J.; Hong, S. Progressive collapse performance of irregular buildings. Struct. Des. Tall Spec. Build. 2011, 20, 721–734. [Google Scholar] [CrossRef]
- Kim, J.; Jung, M. Progressive collapse-resisting capacity of modular mega-frame buildings. Struct. Des. Tall Spec. Build. 2013, 22, 471–484. [Google Scholar] [CrossRef]
- Kordbagh, B.; Mohammadi, M. Influence of seismicity level and height of the building on progressive collapse resistance of steel frames. Struct. Des. Tall Spec. Build. 2017, 26, e1305. [Google Scholar] [CrossRef]
- Naji, A.; Ommetalab, M.R. Horizontal bracing to enhance progressive collapse resistance of steel moment frames. Struct. Des. Tall Spec. Build. 2019, 28, e1563. [Google Scholar] [CrossRef]
- Zhang, J.-Z.; Li, G.-Q.; Jiang, J. Collapse of steel-concrete composite frame under edge-column loss—Experiment and its analysis. Eng. Struct. 2020, 209, 109951. [Google Scholar] [CrossRef]
- Gade, V.P.; Sahoo, D.R. Evaluation of collapse-resistance of special truss moment frames as per FEMAp695 approach. Eng. Struct. 2016, 126, 505–515. [Google Scholar] [CrossRef]
- Kim, J.; Park, J.-H.; Lee, T.-H. Sensitivity analysis of steel buildings subjected to column loss. Eng. Struct. 2011, 33, 421–432. [Google Scholar] [CrossRef]
- Kiakojouri, F.; Sheidaii, M.; De Biagi, V.; Chiaia, B. Progressive collapse assessment of steel moment-resisting frames using static-and dynamic-incremental analyses. J. Perform. Constr. Facil. 2020, 34, 04020025. [Google Scholar] [CrossRef]
- Hadjioannou, M.; Williamson, E.B.; Engelhardt, M.D. Collapse Simulations of Steel-Concrete Composite Floors under Column Loss Scenarios. J. Struct. Eng. 2020, 146, 04020275. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Bao, Y. Full-scale test of a steel–concrete composite floor system with moment-resisting connections under a middle-edge column removal scenario. J. Struct. Eng. 2020, 146, 04020067. [Google Scholar] [CrossRef]
- Naji, A.; Khodaverdi Zadeh, M. Progressive collapse analysis of steel braced frames. Pract. Period. Struct. Des. 2019, 24, 04019004. [Google Scholar] [CrossRef]
- Fu, F. Progressive collapse analysis of high-rise building with 3-D finite element modeling method. J. Constr. Steel Res. 2009, 65, 1269–1278. [Google Scholar] [CrossRef]
- Fu, F. 3-D nonlinear dynamic progressive collapse analysis of multi-storey steel composite frame buildings—Parametric study. Eng. Struct. 2010, 32, 3974–3980. [Google Scholar] [CrossRef]
- Gao, S.; Xu, M.; Zhang, S. Dynamic analysis of concrete-filled steel tube composite frame against progressive collapse based on benchmark model. Adv. Struct. Eng. 2018, 21, 1021–1035. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W. Theoretical evaluation method for the progressive collapse resistance of steel frame buildings. J. Constr. Steel Res. 2021, 179, 106576. [Google Scholar] [CrossRef]
- Zhang, W.-J.; Li, G.-Q.; Zhang, J.-Z. Progressive collapse mechanism of steel framed-structures subjected to a middle-column loss. Adv. Steel. Constr. 2021, 17, 199–209. [Google Scholar]
- Tian, Y.; Lin, K.; Zhang, L.; Lu, X.; Xue, H. Novel seismic–progressive collapse resilient super-tall building system. J. Build. Eng. 2021, 41, 102790. [Google Scholar] [CrossRef]
- Chen, X.; Wang, H.; Chan, A.H.; Agrawal, A.K.; Cheng, Y. Collapse simulation of masonry arches induced by spreading supports with the combined finite–discrete element method. Comput. Part. Mech. 2021, 8, 721–735. [Google Scholar] [CrossRef]
- Peng, J.; Hou, C.; Shen, L. Progressive collapse analysis of corner-supported composite modular buildings. J. Build. Eng. 2022, 48, 103977. [Google Scholar] [CrossRef]
- Gardner, L.; Wang, F.; Liew, A. Influence of strain hardening on the behavior and design of steel structures. Int. J. Struct. Stab. Dyn. 2011, 11, 855–875. [Google Scholar] [CrossRef]
- Liew, A.; Gardner, L. Ultimate capacity of structural steel cross-sections under compression, bending and combined loading. Structures 2015, 1, 2–11. [Google Scholar] [CrossRef]
- Yun, X.; Gardner, L. Stress-strain curves for hot-rolled steels. J. Constr. Steel Res. 2017, 133, 36–46. [Google Scholar] [CrossRef]
- Desayi, P.; Krishnan, S. Equation for the stress-strain curve of concrete. Matériaux Constr. 1978, 11, 339–345. [Google Scholar]
- BS. Eurocode 2: Design of Concrete Structures: Part 1-1: General Rules and Rules for Buildings; British Standards Institution: London, UK, 2004. [Google Scholar]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Deb, T.; Yuen, T.Y.; Lee, D.; Halder, R.; You, Y.C. Bi-directional collapse fragility assessment by DFEM of unreinforced masonry buildings with openings and different confinement configurations. Earthq. Eng. Struct. Dyn. 2021, 50, 4097–4120. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Ren, W.; Sneed, L.H.; Yang, Y.; He, R. Numerical simulation of prestressed precast concrete bridge deck panels using damage plasticity model. Int. J. Concr. Struct. 2015, 9, 45–54. [Google Scholar] [CrossRef] [Green Version]
- Yan, D.; Lin, G. Dynamic behaviour of concrete in biaxial compression. Mag. Concr. Res. 2007, 59, 45–52. [Google Scholar] [CrossRef]
- Couwenberg, R.P.P.; Hordijk, D.; Zegers, S. Progressive Collapse of Reinforced Concrete Structures. Master’s Thesis, Faculty of Architecture of the TU/e, Eindhoven, The Netherlands, 2013. [Google Scholar]
- EN 1991-1-4:2005; Eurocode 1: Actions on Structures-Part 1–4: General Actions-Wind Actions. The European Union: Maastricht, The Netherlands, 2005.
- GSA. Progressive Collapse Analysis and Design Guidelines for New Federal Office Buildings and Major Modernization Projects; General Services Administration: Washington, DC, USA, 2003.





| Steel Grade | E (N/mm2) | fy (N/mm2) | fu (N/mm2) | % | % |
|---|---|---|---|---|---|
| S235 | 210,000 | 235 | 360 | 0.11 | 20.83 |
| S275 | 210,000 | 275 | 430 | 0.13 | 21.63 |
| S355 | 210,000 | 355 | 490 | 0.17 | 16.53 |
| S440 | 210,000 | 440 | 550 | 0.21 | 12.00 |
| Dilation Angle () | Eccentricity () | Viscosity Parameter | ||
|---|---|---|---|---|
| 30 | 0.1 | 1.16 | 0.6666 | 0.0004 |
| Structural Element | Dimensions (mm) | Longitudinal Reinforcement | ||
|---|---|---|---|---|
| Breadth (mm) | Depth (mm) | Top | Bottom | |
| Beams | 450 | 600 | 6- #20 | 4- #20 |
| Columns | 450 | 450 | 2- #20 | 2- #20 |
| Columns Steel Members Properties | ||||||
|---|---|---|---|---|---|---|
| Stories | Section | Type | Overall Depth (mm) | Width (mm) | Thickness | |
| Flange (mm) | Web (mm) | |||||
| 01: 09 | UKC356 × 406 × 634 | I-beam | 474.6 | 424 | 77 | 47.6 |
| 10: 18 | UKC356 × 406 × 551 | I-beam | 455.6 | 418.5 | 67.5 | 42.1 |
| 19: 25 | UKC356 × 406 × 287 | I-beam | 393.6 | 399 | 36.5 | 22.6 |
| Beams Steel Members Properties | ||||||
| Beam ID | Section | Type | Overall Depth (mm) | Width (mm) | Thickness | |
| Flange (mm) | Web (mm) | |||||
| B1 | UKB533 × 312 × 150 | I-beam | 542.5 | 312 | 20.3 | 12.7 |
| B2 | UKB356 × 171 × 67 | I-beam | 363.4 | 173.2 | 15.7 | 9 |
| Bracing Steel Members Properties | ||||||
| Stories | Section | Type | Outer Diameter (mm) | Thickness (mm) | Place Bracing (Bay Number) | |
| 01: 09 | CHHF406.4 × 16 | Circular-Tube | 406.4 | 16 | 3 | |
| CHHF323.9 × 10 | Circular-Tube | 323.9 | 10 | 1, 2, 4 and 5 | ||
| 10: 18 | CHHF355.6 × 14.2 | Circular-Tube | 355.6 | 14.2 | 3 | |
| CHHF244.5 × 10 | Circular-Tube | 244.5 | 10 | 1, 2, 4 and 5 | ||
| 19: 25 | CHHF323.9 × 6.3 | Circular-Tube | 323.9 | 6.3 | 3 | |
| CHHF219.1 × 5 | Circular-Tube | 219.1 | 5 | 1, 2, 4 and 5 | ||
| Case | Steel (fy) MPa | Concrete (fcm) MPa | Rebar (fy) MPa | Bottom Rebar mm2/m | Top Rebar mm2/m | Collapse Column | Beams | Bracing Location | |
|---|---|---|---|---|---|---|---|---|---|
| Outer | Inner | ||||||||
| 1 | 235 | 40 | 235 | 566 | 393 | C2 | B2 | B1 | Bays 2, 4 |
| 2 | 235 | 35 | 355 | 1005 | 393 | C5 | B1 | B1 | Bays 1, 5 |
| 3 | 275 | 25 | 275 | 1571 | 1005 | C3 | B2 | B1 | Bays 2, 4 |
| 4 | 440 | 35 | 355 | 252 | 1005 | C3 | B2 | B2 | Bays 2, 4 |
| 5 | 275 | 40 | 275 | 1272 | 393 | C1 | B2 | B1 | Bays 2, 4 |
| 6 | 275 | 30 | 275 | 1005 | 393 | C5 | B2 | B1 | Bay 3 |
| 7 | 235 | 30 | 235 | 566 | 393 | C4 | B2 | B1 | Bays 1, 5 |
| 8 | 440 | 25 | 235 | 1571 | 1005 | C5 | B1 | B1 | Bays 2, 4 |
| 9 | 275 | 20 | 235 | 566 | 393 | C5 | B1 | B1 | Bay 3 |
| 10 | 440 | 20 | 275 | 393 | 393 | C1 | B1 | B1 | Bays 1, 5 |
| 11 | 355 | 20 | 235 | 1005 | 1005 | C6 | B1 | B2 | Bays 2, 4 |
| 12 | 275 | 30 | 355 | 1005 | 393 | C3 | B2 | B1 | Bay 3 |
| 13 | 440 | 20 | 355 | 393 | 1005 | C5 | B2 | B1 | Bays 1, 5 |
| 14 | 440 | 40 | 355 | 1272 | 1005 | C5 | B2 | B1 | Bay 3 |
| 15 | 275 | 35 | 275 | 1571 | 393 | C5 | B1 | B1 | Bays 2, 4 |
| 16 | 440 | 20 | 235 | 1571 | 393 | C1 | B1 | B1 | Bay 3 |
| 17 | 440 | 20 | 235 | 252 | 1005 | C3 | B2 | B2 | Bay 3 |
| 18 | 275 | 25 | 275 | 393 | 1005 | C4 | B1 | B2 | Bays 2, 4 |
| 19 | 275 | 30 | 355 | 252 | 1005 | C6 | B1 | B1 | Bays 2, 4 |
| 20 | 355 | 20 | 275 | 1005 | 1005 | C6 | B1 | B1 | Bays 2, 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lotfy, S.; Mortagi, M.; El Madawy, M.E. Variable Factors Affecting Progressive Destruction of Composite Steel Tall Building. Buildings 2022, 12, 1704. https://doi.org/10.3390/buildings12101704
Lotfy S, Mortagi M, El Madawy ME. Variable Factors Affecting Progressive Destruction of Composite Steel Tall Building. Buildings. 2022; 12(10):1704. https://doi.org/10.3390/buildings12101704
Chicago/Turabian StyleLotfy, Sameh, Mohamed Mortagi, and Mohamed E. El Madawy. 2022. "Variable Factors Affecting Progressive Destruction of Composite Steel Tall Building" Buildings 12, no. 10: 1704. https://doi.org/10.3390/buildings12101704
APA StyleLotfy, S., Mortagi, M., & El Madawy, M. E. (2022). Variable Factors Affecting Progressive Destruction of Composite Steel Tall Building. Buildings, 12(10), 1704. https://doi.org/10.3390/buildings12101704







