Structural and Heat Transfer Model Analysis of Wall-Mounted Solar Chimney Inlets and Outlets in Single-Story Buildings
Abstract
:1. Introduction
- (1)
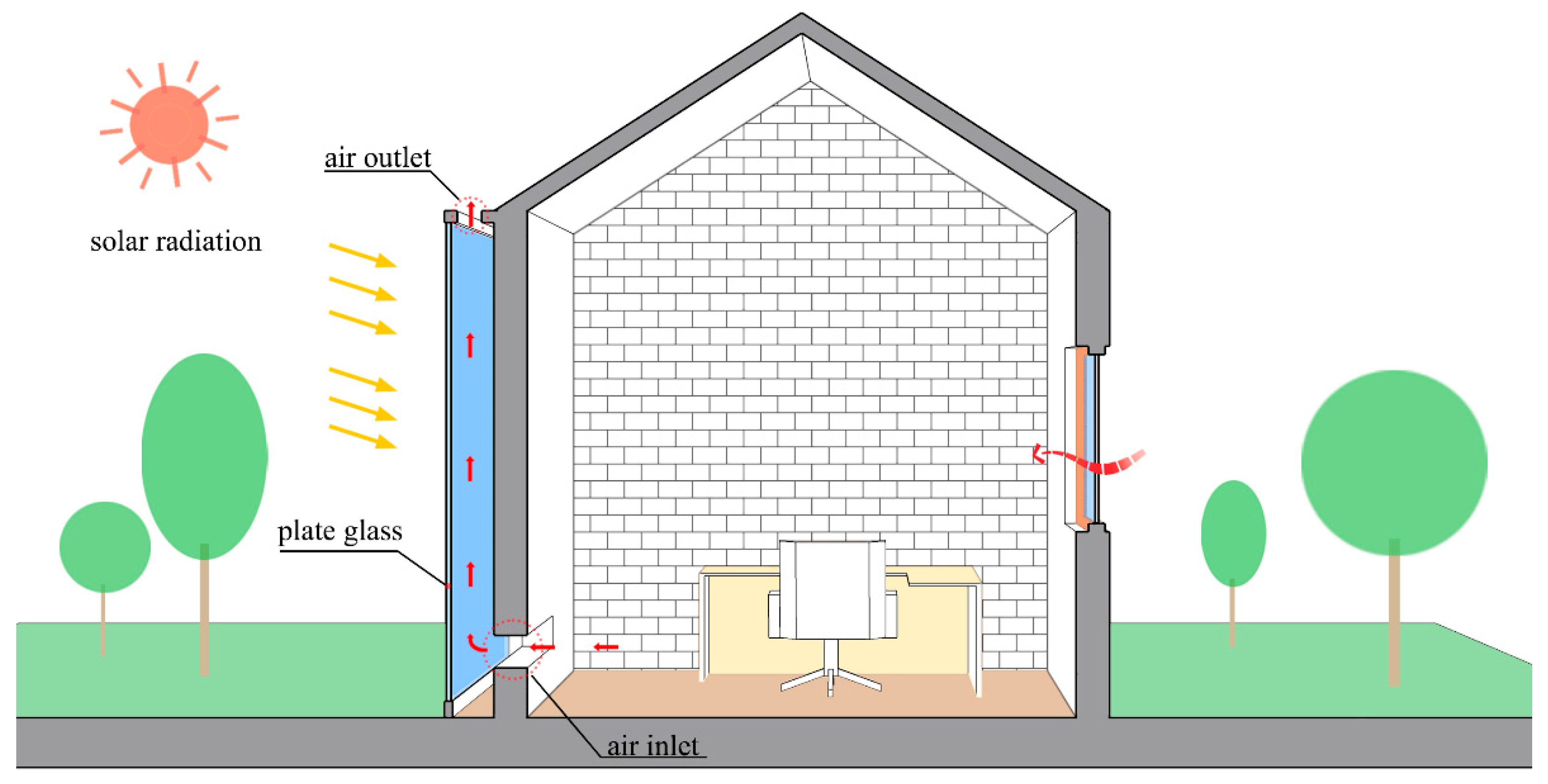
- A wall-mounted solar chimney with an outer glass cover was designed, and the ratio of the inlet and outlet cross-sectional area of the wall-mounted solar chimney is S;
- (2)
- Six physical models of wall-mounted solar chimneys with different S-values were developed based on the different ratios of the inlet and outlet cross-sectional areas of wall-mounted solar chimneys;
- (3)
- The energy input and output processes of each component of the wall-mounted solar chimney were analyzed, and the analytical equations for the heat transfer of each component in the wall-mounted solar chimney were established;
- (4)
- Ansys Fluent steady-state simulations analyzed the air temperature distribution and flow conditions in the wall-mounted solar chimney at different S-values;
- (5)
- Finally, Ansys Fluent transient simulation was applied to analyze the natural ventilation effect of the wall-mounted solar chimney at each moment of actual operation under different S-values.
2. Model Description and Heat Transfer Analysis
2.1. Physical Model Description
2.2. Thermal Balance Analysis of Glass Cover
2.3. Wall Heat Balance Analysis
2.4. Heat Balance Analysis of Airflow Region
3. Simulation Method
3.1. Simulation Condition Setting
- (1)
- The air inside the wall-type solar chimney is an ideal incompressible gas, usually using the Boussinesq assumption;
- (2)
- Ignore the viscous dissipation of air in the flow channel;
- (3)
- The physical properties of the air inside the solar wall chimney are constant, and the air density is the only variable;
- (4)
- Ignore the shell’s heat transfer loss and the outer wall’s radiant heat loss.
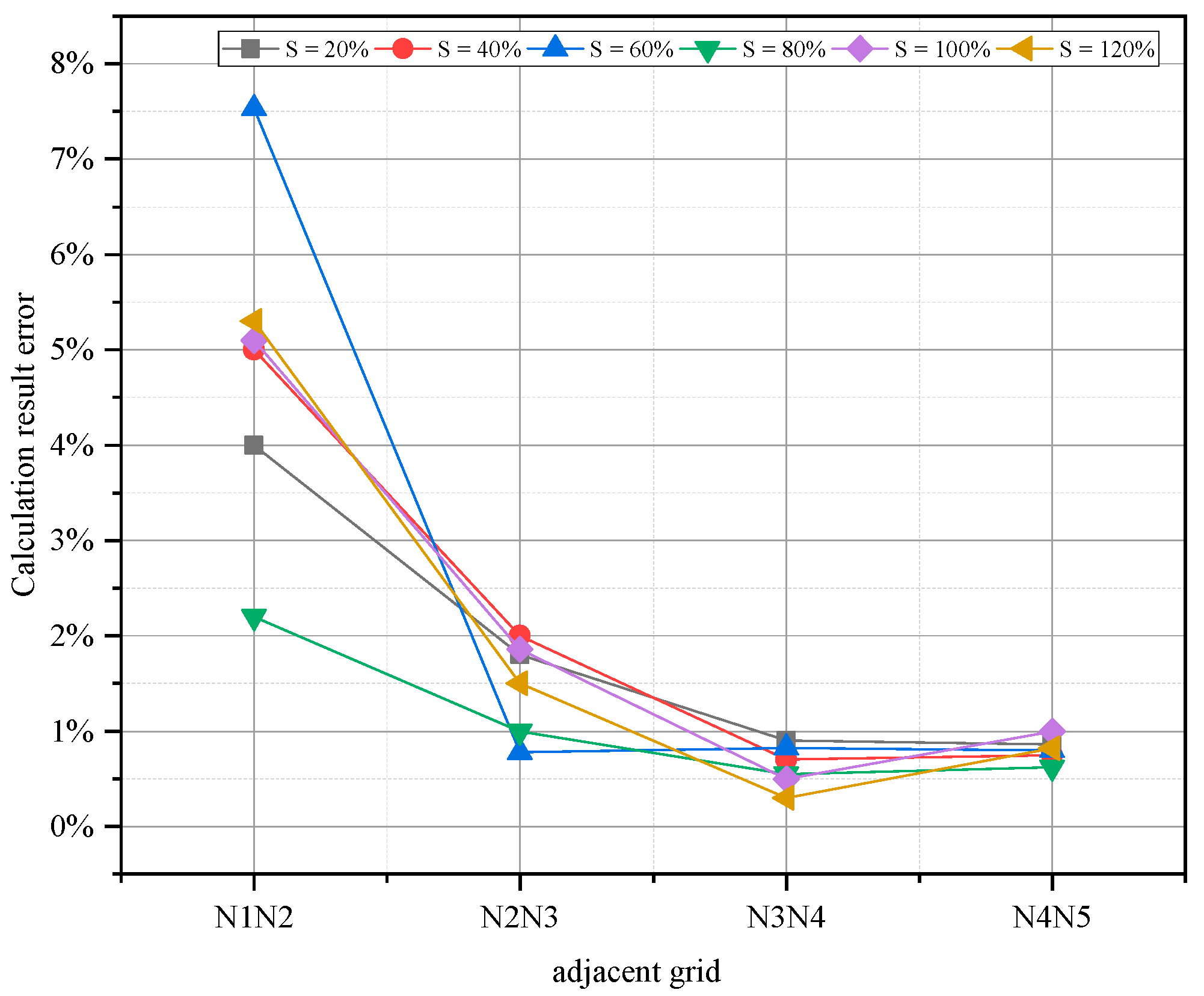
3.2. Physical Computation Grid Validation
3.3. Governing Equations
- (1)
- Conservation of mass equation
- (2)
- Conservation of momentum equation
- (3)
- Energy and heat transfer equation
- (4)
- Turbulent kinetic energy control equation
3.4. Solver and Boundary Condition Settings
- (1)
- The air intake utilized the pressure intake border, the pressure at the inlet was 0 Pa, the inlet airflow temperature was 30 °C, and the inlet size was 100 mm × 1000 mm;
- (2)
- The air outlet was the pressure outlet so in order to study the natural ventilation effect caused by the hot pressure, the outlet pressure was set to 0 Pa, and the outlet size was set to six different sizes according to the S-value;
- (3)
- The size of the glass cover was 3000 mm × 3000 mm × 5 mm, the heat boundary was the convective-radiation mixed boundary, and the convection coefficient was calculated and determined according to the above formula, while the radiation boundary was the semi-transparent radiation boundary, and the inner and outer emissivity were both 0.55;
- (4)
- The thickness of the wall body was 130 mm, the boundary conditions of radiation convection were mixed, and the above formula determined the convective heat transfer coefficient;
- (5)
- The surrounding protective structure was the boundary condition of four adiabatic walls with equal thicknesses, which were 5 mm.
4. Results and Discussion
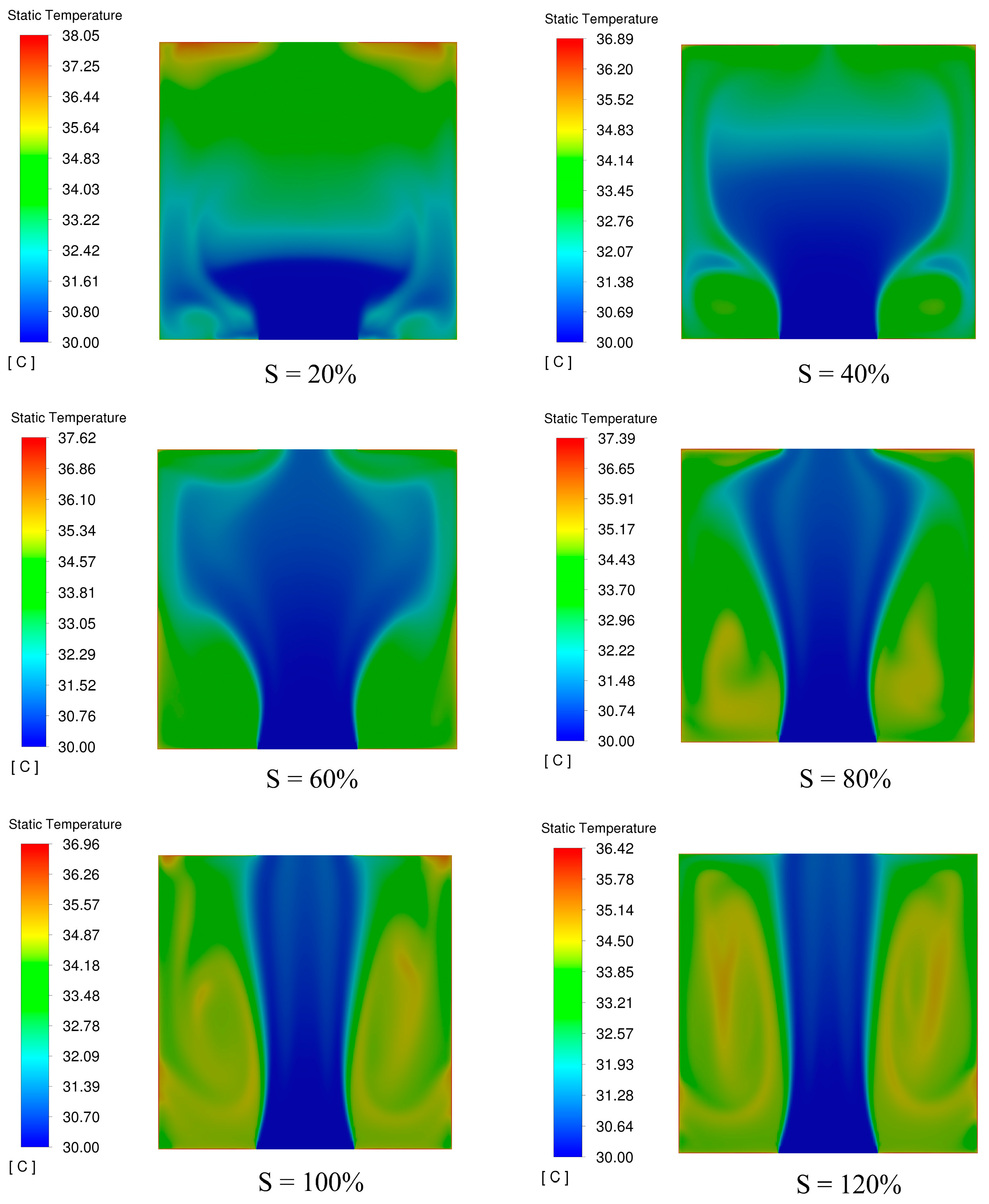
4.1. Overall Comparison of S-Values—Temperature Field Distribution
4.2. Overall Comparison of S-Values—Flow Field Analysis
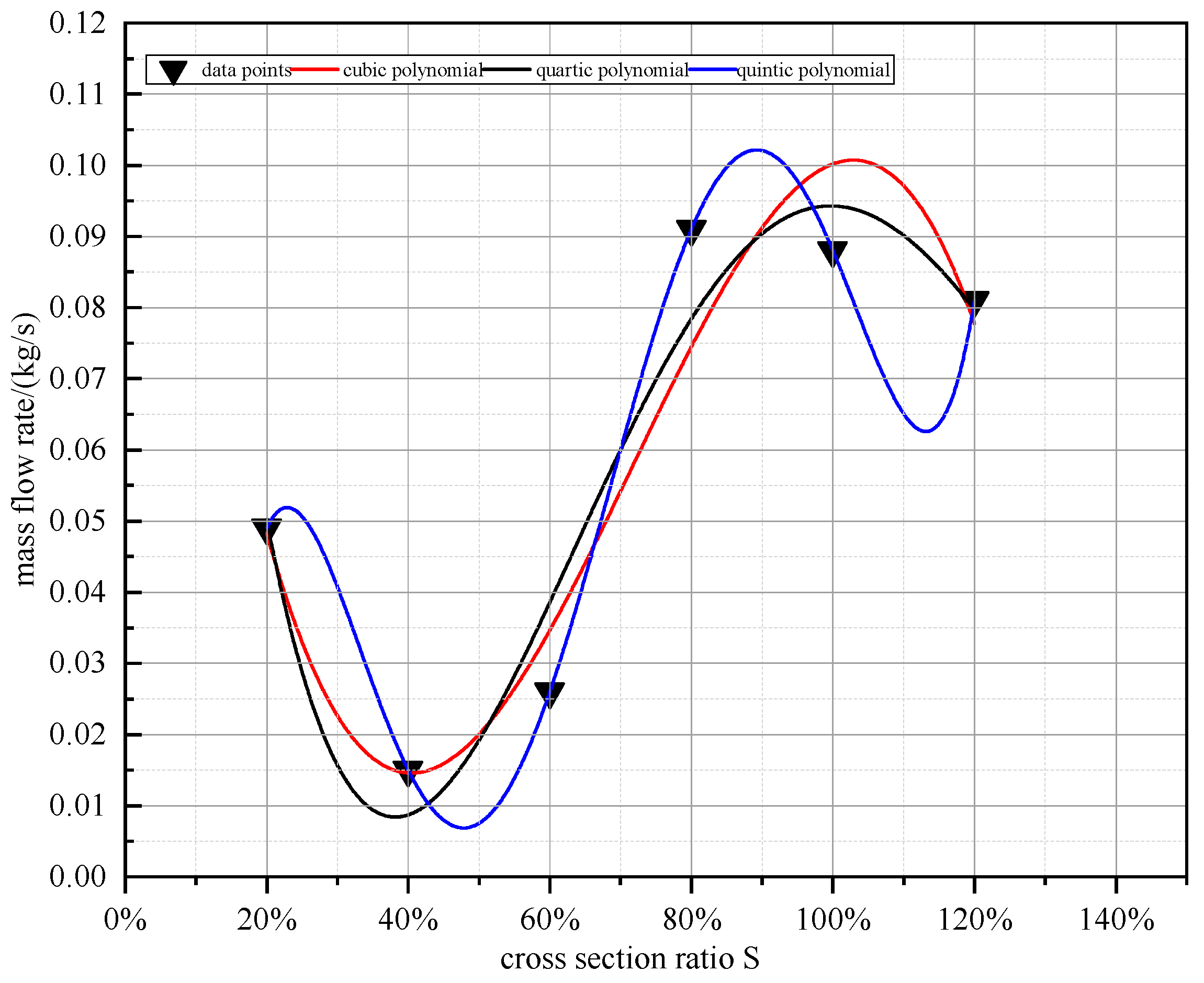
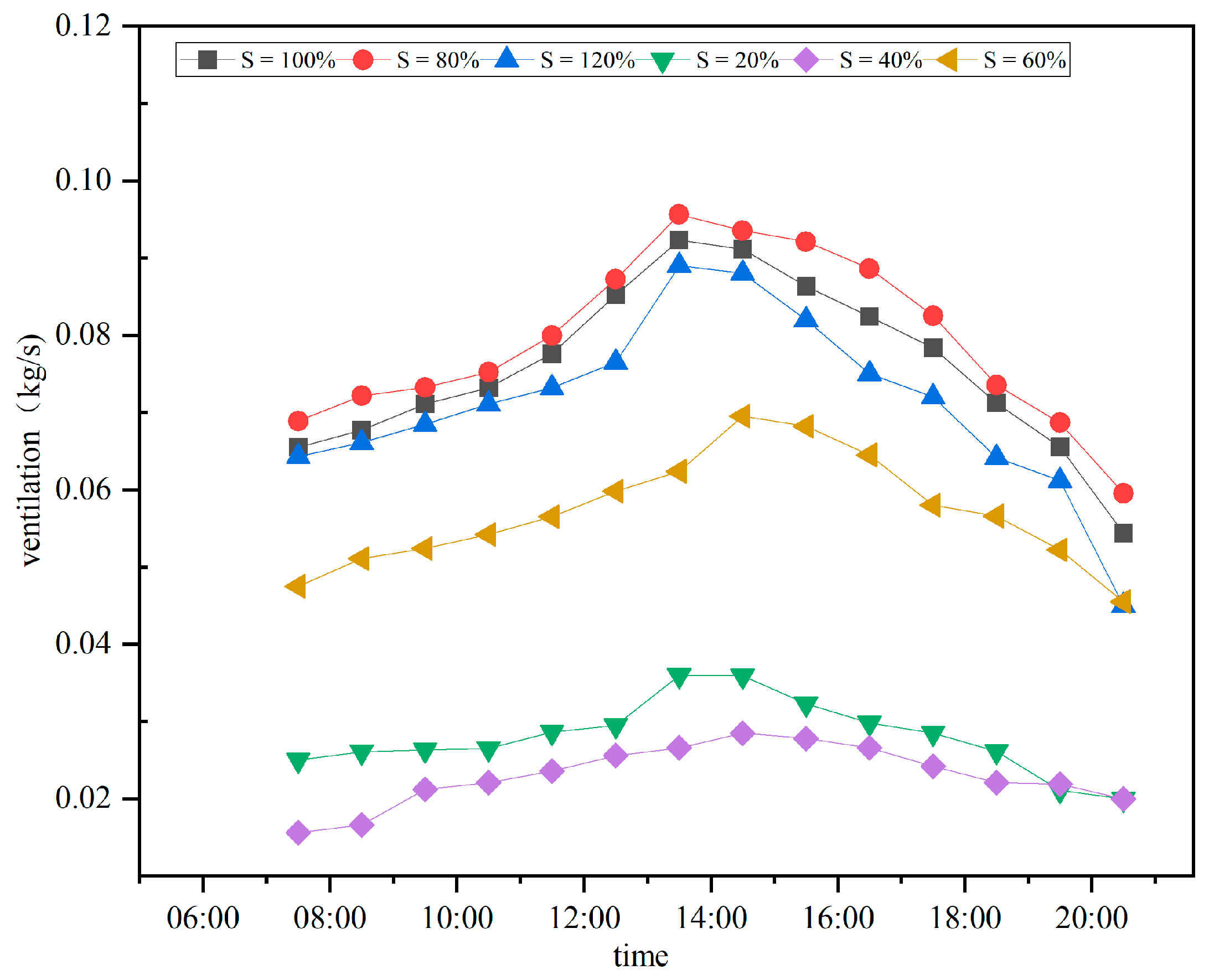
4.3. Analysis of Actual Ventilation Rate
5. Conclusions
- (1)
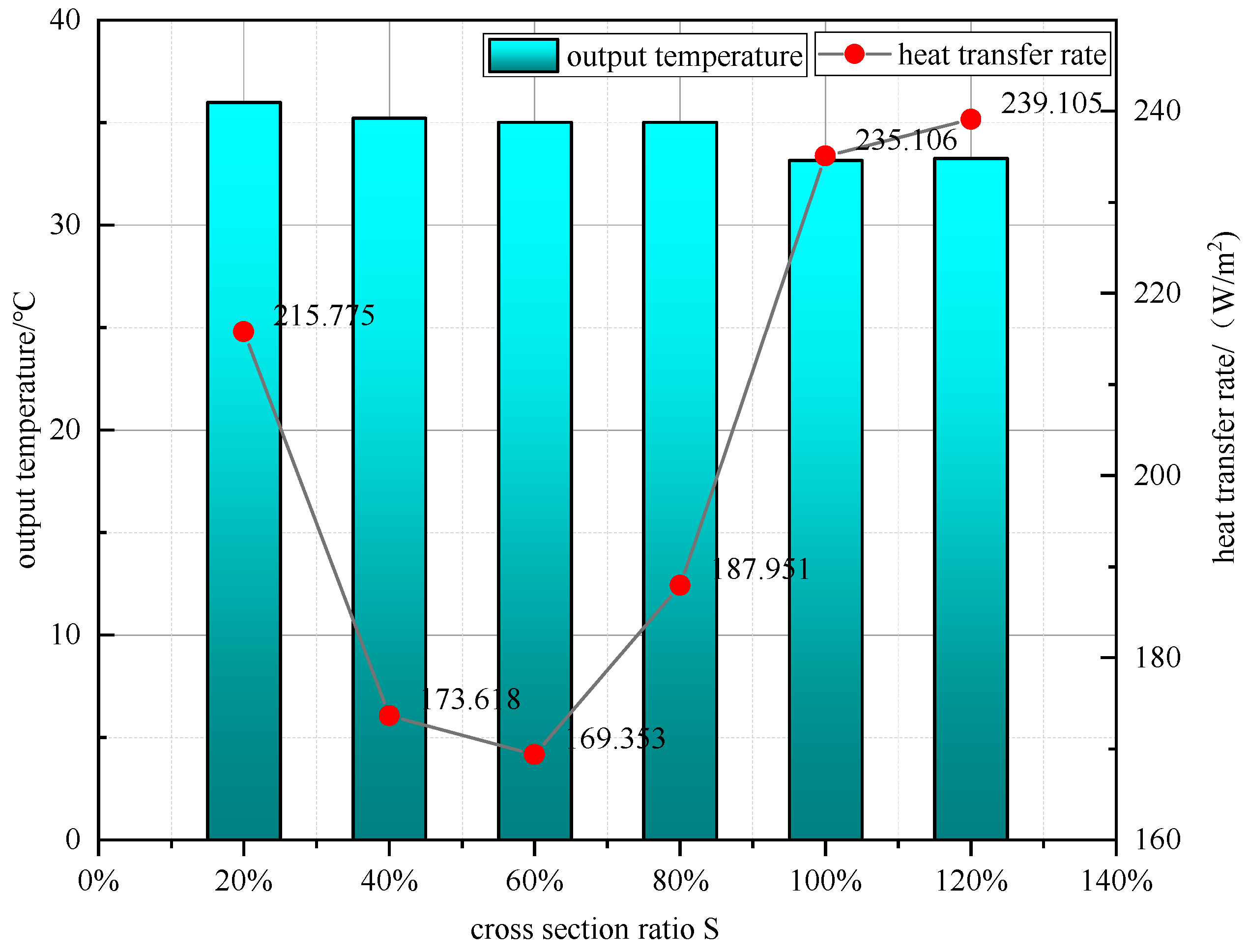
- The maximum local heat flow density of the air inside the wall-mounted solar chimney reached 187.951 W/m2 at S = 80%. When S > 80%, the local heat flow density inside the wall-mounted solar chimney continued to increase. It tended to flow in a steady state at S = 120%;
- (2)
- When S < 80%, the airflow inside the wall-mounted solar chimney did not form vortices. However, at this time, the temperature difference between the components of the air inside the wall-mounted solar chimney was slight, and the buoyancy force formed was not sufficient to provide a higher airflow rate. The natural draft of a wall-mounted solar chimney is at a low level;
- (3)
- At S < 80%, the wall-mounted solar chimney internal airflow state was different. When 80% ≤ S < 100%, the formation of a local vortex occurred, such that the flow of air was repeatedly heated by solar radiation. When the wall-mounted solar chimney internal air buoyancy force increased, the airflow rate increased, and wall-mounted solar chimney ventilation increased rapidly. At S = 80%, the maximum instantaneous ventilation of the wall-mounted solar chimney reached 0.096 kg/s; in the 80% ≤ S < 100% interval, the natural ventilation of the wall-mounted solar chimney was maintained at a high level;
- (4)
- After S ≥ 100%, the airflow in the wall-mounted solar chimney formed a vortex area which further expanded to the point of forming a secondary return flow of air. Although the flow rate of air increased, the formation of secondary reflux caused a significant loss in the efficiency of the overall ventilation of the wall-mounted solar chimney;
- (5)
- S-values in the design of wall-mounted solar chimneys have a non-negligible role, and the proper selection of the S-value range can make wall-mounted solar chimney ventilation achieve the actual engineering design requirements.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Glass cover area | |
| Specific heat capacity of air | |
| Calculation constant | |
| Calculation constant | |
| Turbulent kinetic energy due to mean velocity gradient | |
| Radiant heat transfer coefficient between the outside of the glass cover and the ground | |
| Radiant heat transfer coefficient between the outer surface of the glass cover and the sky | |
| Convective heat transfer coefficient between the glass cover and the outdoor air | |
| Convective heat transfer coefficient between the glass cover and the air inside the chimney | |
| Convective heat transfer coefficient between the surface of the exterior wall and the air inside the chimney | |
| Direct solar irradiation | |
| Solar scattering irradiation | |
| Diffusion flux of component | |
| Turbulent pulsation kinetic energy | |
| Effective thermal conductivity | |
| Airflow rate | |
| Air convection heat transfer strength between the glass cover and the cavity area | |
| Fluid pressure | |
| Prandtl number | |
| Radiative heat exchange between the glass cover and the wall | |
| Convective heat exchange with air on the outside of the glass cover | |
| Convective heat exchange between the inner side of the glass cover and the inner air | |
| Longwave radiation between the glass cover and the sky | |
| Longwave radiation between the glass cover and the ground | |
| Convective heat exchange between the wall and the air in the runner | |
| The air inside the chimney absorbing heat from solar radiation through the glass cover | |
| Heat transfer thermal resistance on the inner surface of the glass cover | |
| Heat transfer thermal resistance on the outer surface of the glass cover | |
| Reynolds number | |
| Outlet-to-inlet airflow path cross-sectional area ratio | |
| Heat generated by a volumetric heat source | |
| Average temperature of the glass cover | |
| Ambient temperature | |
| Building outdoor ground temperature | |
| Sky temperature | |
| Average air temperature inside the chimney | |
| Average indoor air temperature | |
| Average temperature of the exterior wall surface | |
| Velocity of the fluid in the x-direction | |
| Velocity of the fluid in the y-direction | |
| Velocity of the fluid in the z-direction | |
| Height of contact between the glass cover and the internal air | |
| Building outdoor airflow rate | |
| Absorption rate of the glass cover (0.6) | |
| Absorption rate of the exterior wall (0.76) | |
| Reciprocal of the effective Prandtl number of | |
| Reciprocal of the effective Prandtl number of | |
| Transmittance of the glass cover | |
| Glass cover surface emissivity | |
| Dissipation rate of turbulent pulsating momentum | |
| Fluid effective dynamic viscosity | |
| Air density | |
| Stefan–Boltzmann’s constant |
References
- Tariq, R.; Torres-Aguilar, C.E.; Xamán, J.; Zavala-Guillén, I.; Bassam, A.; Ricalde, L.J.; Carvente, O. Digital twin models for optimization and global projection of building-integrated solar chimney. Build. Environ. 2022, 213, 108807. [Google Scholar] [CrossRef]
- Liu, Y.; Ming, T.; Peng, C.; Wu, Y.; Li, W.; de Richter, R.; Zhou, N. Mitigating air pollution strategies based on solar chimneys. Sol. Energy 2021, 218, 11–27. [Google Scholar] [CrossRef]
- Daghistani, F.F. Solar chimney street-lighting pole for ventilating polluted urban areas. Sustain. Cities Soc. 2021, 72, 103057. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, G.; Wu, Q.; Shi, L. Solar chimney performance in buildings under three heating modes: An empirical analysis. Sustain. Energy Technol. Assess. 2022, 52, 102222. [Google Scholar] [CrossRef]
- Liu, B.; Ma, X.; Wang, X.; Dang, C.; Wang, Q.; Bennacer, R. Experimental study of the chimney effect in a solar hybrid double wall. Sol. Energy 2015, 115, 1–9. [Google Scholar] [CrossRef]
- Jianliu, X.; Weihua, L. Study on solar chimney used for room natural ventilation in Nanjing. Energy Build. 2013, 66, 467–469. [Google Scholar] [CrossRef]
- Arce, J.; Jiménez, M.J.; Guzmán, J.D.; Heras, M.R.; Alvarez, G.; Xamán, J. Experimental study for natural ventilation on a solar chimney. Renew. Energy 2009, 34, 2928–2934. [Google Scholar] [CrossRef]
- He, G.; Lv, D. Distributed heat absorption in a solar chimney to enhance ventilation. Sol. Energy 2022, 238, 315–326. [Google Scholar] [CrossRef]
- Ahmed, O.K.; Algburi, S.; Ali, Z.H.; Ahmed, A.K.; Shubat, H.N. Hybrid solar chimneys: A comprehensive review. Energy Rep. 2022, 8, 438–460. [Google Scholar] [CrossRef]
- Jiménez-Xamán, C.; Xamán, J.; Gijón-Rivera, M.; Zavala-Guillén, I.; Noh-Pat, F.; Simá, E. Assessing the thermal performance of a rooftop solar chimney attached to a single room. J. Build. Eng. 2020, 31, 101380. [Google Scholar] [CrossRef]
- Liu, H.; Li, P.; Yu, B.; Zhang, M.; Tan, Q.; Wang, Y.; Zhang, Y. Contrastive Analysis on the Ventilation Performance of a Combined Solar Chimney. Appl. Sci. 2021, 12, 156. [Google Scholar] [CrossRef]
- Hussam, W.K.; Salem, H.J.; Redha, A.M.; Khlefat, A.M.; Al Khatib, F. Experimental and numerical investigation on a hybrid solar chimney-photovoltaic system for power generation in Kuwait. Energy Convers. Manag. X 2022, 15, 100249. [Google Scholar] [CrossRef]
- Bernardes, M.A.d.S.; Voß, A.; Weinrebe, G. Thermal and technical analyses of solar chimneys. Sol. Energy 2003, 75, 511–524. [Google Scholar] [CrossRef]
- Asadi, S.; Fakhari, M.; Fayaz, R.; Mahdaviparsa, A. The effect of solar chimney layout on ventilation rate in buildings. Energy Build. 2016, 123, 71–78. [Google Scholar] [CrossRef]
- Kasaeian, A.B.; Molana, S.; Rahmani, K.; Wen, D. A review on solar chimney systems. Renew. Sustain. Energy Rev. 2017, 67, 954–987. [Google Scholar] [CrossRef]
- Zamora, B. Determining correlations for solar chimneys in buildings with wind interference: A numerical approach. Sustain. Energy Technol. Assess. 2021, 48, 101662. [Google Scholar] [CrossRef]
- Tan, A.Y.K.; Wong, N.H. Influences of ambient air speed and internal heat load on the performance of solar chimney in the tropics. Sol. Energy 2014, 102, 116–125. [Google Scholar] [CrossRef]
- Duan, S. A predictive model for airflow in a typical solar chimney based on solar radiation. J. Build. Eng. 2019, 26, 100916. [Google Scholar] [CrossRef]
- Shi, L.; Cheng, X.; Zhang, L.; Li, Z.; Zhang, G.; Huang, D.; Tu, J. Interaction effect of room opening and air inlet on solar chimney performance. Appl. Therm. Eng. 2019, 159, 113877. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, G.; Yang, W.; Huang, D.; Cheng, X.; Setunge, S. Determining the influencing factors on the performance of solar chimney in buildings. Renew. Sustain. Energy Rev. 2018, 88, 223–238. [Google Scholar] [CrossRef]
- Neves, L.d.O.; Marques da Silva, F. Simulation and measurements of wind interference on a solar chimney performance. J. Wind Eng. Ind. Aerodyn. 2018, 179, 135–145. [Google Scholar] [CrossRef]
- Khosravi, M.; Fazelpour, F.; Rosen, M.A. Improved application of a solar chimney concept in a two-story building: An enhanced geometry through a numerical approach. Renew. Energy 2019, 143, 569–585. [Google Scholar] [CrossRef]
- Sivalakshmi, S.; Raja, M.; Mahudeswaran, R.; Gowtham, G. Thermal performance of wall solar chimney integrated with a room under warm and humid conditions. Mater. Today Proc. 2021, 43, 1892–1895. [Google Scholar] [CrossRef]
- Al-Kayiem, H.H.; Sreejaya, K.V.; Chikere, A.O. Experimental and numerical analysis of the influence of inlet configuration on the performance of a roof top solar chimney. Energy Build. 2018, 159, 89–98. [Google Scholar] [CrossRef]
- Gao, M.; Fan, J.; Furbo, S.; Xiang, Y. Energy and exergy analysis of a glazed solar preheating collector wall with non-uniform perforated corrugated plate. Renew. Energy 2022, 196, 1048–1063. [Google Scholar] [CrossRef]
- Xamán, J.; Vargas-López, R.; Gijón-Rivera, M.; Zavala-Guillén, I.; Jiménez, M.J.; Arce, J. Transient thermal analysis of a solar chimney for buildings with three different types of absorbing materials: Copper plate/PCM/concrete wall. Renew. Energy 2019, 136, 139–158. [Google Scholar] [CrossRef]
- Harris, D.J.; Helwig, N. Solar chimney and building ventilation. Appl. Energy 2007, 84, 135–146. [Google Scholar] [CrossRef]
- Suhendri, S.; Hu, M.; Su, Y.; Darkwa, J.; Riffat, S. Performance evaluation of combined solar chimney and radiative cooling ventilation. Build. Environ. 2022, 209, 108686. [Google Scholar] [CrossRef]
- Hu, S.; Leung, D.Y.C.; Chen, M.Z.Q.; Chan, J.C.Y. Effect of guide wall on the potential of a solar chimney power plant. Renew. Energy 2016, 96, 209–219. [Google Scholar] [CrossRef]
- Shi, L. Theoretical models for wall solar chimney under cooling and heating modes considering room configuration. Energy 2018, 165, 925–938. [Google Scholar] [CrossRef]
- Dahire, H.; Kannan, S.R.; Saw, S.K. Effect of humidity on the performance of rooftop solar chimney. Therm. Sci. Eng. Prog. 2022, 27, 101026. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A.; Blair, N. Solar Engineering of Thermal Processes, Photovoltaics and Wind; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Chantawong, P.; Hirunlabh, J.; Zeghmati, B.; Khedari, J.; Teekasap, S.; Win, M.M. Investigation on thermal performance of glazed solar chimney walls. Sol. Energy 2006, 80, 288–297. [Google Scholar] [CrossRef]
- Ghalamchi, M.; Kasaeian, A.; Ghalamchi, M.; Mirzahosseini, A.H. An experimental study on the thermal performance of a solar chimney with different dimensional parameters. Renew. Energy 2016, 91, 477–483. [Google Scholar] [CrossRef]
- Bacharoudis, E.; Vrachopoulos, M.G.; Koukou, M.K.; Margaris, D.; Filios, A.E.; Mavrommatis, S.A. Study of the natural convection phenomena inside a wall solar chimney with one wall adiabatic and one wall under a heat flux. Appl. Therm. Eng. 2007, 27, 2266–2275. [Google Scholar] [CrossRef] [Green Version]
- He, G.; Zhang, J.; Hong, S. A new analytical model for airflow in solar chimneys based on thermal boundary layers. Sol. Energy 2016, 136, 614–621. [Google Scholar] [CrossRef]
- Shahreza, A.R.; Imani, H. Experimental and numerical investigation on an innovative solar chimney. Energy Convers. Manag. 2015, 95, 446–452. [Google Scholar] [CrossRef]
- Ren, X.-H.; Liu, R.-Z.; Wang, Y.-H.; Wang, L.; Zhao, F.-Y. Thermal driven natural convective flows inside the solar chimney flush-mounted with discrete heating sources: Reversal and cooperative flow dynamics. Renew. Energy 2019, 138, 354–367. [Google Scholar] [CrossRef]
- Zhai, X.Q.; Song, Z.P.; Wang, R.Z. A review for the applications of solar chimneys in buildings. Renew. Sustain. Energy Rev. 2011, 15, 3757–3767. [Google Scholar] [CrossRef]
- Saifi, N.; Settou, N.; Dokkar, B.; Negrou, B.; Chennouf, N. Experimental Study And Simulation Of Airflow In Solar Chimneys. Energy Procedia 2012, 18, 1289–1298. [Google Scholar] [CrossRef]
- Maia, C.B.; Castro Silva, J.O.; Cabezas-Gómez, L.; Hanriot, S.M.; Ferreira, A.G. Energy and exergy analysis of the airflow inside a solar chimney. Renew. Sustain. Energy Rev. 2013, 27, 350–361. [Google Scholar] [CrossRef]
- Murena, F.; Gaggiano, I.; Mele, B. Fluid dynamic performances of a solar chimney plant: Analysis of experimental data and CFD modelling. Energy 2022, 249, 123702. [Google Scholar] [CrossRef]
- Lechowska, A.; Szczepanik-Ścisło, N.; Schnotale, J.; Stelmach, M.; Pyszczek, T. CFD modelling of transient thermal performance of solar chimney used for passive ventilation in a building. IOP Conf. Ser. Mater. Sci. Eng. 2018, 415, 012049. [Google Scholar] [CrossRef]
- Khanal, R.; Lei, C. A numerical investigation of buoyancy induced turbulent air flow in an inclined passive wall solar chimney for natural ventilation. Energy Build. 2015, 93, 217–226. [Google Scholar] [CrossRef]
- Khanal, R.; Lei, C. Flow reversal effects on buoyancy induced air flow in a solar chimney. Sol. Energy 2012, 86, 2783–2794. [Google Scholar] [CrossRef]
- Nguyen, Y.Q.; Nguyen, V.T.; Tran, L.T.; Wells, J.C. CFD Analysis of Different Ventilation Strategies for a Room with a Heated Wall. Buildings 2022, 12, 1300. [Google Scholar] [CrossRef]
- Costa, R.; Clain, S.; Machado, G.J.; Nóbrega, J.M. Very high-order accurate finite volume scheme for the steady-state incompressible Navier–Stokes equations with polygonal meshes on arbitrary curved boundaries. Comput. Methods Appl. Mech. Eng. 2022, 396, 115064. [Google Scholar] [CrossRef]
- Mandal, D.K.; Pradhan, S.; Chakraborty, R.; Barman, A.; Biswas, N. Experimental investigation of a solar chimney power plant and its numerical verification of thermo-physical flow parameters for performance enhancement. Sustain. Energy Technol. Assess. 2022, 50, 101786. [Google Scholar] [CrossRef]
- Guo, P.; Wang, S.; Lei, Y.; Li, J. Numerical simulation of solar chimney-based direct airside free cooling system for green data centers. J. Build. Eng. 2020, 32, 101793. [Google Scholar] [CrossRef]
- Suárez-López, M.J.; Blanco-Marigorta, A.M.; Gutiérrez-Trashorras, A.J.; Pistono-Favero, J.; Blanco-Marigorta, E. Numerical simulation and exergetic analysis of building ventilation solar chimneys. Energy Convers. Manag. 2015, 96, 1–11. [Google Scholar] [CrossRef]
- Ayadi, A.; Nasraoui, H.; Bouabidi, A.; Driss, Z.; Bsisa, M.; Abid, M.S. Effect of the turbulence model on the simulation of the air flow in a solar chimney. Int. J. Therm. Sci. 2018, 130, 423–434. [Google Scholar] [CrossRef]
- Bassiouny, R.; Koura, N.S.A. An analytical and numerical study of solar chimney use for room natural ventilation. Energy Build. 2008, 40, 865–873. [Google Scholar] [CrossRef]
- Aliaga, D.M.; Feick, R.; Brooks, W.K.; Mery, M.; Gers, R.; Levi, J.F.; Romero, C.P. Modified solar chimney configuration with a heat exchanger: Experiment and CFD simulation. Therm. Sci. Eng. Prog. 2021, 22, 100850. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, J.; Li, J.; Gao, S.; Zhou, R.; Liu, H.; Chen, Y. Climate change in Urumqi City during 1960–2013. Quat. Int. 2015, 358, 93–100. [Google Scholar] [CrossRef]



| Model | Number of Grids |
|---|---|
| S = 20% | N1 = 1,500,325 N2 = 2,912,532 N3 = 3,598,568 N4 = 3,766,896 N5 = 4,885,214 |
| S = 40% | N1 = 1,476,323 N2 = 2,596,512 N3 = 3,432,521 N4 = 3,710,120 N5 = 4,832,314 |
| S = 60% | N1 = 1,442,361 N2 = 2,493,256 N3 = 3,364,896 N4 = 3,642,321 N5 = 4,765,425 |
| S = 80% | N1 = 1,411,532 N2 = 2,437,452 N3 = 3,201,458 N4 = 4,064,521 N5 = 4,654,232 |
| S = 100% | N1 = 1,386,526 N2 = 2,013,652 N3 = 3,186,754 N4 = 3,341,263 N5 = 4,412,589 |
| S = 120% | N1 = 1,346,897 N2 = 2,298,546 N3 = 2,965,236 N4 = 3,515,478 N5 = 4,146,582 |
| Direction | Direct Irradiation | Vertical Scattered Radiation | Horizontal Scattered Radiation | Ground Vertical Reflected Radiation |
|---|---|---|---|---|
| Solar irradiance (W/m2) | 853.125 | 100.462 | 112.172 | 81.6977 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Z.; Wang, W.; Chen, Y.; Song, J. Structural and Heat Transfer Model Analysis of Wall-Mounted Solar Chimney Inlets and Outlets in Single-Story Buildings. Buildings 2022, 12, 1790. https://doi.org/10.3390/buildings12111790
Fang Z, Wang W, Chen Y, Song J. Structural and Heat Transfer Model Analysis of Wall-Mounted Solar Chimney Inlets and Outlets in Single-Story Buildings. Buildings. 2022; 12(11):1790. https://doi.org/10.3390/buildings12111790
Chicago/Turabian StyleFang, Zhicheng, Wanjiang Wang, Yanhui Chen, and Junkang Song. 2022. "Structural and Heat Transfer Model Analysis of Wall-Mounted Solar Chimney Inlets and Outlets in Single-Story Buildings" Buildings 12, no. 11: 1790. https://doi.org/10.3390/buildings12111790
APA StyleFang, Z., Wang, W., Chen, Y., & Song, J. (2022). Structural and Heat Transfer Model Analysis of Wall-Mounted Solar Chimney Inlets and Outlets in Single-Story Buildings. Buildings, 12(11), 1790. https://doi.org/10.3390/buildings12111790








