Center of Stiffness, Principal Axes and Principal Start Point of Thin-Walled Open-Sections of Cores: A New Modified Calculation Technique Based on Vlasov Torsion Theory
Abstract
:1. Introduction
2. Methodology
- Having known the geometric shape of the thin-walled cross-section of a core, the adoption of a temporary Cartesian three-orthogonal reference system, OXYZ, that will be used for the study of a thin-walled open section and calculation for the center of gravity, G, as well as for the orientation of the principal axes and of the cross-section of the core.
- The calculation of the principal moment of inertia ( and ) of the thin-walled cross-section about the principal axes and passing through the gravity center G of the core cross-section.
- The calculation of diagrams of coordinate-functions of the thin-walled cross-section with regard to gravity reference system .
- The calculation of the location of the shear center (that is also known as elastic center) K of the thin-walled open cross-section of the core, using a repetitive mathematical procedure.
- The calculation of the position of the principal start point of the thin-walled cross-section of the core. It is worth noting that this principal start point of the open section defines the origin point where the calculation of the sectorial coordinates is based. Only referring to the principal start point, the numerical value of the warping moment of inertia becomes minimum and this value is the exact value of according to Vlasov torsion theory.
- The calculation of the numerical value of the warping moment of inertia (or warping constant according other researchers, Bernuzzi et al. [30]) of the thin-walled cross-section of the core.
- The calculation of the warping stiffness of the core.
3. The Modification of the Vlasov Torsion Theory on Cores with Thin-Walled Open Section
3.1. General
- The cross-sections of a thin-walled core remain undeformed into their level, namely each cross-section operates as one undeformed disk. This assumption is the known Bernoulli’s assumption (or assumption by Bernoulli-Navier) from the technical bending theory that applies on beams. According to this assumption, each cross-section of thin-walled is moved into its level as undeformed disk having three degrees of freedom (namely two translational along the two principal axes and a rotation about the longitudinal axis of the core.) For this purpose, we must insert into the thin-walled cross-section a point P, that possesses the above-mentioned three degrees of freedom (Figure 1). This point is called the “pole” of the thin-walled cross-section and the line that passes through this pole, and is parallel with the longitudinal principal axis (that is perpendicular on the disk of the thin-walled cross-section, namely along to Z-axis), is called the polar axis of the core.
- The shear deformations of the above-mentioned structural member (namely the core) are considered null (assumption by Bernoulli).
- The perpendicular lines that belong at the disk of the thin-walled open cross-section remain perpendicular and at the new position of the disk. This is the Kirchhoff assumption in the study of the thin plates.

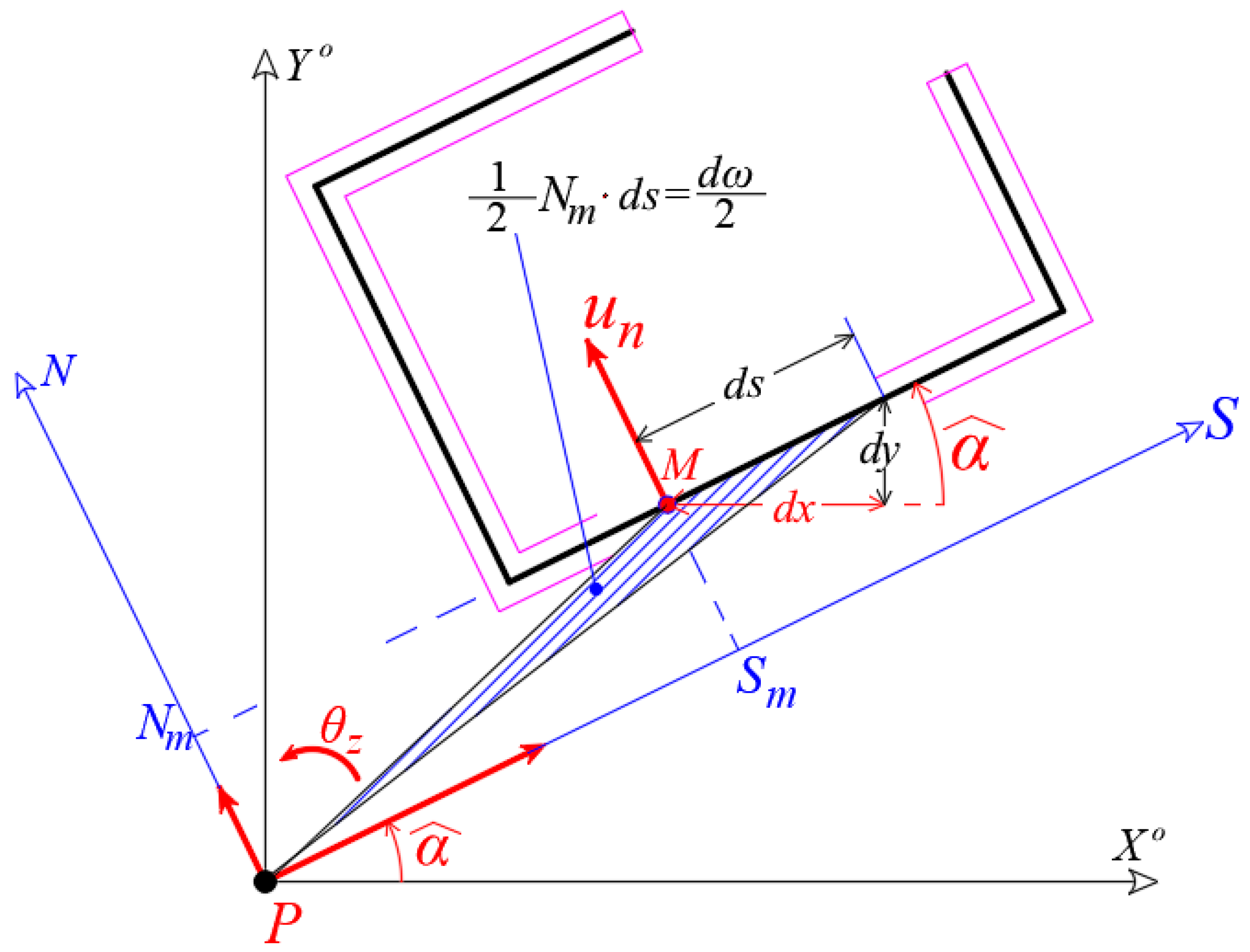
3.2. The Warping Phenomenon That Gives Normal Stresses on the Thin-Walled Open Cross-Section of Core
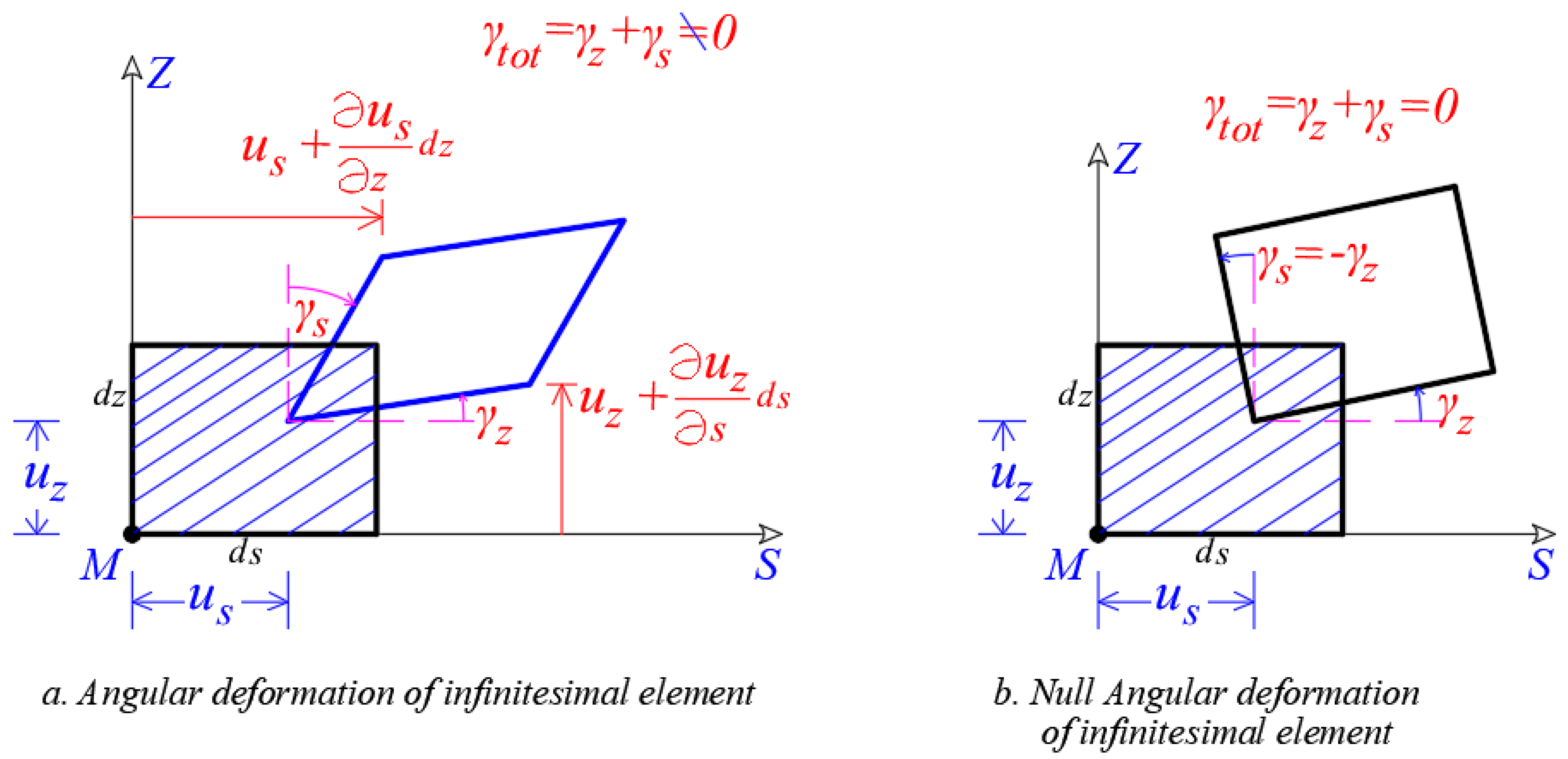
- is the function of the Cartesian Coordinate x of the point M at the position s,is the function of the Cartesian Coordinate y of the point M at the position s,
- is the function of the Sectorial Area (or Sectorial Coordinate) of the point M. Function , also, is known as «function of warping» or «measurement of warping» and as it will be proven bellow, its graphical image defines the distribution of the normal stresses on the cross-section of the thin-walled open core, in the case where core is loading with external bi-moment and simultaneously there is obstacle of the free torsion of the core.
- and are the angles of the core cross-section about the horizontal axes, respectively.
- and are the functions of coordinates of the core cross-section referring to local reference system .
- is the axial force of the core (along Z-axis), with cross-section area A and modulus of elasticity E of material:
- is the bending moment at level z that acts on the cross-section of the core about y-axis, according to Bernoulli’s bending technical theory for the compact beams. is the moment of inertia of the cross-section about the y-axis that passes through the gravity center G of the thin-walled open cross-section, so as the product second moment of area as well as the product first moment of area to be null:
- is the bending moment at level z that acts on the cross-section of the core about x-axis, according to Bernoulli’s bending technical theory for the compact beams. is the moment of inertia of the cross-section about the x-axis that passes through the gravity center G of the thin-walled open cross-section, so as the product second moment of area as well as the product first moment of area to be null:
- and are the bending moments at level z on the cross-section of the core about the principal directions and , respectively, that passe through the gravity center G of the open cross-section of the core.
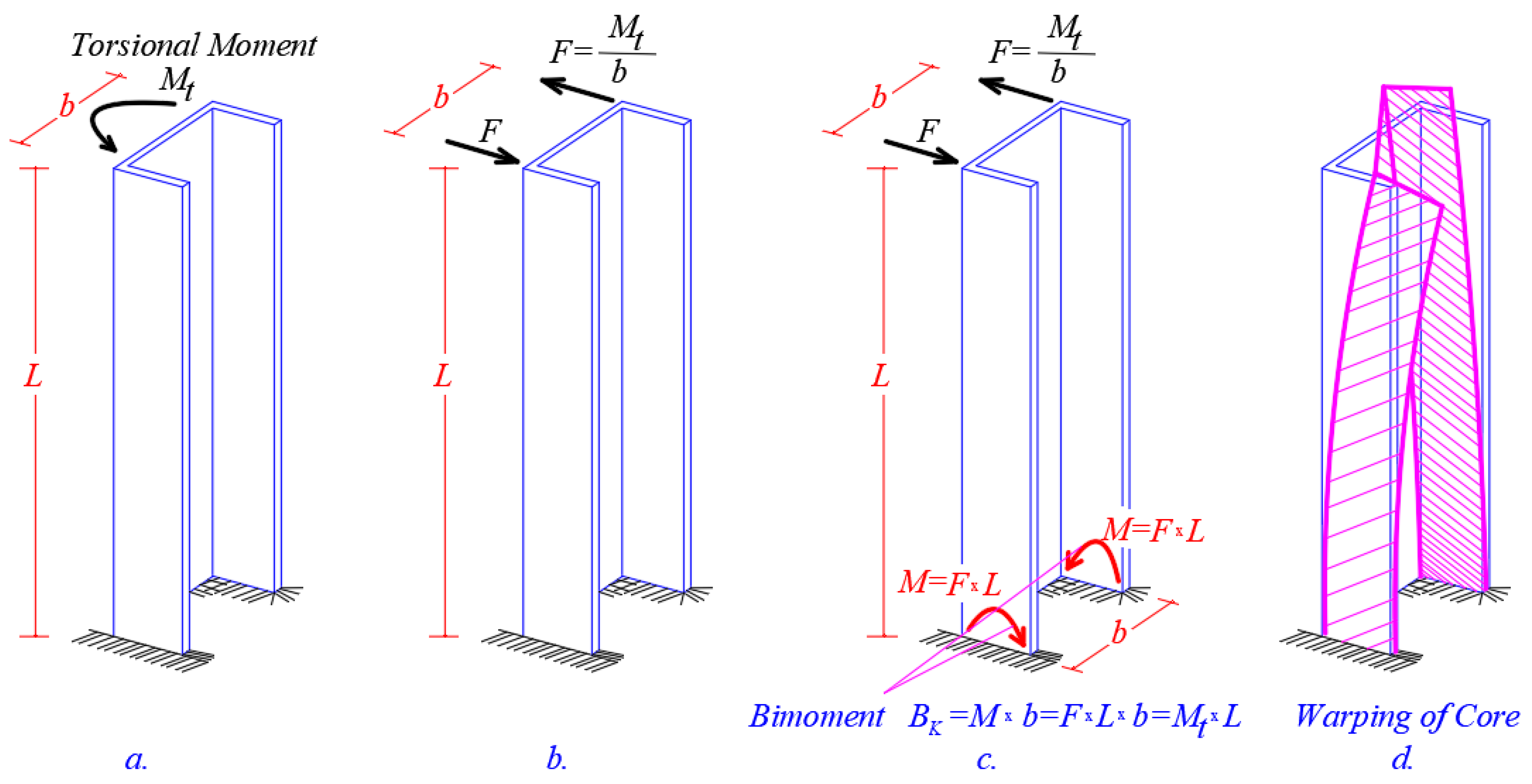
- is the bi-moment or also known as “warping moment” at level z that acts on the open cross-section of the core (furthermore see Figure 4 and Figure 5). The parameter is the “Warping or Sectorial Moment of Inertia” of the open cross-section of the core and has dimensions of length to the sixth power (). In order to calculate the Sectorial Moment of Inertia the following two assumptions has to be always true:
- (i)
- The calculation of must referred to principal pole P of the open cross-section, where this pole coincides always with the shear center (also called elastic center K) of the open cross-section;
- (ii)
- The principal start point of the open cross-section has to be used always.
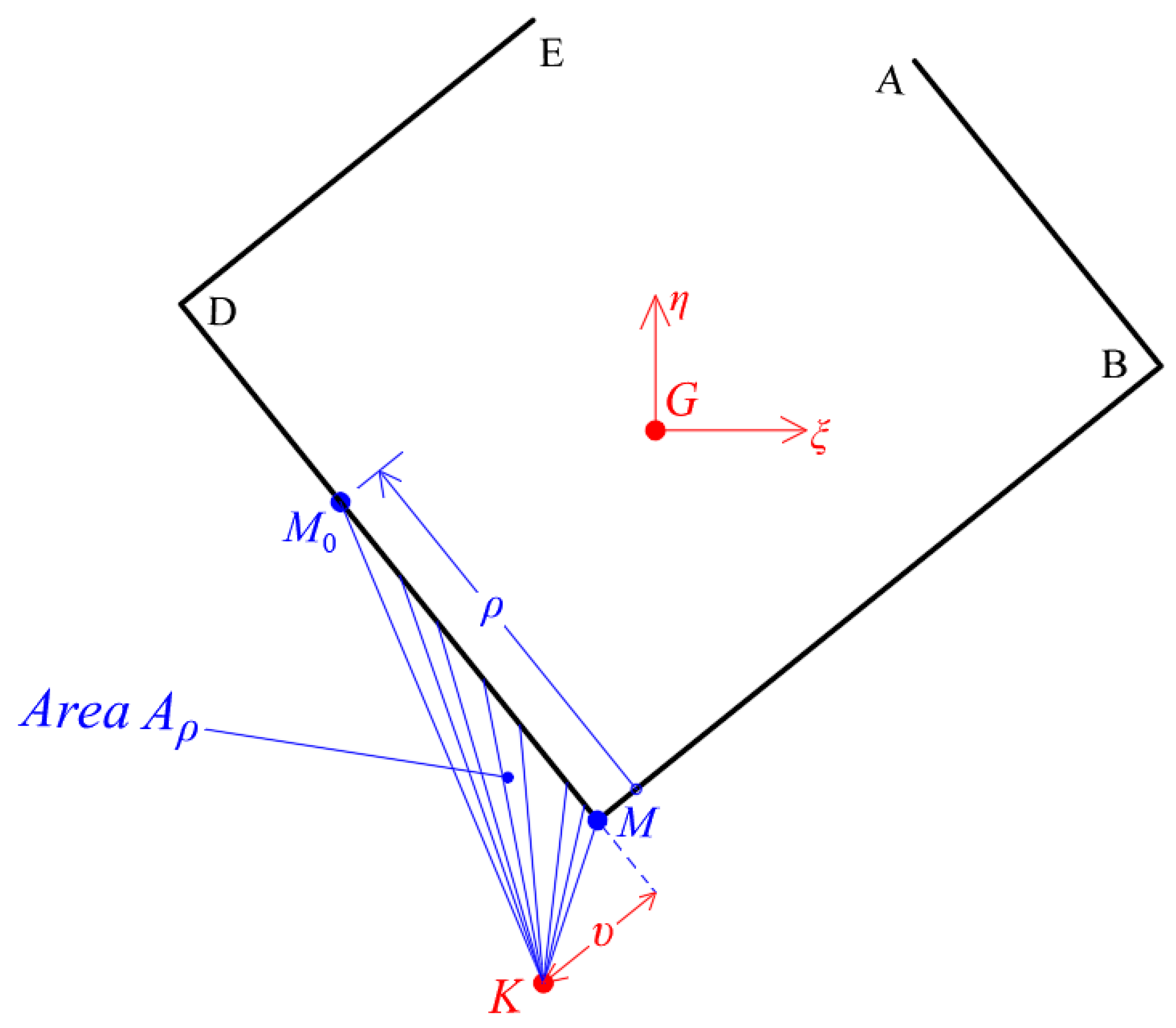
3.3. Determination of the Elastic Center K of the Thin-Walled Open Cross-Section
3.4. Calculation of the Principal Start Point of the Thin-Walled Open Cross-Section
- the final diagram of the sectorial coordinates ; and
- the sectorial moment of inertia of the thin-walled open cross-section.
3.5. The Concept of the Bi-Moment
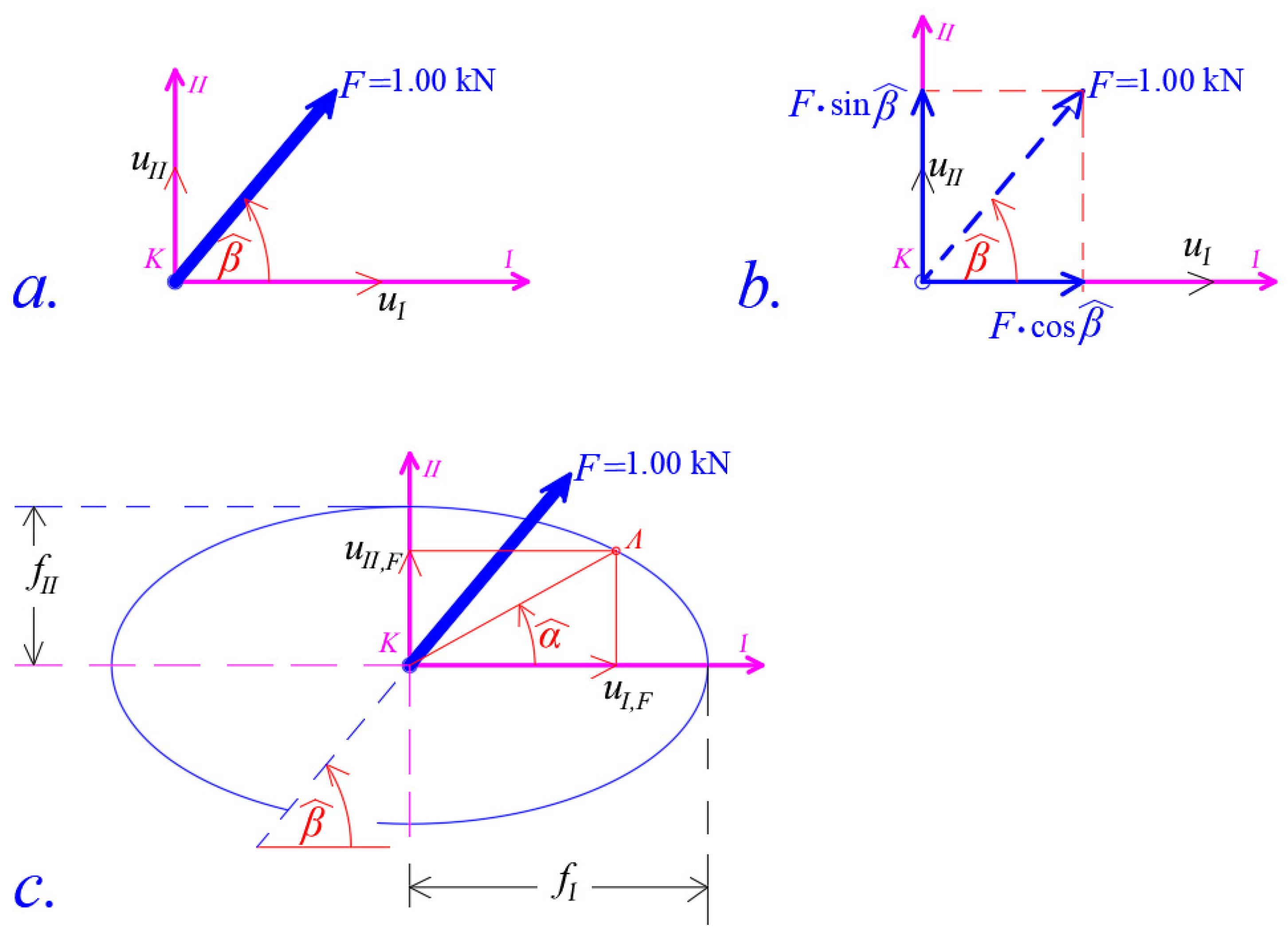
3.6. Principal Elasticity Axes I and II of the Thin-Walled Open Cross-Section
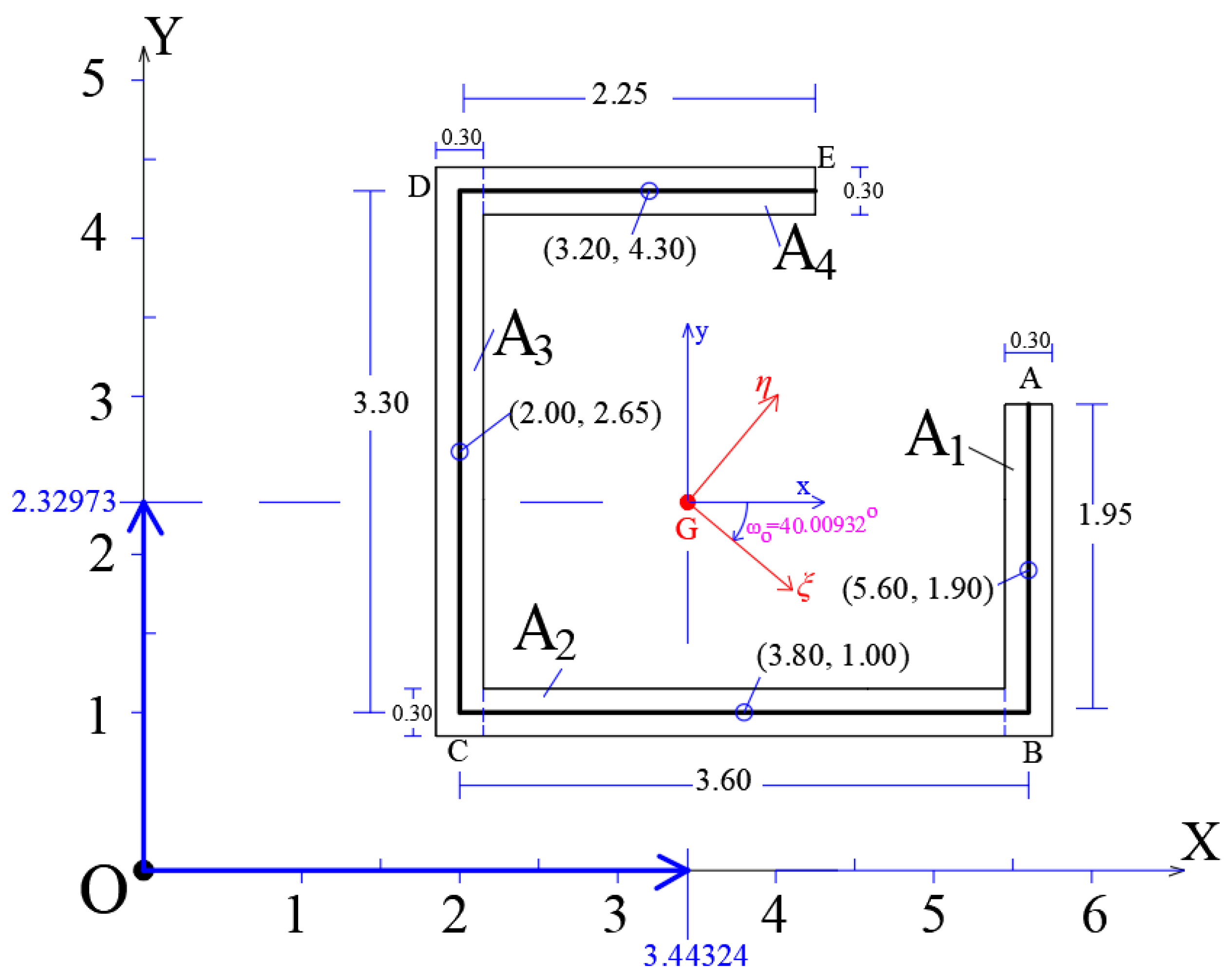
4. Numerical Example
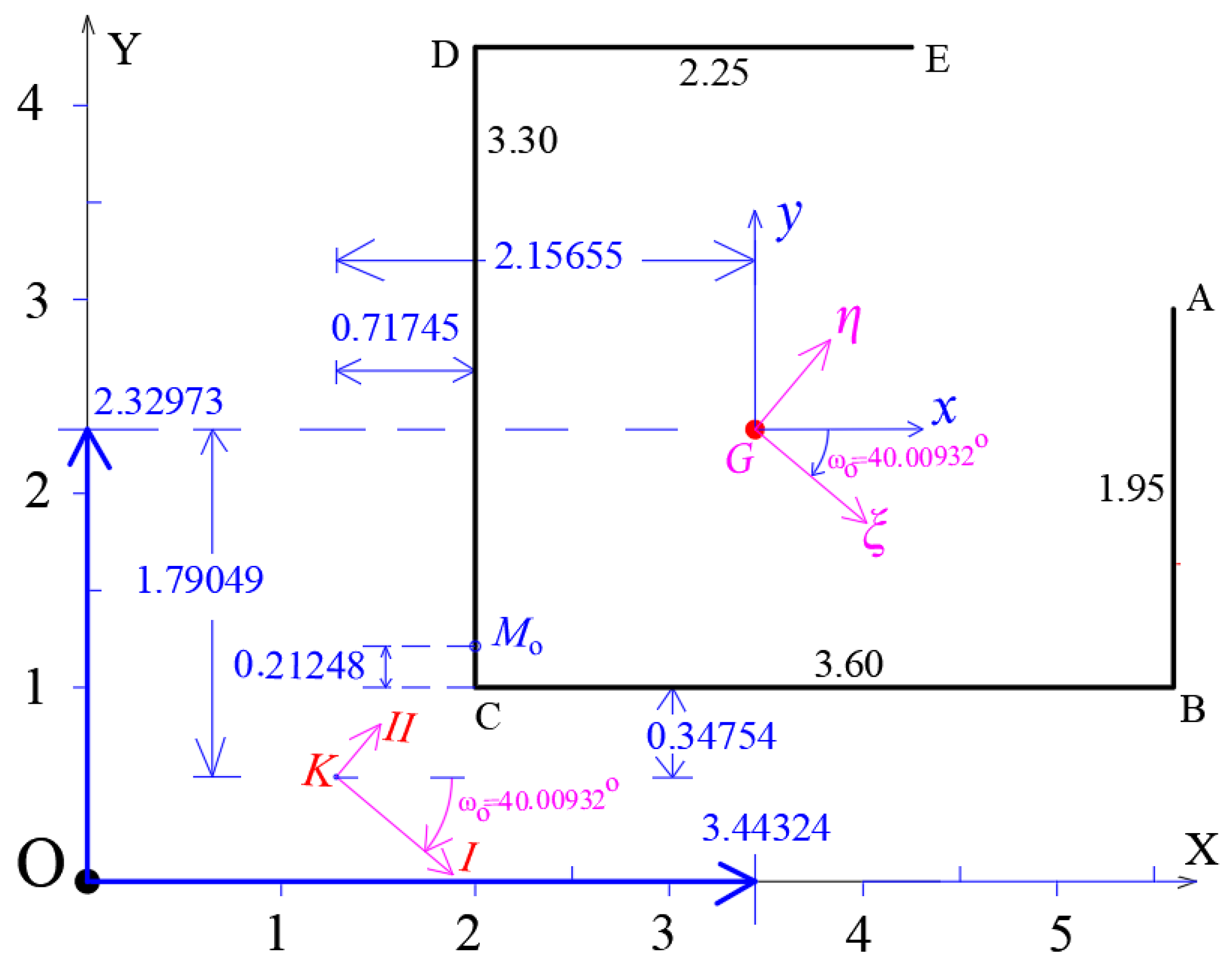
4.1. Gravity Center G of the Thin-Walled Open Cross-Section and the Principal Centro-Gravity Directions and of the Cross-Section

| Number | |||||||
|---|---|---|---|---|---|---|---|
| A1 | 2.15676 | −0.42973 | 0.23153 | 0.00473 | 0.34787 | 2.93523 | −0.5839 |
| A2 | 0.35676 | −1.32973 | 0.00743 | 0.89843 | 1.75792 | 1.02443 | −0.46965 |
| A3 | −1.44324 | 0.32027 | 1.16640 | 0.00810 | 1.27718 | 2.25769 | −0.49921 |
| A4 | −0.24324 | 1.97027 | 0.00473 | 0.23153 | 2.45036 | 0.26880 | −0.30193 |
| Sum | 5.83333 | 6.48615 | −1.85468 |
4.2. Principal Moments of Inertia ( and ) of the Thin-Walled Section about the Principal Directions and of the Gravity Center G of the Cross-Section
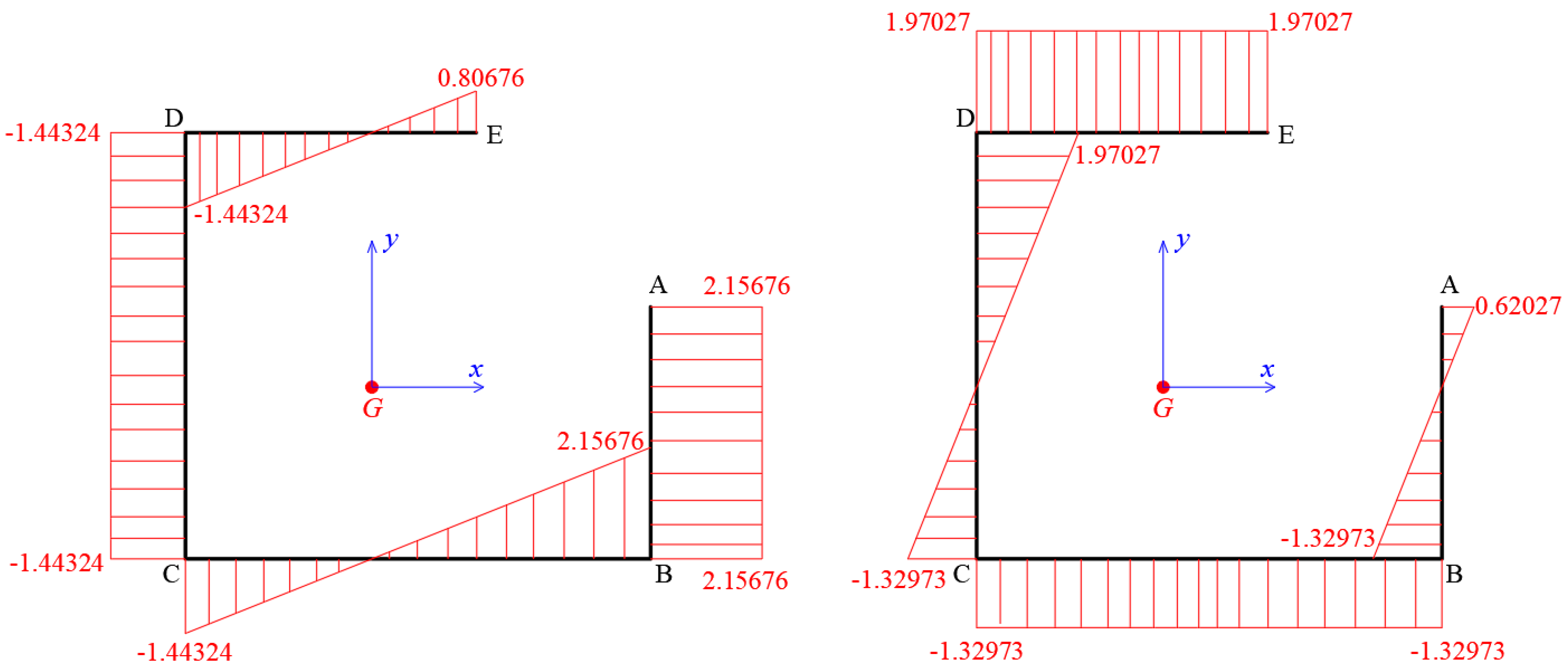
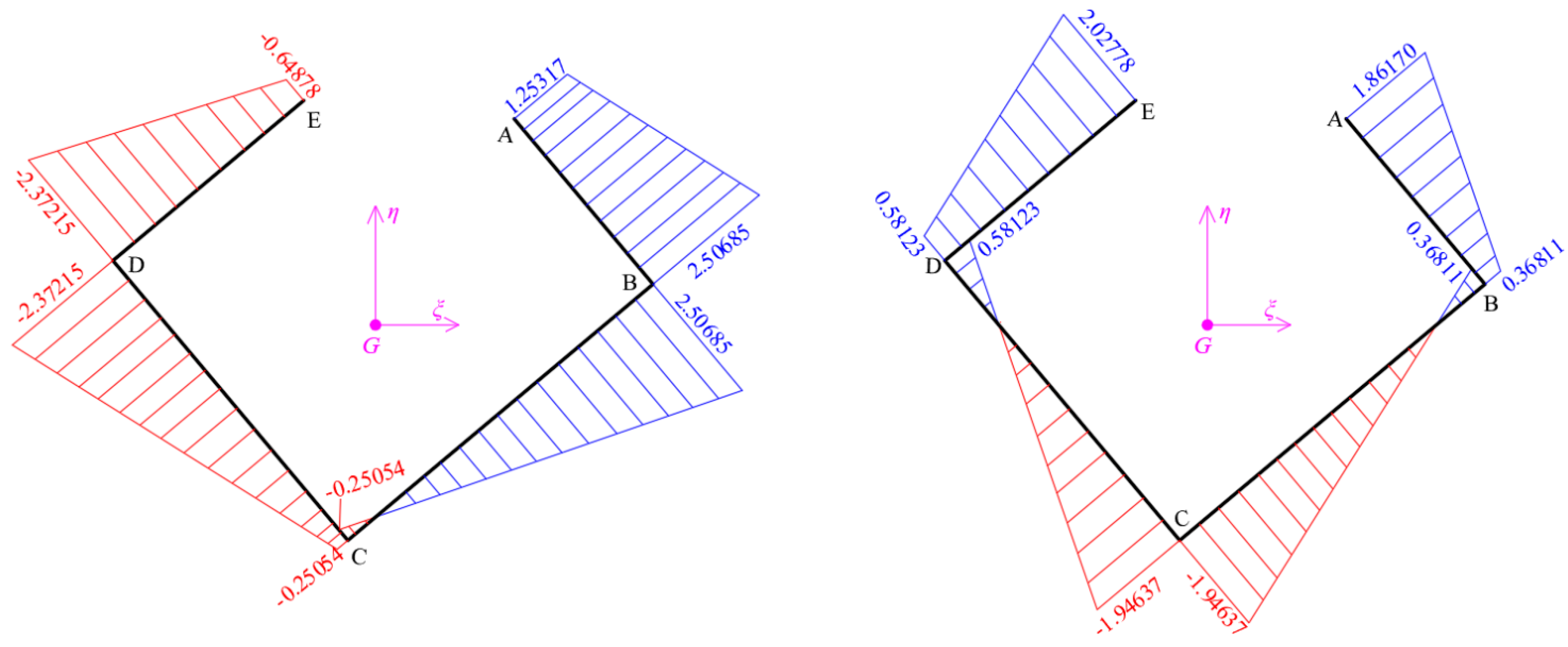
4.3. Calculation of Diagrams of Functions of Coordinates of the Thin-Walled Cross-Section at Cartesian Reference 3D-System
4.4. Elastic Center (Center of Stiffness) K of the Thin-Walled Cross-Section. Iterate Procedure for the Exact Location of Center K
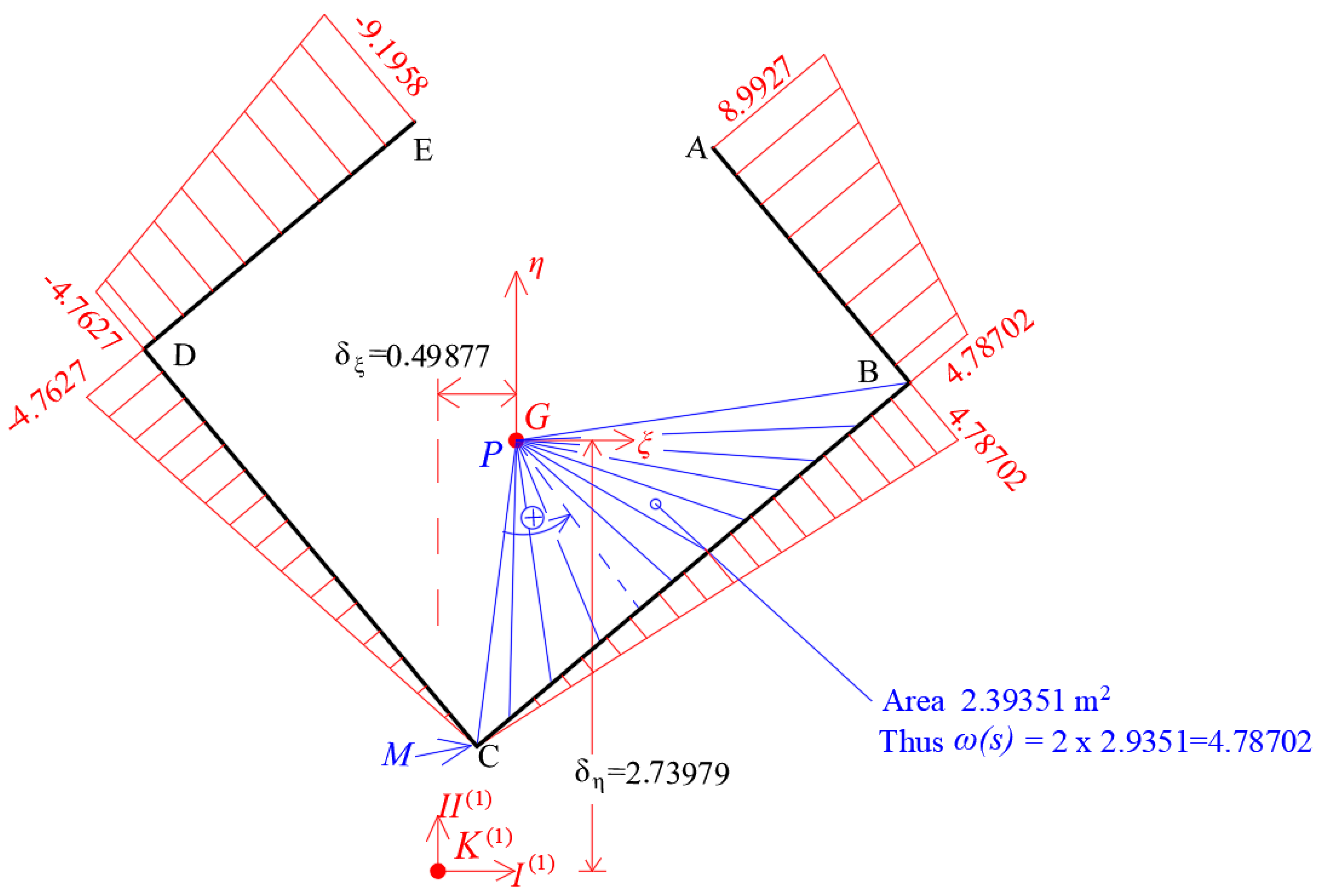
| Function ξ(s) | Function ω(s) | ||||||
|---|---|---|---|---|---|---|---|
| Number | e | Li | a | b | c | d | Iη,ω,i (Figure 3) |
| B-A | 0.30 | 1.95 | 2.50685 | 1.25317 | 4.78702 | 8.99270 | 7.320465 |
| C-B | 0.30 | 3.60 | −0.25054 | 2.50685 | 0. | 4.78702 | 4.104242 |
| C-D | 0.30 | 3.30 | −0.25054 | −2.37215 | 0. | −4.76270 | 3.925162 |
| D-E | 0.30 | 2.25 | −2.37215 | −0.64878 | −4.76270 | −9.19580 | 6.686042 |
| Sum | 22.035912 | ||||||
| Function η(s) | Function ω(s) | ||||||
|---|---|---|---|---|---|---|---|
| Number | e | Li | a | b | c | d | Iξ,ω,i (Figure 3) |
| B-A | 0.30 | 1.95 | 0.36811 | 1.86170 | 4.78702 | 8.99270 | 4.799927 |
| C-B | 0.30 | 3.60 | −1.94637 | 0.36811 | 0. | 4.78702 | −1.042735 |
| C-D | 0.30 | 3.30 | −1.94637 | 0.58123 | 0. | −4.76270 | 0.616029 |
| D-E | 0.30 | 2.25 | 0.58123 | 2.02778 | −4.76270 | −9.19580 | −6.506244 |
| Sum | −2.133022 | ||||||
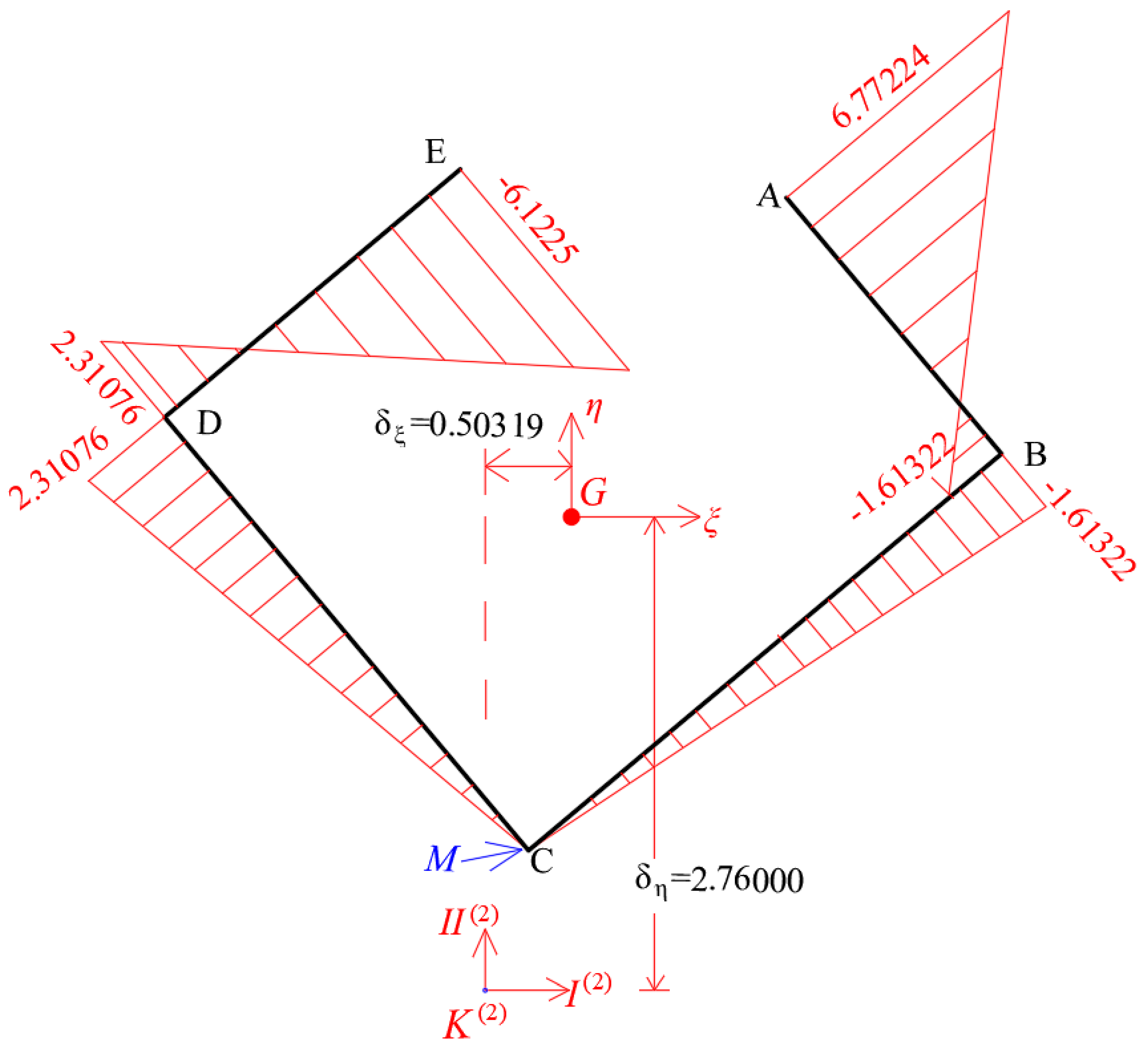
4.5. Calculation of the Principal Start Point of the Thin-Walled Open Cross-Section of the Core
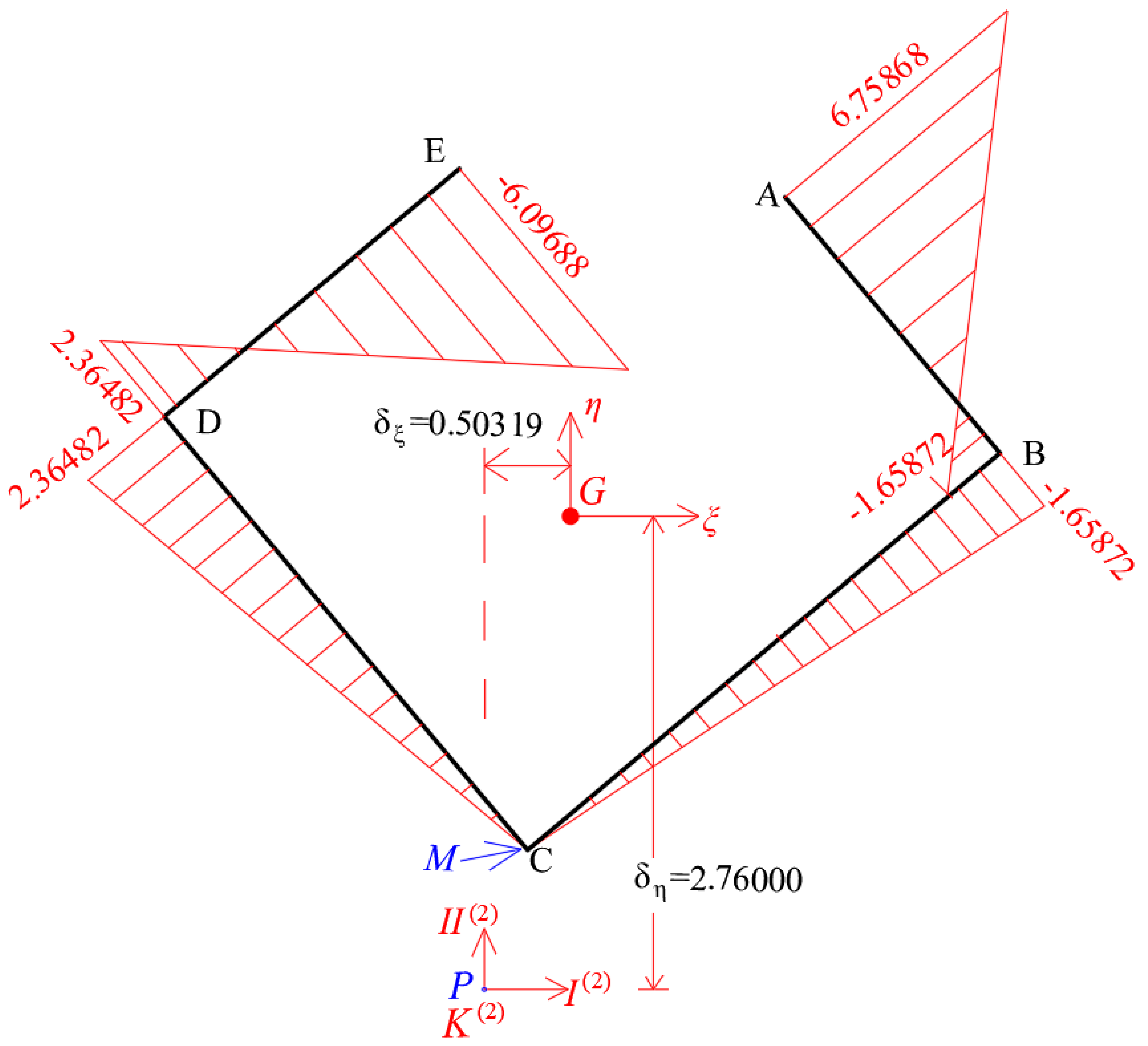
| Function ω(s) | |||||
|---|---|---|---|---|---|
| Number | e | Li | a | b | |
| B-A | 0.30 | 1.95 | −1.65872 | 6.75868 | 1.491738 |
| C-B | 0.30 | 3.60 | 0 | −1.65872 | −0.89571 |
| C-D | 0.30 | 3.30 | 0 | 2.36482 | 1.170586 |
| D-E | 0.30 | 2.25 | 2.36482 | −6.09688 | −1.25957 |
| Sum | 0.507045 | ||||
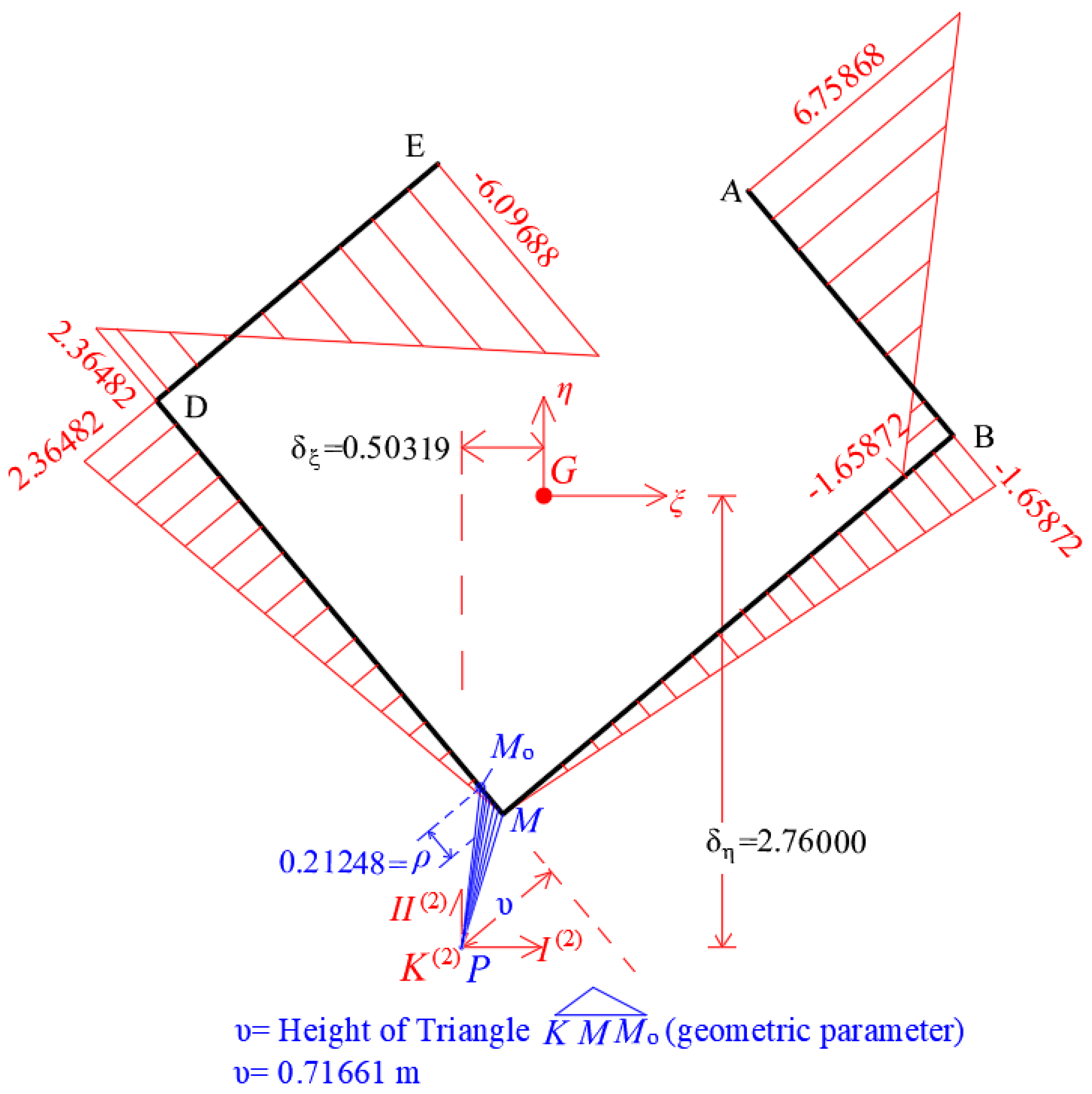

4.6. Warping Moment of Inertia of the Thin-Walled Open Cross-Section
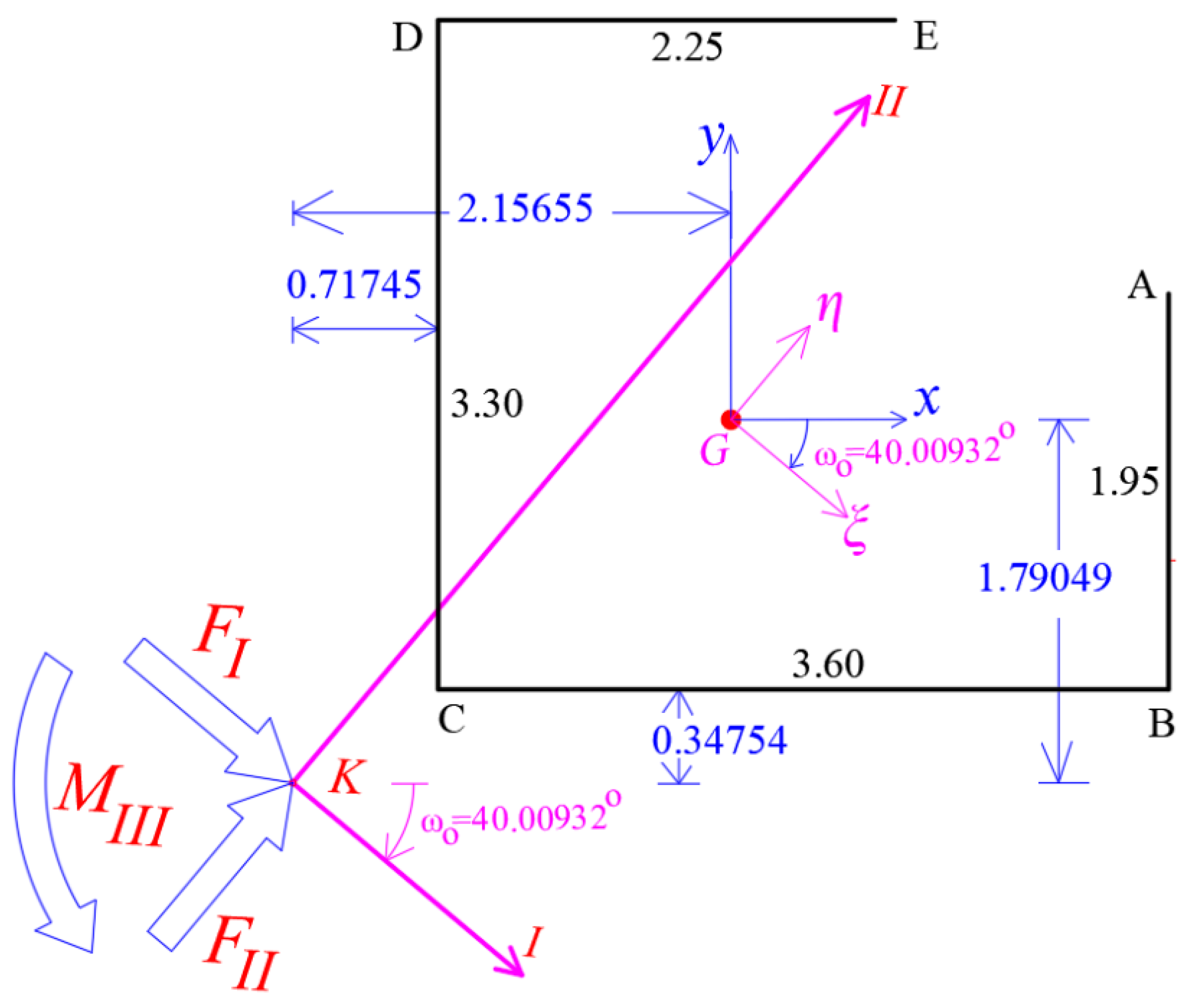
4.7. Lateral Static Loading on the Core
- (i)
- A lateral force applying on the top of the core on the elastic center K of the section, along the principal I-axis.
- (ii)
- A lateral force applying on the top of the core on the elastic center K of the section, along the principal II-axis.
- (iii)
- A torsional moment applying on the top of the core about the vertical III-axis of the section.
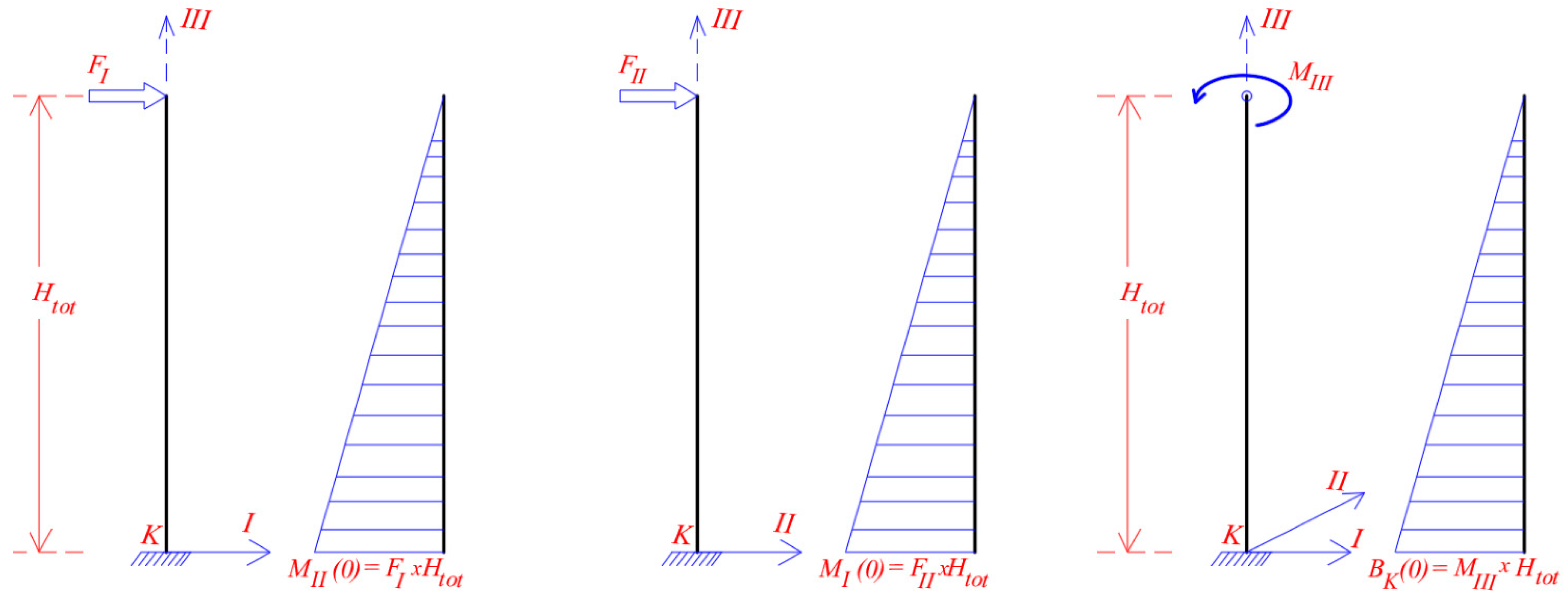
5. Conclusions
- (i)
- If a lateral static force F is applying on the elastic center K of a thin-walled open cross-section (having random orientation), then the rotation about the vertical III-axis is null, hence the point K is center of the bending of the cross-section.
- (ii)
- If a torsional moment (about the vertical III-axis) is applying on the elastic center K of a thin-walled open cross-section of core, then the horizontal displacements and of the point K are null, hence the point K is the center of twist of the cross-section.
- (iii)
- For a random lateral static force F that is acting on any point of the thin-walled open cross-section, and if we consider that the rotation (about the vertical axis) of the cross-section has been fixed, then the equivalent base shear-force of the cross-section is passed through point K. Hence, the point K is the center of shear of the thin-walled open cross-section.
- (iv)
- The product warping moments of inertia and are always null, with regard to the principal elastic Cartesian reference 3D-system K,I,II,III. In a similar way, the product moment of inertia is always null, with reference to the center-gravity Cartesian reference 3D-system .
- (v)
- If a lateral static force is applying on the elastic center K of a thin-walled open cross-section having the same orientation with I-axis, then the cross-section is moving parallel to itself along the I-axis, while along the II-axis the displacement is null. For this reason, the I-axis is called principal I-Axis of the cross-section.
- (vi)
- If a lateral static force is applied on the elastic center K of a thin-walled open cross-section having the same orientation with II-axis, then the cross-section is moving parallel to itself along the II-axis, while along the I-axis the displacement is null. For this reason, the II-axis is called principal II-Axis of the cross-section.
- (vii)
- If there is an axis of symmetry at the cross-section, then it is always principal axis of the cross-section.
- (viii)
- If a lateral static force that is applying on the elastic center K of a thin-walled open cross-section (hence the rotation about the vertical axis is null) and this force rotating slowly (to do not develop inertia forces) about the vertical axis K,III for 360 degrees, then the trace in plan of the point K displacement is forming an ellipse.
- (ix)
- If on the thin-walled open cross-section acts a bending moment about the principal center-gravity -axis, then pure bending is developing as it defined by the Bernoulli’s bending technical theory of beams, hence, the normal stresses are developed on total cross-section (Equation (16)).
- (x)
- If on the thin-walled open cross-section acts a bending moment about the principal center-gravity -axis, then pure bending is developing as it defined by the Bernoulli’s bending technical theory of beams, hence, the normal stresses are developed on total cross-section (Equation (16)).
- (xi)
- The recovery elastic forces , are depended from the moments of inertia and of the core, but these forces are acting on the elastic center K of the cross-section.
- (xi)
- The warping moment of inertia has to be calculated with regard to principal elastic Cartesian reference 3D-system K,I,II,III (and referring to principal start point ) where the product warping moments of inertia and are null. Only then, the value of the is minimum.
- (xiii)
- The normal stresses that are developed on the thin-walled open cross-section are given by Equation (16), that combines the bi-axial bending of the beam with axial force, as has been defined by the Bernoulli’s bending technical theory, with the Vlasov torsion theory on cores with thin-walled open cross-section.
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Vlasov, V.Z. Thin-Walled Elastic Bars, 2nd ed.; Fizmatgiz: Moscow, Russia, 1959. (In Russian) [Google Scholar]
- Vlasov, V.Z. Thin-Walled Elastic Bars, 2nd ed.; Israel Program for Scientific Translations: Jerusalem, Israel, 1961. (In English) [Google Scholar]
- Xenidis, H.; Morfidis, K.; Avramidis, I.E. Modeling of two-cell cores for three-dimensional analysis of multi-story buildings. Struct. Des. Tall Build. 2000, 9, 343–363. [Google Scholar] [CrossRef]
- Beck, H. Contribution to the Analysis of Coupled Shear Walls. ACI J. Proc. 1962, 59, 1055–1070. Available online: https://www.concrete.org/publications/internationalconcreteabstractsportal/m/details/id/7951 (accessed on 28 August 2022).
- MacLeod, I.A. Lateral stiffness of shear walls with openings in tall buildings. In Tall Buildings; Pergamon: London, UK, 1967; pp. 223–244. [Google Scholar]
- Schwaighofer, J. Ein Beitrag zum Windscheiben-Problem. Der Bauing. 1969, 44, 370–373. [Google Scholar]
- Schwaighofer, J.; Microys, H.F. Analysis of shear walls using standard computer programs. ACI J. Proc. 1969, 66, 1005–1007. [Google Scholar]
- Heidebrecht, A.C.; Swift, R.D. Analysis of Asymmetrical Coupled Shear Walls. J. Struct. Div. 1971, 97, 1407–1422. [Google Scholar] [CrossRef]
- MacLeod, I. Analysis of shear wall buildings by the frame method. Proc. Inst. Civ. Eng. 1973, 55, 593–603. [Google Scholar] [CrossRef]
- MacLeod, I.A.; Green, D.R. Frame Idealization for Shear Wall Systems; The Structural Engineer: London, UK, 1973; Volume 51, pp. 71–74. Available online: https://www.istructe.org/journal/volumes/volume-51-(published-in-1973)/issue-2/frame-idealization-for-shear-wall-support-systems/ (accessed on 28 August 2022).
- MacLeod, I. General frame element for shear wall analysis. Proc. Inst. Civ. Eng. 1976, 61, 785–790. [Google Scholar] [CrossRef]
- MacLeod, I.A.; Hosny, H.M. Frame Analysis of Shear Wall Cores. J. Struct. Div. 1977, 103, 2037–2047. [Google Scholar] [CrossRef]
- MacLeod, I.A. Structural Analysis of Wall Systems; The Structural Engineer: London, UK, 1977; Volume 55, pp. 487–495. [Google Scholar]
- Smith, B.S.; Abate, A. Analysis of non-planar shear wall assemblies by analogous frame. Proc. Inst. Civ. Eng. 1981, 71, 395–406. [Google Scholar] [CrossRef]
- Lew, I.P.; Narov, F. Three-Dimensional Equivalent Frame Analysis of Shear Walls. Concr. Int. Des. Constr. 1983, 5, 25–30. Available online: https://www.concrete.org/publications/internationalconcreteabstractsportal/m/details/id/15106 (accessed on 28 August 2022).
- Smith, B.S.; Girgis, A. Simple Analogous Frames for Shear Wall Analysis. J. Struct. Eng. 1984, 110, 2655–2666. [Google Scholar] [CrossRef]
- Kheyroddin, A.; Abdollahzadeh, D.; Mastali, M. Improvement of open and semi-open core wall system in tall buildings by closing of the core section in the last story. Int. J. Adv. Struct. Eng. 2014, 6, 67. [Google Scholar] [CrossRef] [Green Version]
- Girgis, A.M.; Stafford-Smith, B. Torsion analysis of building cores partially closed by beams. In Proceedings of the Symposium on the Behaviour of Building Systems and Components, Vanderbilt University, Nashville, TN, USA, 8–9 March 1979; pp. 211–227. [Google Scholar]
- Stafford-Smith, B.; Girgis, A.M. Deficiencies in the Wide Column Analogy for Shear Wall Core Analysis. Concr. Int. 1986, 58–61. Available online: https://www.concrete.org/publications/internationalconcreteabstractsportal.aspx?m=details&i=9586 (accessed on 28 August 2022).
- Avramidis, I.E. Zur Kritik des Aquivalenten Rahmenmodells fur Wandscheiben und Hochhauskerne. Bautechnik 1991, 68, S275–S285. Available online: https://pascal-francis.inist.fr/vibad/index.php?action=getRecordDetail&idt=19854325 (accessed on 28 August 2022).
- Carpinteri, A.; Lacidogna, G.; Nitti, G. Open and closed shear-walls in high-rise structural systems: Static and dynamic analysis. Curved Layer. Struct. 2016, 3, 154–171. [Google Scholar] [CrossRef] [Green Version]
- Zulli, D. A one-dimensional beam-like model for double-layered pipes. Int. J. Non-Linear Mech. 2019, 109, 50–62. [Google Scholar] [CrossRef]
- Latalski, J.; Zulli, D. Generalized Beam Theory for Thin-Walled Beams with Curvilinear Open Cross-Sections. Appl. Sci. 2020, 10, 7802. [Google Scholar] [CrossRef]
- Alsheikh, A.M.S.; Rees, D.W.A. General Stiffness Matrix for a Thin-Walled, Open-Section Beam Structure. World J. Mech. 2021, 11, 205–236. [Google Scholar] [CrossRef]
- Choi, I.S.; Jang, G.-W.; Choi, S.; Shin, D.; Kim, Y.Y. Higher order analysis of thin-walled beams with axially varying quadrilateral cross sections. Comput. Struct. 2017, 179, 127–139. [Google Scholar] [CrossRef]
- Chuong, N.T.; Quy, D.X. On the Thin-Walled Theory’s Application to Calculate the Semi-enclosed Core Structure of High-Rise Buildings. In Modern Mechanics and Applications; Tien Khiem, N., Van Lien, T., Xuan Hung, N., Eds.; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Lee, J. Center of gravity and shear center of thin-walled open-section composite beams. Compos. Struct. 2001, 52, 255–260. [Google Scholar] [CrossRef]
- Pavazza, R.; Matoković, A.; Vukasović, M. A theory of torsion of thin-walled beams of arbitrary open sections with influence of shear. Mech. Based Des. Struct. Mach. 2022, 50, 206–241. [Google Scholar] [CrossRef]
- Yu, W.; Hodges, D.H.; Volovoi, V.V.; Fuchs, E.D. A generalized Vlasov theory for composite beams. Thin-Walled Struct. 2005, 43, 1493–1511. [Google Scholar] [CrossRef]
- Bernuzzi, C.; Montanino, A.; Simoncelli, M. Torsional behaviour of thin-walled members with regular perforation systems. ce/papers 2021, 4, 343–350. [Google Scholar] [CrossRef]
- Nitti, G.; Lacidogna, G.; Carpinteri, A. Structural Analysis of High-rise Buildings under Horizontal Loads: A Study on the Piedmont Region Headquarters Tower in Turin. Open Constr. Build. Technol. J. 2019, 13, 81–96. [Google Scholar] [CrossRef]
| Number | bx | by | |||||
|---|---|---|---|---|---|---|---|
| A1 | 0.30 | 2.10 | 0.63 | 5.60 | 1.90 | 3.528 | 1.197 |
| A2 | 3.30 | 0.30 | 0.99 | 3.80 | 1.00 | 3.762 | 0.990 |
| A3 | 0.30 | 3.60 | 1.08 | 2.00 | 2.65 | 2.160 | 2.862 |
| A4 | 2.10 | 0.30 | 0.63 | 3.20 | 4.30 | 2.016 | 2.709 |
| Sum | 11.466 | 7.758 |
| Function ξ(s) | Function ω(s) | ||||||
|---|---|---|---|---|---|---|---|
| Number | e | Li | a | b | c | d | Iη,ω (Figure 3) |
| B-A | 0.30 | 1.95 | 2.50685 | 1.25317 | −1.61322 | 6.77224 | 2.32447 |
| C-B | 0.30 | 3.60 | −0.25054 | 2.50685 | 0. | −1.61322 | −1.38312 |
| C-D | 0.30 | 3.30 | −0.25054 | −2.37215 | 0. | 2.31076 | −1.90440 |
| D-E | 0.30 | 2.25 | −2.37215 | −0.64878 | 2.31076 | −6.12250 | 1.12564 |
| Sum | 0.16258 | ||||||
| Function η(s) | Function ω(s) | ||||||
|---|---|---|---|---|---|---|---|
| Number | e | Li | a | b | c | d | Iξ,ω (Figure 3) |
| B-A | 0.30 | 1.95 | 0.36811 | 1.86170 | −1.61322 | 6.77224 | 2.29297 |
| C-B | 0.30 | 3.60 | −1.94637 | 0.36811 | 0. | −1.61322 | 0.35140 |
| C-D | 0.30 | 3.30 | −1.94637 | 0.58123 | 0. | 2.31076 | −0.29888 |
| D-E | 0.30 | 2.25 | 0.58123 | 2.02778 | 2.31076 | −6.12250 | −2.36440 |
| Sum | −0.01892 | ||||||
| Function ω(s) | Function ω(s) | ||||||
|---|---|---|---|---|---|---|---|
| Number | e | Li | a | b | c | d | Iωi (Figure 3) |
| B-A | 0.30 | 1.95 | −1.811 | 6.6064 | −1.811 | 6.6064 | 6.81721 |
| C-B | 0.30 | 3.60 | −0.15228 | −1.811 | −0.15228 | −1.811 | 1.28833 |
| C-D | 0.30 | 3.30 | −0.15228 | 2.21256 | −0.15228 | 2.21256 | 1.51196 |
| D-E | 0.30 | 2.25 | 2.21256 | −6.24914 | 2.21256 | −6.24914 | 6.77713 |
| Sum | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makarios, T.K.; Athanatopoulou, A. Center of Stiffness, Principal Axes and Principal Start Point of Thin-Walled Open-Sections of Cores: A New Modified Calculation Technique Based on Vlasov Torsion Theory. Buildings 2022, 12, 1804. https://doi.org/10.3390/buildings12111804
Makarios TK, Athanatopoulou A. Center of Stiffness, Principal Axes and Principal Start Point of Thin-Walled Open-Sections of Cores: A New Modified Calculation Technique Based on Vlasov Torsion Theory. Buildings. 2022; 12(11):1804. https://doi.org/10.3390/buildings12111804
Chicago/Turabian StyleMakarios, Triantafyllos K., and Asimina Athanatopoulou. 2022. "Center of Stiffness, Principal Axes and Principal Start Point of Thin-Walled Open-Sections of Cores: A New Modified Calculation Technique Based on Vlasov Torsion Theory" Buildings 12, no. 11: 1804. https://doi.org/10.3390/buildings12111804
APA StyleMakarios, T. K., & Athanatopoulou, A. (2022). Center of Stiffness, Principal Axes and Principal Start Point of Thin-Walled Open-Sections of Cores: A New Modified Calculation Technique Based on Vlasov Torsion Theory. Buildings, 12(11), 1804. https://doi.org/10.3390/buildings12111804








