1. Introduction
The flow perturbations generated by a building are strongly related to that building’s configurations. Studies of wind effects on basic rectangular-shaped buildings showed that building shape exerted great influences on wind characteristics around the buildings [
1,
2]. Spherical structures are widely used in public venues or landmarks because of their large column-free spaces, beautiful shapes, and advantages in efficiency and economy. Usually, strong impinging and flow separation occur for wind flow around spherical structures because of their curved shapes. The curved shape also makes estimation of wind pressure on a spherical structure a difficult task. Buildings with spherical structures are wind-sensitive and prone to damage under wind loads because they are usually built using lightweight materials. There have been reports of collapse of curve-shaped storage domes during strong wind [
3]. Therefore, the study of wind loads on spherical structures is crucial for developing wind-resistant designs.
The most widely used type of spherical structure is a hemisphere. Wind tunnel experiments and computational fluid dynamics (CFD) techniques have been used to investigate the air flow around and wind loads on a surface-mounted hemisphere. Toy et al. [
4] performed an initial investigation into the flow past a hemispherical dome immersed in two thick boundary layers by conducting wind tunnel experiments. They determined that, with increased turbulence intensity in the boundary layer, the separation region and reattachment point moved downstream. Savory and Toy [
5] conducted experiments to study the effects of model surface roughness and three turbulent boundary layers on the mean pressure distributions and near-wake changes. Air flows around a surface-mounted hemisphere were numerically investigated at Reynolds numbers ranging from 3.5 × 10
4 to 6.4 × 10
4 [
6,
7]. The aforementioned authors concluded that the air flow around a surface-mounted hemisphere, especially in the reverse-flow region behind the structure, is highly dependent on the Reynolds number. Kharoua and Khezzar [
8] conducted large eddy simulations to study the turbulent flow around smooth and rough hemispherical domes at a Reynolds number of 1.4 × 10
5. They found that the separation phenomenon occurs before the apex of a rough dome and shifts forward for a smooth dome. The turbulence-affected region is more larger in the wake of a rough dome. Cheng and Fu [
3] performed a series of wind tunnel tests to investigate the effects of the Reynolds number on the aerodynamic characteristics of hemispherical domes in smooth and turbulent boundary layer flows. The results of the aforementioned studies have indicated that the pressure distributions become relatively stable at
Re > 3.0 × 10
5 in a smooth flow. In turbulent flow, the mean and root-mean-square pressure distributions become independent of the Reynolds number when
Re = 1.0 − 2.0 × 10
5.
In an actual project, various types of spherical structures exist due to different build positions and design styles. In addition to hemispheres, some structures that are smaller or larger than a hemisphere are used in building projects. Moreover, in certain cases, a whole sphere may exist above the ground under some supports [
9]. Wind loads acting on nonhemispherical domes have gained considerable research interest. Meroney et al. [
10] calculated the mean pressure distributions over single and paired domes formed from truncated hemispheres. Surface roughness was found to reduce the mean suction for a single dome. Moreover, wake effects were found to modify the mean suction for paired domes. Yousef et al. [
11] and Li et al. [
12] have investigated the wind loads induced by tornadoes acting on dome structures smaller than a hemisphere. Tsutsui [
13] investigated the flow around a whole sphere placed at various heights above a plane. Sadeghi et al. [
14] numerically studied the wind effect on spherical, grooved, and scallop domes in a smooth flow based on a Reynolds-averaged Navier–Stokes (RANS) model. They determined the wind pressure patterns on spherical domes with rise–span ratios ranging from 0 to 0.7. Taylor [
15] conducted wind tunnel experiments to investigate the aerodynamic pressure distributions on rough hemispherical domes with different wall-height-to-diameter ratios in two turbulent boundary layers. The aforementioned investigation confirmed that the pressure distribution becomes independent of the Reynolds number at a large
Re value and turbulence intensity. Chen et al. [
16] studied the aeroelastic instability of spherical inflatable membrane structures with a large rise–span ratio using a wind tunnel experiment. Uematsu et al. [
17] and Sun et al. [
18] measured the mean and fluctuating wind pressure acting on spherical domes with different rise–span and wall-height–span ratios in a turbulent boundary layer. Park et al. [
19] studied the external and internal pressure characteristics of dome roofs with openings and low rise–span ratios via wind tunnel experiments.
The wind loads acting on spherical structures are complex, and predicting the surface pressure directly is difficult because of the existence of various types of structural configurations in engineering. Although some studies have investigated wind pressure distributions on a spherical structure, most of them have examined structures that are hemispheres or smaller. Thus, a research gap exists regarding the wind pressure distributions on structures whose shape falls between a hemisphere and a whole sphere. Most studies have been conducted under a smooth inflow condition or in a thin boundary layer for flows with a low Reynolds number. However, investigations in a fully developed turbulent boundary layer for flows with a high Reynolds number are essential for engineering applications.
In this study, commonly used turbulence models in wind engineering were assessed through comparisons of wind pressure measurements for a hemisphere. The optimal turbulence model was selected to ensure high accuracy in predicting the wind pressure on a curved surface. By using the optimal CFD model, numerous numerical simulations were conducted to determine the mean wind loads on various types of spherical structures with different apex-height-to-diameter ratios (ARs). The studied structural types ranged from different truncated spheres to whole spheres located at different distances above the ground. Full-scale simulations were performed for a flow with a high Reynolds number in a turbulent boundary layer. This can ensure that the pressure distribution is independent of the Reynolds number. The variation rules of the mean wind pressure over the structural surface as well as the variation tendency of the mean drag and lift force coefficients were determined. Finally, suggestions were presented for wind-resistant design of spherical structures on the basis of the obtained results.
2. Turbulence Model Evaluations
Commonly used turbulence models in wind engineering and the numerical algorithms used in this study were evaluated to ensure the accuracy of CFD techniques in predicting wind pressures on a curved surface. The examined RANS models were a standard
k–
ε model, a renormalisation group (RNG)
k–
ε model [
20], an LK
k–
ε model [
21], and a shear stress transport (SST)
k–
ω model [
22].
In a standard
k–
ε model, the production term
Pk is computed as follows:
where
νt is the turbulent viscosity and
S is the magnitude of the strain rate, which is defined as follows:
where
xj (
j = 1, 2, 3) represents the three directions of the coordinates.
In an LK
k–
ε model, the production term
Pk is simply modified from a standard
k–
ε model and computed as follows:
where
Ω is the magnitude of the vorticity rate and is defined as follows:
For an SST
k–
ω model, the transport equations of both the turbulent kinetic energy
k and turbulent frequency
ω are solved. The wind tunnel measurements of wind pressure on a hemisphere conducted by Cheng and Fu [
3] for a smooth inflow condition (uniform inflow velocity of 9 m/s) were used to validate the CFD models. The diameter of the hemisphere
d was 0.5 m. The Reynolds number determined from the inflow velocity and the diameter is approximately 3.0 × 10
5. The distance from the sphere centre to the outlet of the computational domain is 15
d. The top boundary and two lateral boundaries of the domain were set to be symmetrical. The pressure outlet condition was given to the outlet boundary. The same unstructured mesh system with a grid number of 2,000,000 was used for all the simulations. The size of the first mesh on the wall surface was controlled carefully to ensure that the nondimensional distance (
y+) is approximately 30 in most regions. This satisfies the criterion for using a wall function. The second-order Upwind scheme was used for the convection term. The SIMPLE algorithm was used for the pressure–velocity calculations.
The values of the mean pressure coefficient (
Cp) in different simulations were compared. The parameter
Cp is defined as follows:
where
P is the mean pressure on the surface of the sphere,
P∞ is the mean pressure in the free stream,
ρ is the density of the air (
ρ = 1.225 kg/m
3), and
Uref is the inflow mean streamwise velocity at the reference height (
Uref = 9 m/s for this validation model).
Figure 1 displays the distributions of
Cp along the centre meridian in different simulations. Further,
γ is the angle between the line connecting one point on the sphere surface to the sphere’s centre (red line) and the negative
x-direction. Another set of simulations were conducted with the SST
k–
ω model by using a coarse mesh system to check the mesh sensitivity. A relatively large discrepancy was observed between the experimental results and the results of the standard
k–
ε model for
γ = 20–120°. Small differences were observed between the results of the LK
k–
ε, RNG
k–
ε, and SST
k–
ω models. Moreover, the
Cp values calculated using these turbulence models exhibited good agreement with the experimental results from
γ = 0–160°. The results were not sensitive to the mesh density for RANS models. In small leeward regions for
γ = 160–180°, the results were sensitive to the turbulence model adopted. Positive pressures were observed in both the experiments and CFD simulations at the leeward surface near the ground.
Figure 2 presents comparisons of the mean streamlines and normalised turbulent kinetic energy in the centre plane of the domain. An excessive generation of turbulent kinetic energy around the structure was observed in the standard
k–
ε model. Compared with the standard
k–
ε model, the revised
k–
ε models and SST
k–
ω model exhibited considerably lower
k values. The most effective reduction in
k was from LK
k–
ε model because of the modification in Equation (3). Considerable overestimations of
k in the standard
k–
ε model have been reported by Mochida et al. [
23] and Tominaga et al. [
24] in their simulations of wind flow around an isolated high-rise building. The poor prediction of
Cp in the standard
k–
ε model (
Figure 1) was likely due to the excessive generation of
k in the impinging and separation region. A small recirculation was observed in front of the structure near the ground in all the simulations. This recirculation caused the
Cp value to decrease marginally and then increase in the regions where
γ < 15°. Clear recirculation was observed behind the structure in the simulations conducted with the LK
k–
ε, RNG
k–
ε and SST
k–
ω models. In the core of recirculation, the turbulent kinetic energy is usually large because of the strong turbulent motion. Overall, in contrast to the standard
k–
ε model, the revised
k–
ε models and SST
k–
ω model could accurately predict
Cp over the entire surface of the hemisphere except for a small leeward region. Although the LK
k–
ε model is the simplest modification of the standard
k–
ε model, it exhibited excellent performance in predicting
Cp on a curved surface. However, evaluations of the LK
k–
ε model are still essential in wind engineering. The SST
k–
ω model was selected in this study to investigate the wind loads on various types of spherical structures because this model can accurately predict separating flows under adverse pressure gradients and is widely used in wind engineering for predicting mean pressure [
25].
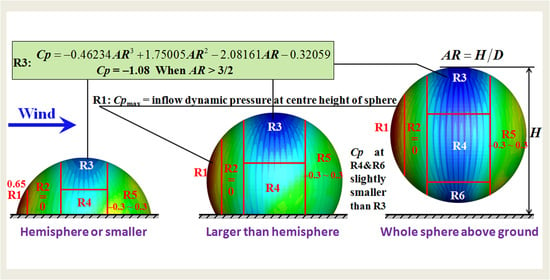
5. Design Suggestions
This section provides suggestions for wind-resistant design of spherical structures based on the results. In the Japanese code governing the design of spherical structures [
27], the whole surface of a dome structure (including the truncated hemisphere) with a rise–span ratio of less than 0.5 is divided into four regions to obtain separate mean pressure coefficients for wind-resistant design. Similar to the aforementioned Japanese code, this study divided the surface of a sphere into six regions (
Figure 14). Region R1, which is located at the windward surface, is subjected to strong positive pressure due to the impinging effect of wind. Region R2 is the transition area from positive to negative pressures, and zero pressure is appropriate. The position of R2 can be determined according to the position angle of zero pressure shown in
Figure 10. R3 (top region) and R4 (two side regions) are subjected to a strong suction effect, and the largest negative pressure appears in R3. R5 covers a large area of the rear surface but is not consequential for wind-resistant design because the wind pressure in this region is small. If the inflow dynamic pressure at the apex height
H is used as a reference, a
Cp value of −0.3 to 0.3 is recommended for R5. The bottom region R6 and its two small adjacent regions only exist when the spherical structure is a whole sphere. To develop a wind-resistant design for a spherical structure, determining the maximum positive pressure acting on the windward wall and the maximum negative pressures at the top region are important. When the spherical structure is equal to or smaller than a hemisphere, a
Cp value of 0.6–0.7 is suggested for R1. For structures larger than a hemisphere, the pressure in R1 can be obtained from the inflow dynamic pressure at the centre height of the sphere because the inflow dynamic pressure changes to being static pressure near this height according to Bernoulli’s theorem. For all types of spherical structures, if the inflow dynamic pressure at the apex height
H is used as a reference, the polynomial approximation equation presented in this study (Equation (11)) is suggested for evaluation of
Cp in R3. The limitations of using Equation (11) arise from the limited number of simulation models in which a whole sphere is located above the ground. As shown in
Figure 11, the change in the area-averaged
Cp value in the top region was small for Models 16–18. Therefore, when a whole sphere is located far from the ground, a
Cp value of −1.08 is suggested for R3. A
Cp value smaller than that in R3 is appropriate for the side region R4 and bottom region R6. In an actual project, a support structure is usually connected to R6 when a whole sphere is located above the ground. As a result, the pressure acting on R6 may be affected by the support structures.
6. Conclusions
In this study, four RANS turbulence models that are commonly used in wind engineering were evaluated with respect to prediction of the mean wind loads acting on a hemisphere. The best turbulence model (SST k–ω model) was selected to investigate the wind pressures acting on various types of spherical structures with different ARs. Design suggestions were presented based on the obtained results.
The results indicated that, in a large area of the windward surface, the pressures were positive due to the impinging effect of wind. The maximum positive pressure gradually increased with AR. The largest positive Cp was 0.6–0.7 for a hemisphere and for structures smaller than a hemisphere. For structures larger than a hemisphere, the largest positive pressure nearly equalled the inflow dynamic pressure at the centre height of the sphere. The structures were subjected to a strong suction effect at the crown of the sphere as well as its two side and bottom regions (if they exist). This strong suction effect gradually strengthened as AR increased. For a whole sphere located above the ground, the suction effect at the side and bottom regions was strong and only marginally weaker than that at the top region. The strongest suction effect occurred at the apex position in all the models. In most regions of the rear surface, the pressure was small. By using the inflow dynamic pressure at the apex height as a reference in each case, the negative Cp over the crown area was averaged. Moreover, a polynomial approximation function was derived for quickly determining the strongest suction effect for all types of spherical structures.
The drag coefficient CD increased rapidly with AR and reached its maximum value when the structure was close to a whole sphere. Subsequently, the CD value suddenly decreased because of the appearance of negative pressures in the lower part of the windward wall and large-area positive-pressure regions at the rear surface. The total lift coefficient CL increased rapidly with AR and reached its maximum value in Model 9. CL suddenly decreased in Model 12 because of the appearance of a strong suction effect at the bottom of the structure. The strong suction effect acting on the top area contributed considerably to total lift. For a whole sphere located far from the ground, the changes in both CD and CL were small.
Based on the obtained results, suggestions were proposed for wind-resistant design of spherical structures. This study had its limitations, suggesting future work. The predicted result by the RANS model was not satisfactory in a small leeward region. More simulation models are still necessary to be conducted to generalize the results.