Probabilistic Assessment of Buildings Subjected to Multi-Level Earthquake Loading Based on the PBSD Concept
Abstract
:1. Introduction
2. Probabilistic Assessment Approach to Extract Structural Risk
2.1. Deterministic Response Using OpenSees
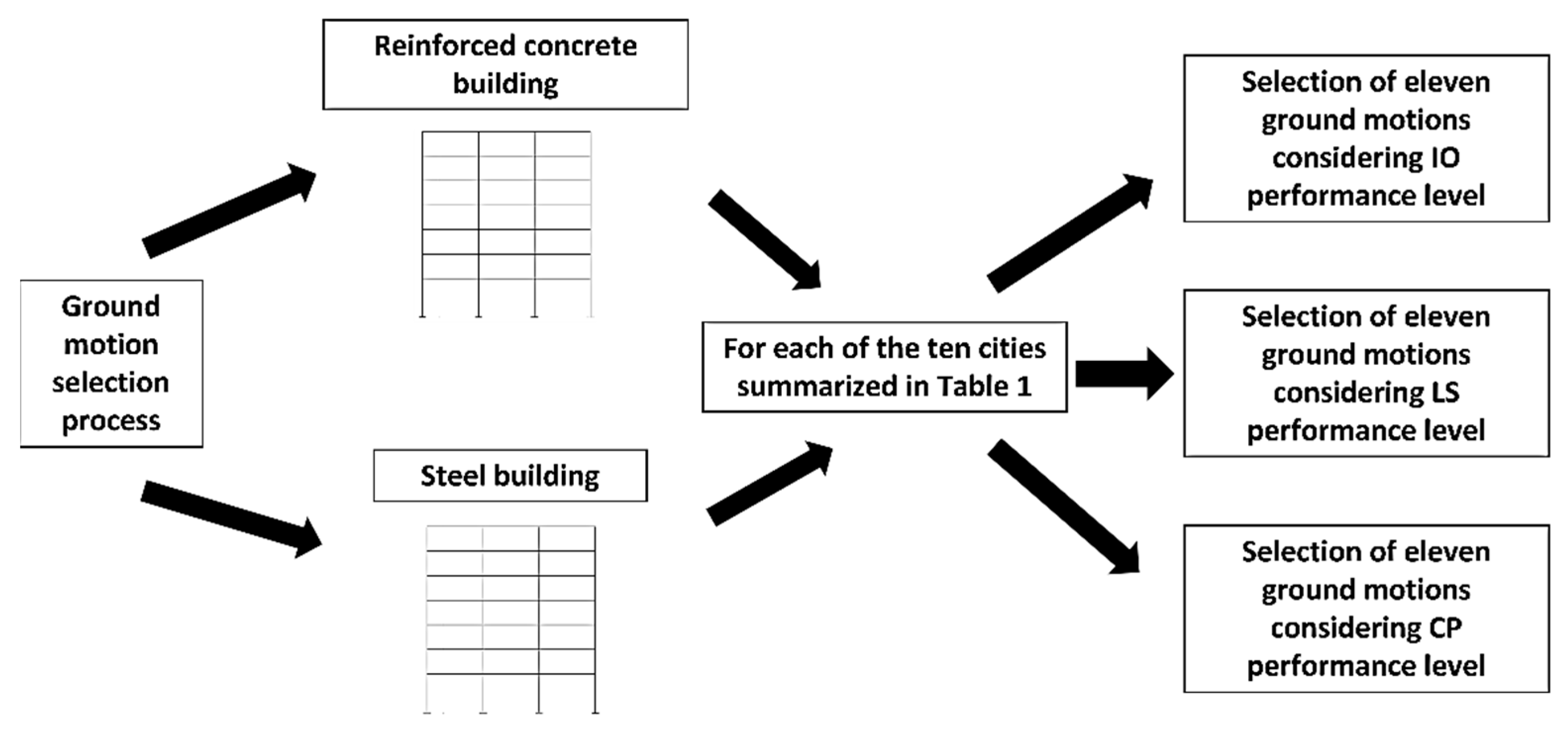
2.2. Seismic Load Selection and Performance Levels
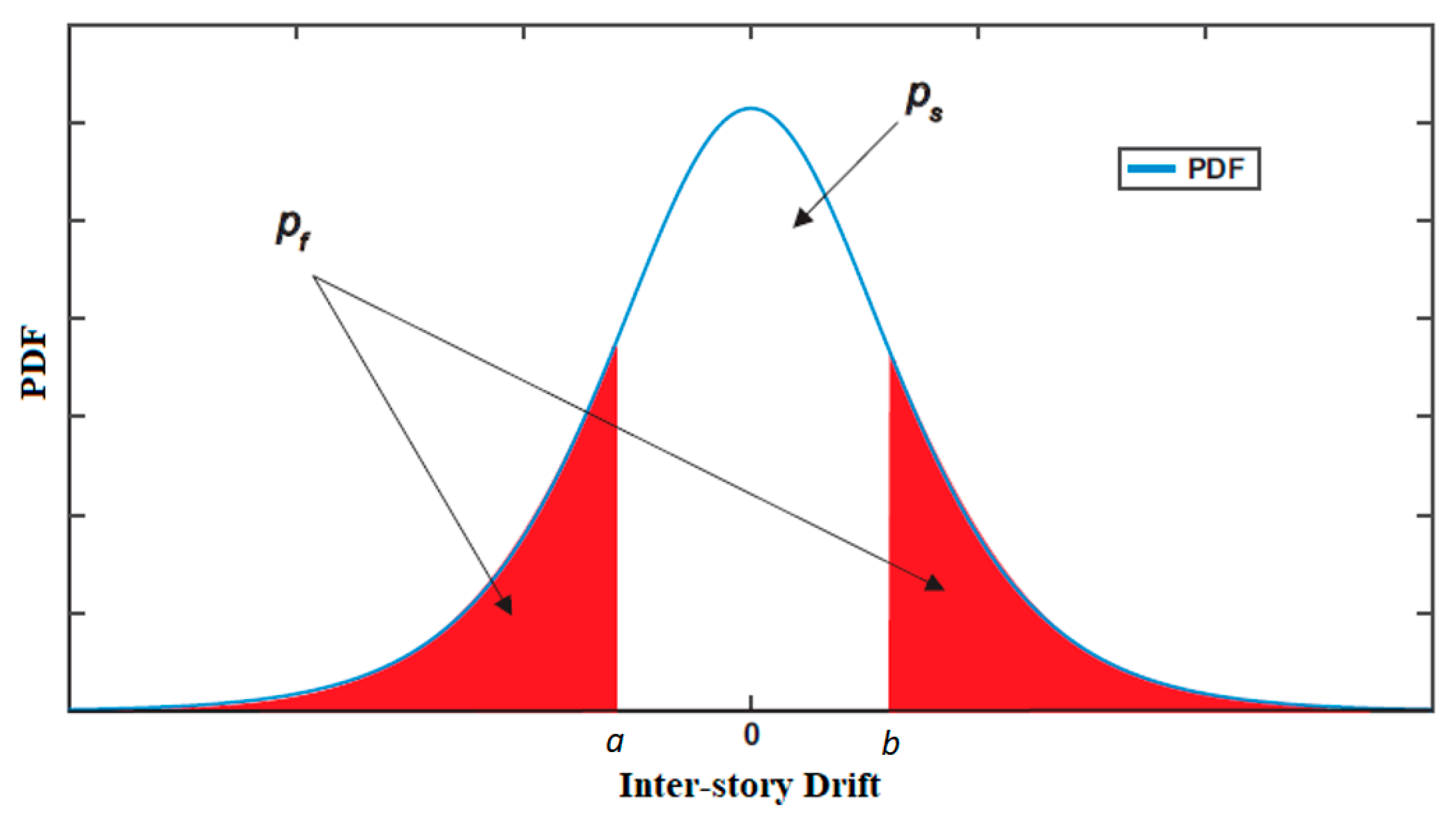
2.3. Probability Density Functions (PDFs) of Inter-Story Drifts
2.4. Calculation of Reliability Index
2.5. Flowchart of the Probabilistic Approach
3. Numerical Examples for the Implementation of the Probabilistic Approach
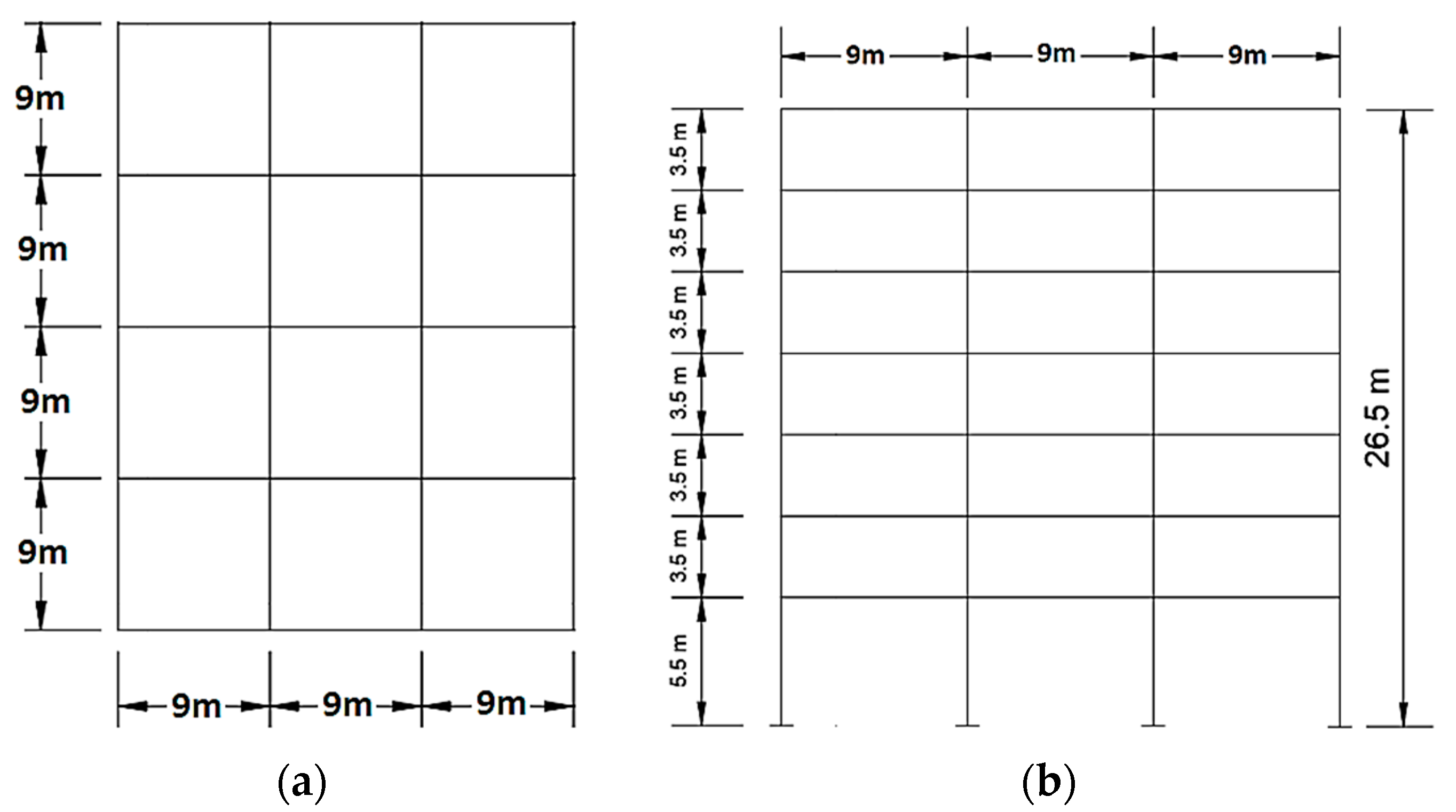
3.1. Structural Models and Locations
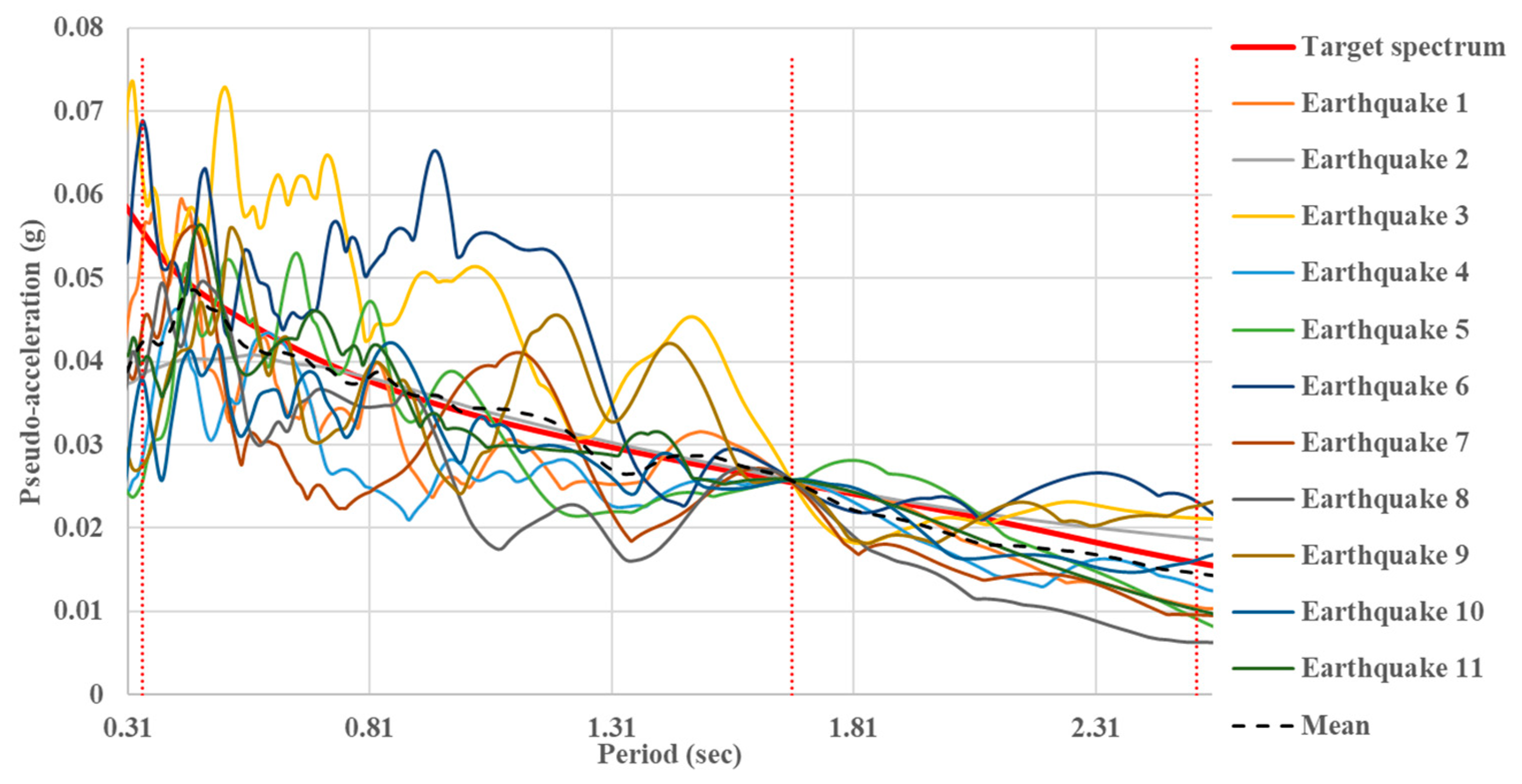
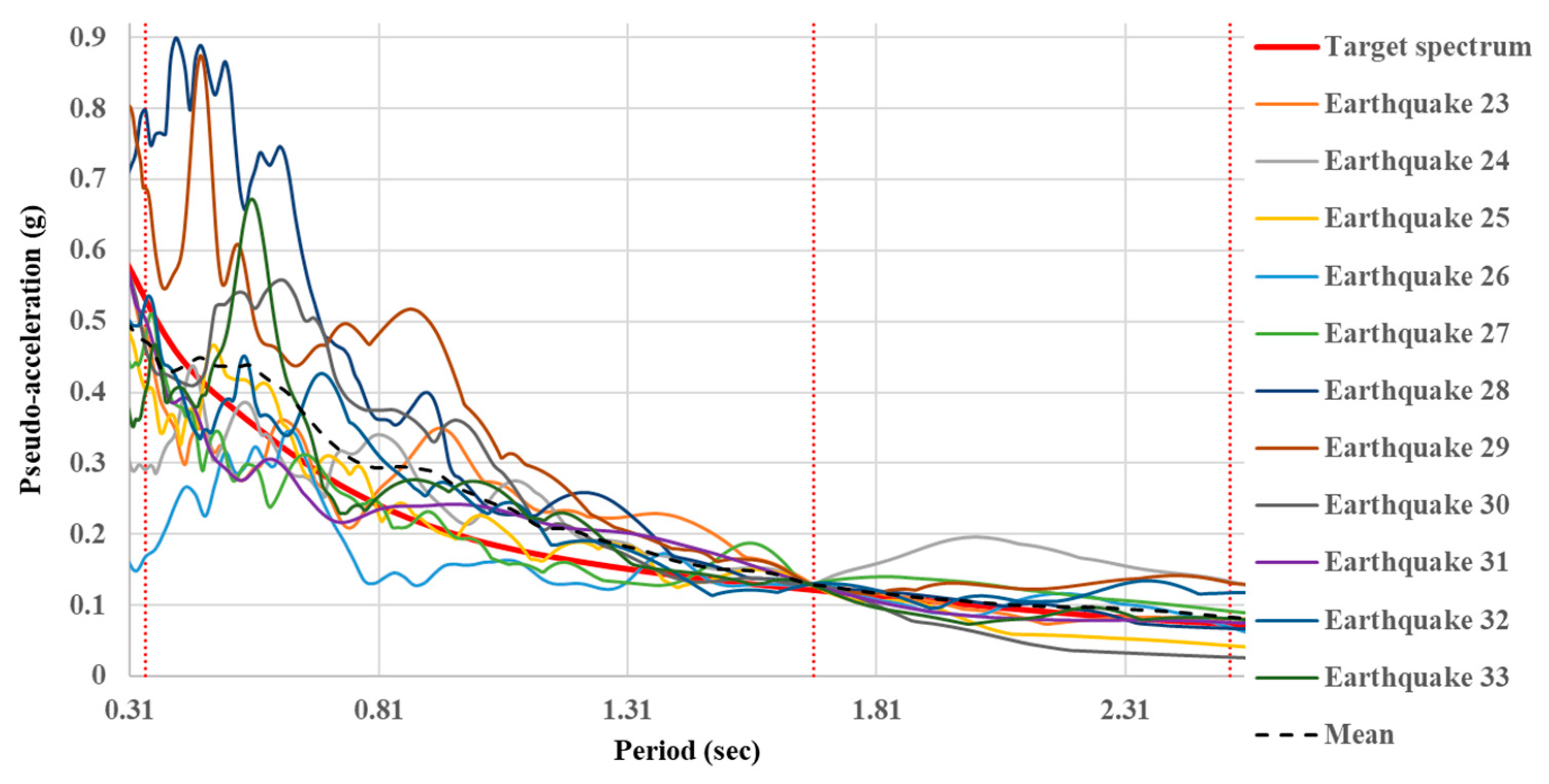
3.2. Selection of Representative Ground Motions
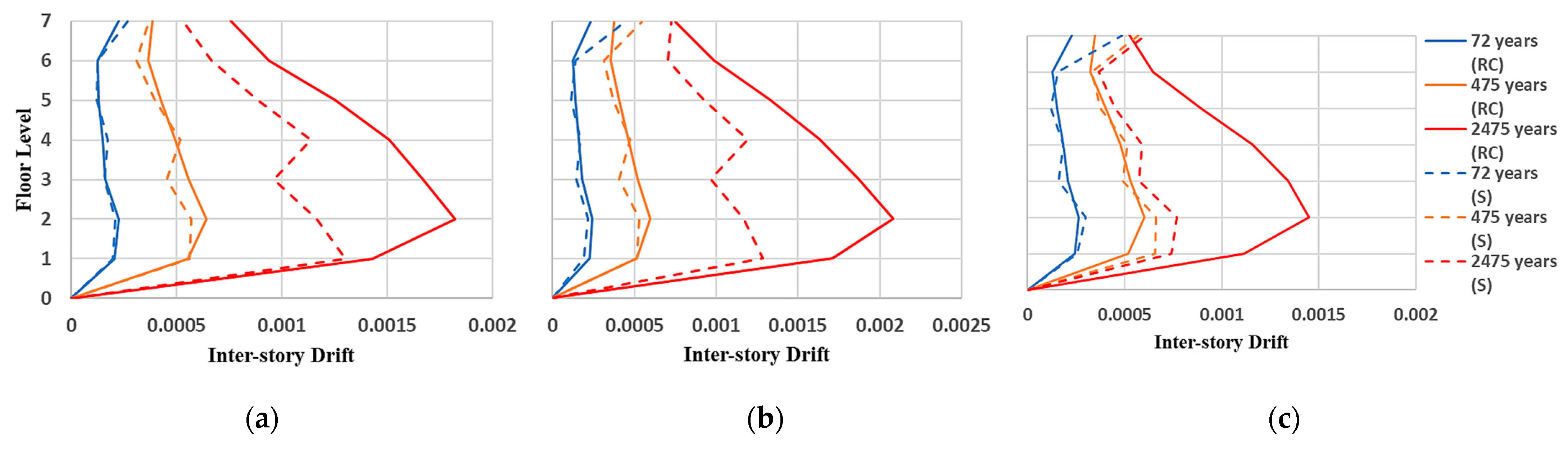
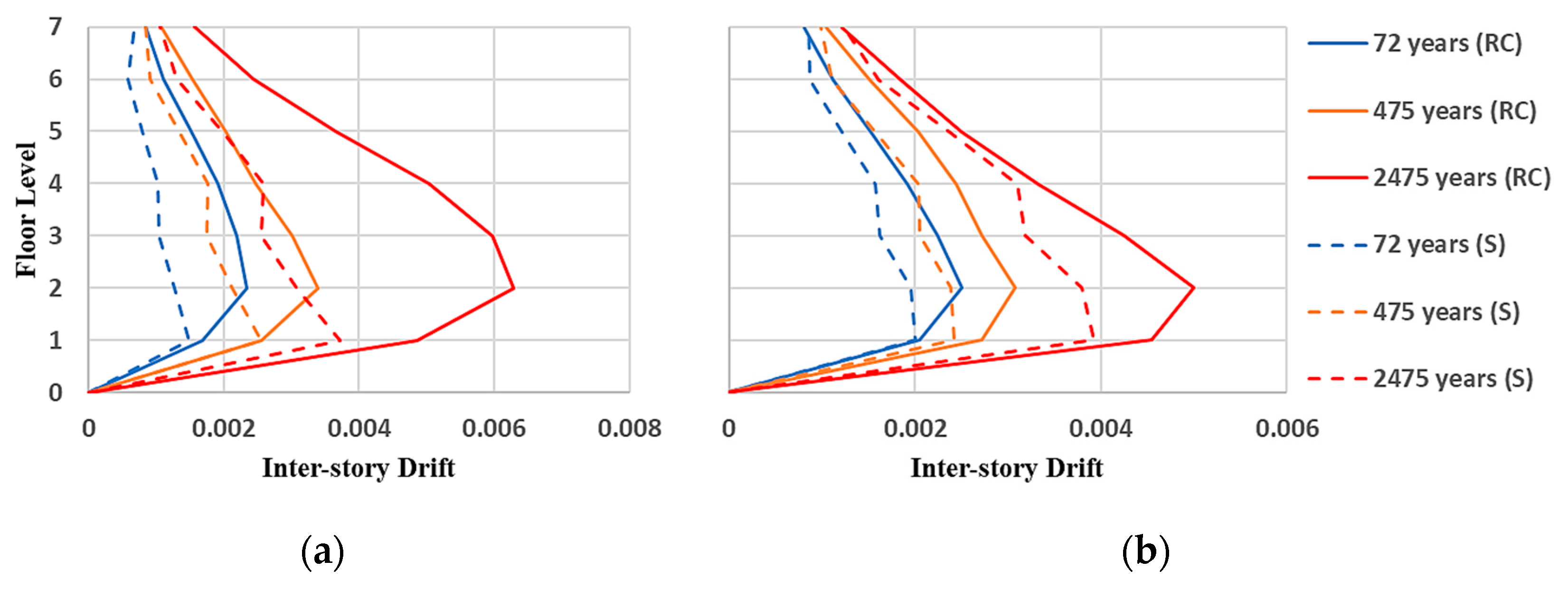
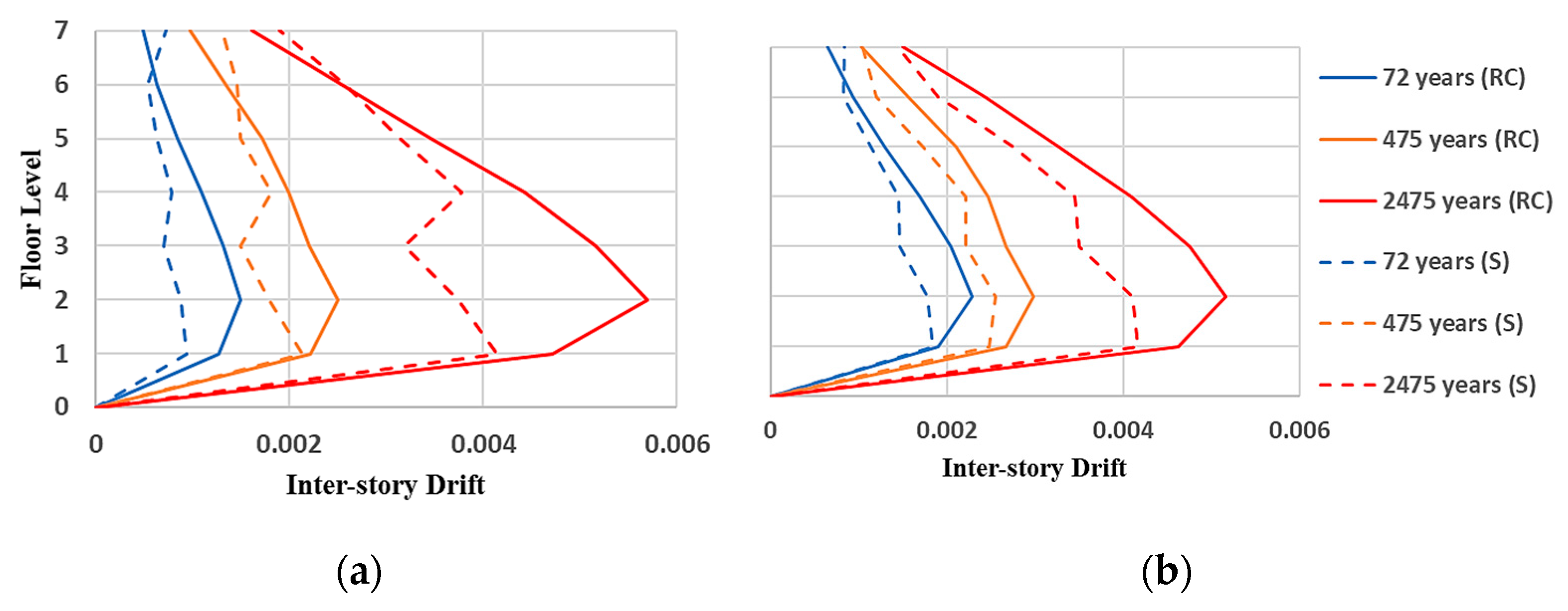
3.3. Derterministic Seismic Response of Buildings
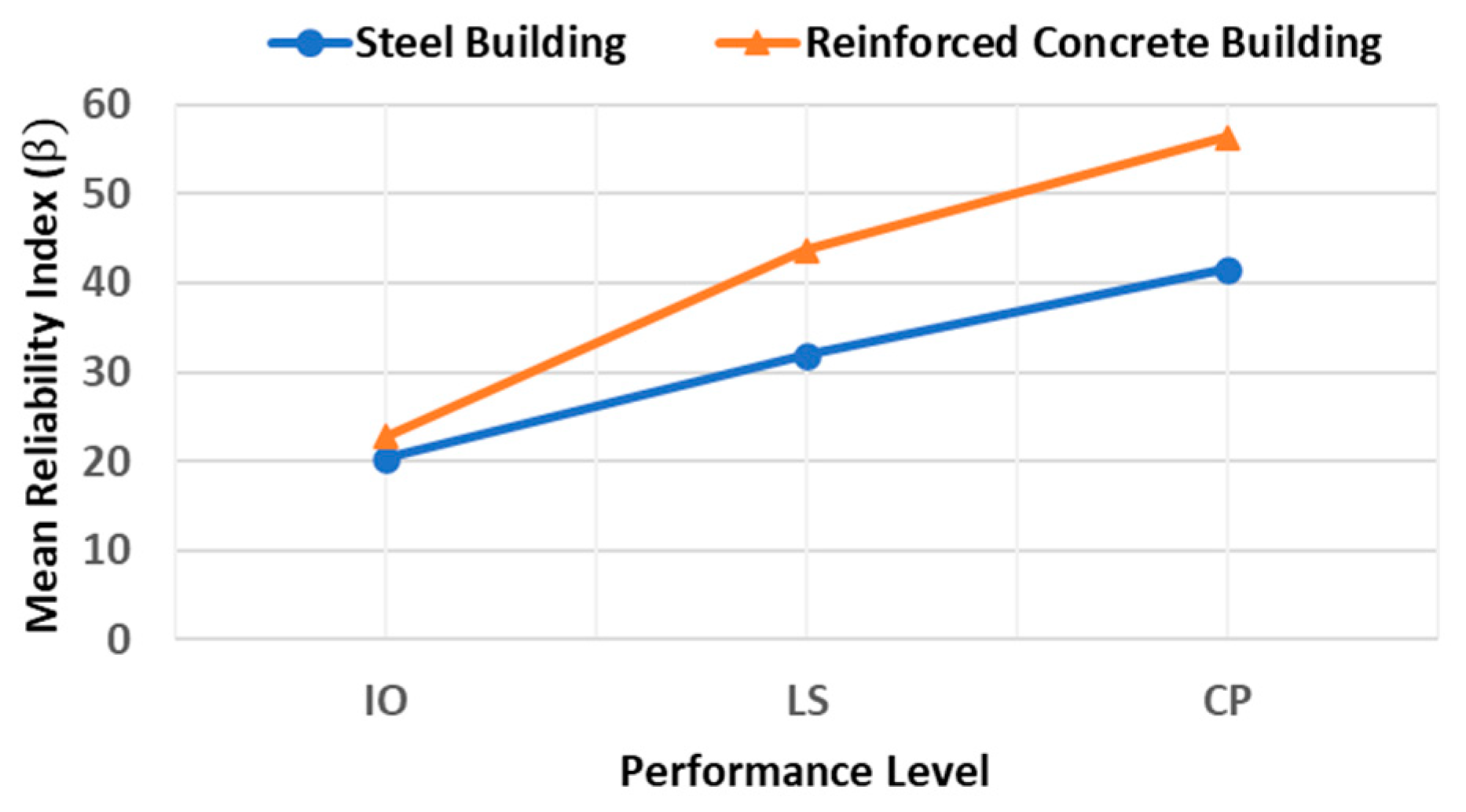
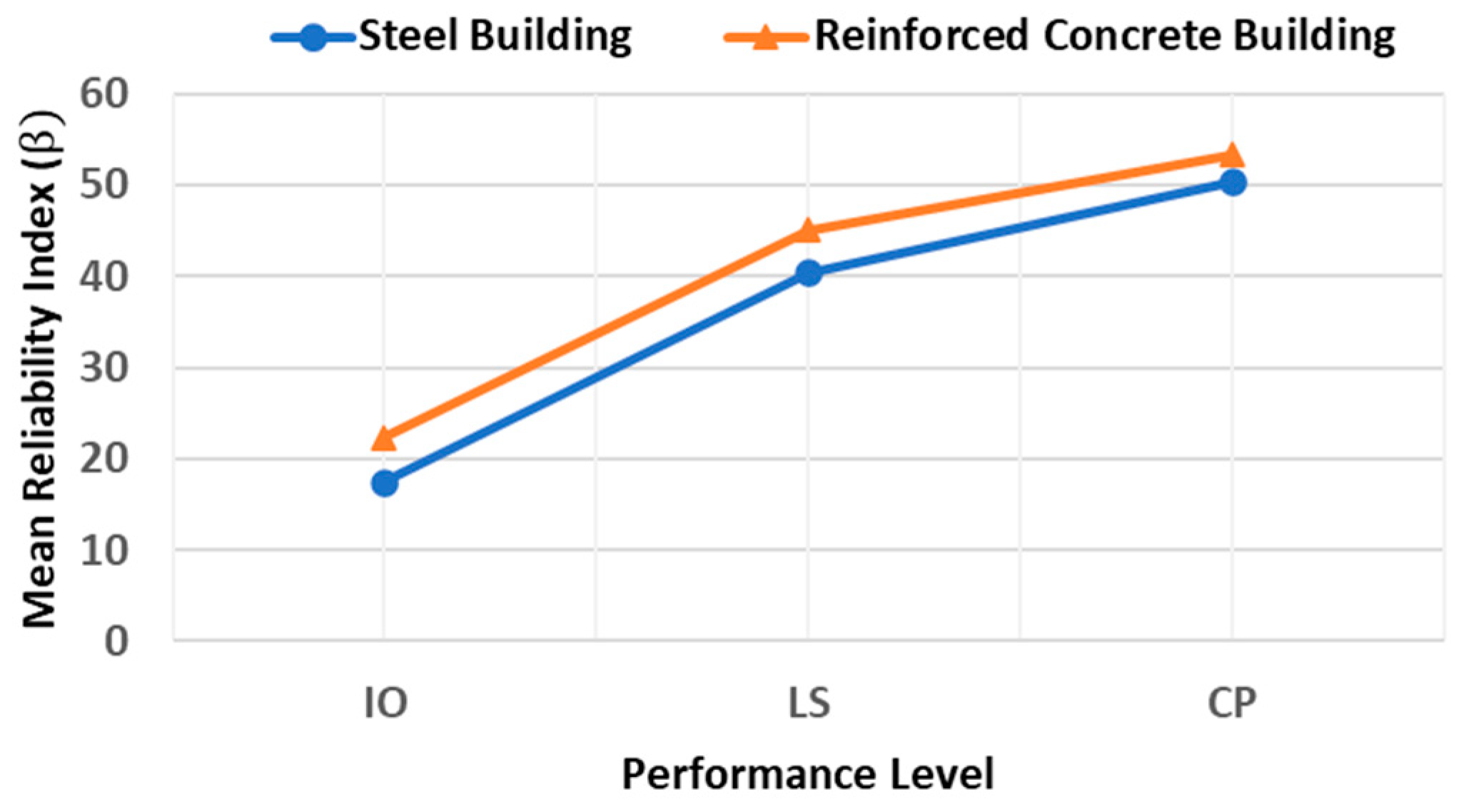
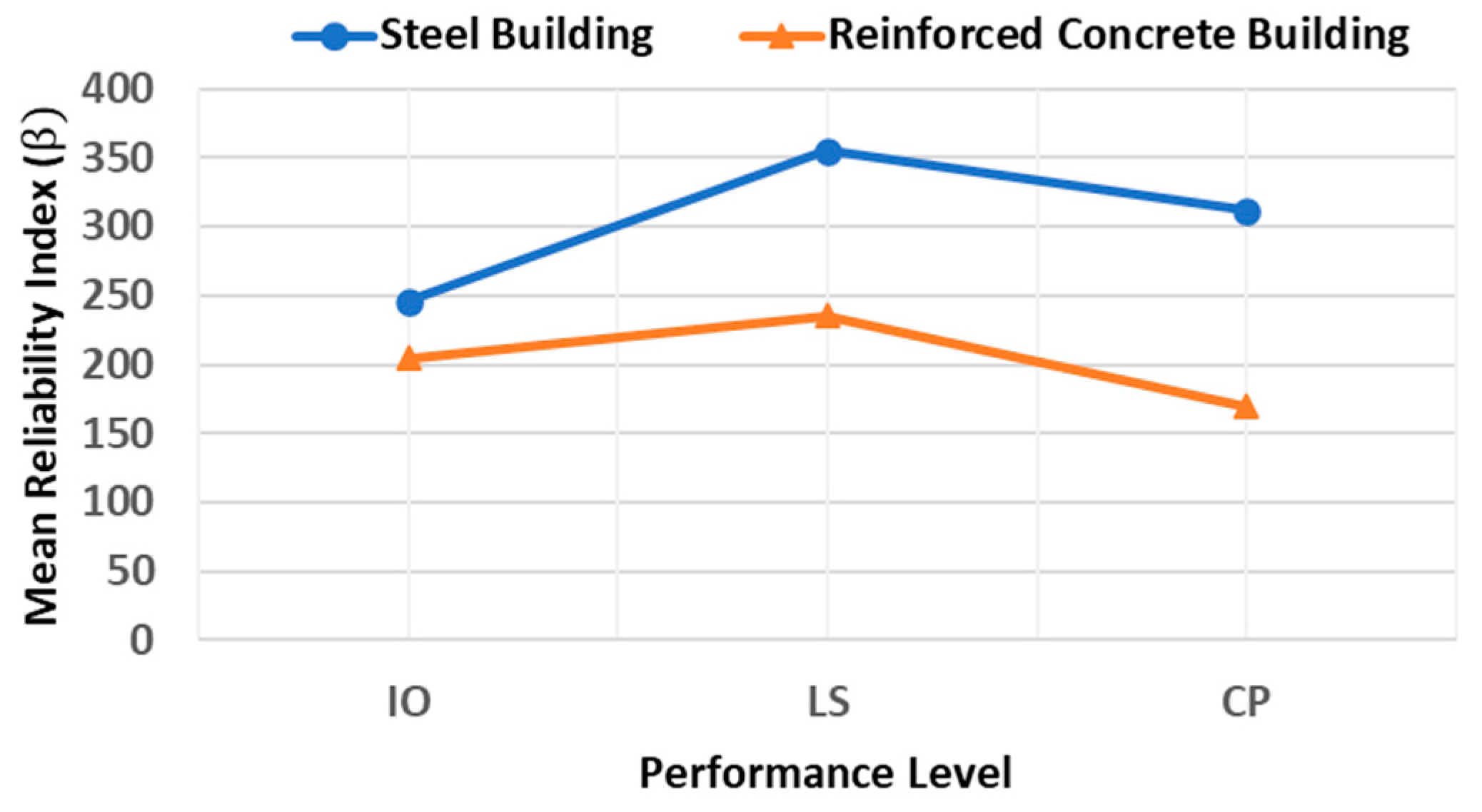
3.4. Structural Reliability of Buildings Using the Probabilistic Approach
4. Conclusions
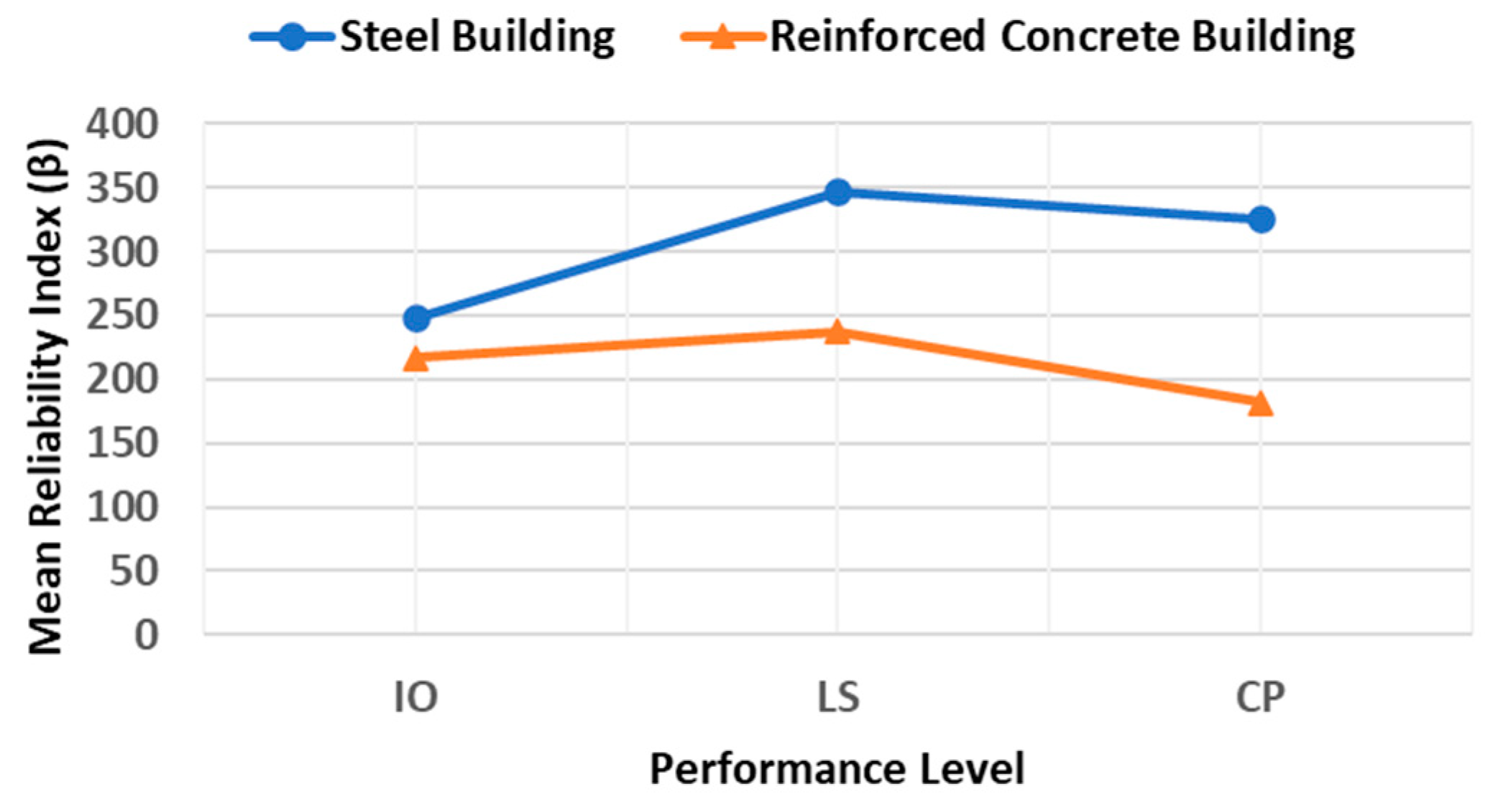
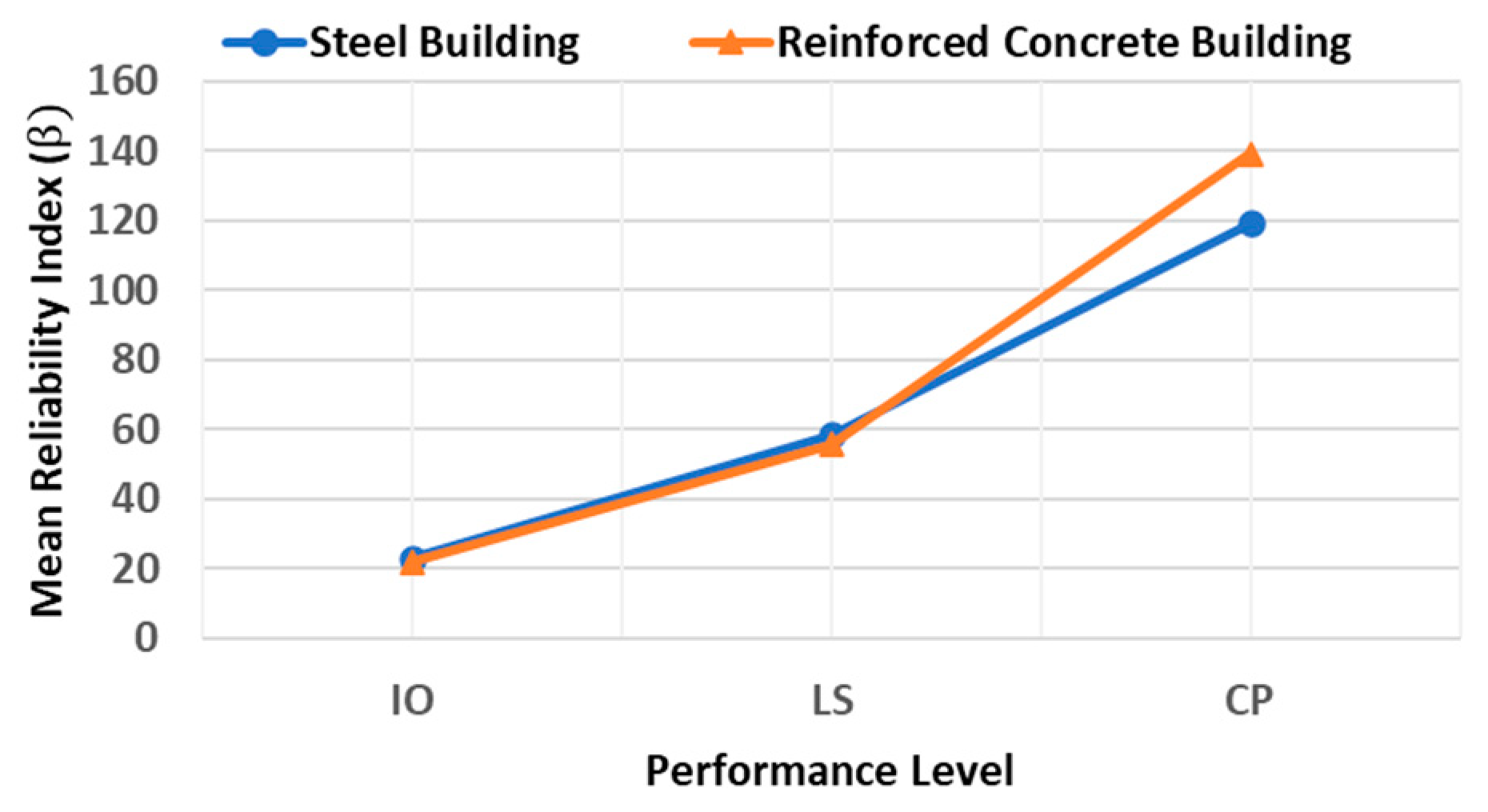
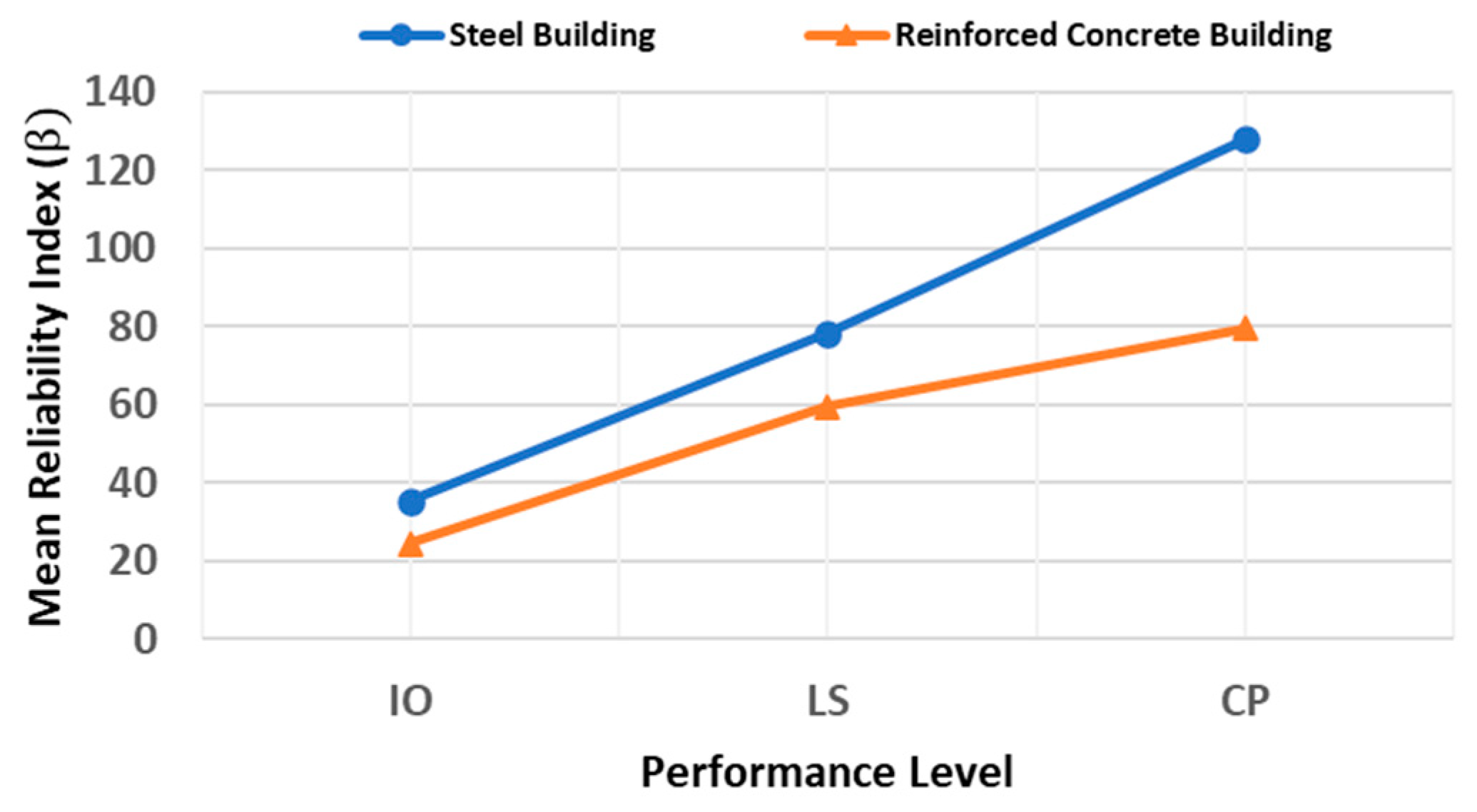
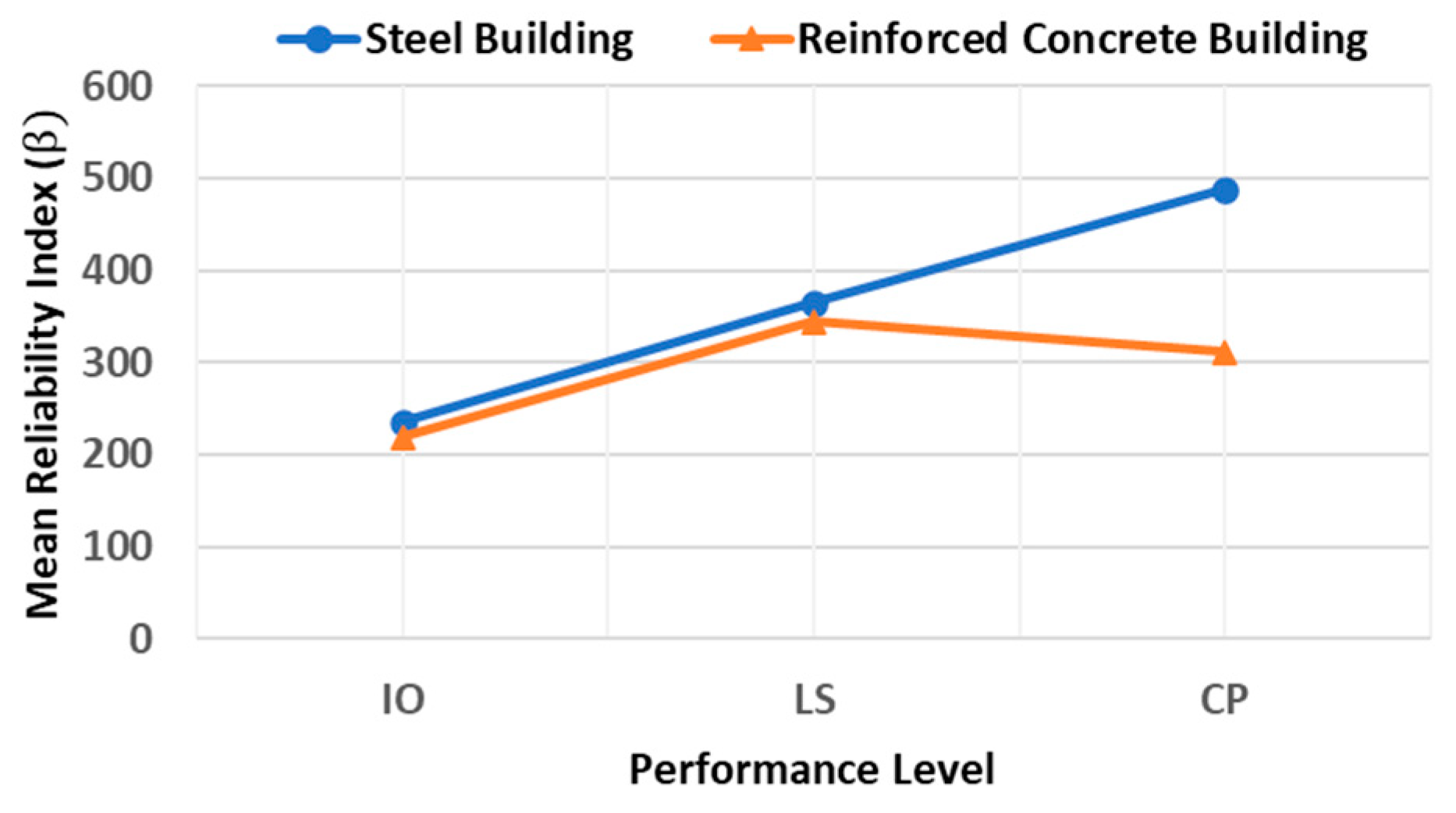
- A novel probabilistic approach was implemented to extract the structural risk of steel and reinforced concrete buildings in different locations (seismic zones A, B, C, and D) in Mexico. The mean values of maximum inter-story drift demonstrated that buildings located in earthquake-prone regions in Mexico (seismic zone D) present the largest deformations. This is an anticipated scenario, since it is expected that very strong earthquakes occur in these regions.
- Buildings located in regions with a very low seismic activity in Mexico (seismic zone A) exhibited the smallest inter-story drifts. This is logical given the low magnitude earthquakes commonly occurring in those areas. Thus, seismic loading is never significant in these locations. On the other hand, buildings located in zones with the highest seismic hazard (seismic zone D) in Mexico presented the lowest values of reliability index (). In contrast, those located in seismic zone A (lowest seismic risk) showed the highest values of reliability index (). This may reflect the tendency of building codes to protect buildings designed in earthquake-prone areas.
- In general, for almost every case under study, it is observed that the structural reliability of buildings increased from IO to LS and LS to CP, respectively, which can reflect a higher structural safety for buildings subjected to very intense ground motions.
- It was demonstrated that the main PDF controlling the stochastic behavior of inter-story drift is the GEV distribution. This is an important observation that implies that the randomness of damage in buildings can be studied using this PDF in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- MCBC. Mexico City Building Code. In Complementary Technical Norms for Earthquake Resistant Design; Government of Mexico City: Mexico City, Mexico, 2017. [Google Scholar]
- IBC. International Building Code; International Code Council: Washington, DC, USA, 2012. [Google Scholar]
- Esteva, L. The Mexico earthquake of September 19, 1985—Consequences, lessons, and impact on research and practice. Earthq. Spectra 1988, 4, 413–426. [Google Scholar] [CrossRef]
- Kroll, C.A.; Landis, J.D.; Shen, Q.; Stryker, S. Economic impacts of the Loma Prieta earthquake: A focus on small business. Berk. Plan. J. 1991, 5, 39–58. [Google Scholar] [CrossRef] [Green Version]
- Kircher, C.A.; Reitherman, R.K.; Whitman, R.V.; Arnold, C. Estimation of earthquake losses to buildings. Earthq. Spectra 1997, 13, 703–720. [Google Scholar] [CrossRef]
- Olshansky, R.B.; Johnson, L.A.; Topping, K.C. Rebuilding communities following disaster: Lessons from Kobe and Los Angeles. Built Environ. 2006, 32, 354–374. Available online: https://www.jstor.org/stable/23289510 (accessed on 10 September 2022). [CrossRef]
- SEAOC Vision 2000. Performance Based Seismic Engineering of Buildings; Structural Engineers Association of California (SEAOC): Los Angeles, CA, USA, 1995. [Google Scholar]
- ATC-40; Seismic Evaluation and Retrofit of Concrete Buildings. Applied Technology Council (ATC): Los Angeles, CA, USA, 1996.
- FEMA-273; NEHRP Guidelines for the Seismic Rehabilitation of Buildings. Federal Emergency Management Agency (FEMA): Los Angeles, CA, USA, 1997.
- FEMA-350; Recommended Seismic Design Criteria for New Steel Moment-Frame Buildings. Federal Emergency Management Agency (FEMA): Los Angeles, CA, USA, 2000.
- Haukaas, T.; Der Kiureghian, A. Parameter sensitivity and importance measures in nonlinear finite element reliability analysis. J. Eng. Mech. 2005, 131, 1013–1026. [Google Scholar] [CrossRef]
- Der Kiureghian, A.; Haukaas, T.; Fujimura, K. Structural reliability software at the University of California, Berkeley. Struct. Saf. 2006, 28, 44–67. [Google Scholar] [CrossRef]
- Haukaas, T.; Der Kiureghian, A. Strategies for finding the design point in non-linear finite element reliability analysis. Probabilistic Eng. Mech. 2006, 21, 133–147. [Google Scholar] [CrossRef]
- Koo, H.; Der Kiureghian, A.; Fujimura, K. Design-point excitation for non-linear random vibrations. Probabilistic Eng. Mech. 2005, 20, 136–147. [Google Scholar] [CrossRef]
- Au, S.K.; Beck, J.L. First excursion probabilities for linear systems by very efficient importance sampling. Probabilistic Eng. Mech. 2001, 16, 193–207. [Google Scholar] [CrossRef]
- Ching, J.; Au, S.K.; Beck, J.L. Reliability estimation for dynamical systems subject to stochastic excitation using subset simulation with splitting. Comput. Methods Appl. Mech. Eng. 2005, 194, 1557–1579. [Google Scholar] [CrossRef]
- Au, S.K.; Beck, J.L. A new adaptive importance sampling scheme for reliability calculations. Struct. Saf. 1999, 21, 135–158. [Google Scholar] [CrossRef]
- Hamburger, R.O.; Foutch, D.A.; Cornell, C.A. Translating research to practice: FEMA/SAC performance-based design procedures. Earthq. Spectra 2003, 19, 255–267. [Google Scholar] [CrossRef]
- Cornell, C.A.; Jalayer, F.; Hamburger, R.O.; Foutch, D.A. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines. J. Struct. Eng. 2002, 128, 526–533. [Google Scholar] [CrossRef] [Green Version]
- Yun, S.Y.; Hamburger, R.O.; Cornell, C.A.; Foutch, D.A. Seismic performance evaluation for steel moment frames. J. Struct. Eng. 2002, 128, 534–545. [Google Scholar] [CrossRef]
- Wen, Y.K. Reliability and performance-based design. Struct. Saf. 2001, 23, 407–428. [Google Scholar] [CrossRef]
- Liao, W.C.; Goel, S.C. Performance-based seismic design of RC SMF using target drift and yield mechanism as performance criteria. Adv. Struct. Eng. 2014, 17, 529–542. [Google Scholar] [CrossRef]
- Franchin, P.; Petrini, F.; Mollaioli, F. Improved risk-targeted performance-based seismic design of reinforced concrete frame structures. Earthq. Eng. Struct. Dyn. 2018, 47, 49–67. [Google Scholar] [CrossRef]
- Harris, J.; Speicher, M. Assessment of performance-based seismic design methods in ASCE 41 for new steel buildings: Special moment frames. Earthq. Spectra 2018, 34, 977–999. [Google Scholar] [CrossRef]
- ASCE 41-13; Seismic Evaluation and Retrofit of Existing Buildings. American Society of Civil Engineers (ASCE): Reston, VA, USA, 2014.
- ASCE 7-16; Minimum Design Loads for Buildings and Other Structures. American Society of Civil Engineers (ASCE): Reston, VA, USA, 2016.
- Gaxiola-Camacho, J.R.; Azizsoltani, H.; Villegas-Mercado, F.J.; Haldar, A. A novel reliability technique for implementation of performance-based seismic design of structures. Eng. Struct. 2017, 142, 137–147. [Google Scholar] [CrossRef] [Green Version]
- Gaxiola-Camacho, J.R.; Haldar, A.; Azizsoltani, H.; Valenzuela-Beltran, F.; Reyes-Salazar, A. Performance-based seismic design of steel buildings using rigidities of connections. ASCE ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2018, 4, 04017036. [Google Scholar] [CrossRef]
- Gaxiola-Camacho, J.R.; Haldar, A.; Reyes-Salazar, A.; Valenzuela-Beltran, F.; Vazquez-Becerra, G.E.; Vazquez-Hernandez, A.O. Alternative reliability-based methodology for evaluation of structures excited by earthquakes. Earthq. Struct. 2018, 14, 361–377. [Google Scholar] [CrossRef]
- Moghaddam, H.; Hajirasouliha, I.; Gelekolai, S.M.H. Performance-based seismic design of moment resisting steel frames: Adaptive optimisation framework and optimum design load pattern. Structures 2021, 33, 1690–1704. [Google Scholar] [CrossRef]
- Monjardin-Quevedo, J.G.; Reyes-Salazar, A.; Tolentino, D.; Gaxiola-Camacho, O.D.; Vazquez-Becerra, G.E.; Gaxiola-Camacho, J.R. Seismic reliability of steel SMFs with deep columns based on PBSD philosophy. Structures 2022, 42, 1–15. [Google Scholar] [CrossRef]
- Demir, A. Investigation of the effect of real ground motion record number on seismic response of regular and vertically irregular RC frames. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; Volume 39, pp. 1074–1091. [Google Scholar] [CrossRef]
- Mazzoni, S.; McKenna, F.; Scott, M.H.; Fenves, G.L. The Open System for Earthquake Engineering Simulation (OpenSEES) User Command-Language Manual. 2006. Available online: https://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.476.1843 (accessed on 10 September 2022).
- Demir, A.; Palanci, M.; Kayhan, A.H. Probabilistic assessment for spectrally matched real ground motion records on distinct soil profiles by simulation of SDOF systems. Earthq. Struct. 2021, 21, 395–411. [Google Scholar] [CrossRef]
- Nowak, A.S.; Collins, K.R. Reliability of Structures; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Vazquez-Ontiveros, J.R.; Vazquez-Becerra, G.E.; Quintana, J.A.; Carrion, F.J.; Guzman-Acevedo, G.M.; Gaxiola-Camacho, J.R. Implementation of PPP-GNSS measurement technology in the probabilistic SHM of bridge structures. Measurement 2021, 173, 108677. [Google Scholar] [CrossRef]
- Lemaire, M. Structural Reliability; Wiley-ISTE: New York, NY, USA, 2009. [Google Scholar]






| City | Reinforced Concrete (s) | Steel (s) |
|---|---|---|
| Agua Prieta, Sonora | 1.6828 | 1.196 |
| Cd. Victoria, Tamaulipas | 1.8024 | 1.162 |
| Culiacan, Sinaloa | 1.8024 | 1.2846 |
| Mexicali, Baja California | 0.8416 | 1.1115 |
| Torreon, Coahuila | 1.8024 | 1.1929 |
| Chilpancingo, Guerrero | 0.9057 | 1.2950 |
| Guadalajara, Jalisco | 1.5675 | 1.3042 |
| Mérida, Yucatan | 1.8024 | 1.3042 |
| Oaxaca de Juarez, Oaxaca | 1.2745 | 1.2772 |
| Villahermosa, Tabasco | 1.6136 | 1.3042 |
| City | Seismic Zone | Location on Map |
|---|---|---|
| Agua Prieta, Sonora | C | 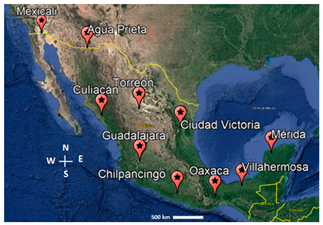 |
| Ciudad Victoria, Tamaulipas | A | |
| Culiacan, Sinaloa | B | |
| Mexicali, Baja California | D | |
| Torreon, Coahuila | A | |
| Chilpancingo, Guerrero | D | |
| Guadalajara, Jalisco | C | |
| Merida, Yucatan | A | |
| Oaxaca de Juarez, Oaxaca | D | |
| Villahermosa, Tabasco | B |
| Selected Ground Motions | ||
|---|---|---|
| Probability of Exceedance | Return Period (Years) | Performance Level |
| 50% in 50 years | 72 | IO |
| 10% in 50 years | 475 | LS |
| 2% in 50 years | 2475 | CP |
| Ground Motion | Performance Level | Station Name | Magnitude | Scale Factor |
|---|---|---|---|---|
| Earthquake 1 | IO | Cerro de Piedra | 4.90 | 0.88 |
| Earthquake 2 | IO | La Venta | 6.80 | 0.88 |
| Earthquake 3 | IO | Mesa Vibradora | 6.30 | 0.87 |
| Earthquake 4 | IO | Huamuxtitlan | 6.4 | 1.0 |
| Earthquake 5 | IO | Texcoco Chimalhuacan | 6.30 | 1.0 |
| Earthquake 6 | IO | Sismex Ciudad Universitaria | 6.40 | 0.74 |
| Earthquake 7 | IO | Ciudad Serdan | 6.5 | 1.5 |
| Earthquake 8 | IO | Chila de las Flores | 6.5 | 1.1 |
| Earthquake 9 | IO | Las Mesas | 6.80 | 0.88 |
| Earthquake 10 | IO | Sismex Hospital ABC | 7.00 | 1.1 |
| Earthquake 11 | IO | Mezontepec | 6.5 | 1.4 |
| Earthquake 12 | LS | Papanoa | 6.80 | 1.3 |
| Earthquake 13 | LS | Cerro de Piedra | 4.70 | 0.84 |
| Earthquake 14 | LS | El Ocotito | 6.80 | 1.1 |
| Earthquake 15 | LS | Las Canteras | 6.5 | 1.1 |
| Earthquake 16 | LS | Atoyac | 6.80 | 1.4 |
| Earthquake 17 | LS | Apatzingan | 6.10 | 1.9 |
| Earthquake 18 | LS | Caleta de Campos | 6.20 | 1.6 |
| Earthquake 19 | LS | San Marcos | 6.20 | 1.1 |
| Earthquake 20 | LS | Las Vigas | 6.30 | 1.6 |
| Earthquake 21 | LS | San Luis de la Loma 2 | 6.1 | 0.93 |
| Earthquake 22 | LS | San Martin los Canseco | 6.5 | 1.3 |
| Earthquake 23 | CP | Las Negras | 6.5 | 0.94 |
| Earthquake 24 | CP | La Union | 6.80 | 0.96 |
| Earthquake 25 | CP | Rio Grande | 6.5 | 1.5 |
| Earthquake 26 | CP | Caleta de Campos | 6.5 | 0.85 |
| Earthquake 27 | CP | Aeropuerto Zihuatanejo | 6.30 | 1.0 |
| Earthquake 28 | CP | Petatlan II | 7.2 | 2.1 |
| Earthquake 29 | CP | Sicartsa Aceracion | 7.00 | 1.4 |
| Earthquake 30 | CP | San Marcos | 6.30 | 1.2 |
| Earthquake 31 | CP | Caleta de Campos | 6.80 | 0.99 |
| Earthquake 32 | CP | Villita Margen Derecha | 6.80 | 1.4 |
| Earthquake 33 | CP | Chilpancingo | 6.30 | 0.72 |
| Return Period (Years) | Performance Level | Permissible Inter-Story Drift |
|---|---|---|
| 72 | IO | ±0.007 |
| 475 | LS | ±0.025 |
| 2475 | CP | ±0.050 |
| Location | Steel Buildings | Reinforced Concrete Buildings | ||||
|---|---|---|---|---|---|---|
| IO | LS | CP | IO | LS | CP | |
| Agua Prieta, Sonora | GEV | GEV | GEV | GEV | GEV | GEV |
| Ciudad Victoria, Tamaulipas | GEV | GEV | GEV | GEV | GEV | GEV |
| Villahermosa, Tabasco | Stable | GEV | GEV | GEV | GEV | GEV |
| Chilpancingo, Guerrero | Stable | GEV | GEV | GEV | GEV | GEV |
| Culiacan, Sinaloa | GEV | GEV | GEV | GEV | GEV | GEV |
| Guadalajara, Jalisco | GEV | GEV | GEV | GEV | GEV | Stable |
| Merida, Yucatan | tLS | GEV | GEV | GEV | GEV | Stable |
| Mexicali, Baja California | GEV | GEV | GEV | GEV | Stable | GEV |
| Oaxaca de Juarez, Oaxaca | Stable | GEV | GEV | GEV | Stable | GEV |
| Torreon, Coahuila | tLS | GEV | GEV | GEV | GEV | GEV |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monjardin-Quevedo, J.G.; Valenzuela-Beltran, F.; Reyes-Salazar, A.; Leal-Graciano, J.M.; Torres-Carrillo, X.G.; Gaxiola-Camacho, J.R. Probabilistic Assessment of Buildings Subjected to Multi-Level Earthquake Loading Based on the PBSD Concept. Buildings 2022, 12, 1942. https://doi.org/10.3390/buildings12111942
Monjardin-Quevedo JG, Valenzuela-Beltran F, Reyes-Salazar A, Leal-Graciano JM, Torres-Carrillo XG, Gaxiola-Camacho JR. Probabilistic Assessment of Buildings Subjected to Multi-Level Earthquake Loading Based on the PBSD Concept. Buildings. 2022; 12(11):1942. https://doi.org/10.3390/buildings12111942
Chicago/Turabian StyleMonjardin-Quevedo, J. Guadalupe, Federico Valenzuela-Beltran, Alfredo Reyes-Salazar, J. Martin Leal-Graciano, Xochitl G. Torres-Carrillo, and J. Ramon Gaxiola-Camacho. 2022. "Probabilistic Assessment of Buildings Subjected to Multi-Level Earthquake Loading Based on the PBSD Concept" Buildings 12, no. 11: 1942. https://doi.org/10.3390/buildings12111942
APA StyleMonjardin-Quevedo, J. G., Valenzuela-Beltran, F., Reyes-Salazar, A., Leal-Graciano, J. M., Torres-Carrillo, X. G., & Gaxiola-Camacho, J. R. (2022). Probabilistic Assessment of Buildings Subjected to Multi-Level Earthquake Loading Based on the PBSD Concept. Buildings, 12(11), 1942. https://doi.org/10.3390/buildings12111942







