Application of the Coupled Markov Chain in Soil Liquefaction Potential Evaluation
Abstract
1. Introduction
2. Materials and Methods
2.1. Coupled Markov Chain (CMC)
2.1.1. Transition Probability Matrix
2.1.2. Markov Chain
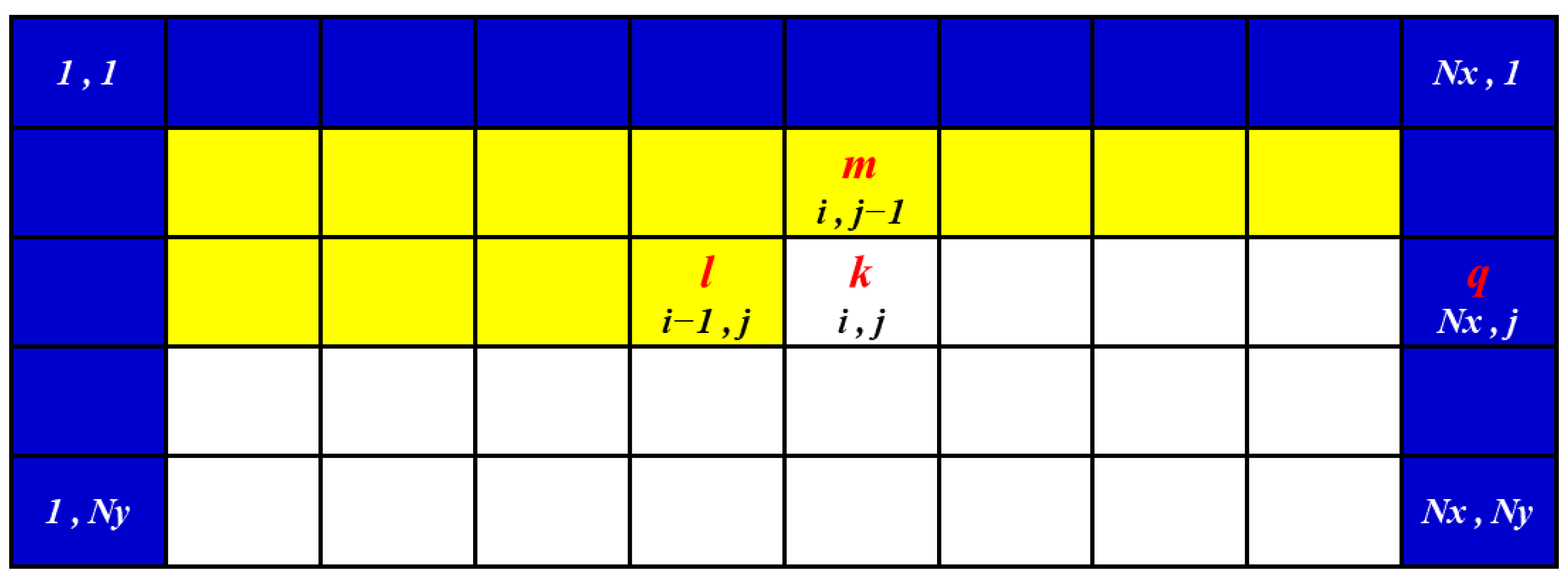
2.1.3. Two-Dimensional Markov Chain
2.1.4. Estimation of the Transition-Probability Matrix
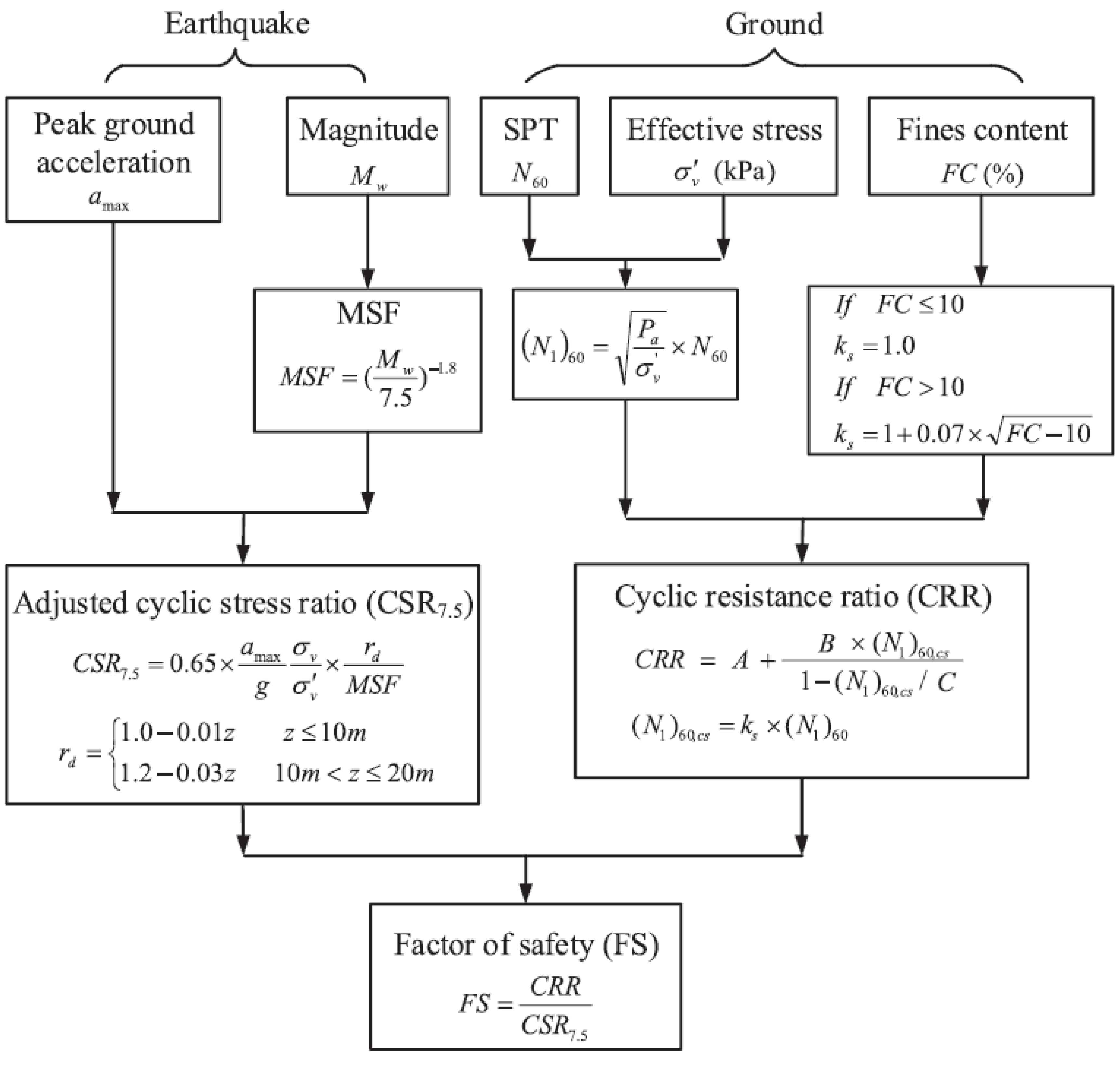
2.2. Liquefaction-Potential Evaluation
2.2.1. Hyperbolic Function (HBF) [1]
2.2.2. JRA Method (2017) [48,49]
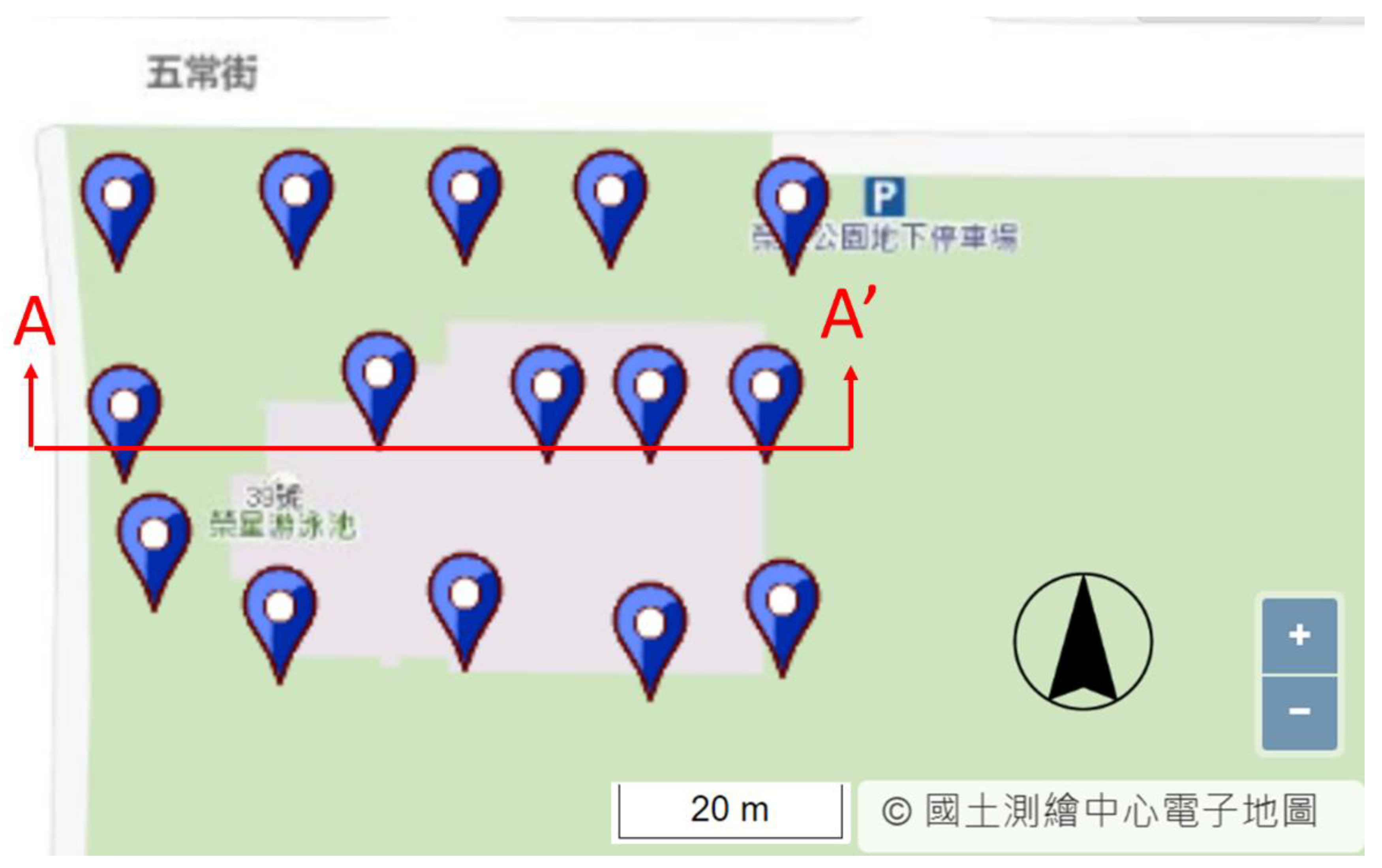
2.3. Drilling Data
3. Results and Discussion
3.1. Testing the Accuracy of the CMC and Selecting the Suitable Grid Size
| Borehole Scheme | Hole 6 | Hole 7 | Hole 8 | Hole 9 | Hole 10 |
|---|---|---|---|---|---|
| Scheme 1 | √ | √ | √ | √ | |
| Scheme 2 | √ | √ | √ | √ | |
| Scheme 3 | √ | √ | √ | √ |
3.2. Comparison and Analysis of the Soil Liquefaction Potential Evaluations under the Two Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hwang, J.-H.; Khoshnevisan, S.; Juang, C.H.; Lu, C.-C. Soil liquefaction potential evaluation–An update of the HBF method focusing on research and practice in Taiwan. Eng. Geol. 2021, 280, 105926. [Google Scholar] [CrossRef]
- Baise, L.G.; Lenz, J.A. Guidelines for Regional Liquefaction Hazard Mapping; Tufts University, Department of Civil and Environmental Engineering: Medford, MA, USA, 2006. [Google Scholar]
- Chung, J.-W.; Rogers, J.D. Simplified method for spatial evaluation of liquefaction potential in the St. Louis area. J. Geotech. Geoenviron. Eng. 2011, 137, 505–515. [Google Scholar] [CrossRef]
- Pokhrel, R.M.; Kuwano, J.; Tachibana, S. Geostatistical analysis for spatial evaluation of liquefaction potential in Saitama City. Lowland Technol. Int. 2012, 14, 45–51. [Google Scholar]
- Pokhrel, R.M.; Kuwano, J.; Tachibana, S. A kriging method of interpolation used to map liquefaction potential over alluvial ground. Eng. Geol. 2013, 152, 26–37. [Google Scholar] [CrossRef]
- Thompson, E.; Wald, D.J.; Worden, C. A VS30 Map for California with Geologic and Topographic ConstraintsA VS30 Map for California with Geologic and Topographic Constraints. Bull. Seismol. Soc. Am. 2014, 104, 2313–2321. [Google Scholar] [CrossRef]
- Thompson, E.M.; Baise, L.G.; Kayen, R.E.; Tanaka, Y.; Tanaka, H. A geostatistical approach to mapping site response spectral amplifications. Eng. Geol. 2010, 114, 330–342. [Google Scholar] [CrossRef]
- Wang, L.; Wu, C.; Gu, X.; Liu, H.; Mei, G.; Zhang, W. Probabilistic stability analysis of earth dam slope under transient seepage using multivariate adaptive regression splines. Bull. Eng. Geol. Environ. 2020, 79, 2763–2775. [Google Scholar] [CrossRef]
- Zhang, D.-M.; Zhang, J.-Z.; Huang, H.-W.; Qi, C.-C.; Chang, C.-Y. Machine learning-based prediction of soil compression modulus with application of 1D settlement. J. Zhejiang Univ. Sci. A 2020, 21, 430–444. [Google Scholar] [CrossRef]
- Gong, W.; Tang, H.; Wang, H.; Wang, X.; Juang, C.H. Probabilistic analysis and design of stabilizing piles in slope considering stratigraphic uncertainty. Eng. Geol. 2019, 259, 105162. [Google Scholar] [CrossRef]
- Wang, X.; Li, Z.; Wang, H.; Rong, Q.; Liang, R.Y. Probabilistic analysis of shield-driven tunnel in multiple strata considering stratigraphic uncertainty. Struct. Saf. 2016, 62, 88–100. [Google Scholar] [CrossRef]
- Elkateb, T.; Chalaturnyk, R.; Robertson, P.K. An overview of soil heterogeneity: Quantification and implications on geotechnical field problems. Can. Geotech. J. 2003, 40, 1–15. [Google Scholar] [CrossRef]
- Kawa, M.; Puła, W. 3D bearing capacity probabilistic analyses of footings on spatially variable c–φ soil. Acta Geotech. 2020, 15, 1453–1466. [Google Scholar] [CrossRef]
- Lloret-Cabot, M.; Fenton, G.A.; Hicks, M.A. On the estimation of scale of fluctuation in geostatistics. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2014, 8, 129–140. [Google Scholar] [CrossRef]
- Elfeki, A.; Dekking, M. A Markov chain model for subsurface characterization: Theory and applications. Math. Geol. 2001, 33, 569–589. [Google Scholar] [CrossRef]
- Qi, X.-H.; Li, D.-Q.; Phoon, K.-K.; Cao, Z.-J.; Tang, X.-S. Simulation of geologic uncertainty using coupled Markov chain. Eng. Geol. 2016, 207, 129–140. [Google Scholar] [CrossRef]
- Chen, F.; Wang, L.; Zhang, W. Reliability assessment on stability of tunnelling perpendicularly beneath an existing tunnel considering spatial variabilities of rock mass properties. Tunn. Undergr. Space Technol. 2019, 88, 276–289. [Google Scholar] [CrossRef]
- Dalong, J.; Zhichao, S.; Dajun, Y. Effect of spatial variability on disc cutters failure during TBM tunneling in hard rock. Rock Mech. Rock Eng. 2020, 53, 4609–4621. [Google Scholar] [CrossRef]
- Gong, W.; Juang, C.H.; Martin II, J.R.; Tang, H.; Wang, Q.; Huang, H. Probabilistic analysis of tunnel longitudinal performance based upon conditional random field simulation of soil properties. Tunn. Undergr. Space Technol. 2018, 73, 1–14. [Google Scholar] [CrossRef]
- Pan, Q.; Dias, D. Probabilistic evaluation of tunnel face stability in spatially random soils using sparse polynomial chaos expansion with global sensitivity analysis. Acta Geotech. 2017, 12, 1415–1429. [Google Scholar] [CrossRef]
- Pan, Y.; Yao, K.; Phoon, K.K.; Lee, F.H. Analysis of tunnelling through spatially-variable improved surrounding–A simplified approach. Tunn. Undergr. Space Technol. 2019, 93, 103102. [Google Scholar] [CrossRef]
- Zhang, J.-Z.; Huang, H.-W.; Zhang, D.-M.; Zhou, M.-L.; Tang, C.; Liu, D.-J. Effect of ground surface surcharge on deformational performance of tunnel in spatially variable soil. Comp. Geotech. 2021, 136, 104229. [Google Scholar] [CrossRef]
- Zhang, W.; Han, L.; Gu, X.; Wang, L.; Chen, F.; Liu, H. Tunneling and deep excavations in spatially variable soil and rock masses: A short review. Undergr. Space 2020, 7, 380–407. [Google Scholar] [CrossRef]
- Hu, Q. Risk Analysis and Its Application for Tunnel Works Based on Research of Stratum and Soil Spatial Variability. Ph.D. Thesis, Tongji University, Shanghai, China, 2006. [Google Scholar]
- Li, Z.; Wang, X.; Wang, H.; Liang, R.Y. Quantifying stratigraphic uncertainties by stochastic simulation techniques based on Markov random field. Eng. Geol. 2016, 201, 106–122. [Google Scholar] [CrossRef]
- De Marsily, G.; Delay, F.; Gonçalvès, J.; Renard, P.; Teles, V.; Violette, S. Dealing with spatial heterogeneity. Hydrogeol. J. 2005, 13, 161–183. [Google Scholar] [CrossRef]
- Chiles, J.-P.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty; John Wiley & Sons: New York, NY, USA, 2009; Volume 497. [Google Scholar]
- Cross, G.R.; Jain, A.K. Markov random field texture models. IEEE Trans. Pattern Anal. Mach. Intell. 1983, 1, 25–39. [Google Scholar] [CrossRef]
- Wang, X. Uncertainty quantification and reduction in the characterization of subsurface stratigraphy using limited geotechnical investigation data. Undergr. Space 2020, 5, 125–143. [Google Scholar] [CrossRef]
- Carle, S.F.; Labolle, E.M.; Weissmann, G.S.; Van Brocklin, D.; Fogg, G.E. Conditional simulation of hydrofacies architecture: A transition probability/Markov approach. Hydrogeol. Models Sediment. Aquifers Concepts Hydrogeol. Environ. Geol. 1998, 1, 147–170. [Google Scholar]
- Wang, H.; Wellmann, J.F.; Li, Z.; Wang, X.; Liang, R.Y. A segmentation approach for stochastic geological modeling using hidden Markov random fields. Math. Geosci. 2017, 49, 145–177. [Google Scholar] [CrossRef]
- Wang, X.; Wang, H.; Liang, R.Y.; Zhu, H.; Di, H. A hidden Markov random field model based approach for probabilistic site characterization using multiple cone penetration test data. Struct. Saf. 2018, 70, 128–138. [Google Scholar] [CrossRef]
- Wang, X.; Wang, H.; Liang, R.Y. A method for slope stability analysis considering subsurface stratigraphic uncertainty. Landslides 2018, 15, 925–936. [Google Scholar] [CrossRef]
- Cao, W.; Zhou, A.; Shen, S.-L. An analytical method for estimating horizontal transition probability matrix of coupled Markov chain for simulating geological uncertainty. Comp. Geotech. 2021, 129, 103871. [Google Scholar] [CrossRef]
- Li, J.; Cai, Y.; Li, X.; Zhang, L. Simulating realistic geological stratigraphy using direction-dependent coupled Markov chain model. Comp. Geotech. 2019, 115, 103147. [Google Scholar] [CrossRef]
- Deng, Z.-P.; Jiang, S.-H.; Niu, J.-T.; Pan, M.; Liu, L.-L. Stratigraphic uncertainty characterization using generalized coupled Markov chain. Bull. Eng. Geol. Environ. 2020, 79, 5061–5078. [Google Scholar] [CrossRef]
- Zhang, J.-Z.; Liu, Z.-Q.; Zhang, D.-M.; Huang, H.-W.; Phoon, K.-K.; Xue, Y.-D. Improved coupled Markov chain method for simulating geological uncertainty. Eng. Geol. 2022, 298, 106539. [Google Scholar] [CrossRef]
- Deng, Z.-P.; Li, D.-Q.; Qi, X.-H.; Cao, Z.-J.; Phoon, K.-K. Reliability evaluation of slope considering geological uncertainty and inherent variability of soil parameters. Comp. Geotech. 2017, 92, 121–131. [Google Scholar] [CrossRef]
- Zhang, J.-Z.; Huang, H.-W.; Zhang, D.-M.; Phoon, K.K.; Liu, Z.-Q.; Tang, C. Quantitative evaluation of geological uncertainty and its influence on tunnel structural performance using improved coupled Markov chain. Acta Geotech. 2021, 16, 3709–3724. [Google Scholar] [CrossRef]
- Elfeki, A.M. Reducing concentration uncertainty using the coupled Markov chain approach. J. Hydrol. 2006, 317, 1–16. [Google Scholar] [CrossRef]
- Shi, C.; Wang, Y. Nonparametric and data-driven interpolation of subsurface soil stratigraphy from limited data using multiple point statistics. Can. Geotech. J. 2021, 58, 261–280. [Google Scholar] [CrossRef]
- Gong, W.; Zhao, C.; Juang, C.H.; Zhang, Y.; Tang, H.; Lu, Y. Coupled characterization of stratigraphic and geo-properties uncertainties–A conditional random field approach. Eng. Geol. 2021, 294, 106348. [Google Scholar] [CrossRef]
- Zhao, C.; Gong, W.; Li, T.; Juang, C.H.; Tang, H.; Wang, H. Probabilistic characterization of subsurface stratigraphic configuration with modified random field approach. Eng. Geol. 2021, 288, 106138. [Google Scholar] [CrossRef]
- Elfeki, A.; Dekking, F. Modelling subsurface heterogeneity by coupled Markov chains: Directional dependency, Walther’s law and entropy. Geotech. Geol. Eng. 2005, 23, 721–756. [Google Scholar] [CrossRef]
- Li, W.; Zhang, C.; Burt, J.E.; Zhu, A.-X.; Feyen, J. Two-dimensional Markov chain simulation of soil type spatial distribution. Soil Sci. Soc. Am. J. 2004, 68, 1479–1490. [Google Scholar] [CrossRef]
- Youd, T.L.; Idriss, I.M. Liquefaction resistance of soils: Summary report from the 1996 NCEER and 1998 NCEER/NSF workshops on evaluation of liquefaction resistance of soils. J. Geotech. Geoenviron. Eng. 2001, 127, 297–313. [Google Scholar] [CrossRef]
- Tokimatsu, K.; Yoshimi, Y. Empirical correlation of soil liquefaction based on SPT N-value and fines content. Soils Found. 1983, 23, 56–74. [Google Scholar] [CrossRef]
- Japan Road Association. Design code and explanations for roadway bridges. In Part V–Seismic Resistance Design, Japan; Japan Road Association: Tokyo, Japan, 1996. [Google Scholar]
- Institute, P.W.R. Evaluation Method for Liquefaction Strength of Fine-Grained Sand; Public Works Research Institute: Ibaraki, Japan, 2017. [Google Scholar]
- Cetin, K.; Seed, R.; Der Kiureghian, A.; Tokimatsu, K.; Harder, L.; Kayen, R. SPT-Based probabilistic and deterministic assessment of seismic soil liquefaction initiation hazard. In Pacific Earthquake Engineering Research Report No. PEER-2000/05; Pacific Gas and Electric Company (PG&E): San Francisco, CA, USA, 2000. [Google Scholar]
- Iwasaki, T.; Arakawa, T.; Tokida, K.-I. Simplified procedures for assessing soil liquefaction during earthquakes. Int. J. Soil Dynam. Earthq. Eng. 1984, 3, 49–58. [Google Scholar] [CrossRef]
- Chien, W.-Y.; Lu, Y.-C.; Juang, C.H.; Dong, J.-J.; Hung, W.-Y. Effect of stratigraphic model uncertainty at a given site on its liquefaction potential index: Comparing two random field approaches. Eng. Geol. 2022, 309, 106838. [Google Scholar] [CrossRef]
- Gholampour, A. Site-scale liquefaction potential analysis using a sectional random field model. Eng. Geol. 2022, 297, 106485. [Google Scholar] [CrossRef]
- Guan, Z.; Wang, Y. CPT-based probabilistic liquefaction assessment considering soil spatial variability, interpolation uncertainty and model uncertainty. Comp. Geotech. 2022, 141, 104504. [Google Scholar] [CrossRef]
- Wang, Y.; Shu, S.; Wu, Y. Reliability analysis of soil liquefaction considering spatial variability of soil property. J. Earthq. Tsunami 2022, 16, 2250002. [Google Scholar] [CrossRef]
- Krumbein, W. Statistical models in sedimentology 1. Sedimentology 1968, 10, 7–23. [Google Scholar] [CrossRef]
- Doveton, J.H. Theory and Applications of Vertical Variability Measures from Markov Chain Analysis; AAPG: Tulsa, OK, USA, 1994. [Google Scholar]
- Qi, X.-H.; Li, D.-Q.; Phoon, K.-K. Estimation of horizontal transition probability matrix for coupled Markov chain. Jpn. Geotech. Soc. Special Publ. 2016, 2, 2423–2428. [Google Scholar] [CrossRef]
- Bolton Seed, H.; Tokimatsu, K.; Harder, L.; Chung, R.M. Influence of SPT procedures in soil liquefaction resistance evaluations. J. Geotech. Eng. 1985, 111, 1425–1445. [Google Scholar] [CrossRef]
- Iwasaki, T.; Tokida, K.; Tatsuoka, F.; Watanabe, S.; Yasuda, S.; Sato, H. Microzonation for soil liquefaction potential using simplified methods. In Proceedings of the 3rd International Conference on Microzonation, Seattle, WA, USA, 28 June–1 July 1982; pp. 1310–1330. [Google Scholar]
- Tatsuoka, F.; Iwasaki, T.; Tokida, K.-I.; Yasuda, S.; Hirose, M.; Imai, T.; Kon-No, M. Standard penetration tests and soil liquefaction potential evaluation. Soils Found. 1980, 20, 95–111. [Google Scholar] [CrossRef]
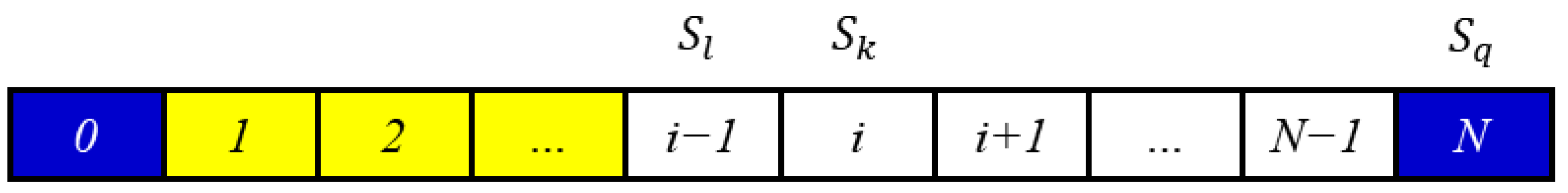

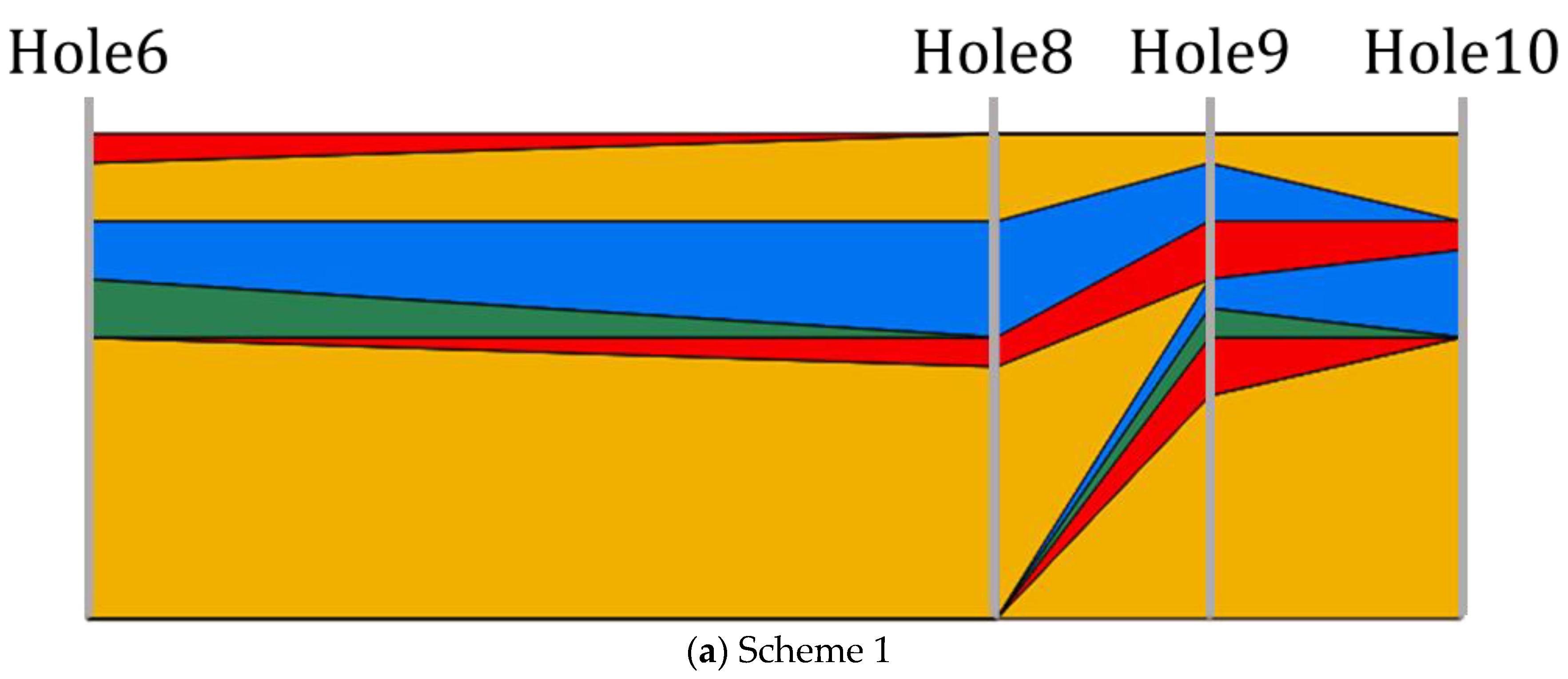
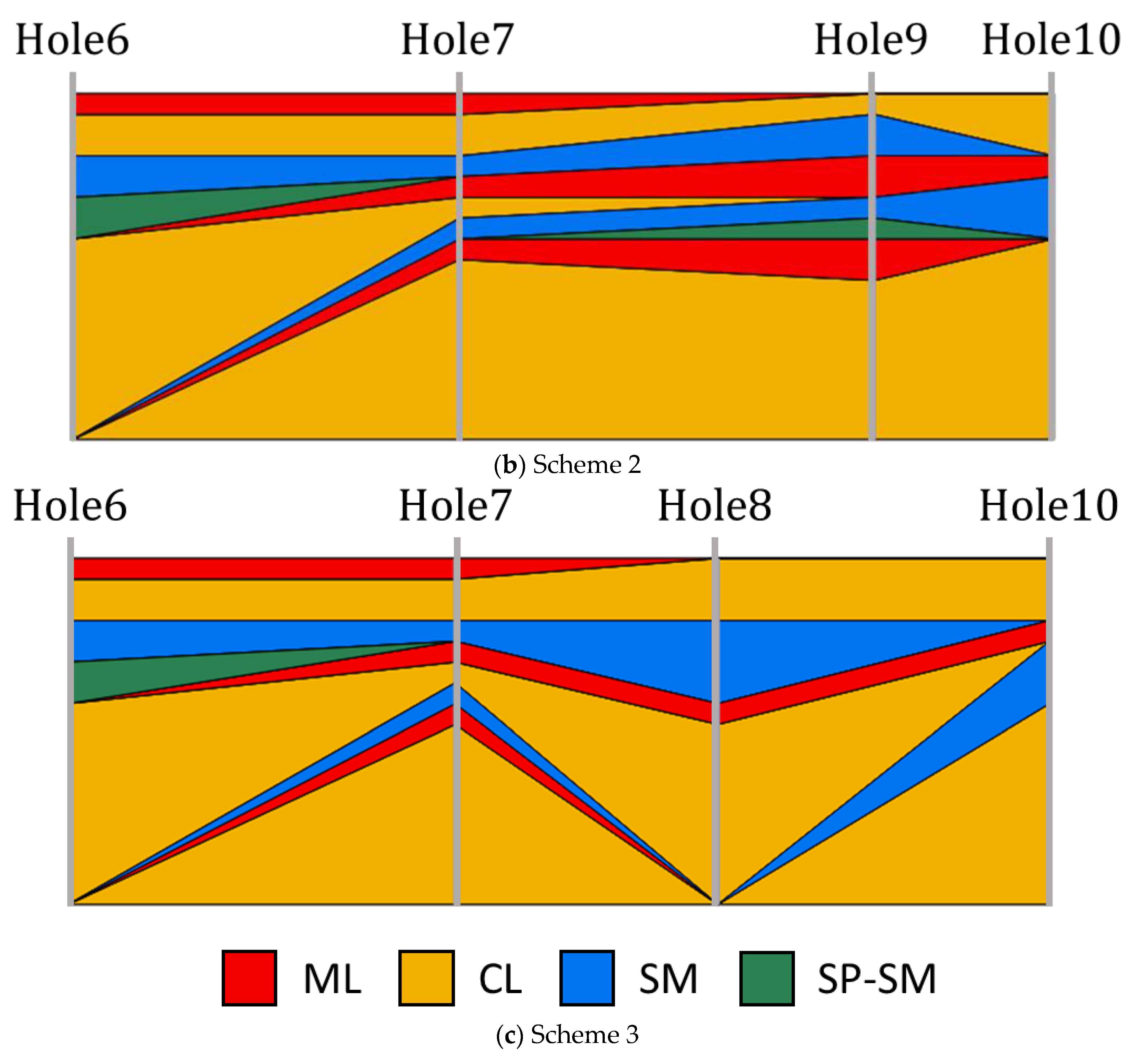
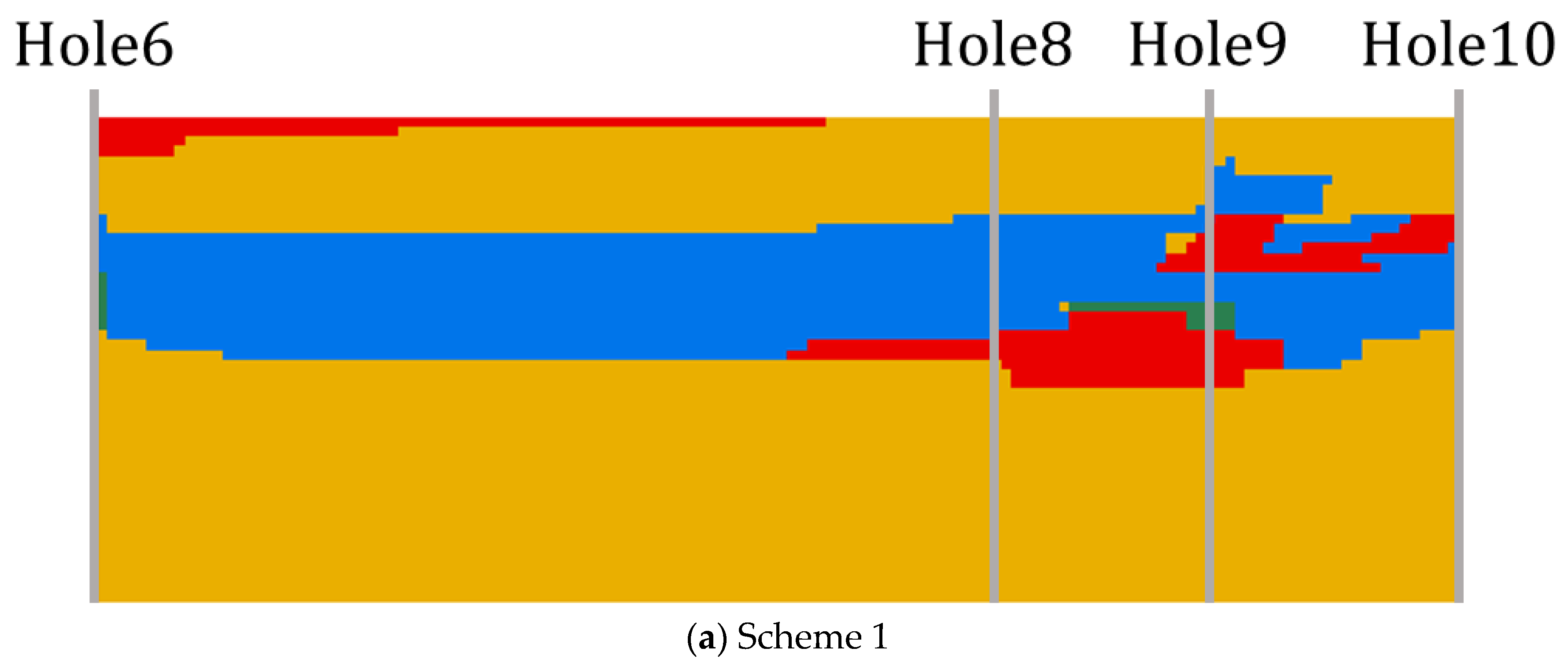






| USCS | Mean | COV | N Mean | N COV | FC Mean (%) | FC COV |
|---|---|---|---|---|---|---|
| ML | 18.64 | 0.04 | 7 | 0.67 | 70 | 0.21 |
| CL | 18.15 | 0.04 | 6 | 0.43 | 97 | 0.05 |
| SM | 19.03 | 0.05 | 9 | 0.40 | 45 | 0.45 |
| SP-SM | 18.25 | 0.06 | 10 | 0.21 | 10 | 0.74 |
| (a) Scheme 1 | ||||
| Soil Type | ML | CL | SM | SP-SM |
| ML | 0.7727 | 0.1364 | 0.0909 | 0.0000 |
| CL | 0.0077 | 0.969 | 0.0233 | 0.0000 |
| SM | 0.0555 | 0.0278 | 0.8611 | 0.0556 |
| SP-SM | 0.1111 | 0.1111 | 0.0000 | 0.7778 |
| (b) Scheme 2 | ||||
| Soil Type | ML | CL | SM | SP-SM |
| ML | 0.7586 | 0.1724 | 0.0690 | 0.0000 |
| CL | 0.0078 | 0.9609 | 0.0313 | 0.0000 |
| SM | 0.1000 | 0.0333 | 0.8000 | 0.0667 |
| SP-SM | 0.1111 | 0.1111 | 0.0000 | 0.7778 |
| (c) Scheme 3 | ||||
| Soil Type | ML | CL | SM | SP-SM |
| ML | 0.7000 | 0.2500 | 0.0500 | 0.0000 |
| CL | 0.0073 | 0.9635 | 0.0292 | 0.0000 |
| SM | 0.0909 | 0.0303 | 0.8485 | 0.0303 |
| SP-SM | 0.0000 | 0.1667 | 0.0000 | 0.8333 |
| Borehole Scheme | Simulation Sequence | |||
|---|---|---|---|---|
| Scheme 1 | 4.1 | 6.6 | 6.6 | From right to left |
| Scheme 2 | 9.2 | 10.1 | 10.1 | From right to left |
| Scheme 3 | 22.9 | 15.1 | 22.9 | From left to right |
| (a) Scheme 1 | ||||
| Soil Type | ML | CL | SM | SP-SM |
| ML | 0.9573 | 0.0256 | 0.0171 | 0.0000 |
| CL | 0.0012 | 0.9952 | 0.0036 | 0.0000 |
| SM | 0.0095 | 0.0048 | 0.9762 | 0.0095 |
| SP-SM | 0.0207 | 0.0207 | 0.0000 | 0.9586 |
| (b) Scheme 2 | ||||
| Soil Type | ML | CL | SM | SP-SM |
| ML | 0.9695 | 0.0218 | 0.0087 | 0.0000 |
| CL | 0.0008 | 0.9960 | 0.0032 | 0.0000 |
| SM | 0.0121 | 0.0040 | 0.9758 | 0.0081 |
| SP-SM | 0.0138 | 0.0138 | 0.0000 | 0.9724 |
| (c) Scheme 3 | ||||
| Soil Type | ML | CL | SM | SP-SM |
| ML | 0.9816 | 0.0153 | 0.0031 | 0.0000 |
| CL | 0.0003 | 0.9984 | 0.0013 | 0.0000 |
| SM | 0.0046 | 0.0015 | 0.9924 | 0.0015 |
| SP-SM | 0.0000 | 0.0087 | 0.0000 | 0.9913 |
| Borehole Scheme | Accuracy (%) | ||||
|---|---|---|---|---|---|
| Hole No. | |||||
| 6 | 7 | 8 | 9 | 10 | |
| Scheme 1 Kriging | - | 55.3 | - | - | - |
| Scheme 1 CMC | - | 71.6 | - | - | - |
| Scheme 2 Kriging | - | - | 52.8 | - | - |
| Scheme 2 CMC | - | - | 76.3 | - | - |
| Scheme 3 Kriging | - | - | - | 44.3 | - |
| Scheme 3 CMC | - | - | - | 70.0 | - |
| Scheme | Grid Size (m) | Simulation Sequence | Accuracy (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Hole No. | ||||||||||
| 6 | 7 | 8 | 9 | 10 | ||||||
| 1 | 0.5 | 4.1 | 6.6 | 6.6 | From right to left | - | 71.6 | - | - | - |
| 1.0 | 2.0 | 3.2 | 3.2 | From right to left | - | 71.4 | - | - | - | |
| 2.0 | 1.0 | 1.6 | 1.6 | From right to left | - | 71.6 | - | - | - | |
| 2.5 | 1.0 | 1.3 | 1.3 | From right to left | - | 69.5 | - | - | - | |
| 2 | 0.5 | 9.2 | 10.1 | 10.1 | From right to left | - | - | 76.3 | - | - |
| 1.0 | 4.5 | 4.9 | 4.9 | From right to left | - | - | 75.8 | - | - | |
| 2.0 | 2.1 | 2.4 | 2.4 | From right to left | - | - | 75.2 | - | - | |
| 2.5 | 1.7 | 1.9 | 1.9 | From right to left | - | - | 73.2 | - | - | |
| 3 | 0.5 | 22.9 | 15.1 | 22.9 | From left to right | - | - | - | 70.0 | - |
| 1.0 | 11.4 | 7.5 | 11.4 | From left to right | - | - | - | 69.9 | - | |
| 2.0 | 5.6 | 3.7 | 5.6 | From left to right | - | - | - | 69.5 | - | |
| 2.5 | 4.4 | 2.9 | 4.4 | From left to right | - | - | - | 68.0 | - | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, H.-C.; Li, A.-J.; Lu, C.-W.; Chen, C.-N. Application of the Coupled Markov Chain in Soil Liquefaction Potential Evaluation. Buildings 2022, 12, 2095. https://doi.org/10.3390/buildings12122095
Wen H-C, Li A-J, Lu C-W, Chen C-N. Application of the Coupled Markov Chain in Soil Liquefaction Potential Evaluation. Buildings. 2022; 12(12):2095. https://doi.org/10.3390/buildings12122095
Chicago/Turabian StyleWen, Hsiu-Chen, An-Jui Li, Chih-Wei Lu, and Chee-Nan Chen. 2022. "Application of the Coupled Markov Chain in Soil Liquefaction Potential Evaluation" Buildings 12, no. 12: 2095. https://doi.org/10.3390/buildings12122095
APA StyleWen, H.-C., Li, A.-J., Lu, C.-W., & Chen, C.-N. (2022). Application of the Coupled Markov Chain in Soil Liquefaction Potential Evaluation. Buildings, 12(12), 2095. https://doi.org/10.3390/buildings12122095







