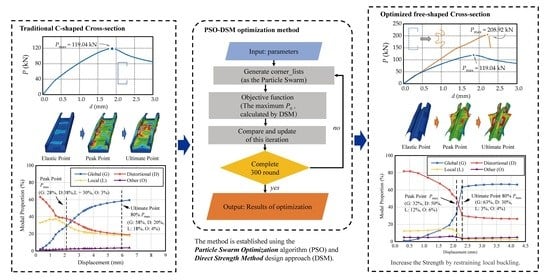
Free-Form Shape Optimization of Advanced High-Strength Steel Members
Abstract
1. Introduction
2. Modal analysis and Member Selection
2.1. Elastic Buckling Analysis and Nonlinear Shell FE Models
- -
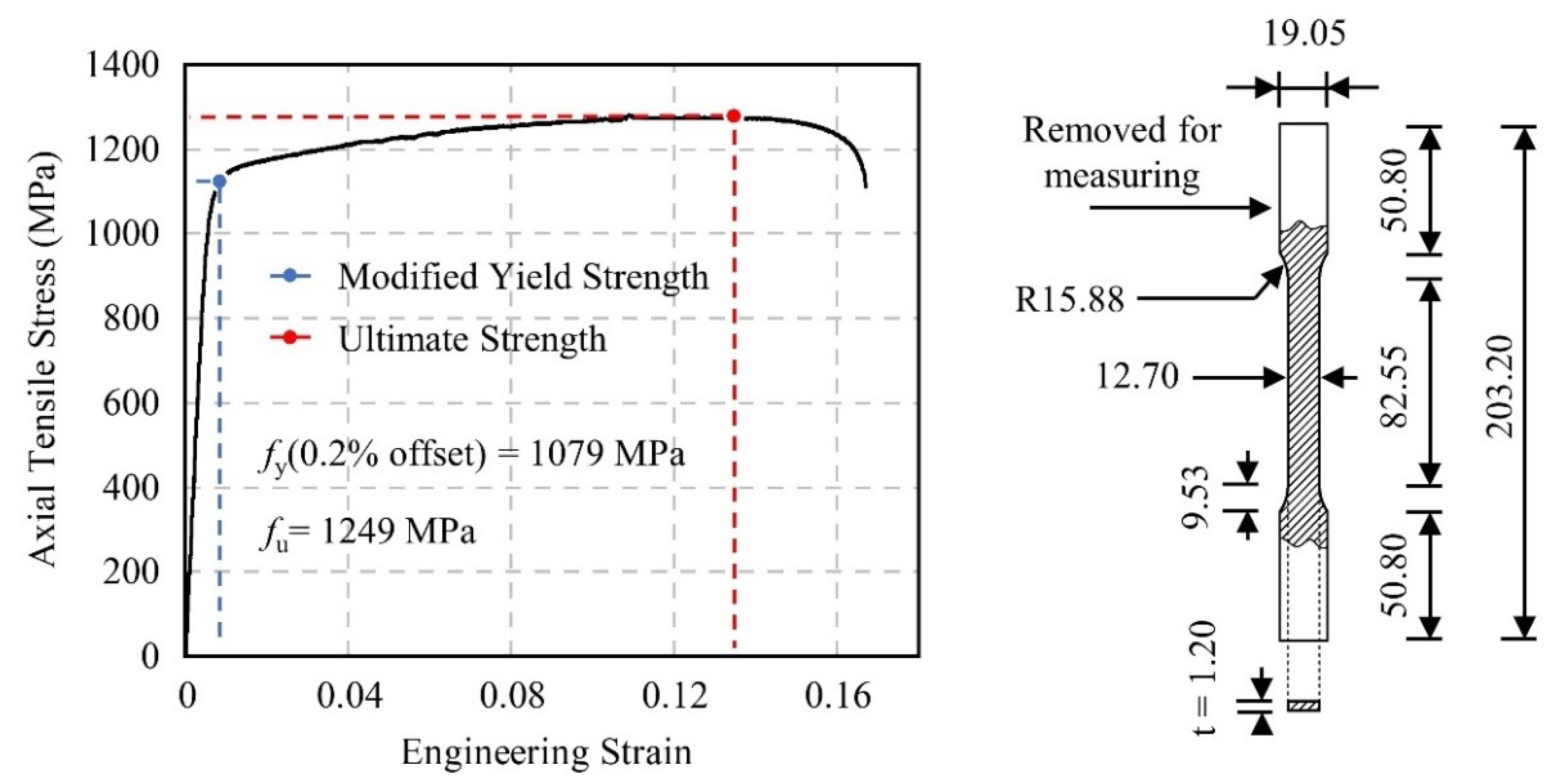
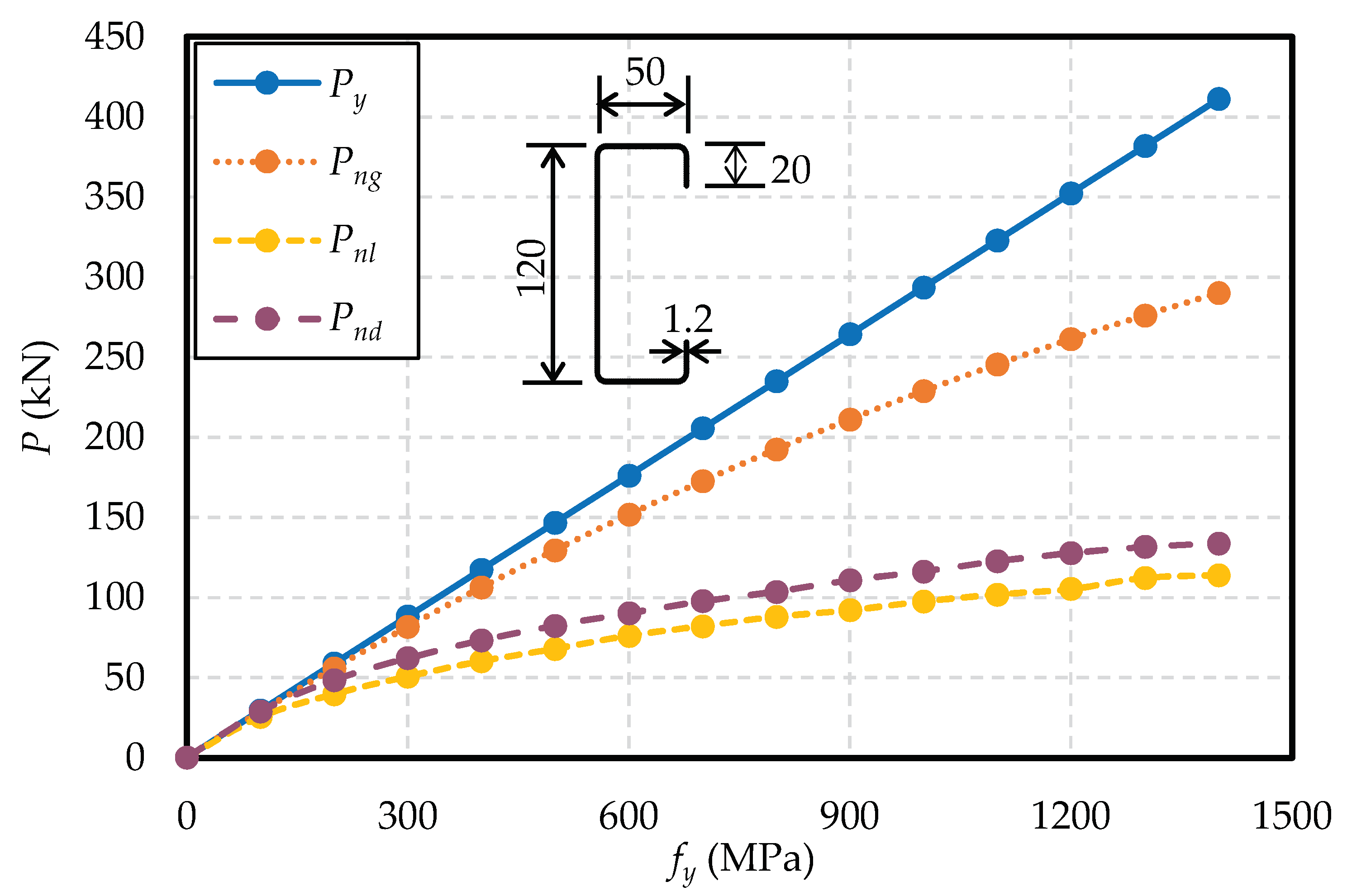
- Material model: based on the coupon test as shown in Figure 1 of the Q&P1180 AHSS material. The yield strength fy is 1079 MPa, and the Young’s modulus E is 203 GPa.
- -
- Element type: S4R, which is a general-purpose type of shell element that has four nodes (linear formulation) with reduced integration.
- -
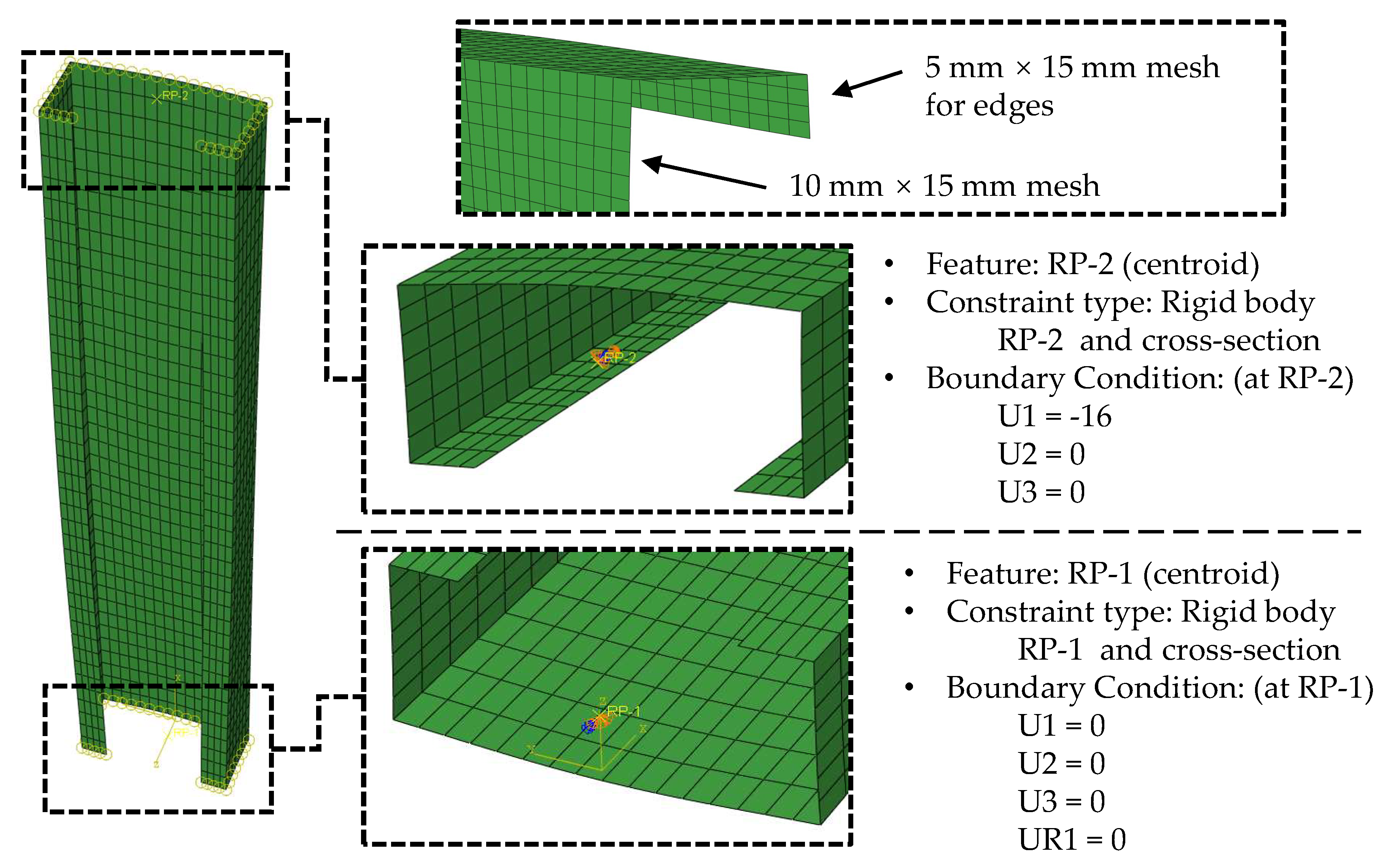
- Mesh size: about 10 mm × 15 mm, resulting in a fine mesh. The lip has slightly finer mesh, such as 5 mm × 15 mm. Mesh sensitivity studies were conducted to determine this mesh size, which ensures a reasonable accuracy while balancing computational costs.
- -
- Boundary conditions: globally pinned but warping fixed. Centroid RP-1 and RP-2 are defined as the reference points for end sections. The boundary conditions listed in Figure 2 were applied through the reference points.
- -
- Solution scheme: Rik’s method in ABAQUS; the way of convergence judgment follows the traditional theory [44].
- -
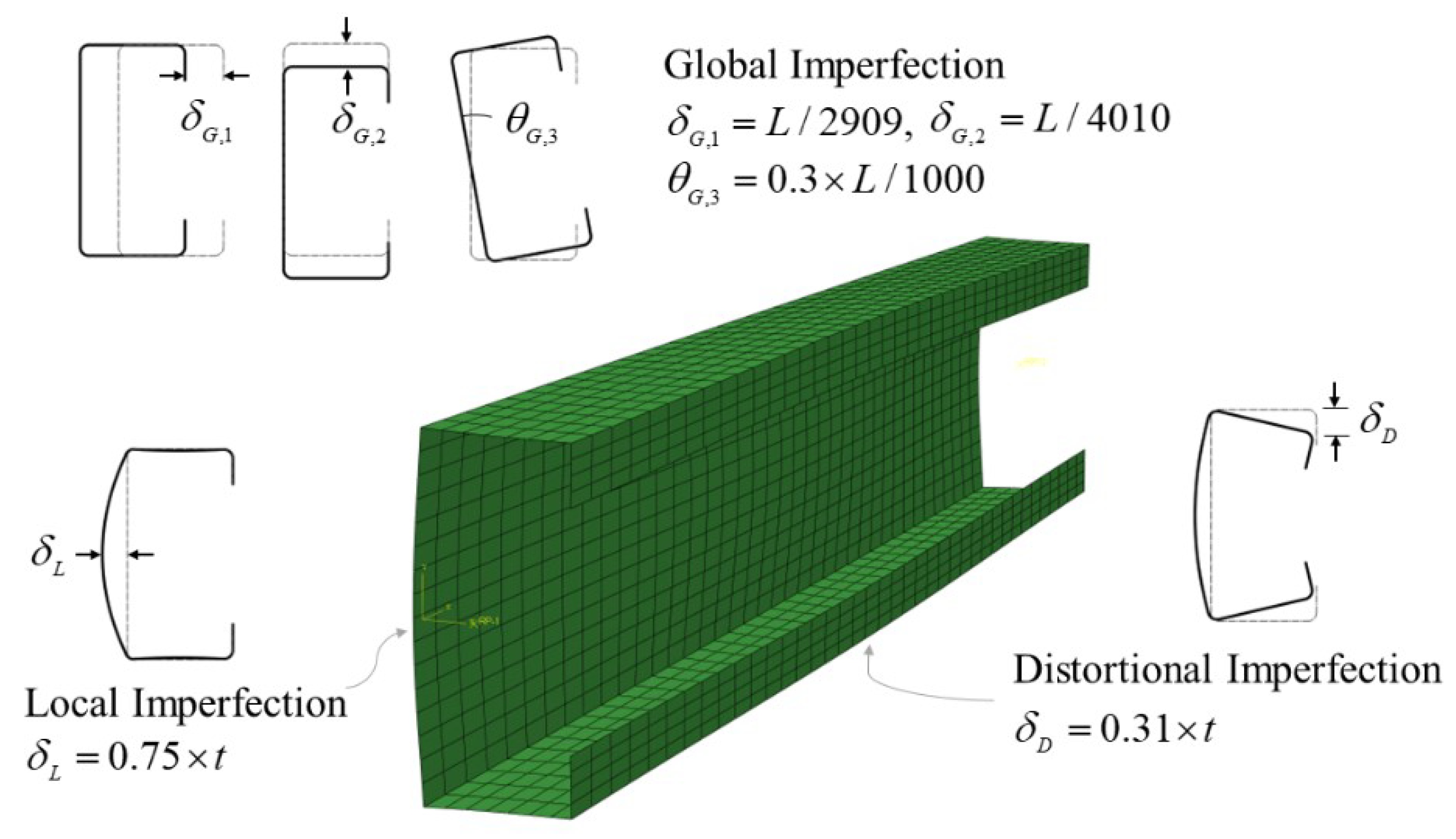
- Geometric imperfections: The initial imperfections are defined according to the one-dimensional spectrum method [45]. For the five initial imperfections in the one-dimensional spectrum method illustrated in Figure 3, based on the existing test results [46], the following amplitudes are adopted: overall buckling imperfection δG,1 = L/2909, δG,2 = L/4010, θG,3 = 0.3 × L/1000; local buckling imperfections δL = 0.75 × t; distortion buckling imperfection δL = 0.31 × t; where L is the member length and t is the cross-section thickness.
- -
- Residual stress: this effect was ignored in the model [47].
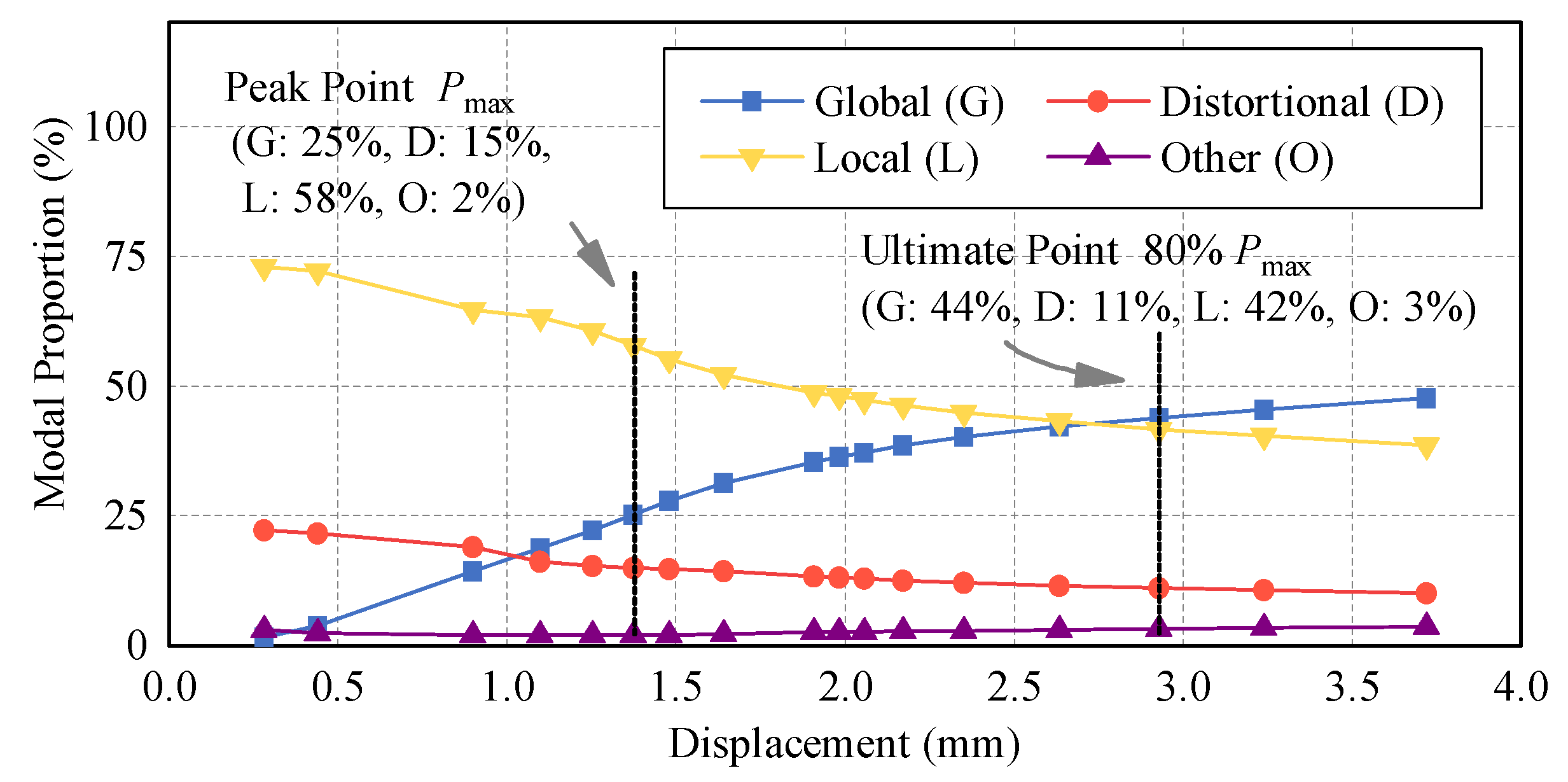
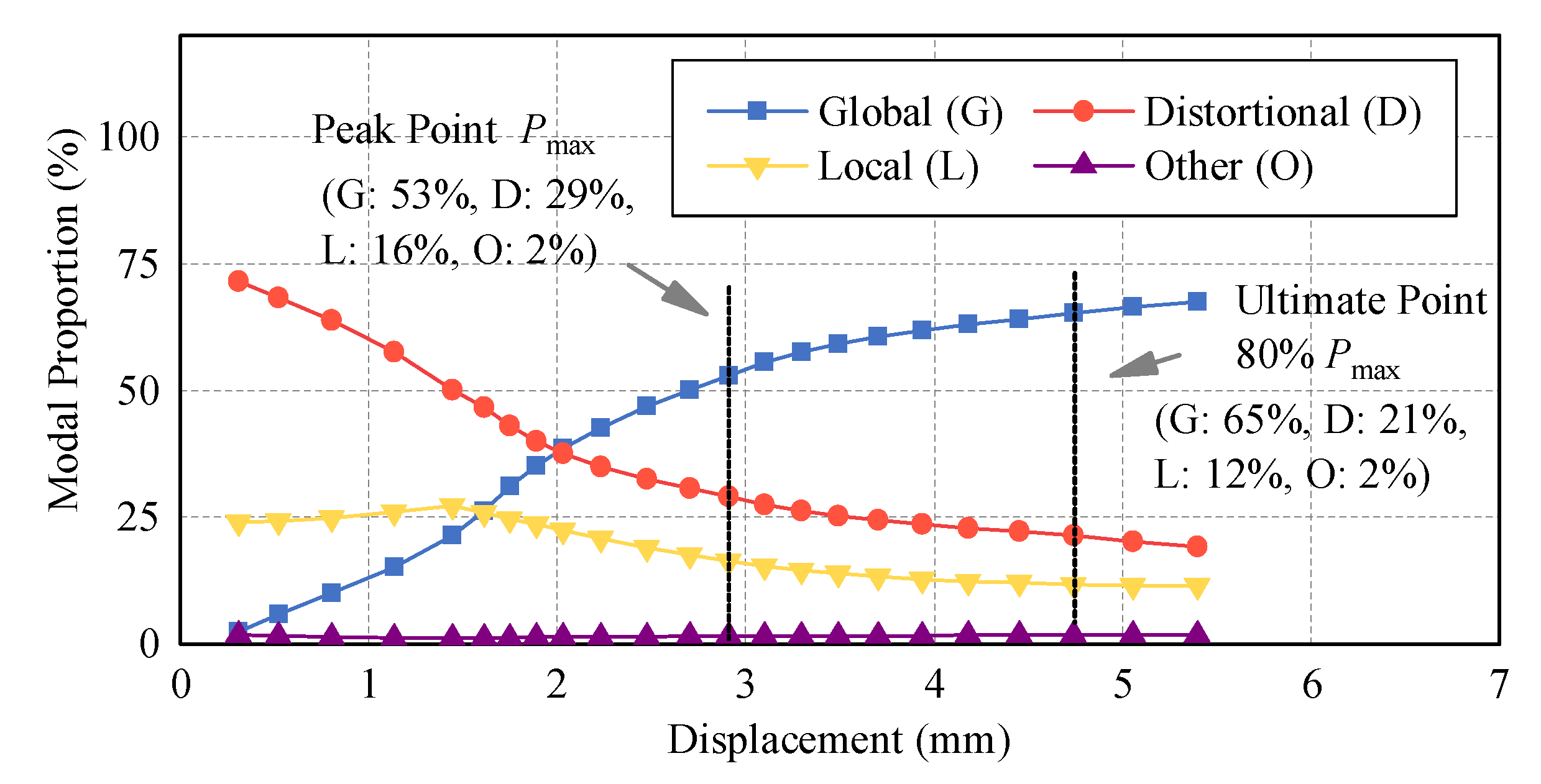
2.2. Modal Analysis
2.3. Limiting Factors of Axial Load Capacity
3. Construction of Cross-Section Optimization Model
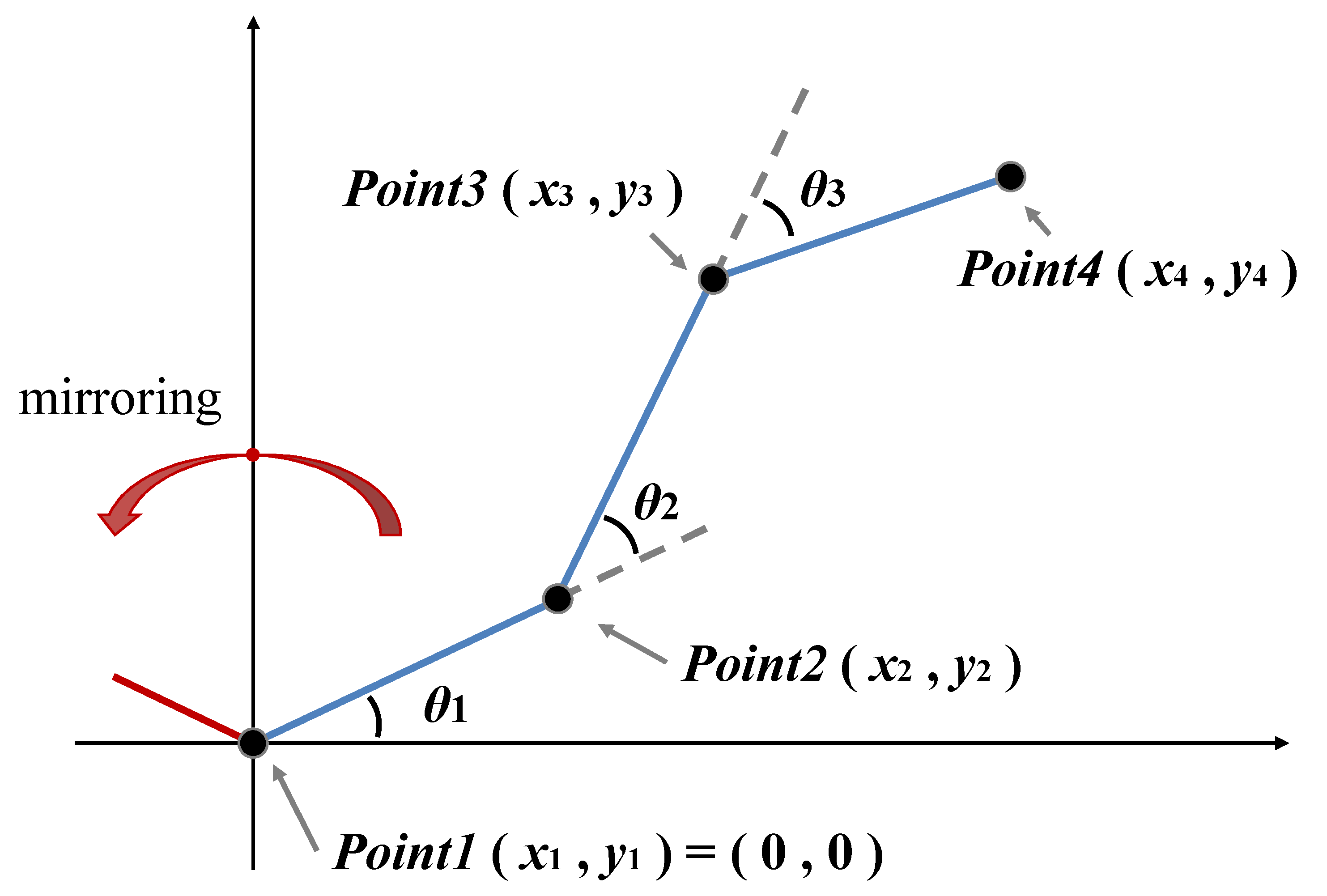
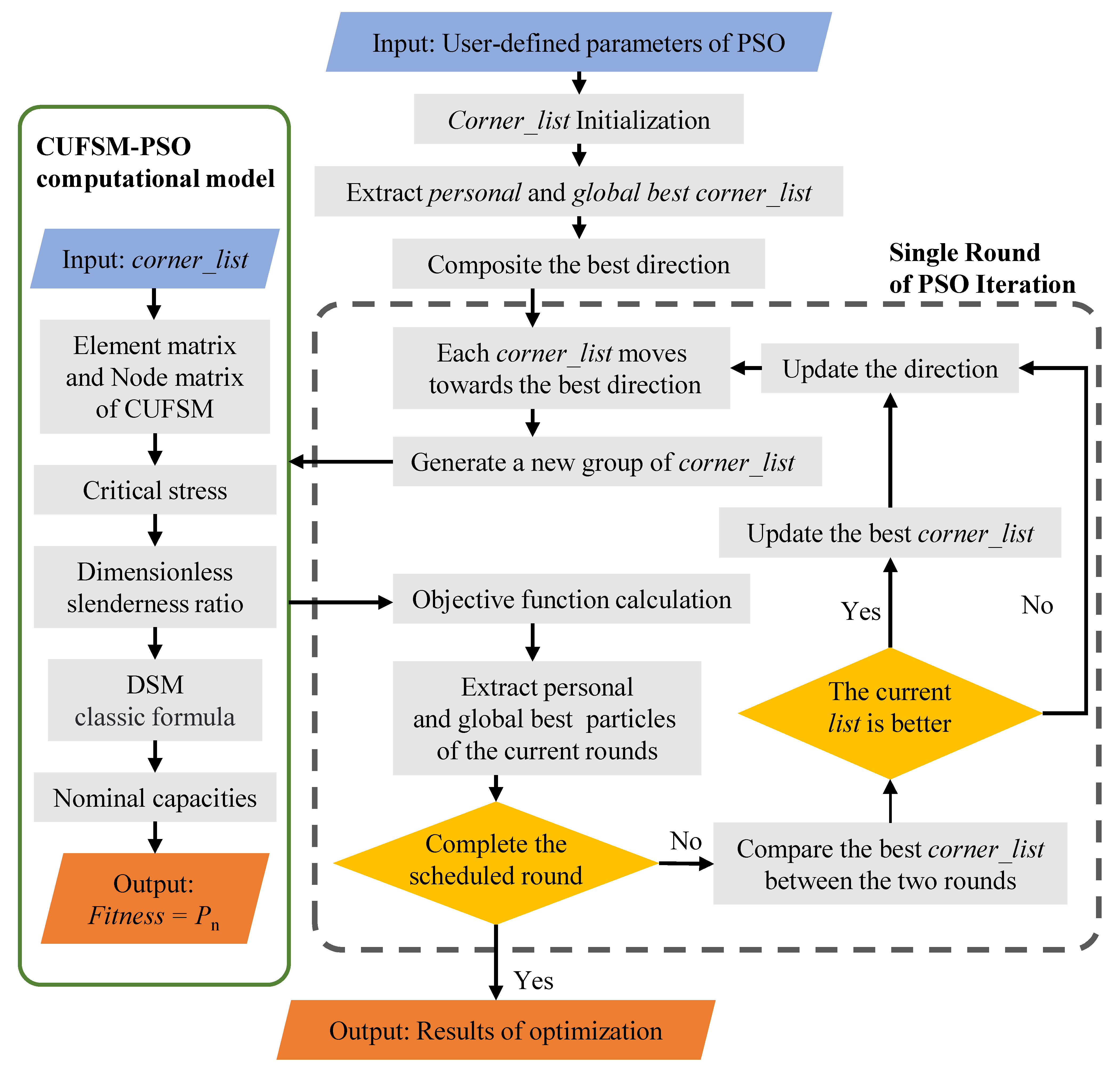
3.1. Definition of Free-Form Cross-Section in PSO
3.2. Objective Function and Constraint Conditions
- (1)
- The included angle between two adjacent elements shall not be less than 90°. Since the free-form shape of the cross-section in this paper is the complete cross-section obtained by first forming the polyline on the right side of the y-axis, and then mirror folding the y-axis, the first element needs to meet the state shown in Figure 12a, so as to meet the requirement that the included angle between element1 and the folded element is not less than 90°. For other elements, the included angle of adjacent elements shall not be less than 90° according to the restrictions in Figure 12b. The code for this condition in optimization is shown as Equation (12), where θ1 is the corner of the first element, and θi (i = 2, 3, 4, …) is the corner of the subsequent elements:
- (2)
- The member element itself does not cross and tie, as shown in Figure 12c. Note that since the cross-section is a complete cross-section obtained by folding the mirror image of the y-axis, if the one-sided cross-section intersects the y-axis of the symmetry axis, the self-inter cross-section of the complete cross-section will also occur, as shown in Figure 12d, which also needs to be avoided. The code for this condition in optimization is shown as Equations (13) and (14), where xi is the abscissa of the point, (xm, ym) and (xm+1, ym+1) are the end-node coordinates of the m-th element, (xn, yn) and (xn+1, yn+1) are the end-node coordinates of the n-th element, f(x, y) is the functional expression of the m-th element:
3.3. Optimizing Processes and Parameters
4. Optimization Results and FE Verification
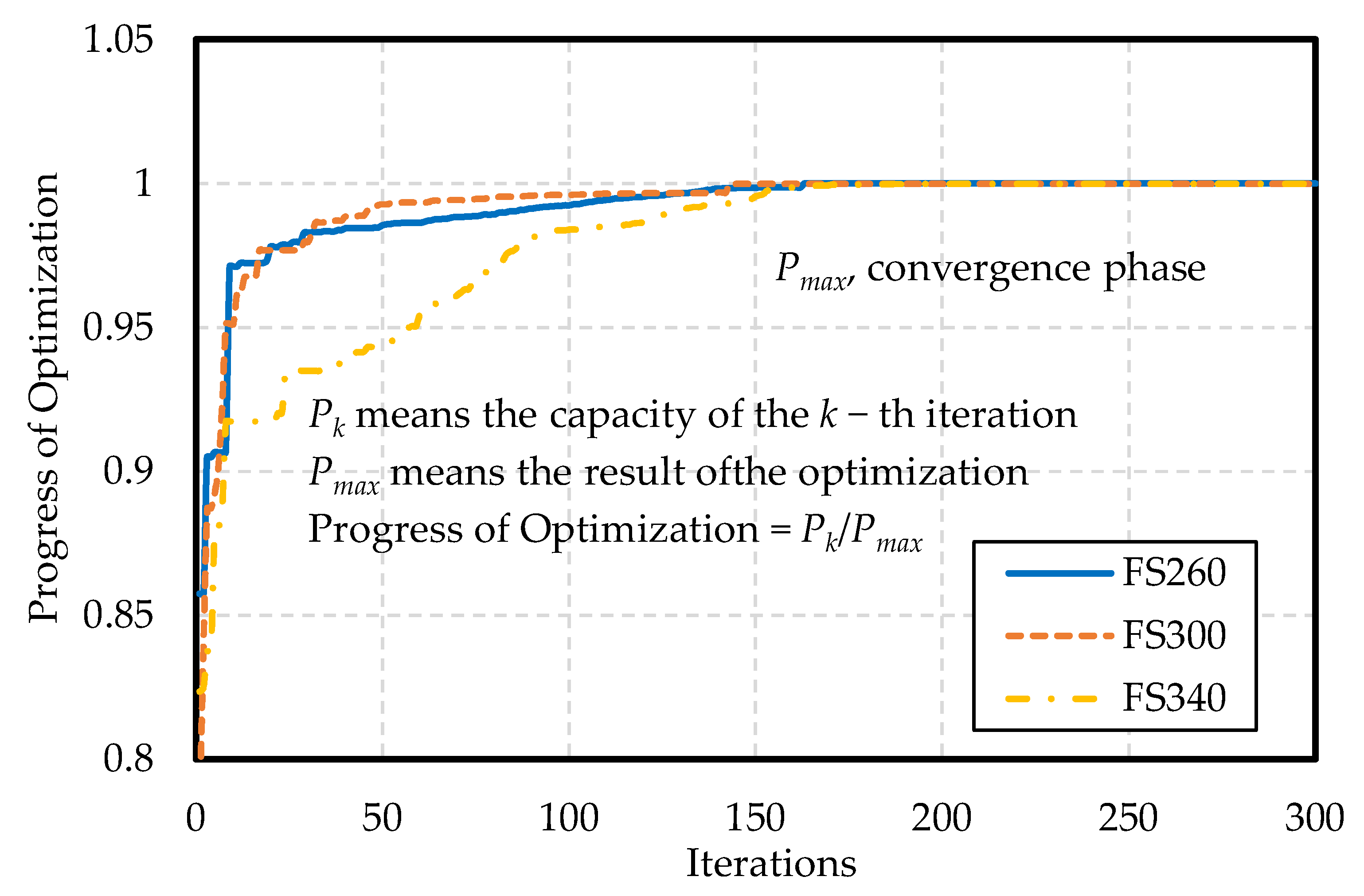
4.1. Optimization Path and Optimization Result
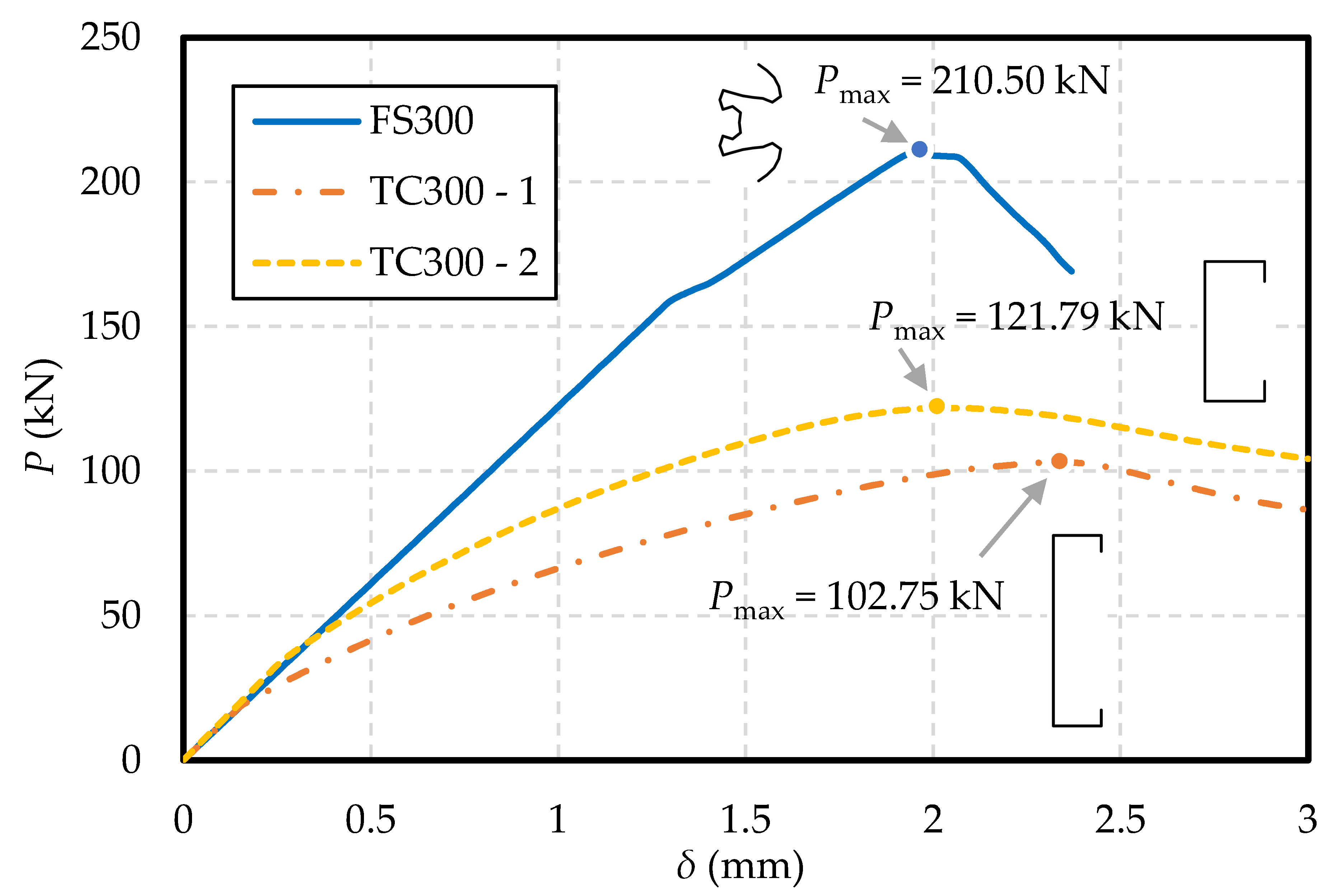
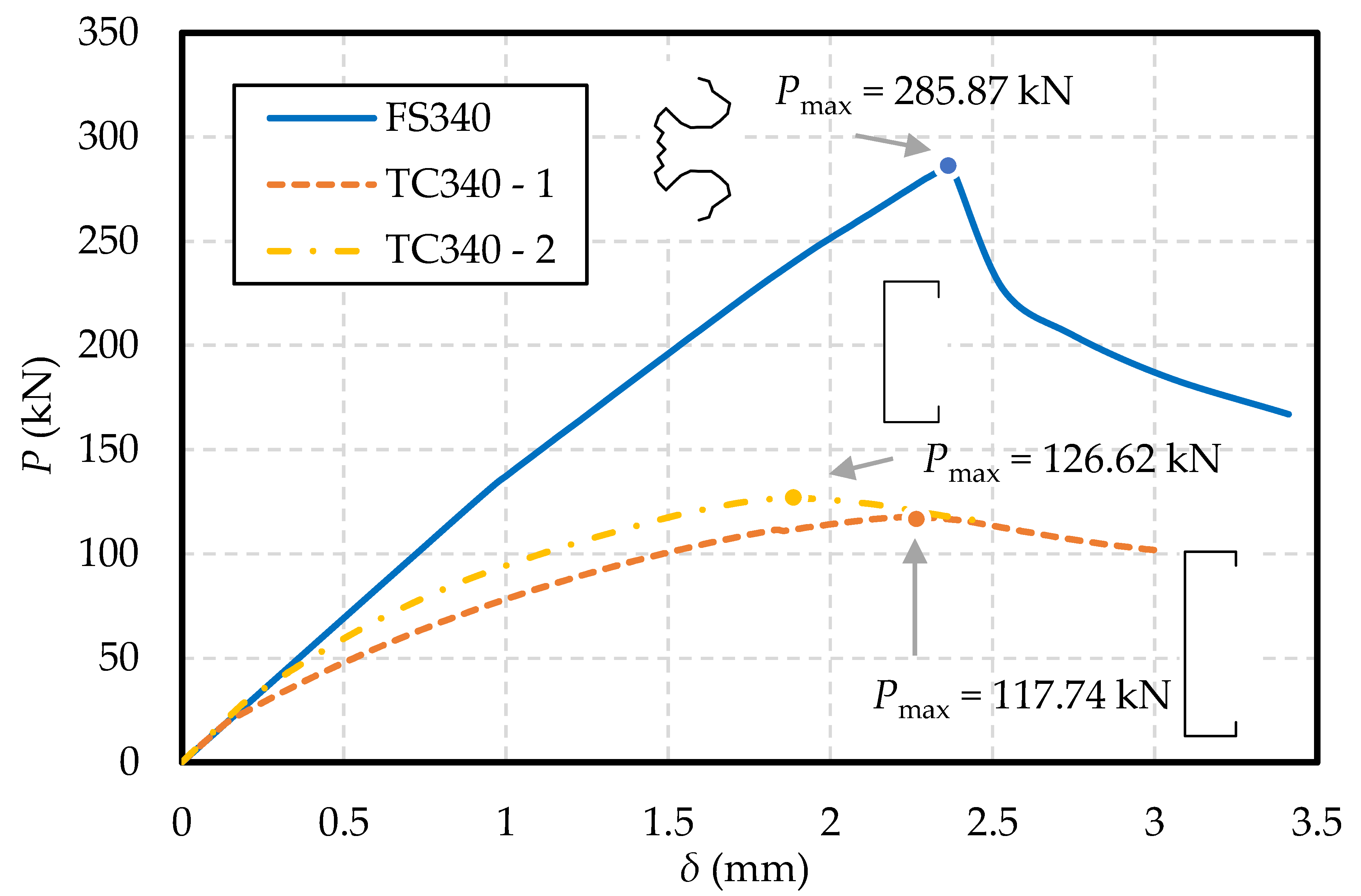
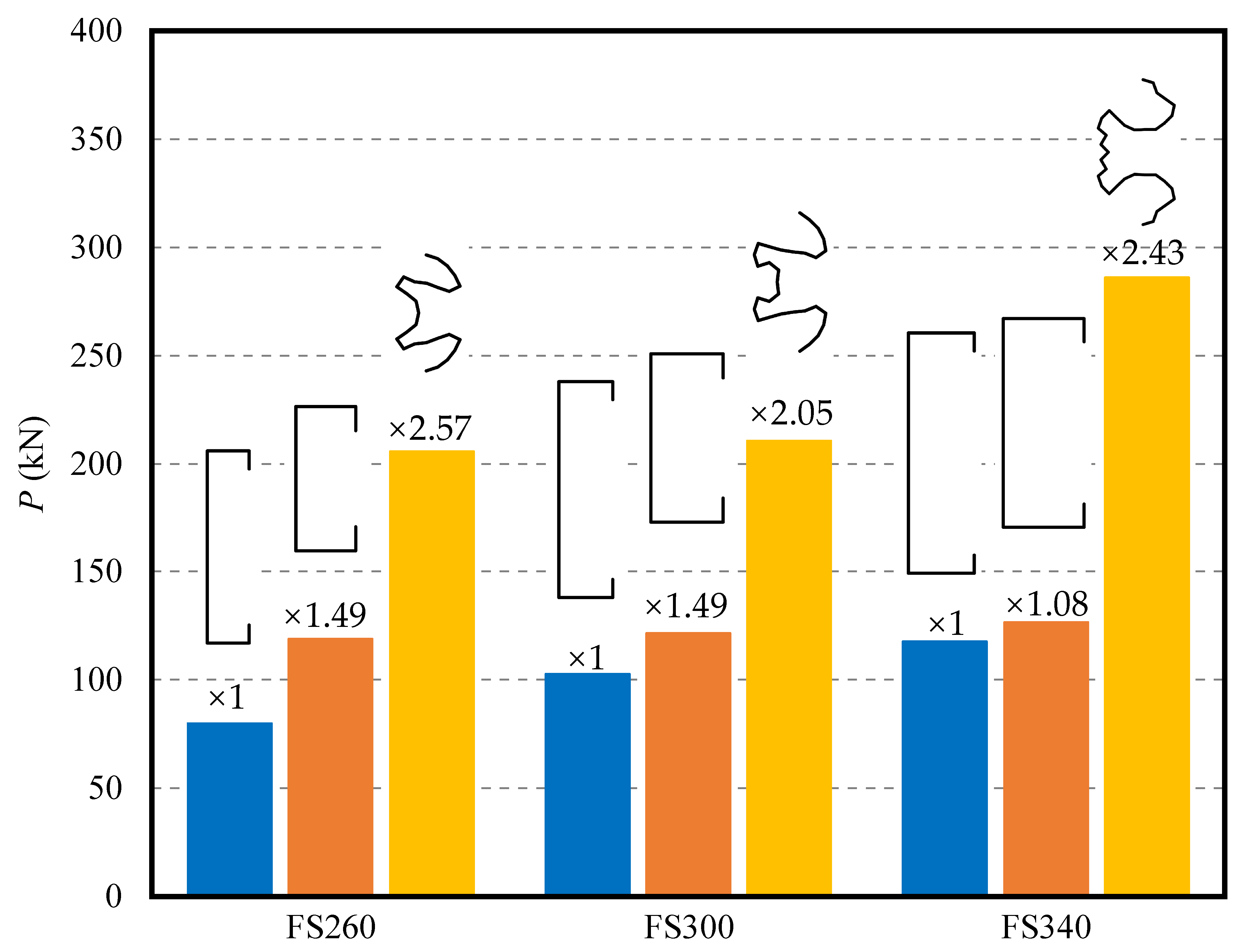
4.2. FE Verification
- (1)
- The bearing capacity results of FE simulation are basically consistent with those of PSO optimization.
- (2)
- The PSO-CUFSM in this paper has a remarkable effect. For the free-form shape of cross-sections of FS260, FS300, and FS340, the maximum bearing capacity can be increased by 2.57, 2.05, and 2.43 times, respectively, effectively improving the material utilization of AHSS members.
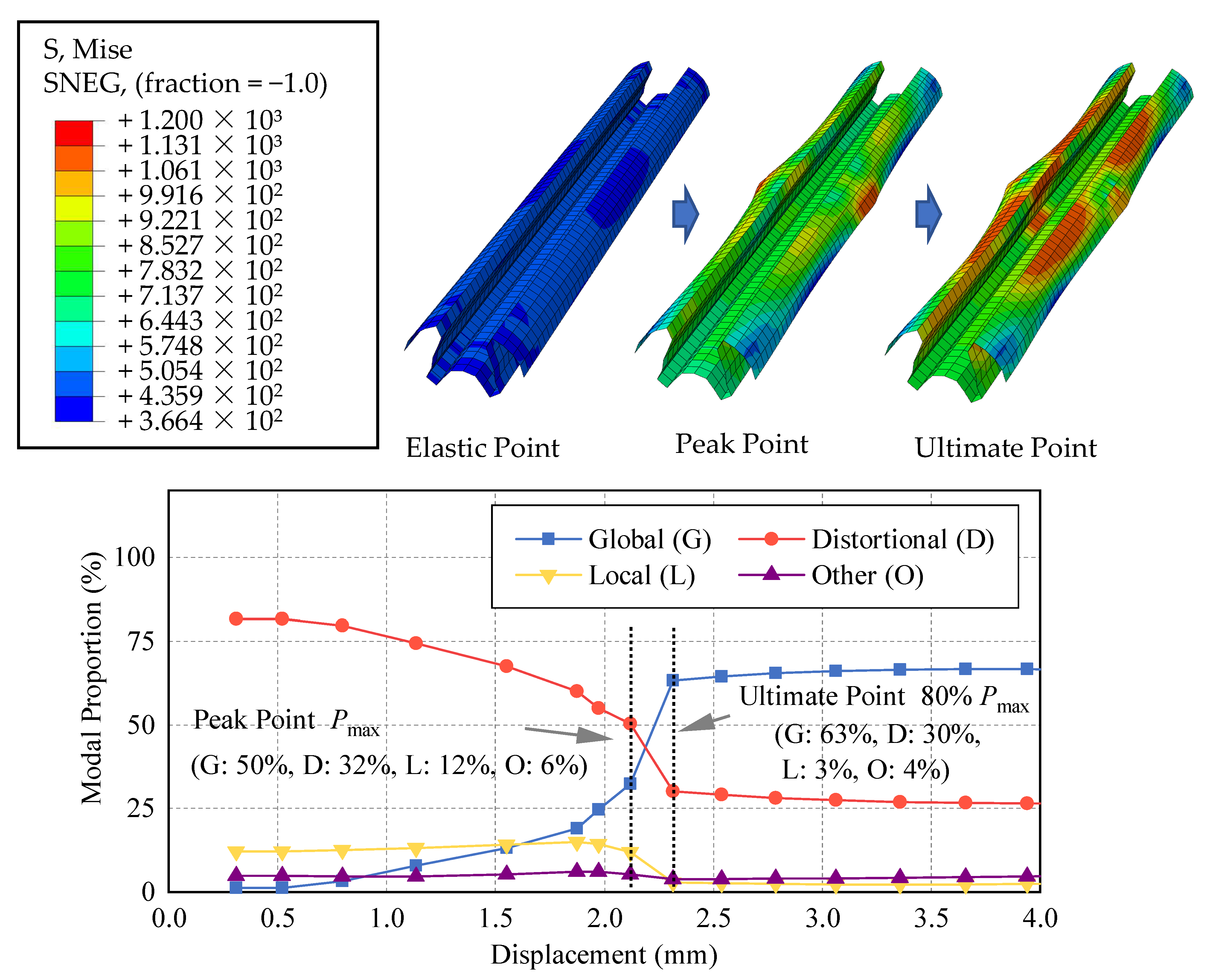
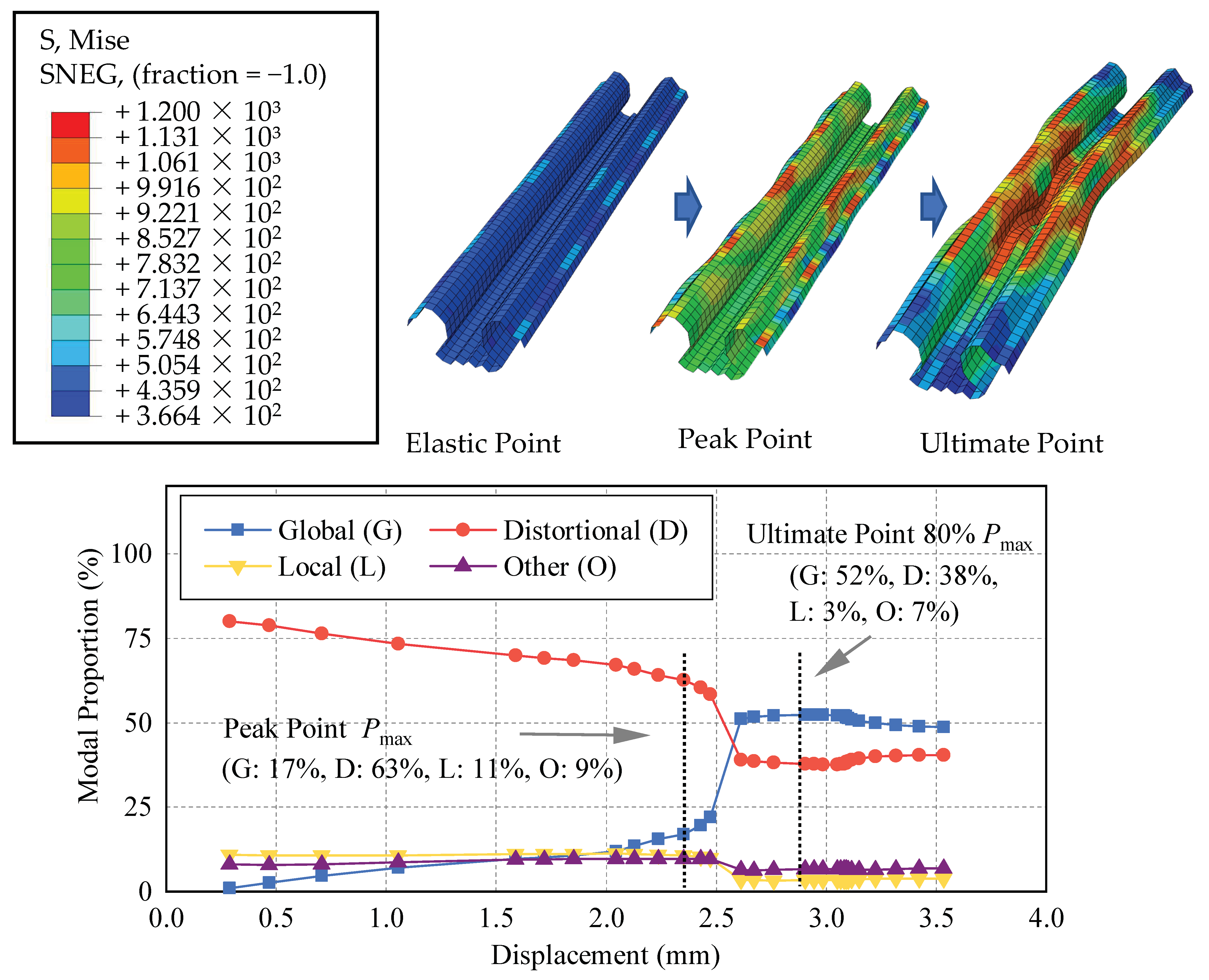
4.3. Modal Verification
5. Discussion
6. Conclusions
- (1)
- Through nonlinear FE modal identification and classification, it can be seen that the critical stress of the local buckling (L) of the traditional cross-section is low; hence local buckling (L) occurs early, and the interaction with distortional buckling (D) limits the bearing capacity. The optimized cross-section restrains the early occurrence of (L), reduces the coupling effect of local buckling (L) and distortional buckling (D), and thus improves the bearing capacity.
- (2)
- The proposed PSO-DSM method shows promising optimal results, although the DSM was only approximately applied to AHSS sections. Based on the further validation with nonlinear FE results, for the three groups of optimizations, the load bearing capacity was increased by 2.57, 2.05, and 2.43 times, respectively, compared to that of the traditional cross-sections.
- (3)
- The free-form shape optimization mainly restricts the local buckling in the optimization direction. The three groups of optimized cross-sections are similar, and the optimized cross-sections all have web stiffeners, a flange bending inward, and a large area curling outward. In this study, it is defined as “a cross-section similar to Ω shape”.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hancock, G.J. Cold-formed steel structures. J. Constr. Steel Res. 2003, 59, 473–487. [Google Scholar] [CrossRef]
- Li, Y.; Huang, B. Research on load-bearing performance of new fabricated steel structure beam-column joints with energydissipating elements. Structures 2022, 38, 492–501. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, T.; Wu, H.; Guan, Y.; Zhang, L. Cyclic performance of steel frame fabricated with cold-formed steel composite wall structure. Eng. Struct. 2022, 270, 114892. [Google Scholar] [CrossRef]
- Yang, H.; Wang, H.; Qian, H.; Jin, X.; Chen, D.; He, Y.; Li, Q.; Fan, F. Mechanical performance of pre-engineered closed section beam-column connections in CFS frames: Experimental investigation. Structures 2022, 39, 164–174. [Google Scholar] [CrossRef]
- Zhang, Z.-W.; Bai, G.-L.; Qin, C.-G.; Li, J.-R.; Liu, H.-Q. Shaking table test of fabricated concrete shear wall structure and study on damage mechanism of strong earthquake. Structures 2022, 43, 645–656. [Google Scholar] [CrossRef]
- Dar, M.A.; Subramanian, N.; Anbarasu, M.; Ghowsi, A.F.; Arif, P.A.; Dar, A. Testing and FE simulation of lightweight CFS composite built-up columns: Axial strength and deformation behaviour. Thin-Walled Struct. 2021, 167, 108222. [Google Scholar] [CrossRef]
- Sangeetha, P.; Vaishnavi, M.; Modhagapriyan, A.; Rajarajan, T. Effect of batten plates on the unlipped channel CFS built- up column under axial compression. Mater. Today Proc. 2022, 66, 1796–1804. [Google Scholar] [CrossRef]
- Rajanayagam, H.; Upasiri, I.; Poologanathan, K.; Gatheeshgar, P.; Sherlock, P.; Konthesingha, C.; Nagaratnam, B.; Perera, D. Thermal Performance of LSF Wall Systems with Vacuum Insulation Panels. Buildings 2021, 11, 621. [Google Scholar] [CrossRef]
- Naser, M.; Degtyareva, N. Temperature-induced instability in cold-formed steel beams with slotted webs subject to shear. Thin-Walled Struct. 2019, 136, 333–352. [Google Scholar] [CrossRef]
- Torabian, S.; Zheng, B.; Schafer, B.W. Experimental response of cold-formed steel lipped channel beam-columns. Thin-Walled Struct. 2015, 89, 152–168. [Google Scholar] [CrossRef]
- Hasanali, M.; Mojtabaei, S.M.; Clifton, G.C.; Hajirasouliha, I.; Torabian, S.; Lim, J.B. Capacity and design of cold-formed steel warping-restrained beam-column elements. J. Constr. Steel Res. 2022, 190, 107139. [Google Scholar] [CrossRef]
- Anbarasu, M.; Dar, M.A. Axial capacity of CFS built-up columns comprising of lipped channels with spacers: Nonlinear response and design. Eng. Struct. 2020, 213, 110559. [Google Scholar] [CrossRef]
- Singh, R.; Samanta, A. Numerical finite element simulation and structural behaviour of cold-formed steel members. Mater. Today Proc. 2022, 65, 3300–3305. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, T.; Zhang, L.; Ding, J.; Zhang, X. Distortional buckling behavior of cold-formed steel built-up closed section columns. Thin-Walled Struct. 2021, 166, 108069. [Google Scholar] [CrossRef]
- Defining Steels-AHSS Guidelines. 10 October 2021. Available online: https://ahssinsights.org/metallurgy/steel-grades/ (accessed on 10 October 2021).
- Srivastava, A.K.; Patra, P.K.; Jha, R. AHSS applications in Industry 4.0: Determination of optimum processing parameters during coiling process through unsupervised machine learning approach. Mater. Today Commun. 2022, 31, 103625. [Google Scholar] [CrossRef]
- Yang, H.; Wang, H.; Yang, Z.; Huang, Y.; Li, D.; Peng, Y.; Wu, P. In situ neutron diffraction and crystal plasticity analysis on Q&P1180 steel during plastic deformation. Mater. Sci. Eng. A 2021, 802, 140425. [Google Scholar]
- Sedaghat-Nejad, R.; Shahverdi, H.R.; Askari-Paykani, M. Introduction and mechanical evaluation of a novel 3rd-generation medium manganese AHSS with 86 GPa% of PSE. Mater. Sci. Eng. A 2022, 843, 143104. [Google Scholar] [CrossRef]
- Leng, J.; Li, Z.; Guest, J.K.; Schafer, B.W. Shape optimization of cold-formed steel columns with fabrication and geometric end-use constraints. Thin-Walled Struct. 2014, 85, 271–290. [Google Scholar] [CrossRef]
- Coimbra, K.F.; Alves, V.N.; Sarmanho, A.M.C.; Neiva, L.H.D.A. Optimization of rack-section cold-formed profiles columns. J. Constr. Steel Res. 2022, 196, 107422. [Google Scholar] [CrossRef]
- Öztürk, F.; Mojtabaei, S.M.; Şentürk, M.; Pul, S.; Hajirasouliha, I. Buckling behaviour of cold-formed steel sigma and lipped channel beam–column members. Thin-Walled Struct. 2022, 173, 108963. [Google Scholar] [CrossRef]
- GB/T 700-2006; Carbon Structural Steels. China Standard Press: Beijing, China, 2006. (In Chinese)
- Yuting, Z.; Yingkai, L.; Ruoqiang, F. A two-level optimization framework for new family of CFS sections. J. Constr. Steel Res. 2022, 197, 107460. [Google Scholar] [CrossRef]
- Ye, J.; Mojtabaei, S.M.; Hajirasouliha, I. Local-flexural interactive buckling of standard and optimised cold-formed steel columns. J. Constr. Steel Res. 2018, 144, 106–118. [Google Scholar] [CrossRef]
- Karim, A.; Adeli, H. Global optimum design of cold-formed steel hat-shape beams. Thin-Walled Struct. 1999, 35, 275–288. [Google Scholar] [CrossRef]
- Tian, Y.; Lu, T. Minimum weight of cold-formed steel sections under compression. Thin-Walled Struct. 2004, 42, 515–532. [Google Scholar] [CrossRef]
- Lee, J.; Kim, S.-M.; Park, H.-S.; Woo, B.-H. Optimum design of cold-formed steel channel beams using micro Genetic Algorithm. Eng. Struct. 2004, 27, 17–24. [Google Scholar] [CrossRef]
- Lee, J.; Kim, S.-M.; Park, H.S. Optimum design of cold-formed steel columns by using micro genetic algorithms. Thin-Walled Struct. 2006, 44, 952–960. [Google Scholar] [CrossRef]
- Schafer, B.W. Advances in the Direct Strength Method of cold-formed steel design. Thin-Walled Struct. 2019, 140, 533–541. [Google Scholar] [CrossRef]
- Liu, H.; Igusa, T.; Schafer, B. Knowledge-based global optimization of cold-formed steel columns. Thin-Walled Struct. 2004, 42, 785–801. [Google Scholar] [CrossRef]
- Leng, J.; Guest, J.K.; Schafer, B.W. Shape optimization of cold-formed steel columns. Thin-Walled Struct. 2011, 49, 1492–1503. [Google Scholar] [CrossRef]
- Leng, J.; Li, Z.; Guest, J.K.; Schafer, B.W. Shape optimization of cold-formed steel columns with manufacturing con-straints and limited number of rollers. In Proceedings of the Structural Stability Research Council Annual Stability Conference 2013, SSRC 2013, St. Louis, MO, USA, 16–20 April 2013; pp. 313–331. [Google Scholar]
- Moharrami, M.; Louhghalam, A.; Tootkaboni, M. Optimal folding of cold formed steel cross sections under compression. Thin-Walled Struct. 2014, 76, 145–156. [Google Scholar] [CrossRef]
- Ye, J.; Hajirasouliha, I.; Becque, J.; Pilakoutas, K. Development of more efficient cold-formed steel channel sections in bending. Thin-Walled Struct. 2016, 101, 1–13. [Google Scholar] [CrossRef]
- Li, Z.; Leng, J.; Guest, J.K.; Schafer, B.W. Two-level optimization for a new family of cold-formed steel lipped channel sections against local and distortional buckling. Thin-Walled Struct. 2016, 108, 64–74. [Google Scholar] [CrossRef]
- Akchurin, D.; Ding, C.; Xia, Y.; Blum, H.; Schafer, B.W.; Li, Z. Optimization of cold-formed steel members considering reduced stiffness and strength due to cross-sectional instabilities. In Proceedings of the Structural Stability Research Council-Proceedings of the 2022 Annual Stability Conference, Denver, CO, USA, 22–25 March 2022. [Google Scholar]
- Gatheeshgar, P.; Poologanathan, K.; Gunalan, S.; Tsavdaridis, K.D.; Nagaratnam, B.; Iacovidou, E. Optimised cold-formed steel beams in modular building applications. J. Build. Eng. 2020, 32, 101607. [Google Scholar] [CrossRef]
- Leng, J. Optimization techniques for structural design of cold-formed steel structures. In Recent Trends in Cold-Formed Steel Construction; Woodhead Publishing: Sawston, UK, 2016; pp. 129–151. [Google Scholar] [CrossRef]
- Ding, C.; Xia, Y.; Akchurin, D.; Li, Z.; Blum, H.; Schafer, B.W. Simulation of compressive strength of wall studs cold-formed from ad-vanced high strength steels. In Proceedings of the Structural Stability Research Council-Proceedings of the 2022 Annual Stability Conference, Denver, CO, USA, 22–25 March 2022. [Google Scholar]
- Ding, C.; Xia, Y.; Akchurin, D.; Blum, H.B.; Li, Z.; Schafer, B.W. Structural Behavior Of Advanced High Strength Steel: Ductility, Connections, Members. In Proceedings of theCold-Formed Steel Research Consortium (CFSRC) Colloquium, Baltimore, MD, USA, 17–19 October 2022. [Google Scholar]
- Ádány, S.; Schafer, B.W. Buckling mode decomposition of single-branched open cross-section members via finite strip method: Application and examples. Thin-Walled Struct. 2006, 44, 585–600. [Google Scholar] [CrossRef]
- Sibalija, T.V. Particle swarm optimisation in designing parameters of manufacturing processes: A review (2008–2018). Appl. Soft Comput. 2019, 84, 105743. [Google Scholar] [CrossRef]
- Li, Z.; Schafer, B. Application of the finite strip method in cold-formed steel member design. J. Constr. Steel Res. 2010, 66, 971–980. [Google Scholar] [CrossRef]
- Crisfield, M. A fast incremental/iterative solution procedure that handles “snap-through”. Comput. Struct. 1981, 13, 55–62. [Google Scholar] [CrossRef]
- Zeinoddini, V.; Schafer, B. Simulation of geometric imperfections in cold-formed steel members using spectral representation approach. Thin-Walled Struct. 2012, 60, 105–117. [Google Scholar] [CrossRef]
- Deng, T. Buckling Bearing Capacity and Optimization of Section Form of Cold Formed Advanced High Strength Steel Member. Master’s Thesis, Southeast University, Nanjing, China, 2022. (In Chinese). [Google Scholar]
- Schafer, B.; Li, Z.; Moen, C. Computational modeling of cold-formed steel. Thin-Walled Struct. 2010, 48, 752–762. [Google Scholar] [CrossRef]
- Li, X. Research on Mechanical Properties of Advanced High Strength Steel Considering Cold Working Effect. Master’s Thesis, Southeast University, Nanjing, China, 2022. (In Chinese). [Google Scholar]
- Li, Z.; Ádány, S.; Schafer, B. Modal identification for shell finite element models of thin-walled members in nonlinear collapse analysis. Thin-Walled Struct. 2013, 67, 15–24. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), Anchorage, AK, USA, 4–9 May 1998. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks Proceedings, Perth, WA, Australia, 27 November–1 December 1995; Volume 1–6, pp. 1942–1948. [Google Scholar]
- GB 50018-2002; Technical Code of Cold-Formed Thin-wall Structures. China Ministry of Construction: Beijing, China, 2002. (In Chinese)







| Parameter Symbol | Parameter Name | Amplitude | Note |
|---|---|---|---|
| n_particle | Number of particles | 50 | Number of particles in a single particle swarm (number of cross-sections) |
| n_order | Order of the particle | Positive integer | Number of elements of a single particle (number of polyline segments) |
| len_element | Length of element | 10 mm | The length of a single polyline segment |
| t_element | Thickness of element | 1.2 mm | The actual thickness of the member cross-section, selected from the material properties test of Figure 1 |
| w | Weight of inertia | 0.9 | Increase the randomness of motion, selected according to reference [50] |
| r1 | Personal learning factors | 1.0 | Increase the randomness of motion, selected according to reference [51] |
| r2 | Global learning factors | 2.0 | Increase the randomness of motion, selected according to reference [51] |
| max_gen | Maximum number of iterations | 300 | The iteration upper bound, where the optimization terminates. |
| pop_range | Motion boundary | (−0.5, 0.5) | Corner of a single round is limited to the interval (−π/2, π/2). |
| speed_range | Velocity boundary | (−0.5, 0.5) | Corner of a single round is limited to the interval (−π/2, π/2). |
| fy | Yield strength | 1079 MPa | Material parameters of CUFSM, selected from the material properties test of Figure 1 |
| E | Elasticity modulus | 203 GPa | Material parameters of CUFSM, selected from the material properties test of Figure 1 |
| ID | Iteration k | 1 | 75 | 150 | 225 (Convergence) |
|---|---|---|---|---|---|
| FS260 | Cross-Section k |  | 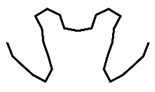 | 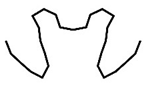 | 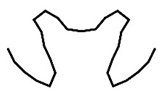 |
| Pk (kN) | 179.16 | 206.55 | 208.61 | 208.92 | |
| FS300 | Cross-Section k |  | 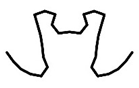 |  | 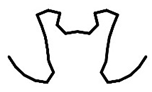 |
| Pk (kN) | 192.37 | 234.46 | 235.08 | 235.10 | |
| FS340 | Cross-Section k | 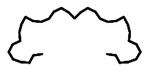 | 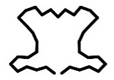 | 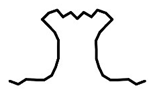 | 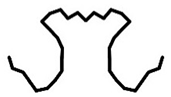 |
| Pk (kN) | 221.05 | 259.06 | 267.26 | 268.42 |
| Optimize Grouping | C Cross-Section | Web h (mm) | Flange b (mm) | Hemming a (mm) | Cross-Section Sketch |
|---|---|---|---|---|---|
| FS260 | TC260-1 | 160 | 35 | 15 | 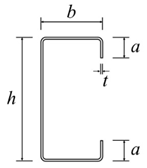 |
| TC260-2 | 120 | 50 | 20 | ||
| FS300 | TC300-1 | 180 | 45 | 15 | |
| TC300-2 | 140 | 60 | 20 | ||
| FS340 | TC340-1 | 200 | 55 | 15 | |
| TC340-2 | 160 | 70 | 20 |
| Specimen | Pmax, PSO (MPa) | Pmax, FEM (MPa) | Variation (Pmax, PSO–Pmax, FEM)/Pmax, PSO |
|---|---|---|---|
| FS260 | 208.92 | 205.65 | 1.57% |
| FS300 | 235.10 | 210.50 | 10.46% |
| FS340 | 268.42 | 285.87 | −6.50% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, L.; Deng, T.; Niu, Y.; Li, Z. Free-Form Shape Optimization of Advanced High-Strength Steel Members. Buildings 2022, 12, 2101. https://doi.org/10.3390/buildings12122101
Yin L, Deng T, Niu Y, Li Z. Free-Form Shape Optimization of Advanced High-Strength Steel Members. Buildings. 2022; 12(12):2101. https://doi.org/10.3390/buildings12122101
Chicago/Turabian StyleYin, Lingfeng, Tianyang Deng, Yu Niu, and Zhanjie Li. 2022. "Free-Form Shape Optimization of Advanced High-Strength Steel Members" Buildings 12, no. 12: 2101. https://doi.org/10.3390/buildings12122101
APA StyleYin, L., Deng, T., Niu, Y., & Li, Z. (2022). Free-Form Shape Optimization of Advanced High-Strength Steel Members. Buildings, 12(12), 2101. https://doi.org/10.3390/buildings12122101