Shaking Table Testing of a Low-Rise Reinforced Concrete Intermediate Moment Resisting Frame
Abstract
:1. Introduction
2. Design of Selected Moment-Resisting Frame
2.1. Lateral Seismic Forces
2.2. Design of Beams
2.3. Design of Columns
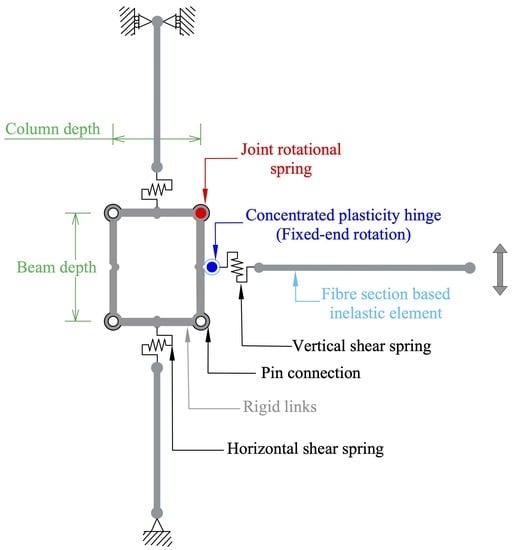
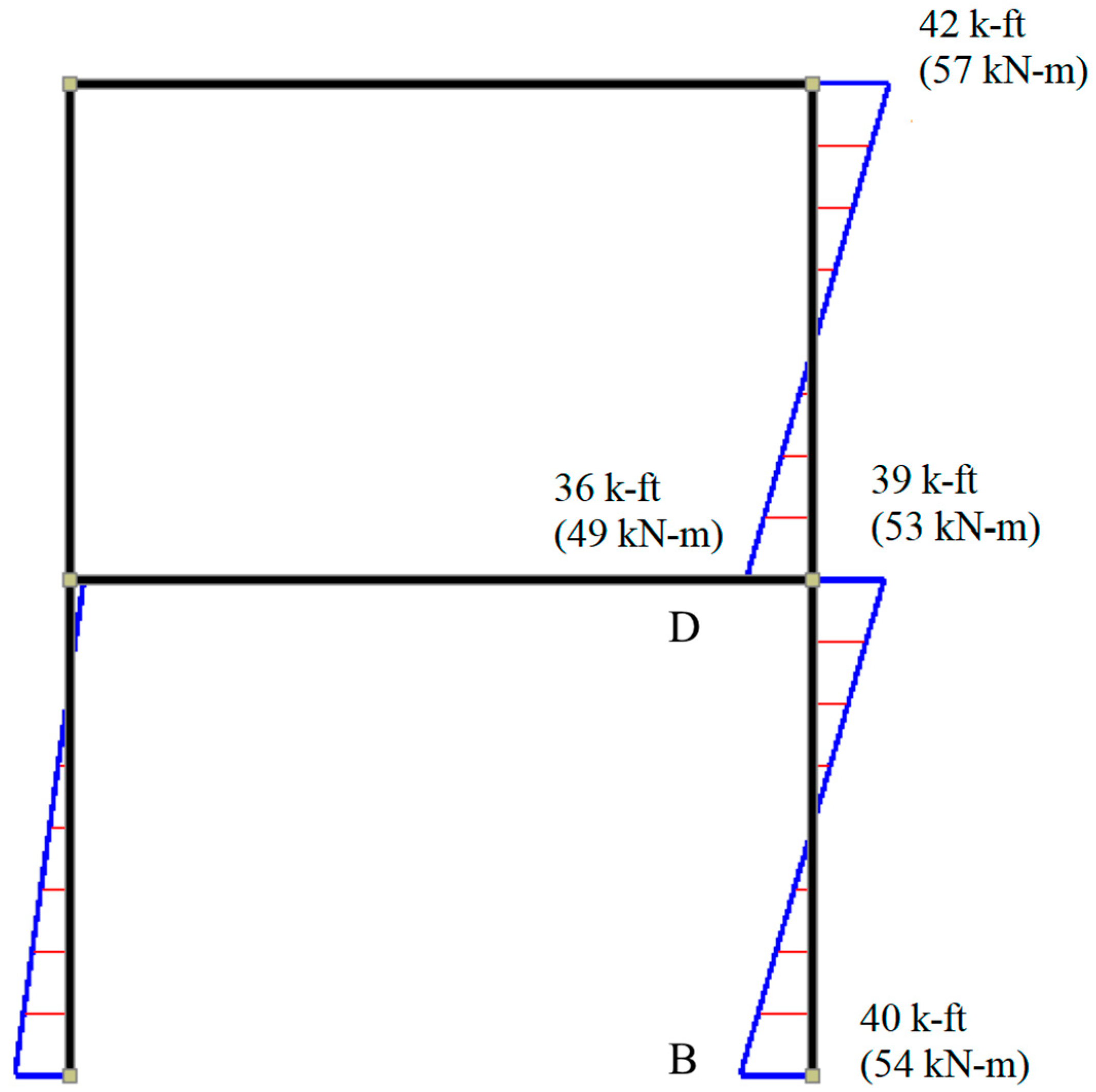
2.4. Design of Beam–column Joints
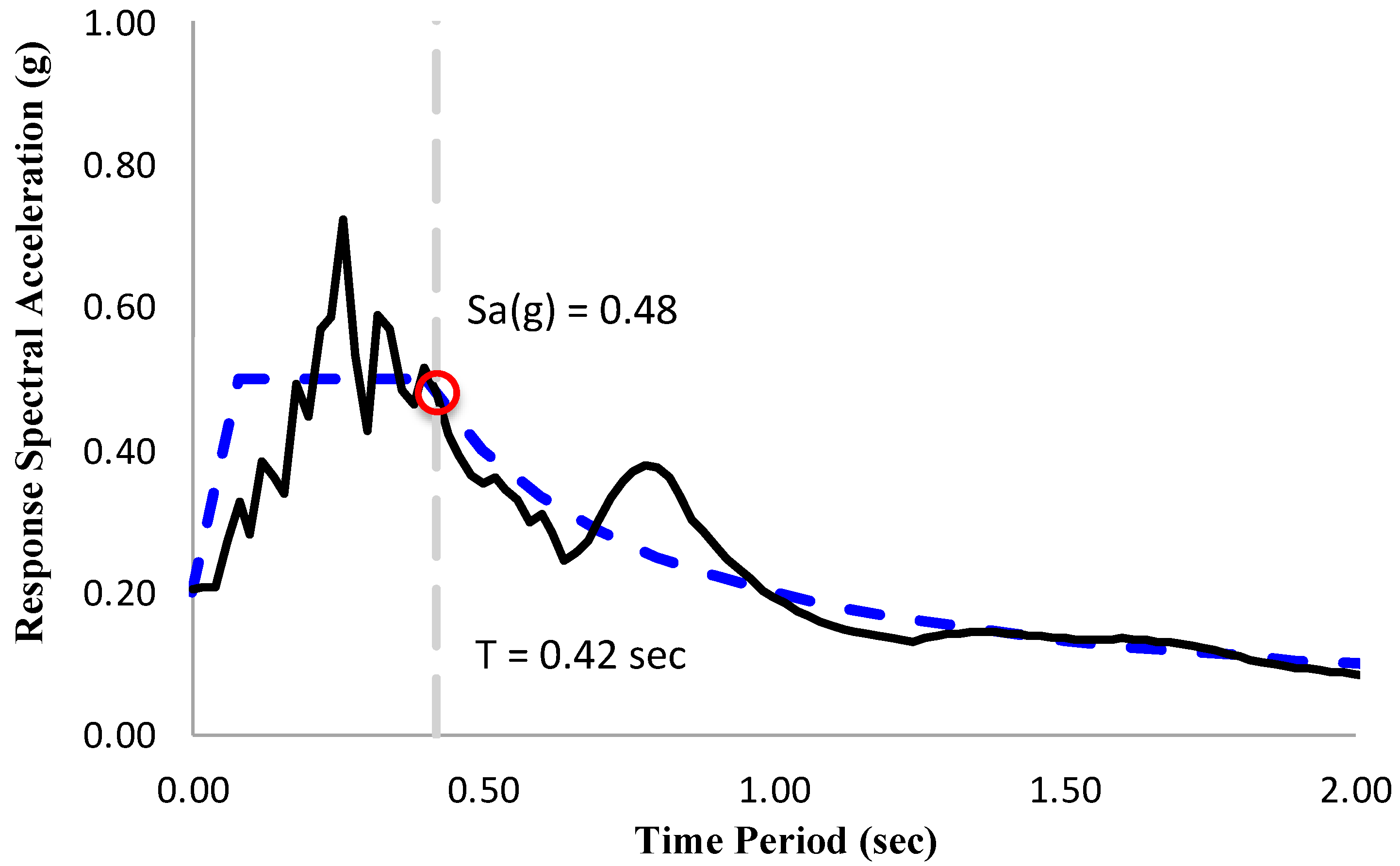
3. Shake-Table Tests on Selected Frame
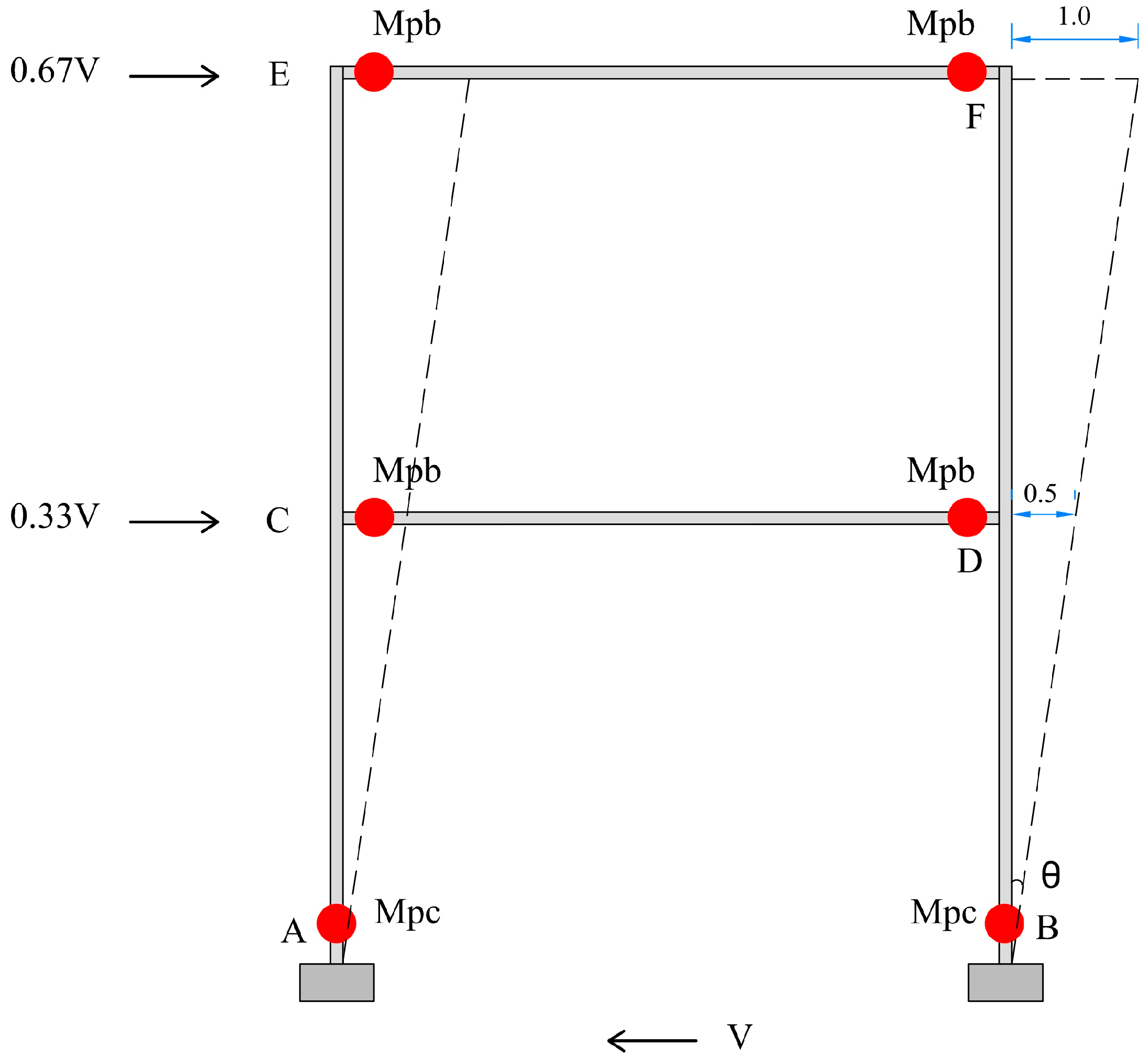
4. Seismic Design Factors for Selected Frame
4.1. Overstrength Factor
4.2. Ductility Factor
4.3. Response Modification Coefficient
5. Assessment of Beam–Column Joint
5.1. Efficiency of Beam–Column Joint
5.2. Shear Strength of Beam–Column Joint
6. Discussions
7. Conclusions
- The analysis of the beam indicates overstrength equal to 1.17 for flexural strength and 1.40 for shear strength. The corresponding flexural and shear overstrength obtained for columns are 1.15 and 2.50, respectively;
- The factored shear force computed in accordance with the ACI-318-19 provisions 18.4.2.3 (a) and 18.4.2.3 (b) gives roughly similar shear force, with the procedure (a) giving relatively high shear force by 7% in comparison to procedure (b);
- The updated model for the shear strength of concrete included in ACI-318-19 gives a strength 31% less than the previous simple model;
- The analytical model gives overstrength equal to 1.17 for the shear capacity of the joint for design base action. This confirms the efficacy of the joint laterally supported by beams on three faces despite its lack of shear reinforcement. However, it must be ensured that the concrete has compressive strength equal to or more than 28 MPa.
- The selected frame exhibited flexural mechanism in beams under base motions with sustained maximum acceleration up to 0.40 g. Only a few slight cracks were developed in beam–column joints under base motions with a sustained maximum acceleration equal to 0.45 g. The joints incurred extensive damage under base motion with sustained maximum acceleration of 0.70 g;
- The selected frame achieved an overstrength factor equal to 2.50, which is 20% less than the value suggested by the ASCE/SEI-7-22. The ductility factor determined is equal to 2.40, which is 44% higher than the ductility factor inherently available in the response modification coefficient suggested by the ASCE/SEI-7-22 for the selected frame. This gives a response modification coefficient equal to 6.0, which is 20% higher than the value suggested by the ASCE/SEI-7-22;
- The available analytical model for yield drifts provided an estimate of the ductility factor 33% less than the experimental value. This is due to the fact that such models are based on the response of beam–column connection sub-assemblages lacking slab effects;
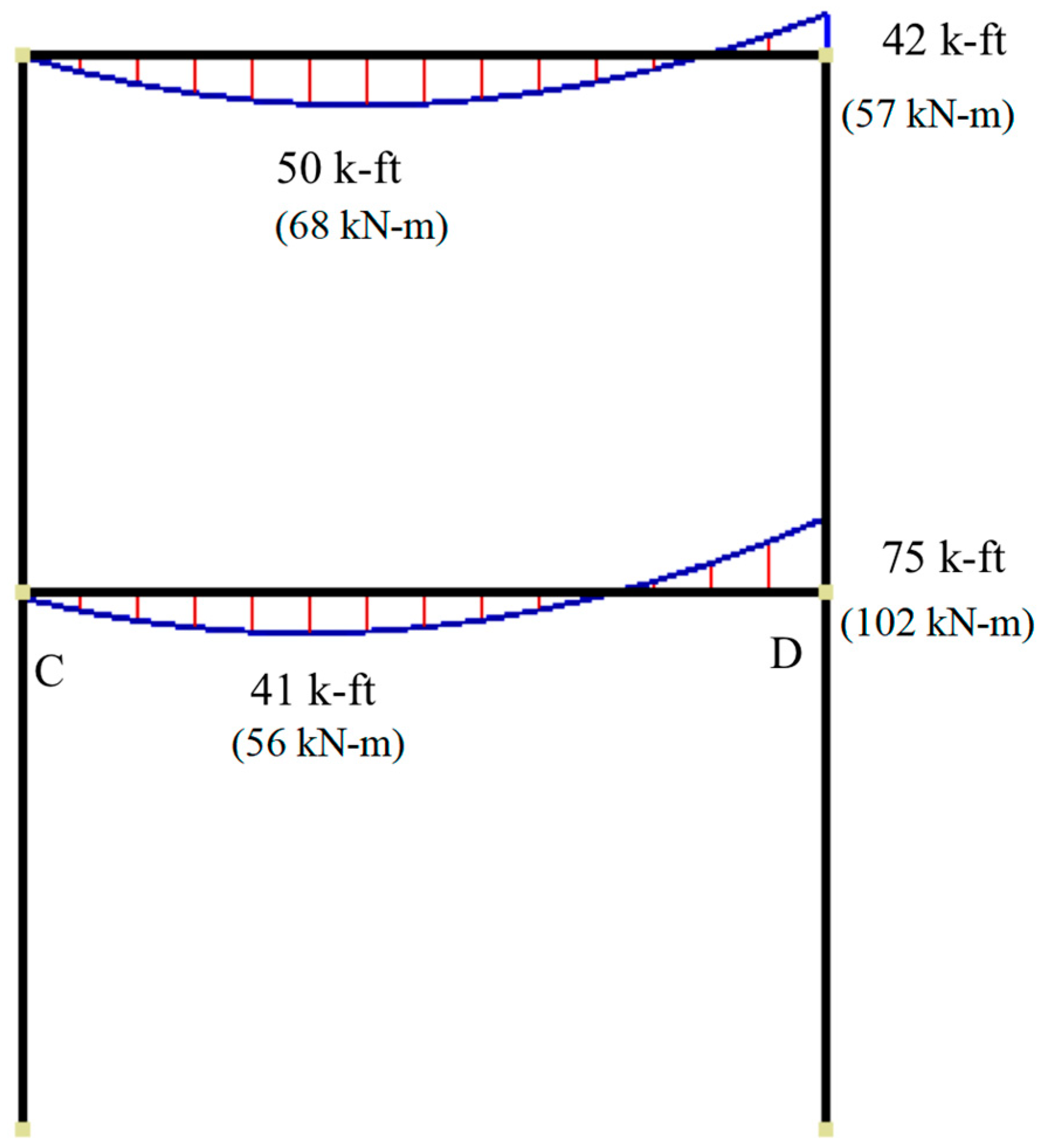
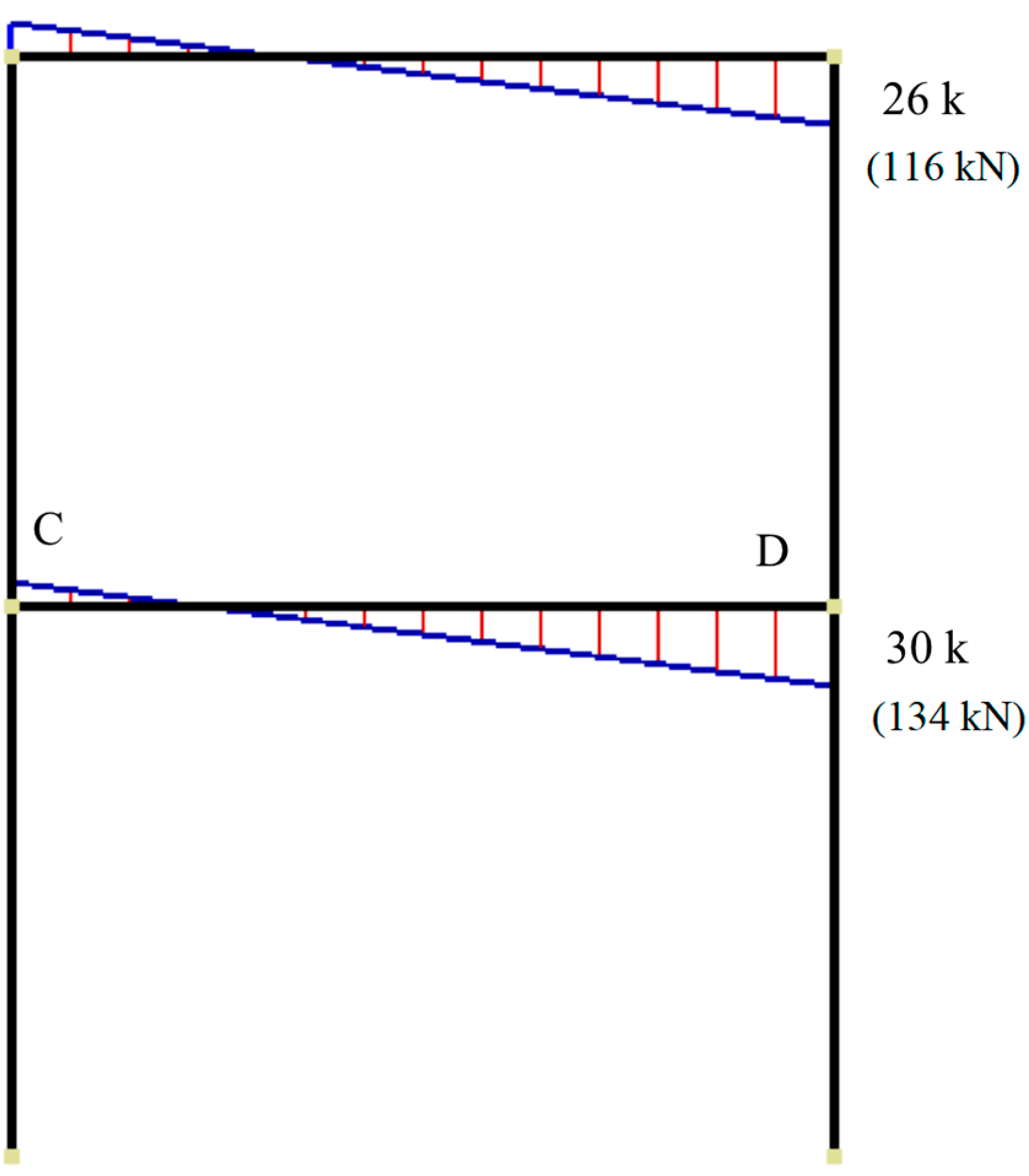
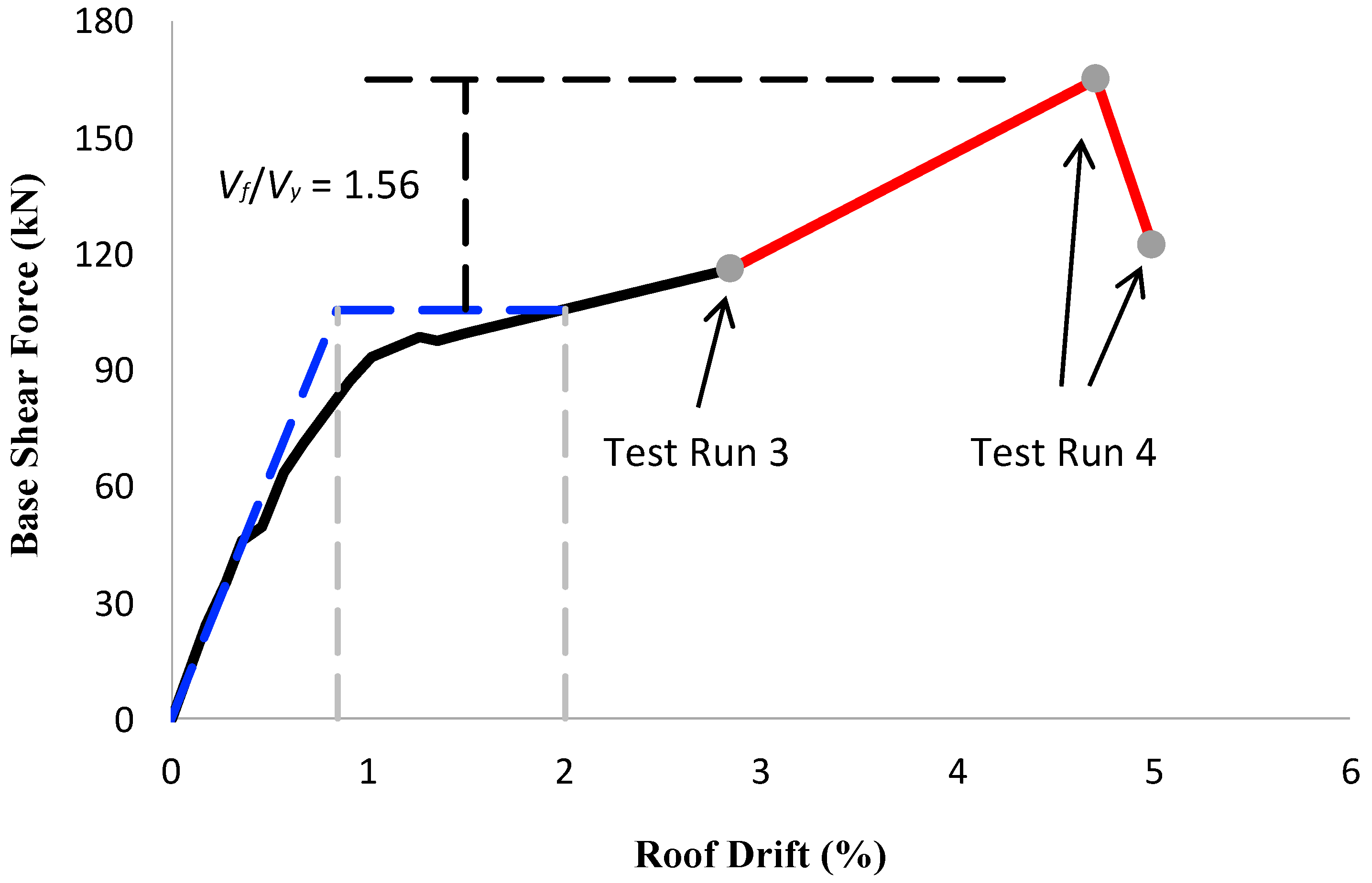
- The virtual work method based on the presumed beam-sway plastic mechanism predicted the peak base shear of the selected frame at roof drift of 2% with sufficient accuracy; it was slightly overestimated by 7%. However, this method underestimated the maximum resistance of the frame at the roof drift of 4.20% by 31%. This is due to the fact that the method ignored the material overstrength and slab contribution to flexural strength. Re-calculating Vmax using Equation (8) and amplifying the bending moment capacity of the beam by flexural overstrength of 1.85 gives Vmax equal to 188 kN. This is approximately 14% higher than the experimentally observed maximum resistance of 165 kN;
- The efficiency of joint that defines the ratio of force causing failure of the joint to the force developed in the frame at the maximum permissible drift is equal to 1.56 (or 156%). This measured efficiency is significantly higher than the values reported previously [28,29]. This increase is attributed to the material overstrength and the fact that the joint was confined by beams on three faces and the concrete strength is 28 MPa;
- Analysis of beam–column joints based on the experimental response at the roof drift equal to 4.70% gives overstrength equal to 1.58 for joint shear strength in comparison to nominal shear strength determined in accordance with the ACI-318-19 (18.8.4.3). The measured high overstrength confirms the efficacy of the beam–column joint confined by beams on three faces despite the fact it lacks shear reinforcement. However, it is a must to use concrete that has compressive strength equal to or more than 28 MPa. The inherent minimal confinement is sufficient to ensure satisfactory seismic behavior.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| joint area | |
| area of longitudinal steel reinforcement in tension | |
| deflection amplification factor | |
| seismic response coefficient | |
| coefficient for upper limit on fundamental time period, 1.5 for SD1 equal to 0.20 | |
| Vertical distribution factor | |
| effect of earthquake-induced forces | |
| Young’s modulus of concrete | |
| Young’s modulus of steel | |
| lateral seismic design forces at level x | |
| lateral seismic forces at level x at lateral force causing failure of the joint | |
| compressive strength of concrete | |
| yield strength of steel | |
| acceleration due to gravity equal to 32.17 ft/s2 (9.81 m/s2) | |
| depth of beam | |
| story height below level x | |
| earthquake importance factor based on the use and occupancy of the frame | |
| length of beam | |
| floor mass of test model | |
| additional floor mass for test model | |
| nominal moment strength | |
| Mnb | the sum of the nominal flexural strengths of the beams that framing into the joint and measured at the faces of the joint |
| Mnc | the sum of the nominal flexural strengths of the columns that framing into the joint and measured at the faces of the joint |
| floor mass of prototype of test model | |
| plastic moment of beam section | |
| plastic moment of column section | |
| prototype-to-model mass ratio | |
| factored design moment | |
| factored axial load | |
| response modification coefficient | |
| ductility factor | |
| design spectral response acceleration parameter in the short period range | |
| design spectral response acceleration parameter for structural period equal to 1.0 s | |
| scale factor | |
| s | center-to-center spacing of transverse reinforcements (ties) |
| fundamental period of the frame | |
| tensile force in longitudinal reinforcement of beam in tension | |
| design lateral strength, design base shear force | |
| shear strength of concrete | |
| column shear force | |
| peak lateral force causing failure of the joint | |
| maximum lateral strength, up to permissible maximum design drift | |
| nominal shear strength | |
| story shear force | |
| factored shear force | |
| nominal shear strength of joint | |
| factored shear strength of joint | |
| effective seismic weight of frame | |
| virtual external work | |
| virtual internal work | |
| effective yield displacement | |
| maximum displacement corresponding to maximum permissible design drift | |
| strain of steel corresponding to yield stress | |
| displacement ductility ratio | |
| overstrength factor | |
| strength reduction factor | |
| story drift | |
| effective yield drift |
References
- Gulkan, P.; Sozen, M.A. Inelastic response of reinforced concrete structures to earthquake motions. ACI Struct. J. 1974, 89, 89–98. [Google Scholar] [CrossRef] [Green Version]
- Blume, J.A.; Newmark, N.M.; Corning, L.H. Design of Multistory Reinforced Concrete Buildings for Earthquake Motions; Portland Cement Association: Skokie, IL, USA, 1961; 318p. [Google Scholar]
- Park, R.; Paulay, T. Reinforced Concrete Structures; John Wiley & Sons, Inc.: New York, NY, USA, 1975; 768p. [Google Scholar]
- American Society of Civil Engineers. Minimum Design Loads and Associated Criteria for Buildings and Other Structures; ASCE/SEI 7-22; American Society of Civil Engineers: Reston, VA, USA, 2021; 1046p. [Google Scholar]
- IBC-2021—International Building Code; International Code Council: Washington, DC, USA, 2020.
- Building Code Requirements for Structural Concrete; ACI-318-19; American Concrete Institute: Farmington Hills, MI, USA, 2019; 822p.
- Hanson, N.W.; Connor, H.W. Seismic resistance of reinforced concrete beam-column joints. J. Struct. Div. ASCE 1967, 93, 533–560. [Google Scholar] [CrossRef]
- Meinheit, D.F.; Jirsa, J.O. Shear Strength of Reinforced Concrete Beam-Column Joints; Report No. 77-1; Department of Civil Engineering, Structures Research Laboratory, University of Texas at Austin: Austin, TX, USA, 1977; 291p. [Google Scholar]
- Recommendation for Design of Beam-Column Connections in Monolithic Reinforced Concrete Structures—ACI-ASCE Committee 352; ACI 352R-02; American Concrete Institute: Farmington Hills, MI, USA, 2019; 822p.
- Chopra, K.A. Dynamics of Structures, Theory and Applications to Earthquake Engineering, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2016; 992p. [Google Scholar]
- Goel, R.K.; Chopra, A.K. Period formulas for moment-resisting frame buildings. J. Struct. Eng. ASCE 1997, 123, 1454–1461. [Google Scholar] [CrossRef] [Green Version]
- Goel, R.K.; Chopra, A.K. Period formulas for concrete shear wall buildings. J. Struct. Eng. ASCE 1998, 124, 426–433. [Google Scholar] [CrossRef] [Green Version]
- Rosenblueth, E.; Contreras, H. Approximate design for multicomponent earthquakes. J. Eng. Mech. Div. ASCE 1977, 103, 881–893. [Google Scholar] [CrossRef]
- Wight, J.K. Reinforced Concrete: Mechanics and Design, 7th ed.; Pearson Education Inc.: Hoboken, NJ, USA, 2016; 1144p. [Google Scholar]
- MacGregor, J.G.; Hanson, J.M. Proposed changes in shear provisions for reinforced and pre-stressed concrete beams. ACI J. Proc. 1969, 66, 276–288. [Google Scholar] [CrossRef]
- Kuchma, D.; Wei, S.; Sanders, D.; Belarbi, A.; Novak, L. Development of the one-way shear design provisions of ACI 318-19. ACI Struct. J. 2019, 116, 285–295. [Google Scholar] [CrossRef]
- Sneed, L.H.; Ramirez, J. Influence of effective depth on the shear strength of concrete beams—Experimental study. ACI Struct. J. 2010, 107, 554–562. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Yu, Q.; Gerstle, W.; Hanson, J.; Ju, J. Justification of ACI 446 code provisions for shear design of reinforced concrete beams. ACI Struct. J. 2007, 104, 601–610. [Google Scholar] [CrossRef]
- Angelakos, D.; Bentz, E.C.; Collins, M.D. Shear strength of large members. ACI Struct. J. 2001, 98, 290–300. [Google Scholar]
- Lubell, A.S.; Sherwood, E.G.; Bentz, E.C.; Collins, M.P. Safe shear design of large wide beams. Concr. Int. 2004, 26, 66–78. [Google Scholar]
- Brown, M.D.; Bayrak, O.; Jirsa, J.O. Design for shear based on loading conditions. ACI Struct. J. 2006, 103, 541–550. [Google Scholar] [CrossRef]
- Sozen, M.A. Seismic behavior of reinforced concrete buildings. In Earthquake Engineering; Bozorgnia, Y., Bertero, V.V., Eds.; CRC Press: New York, NY, USA, 2004; pp. 601–642. [Google Scholar]
- Moncarz, P.; Krawinkler, H. Theory and Application of Experimental Model Analysis in Earthquake Engineering; Report No. 50; Department of Civil and Environmental Engineering, John Blume Earthquake Engineering Center, Stanford University: Stanford, CA, USA, 1981; 263p. [Google Scholar]
- El-Attar, A.-G.; White, R.N.; Gergely, P. Shake Table Test of a 1/6 Scale Two-Story Lightly Reinforced Concrete Building; Report No. 50; Department of Civil and Environmental Engineering, National Center for Earthquake Engineering Research, State University of New York: Buffalo, NY, USA, 1991; 263p. [Google Scholar]
- Newmark, N.M.; Hall, W.J. Earthquake Spectra and Design; Earthquake Engineering Research Institute: Oakland, CA, USA, 1982; 103p. [Google Scholar]
- Federal Emergency Management Agency (FEMA). Quantification of Building Seismic Performance Factors; FEMA-P-695; FEMA: Washington, DC, USA, 2009; 421p. [Google Scholar]
- Priestley, M.J.N.; Calvi, G.M.; Kowalsky, M.J. Displacement Based Seismic Design of Structures; IUSS Press: Pavia, Italy, 2007; 721p. [Google Scholar]
- Nilsson, I.H.E.; Losberg, A. Reinforced concrete corners and joints subjected to bending moment. J. Struct. Div. ASCE 1976, 102, 1229–1254. [Google Scholar] [CrossRef]
- Balint, P.S.; Taylor, H.P.J. Reinforcement Detailing of Frame Corner Joints with Particular Reference to Opening Corners; Technical Report; Cement and Concrete Association: London, UK, 1972; 16p. [Google Scholar]
- French, C.W.; Moehle, J.P. Effect of foor slab on behavior of slab-beam-column connections. ACI Symp. Pap. 1991, 123, 225–258. [Google Scholar] [CrossRef]
- Masoudi, M.; Khajevand, S. Revisiting flexural overstrength in RC beam-and-slab floor systems for seismic design and evaluation. Bull. Earthq. Eng. 2020, 18, 5309–5341. [Google Scholar] [CrossRef]
- Kassem, M.M.; Nazri, F.M.; Farsangi, E.N.; Ozturk, B. Improved vulnerability index methodology to quantify seismic risk and loss assessment in reinforced concrete buildings. J. Earthq. Eng. 2022, 26, 6172–6207. [Google Scholar] [CrossRef]
- Tariq, H.; Jampole, E.A.; Bandelt, M.J. Development and application of spring hinge models to simulate reinforced ductile concrete structural components under cyclic loading. ASCE J. Struct. Eng. 2021, 147, 04020322-1–04020322-20. [Google Scholar] [CrossRef]
- Ahmad, N.; Rizwan, M.; Ilyas, B.; Hussain, S.; Khan, M.U.; Shakeel, H.; Ahmad, M.E. Nonlinear Modeling of RC Substandard Beam–Column Joints for Building Response Analysis in Support of Seismic Risk Assessment and Loss Estimation. Buildings 2022, 12, 1758. [Google Scholar] [CrossRef]
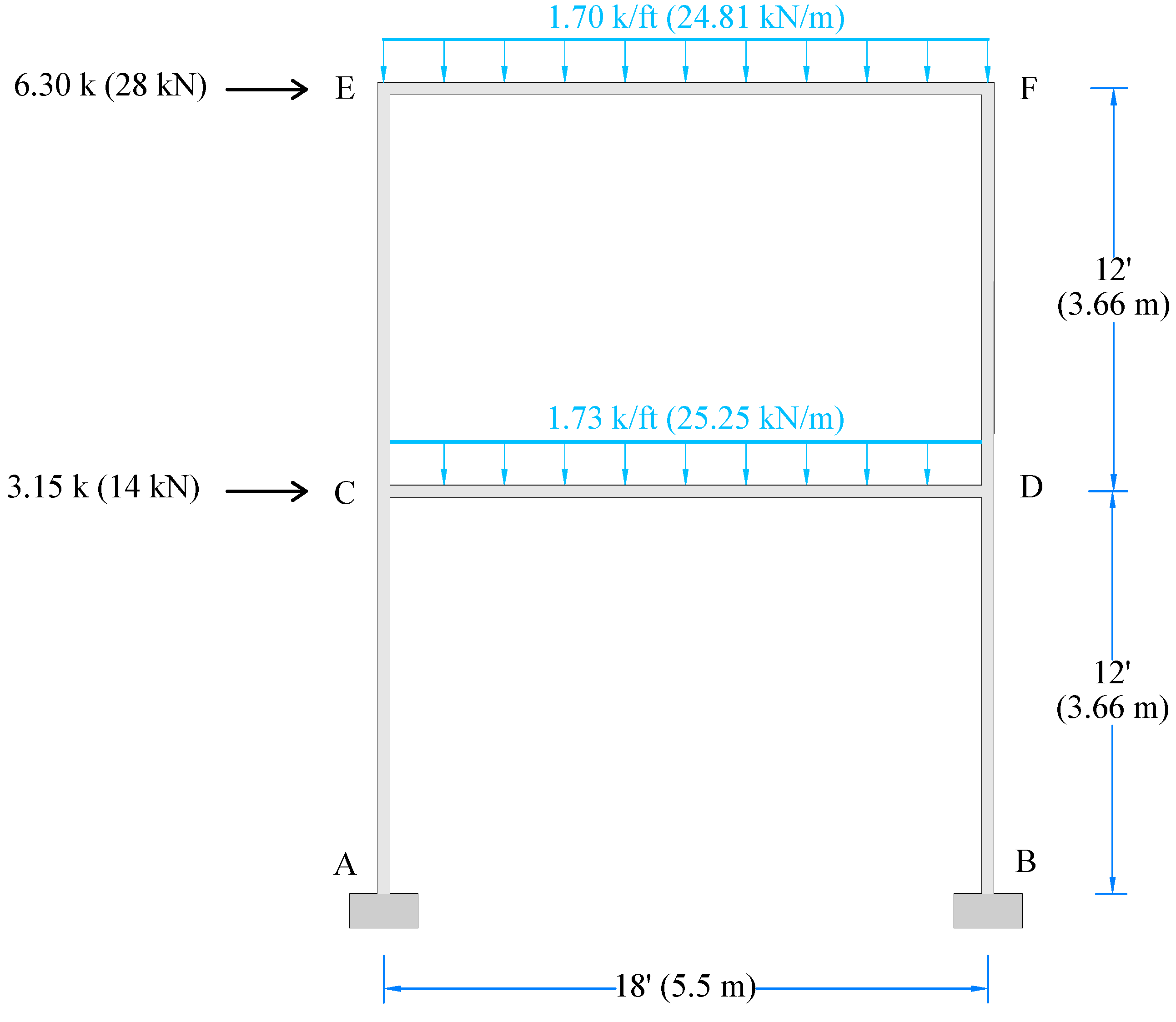







| Member | Depth in. (mm) | Width in. (mm) | Clear Span in. (mm) | fc′ ksi (MPa) | Ec ksi (GPa) | fy ksi (MPa) | Es ksi (GPa) |
|---|---|---|---|---|---|---|---|
| Beams: | 18 (457) | 12 (305) | 204 (5182) | 4 (28) | 3605 (24.86) | 60 (414) | 29,000 (200) |
| Columns: | 12 (305) | 12 (305) | 138 (3505) | 4 (28) | 3605 (24.86) | 60 (414) | 29,000 (200) |
| SDC | SDS | SD1 | Soil | Ie | R | Ωo | Cd |
|---|---|---|---|---|---|---|---|
| C | 0.5 | 0.2 | B | 1.25 | 5.0 | 3 | 4.5 |
| Test Runs | PHA * (g) | Remarks |
|---|---|---|
| 1 | 0.20 | - |
| 2 | 0.40 | Horizontal and vertical flexural cracks at the beam–joint interface. |
| 3 | 0.45 | Aggravation of horizontal flexural cracks at the beam ends. Occurrence of slight cracks in beam–column joints |
| 4 | 0.70 | Extensive damages occurred at the beam–column joint panels on both floor levels. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, S.; Shakeel, H.; Ali, A.; Rizwan, M.; Ahmad, N. Shaking Table Testing of a Low-Rise Reinforced Concrete Intermediate Moment Resisting Frame. Buildings 2022, 12, 2104. https://doi.org/10.3390/buildings12122104
Hussain S, Shakeel H, Ali A, Rizwan M, Ahmad N. Shaking Table Testing of a Low-Rise Reinforced Concrete Intermediate Moment Resisting Frame. Buildings. 2022; 12(12):2104. https://doi.org/10.3390/buildings12122104
Chicago/Turabian StyleHussain, Sida, Hamna Shakeel, Asif Ali, Muhammad Rizwan, and Naveed Ahmad. 2022. "Shaking Table Testing of a Low-Rise Reinforced Concrete Intermediate Moment Resisting Frame" Buildings 12, no. 12: 2104. https://doi.org/10.3390/buildings12122104
APA StyleHussain, S., Shakeel, H., Ali, A., Rizwan, M., & Ahmad, N. (2022). Shaking Table Testing of a Low-Rise Reinforced Concrete Intermediate Moment Resisting Frame. Buildings, 12(12), 2104. https://doi.org/10.3390/buildings12122104