Axial Compression Test and Numerical Investigation of Concrete-Filled Double-Skin Elliptical Tubular Short Columns
Abstract
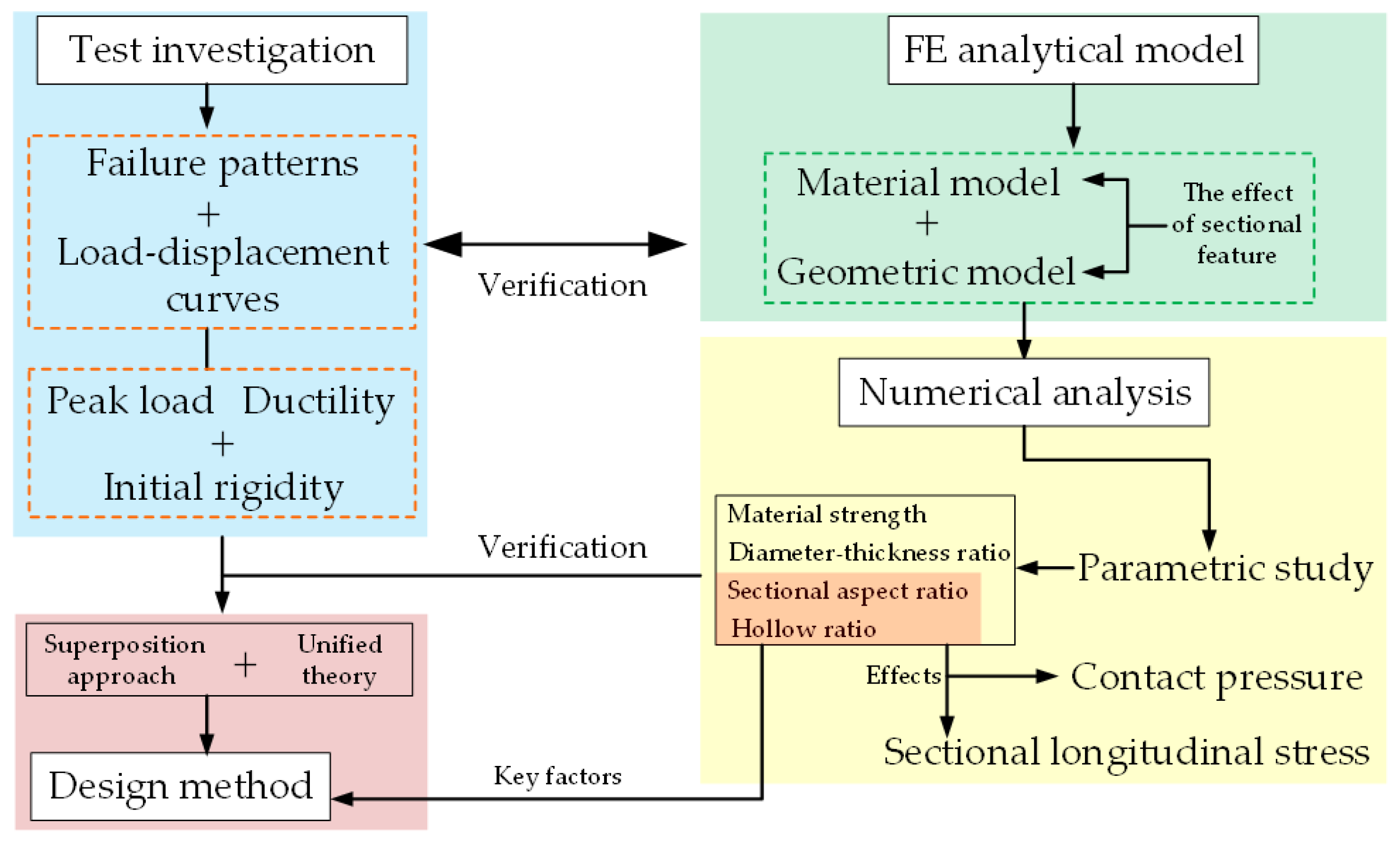
:1. Introduction
2. Experimental Program
2.1. Specimen Design
2.2. Material Property
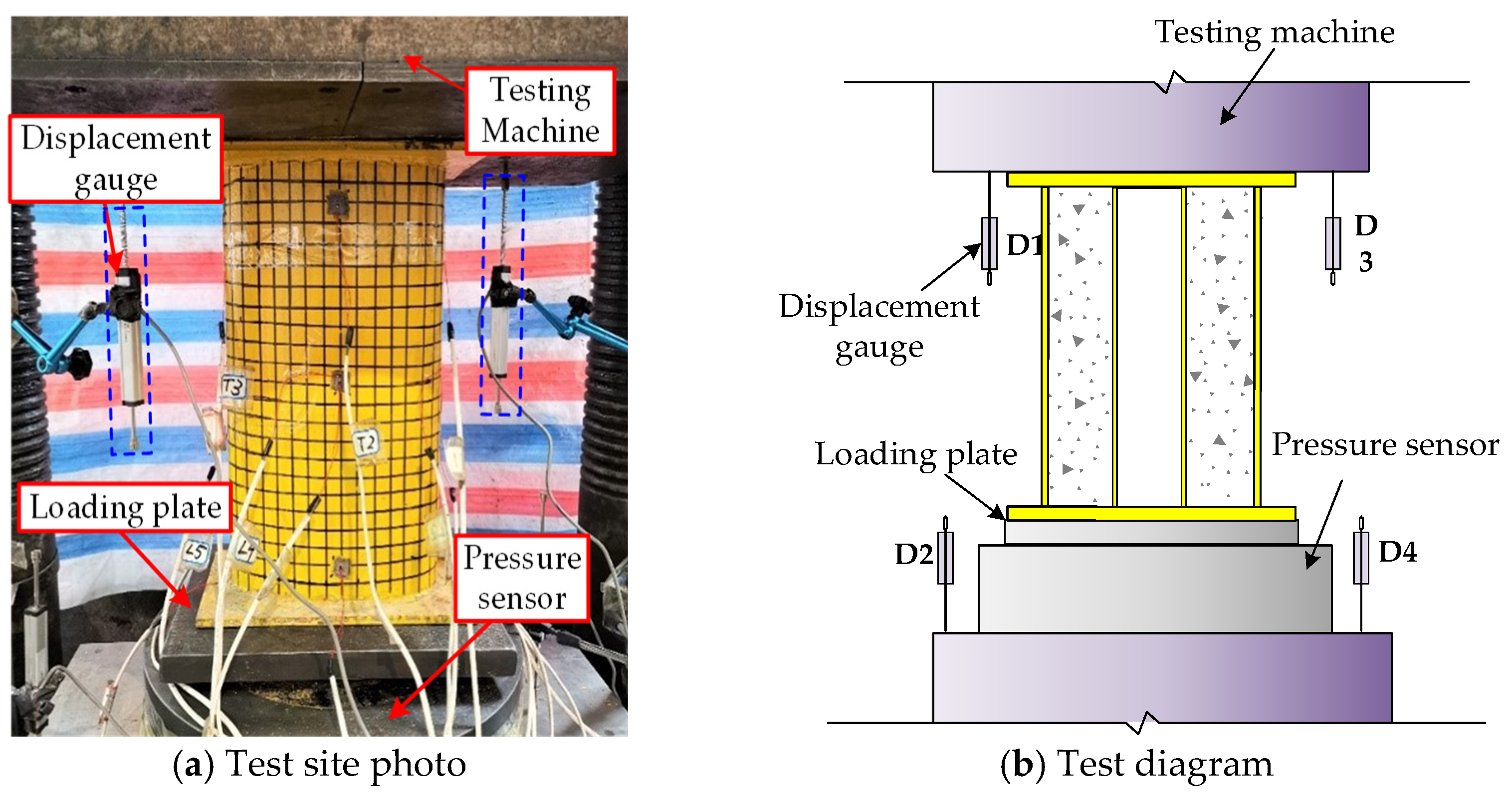
2.3. Loading Device and Measurement Content
3. Test Results and Analyses
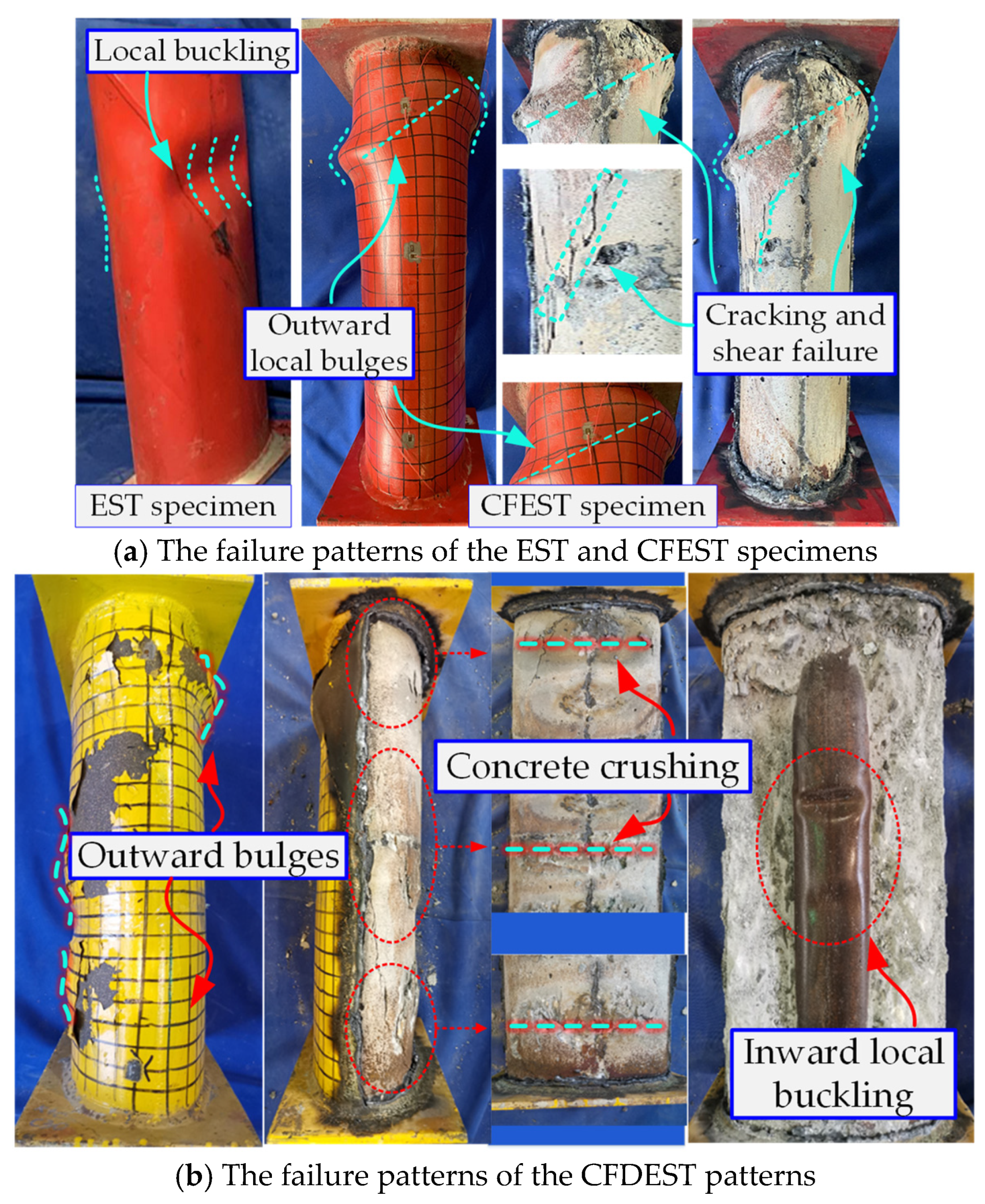
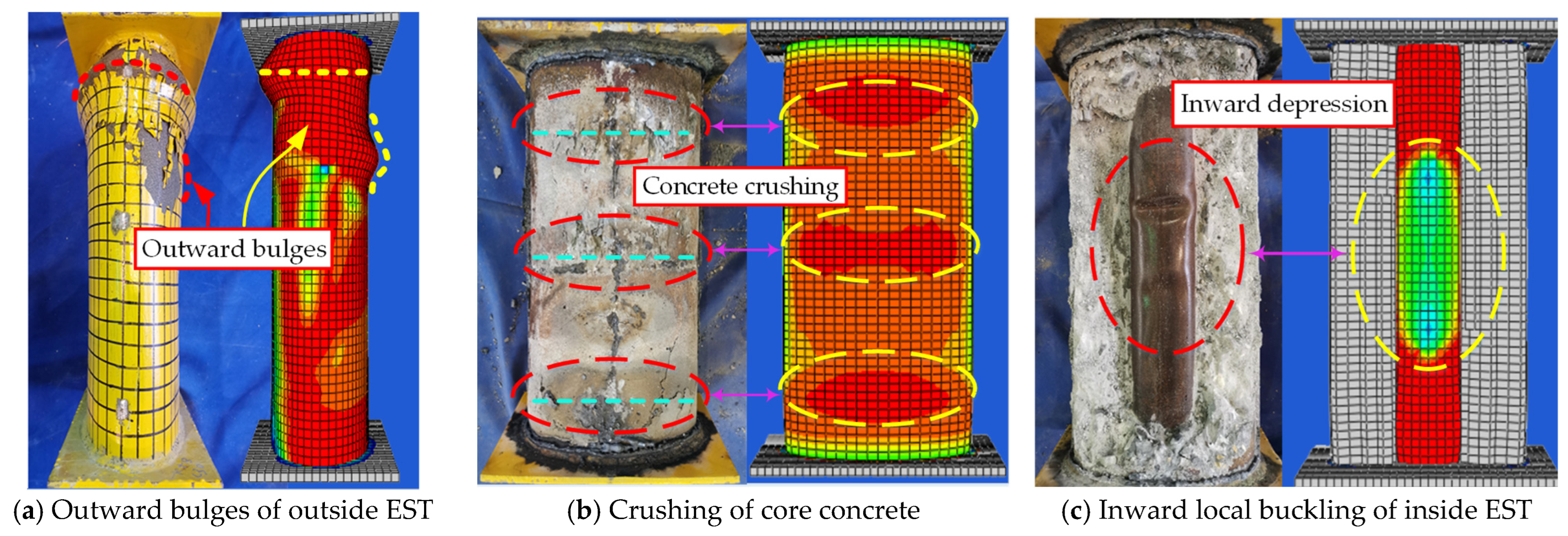
3.1. Failure Patterns
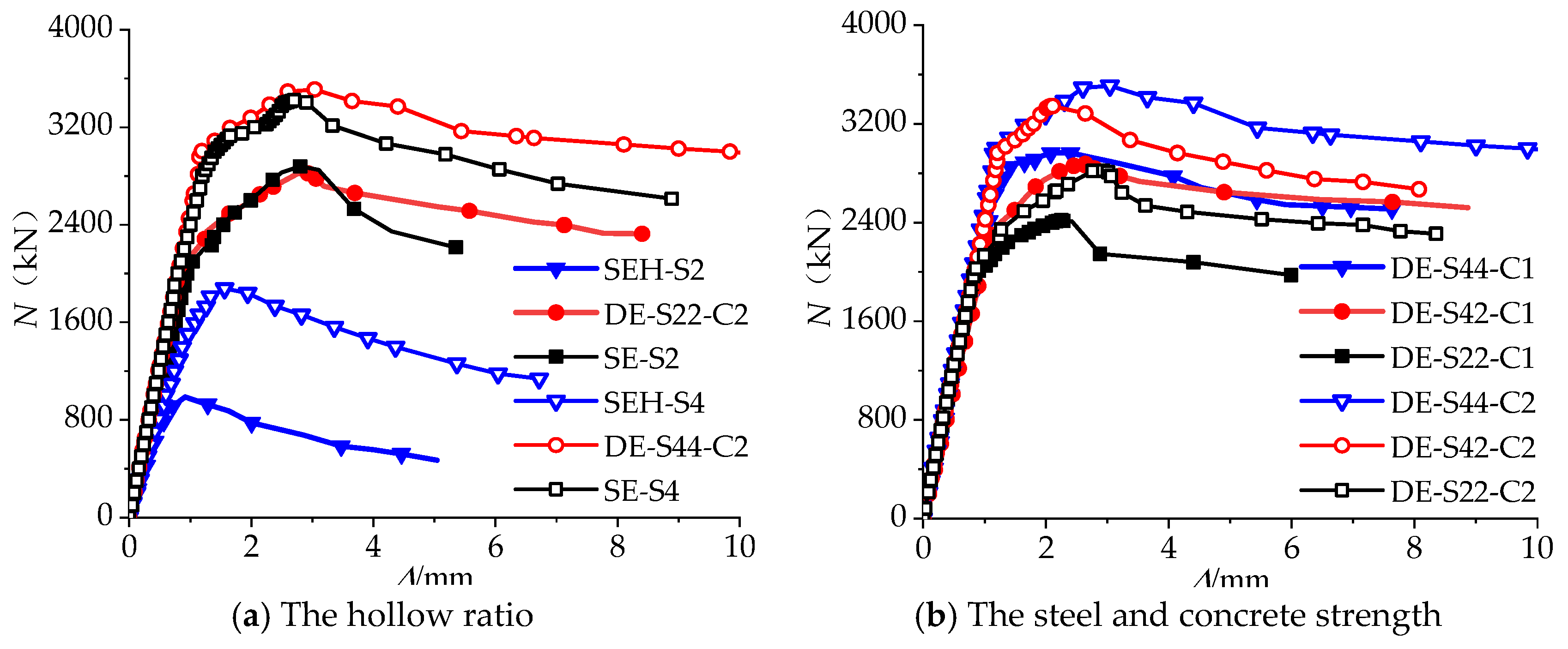
3.2. Axial Pressure versus Axial Displacement Curves
- (1)
- Due to the lack of a core concrete support effect, the N–Δ curves of the EST specimens displayed an obvious and rapid decline trend after their peak loads. Similarly, an obvious descent was also observed in N–Δ relationships of the CFEST short columns, owing to their brittle shear failure of the inside concrete infills.
- (2)
- Along with an increment in hollow ratio, the sectional area and initial rigidity of the test specimen gradually decreased. However, due to the good confining effect of the inside and outside ESTs on the inside core concrete, the brittle characteristics of the plain concrete were effectively suppressed and the descending section of the N–Δ curve was gentler.
- (3)
- The increment in steel material strength barely offered any effect on the curve’s initial rigidity and decreasing segment of the CFDEST short column. Accompanied by an increment in concrete yield stress, the initial rigidity of the axially compressed CFDEST short column was improved. However, because the brittle characteristics of concrete would become more obvious along with the improvement in strength, the slope of the decline section of the N–Δ relationship was heightened.
3.3. The Peak Load and Initial Rigidity
- (1)
- Compared with the axially compressed CFEST short columns, although the sectional area of the CFDEST short columns decreased by about 10.0%, their axial peak loads were not weakened. For instance, the initial rigidity of specimens DE-S44-C2 and DE-S22-C2 was, respectively, 26.6% and 22.7% lower than that of specimens SE-S4 and SE-S2, while the differences in axial peak load were only 0.3% and 3.6%. This may be attributed to the excellent confinement on the inside core concrete furnished by the outside and inside ESTs.
- (2)
- Since the cross-sectional area value of the outside EST is much larger than that of the inside EST, the impression of strength improvement outside EST on the axial peak force of the CFDEST stub column is much greater than that of the inside EST. When the strength of the outside EST changed from 421.5 MPa to 270.3 MPa, the axial peak loads of the specimens DE-S22-C1 and DE-S22-C2 were, respectively, 18.8% and 18.5% lower than those of specimens DE-S42-C1 and DE-S42-C2. On the condition that the strength of the inside EST increased from 270.3 MPa to 421.5 MPa, the axial peak loads of the specimens DE-S44-C1 and DE-S44-C2 were only 3.2% and 5.0% higher than those of specimens DE-S42-C1 and DE-S42-C2, respectively.
- (3)
- The results indicated that the axial peak pressure and initial rigidity of the CFDEST short column were highly improved along with the enhancement in concrete stress. The axial peak loads of specimens DE-S44-C2, DE-S42-C2 and DE-S22-C2 (fcu = 58.3 MPa) were, respectively, 18.3%, 16.3% and 16.6% higher than those of specimens DE-S44-C1, DE-S42-C1 and DE-S22-C1 (fcu = 38.6 MPa) and the initial rigidity increased 11.1%, 13.6% and 12.1% correspondingly.
3.4. Ductility Index
- (1)
- Compared with specimens SEH-S2 and SEH-S4, the DIs of specimens SE-S2-C2 and SE-S4-C2, respectively, increased 101.9% and 60.4%. This phenomenon is caused by the support action furnished by the inside core concrete infills; hence, the local buckling behaviour is inhibited and the ductility of the column is significantly improved.
- (2)
- Compared to the specimens SE-S2-C2 and SE-S4-C2, the specimens DE-S22-C2 and DE-S44-C2, respectively, offered increments of 13.9% and 6.5% in DIs, which are induced by the excellent support effect stemming from outside and inside steel tubes.
- (3)
- The DIs of specimens DE-S44-C1, DE-S42-C1 and DE-S22-C1 were, respectively, 3.2%, 3.4% and 3.0% higher than those of specimens DE-S44-C2, DE-S42-C2 and DE-S22-C2. The comparison reflected that the DI of the axially compressed CFDEST stub column decreased with the increase in concrete strength, due to the brittle feature of the inside concrete with higher compressive strength.
4. Numerical Analyses
4.1. FE Modelling
4.1.1. Material Model
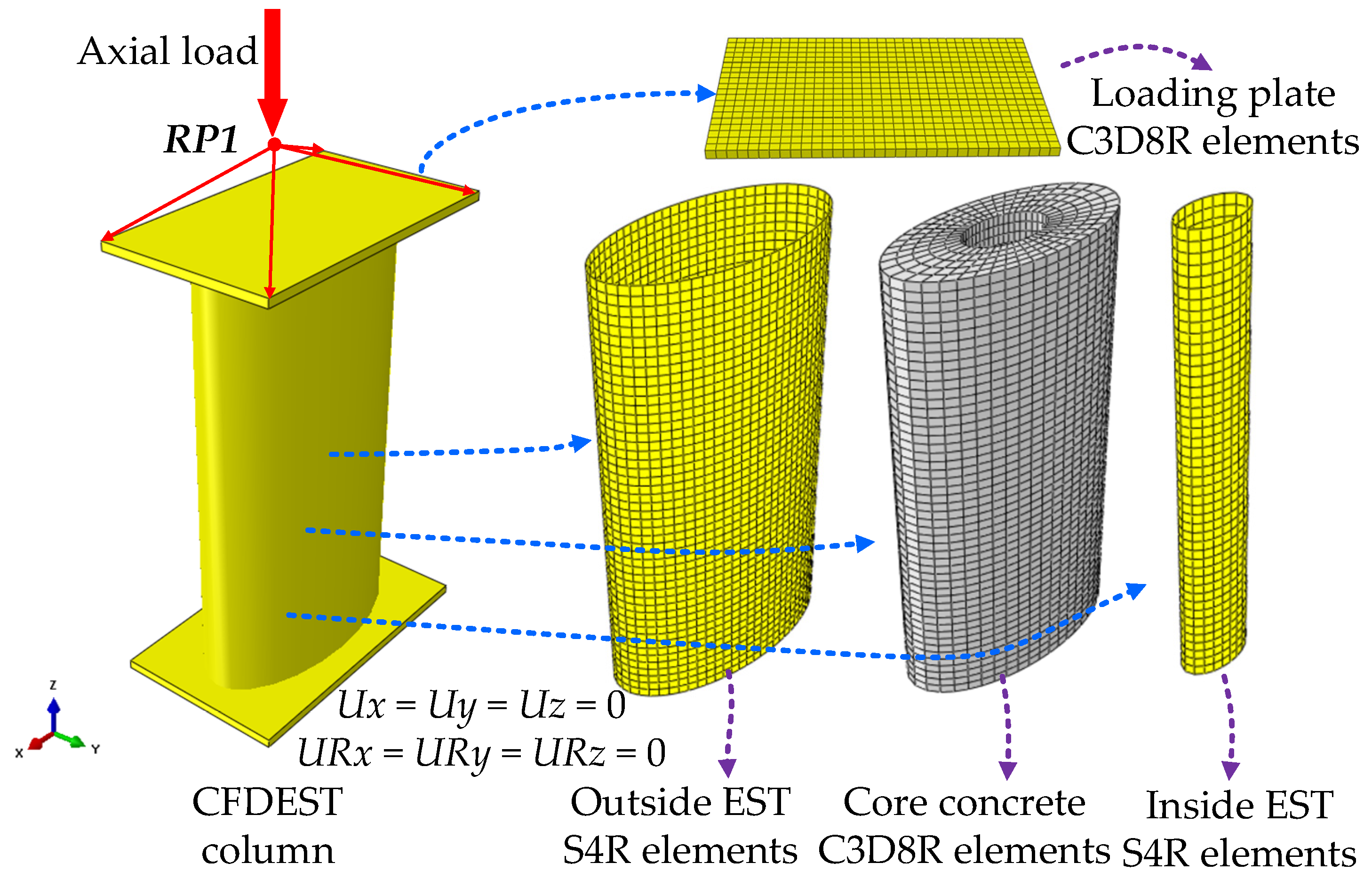
4.1.2. Geometric Model
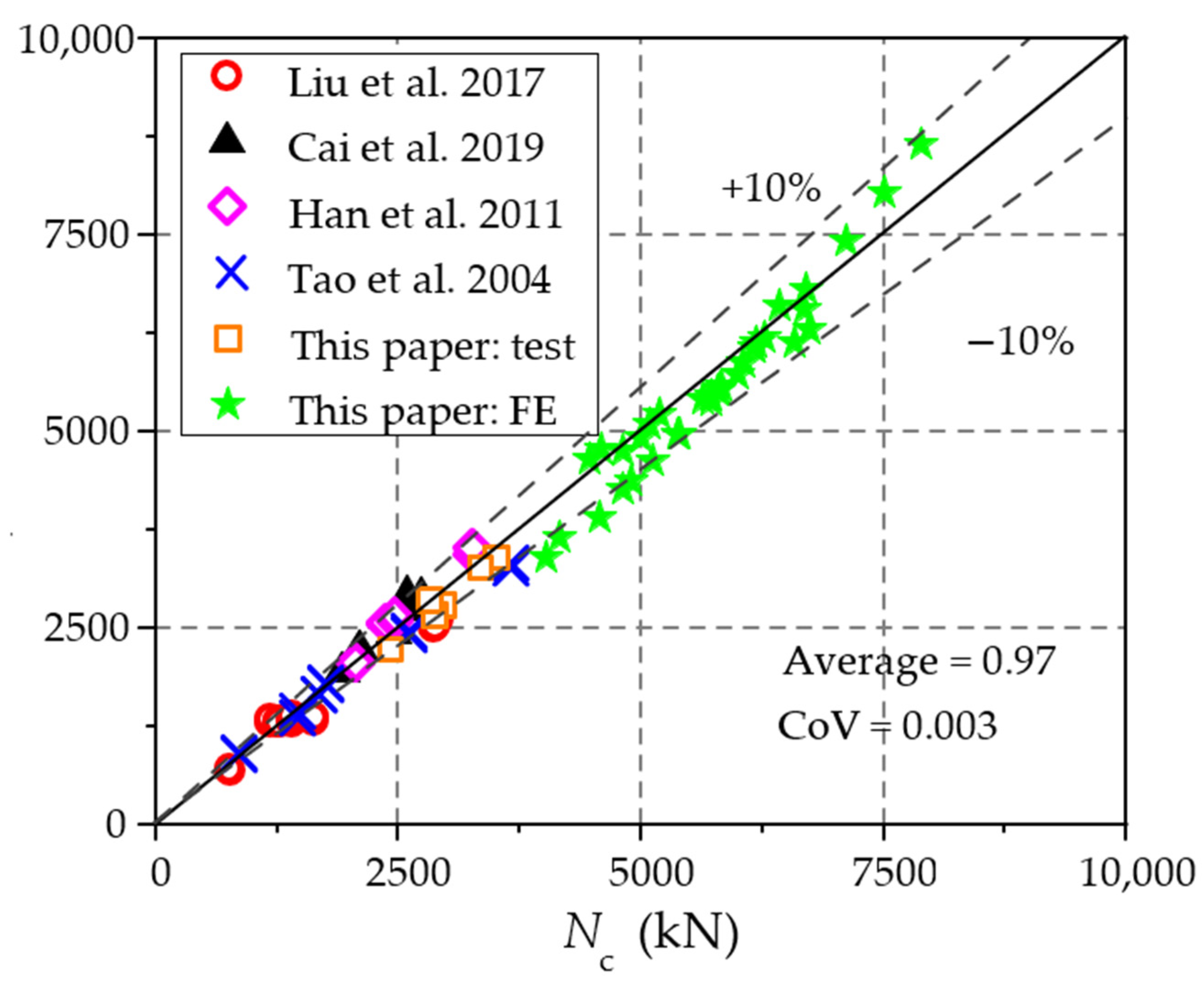
4.2. Test Validation
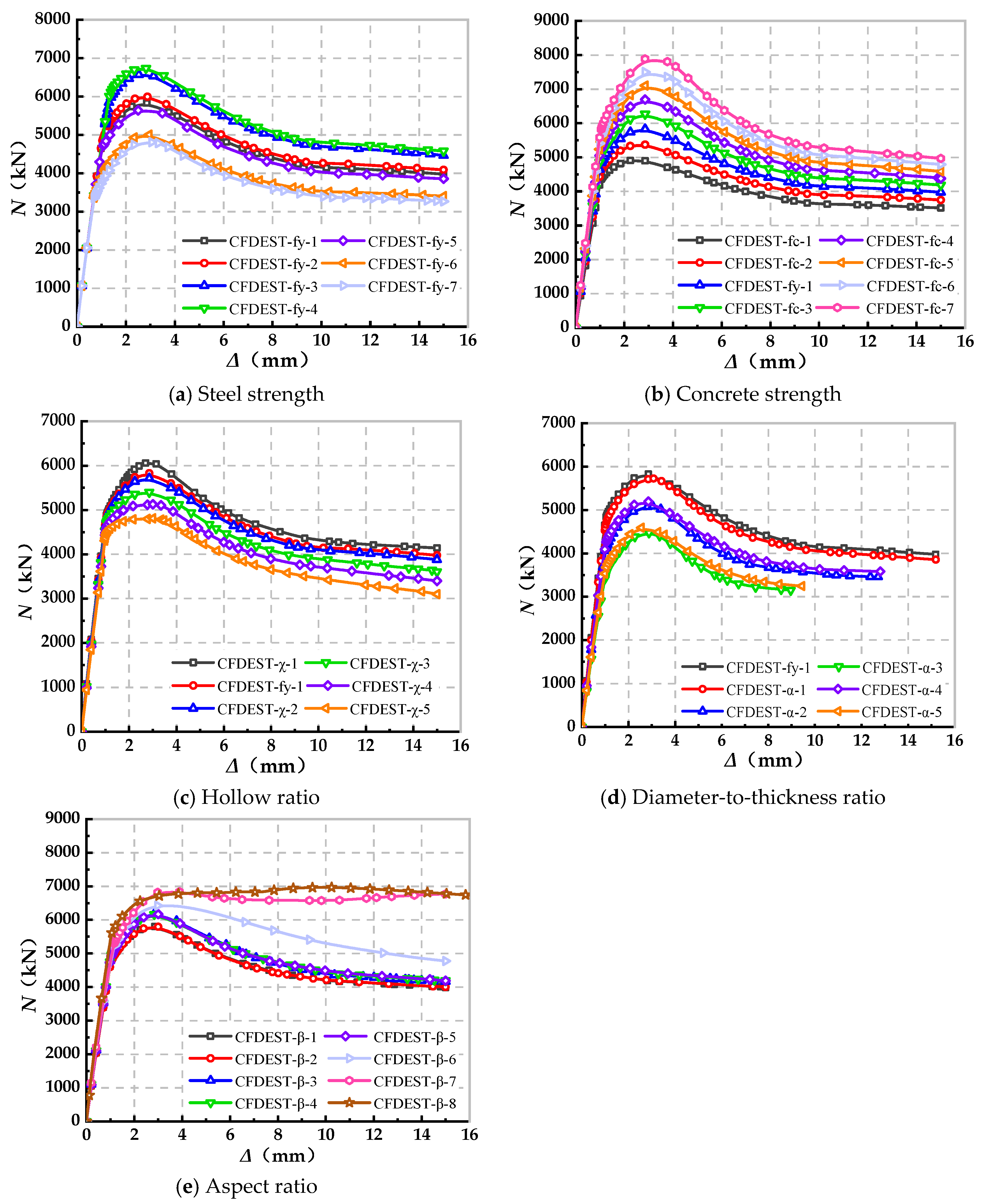
4.3. Parametric Analysis
- (1)
- The peak force of the axially compressed CFDEST stub column is enhanced by the increments in steel and concrete strengths and declined with the increasing hollow ratio, diameter/thickness ratio and sectional aspect ratio;
- (2)
- The initial rigidity of the axially compressed CFDEST short column grows with the increase in concrete stress and decreases with the increments in sectional hollow ratio and diameter/thickness ratio. However, the steel strength and the sectional aspect ratio barely have any effect on the initial rigidity;
- (3)
- The ductility index of the column decreases with the increments in concrete strength, diameter/thickness ratio, hollow ratio and sectional aspect ratio.
4.4. Contact Pressure
4.5. Longitudinal Stress Distribution of the Core Concrete
- (1)
- Along with the growth in sectional hollow ratio, the longitudinal compressed stress of the core concrete between two elliptical steel tubular sections decreases gradually. As the analysis in Section 4.4 showed, the growth in the sectional hollow ratio leads to a gradual decrement in the sectional area of the inside concrete infills and, therefore, the expansion value of the inside core concrete infills would be decreased obviously, which will result in a decrease in confining stress between the inside concrete and outside steel tube. Hence, the peak compressive stress of the inside core concrete decreases accordingly (illustrated in Figure 14a).
- (2)
- Along with the increment in the sectional aspect ratio, the amplitude of change in curvature at different points of the cross-section grows; therefore, the longitudinal compressed stress distribution of the inside concrete under the maximum pressure load begins to show significant heterogeneity. Based on the results shown in Refs. [30,51], it is known that the average confining stress of CFST column with elliptical cross-section decreases with the growth in the sectional aspect ratio, which leads to a gradual fall in concrete’s average longitudinal compressive stress (seen in Figure 14b). The analytical result is consistent with the findings in Section 4.3 and Section 4.4.
- (3)
- In addition, since both the thickness of the concrete layer and the curvature of the EST keep decreasing from the long-axis end to the short-axis end, the confining stress around the long axis is much higher than that around the short axis. As a consequence, the high longitudinal compressed stress of the concrete mainly locates at the region along the long axis, while the longitudinal compressed stress along the short-axis direction is much smaller.
5. Design Method
5.1. Calculation Formulae
5.2. Validation
6. Conclusions
- (1)
- The experimental study reveals that the failure morphologies of the axially compressed CFDEST stub columns majorly contain the outward local bulges of the outside EST, the inward bulges of the inside EST and the crushing of the core concrete.
- (2)
- In light of the experimental study, FE modelling for analysing the axial performance of the CFDEST short column is built and validated by the test outcomes. Then, systematic parametric analyses of their effects on the axial loading mechanical responses of the CFDEST short column are performed.
- (3)
- The increase in the hollow ratio would lead to successive decreases in the lateral expansion of compressive core concrete and the confinement furnished by the outside steel tube. As a result, both the axial compress capacity and ductility of the CFDEST short column may be gradually weakened within the parameter analytical scope.
- (4)
- For the axially compressed CFDEST short column, the confining stress provided by the outside EST on core concrete shows obvious heterogeneity, due to the difference in curvature at various points of the cross-section. With an increment in the sectional aspect ratio of the elliptical cross-section, the average confining pressure on concrete is gradually decreased; therefore, its axial load-bearing capacity and ductility coefficient decrease as well.
- (5)
- This paper proposes a design method for evaluating the axial compress capacity of the CFDEST short column. The calculation formulae are proven to have good accuracy and reliability in prediction.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shams, M.; Saadeghvaziri, M.A. State of the art of concrete-filled steel tubular columns. ACI Struct. J. 1997, 94, 558–571. [Google Scholar]
- Ma, W.C.; Tian, Y.; Zhao, H.L.; Orton, S.L. Time-dependent behavior of reinforced concrete columns subjected to high sustained loads. J. Struct. Eng. 2022, 148, 04022161. [Google Scholar] [CrossRef]
- Wu, L.W.; Tian, Y.; Su, Y.P.; Chen, H.B. Seismic performance of precast composite shear walls reinforced by concrete-filled steel tubes. Eng. Struct. 2018, 162, 72–83. [Google Scholar] [CrossRef]
- Liao, J.; Asteris, P.G.; Cavaleri, L.; Mohammed, A.S.; Lemonis, M.E.; Tsoukalas, M.Z.; Skentou, A.D.; Maraveas, C.; Koopialipoor, M.; Armaghani, D.J. Novel fuzzy-based optimization approaches for the prediction of ultimate axial load of circular concrete-filled steel tubes. Buildings 2021, 11, 629. [Google Scholar] [CrossRef]
- Al-Shaar, A.A.; Göğüş, M.T. Flexural behavior of lightweight concrete and self-compacting concrete-filled steel tube beams. J. Constr. Steel Res. 2018, 149, 153–164. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhou, X.H.; Yan, B.; Gan, D. Shear strength of stiffened square thin-walled concrete-filled steel tubular columns. J. Build. Eng. 2022, 58, 104968. [Google Scholar] [CrossRef]
- Le, K.B.; Cao, V.V. Numerical study of circular concrete filled steel tubes subjected to pure torsion. Buildings 2021, 11, 397. [Google Scholar] [CrossRef]
- Ramírez Ortiz, C.; Gutierrez Amador, A.D.; Ramírez Duque, J.L. Numerical analysis of the seismic behavior of a steel beam-to-concrete-filled steel tubular column connection using external diaphragms. Buildings 2022, 12, 1217. [Google Scholar] [CrossRef]
- Stephens, M.T.; Lehman, D.E.; Roeder, C.W. Seismic performance modeling of concrete-filled steel tube bridges: Tools and case study. Eng. Struct. 2018, 165, 88–105. [Google Scholar] [CrossRef]
- Kang, X.; Liu, Y.; Zhao, S. Design calculation for concrete-filled steel tube under soft lateral impact. Buildings 2022, 12, 1618. [Google Scholar] [CrossRef]
- Wang, Z.G.; Wu, H.; Fang, Q.; Wu, J. Experimental study on the residual axial capacity of ultra high performance cementitious composite filled steel tube (UHPCC-FST) column under contact explosion. Thin-Walled Struct. 2020, 147, 106515. [Google Scholar] [CrossRef]
- Moradi, M.J.; Daneshvar, K.; Ghazi-nader, D.; Hajiloo, H. The prediction of fire performance of concrete-filled steel tubes (CFST) using artificial neural network. Thin-Walled Struct. 2021, 161, 107499. [Google Scholar] [CrossRef]
- Alraeeini, A.S.; Nikbakht, E. Corrosion effect on the flexural behaviour of concrete filled steel tubulars with single and double skins using engineered cementitious composite. Structures 2022, 44, 1680–1694. [Google Scholar] [CrossRef]
- Eurocode 4 1994-1-1:2004; Design of Composite Steel and Concrete Structures-Part 1-1: General Rules and Rules for Buildings. CEN: Brussels, Belgium, 2004.
- Han, L.H. Concrete Filled Steel Tubular Structures—Theory and Practice, 3rd ed.; Science Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- AISC 360-05; Specification for Structural Steel Buildings. AISC: Chicago, IL, USA, 2005.
- GB 50396-2014; Technical Code for Concrete Filled Steel Tubular Structures. Architecture Industrial Press of China: Beijing, China, 2014. (In Chinese)
- Chang, Z.H.; Azmi, M.R.; Yatim, M.Y.M. Behaviour of Concrete-Filled Double Skin Tubular Short Column with Plate Stiffeners Welded Intermittently under Axial Compression. Buildings 2022, 12, 567. [Google Scholar] [CrossRef]
- Yu, P.; Ren, Z.; Yun, W.; Zhao, Y.; Xu, J. Performance of bolt-welded CFST short columns with different initial imperfections: Experimental and numerical studies. Buildings 2022, 12, 1352. [Google Scholar] [CrossRef]
- Tiwary, A.K. Experimental investigation into mild steel circular concrete-filled double skin steel tube columns. J. Constr. Steel Res. 2022, 198, 107527. [Google Scholar] [CrossRef]
- Hassanein, M.F.; Silvestre, N. New confining stress-based design for rubberised concrete-filled single/double-skin steel tubular short columns. J. Constr. Steel Res. 2022, 197, 107435. [Google Scholar] [CrossRef]
- Li, W.; Wang, T.; Han, L.H. Seismic performance of concrete-filled double-skin steel tubes after exposure to fire: Experiments. J. Constr. Steel Res. 2019, 154, 209–223. [Google Scholar] [CrossRef]
- Hou, C.; Han, L.H.; Zhao, X.L. Behaviour of circular concrete filled double skin tubes subjected to local bearing force. Thin-Walled Struct. 2015, 93, 36–53. [Google Scholar] [CrossRef]
- Vernardos, S.; Gantes, C. Experimental behavior of concrete-filled double-skin steel tubular (CFDST) stub members under axial compression: A comparative review. Structures 2019, 22, 383–404. [Google Scholar] [CrossRef]
- Hassanein, M.F.; Kharoob, O.F. Compressive strength of circular concrete-filled double skin tubular short columns. Thin-Walled Struct. 2014, 77, 165–173. [Google Scholar] [CrossRef]
- Ayough, P.; Ramli Sulong, N.H.; Ibrahim, Z.H. Analysis and review of concrete-filled double skin steel tubes under compression. Thin-Walled Struct. 2020, 148, 106495. [Google Scholar] [CrossRef]
- Ren, Q.X.; Han, L.H.; Lam, D.; Hou, C. Experiments on special-shaped CFST stub columns under axial compression. J. Constr. Steel Res. 2014, 98, 123–133. [Google Scholar] [CrossRef]
- Shen, Y.; Tu, Y.; Huang, W. Flexural strength evaluation of multi-cell composite L-shaped concrete-filled steel tubular beams. Buildings 2022, 12, 39. [Google Scholar] [CrossRef]
- Fang, H.; Chan, T.M.; Young, B. Structural performance of concrete-filled cold-formed high-strength steel octagonal tubular stub columns. Eng. Struct. 2021, 239, 112360. [Google Scholar] [CrossRef]
- Wang, J.F.; Liu, W.; Shen, Q.H.; Li, J.Z.; Han, Z.H. Experimental investigation and theoretical analysis of axially-loaded concrete-filled elliptical tubes with circumferential gaps. Thin-Walled Struct. 2022, 181, 110100. [Google Scholar] [CrossRef]
- Cai, Y.C.; Quach, W.M.; Young, B. Experimental and numerical investigation of concrete-filled hot-finished and cold-formed steel elliptical tubular stub columns. Thin-Walled Struct. 2019, 145, 106437. [Google Scholar] [CrossRef]
- Xing, W.B.; Shen, Q.H.; Wang, J.F.; Sheng, M.Y. Performance and design of oval-ended elliptical CFT columns under combined axial compression-torsion. J. Constr. Steel Res. 2020, 172, 106148. [Google Scholar] [CrossRef]
- Yang, H.; Lam, D.; Gardner, L. Testing and analysis of concrete-filled elliptical hollow sections. Testing and analysis of concrete-filled elliptical hollow sections. Eng. Struct. 2008, 30, 3771–3781. [Google Scholar] [CrossRef]
- Yang, H.; Liu, F.Q.; Chan, T.M.; Wang, W. Behaviours of concrete-filled cold-formed elliptical hollow section beam-columns with varying aspect ratios. Thin-Walled Struct. 2017, 120, 9–28. [Google Scholar] [CrossRef]
- Dai, X.; Lam, D. Numerical modelling of the axial compressive behaviour of short concrete-filled elliptical steel columns. J. Constr. Steel Res. 2010, 66, 931–942. [Google Scholar] [CrossRef]
- Mahgub, M.; Ashour, A.; Lam, D.; Dai, X. Tests of self-compacting concrete filled elliptical steel tube columns. Thin-Walled Struct. 2017, 110, 27–34. [Google Scholar] [CrossRef] [Green Version]
- Jamaluddin, N.; Lam, D.; Dai, X.H.; Ye, J. An experimental study on elliptical concrete filled columns under axial compression. J. Constr. Steel Res. 2013, 87, 6–16. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.Q.; Wang, Y.Y.; Chan, T.M. Behaviour of concrete-filled cold-formed elliptical hollow sections with varying aspect ratios. Thin-Walled Struct. 2017, 110, 47–61. [Google Scholar] [CrossRef]
- Hassanein, M.F.; Patel, V.I.; Hadidy, A.M.; Abadi, H.A.; Elchalakanid, M. Structural behaviour and design of elliptical high-strength concrete-filled steel tubular short compression members. Eng. Struct. 2018, 173, 495–511. [Google Scholar] [CrossRef]
- Ren, Q.X.; Han, L.H.; Lam, D.; Li, W. Tests on elliptical concrete filled steel tubular (CFST) beams and columns. J. Constr. Steel Res. 2014, 99, 149–160. [Google Scholar] [CrossRef]
- Zhang, T.; Gong, Y.Z.; Ding, F.X.; Liu, X.M.; Yu, Z.W. Experimental and numerical investigation on the flexural behavior of concrete-filled elliptical steel tube (CFET). J. Build. Eng. 2021, 41, 102412. [Google Scholar] [CrossRef]
- Uenaka, K.; Tsunokake, H. Behavior of concrete filled elliptical steel tubular deep beam under bending-shear. Structures 2017, 10, 89–95. [Google Scholar] [CrossRef]
- Uenaka, K.; Tsunokake, H. Concrete filled elliptical steel tubular members with large diameter-to-thickness ratio subjected to bending. Structures 2016, 5, 58–66. [Google Scholar] [CrossRef]
- Wang, J.F.; Tao, S.Q.; Shen, Q.H.; Sheng, M.Y. Mechanical performance and bearing capacity calculation of elliptical CFST members subjected to compression, bending and torsion. Prog. Steel Build. Struct. 2022, 24, 45–55. (In Chinese) [Google Scholar]
- Xu, Y.W.; Yao, J.; Hu, F.; Zhou, Y.; Jiang, S. Seismic behavior of elliptical concrete-filled steel tubular columns under combined axial compression and cyclic lateral loading. Adv. Mater. Sci. Eng. 2021, 1, 5892788. [Google Scholar] [CrossRef]
- Espinos, A.; Romero, M.L.; Serra, E.; Hospitaler, A. Experimental investigation on the fire behaviour of rectangular and elliptical slender concrete-filled tubular columns. Thin-Walled Struct. 2015, 93, 137–148. [Google Scholar] [CrossRef]
- Espinos, A.; Romero, M.L.; Portolés, J.M.; Hospitaler, A. Ambient and fire behavior of eccentrically loaded elliptical slender concrete-filled tubular columns. J. Constr. Steel Res. 2014, 100, 97–107. [Google Scholar] [CrossRef]
- Ahmed, M.; Ci, J.C.; Yan, X.F.; Chen, S.C. Nonlinear analysis of elliptical concrete-filled stainless steel tubular short columns under axial compression. Structures 2021, 32, 1347–1385. [Google Scholar] [CrossRef]
- Sheehan, T.; Dai, X.H.; Chan, T.M.; Lam, D. Structural response of concrete-filled elliptical steel hollow sections under eccentric compression. Eng. Struct. 2012, 45, 314–323. [Google Scholar] [CrossRef] [Green Version]
- McCann, F.; Gardner, L.; Qiu, W. Experimental study of slender concrete-filled elliptical hollow section beam-columns. J. Constr. Steel Res. 2015, 113, 185–194. [Google Scholar] [CrossRef]
- Shen, Q.H.; Li, J.Z.; Wang, J.F. Experimental, numerical and design investigations on the performance of axially-loaded ECFT stub columns with spherical-cap gaps. Structures 2022, 46, 109–127. [Google Scholar] [CrossRef]
- GB/T2975-2018; Steel and Steel Products-Location and Preparation of Samples and Test Pieces for Mechanical Testing. General Administration for National Market Supervision: Beijing, China, 2018. (In Chinese)
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. Ministry of Housing and Urban-Rural Construction of the People’s Republic of China: Beijing, China, 2019. (In Chinese)
- Shen, Q.H.; Wang, F.Q.; Wang, J.F.; Ma, X.F. Cyclic behaviour and design of cold-formed round-ended concrete-filled steel tube columns. J. Constr. Steel Res. 2022, 190, 107089. [Google Scholar] [CrossRef]
- Wang, J.F.; Xiao, Q.; Shen, Q.H.; Sheng, M.Y. Analysis on the axial behavior of CFRP wrapped circular CFST stub columns with initial concrete imperfection. Prog. Steel Build. Struct. 2021, 23, 44–53. (In Chinese) [Google Scholar]
- Huang, H.; Han, L.H.; Tao, Z.; Zhao, X.L. Analytical behaviour of concrete-filled double skin steel tubular (CFDST) stub columns. J. Constr. Steel Res. 2010, 66, 542–555. [Google Scholar] [CrossRef]
- Han, L.H.; Ren, Q.X.; Li, W. Tests on stub stainless steel–concrete–carbon steel double-skin tubular (DST) columns. J. Constr. Steel Res. 2011, 67, 437–452. [Google Scholar] [CrossRef]
- Tao, Z.; Han, L.H.; Zhao, X.L. Behaviour of concrete-filled double skin (CHS inner and CHS outer) steel tubular stub columns and beam-columns. J. Constr. Steel Res. 2004, 60, 1129–1158. [Google Scholar] [CrossRef]

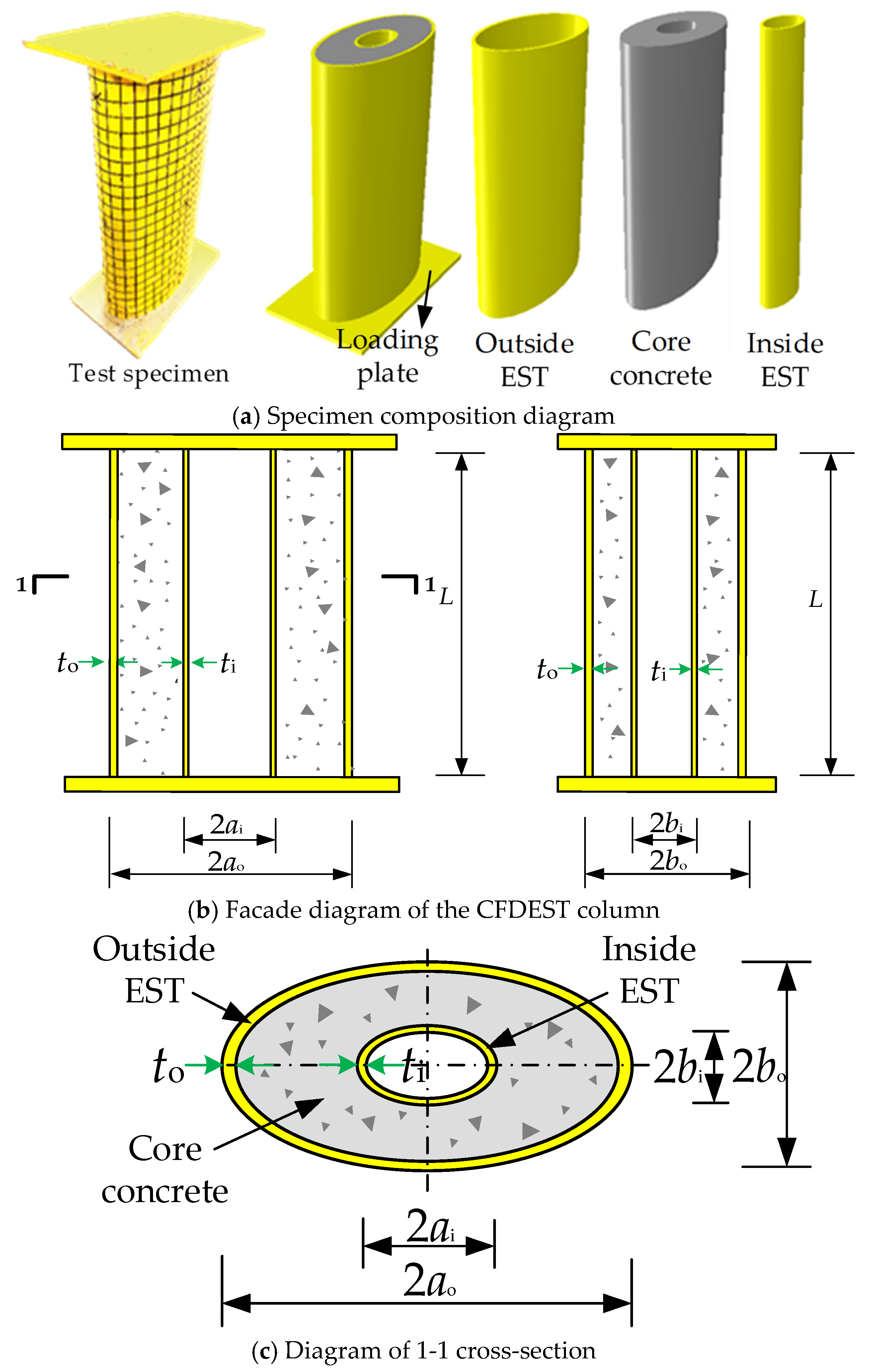




| Specimen ID | 2ao × 2bo × to/mm | 2ai × 2bi × ti/mm | fyo | fyi | fcu |
|---|---|---|---|---|---|
| SEH-S2 | 280 × 140 × 6 | — | 270.3 | — | — |
| SEH-S4 | 280 × 140 × 6 | — | 421.5 | — | — |
| SE-S2 | 280 × 140 × 6 | — | 270.3 | — | 58.3 |
| SE-S4 | 280 × 140 × 6 | — | 421.5 | — | 58.3 |
| DE-S44-C1 | 280 × 140 × 6 | 95 × 53 × 4 | 421.5 | 433.7 | 38.6 |
| DE-S42-C1 | 280 × 140 × 6 | 95 × 53 × 4 | 421.5 | 276.2 | 38.6 |
| DE-S22-C1 | 280 × 140 × 6 | 95 × 53 × 4 | 270.3 | 276.2 | 38.6 |
| DE-S44-C2 | 280 × 140 × 6 | 95 × 53 × 4 | 421.5 | 433.7 | 58.3 |
| DE-S42-C2 | 280 × 140 × 6 | 95 × 53 × 4 | 421.5 | 276.2 | 58.3 |
| DE-S22-C2 | 280 × 140 × 6 | 95 × 53 × 4 | 270.3 | 276.2 | 58.3 |
| ID | fy/MPa | fu/MPa | εy/% | Es/MPa | δ/% |
|---|---|---|---|---|---|
| S-a | 270.3 | 368.9 | 0.31 | 203.6 | 23.5 |
| S-b | 421.5 | 485.6 | 0.37 | 205.8 | 21.1 |
| S-c | 276.2 | 352.8 | 0.31 | 202.1 | 24.2 |
| S-d | 433.7 | 491.1 | 0.38 | 206.2 | 20.6 |
| Specimen ID | Δy/mm | Δ0.85/mm | DI | Ki/kN·mm−1 | Nut/kN |
|---|---|---|---|---|---|
| SEH-S2 | 0.65 | 1.39 | 2.14 | 1505.8 | 985 |
| SEH-S4 | 1.09 | 3.57 | 3.28 | 1730.2 | 1881 |
| SE-S2-C2 | 0.84 | 3.63 | 4.32 | 3233.7 | 2723 |
| SE-S4-C2 | 1.03 | 5.42 | 5.26 | 3405.2 | 3501 |
| DE-S44-C1 | 1.32 | 7.63 | 5.78 | 2250.1 | 2966.8 |
| DE-S42-C1 | 1.31 | 7.42 | 5.42 | 2200.3 | 2874.4 |
| DE-S22-C1 | 1.08 | 5.12 | 5.07 | 2230.1 | 2419.6 |
| DE-S44-C2 | 1.40 | 7.84 | 5.60 | 2500.2 | 3510.2 |
| DE-S42-C2 | 1.34 | 7.29 | 5.24 | 2499.9 | 3344.3 |
| DE-S22-C2 | 1.13 | 5.56 | 4.92 | 2500.0 | 2822.0 |
| Parameters | Specimen ID | 2ao × 2bo × to × L | 2ai × 2bi × ti × L | fyo | fyi | fcu | χ | Nu | Ki | Δ0.85 | DI |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Steel strength | CFDEST-fy-1 | 400 × 200 × 8 × 600 | 160 × 80 × 4 × 600 | 355 | 355 | 50 | 15% | 5829.4 | 4754.1 | 5.68 | 4.63 |
| CFDEST-fy-2 | 400 × 200 × 8 × 600 | 160 × 80 × 4 × 600 | 355 | 460 | 50 | 15% | 5997.4 | 4754.1 | 5.83 | 4.62 | |
| CFDEST-fy-3 | 400 × 200 × 8 × 600 | 160 × 80 × 4 × 600 | 460 | 355 | 50 | 15% | 6573.8 | 4754.1 | 5.67 | 4.10 | |
| CFDEST-fy-4 | 400 × 200 × 8 × 600 | 160 × 80 × 4 × 600 | 460 | 460 | 50 | 15% | 6735.8 | 4754.1 | 5.88 | 4.15 | |
| CFDEST-fy-5 | 400 × 200 × 8 × 600 | 160 × 80 × 4 × 600 | 355 | 235 | 50 | 15% | 5634.0 | 4754.1 | 5.76 | 4.86 | |
| CFDEST-fy-6 | 400 × 200 × 8 × 600 | 160 × 80 × 4 × 600 | 235 | 355 | 50 | 15% | 5005.1 | 4754.1 | 5.49 | 5.21 | |
| CFDEST-fy-7 | 400 × 200 × 8 × 600 | 160 × 80 × 4 × 600 | 235 | 235 | 50 | 15% | 4809.7 | 4754.1 | 5.59 | 5.53 | |
| Concrete strength | CFDEST-fc-1 | 400 × 200 × 8 × 600 | 160 × 80 × 4 × 600 | 355 | 355 | 30 | 15% | 4903.9 | 4276.9 | 6.11 | 5.33 |
| CFDEST-fc-2 | 400 × 200 × 8 × 600 | 160 × 80 × 4 × 600 | 355 | 355 | 40 | 15% | 5372.7 | 4518.3 | 5.91 | 4.97 | |
| CFDEST-fc-3 | 400 × 200 × 8 × 600 | 160 × 80 × 4 × 600 | 355 | 355 | 60 | 15% | 6269.7 | 4989.3 | 5.68 | 4.52 | |
| CFDEST-fc-4 | 400 × 200 × 8 × 600 | 160 × 80 × 4 × 600 | 355 | 355 | 70 | 15% | 6695.1 | 5216.2 | 5.51 | 4.29 | |
| CFDEST-fc-5 | 400 × 200 × 8 × 600 | 160 × 80 × 4 × 600 | 355 | 355 | 80 | 15% | 7106.0 | 5433.2 | 5.46 | 4.17 | |
| CFDEST-fc-6 | 400 × 200 × 8 × 600 | 160 × 80 × 4 × 600 | 355 | 355 | 90 | 15% | 7503.7 | 5644.2 | 5.53 | 4.16 | |
| CFDEST-fc-7 | 400 × 200 × 8 × 600 | 160 × 80 × 4 × 600 | 355 | 355 | 100 | 15% | 7888.4 | 5846.9 | 5.54 | 4.11 | |
| Hollow ratio | CFDEST-χ-1 | 400 × 200 × 8 × 600 | 120 × 60 × 4 × 600 | 355 | 355 | 50 | 10% | 6059.4 | 4783.0 | 5.46 | 4.31 |
| CFDEST-χ-2 | 400 × 200 × 8 × 600 | 180 × 90 × 4 × 600 | 355 | 355 | 50 | 20% | 5715.7 | 4724.2 | 5.65 | 4.67 | |
| CFDEST-χ-3 | 400 × 200 × 8 × 600 | 220 × 110 × 4 × 600 | 355 | 355 | 50 | 30% | 5400.3 | 4630.3 | 5.68 | 4.87 | |
| CFDEST-χ-4 | 400 × 200 × 8 × 600 | 250 × 125 × 4 × 600 | 355 | 355 | 50 | 40% | 5127.3 | 4528.4 | 5.79 | 5.11 | |
| CFDEST-χ-5 | 400 × 200 × 8 × 600 | 280 × 140 × 4 × 600 | 355 | 355 | 50 | 50% | 4809.6 | 4403.3 | 5.71 | 5.23 | |
| Diameter-to-thickness ratio | CFDEST-α-1 | 400 × 200 × 8 × 600 | 160 × 80 × 3 × 600 | 355 | 355 | 50 | 15% | 5726.1 | 4628.4 | 5.53 | 4.47 |
| CFDEST-α-2 | 400 × 200 × 6 × 600 | 160 × 80 × 3 × 600 | 355 | 355 | 50 | 15% | 5087.9 | 4106.4 | 5.19 | 4.19 | |
| CFDEST-α-3 | 400 × 200 × 4 × 600 | 160 × 80 × 3 × 600 | 355 | 355 | 50 | 15% | 4474.3 | 3497.3 | 4.73 | 3.70 | |
| CFDEST-α-4 | 400 × 200 × 6 × 600 | 160 × 80 × 4 × 600 | 355 | 355 | 50 | 15% | 5195.2 | 4189.7 | 5.39 | 4.35 | |
| CFDEST-α-5 | 400 × 200 × 4 × 600 | 160 × 80 × 4 × 600 | 355 | 355 | 50 | 15% | 4591.8 | 3623.0 | 4.56 | 3.60 | |
| Aspect ratio | CFDEST-β-1 | 400 × 200 × 8 × 600 | 140 × 95 × 4 × 600 | 355 | 355 | 50 | 15% | 5803.3 | 4718.1 | 5.62 | 4.57 |
| CFDEST-β-2 | 400 × 200 × 8 × 600 | 115 × 115 × 4 × 600 | 355 | 355 | 50 | 15% | 5796.2 | 4699.2 | 5.90 | 4.78 | |
| CFDEST-β-3 | 360 × 240 × 8 × 600 | 160 × 80 × 4 × 600 | 355 | 355 | 50 | 15% | 6190.4 | 4891.9 | 5.83 | 4.61 | |
| CFDEST-β-4 | 360 × 240 × 8 × 600 | 140 × 95 × 4 × 600 | 355 | 355 | 50 | 15% | 6164.2 | 4854.8 | 5.77 | 4.54 | |
| CFDEST-β-5 | 360 × 240 × 8 × 600 | 115 × 115 × 4 × 600 | 355 | 355 | 50 | 15% | 6169.5 | 4839.7 | 5.99 | 4.70 | |
| CFDEST-β-6 | 300 × 300 × 8 × 600 | 160 × 80 × 4 × 600 | 355 | 355 | 50 | 15% | 6427.4 | 4978.4 | 8.88 | 6.88 | |
| CFDEST-β-7 | 300 × 300 × 8 × 600 | 140 × 95 × 4 × 600 | 355 | 355 | 50 | 15% | 6678.2 | 5057.0 | / | / | |
| CFDEST-β-8 | 300 × 300 × 8 × 600 | 115 × 115 × 4 × 600 | 355 | 355 | 50 | 15% | 6712.7 | 5071.1 | / | / |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Shen, Q.; Wang, J.; Li, B.; Li, G. Axial Compression Test and Numerical Investigation of Concrete-Filled Double-Skin Elliptical Tubular Short Columns. Buildings 2022, 12, 2120. https://doi.org/10.3390/buildings12122120
Li J, Shen Q, Wang J, Li B, Li G. Axial Compression Test and Numerical Investigation of Concrete-Filled Double-Skin Elliptical Tubular Short Columns. Buildings. 2022; 12(12):2120. https://doi.org/10.3390/buildings12122120
Chicago/Turabian StyleLi, Jingzhe, Qihan Shen, Jingfeng Wang, Beibei Li, and Guoqiang Li. 2022. "Axial Compression Test and Numerical Investigation of Concrete-Filled Double-Skin Elliptical Tubular Short Columns" Buildings 12, no. 12: 2120. https://doi.org/10.3390/buildings12122120
APA StyleLi, J., Shen, Q., Wang, J., Li, B., & Li, G. (2022). Axial Compression Test and Numerical Investigation of Concrete-Filled Double-Skin Elliptical Tubular Short Columns. Buildings, 12(12), 2120. https://doi.org/10.3390/buildings12122120