Modeling of Damping Characteristics of Rubber Geopolymer Concrete Based on Finite Element Simulation
Abstract
1. Introduction
2. Materials and Methods
2.1. Test Materials
2.2. Test Plan
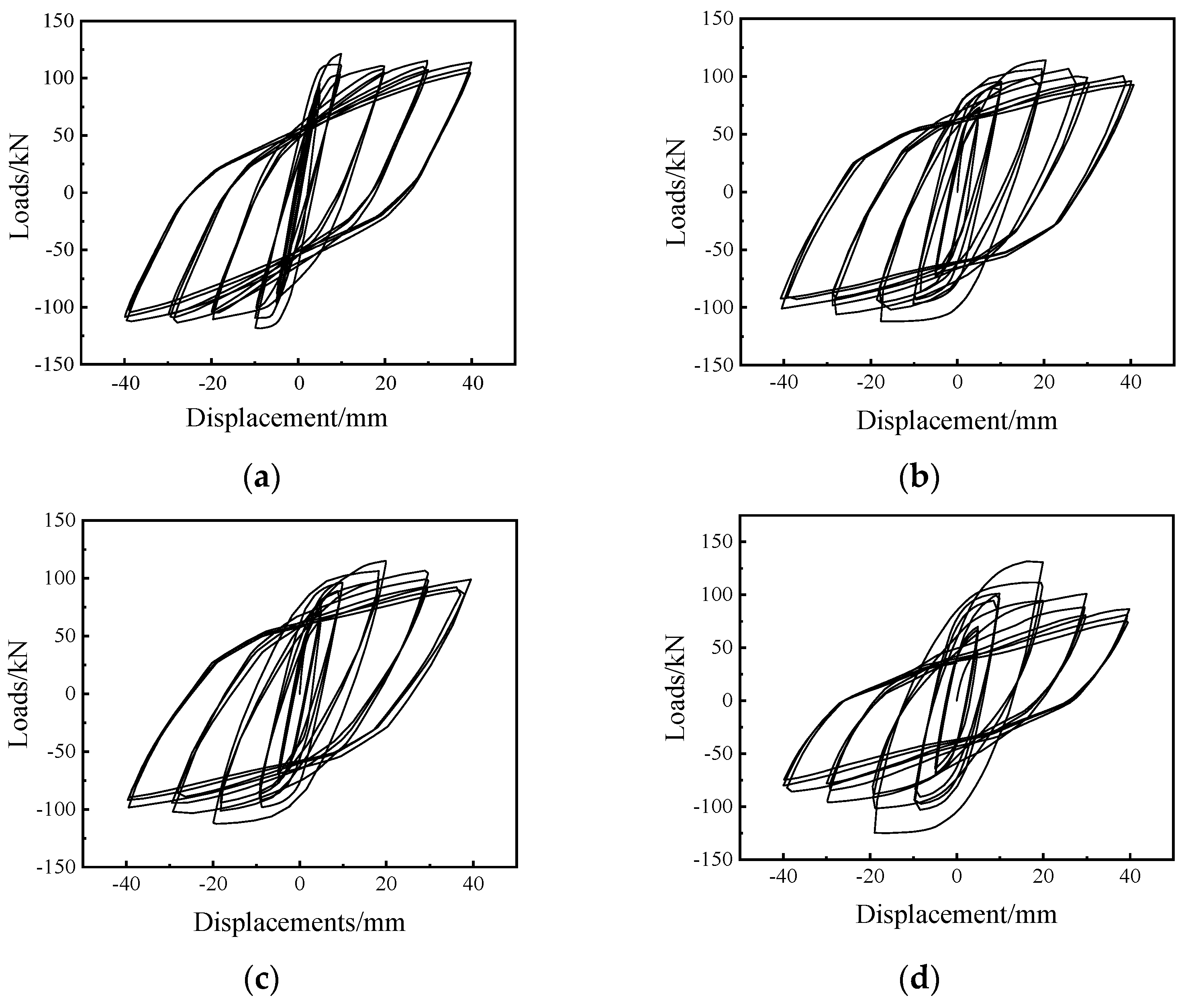
2.3. Test Results
3. Finite Element Simulation
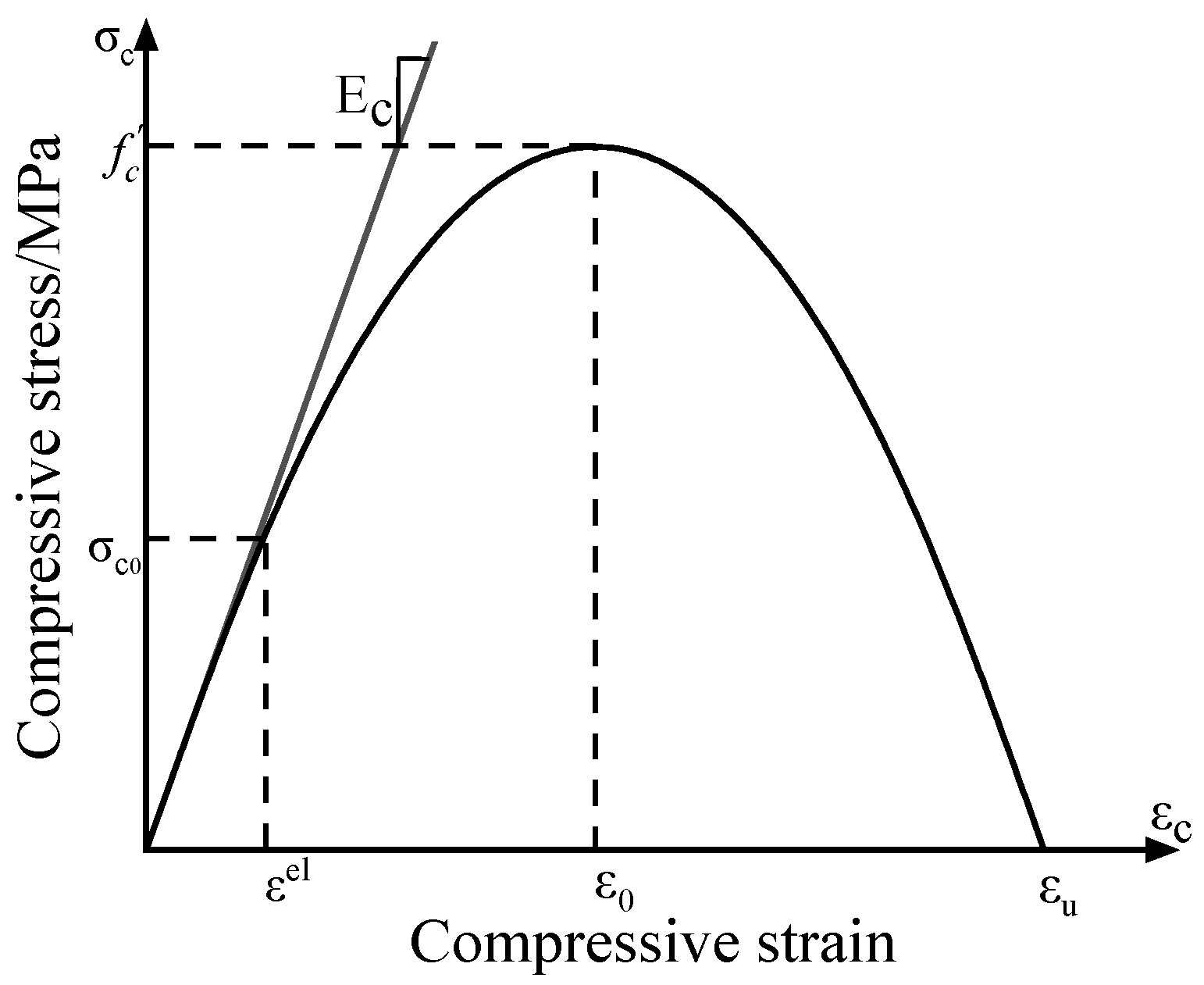
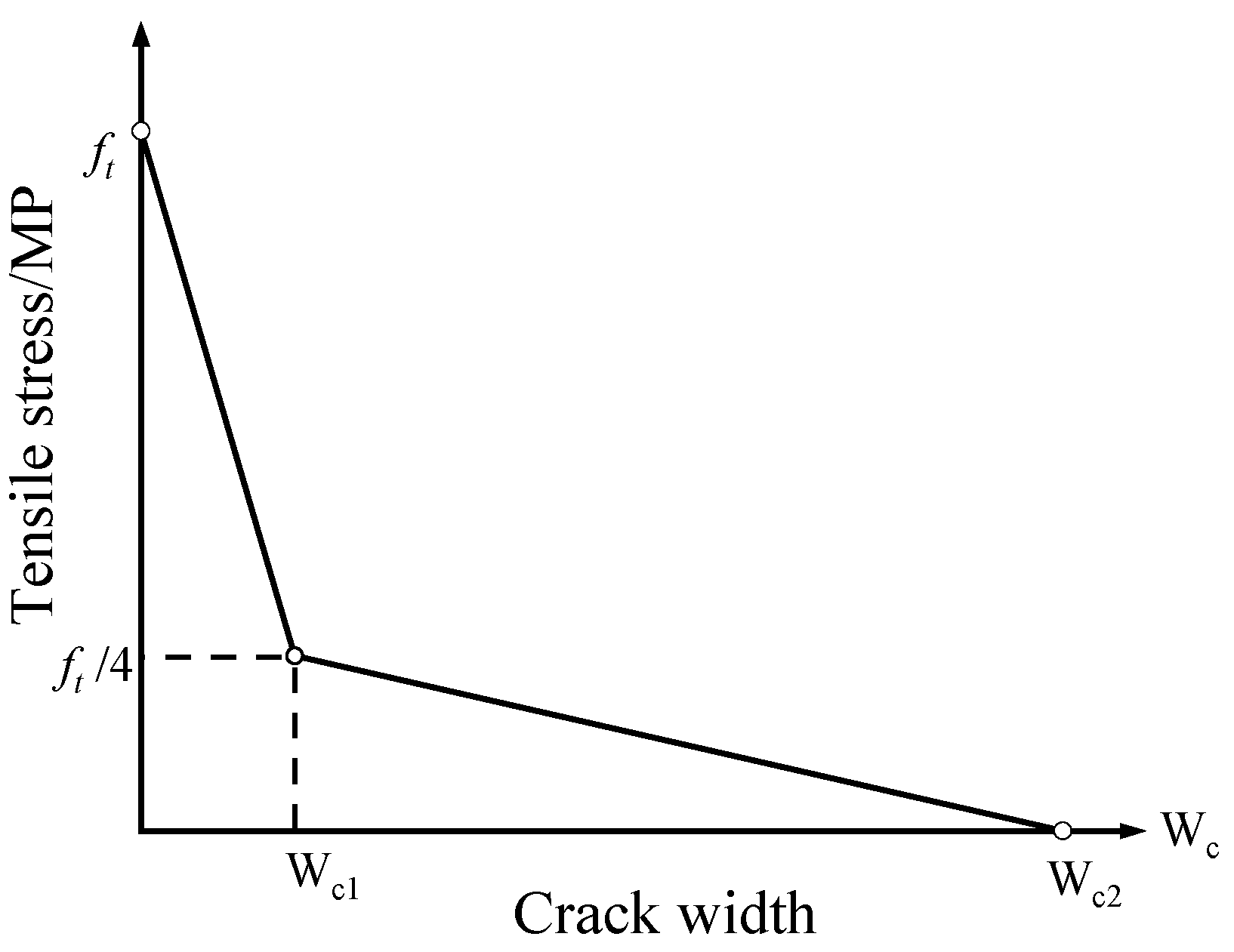
3.1. Constitutive Model
3.2. Material Properties
3.3. Finite Element Modeling
4. Results and Discussion
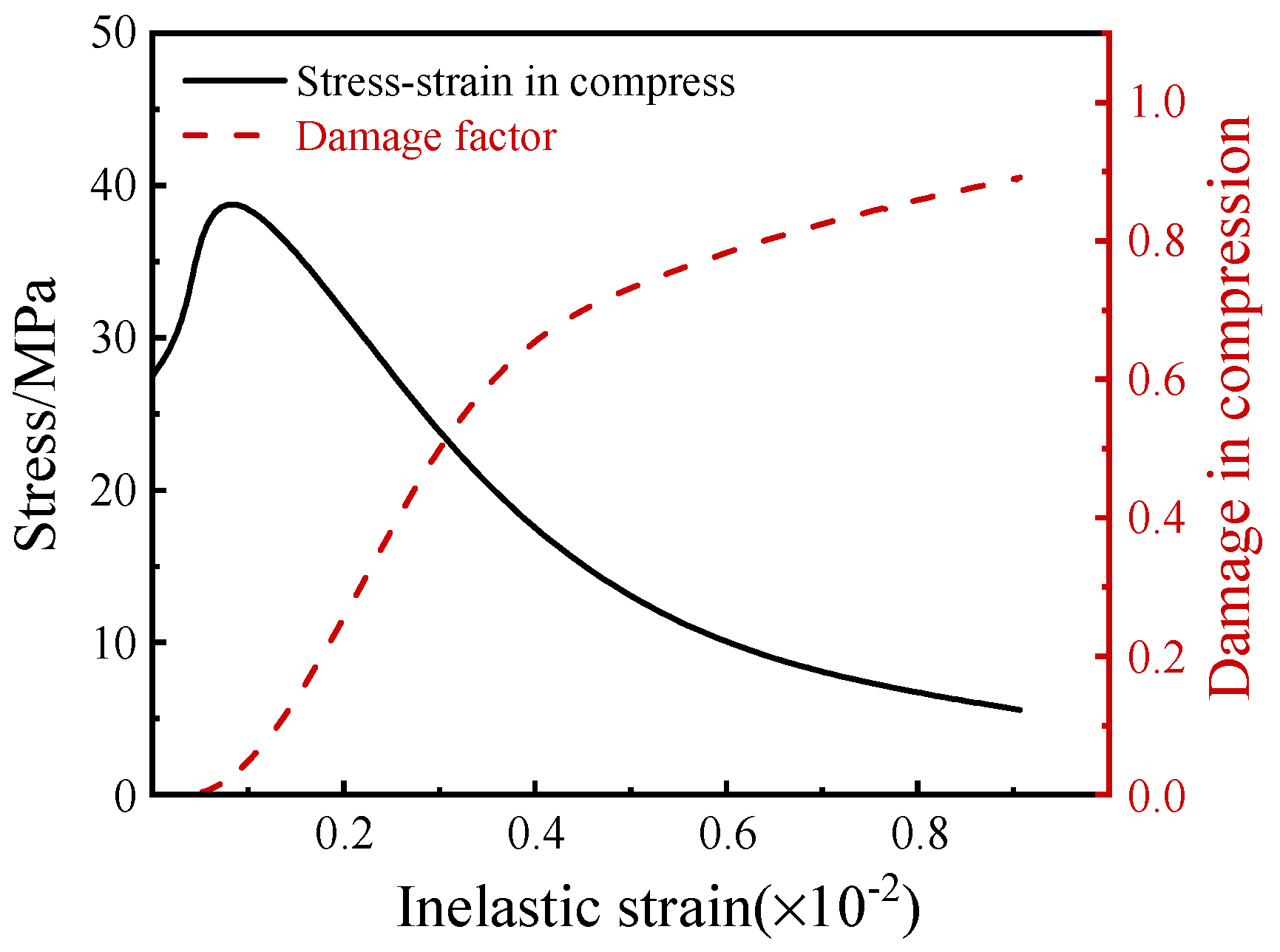
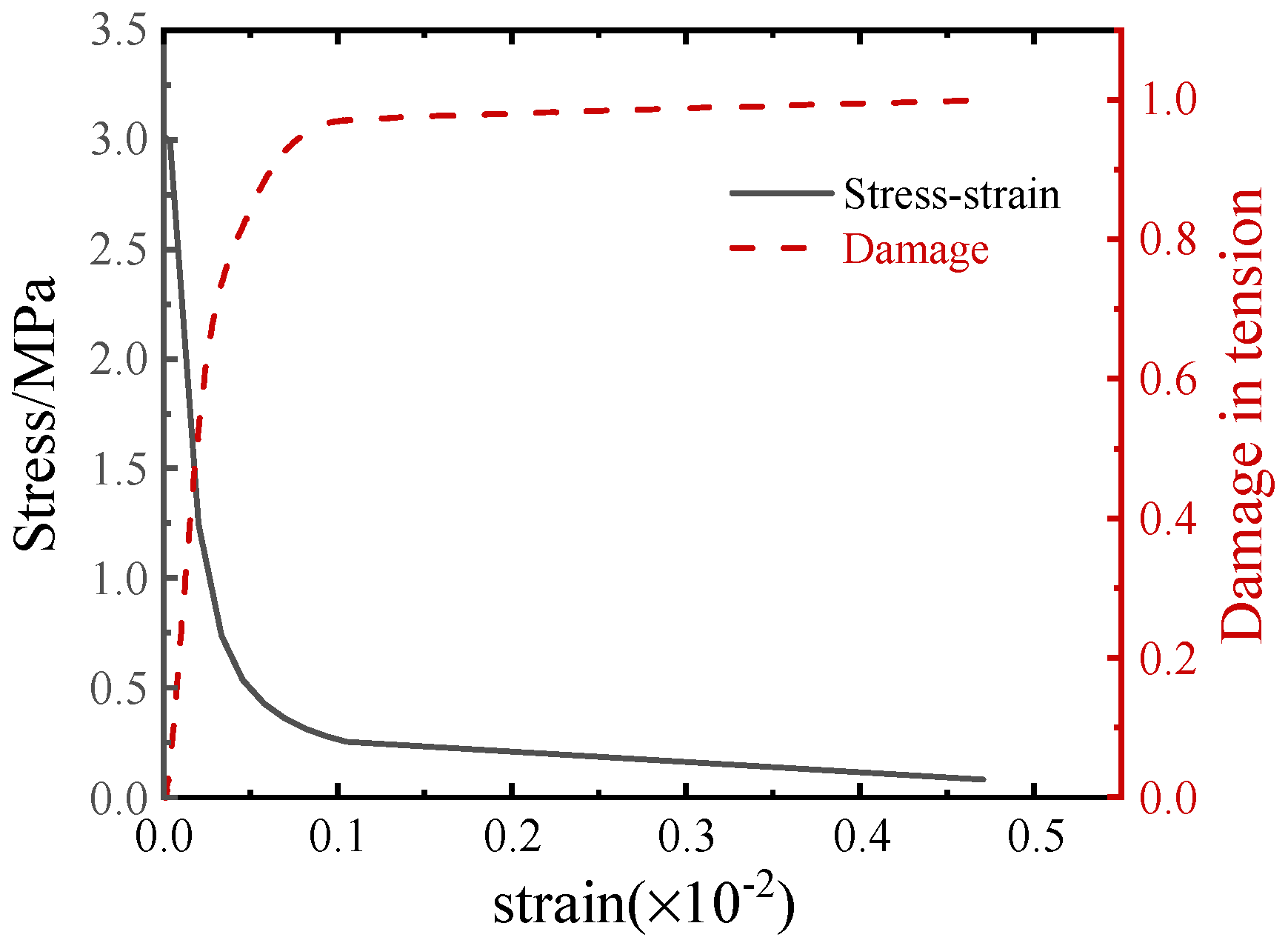
4.1. Plastic Damage and Energy Consumption Analysis
4.1.1. Plastic Damage
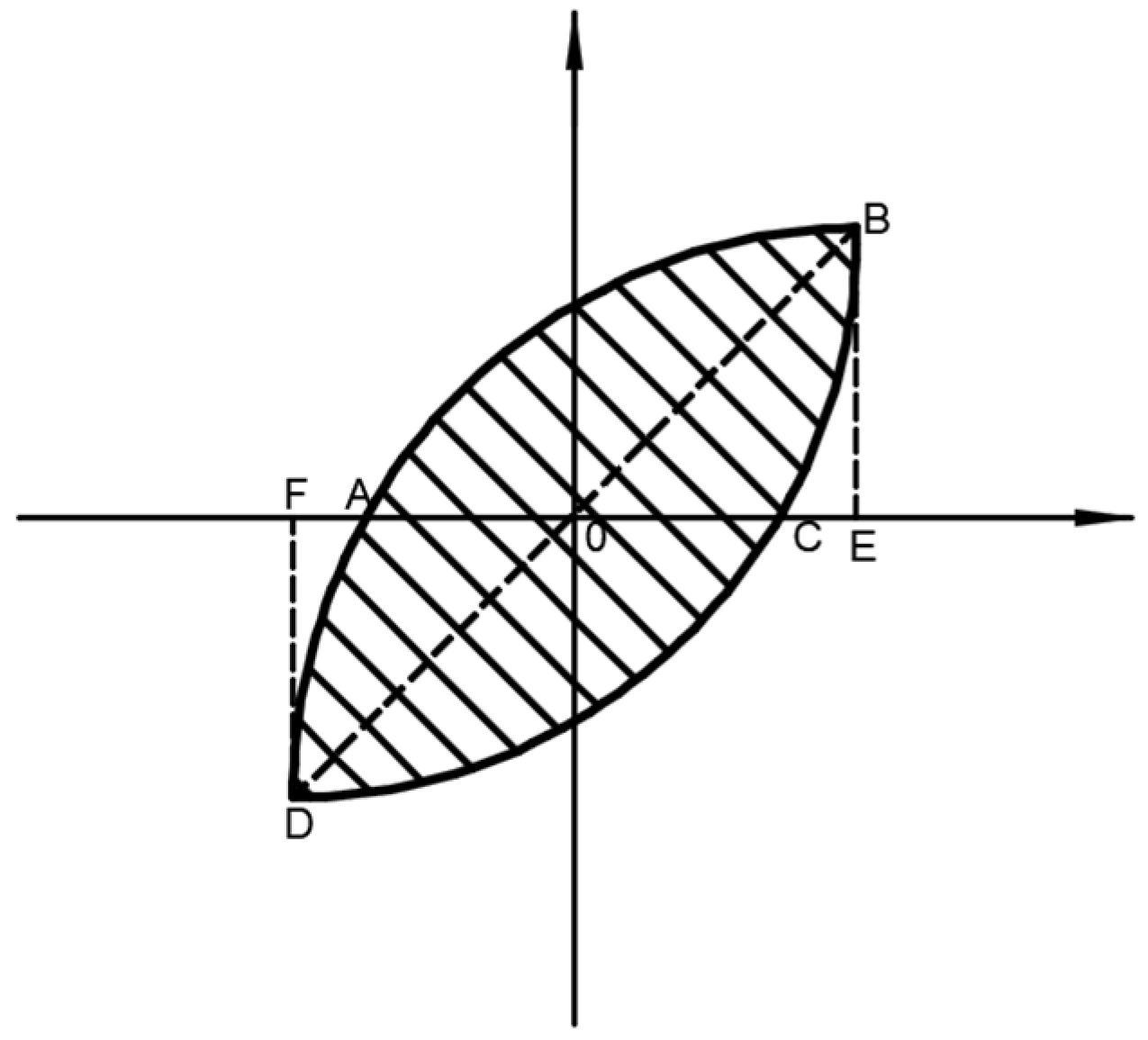
4.1.2. Energy Consumption Analysis of the Rubber Geopolymer Concrete
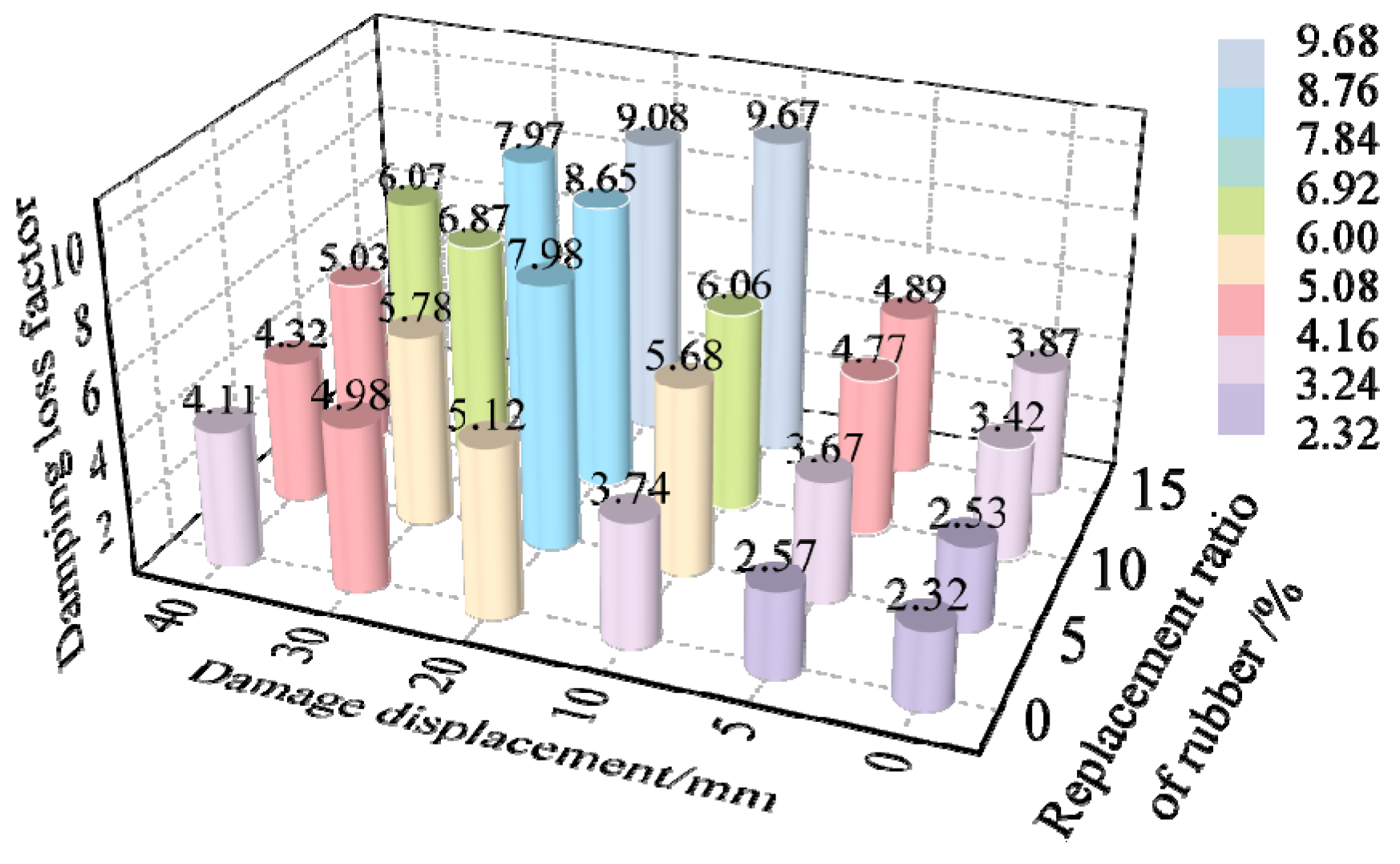
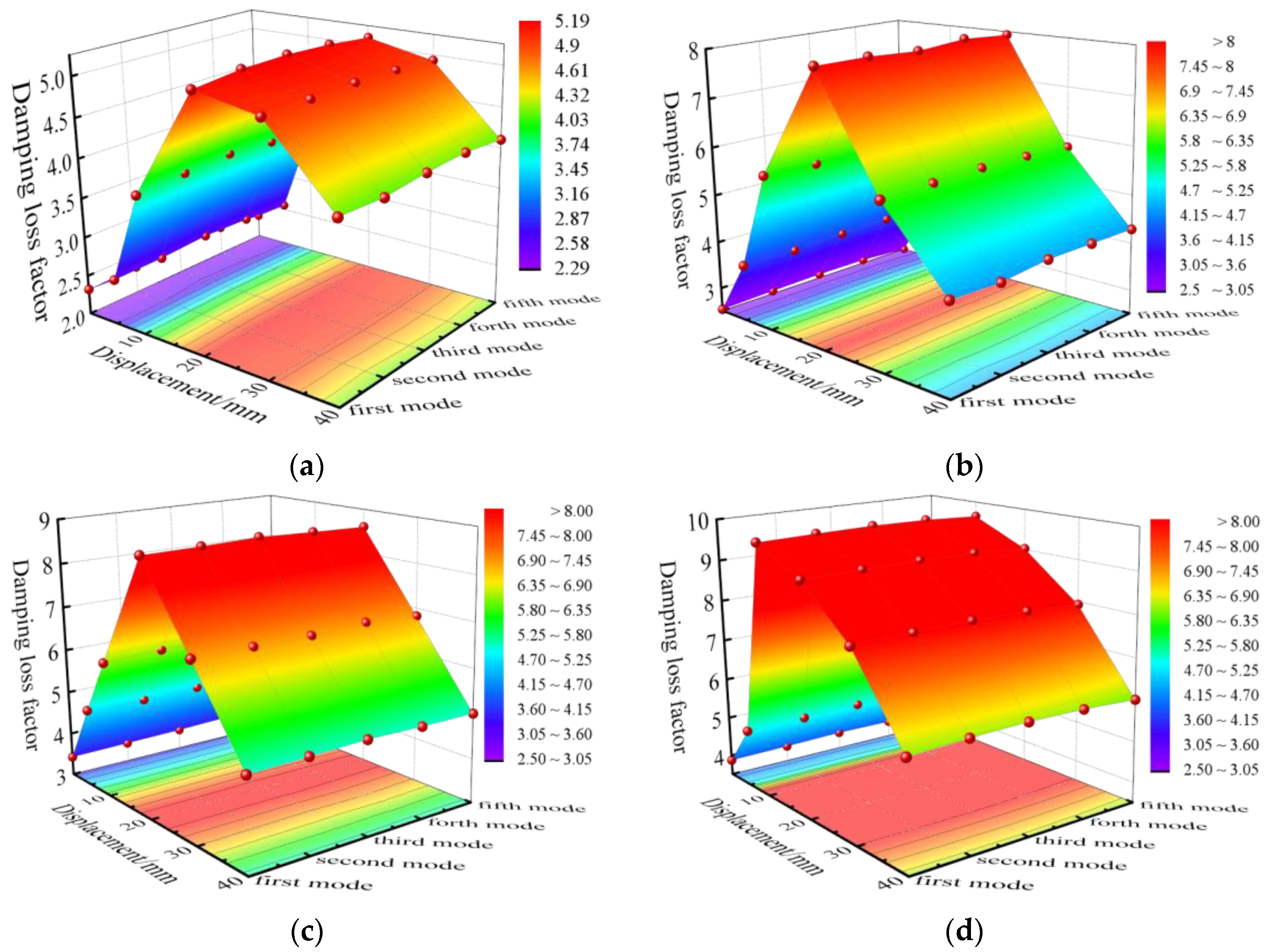
4.2. Analysis of Damping Characteristics of Rubber Geopolymer Concrete
4.3. The State Change of the Cantilever Beam under Different Modes
5. Conclusions
- (1)
- By comparing the numerical simulation results with the experimental results, we found that the rubber particles enhanced the damping performance of the geopolymer concrete, although some differences were observed.
- (2)
- The hysteretic curve and energy dissipation coefficient of geopolymer concrete cantilever beam under repeated loading showed that rubber particles could significantly enhance the energy consumption of concrete beams. When the replacement rate of rubber particles was 10%, the effect of energy dissipation restoring force was optimal.
- (3)
- Analysis of the variation of the first five natural frequencies of the cantilever beam with the damage displacement showed that for certain modes, the natural frequency decreased with an increase in damage displacement, with the decreasing speed gradually slowing. This was mainly because the increase in damage displacement gradually decreased the stiffness of the overall structure, resulting in a decrease in the natural frequency.
- (4)
- Analysis of the damping loss factor of the geopolymer concrete under different modal shapes showed that it was mainly related to the damage displacement and the rubber particle replacement rate rather than its modal shapes.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tripathy, S.K.; Dasu, J.; Murthy, Y.R.; Kapure, G.; Pal, A.R.; Filippov, L.O. Utilisation perspective on water quenched and air cooled blast furnace slags. J. Clean. Prod. 2020, 262, 121354. [Google Scholar] [CrossRef]
- Wang, H.; Wang, X.J.; Gui, F.; Zhang, X.C. The present situation and prospect of blast furnace slag resource utilization. Ind. Miner. 2021, 50, 48–53. (In Chinese) [Google Scholar]
- Provis, J.L.; van Deventer, J.S.J. Geopolymers: Structure, Processing, Properties and Industrial Applications; Woodhead Publishing Materials: Cambridge, UK, 2009. [Google Scholar]
- Thomas, B.S.; Gupta, R.C.; Kalla, P.; Cseteneyi, L. Strength, abrasion and permeation characteristics of cement concrete containing discarded rubber fine aggregates. Constr. Build. Mater. 2014, 59, 204–212. [Google Scholar] [CrossRef]
- Advincula, P.A.; Luong, D.X.; Chen, W.; Raghuraman, S.; Shahsavari, R.; Tour, J.M. Flash graphene from rubber waste. Carbon 2021, 178, 649–656. [Google Scholar] [CrossRef]
- Mohammed, B.S.; Awang, A.B.; Wong, S.S.; Nhavene, C.P. Properties of nano silica modified rubbercrete. J. Clean. Prod. 2016, 119, 66–75. [Google Scholar] [CrossRef]
- Ling, T.C. Effects of compaction method and rubber content on the properties of concrete paving blocks. Constr. Build. Mater. 2012, 28, 164–175. [Google Scholar] [CrossRef]
- Son, K.S.; Hajirasouliha, I.; Pilakoutas, K. Strength and deformability of waste tyre rubber-filled reinforced concrete columns. Constr. Build. Mater. 2011, 25, 218–226. [Google Scholar] [CrossRef]
- Gupta, T.; Chaudhary, S.; Sharma, R.K. Assessment of mechanical and durability properties of concrete containing waste rubber tire as fine aggregate. Constr. Build. Mater. 2014, 73, 562–574. [Google Scholar] [CrossRef]
- Ulker-Kaustell, M.; Karoumi, R. Application of the continuous wavelet transform on the free vibrations of a steel–concrete composite railway bridge. Eng. Struct. 2011, 33, 911–919. [Google Scholar] [CrossRef]
- Dilena, M.; Morassi, A.; Perin, M. Dynamic identification of a reinforced concrete damaged bridge. Mech. Syst. 2011, 25, 2990–3009. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Li, D.; Chen, Y.; Xiang, Z.C. Enhancement of dynamic damping in eco-friendly railway concrete sleepers using waste-tyre crumb rubber. Materials 2018, 11, 1169. [Google Scholar] [CrossRef] [PubMed]
- Ozbay, E.; Lachemi, M.; Sevim, U.K. Compressive strength, abrasion resistance and energy absorption capacity of rubberized concretes with and without slag. Mater. Struct. 2011, 44, 1297–1307. [Google Scholar] [CrossRef]
- Xue, J.; Shinozuka, M. Rubberized concrete: A green structural material with enhanced energy-dissipation capability. Constr. Build. Mater. 2013, 42, 196–204. [Google Scholar] [CrossRef]
- Abdelmonem, A.; El-Feky, M.S.; Nasr, E.S.A.R.; Kohail, M. Performance of high strength concrete containing recycled rubber. Constr. Build. Mater. 2019, 227, 116660. [Google Scholar] [CrossRef]
- Hameed, A.S.; Shashikala, A.P. Suitability of rubber concrete for railway sleepers. Perspect. Sci. 2016, 8, 32–35. [Google Scholar] [CrossRef]
- Pham, T.M.; Chen, W.; Khan, A.M.; Hao, H.; Elchalakani, M.; Tran, T.M. Dynamic Compressive Properties of Lightweight Rubberized Concrete. Constr. Build. Mater. 2019, 238, 117705. [Google Scholar] [CrossRef]
- Sun, J.; Chen, G.Z.; Lv, K.Q.; Wang, A.N. Experimental study on mechanical properties and damping characteristics of rubber geopolymer concrete. Acta Mater. Compos. Sin. 2022, 39, 5321–5332. (In Chinese) [Google Scholar]
- GB/T1499.2-2018; National Standard of the people’s Republic of China, Steel for Reinforced Concrete Part 2: Hot Rolled Ribbed Steel Bar. China Quality Inspection Press: Beijing, China, 2018.
- Zinkaah, O.H.; Alridha, Z.; Alhawat, M. Numerical and theoretical analysis of FRP reinforced geopolymer concrete beams. Case Stud. Constr. Mater. 2022, 16, e01052. [Google Scholar] [CrossRef]
- Hibbitt, K.; Karlsson, B.; Sorensen, P. ABAQUS/Standard User Subroutines Reference Manual; The Pennsylvania State University: State College, PA, USA, 1998. [Google Scholar]
- Wu, P.; Du, K.; Xu, Y.-D.; Chen, W. Meso-scale numerical simulation of corrosion cracking process of reinforced concrete based on brittle cracking model. Bull. Chin. Ceram. Soc. 2018, 37, 2372–2377. [Google Scholar]
- Nie, J.G.; Wang, Y.H. Comparison study of constitutive model of concrete in ABAQUS for static analysis of structures. Eng. Mech. 2013, 30, 59–67, 82. (In Chinese) [Google Scholar]
- Lubliner, J.; Oliver, J.; Oller, S. Plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Mattock, A.H.; Kriz, L.B.; Hognestad, E. Rectangular concrete stress distribution in ultimate strength design. ACI Struct. J. 1961, 57, 875–928. [Google Scholar]
- Comité Euro-International du Béton. CEB-FIP Model Code 1990: Design Code; Thomas Telford Publishing: New York, NY, USA, 1993. [Google Scholar]
- Hu, H.-T.; Liang, J.-I. Ultimate analysis of BWR Mark III reinforced concrete containment subjected to internal pressure. Nucl. Eng. Des. 2000, 195, 1–11. [Google Scholar] [CrossRef]
- Nguyen, K.T.; Ahn, N.; Le, T.A.; Lee, K. Theoretical and experimental study on mechanical properties and flexural strength of fly ash-geopolymer concrete. Constr. Build. Mater. 2016, 105, 65–67. [Google Scholar] [CrossRef]
- Zhou, J.X.; Wei, Z.G.; Mao, H.; Wei, Y.N.; Liu, Y.S. Numerical calculation for isotropic hyperelasticity of constitutive model and verification. Chin. J. Comput. Mech. 2022, 39, 523–530. (In Chinese) [Google Scholar]
- Huang, J.L.; Xie, G.J.; Liu, Z.W. Finite element analysis of super-elastic rubber materials based on the Mooney-Rivlin and Yeoh models. China Rubber/Plast. Technol. Equip. 2008, 34, 22–26. (In Chinese) [Google Scholar]
- Huang, J.L.; Xie, G.J.; Liu, Z.W. FEA of Hyperelastic Rubber Material based on the Mooney-Rivlin and Yeoh models. China Rubber Ind. 2008, 8, 467–471. (In Chinese) [Google Scholar]
- Hu, Z.J.; Shah, Y.I.; Yu, S.L. Cracking analysis of pre-stressed steel–concrete composite girder at negative moment zone. Arab. J. Sci. Eng. 2021, 46, 10771–10783. [Google Scholar] [CrossRef]
- Elchalakani, M.; Karrech, A.; Dong, M.; Ali, M.S.M.; Yang, B. Experiments and finite element analysis of GFRP reinforced geopolymer concrete rectangular columns subjected to concentric and eccentric axial loading. Structures 2018, 14, 273–289. [Google Scholar] [CrossRef]
- Waj, A.; Ybat, B.; Amh, C. Behavior of reinforced concrete deep beam with web openings strengthened with (CFRP) sheet. Structures 2020, 26, 785–800. [Google Scholar]
- Earij, A.; Alfano, G.; Cashell, K.; Zhou, X.M. Nonlinear three–dimensional finite–element modelling of reinforced–concrete beams: Computational challenges and experimental validation. Eng. Fail. Anal. 2017, 82, 92–115. [Google Scholar] [CrossRef]
- JGJ 101-2015; Seismic Test Procedure for Buildings. China Construction Industry Press: Beijing, China, 2015. (In Chinese)
- Cheng, G.L.; Zhu, S.J.; Wu, X.J. A summary of statistical energy analysis method and its loss factor determination. Ship Eng. 2004, 26, 10–15. [Google Scholar]
- Ma, Y.; Kai, Z.; Deng, Z. Wave component solutions of free vibration and mode damping loss factor of finite length periodic beam structure with damping material. Compos. Struct. 2018, 201, 740–746. [Google Scholar] [CrossRef]
- Hu, W.Q.; Wang, M.Q.; Liu, Z.H. Study of design of free-damping from specimen in resonance method. J. Exp. Mech. 2008, 23, 241–247. (In Chinese) [Google Scholar]
- GB/T 18258-2000; Damping Materials, Test Method for Damping Properties. Standards Press of China: Beijing, China, 2000. (In Chinese)
- Yamamoto, T.; Yamada, T.; Izui, K.; Nishiwaki, S. Topology optimization of free-layer damping material on a thin panel for maximizing modal loss factors expressed by only real eigenvalues. J. Sound Vib. 2015, 358, 84–96. [Google Scholar] [CrossRef]
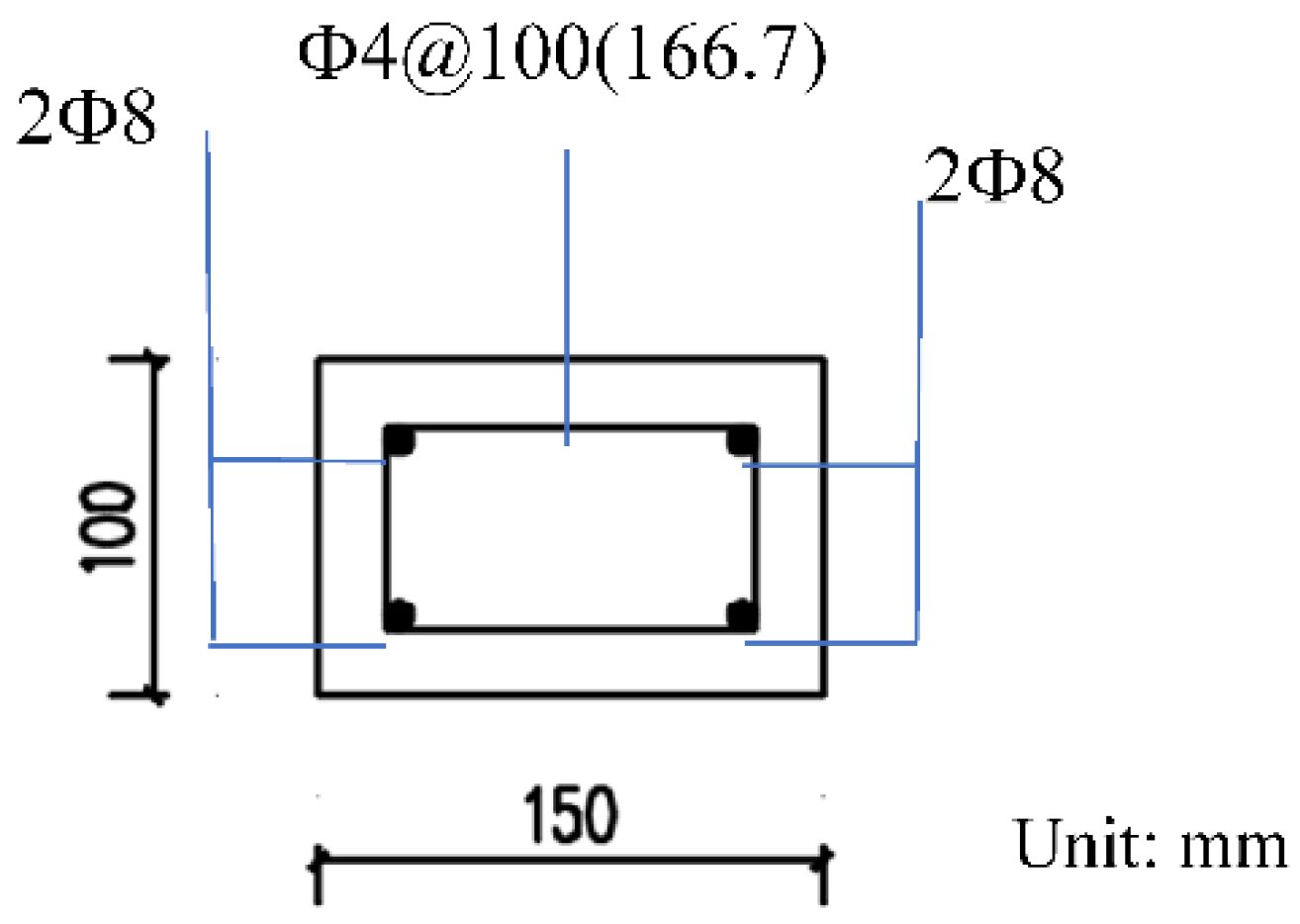
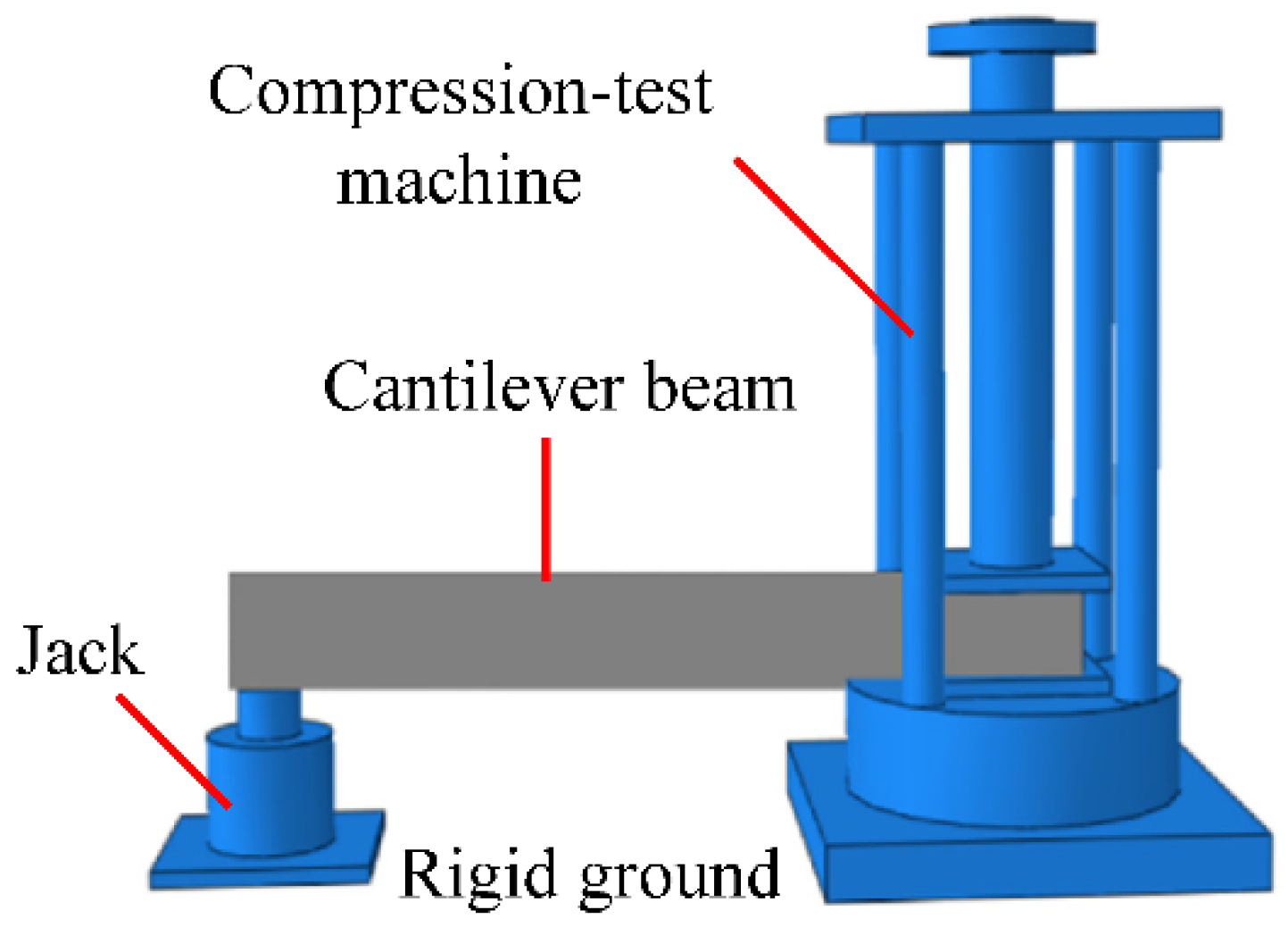
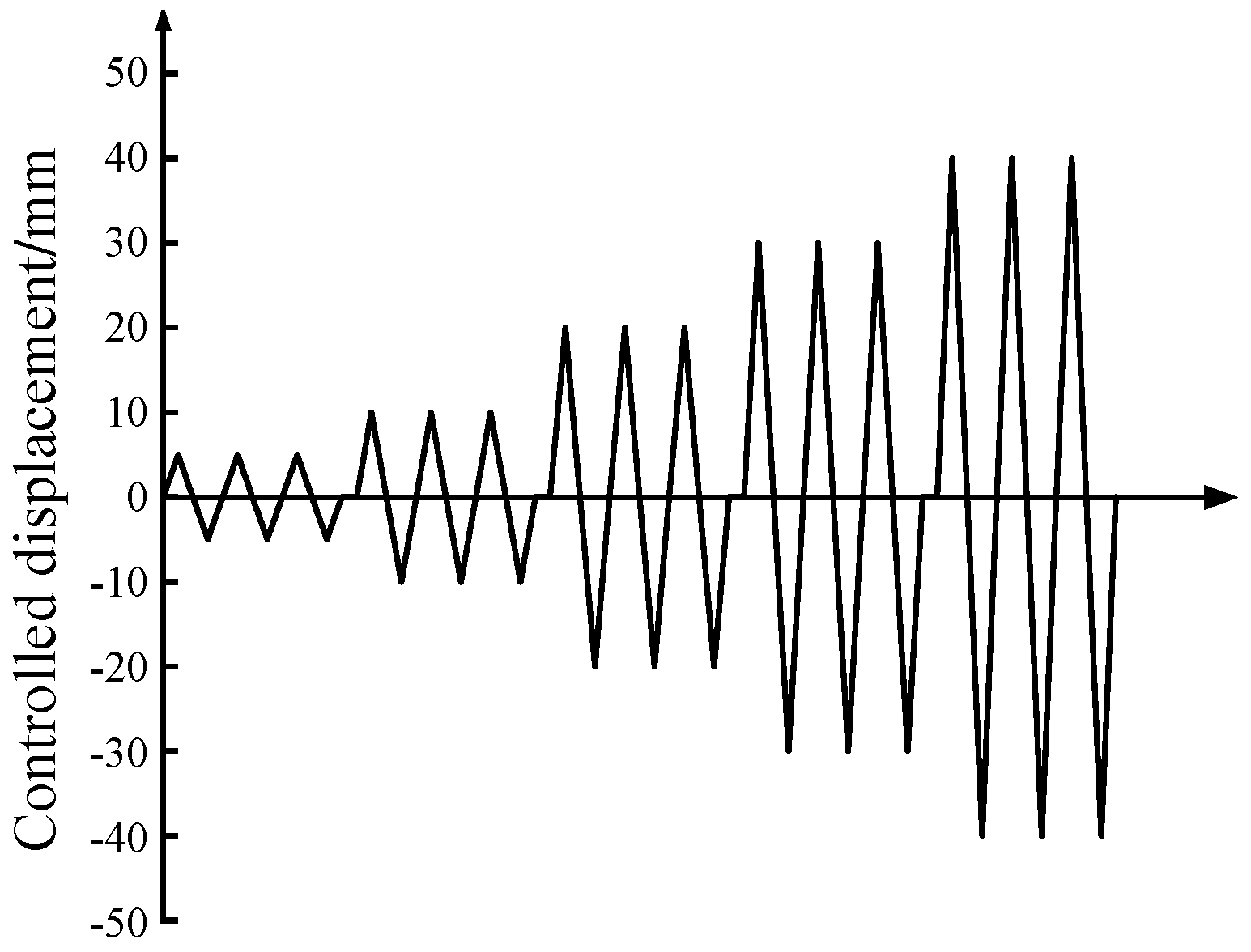
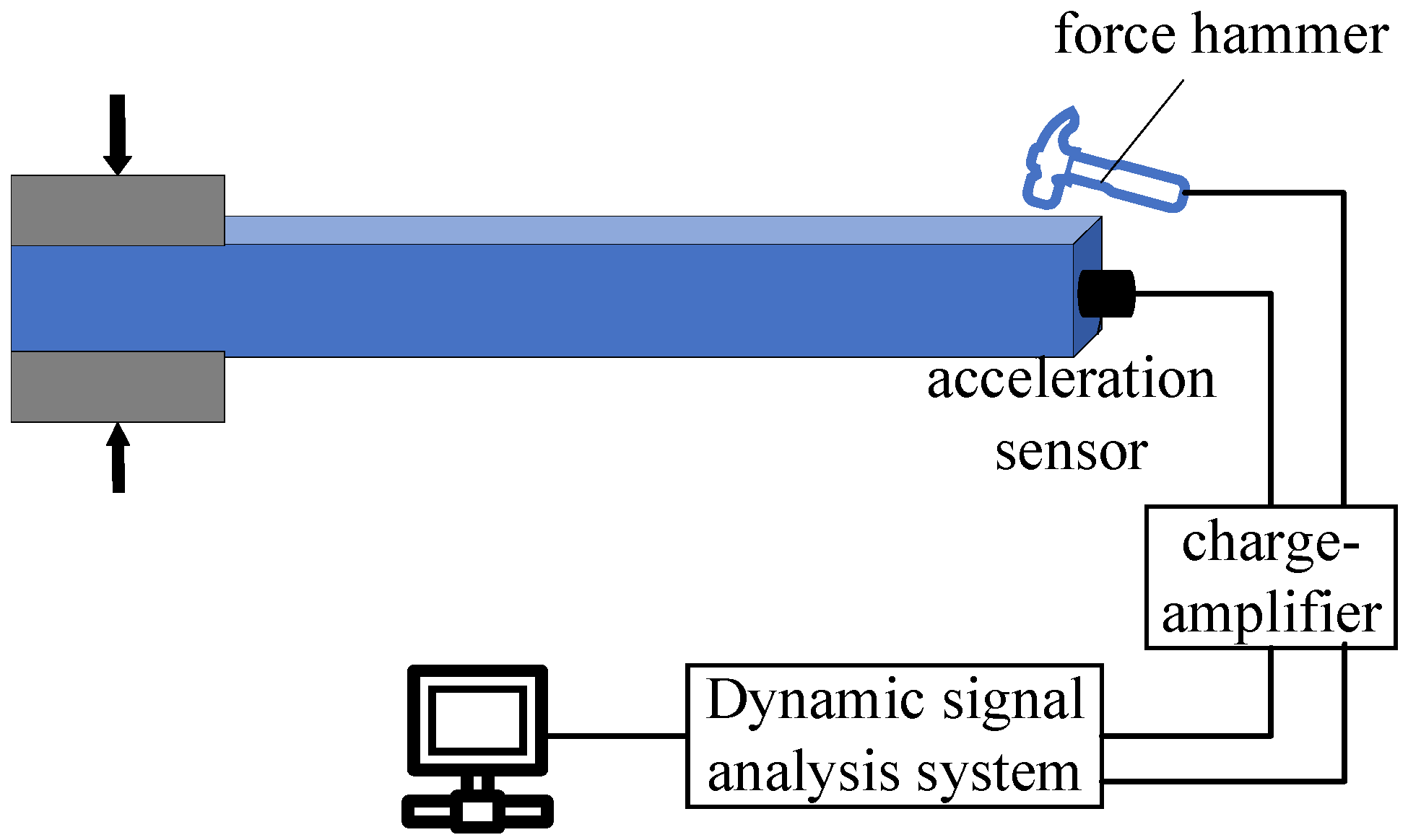




| Test Sample | Compressive Strength/MPa | Splitting Tensile Strength/MPa | Flexural Strength/MPa |
|---|---|---|---|
| GC | 71.88 | 5.06 | 5.58 |
| RGC-5 | 57.74 | 4.69 | 6.08 |
| RGC-10 | 54.74 | 4.59 | 5.51 |
| RGC-15 | 52.84 | 4.01 | 5.41 |
| 38 | 0.1 | 1.16 | 0.667 | 0.076 |
| Material | Diameter/mm | Mass Density/kg/m3 | Elasticity Modulus/GPa | Poisson’s Ratio | Yield Strength/MPa |
|---|---|---|---|---|---|
| hoop-steel | 4 | 7800 | 194.1 | 0.27 | 270 |
| longitudinal-steel | 8 | 7800 | 210 | 0.3 | 360 |
| Sample Label | GC | RGC-5 | RGC-10 | RGC-15 | |
| Total Consumption Energy/J | 15,731.49 | 16,759.11 | 18,415.31 | 16,352.81 | |
| Energy dissipation coefficient | L1 = 5 mm | 0.50 | 1.07 | 1.14 | 1.45 |
| L2 = 10 mm | 0.95 | 1.45 | 1.62 | 1.95 | |
| L3 = 20 mm | 1.39 | 1.63 | 1.82 | 2.15 | |
| L4 = 30 mm | 1.51 | 1.74 | 1.95 | 1.74 | |
| L5 = 40 mm | 1.58 | 1.75 | 2.02 | 1.64 | |
| (mm) | 0 | 5 | 10 | 20 | 30 | 40 | |
|---|---|---|---|---|---|---|---|
| Specimen Label | |||||||
| GPC | (Hz) | 79.5 | 73.5 | 70 | 65 | 61 | 59 |
| (Hz) | 77.3 | 74.1 | 69.3 | 62.5 | 56.4 | 53.5 | |
| Error value (%) | 2.77 | 0.82 | 1 | 3.84 | 5.9 | 9.32 | |
| RGPC-5 | (Hz) | 77 | 74 | 70 | 63 | 58.5 | 54 |
| (Hz) | 74.8 | 73.4 | 68.7 | 61.5 | 56.2 | 51.7 | |
| Error value (%) | 2.86 | 0.81 | 1.86 | 2.38 | 3.93 | 4.26 | |
| RGPC-10 | (Hz) | 76.8 | 71.5 | 69 | 61.2 | 53.6 | 47.5 |
| (Hz) | 73.5 | 71.8 | 68.6 | 58.7 | 51.2 | 46.5 | |
| Error value (%) | 4.3 | 0.42 | 0.58 | 4.08 | 4.48 | 2.11 | |
| RGPC-15 | (Hz) | 75.5 | 68.5 | 55.2 | 51.4 | 48.5 | 45.2 |
| (Hz) | 72.3 | 71.1 | 62.1 | 53.8 | 48.3 | 45.9 | |
| Error value (%) | 2.91 | 3.8 | 12.5 | 4.67 | 0.41 | 1.55 |
| First Mode | Second Mode | Third Mode | Fourth Mode | Fifth Mode | ||
|---|---|---|---|---|---|---|
| /mm | ||||||
| 0 |  | |||||
| f = 73.5 Hz | f = 433.59 Hz | f = 453.22 Hz | f = 580.04 Hz | f = 1141.2 Hz | ||
| 5 |  | |||||
| f = 71.8 Hz | f = 428.08 Hz | f = 447.30 Hz | f = 573.34 Hz | f = 1128.4 Hz | ||
| 10 |  | |||||
| f = 68.6 Hz | f = 404.12 Hz | f = 412.4 Hz | f = 524.23 Hz | f = 1063.4 Hz | ||
| 20 |  | |||||
| f = 58.7 Hz | f = 330.82 Hz | f = 335.9 Hz | f = 348.86 Hz | f = 821.62 Hz | ||
| 30 |  | |||||
| f = 51.2 Hz | f = 220.04 Hz | f = 277.44 Hz | f = 305.34 Hz | f = 682.44 Hz | ||
| 40 |  | |||||
| f = 46.5 Hz | f = 186.18 Hz | f = 241.67 Hz | f = 277.50 Hz | f = 621.01 Hz | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Zhang, D.; Xu, W.; Sun, J. Modeling of Damping Characteristics of Rubber Geopolymer Concrete Based on Finite Element Simulation. Buildings 2022, 12, 2142. https://doi.org/10.3390/buildings12122142
Chen G, Zhang D, Xu W, Sun J. Modeling of Damping Characteristics of Rubber Geopolymer Concrete Based on Finite Element Simulation. Buildings. 2022; 12(12):2142. https://doi.org/10.3390/buildings12122142
Chicago/Turabian StyleChen, Guozhen, Derun Zhang, Wen Xu, and Jie Sun. 2022. "Modeling of Damping Characteristics of Rubber Geopolymer Concrete Based on Finite Element Simulation" Buildings 12, no. 12: 2142. https://doi.org/10.3390/buildings12122142
APA StyleChen, G., Zhang, D., Xu, W., & Sun, J. (2022). Modeling of Damping Characteristics of Rubber Geopolymer Concrete Based on Finite Element Simulation. Buildings, 12(12), 2142. https://doi.org/10.3390/buildings12122142







