Seismic Fragility Analysis of the Aging RC Columns under the Combined Action of Freeze–Thaw Cycles and Chloride-Induced Corrosion
Abstract
:1. Introduction
2. Deterioration Model of RC Structures under the Combined Action of Freeze–Thaw Cycles and Chloride-Induced Corrosion
2.1. Concrete Deterioration Test Results and Analysis
2.1.1. Test Scheme
2.1.2. Materials and Work Method
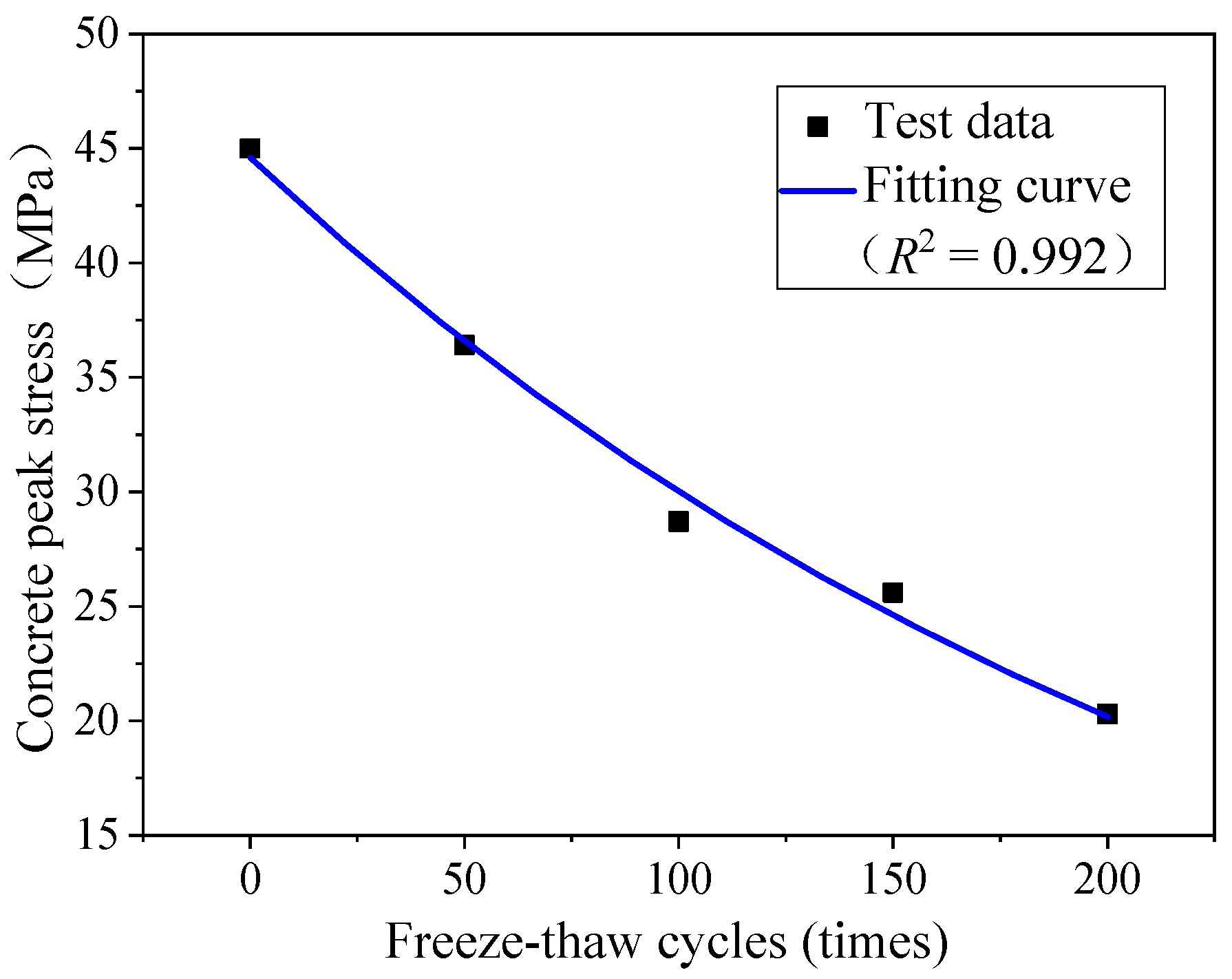
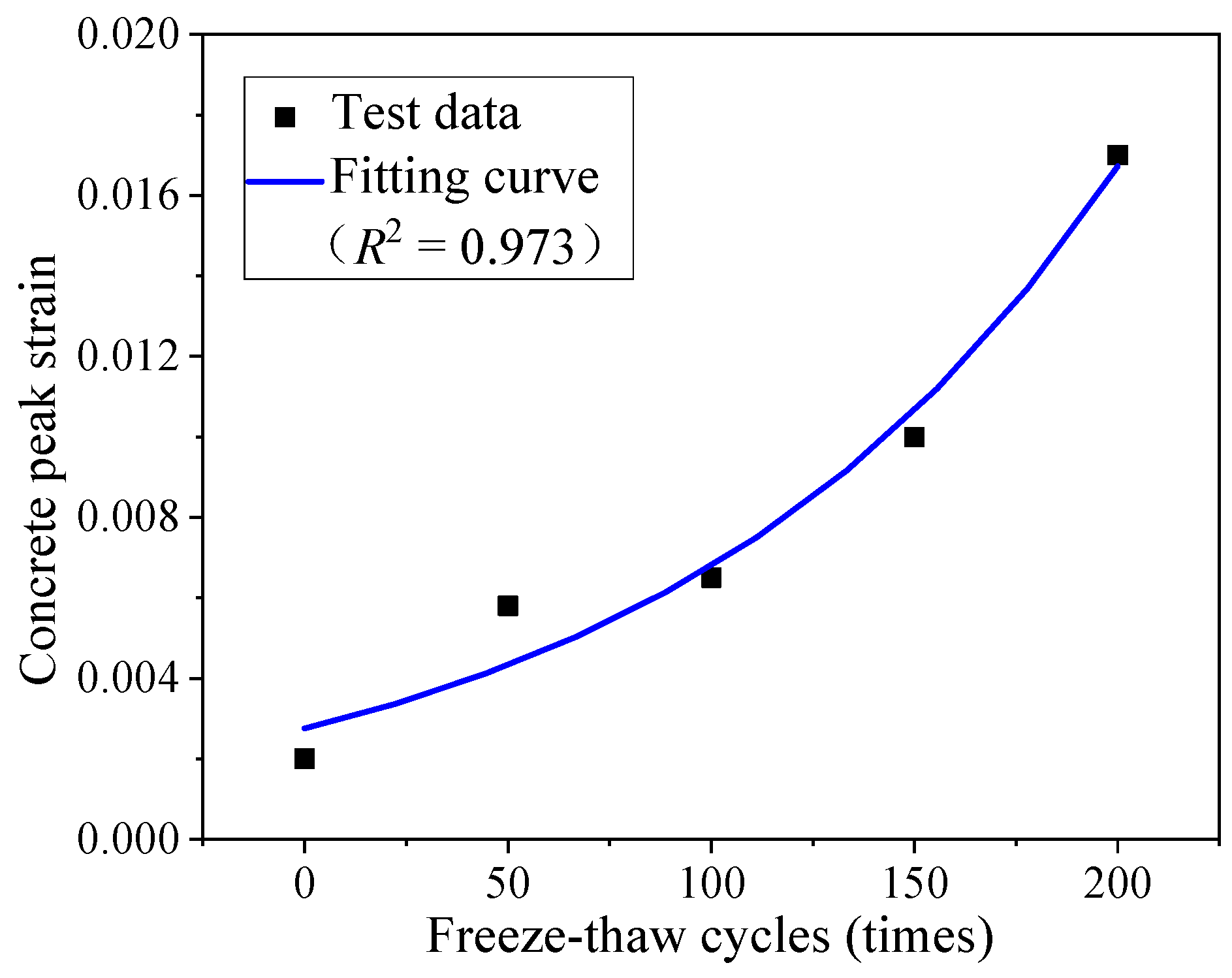
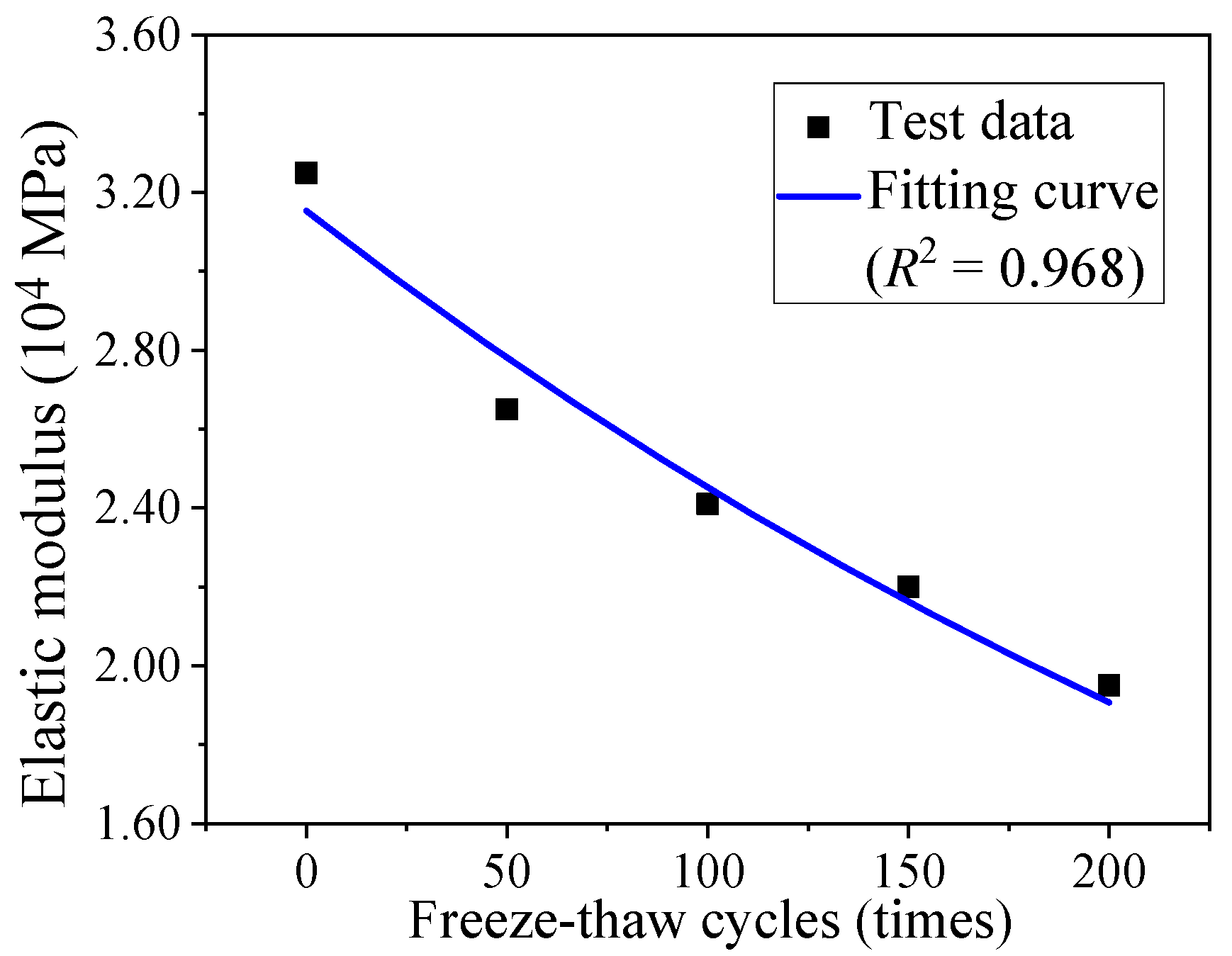
2.1.3. Test Results of the Macro-Structures
2.1.4. Test Results of the Micro-Structures
2.2. Corrosion Initiation Time of Steel
2.3. Time-Dependent Corrosion Mechanisms of Steel Rebar
2.3.1. Corrosion Rate of Steel Rebar
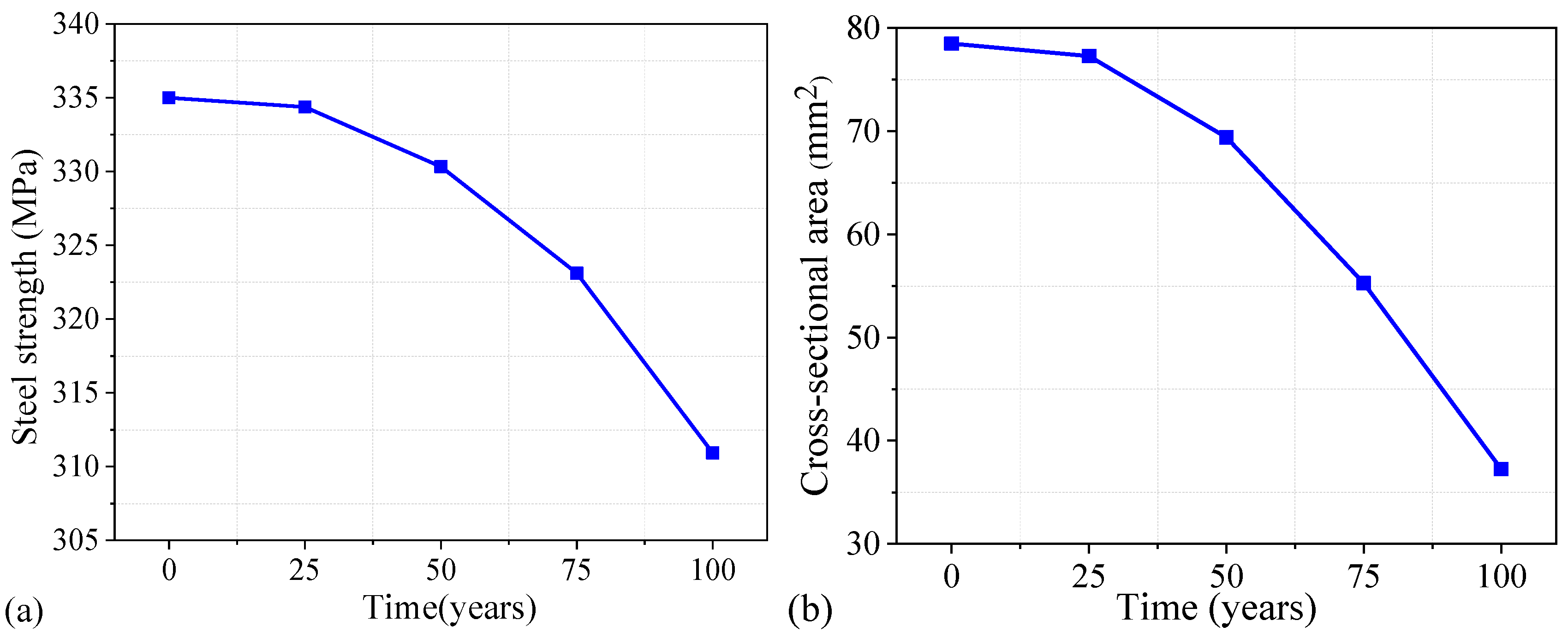
2.3.2. Residual Cross-Sectional Area of Steel
2.3.3. Steel Strength
2.3.4. Steel Ductility
2.4. The Proposed Time-Dependent Deterioration Model of RC Structures under the Combined Action of Freeze–Thaw Cycles and Chloride-Induced Corrosion
2.4.1. Traditional Mander Constitutive Model
2.4.2. The Modified Mander Constitutive Model
3. Time-Dependent Seismic Fragility Function
4. Time-Dependent Seismic Fragility Analysis: Case-Study
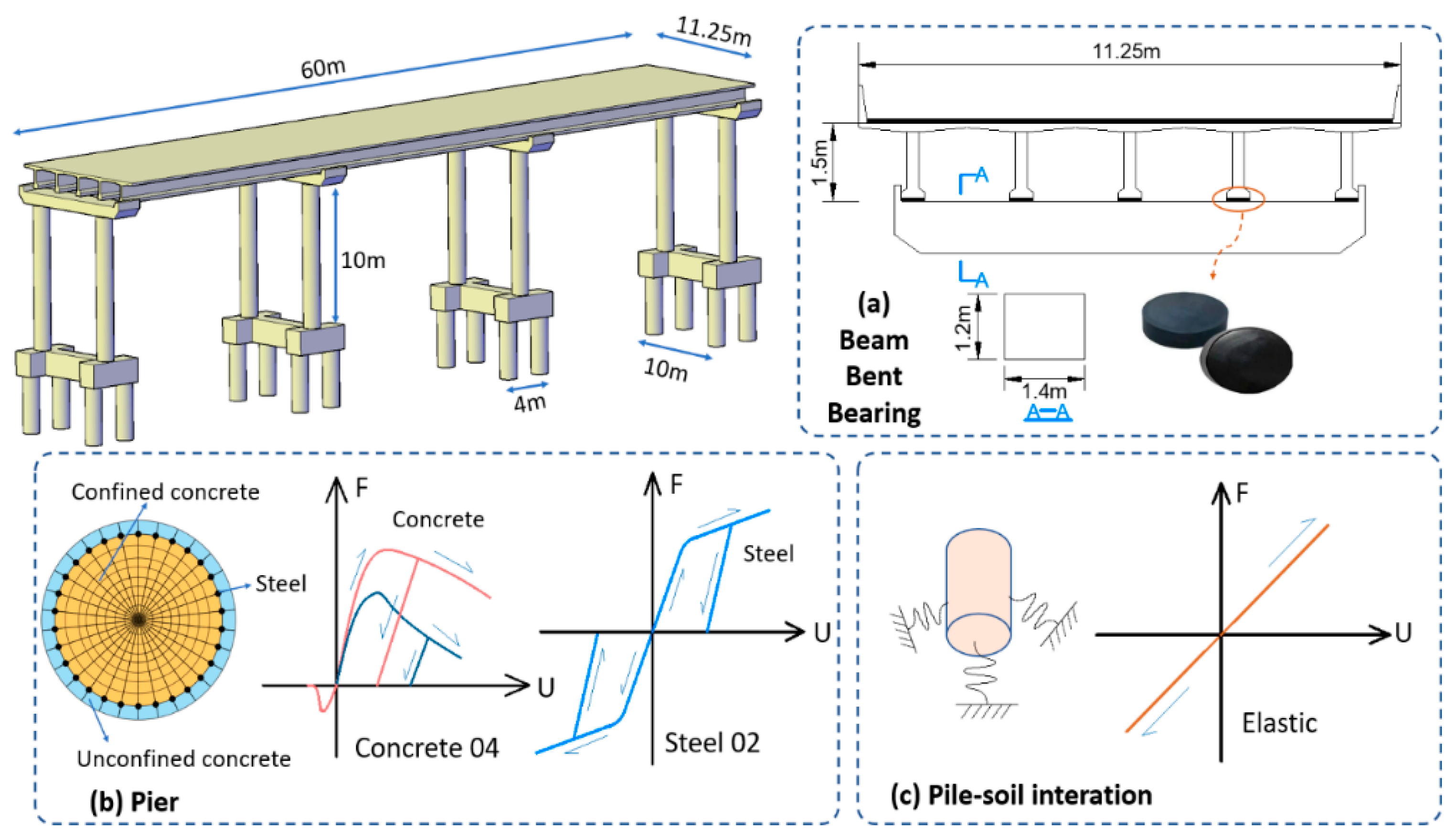
4.1. Bridge Description and FE Modeling
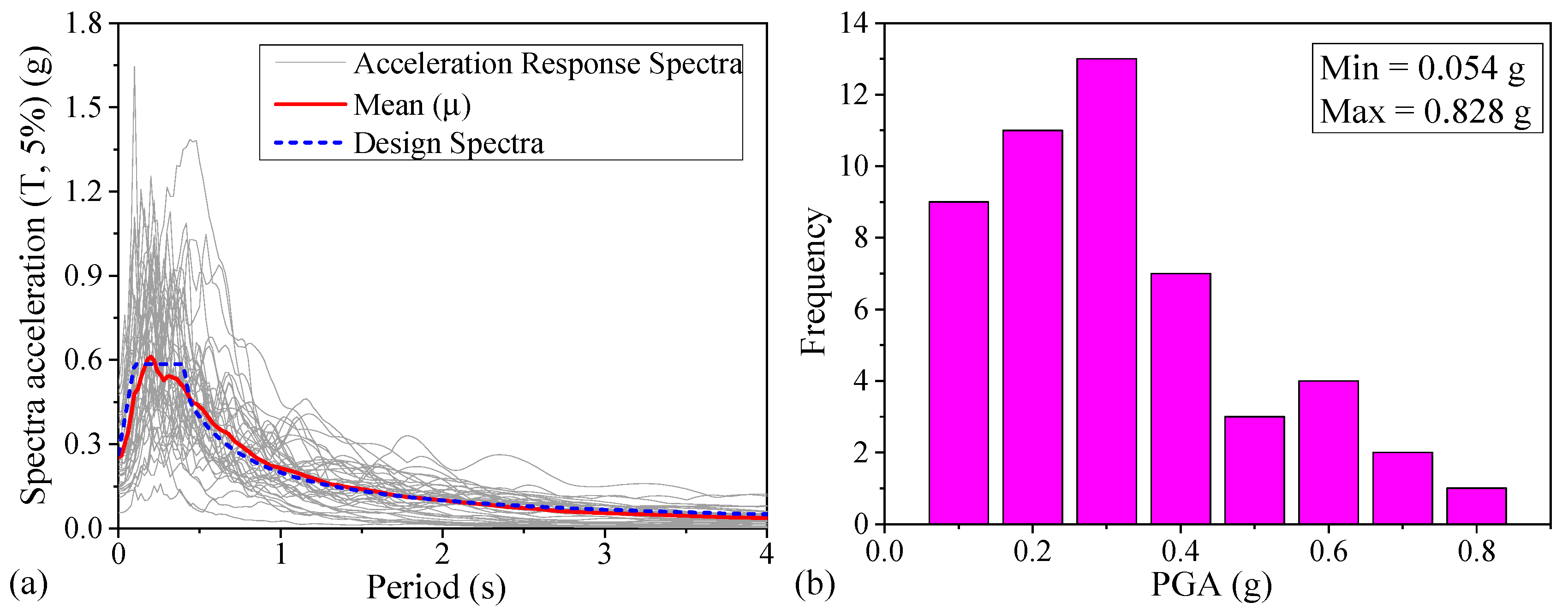
4.2. Selection of the Ground Motions
4.3. Time-Dependent Seismic Fragility Analysis of the Aging RC Columns
4.3.1. Corrosion Initiation Time of Steel Rebar (tcorr)
4.3.2. Time-Dependent Mechanical Properties of the Steel Rebar
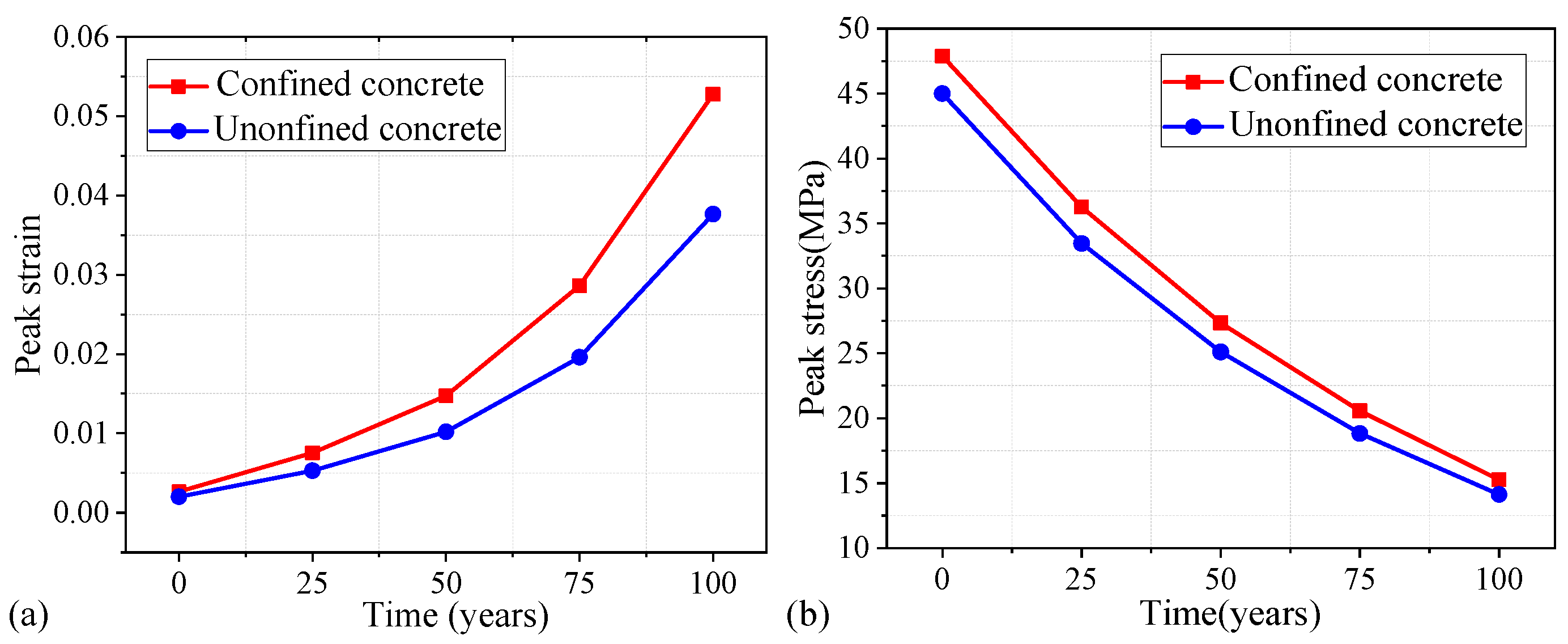
4.3.3. Time-Dependent Mechanical Properties of the Concrete
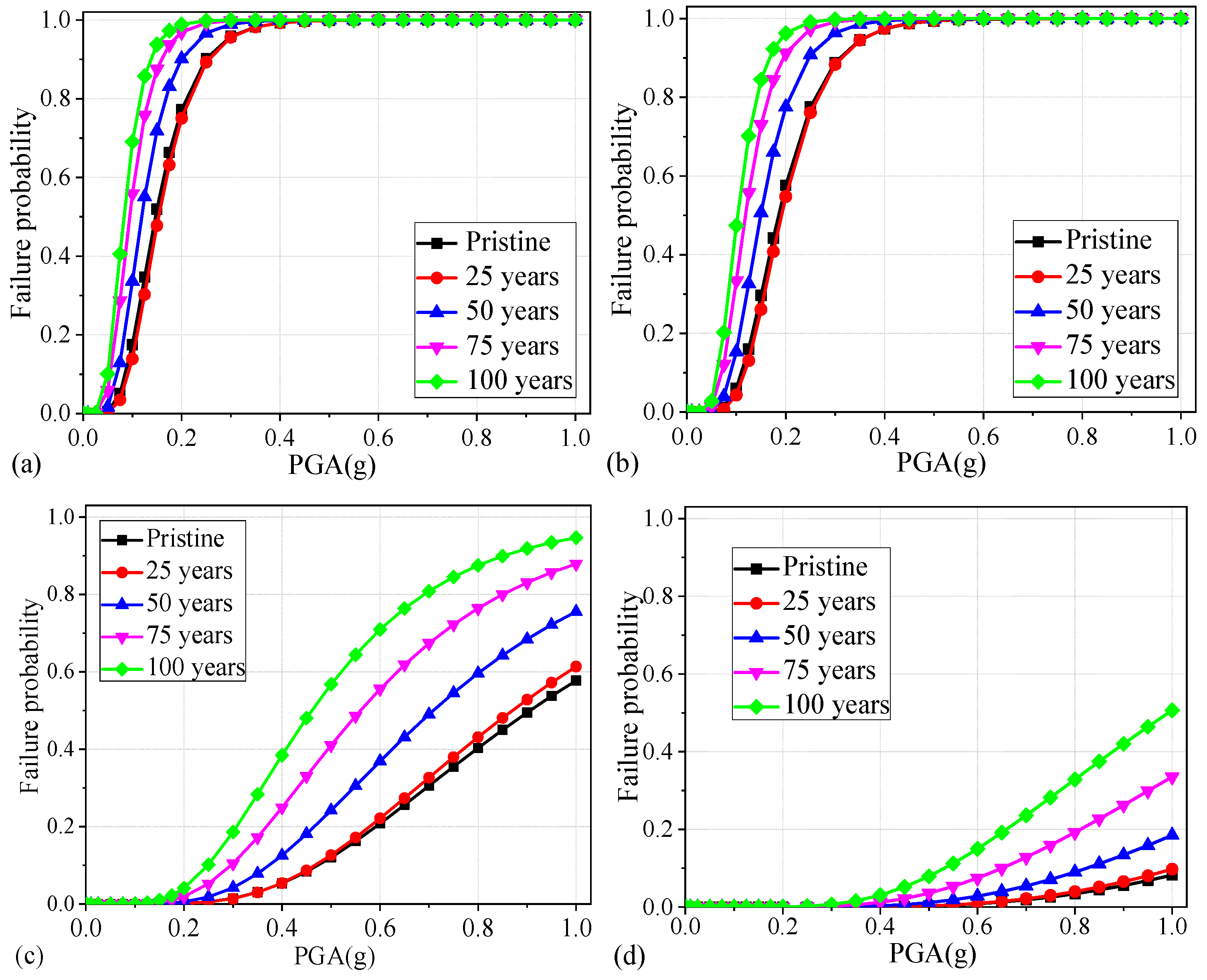
4.3.4. Time-Dependent Seismic Fragility Curves of RC Columns
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duan, A.; Tian, Y.; Dai, J.; Jin, W. A stochastic damage model for evaluating the internal deterioration of concrete due to freeze–thaw action. Mater. Struct. 2014, 47, 1025–1039. [Google Scholar] [CrossRef]
- Si, Z.; Du, X.; Huang, L.; Li, Y. Meso-scale failure of freezing–thawing damage of concrete under uniaxial compression. Appl. Sci. 2020, 10, 1252. [Google Scholar] [CrossRef] [Green Version]
- Qiu, J.; Zhou, Y.; Vatin, N.; Guan, X.; Sultanov, S.; Khemarak, K. Damage constitutive model of coal gangue concrete under freeze-thaw cycles. Constr. Build. Mater. 2020, 264, 120720. [Google Scholar] [CrossRef]
- Li, H.; Li, L.; Li, W.; Xu, L. Seismic fragility assessment framework for highway bridges based on an improved uniform design-response surface model methodology. Bull. Earthq. Eng. 2020, 18, 2329–2353. [Google Scholar] [CrossRef]
- Li, H.; Li, L.; Zhou, G.; Xu, L. Effects of various modeling uncertainty parameters on the seismic response and seismic fragility estimates of the aging highway bridges. Bull. Earthq. Eng. 2020, 18, 6337–6373. [Google Scholar] [CrossRef]
- Cao, D.; Zhao, M.; Ge, W.; Wang, B. Experimental study on the eccentric compressive behaviors of RC columns after freeze-thaw cycles. Recent Adv. Mater. Anal. Monit. Eval. Found. Bridge Eng. 2014, 38–45. [Google Scholar]
- Liu, K.; Yan, J.; Zou, C. A pilot experimental study on seismic behavior of recycled aggregate concrete columns after freeze-thaw cycles. Constr. Build. Mater. 2018, 164, 497–507. [Google Scholar] [CrossRef]
- Xu, S.; Li, A.; Ji, Z.; Wang, Y. Seismic performance of reinforced concrete columns after freeze-thaw cycles. Constr. Build. Mater. 2016, 102, 861–871. [Google Scholar] [CrossRef]
- Hanjari, K. Structural Behaviour of Deteriorated Concrete Structures. Ph.D. Thesis, Chalmers University of Technology-Department of Civil and Environmental Engineering-Division of Structural Engineering, Gothenburg, Sweden, 2010. [Google Scholar]
- Zheng, S.; Zhang, Y.; Pei, P. Experimental study on the seismic performance of reinforced concrete columns under freeze-thaw cycles. J. Build. Struct. 2020, 41, 84–91. [Google Scholar]
- Hasan, M.; Okuyama, H.; Sato, Y.; Ueda, T. Stress-strain model of concrete damaged by freezing and thawing cycles. J. Adv. Concr. Technol. 2004, 2, 89–99. [Google Scholar] [CrossRef] [Green Version]
- Berto, L.; Saetta, A.; Talledo, D. Constitutive model of concrete damaged by freeze–thaw action for evaluation of structural performance of RC elements. Constr. Build. Mater. 2015, 98, 559–569. [Google Scholar] [CrossRef]
- Shen, X.; Jiang, W.; Hou, D.; Hou, D.; Hu, Z.; Yang, J.; Liu, Q. Numerical study of carbonation and its effect on chloride binding in concrete. Cem. Concr. Compos. 2019, 104, 1031–1045. [Google Scholar] [CrossRef]
- Guo, A.; Li, H.; Ba, X.; Guan, X.; Li, H. Experimental investigation on the cyclic performance of reinforced concrete piers with chloride-induced corrosion in marine environment. Eng. Struct. 2015, 105, 1–11. [Google Scholar] [CrossRef]
- Ou, Y.; Fan, H.; Nguyen, N. Long-term seismic performance of reinforced concrete bridges under steel reinforcement corrosion due to chloride attack. Earthq. Eng. Struct. Dyn. 2013, 42, 2113–2127. [Google Scholar] [CrossRef]
- Akiyama, M.; Frangopol, D.; Matsuzaki, H. Life-cycle reliability of RC bridge piers under seismic and airborne chloride hazards. Earthq. Eng. Struct. Dyn. 2011, 40, 1671–1687. [Google Scholar] [CrossRef]
- Li, H.; Li, L.; Zhou, G.; Xu, L. Time-dependent seismic fragility assessment for aging highway bridges subject to non-uniform chloride-induced corrosion. J. Earthq. Eng. 2022, 26, 3523–3553. [Google Scholar] [CrossRef]
- Li, H.; Li, L.; Xu, L. Seismic Response and Fragility Estimates of Highway Bridges Considering Various Modeling Uncertainty Parameters. In Advancements in Geotechnical Engineering; Springer: Cham, Switzerland, 2021; pp. 31–53. [Google Scholar]
- Li, H.; Li, L. Bridge fragility analysis based on an improved uniform design-response surface methodology. J. Vib. Shock. 2018, 37, 245–254. [Google Scholar]
- Wang, B.; Huang, W.; Zheng, S. Study on restoring force performance of corrosion damage steel frame beams under acid atmosphere. Appl. Sci. 2018, 9, 103. [Google Scholar] [CrossRef] [Green Version]
- Val, D.; Stewart, M.; Melchers, R. Effect of reinforcement corrosion on reliability of highway bridges. Eng. Struct. 1998, 20, 1010–1019. [Google Scholar] [CrossRef]
- GB/T 50082-2009. Long-term Performance and Durability of Ordinary Concrete. Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2009.
- Chatterji, S. On the applicability of Fick’s second law to chloride ion migration through Portland cement concrete. Cem. Concr. Res. 1995, 25, 299–303. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Kong, D. Chloride diffusivity analysis of existing concrete based on Fick’s second law. J. Wuhan Univ. Technol.-Mater. Sci. Ed. 2010, 25, 142–146. [Google Scholar] [CrossRef]
- Liu, J.; Jia, Y.; Wang, J. Calculation of chloride ion diffusion in glass and polypropylene fiber-reinforced concrete. J. Constr. Build. Mater. 2019, 215, 875–885. [Google Scholar] [CrossRef]
- Wang, Y.; An, M.; Yu, Z.; Han, B.; Ji, W. Experimental and cellular-automata-based analysis of chloride ion diffusion in reactive powder concrete subjected to freeze–thaw cycling. Constr. Build. Mater. 2018, 172, 760–769. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Luo, W.; Wang, J.; Shi, J.; Zhuang, H.; Wang, Y. Effect of compressive strength and chloride diffusion on life cycle CO2 assessment of concrete containing supplementary cementitious materials. J. Clean. Prod. 2019, 218, 450–458. [Google Scholar] [CrossRef]
- Ma, J.; Lin, P. Simulation approach for random diffusion of chloride in concrete under sustained load with cellular automata. Materials 2022, 15, 4384. [Google Scholar] [CrossRef]
- Wang, Y.; Kun, F. Comparisons of instantaneous chloride diffusion coefficients determined by RCM method and chloride natural diffusion test. Constr. Build. Mater. 2019, 223, 595–604. [Google Scholar] [CrossRef]
- Violetta, B. Life-365 service life prediction model. Concr. Int. 2002, 24, 53–57. [Google Scholar]
- Ge, Y.; Yuan, J.; Yang, W. Influence of freeze-thaw action on bond strength, carbonation and chloride diffusion coefficient of air-entraining concrete. J. Highw. Transp. Res. Dev. 2010, 27 (Suppl. S1), 103–105. [Google Scholar]
- Wang, Y.; Liu, Z.; Fu, K.; Li, Q.; Wang, Y. Experimental studies on the chloride ion permeability of concrete considering the effect of freeze–thaw damage. Constr. Build. Mater. 2020, 236, 117556. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, X.; Fu, B.; Zhang, L. Chloride ion penetration resistance of concrete containing fly ash and silica fume against combined freezing-thawing and chloride attack. Constr. Build. Mater. 2018, 169, 740–747. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wang, Z. Quantitative design of concrete frost resistance. Concrete 2000, 9, 61–64. [Google Scholar]
- Cui, F.; Zhang, H.; Ghosn, M.; Xu, Y. Seismic fragility analysis of deteriorating RC bridge substructures subject to marine chloride-induced corrosion. Eng. Struct. 2018, 155, 61–72. [Google Scholar] [CrossRef]
- Liu, T.; Weyers, R. Modeling the dynamic corrosion process in chloride contaminated concrete structures. Cem. Concr. Res. 1998, 28, 365–379. [Google Scholar] [CrossRef]
- Guo, Y.; Trejo, D.; Yim, S. New model for estimating the time-variant seismic performance of corroding RC bridge columns. J. Struct. Eng. 2015, 141, 1–12. [Google Scholar] [CrossRef]
- Vu, K.; Stewart, M. Structural reliability of concrete bridges including improved chloride-induced corrosion models. Struct. Saf. 2000, 22, 313–333. [Google Scholar] [CrossRef]
- Du, Y.; Clark, L.; Chan, A. Residual capacity of corroded reinforcing bars. Mag. Concr. Res. 2005, 57, 135–147. [Google Scholar] [CrossRef]
- Cui, F.; Li, H.; Dong, X.; Wang, B.; Li, J.; Xue, H.; Qi, M. Improved time-dependent seismic fragility estimates for deteriorating RC bridge substructures exposed to chloride attack. Adv. Struct. Eng. 2021, 24, 437–452. [Google Scholar] [CrossRef]
- Shopov, A.; Bonev, B. Ascertainment of the change of the ductility in corroded steel specimens by experiment. Int. J. Civ. Eng. Technol. 2019, 10, 1551–1560. [Google Scholar]
- Mander, J.; Priestley, M.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef] [Green Version]
- Orakcal, K.; Massone, L.; Ulugtekin, D. A hysteretic constitutive model for reinforced concrete panel elements. Int. J. Concr. Struct. Mater. 2019, 13, 51. [Google Scholar] [CrossRef]
- Sun, L.; Jiang, K.; Zhu, X.; Xu, L. An alternating experimental study on the combined effect of freeze-thaw and chloride penetration in concrete. Constr. Build. Mater. 2020, 252, 119025. [Google Scholar] [CrossRef]
- Yang, D.; Yan, C.; Liu, S.; Ju, Z.; Hu, Z. Stress-strain constitutive model of concrete corroded by saline soil under uniaxial compression. Constr. Build. Mater. 2019, 213, 665–674. [Google Scholar] [CrossRef]
- Qiu, W.; Teng, F.; Pan, S. Damage constitutive model of concrete under repeated load after seawater freeze-thaw cycles. Constr. Build. Mater. 2020, 236, 1154–1171. [Google Scholar] [CrossRef]
- Zhang, D.; Mao, M.; Zhang, S.; Yang, Q. Influence of stress damage and high temperature on the freeze–thaw resistance of concrete with fly ash as fine aggregate. Constr. Build. Mater. 2019, 229, 1168–1179. [Google Scholar] [CrossRef]
- Li, B.; Mao, J.; Nawa, T.; Han, T. Mesoscopic damage model of concrete subjected to freeze-thaw cycles using mercury intrusion porosimetry and differential scanning calorimetry (MIP-DSC). Constr. Build. Mater. 2017, 147, 79–90. [Google Scholar] [CrossRef]
- Sun, M.; Xin, D.; Zou, C. Damage evolution and plasticity development of concrete materials subjected to freeze-thaw during the load process. Mech. Mater. 2019, 139, 576–594. [Google Scholar] [CrossRef]
- Gong, X.; Yu, H.; Wu, C. Research on the constitutive relationship of concrete under uniaxial compression in freeze–thaw environment. Constr. Build. Mater. 2022, 336, 127543. [Google Scholar] [CrossRef]
- Tavares, D.; Padgett, J.; Paultre, P. Fragility curves of typical as-built highway bridges in eastern Canada. Eng. Struct. 2012, 40, 107–118. [Google Scholar] [CrossRef]
- Cornell, C.; Jalayer, F.; Hamburger, R.; Foutch, D. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines. J. Struct. Eng. 2002, 128, 526–533. [Google Scholar] [CrossRef] [Green Version]
- Choi, E.; DesRoches, R.; Nielson, B. Seismic fragility of typical bridges in moderate seismic zones. Eng. Struct. 2004, 26, 187–199. [Google Scholar] [CrossRef]
- JTG/T B02-01. Seismic Design Rules for Highway Bridges in China. Ministry of Transport of the People’s Republic of China: Beijing, China, 2008.
- Li, L.; Luo, G.; Wang, Z.; Zhang, Y.; Yan, Z. Prediction of residual behaviors for post-earthquake damaged reinforced concrete column based on damage distribution model. Eng. Struct. 2021, 234, 111927. [Google Scholar] [CrossRef]
- Stewart, J.; Douglas, J.; Javanbarg, M.; Bozorgnia, Y.; Abrahamson, N.A.; Boore, D.M.; Campbelle, K.W.; Delavaud, E.; Erdik, M.; Stafford, P.J. Selection of ground motion prediction equations for the global earthquake model. Earthq. Spectra 2015, 31, 19–45. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Zhou, G.; Wang, J. Selection of Ground Motion Intensity Measures and Evaluation of the Ground Motion-Related Uncertainties in the Probabilistic Seismic Demand Analysis of Highway Bridges. Buildings 2022, 12, 56–75. [Google Scholar] [CrossRef]
- JTG/T 2231-01. Code for Seismic Design of Highway Bridges. Ministry of Transport of the People’s Republic of China: Beijing, China, 2020.
- Nielson, B.; DesRoches, R. Seismic fragility methodology for highway bridges using a component level approach. Earthq. Eng. Struct. Dyn. 2007, 36, 823–839. [Google Scholar] [CrossRef]
- Li, Q.; Huang, L.; Ye, H.; Fu, C.; Jin, X. Mechanical degradation of reinforced concrete columns corroded under sustained loads. Int. J. Civ. Eng. 2020, 18, 883–901. [Google Scholar] [CrossRef]
- Pan, Y.; Agrawal, A.; Ghosn, M. Seismic fragility of continuous steel highway bridges in New York State. J. Bridge Eng. 2007, 12, 689–699. [Google Scholar] [CrossRef]
- Thanapol, Y.; Akiyama, M.; Frangopol, D. Updating the seismic reliability of existing RC structures in a marine environment by incorporating the spatial steel corrosion distribution: Application to bridge piers. J. Bridge Eng. 2016, 21, 1–17. [Google Scholar] [CrossRef]
- Barbato, M.; Gu, Q.; Conte, J. Probabilistic push-over analysis of structural and soil-structure systems. J. Struct. Eng. 2010, 136, 1330–1341. [Google Scholar] [CrossRef]




| Portland Cement | Mineral Powder | Fly Ash | Fine Aggregate | Coarse Aggregate | Water | Water Reducing Agent | |
|---|---|---|---|---|---|---|---|
| 5–10 mm | 10–20 mm | ||||||
| 8.5% | 3.65% | 8.1% | 30.45% | 13% | 30.3% | 5.5% | 0.5% |
| Number of Freeze–Thaw Cycles | Peak Stress fco (MPa) | Standard Deviation for fco | Peak Strain εco | Standard Deviation for εco | Modulus of Elasticity Ec (104 MPa) | Standard Deviation for Ec | Chloride Ion Diffusion Coefficients D (10−12 m2/s) | Standard Deviation for D |
|---|---|---|---|---|---|---|---|---|
| 0 | 45 | 1.755 | 0.002 | 0.000094 | 3.25 | 0.1495 | 1.003 | 0.0481 |
| 50 | 36.4 | 1.529 | 0.0058 | 0.000282 | 2.65 | 0.1272 | 1.664 | 0.0865 |
| 100 | 28.7 | 1.263 | 0.0065 | 0.000345 | 2.41 | 0.1253 | 2.247 | 0.1258 |
| 150 | 25.6 | 1.229 | 0.010 | 0.00055 | 2.20 | 0.1188 | 2.669 | 0.1655 |
| 200 | 20.3 | 1.035 | 0.017 | 0.00102 | 1.95 | 0.1151 | 4.433 | 0.2926 |
| Parameter (Units) | Distribution | Mean | Standard Deviation | Reference |
|---|---|---|---|---|
| Compressive strength of the unconfined concrete (MPa) | Lognormal | 30.8 | 6.16 | [61] |
| Compressive strength of the confined concrete (MPa) | Lognormal | Equation (27) | 0.2 mean | [62] |
| Peak strain of the unconfined concrete | Lognormal | 0.002 | 0.0004 | [61] |
| Peak strain of the confined concrete | Lognormal | Equation (29) | 0.008 | [62] |
| Ultimate compressive strain of the unconfined concrete | Lognormal | 0.005 | 0.001 | [61] |
| Ultimate compressive strain of the confined concrete | Lognormal | 0.085 | 0.017 | [63] |
| Elastic modulus of concrete (MPa) | Normal | 3.24 × 104 | 3840 | [38] |
| Elastic modulus of steel (MPa) | Normal | 2.0 × 105 | 4000 | [35] |
| Concrete cover depth (mm) | Normal | 50 | 6 | [35] |
| Yield strength of steel (MPa) | Lognormal | Equation (15) | 0.07 mean | [61] |
| Bearing shear modulus (MPa) | Uniform | 1.365 | 0.407 | [40] |
| Rotational stiffness of the foundation (kN m/rad) | Uniform | 1.8 × 107 | 5.2 × 106 | [63] |
| Translation stiffness of foundation (kN/m) | Uniform | 6.2 × 105 | 1.5 × 105 | [63] |
| Deck mass ratios | Uniform | 1.0 | 0.058 | [40] |
| Damping ratio | Normal | 0.045 | 0.0125 | [40] |
| Time (Years) | PSDM | R2 | |
|---|---|---|---|
| 0 | 0.761 | 0.386 | |
| 25 | 0.752 | 0.392 | |
| 50 | 0.764 | 0.435 | |
| 75 | 0.735 | 0.457 | |
| 100 | 0.719 | 0.483 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, F.; Song, L.; Wang, X.; Li, M.; Hu, P.; Deng, S.; Zhang, X.; Li, H. Seismic Fragility Analysis of the Aging RC Columns under the Combined Action of Freeze–Thaw Cycles and Chloride-Induced Corrosion. Buildings 2022, 12, 2223. https://doi.org/10.3390/buildings12122223
Cui F, Song L, Wang X, Li M, Hu P, Deng S, Zhang X, Li H. Seismic Fragility Analysis of the Aging RC Columns under the Combined Action of Freeze–Thaw Cycles and Chloride-Induced Corrosion. Buildings. 2022; 12(12):2223. https://doi.org/10.3390/buildings12122223
Chicago/Turabian StyleCui, Fengkun, Linlin Song, Xingyu Wang, Mian Li, Peng Hu, Shuwen Deng, Xinyue Zhang, and Huihui Li. 2022. "Seismic Fragility Analysis of the Aging RC Columns under the Combined Action of Freeze–Thaw Cycles and Chloride-Induced Corrosion" Buildings 12, no. 12: 2223. https://doi.org/10.3390/buildings12122223
APA StyleCui, F., Song, L., Wang, X., Li, M., Hu, P., Deng, S., Zhang, X., & Li, H. (2022). Seismic Fragility Analysis of the Aging RC Columns under the Combined Action of Freeze–Thaw Cycles and Chloride-Induced Corrosion. Buildings, 12(12), 2223. https://doi.org/10.3390/buildings12122223







