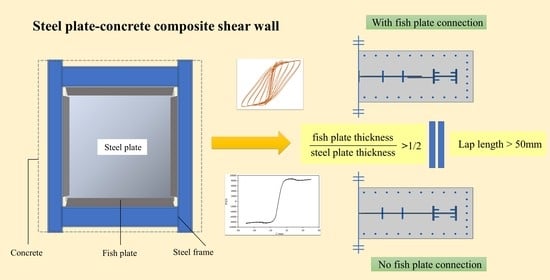
Study on the Seismic Behavior of a Steel Plate–Concrete Composite Shear Wall with a Fishplate Connection
Abstract
1. Introduction
2. Finite Element Model of Steel Plate—Concrete Composite Shear Wall
2.1. Parameter Design of Shear Wall
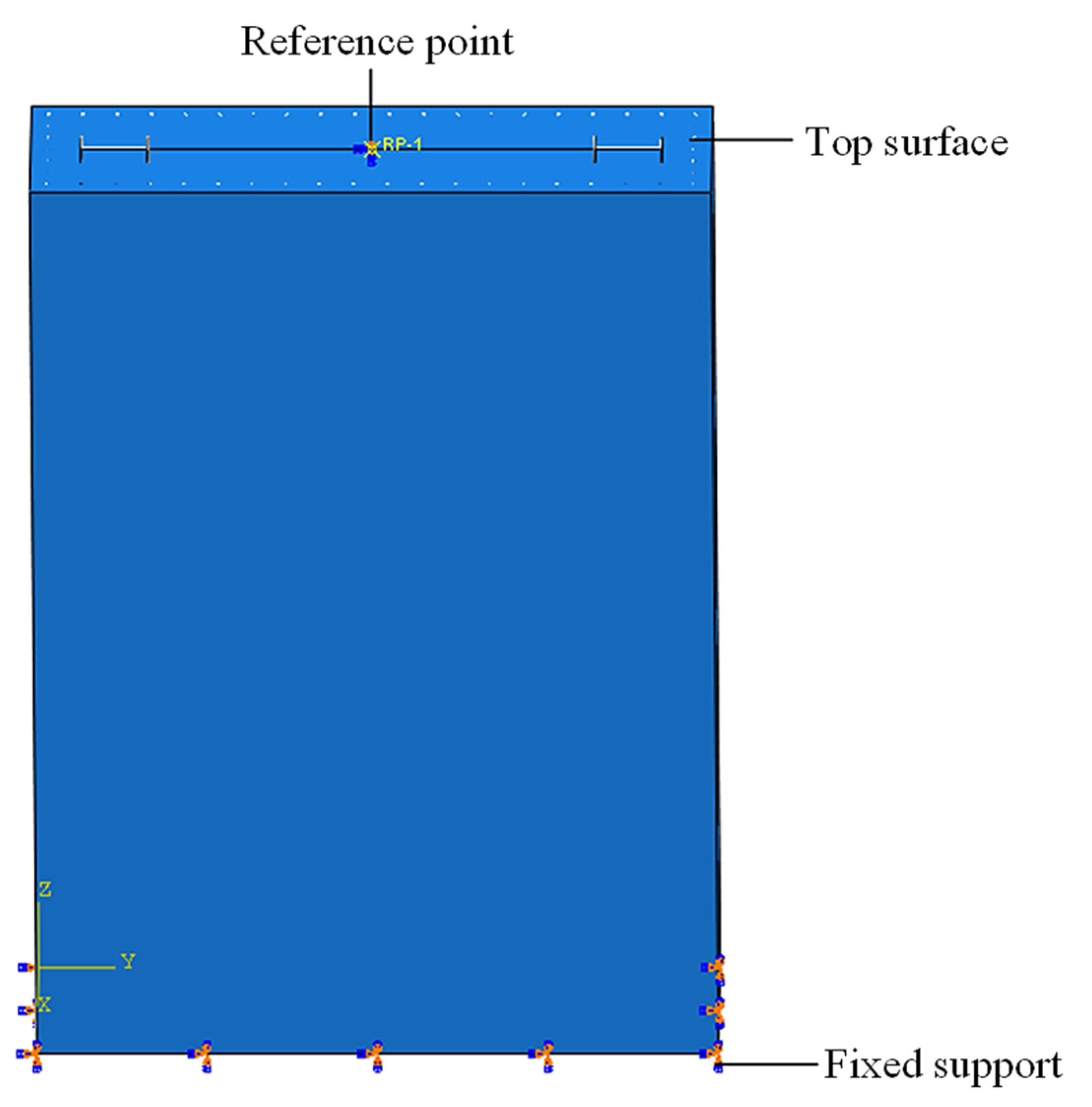
2.2. Establishment of Finite Element Model
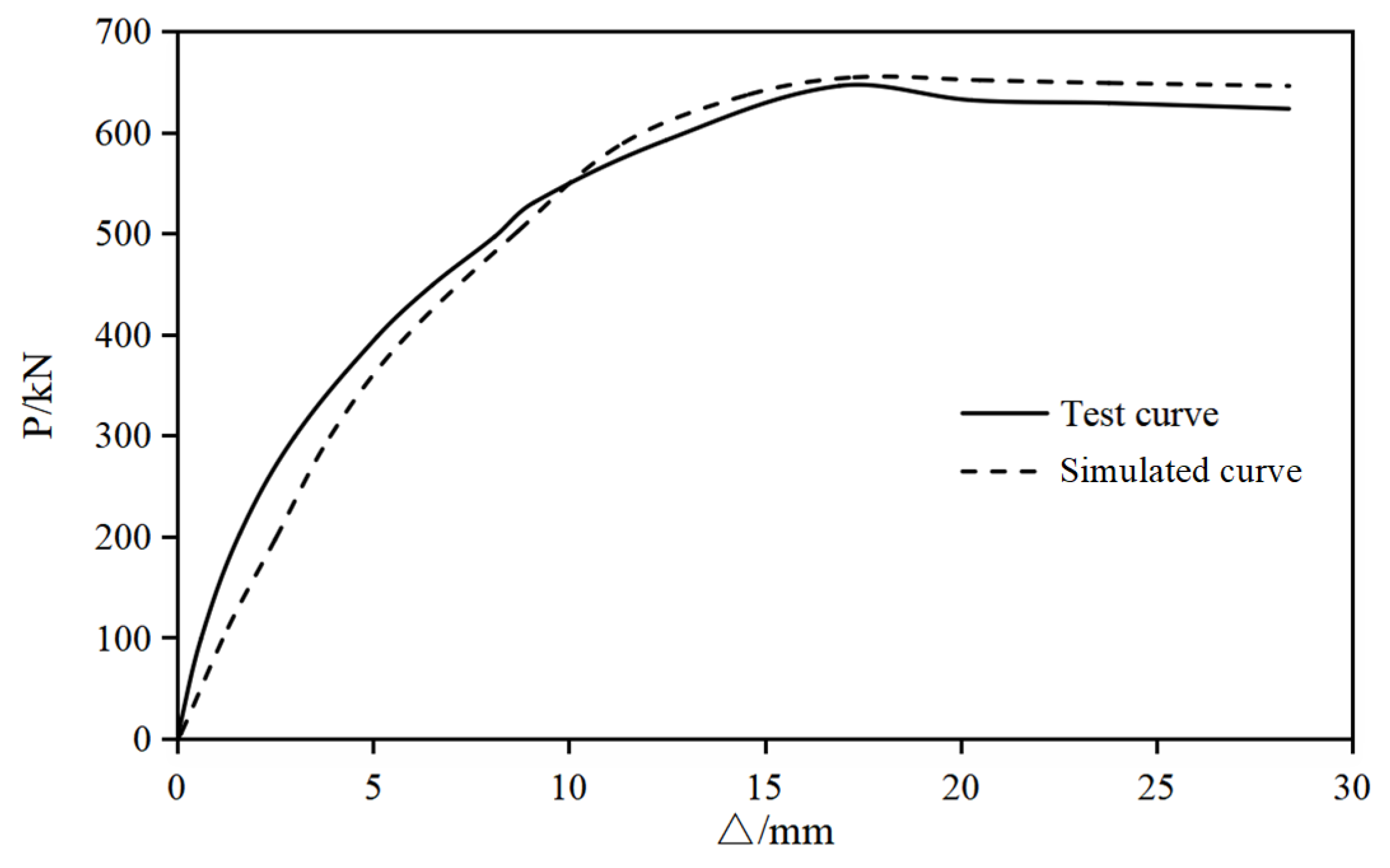
2.3. Simulation Test Verification
3. Parametric Analysis
3.1. Effect of Fishplate Thickness on the Performance of the Composite Wall
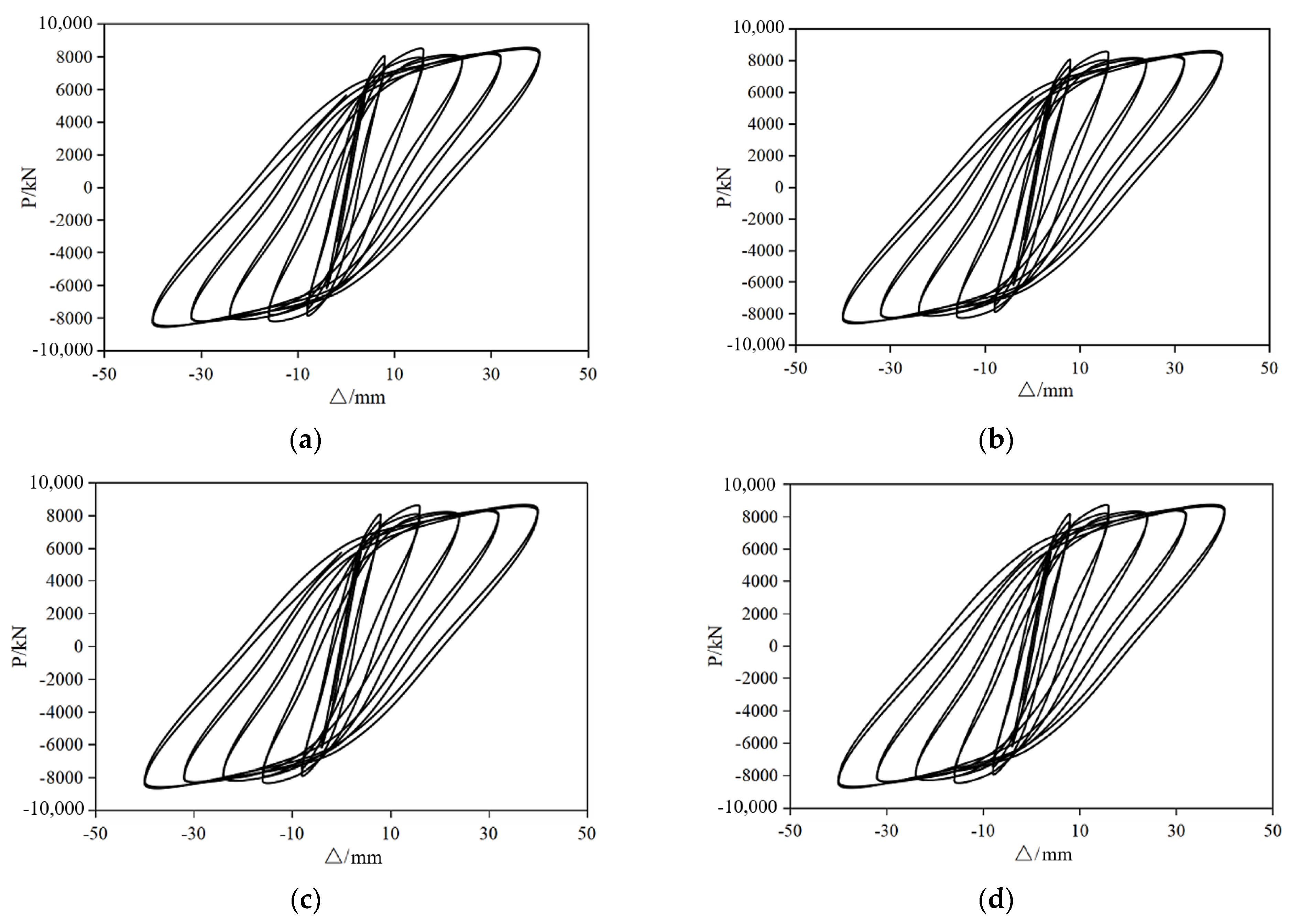
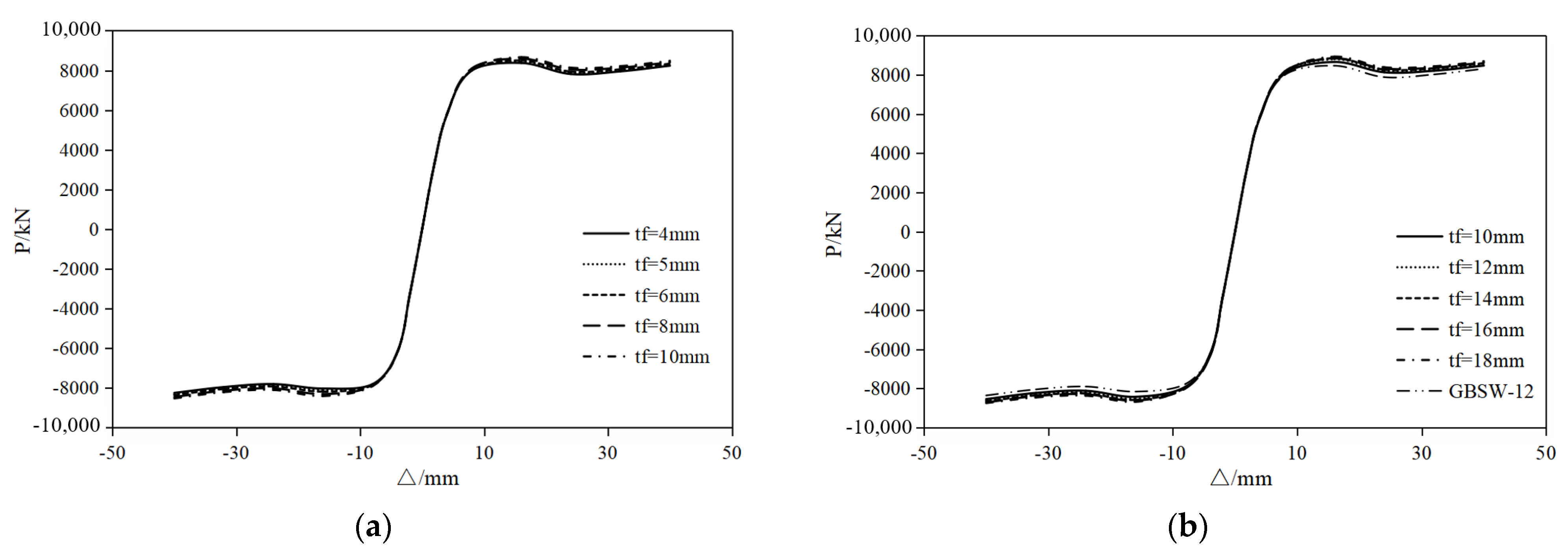
3.1.1. Hysteresis Curve and Skeleton Curve
3.1.2. Stiffness Degradation
3.1.3. Energy Dissipation
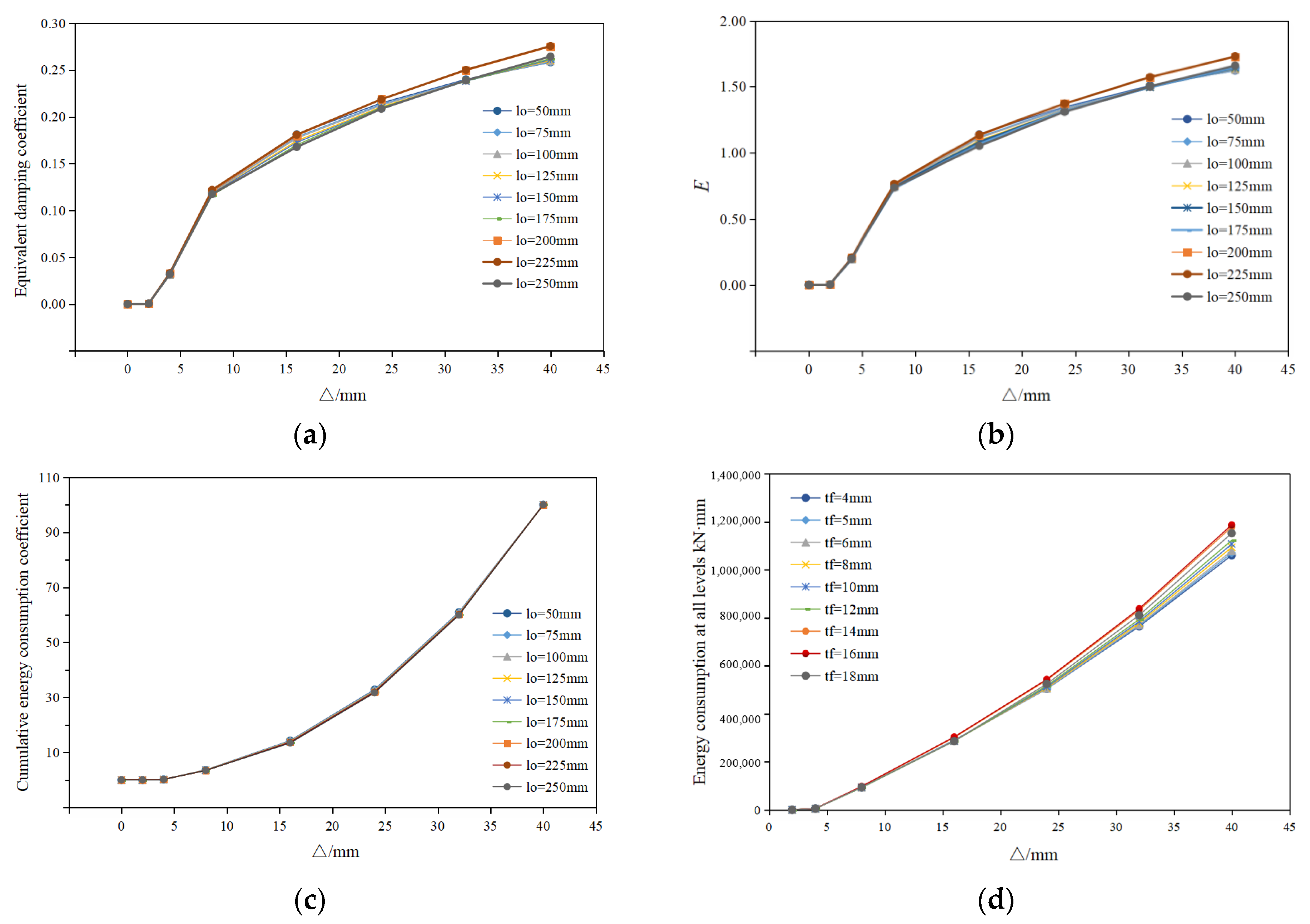
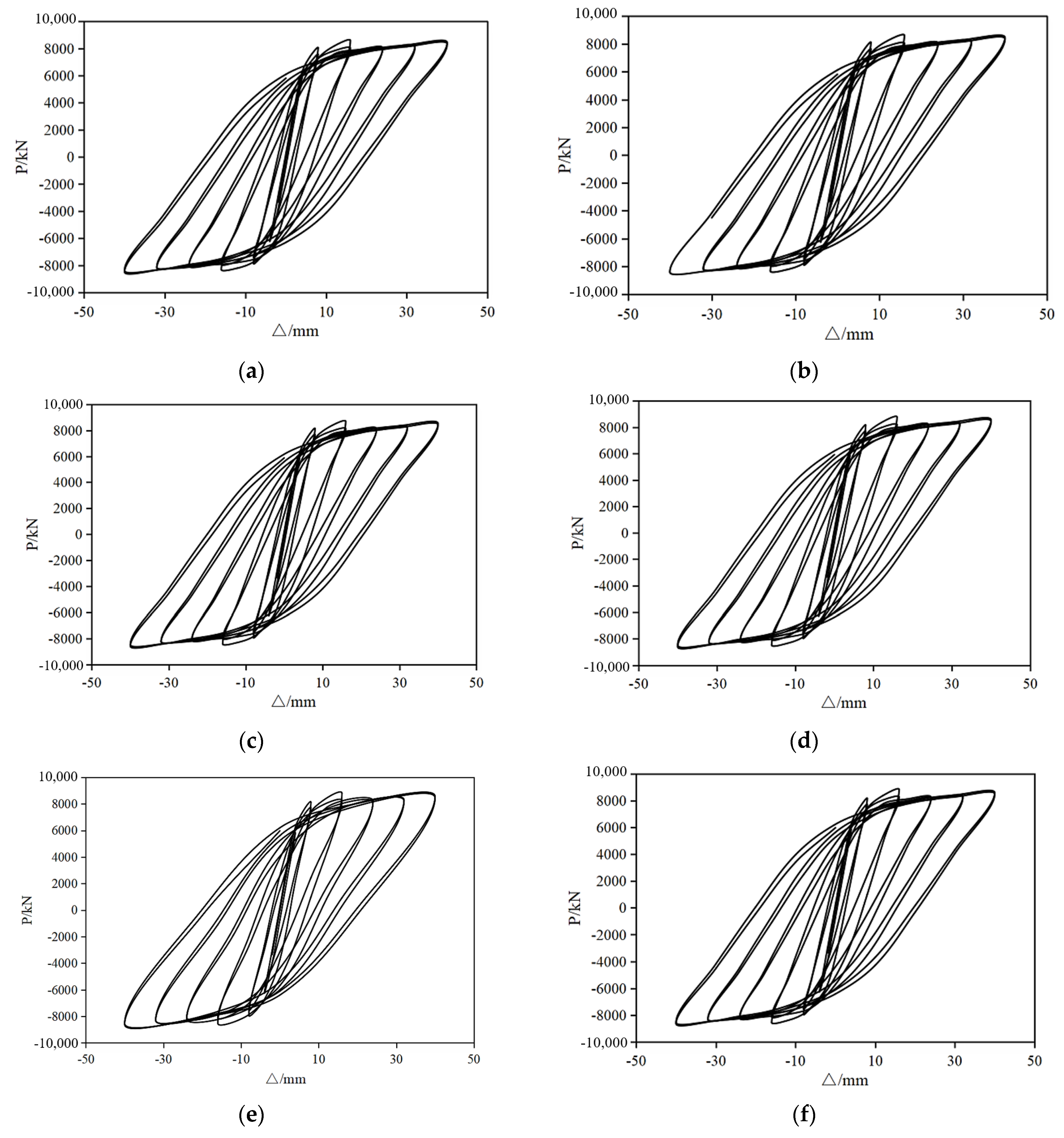
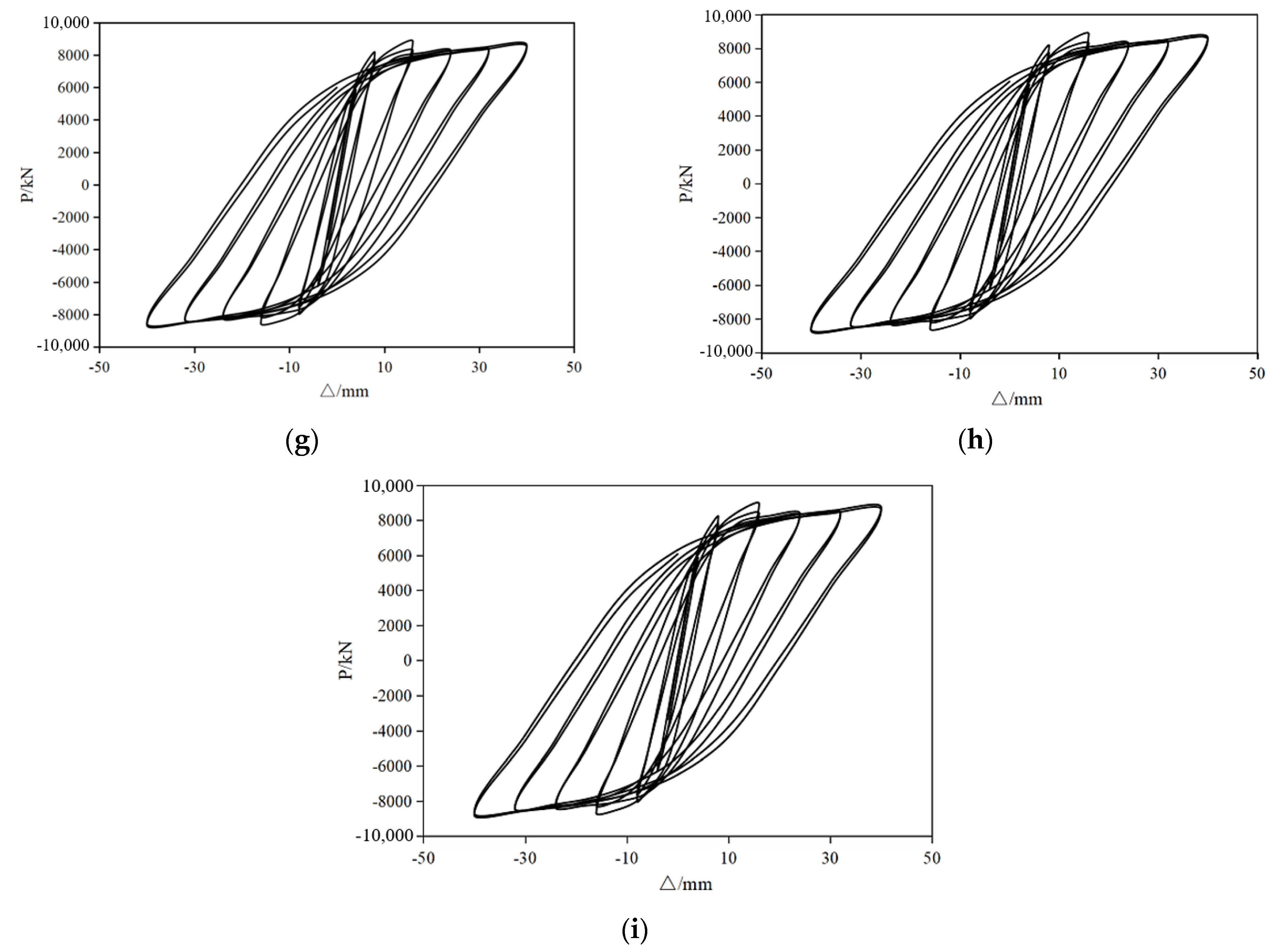
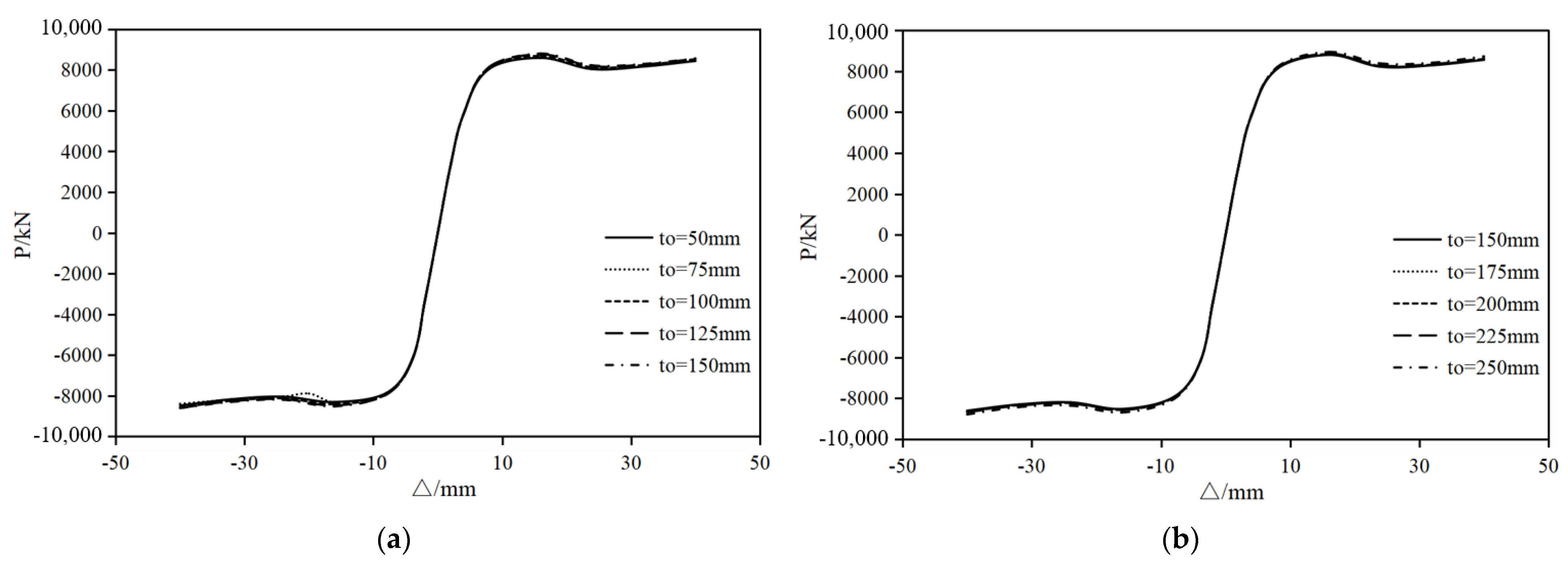
3.2. Effect of Lap Length of Fishplate on Performance of Composite Wall
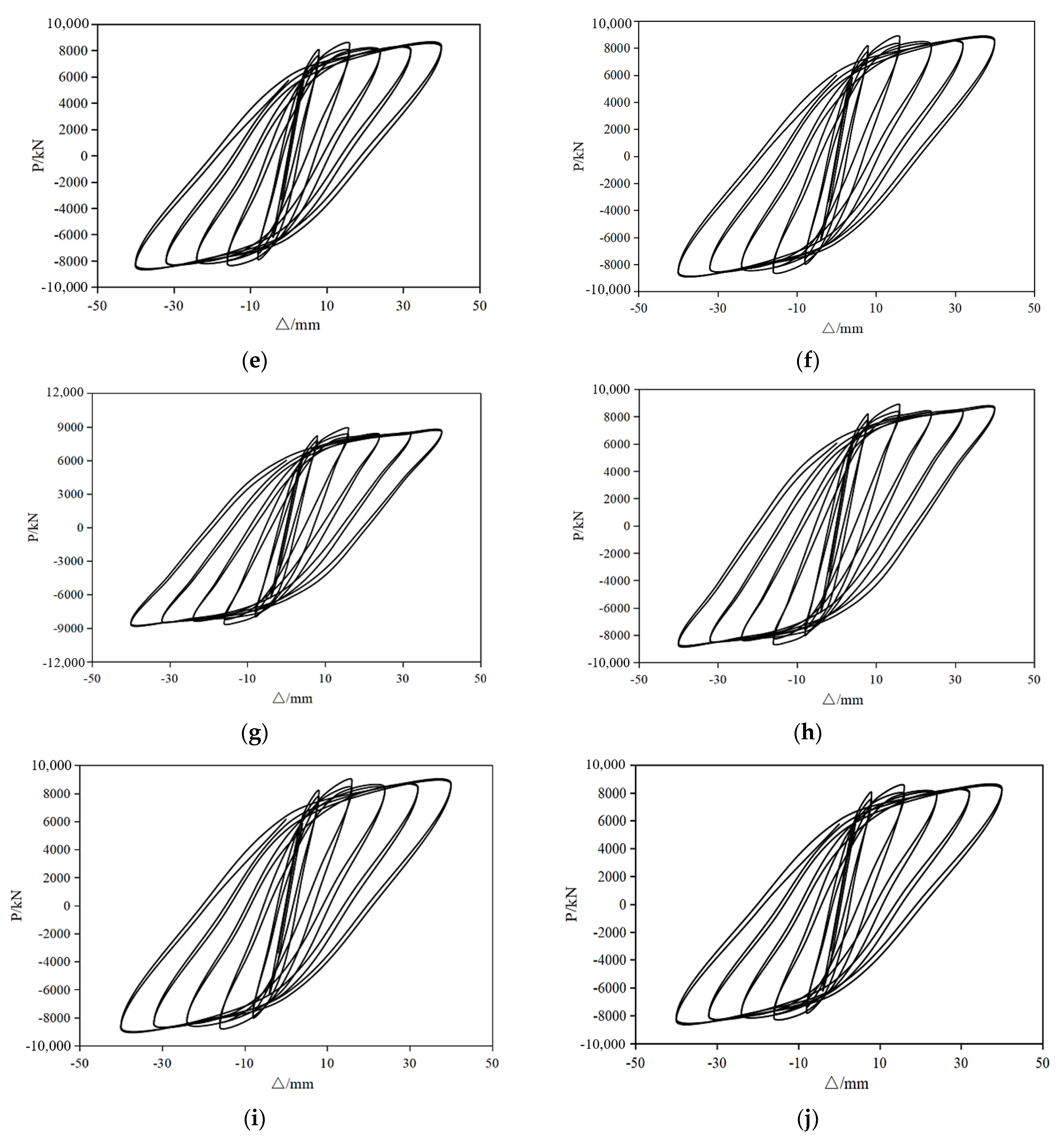
3.2.1. Hysteresis Curve and Skeleton Curve
3.2.2. Stiffness Degradation
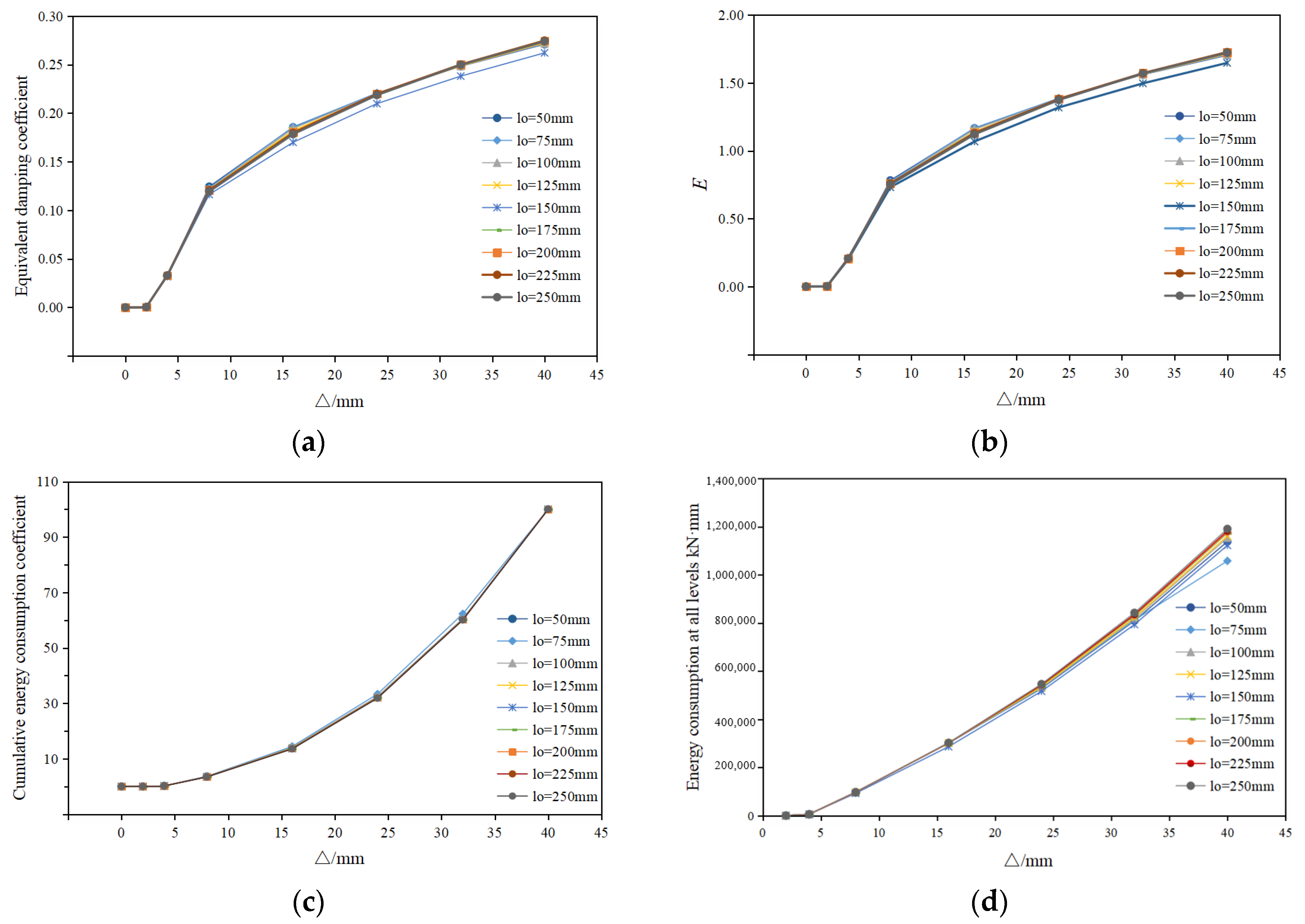
3.2.3. Energy Dissipation
4. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Japan Association of Building Construction Technicians. 100 Typical Examples of Japanese Structural Technology; China Building Industry Press: Beijing, China, 2005. [Google Scholar]
- Ghomi, T. Hysteretic characteristics of unstiffened plate shear panels. Thin. Wall. Struct. 1995, 12, 145–162. [Google Scholar]
- Li, G.Q.; Zhang, X.G.; Shen, Z.Y. Experimental study on shear hysteretic behavior of steel plate encased concrete shear wall panels. Ind. Build. 1995, 30, 32–35. [Google Scholar]
- Wright, H.D. The behaviour of composite walling under construction and service loading. J. Const. Steel. Res. 1995, 35, 257–275. [Google Scholar] [CrossRef]
- Hitaka, T.; Matsui, C. Strength and behavior of steel-concrete composite bearing wall. In Proceedings of the 6th ASCCS Conference on Composite and Hybrid Structures, Los Angeles, CA, USA, 22–24 March 2000. [Google Scholar]
- Emori, K. Compressive and shear strength of concrete filled steel box wall. J. Steel Struct. 2002, 26, 29–40. [Google Scholar]
- Guo, Y.L.; Dong, Q.L. Research and application of steel plate shear wall in high-rise buildings. Steel Constr. 2005, 20, 1–6. [Google Scholar]
- Giannuzzi, D.; Ballarini, R.; Huckelbridge, A., Jr.; Pollino, M.; Valente, M. Braced ductile shear panel: New seismic-resistant framing system. J. Struct. Eng. 2014, 140, 04013050. [Google Scholar] [CrossRef]
- Li, R. Study on Hysteretic Behavior of Steel Plate Shear Wall and Composite Shear Wall. Master Thesis, Harbin Institute of Technology, Harbin, China, 2011. [Google Scholar]
- Cui, L.F.; Jiang, H.J.; Lv, S.W. Comparative study on seismic performance of built-in steel plate and built-in steel truss concrete composite shear wall. J. Build. Struct. 2013, 34, 132–140. [Google Scholar]
- Zhu, A.P. Seismic Behavior of Embedded Steel Plate Reinforced C80 Concrete Composite Shear Walls. Ph.D. Thesis, China Academy of Building Research, Beijing, China, 2015. [Google Scholar]
- Nie, J.G.; Bu, F.M.; Fan, J.S. Experimental research on seismic behavior of low shear-span ratio composite shear wall with double steel plates and infill concrete. J. Build. Struct. 2011, 32, 74–81. [Google Scholar]
- Nie, J.G.; Bu, F.M.; Fan, J.S. Quasi-static test on low shear-span ratio composite shear wall with double steel plates and infill concrete under high axial compression ratio. Eng. Mech. 2013, 30, 60–66. [Google Scholar]
- Bu, F.M.; Nie, J.G.; Fan, J.S. Experimental study on seismic behavior of medium and high shear-span ratio composite shear wall with double steel plates and infill concrete under high axial compression ratio. J. Archit. Struct. 2013, 34, 91–98. [Google Scholar]
- Zhu, A.P.; Xiao, C.Z.; Chen, T.; Tian, C.Y. Experimental study on seismic behavior of embedded steel plate reinforced concrete shear walls with 1.0 shear-span-ratio. China Civ. Eng. J. 2016, 49, 49–56. [Google Scholar]
- Arabzadeh, A.; Hamid, R.K.N.K. Numerical and experimental investigation of composite steel shear wall with opening. Int. J. Steel Struct. 2017, 17, 1379–1389. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Y.; Lu, Z. Experimental study on seismic behavior of steel plate reinforced concrete composite shear wall. Eng. Struct. 2018, 160, 281–292. [Google Scholar] [CrossRef]
- Wang, W.; Ren, Y.Z.; Lu, Z.; Song, J.J.; Han, B.; Zhou, Y. Experimental study of the hysteretic behaviour of corrugated steel plate shear walls and steel plate reinforced concrete composite shear walls. J. Constr. Steel. Res. 2019, 160, 136–152. [Google Scholar] [CrossRef]
- Long, J.T. Study on Seismic Performance of Newly Modular Assembled Single-Layer Composite Shear Wall. Master Thesis, Guangzhou University, Guangzhou, China, 2019. [Google Scholar]
- Chen, Y. Study on Seismic Performance of New Modular Assembled Double-Layer Composite Shear Wall. Master Thesis, Guangzhou University, Guangzhou, China, 2019. [Google Scholar]
- Shallan, O.A.; Maaly, H.M.; Elgiar, M.M.; El-Sisi, A.A. Effect of stiffener characteristics on the seismic behavior and fracture tendency of steel shear walls. Fract. Struct. Integr. 2020, 14, 104–115. [Google Scholar] [CrossRef]
- Guo, Y.L.; Dong, Q.L.; Zhou, M. Elastic behavior and minimum restraining stiffness of buckling-restrained steel plate shear wall. J. Build. Struct. 2009, 30, 40–47. [Google Scholar]
- Astaneh-Asl, A. Seismic Behavior and Design of Composite Steel Plate Shear Walls; Structural Steel Educational Council: Moraga, CA, USA, 2002; pp. 7–8. [Google Scholar]
- Vasdravellis, G.; Valente, M.; Castiglioni, C.A. Dynamic response of composite frames with different shear connection degree. J. Const. Steel. Res. 2009, 65, 2050–2061. [Google Scholar] [CrossRef]
- Li, G.; Qiu, Z.; Yang, Z. Behavior of double fish plate connector between steel plate shear wall structure and steel frame. In Proceedings of the Modular and Offsite Construction (MOC) Summit, Edmonton, AB, Canada, 19–23 May 2015. [Google Scholar]
- El-Sisi, A.A.; Elgiar, M.M.; Maaly, H.M.; Shallan, O.A.; Salim, H.A. Effect of Welding Separation Characteristics on the Cyclic Behavior of Steel Plate Shear Walls. Buildings 2022, 12, 879. [Google Scholar] [CrossRef]
- Paslar, N.; Farzampour, A. Effects of Infill Plate’s Interconnection and Boundary Element Stiffness on Steel Plate Shear Walls’ Seismic Performance. Materials 2022, 15, 5487. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, Z.C.; Zhao, J.; Qu, S.Z. Analysis of mechanical properties of prefabricated composite shear wall connected with fishtail plate. J. China Three Gorges Univ. (Nat. Sci.) 2021, 43, 47–53. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. JGJ/T380-2015 Technical Specification for Steel Plate Shear Walls; China Building Industry Press: Beijing, China, 2015. [Google Scholar]
- GB50010-2010; Code for Design of Concrete Structures. China Building Industry Press: Beijing, China, 2010.
- Jiang, D.Q. Experimental Study on the Flexural Behavior of High Strength Concrete Steel Plate Composite Shear Wall. Master Thesis, China Academy of Building Research, Beijing China, 2011. [Google Scholar]
- Wu, S.Y. Specification of Testing Methods for Earthquake Resistant Building JGJ101-96; China Academy of Building Research: Beijing, China, 2005. [Google Scholar]
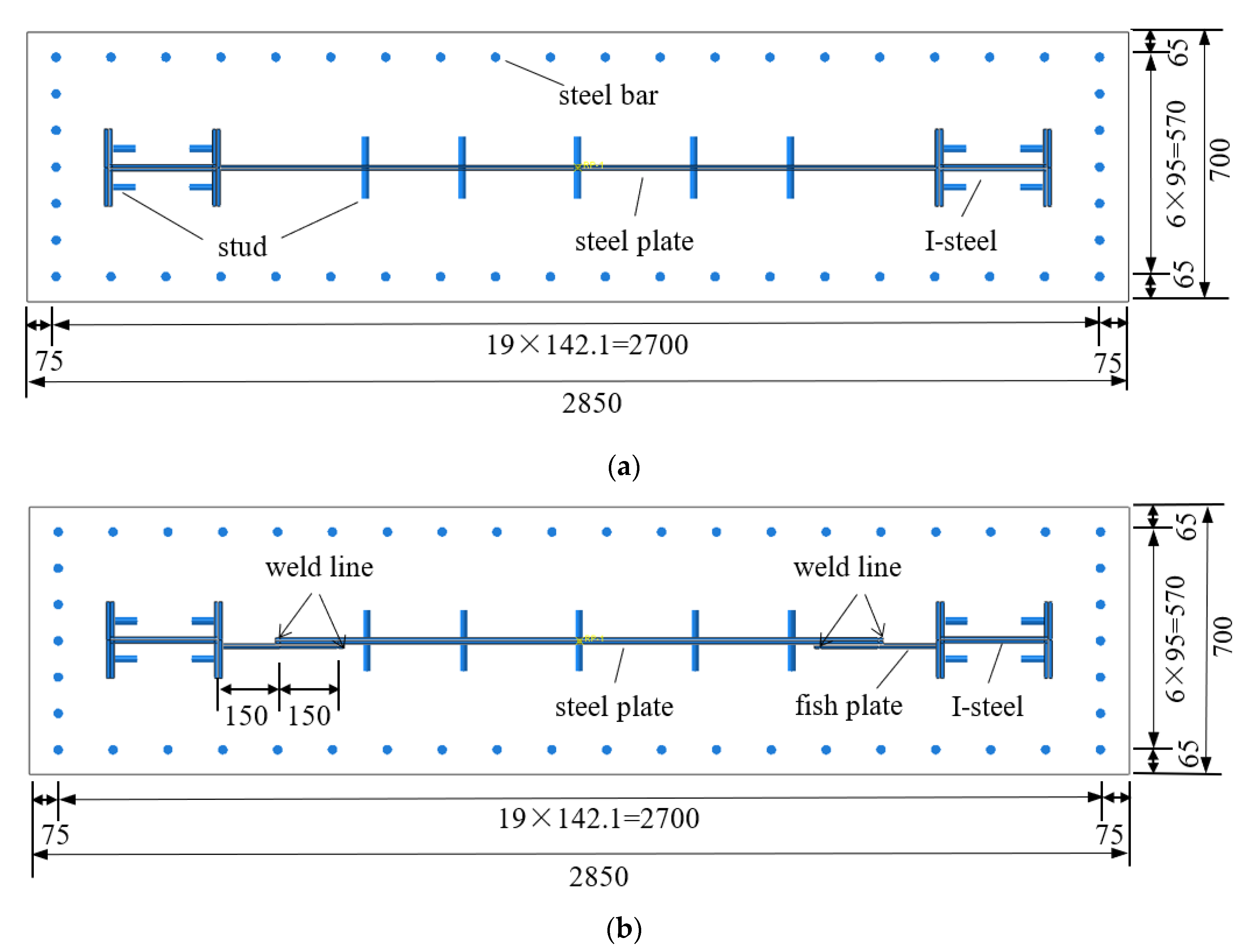
| Model Number | Concrete Strength | Steel Type | Shear Wall H × L × b (mm × mm × mm) | Steel Plate Hs × Ls × bs (mm × mm × mm) | tf (mm) | I-Steel Type | n |
|---|---|---|---|---|---|---|---|
| GBSW | C40 | Q345 | 4200 × 2850 × 700 | 4200 × 1850 × 12 | -- | 300 × 200 × 16 × 20 | 0.3 |
| YWBSW | C40 | Q345 | 4200 × 2850 × 700 | 4200 × 1550 × 12 | 12 | 300 × 200 × 16 × 20 | 0.3 |
| φ | ε | fb0/fc0 | K | η |
|---|---|---|---|---|
| 30 | 0.1 | 1.16 | 0.6667 | 0.0002 |
| Model Number | H/mm | L/mm | b/mm | n | tf/mm | lo/mm | |
|---|---|---|---|---|---|---|---|
| YWBSW-04 | 4200 | 2850 | 700 | 1.5 | 0.3 | 4 | 150 |
| YWBSW-05 | 4200 | 2850 | 700 | 1.5 | 0.3 | 5 | 150 |
| YWBSW-06 | 4200 | 2850 | 700 | 1.5 | 0.3 | 6 | 150 |
| YWBSW-08 | 4200 | 2850 | 700 | 1.5 | 0.3 | 8 | 150 |
| YWBSW-10 | 4200 | 2850 | 700 | 1.5 | 0.3 | 10 | 150 |
| YWBSW-12 | 4200 | 2850 | 700 | 1.5 | 0.3 | 12 | 150 |
| YWBSW-14 | 4200 | 2850 | 700 | 1.5 | 0.3 | 14 | 150 |
| YWBSW-16 | 4200 | 2850 | 700 | 1.5 | 0.3 | 16 | 150 |
| YWBSW-18 | 4200 | 2850 | 700 | 1.5 | 0.3 | 18 | 150 |
| GBSW-12 | 4200 | 2850 | 700 | 1.5 | 0.3 | 0 | 150 |
| Model Number | Yield Load (kN) | Yield Displacement (mm) | Peak Load (kN) |
|---|---|---|---|
| YWBSW-04 | 7255.36 | 6.68 | 8375.60 |
| YWBSW-05 | 7310.48 | 6.76 | 8450.20 |
| YWBSW-06 | 7348.79 | 6.81 | 8499.36 |
| YWBSW-08 | 7449.60 | 6.88 | 8592.40 |
| YWBSW-10 | 7477.37 | 6.95 | 8661.64 |
| YWBSW-12 | 7595.49 | 7.08 | 8800.54 |
| YWBSW-14 | 7642.37 | 7.10 | 8852.78 |
| YWBSW-16 | 7661.60 | 7.13 | 8894.12 |
| YWBSW-18 | 7693.87 | 7.17 | 8931.64 |
| GBSW-12 | 7320.13 | 6.77 | 8470.39 |
| Model Number | Stiffness at Each Stage (kN/mm) | ||||||
|---|---|---|---|---|---|---|---|
| 2 mm | 4 mm | 8 mm | 16 mm | 24 mm | 32 mm | 40 mm | |
| YWBSW-04 | 1648.90 | 1441.33 | 969.71 | 505.80 | 324.92 | 246.96 | 204.26 |
| YWBSW-05 | 1651.23 | 1443.05 | 972.67 | 510.74 | 327.54 | 248.77 | 205.68 |
| YWBSW-06 | 1653.28 | 1444.42 | 974.03 | 514.13 | 329.70 | 250.18 | 206.69 |
| YWBSW-08 | 1657.86 | 1447.85 | 981.56 | 520.47 | 333.96 | 253.07 | 208.73 |
| YWBSW-10 | 1662.38 | 1452.51 | 982.04 | 525.32 | 337.34 | 255.48 | 210.60 |
| YWBSW-12 | 1666.83 | 1455.97 | 988.60 | 532.60 | 340.54 | 258.11 | 212.74 |
| YWBSW-14 | 1672.39 | 1463.60 | 994.47 | 535.56 | 342.66 | 259.61 | 213.76 |
| YWBSW-16 | 1676.72 | 1467.83 | 994.78 | 536.13 | 344.56 | 260.66 | 214.77 |
| YWBSW-18 | 1679.92 | 1465.21 | 995.46 | 540.90 | 347.05 | 262.70 | 216.37 |
| GBSW-12 | 1653.52 | 1447.09 | 969.62 | 510.68 | 327.66 | 249.48 | 206.48 |
| Model Number | Energy Dissipation Coefficient at Each Stage | ||||||
|---|---|---|---|---|---|---|---|
| 2 mm | 4 mm | 8 mm | 16 mm | 24 mm | 32 mm | 40 mm | |
| YWBSW-04 | 0.0022 | 0.1957 | 0.7509 | 1.1392 | 1.3491 | 1.5079 | 1.6220 |
| YWBSW-05 | 0.0023 | 0.1959 | 0.7464 | 1.1206 | 1.3401 | 1.5034 | 1.6236 |
| YWBSW-06 | 0.0023 | 0.1966 | 0.7478 | 1.1123 | 1.3330 | 1.5007 | 1.6292 |
| YWBSW-08 | 0.0025 | 0.1971 | 0.7420 | 1.0949 | 1.3230 | 1.4967 | 1.6358 |
| YWBSW-10 | 0.0026 | 0.1983 | 0.7418 | 1.0843 | 1.3176 | 1.4949 | 1.6409 |
| YWBSW-12 | 0.0027 | 0.1988 | 0.7304 | 1.0677 | 1.3181 | 1.4959 | 1.6465 |
| YWBSW-14 | 00024 | 0.2064 | 0.7568 | 1.1293 | 1.3753 | 1.5662 | 1.7264 |
| YWBSW-16 | 0.0025 | 0.2080 | 0.7660 | 1.1363 | 1.3739 | 1.5717 | 1.7314 |
| YWBSW-18 | 0.0031 | 0.1997 | 0.7377 | 1.0534 | 1.3102 | 1.5012 | 1.6613 |
| GBSW-12 | 0.0024 | 0.1969 | 0.7531 | 1.1170 | 1.3400 | 1.5011 | 1.6267 |
| Model Number | Energy Dissipation at Each Stage (kN·mm) | Cumulative Energy Dissipation | ||||||
|---|---|---|---|---|---|---|---|---|
| 2 mm | 4 mm | 8 mm | 16 mm | 24 mm | 32 mm | 40 mm | ||
| YWBSW-04 | 15 | 5121 | 93,396 | 289,837 | 503,515 | 764,016 | 1,060,538 | 27,164,39 |
| YWBSW-05 | 15 | 5128 | 93,255 | 288,005 | 504,441 | 767,883 | 1,069,748 | 2,728,477 |
| YWBSW-06 | 15 | 5150 | 93,480 | 287,544 | 50,180 | 771,169 | 1,078,773 | 2,741,311 |
| YWBSW-08 | 16 | 5167 | 93,481 | 286,741 | 508,147 | 778,101 | 1,093,915 | 2,765,568 |
| YWBSW-10 | 17 | 5216 | 93,464 | 286,656 | 511,544 | 784,725 | 1,107,389 | 2,789,011 |
| YWBSW-12 | 18 | 5252 | 92,610 | 286,151 | 516,601 | 793,723 | 1,122,878 | 2,817,234 |
| YWBSW-14 | 16 | 5414 | 96,548 | 301,020 | 540,135 | 831,542 | 1,178,551 | 2,953,227 |
| YWBSW-16 | 16 | 5544 | 97,659 | 303,573 | 543,467 | 837,970 | 1,187,486 | 2,975,716 |
| YWBSW-18 | 20 | 5349 | 93,921 | 286,436 | 524,278 | 811,147 | 1,152,644 | 2,873,797 |
| GBSW-12 | 16 | 5188 | 93,822 | 287,285 | 504,169 | 768,920 | 1,076,856 | 2,736,256 |
| Model Number | H/mm | L/mm | b/mm | lo/mm | n | tf/mm | |
|---|---|---|---|---|---|---|---|
| YWBSW-50 | 4200 | 2850 | 700 | 1.5 | 50 | 0.3 | 12 |
| YWBSW-75 | 4200 | 2850 | 700 | 1.5 | 75 | 0.3 | 12 |
| YWBSW-100 | 4200 | 2850 | 700 | 1.5 | 100 | 0.3 | 12 |
| YWBSW-125 | 4200 | 2850 | 700 | 1.5 | 125 | 0.3 | 12 |
| YWBSW-150 | 4200 | 2850 | 700 | 1.5 | 150 | 0.3 | 12 |
| YWBSW-175 | 4200 | 2850 | 700 | 1.5 | 175 | 0.3 | 12 |
| YWBSW-200 | 4200 | 2850 | 700 | 1.5 | 200 | 0.3 | 12 |
| YWBSW-225 | 4200 | 2850 | 700 | 1.5 | 225 | 0.3 | 12 |
| YWBSW-250 | 4200 | 2850 | 700 | 1.5 | 250 | 0.3 | 12 |
| GBSW-12 | 4200 | 2850 | 700 | 1.5 | 0 | 0.3 | 12 |
| Model Number | Yield Load (kN) | Yield Displacement (mm) | Peak Load (kN) |
|---|---|---|---|
| YWBSW-50 | 7414.34 | 6.86 | 8588.51 |
| YWBSW-75 | 7450.31 | 6.86 | 8606.01 |
| YWBSW-100 | 7524.80 | 6.94 | 8685.84 |
| YWBSW-125 | 7581.47 | 7.02 | 8762.45 |
| YWBSW-150 | 7595.49 | 7.08 | 8800.54 |
| YWBSW-175 | 7625.77 | 7.08 | 8827.03 |
| YWBSW-200 | 7632.24 | 7.10 | 8842.33 |
| YWBSW-225 | 7650.07 | 7.11 | 8861.74 |
| YWBSW-250 | 7733.60 | 7.19 | 8945.86 |
| GBSW-12 | 7320.13 | 6.77 | 8470.39 |
| Model Number | Stiffness at Each Stage (kN/mm) | ||||||
|---|---|---|---|---|---|---|---|
| 2 mm | 4 mm | 8 mm | 16 mm | 24 mm | 32 mm | 40 mm | |
| YWBSW-50 | 1661.29 | 1455.76 | 978.85 | 519.25 | 334.04 | 253.95 | 209.57 |
| YWBSW-75 | 1662.79 | 1456.75 | 982.41 | 520.04 | 334.29 | 254.26 | 210.00 |
| YWBSW-100 | 1664.63 | 1458.12 | 988.50 | 525.19 | 337.33 | 256.30 | 211.68 |
| YWBSW-125 | 1666.58 | 1459.59 | 990.17 | 529.61 | 339.05 | 257.11 | 212.20 |
| YWBSW-150 | 1666.83 | 1455.97 | 988.60 | 532.60 | 340.54 | 258.11 | 212.74 |
| YWBSW-175 | 1669.90 | 1461.70 | 991.80 | 534.07 | 341.47 | 258.76 | 213.35 |
| YWBSW-200 | 1671.18 | 1462.39 | 992.28 | 534.87 | 341.85 | 259.04 | 213.68 |
| YWBSW-225 | 1672.72 | 1463.61 | 993.21 | 536.26 | 343.15 | 259.93 | 214.44 |
| YWBSW-250 | 1674.44 | 1465.17 | 1000.44 | 541.97 | 347.03 | 262.40 | 216.65 |
| GBSW-12 | 1653.52 | 1447.09 | 969.62 | 510.68 | 327.66 | 249.48 | 206.48 |
| Model Number | Energy Dissipation Coefficient at Each Stage | ||||||
|---|---|---|---|---|---|---|---|
| 2 mm | 4 mm | 8 mm | 16 mm | 24 mm | 32 mm | 40 mm | |
| YWBSW-50 | 0.0020 | 0.2042 | 0.7812 | 1.1649 | 1.3818 | 1.5595 | 1.7020 |
| YWBSW-75 | 0.0020 | 0.2047 | 0.7720 | 1.1678 | 1.3866 | 1.5635 | 1.7049 |
| YWBSW-100 | 0.0021 | 0.2051 | 0.7628 | 1.1570 | 1.3812 | 1.5610 | 1.7076 |
| YWBSW-125 | 0.0022 | 0.2053 | 0.7628 | 1.1432 | 1.3775 | 1.5625 | 1.7133 |
| YWBSW-150 | 0.0027 | 0.1988 | 0.7304 | 1.0677 | 1.3181 | 1.4959 | 1.6465 |
| YWBSW-175 | 0.0023 | 0.2062 | 0.7601 | 1.1321 | 1.3802 | 1.5677 | 1.7278 |
| YWBSW-200 | 0.0024 | 0.2066 | 0.7582 | 1.1317 | 1.3824 | 1.5711 | 1.7245 |
| YWBSW-225 | 0.0024 | 0.2068 | 0.7577 | 1.1289 | 1.3801 | 1.5711 | 1.7260 |
| YWBSW-250 | 0.0025 | 0.2069 | 0.7498 | 1.1203 | 1.3730 | 1.5688 | 1.7205 |
| GBSW-12 | 0.0024 | 0.1969 | 0.7531 | 1.1170 | 1.3400 | 1.5011 | 1.6267 |
| Model Number | Energy Dissipation at Each Stage (kN·mm) | Cumulative Energy Dissipation | ||||||
|---|---|---|---|---|---|---|---|---|
| 2 mm | 4 mm | 8 mm | 16 mm | 24 mm | 32 mm | 40 mm | ||
| YWBSW-50 | 13 | 5337 | 97,823 | 300,527 | 528,315 | 809,240 | 1,138,599 | 2,879,853 |
| YWBSW-75 | 13 | 5362 | 97,558 | 301,911 | 530,504 | 812,222 | 1,058,073 | 2,805,643 |
| YWBSW-100 | 14 | 5377 | 96,931 | 302,532 | 533,457 | 818,049 | 1,153,845 | 2,910,203 |
| YWBSW-125 | 14 | 5485 | 96,895 | 301,554 | 535,034 | 821,523 | 1,161,090 | 2,921,595 |
| YWBSW-150 | 18 | 5252 | 92,610 | 286,151 | 516,601 | 793,723 | 1,122,878 | 2,817,234 |
| YWBSW-175 | 15 | 5417 | 96,540 | 301,152 | 540,103 | 829,464 | 1,173,662 | 2,946,353 |
| YWBSW-200 | 16 | 5418 | 96,365 | 301,472 | 541,586 | 832,184 | 1,176,720 | 2,953,761 |
| YWBSW-225 | 16 | 5441 | 96,399 | 301,549 | 542,895 | 835,344 | 1,182,591 | 2,964,236 |
| YWBSW-250 | 17 | 5449 | 95,958 | 302,268 | 546,391 | 842,343 | 1,191,089 | 2,983,515 |
| GBSW-12 | 16 | 5188 | 93,822 | 287,285 | 504,169 | 768,920 | 1,076,856 | 2,736,256 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Sang, X.; Shang, K.; Zhang, Y.; Ju, J. Study on the Seismic Behavior of a Steel Plate–Concrete Composite Shear Wall with a Fishplate Connection. Buildings 2022, 12, 2245. https://doi.org/10.3390/buildings12122245
Wang Y, Sang X, Shang K, Zhang Y, Ju J. Study on the Seismic Behavior of a Steel Plate–Concrete Composite Shear Wall with a Fishplate Connection. Buildings. 2022; 12(12):2245. https://doi.org/10.3390/buildings12122245
Chicago/Turabian StyleWang, Yimin, Xiuxing Sang, Kaiguang Shang, Yushuo Zhang, and Jinsan Ju. 2022. "Study on the Seismic Behavior of a Steel Plate–Concrete Composite Shear Wall with a Fishplate Connection" Buildings 12, no. 12: 2245. https://doi.org/10.3390/buildings12122245
APA StyleWang, Y., Sang, X., Shang, K., Zhang, Y., & Ju, J. (2022). Study on the Seismic Behavior of a Steel Plate–Concrete Composite Shear Wall with a Fishplate Connection. Buildings, 12(12), 2245. https://doi.org/10.3390/buildings12122245