Numerical Investigation on Blast Response of Cold-Formed Steel Framing Protected with Functionally Graded Composite Material
Abstract
:1. Introduction
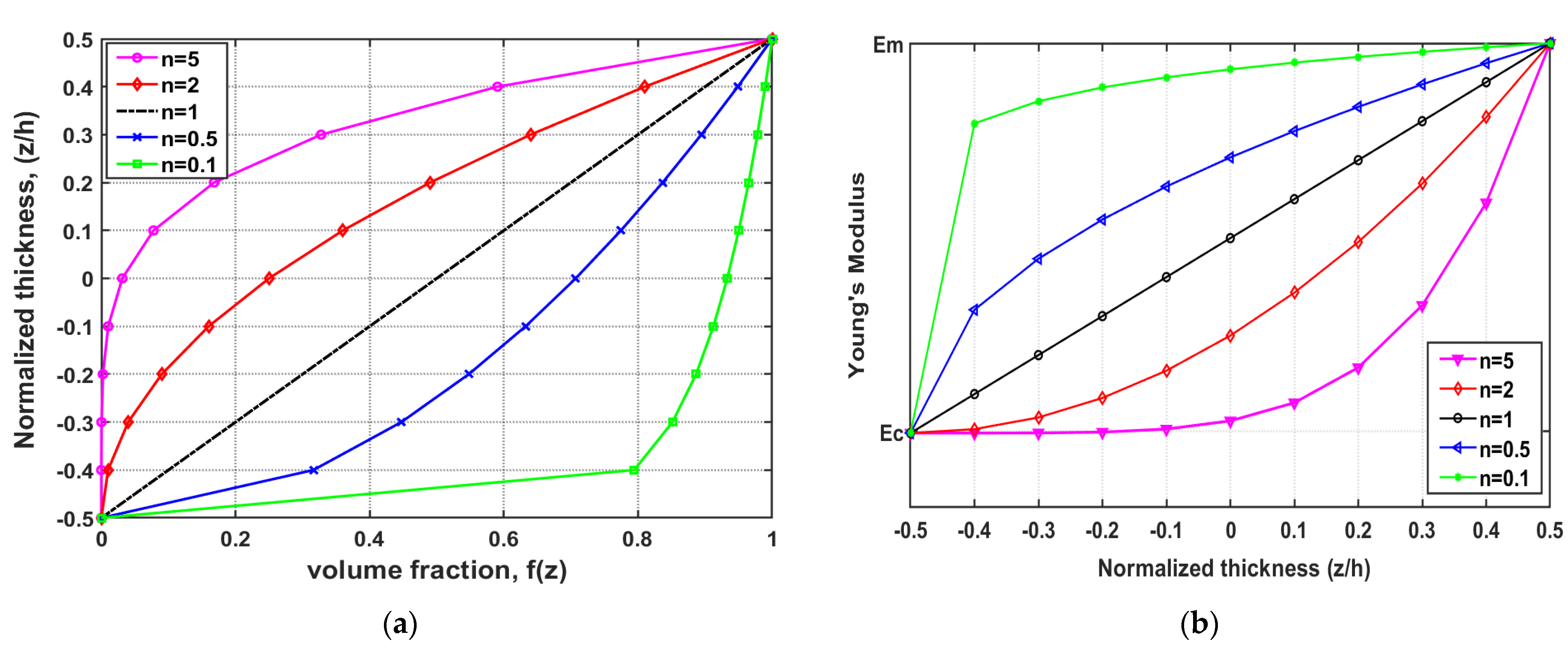
2. Mechanical Properties of Functionally Graded Material Composite Panel
3. Blast Load FE Modeling of the CFS Wall System
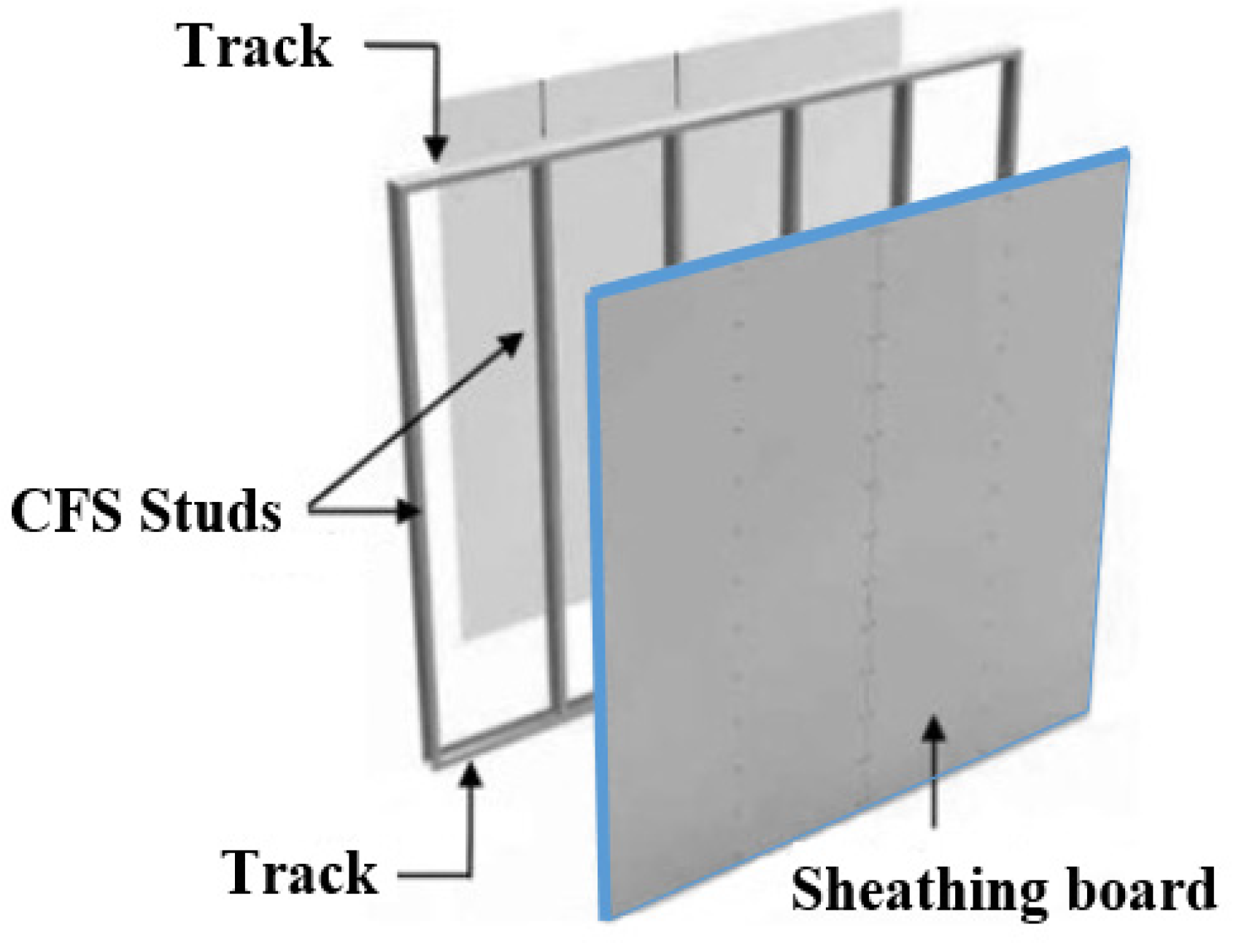
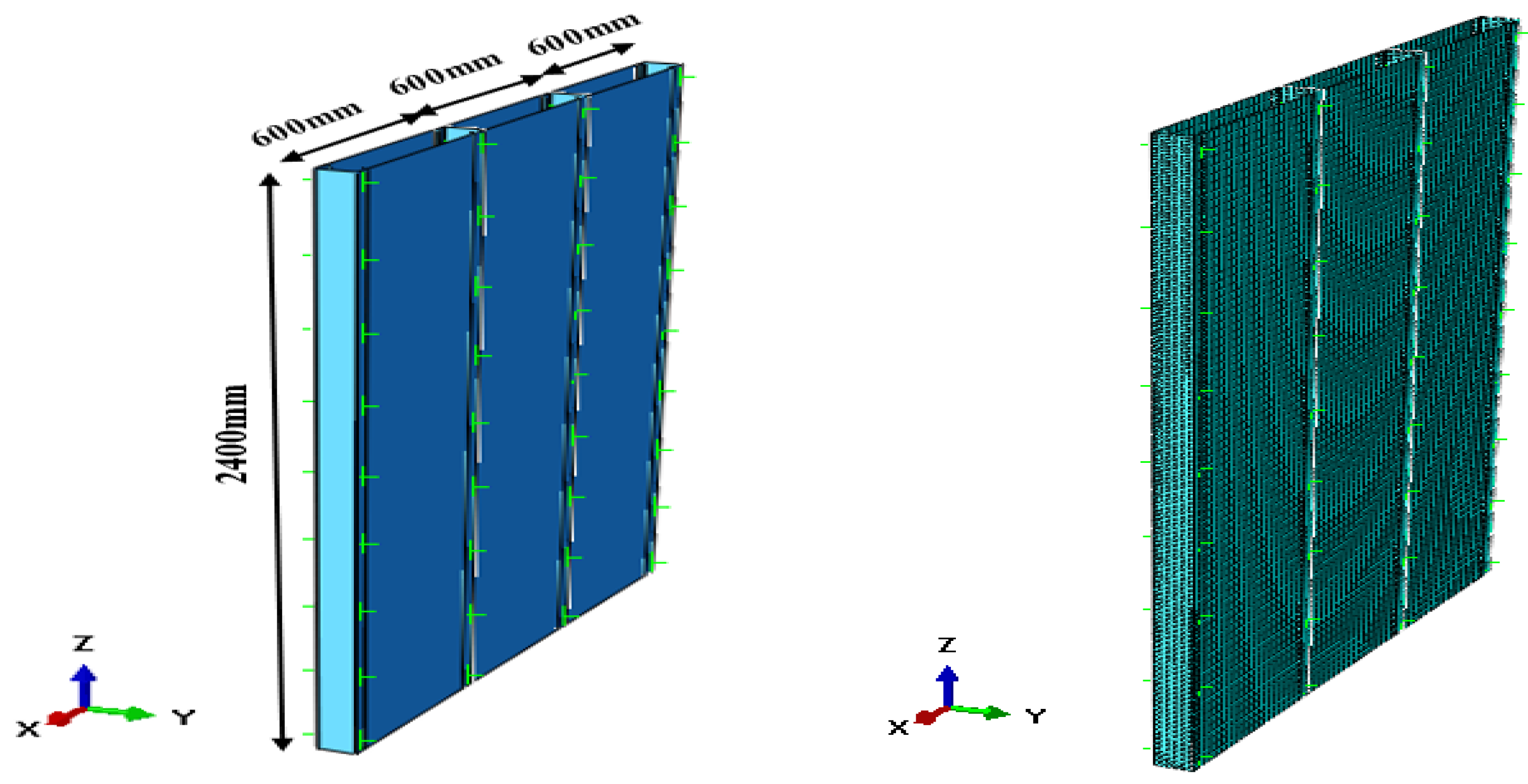
3.1. CFS Wall Geometry
3.2. FGM Board Modeling
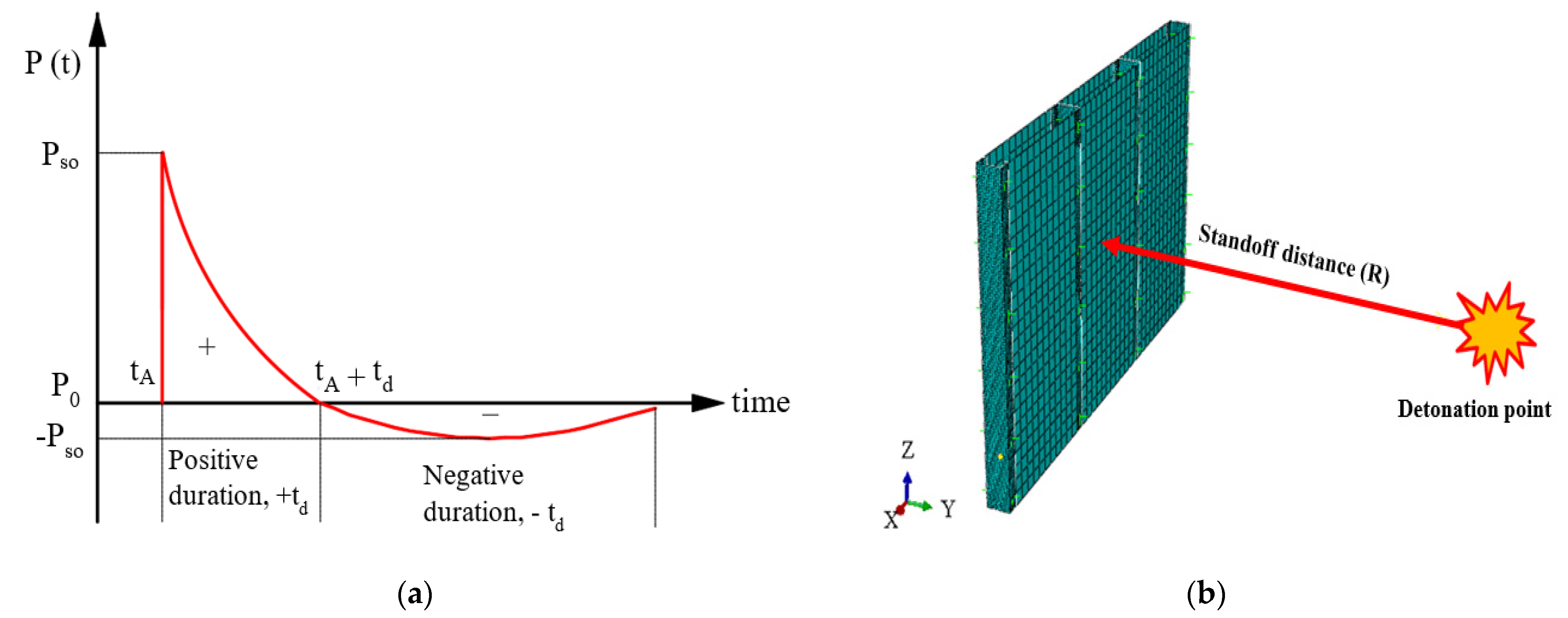
3.3. Blast Loading
4. Results and Discussion
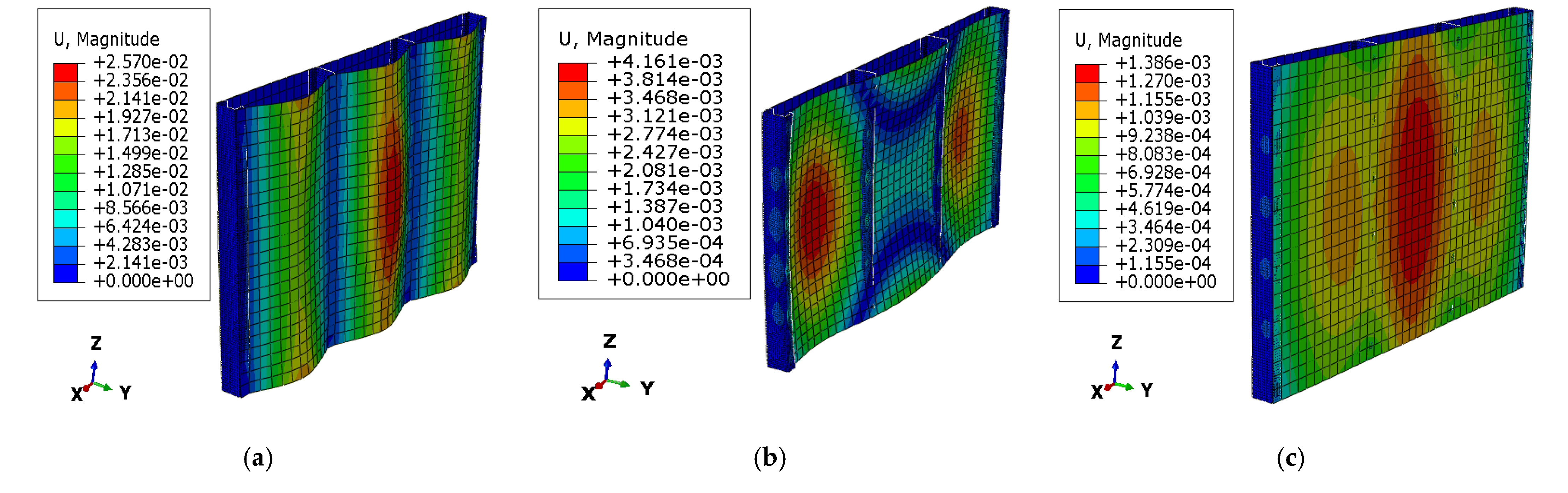
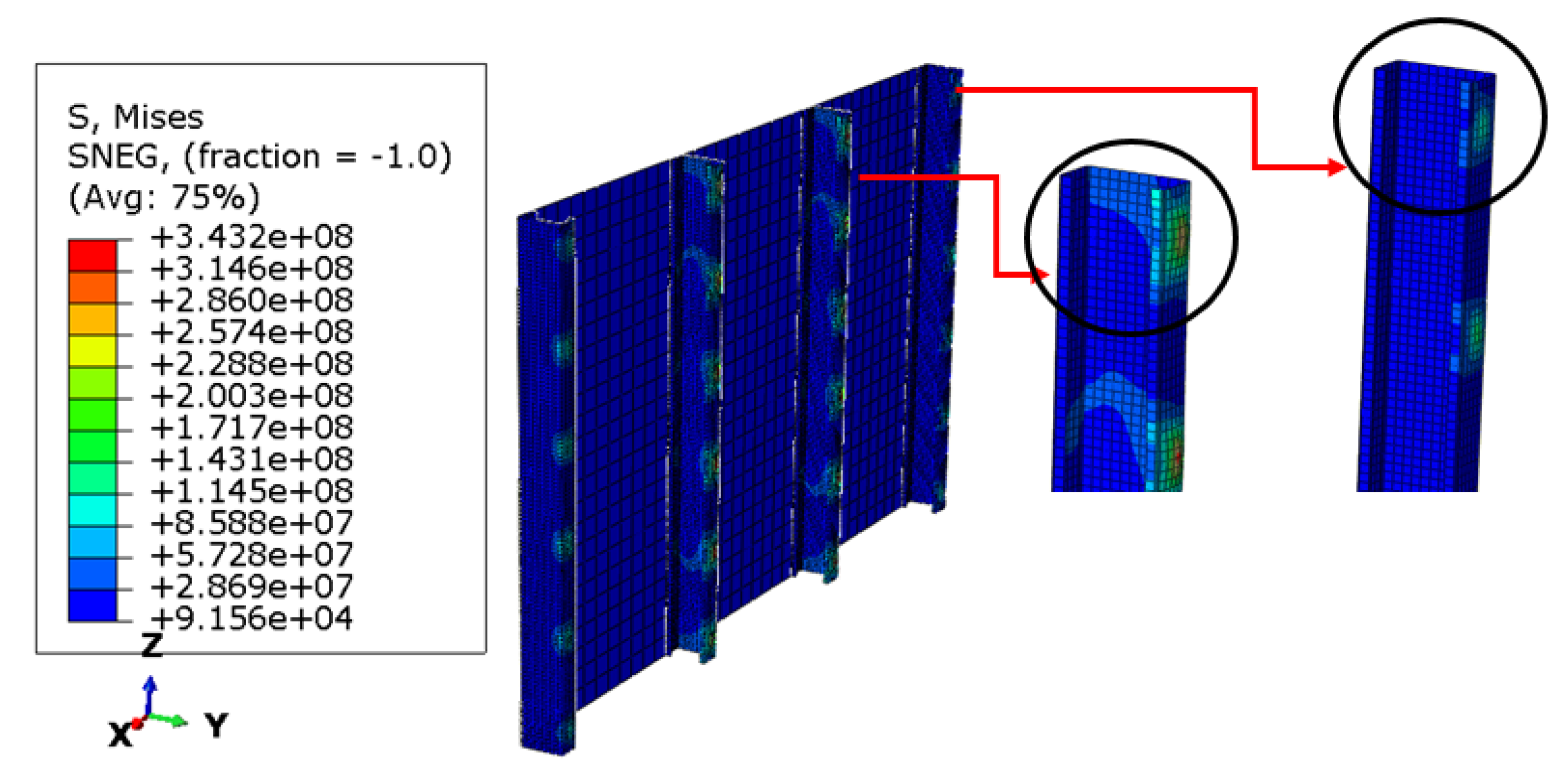
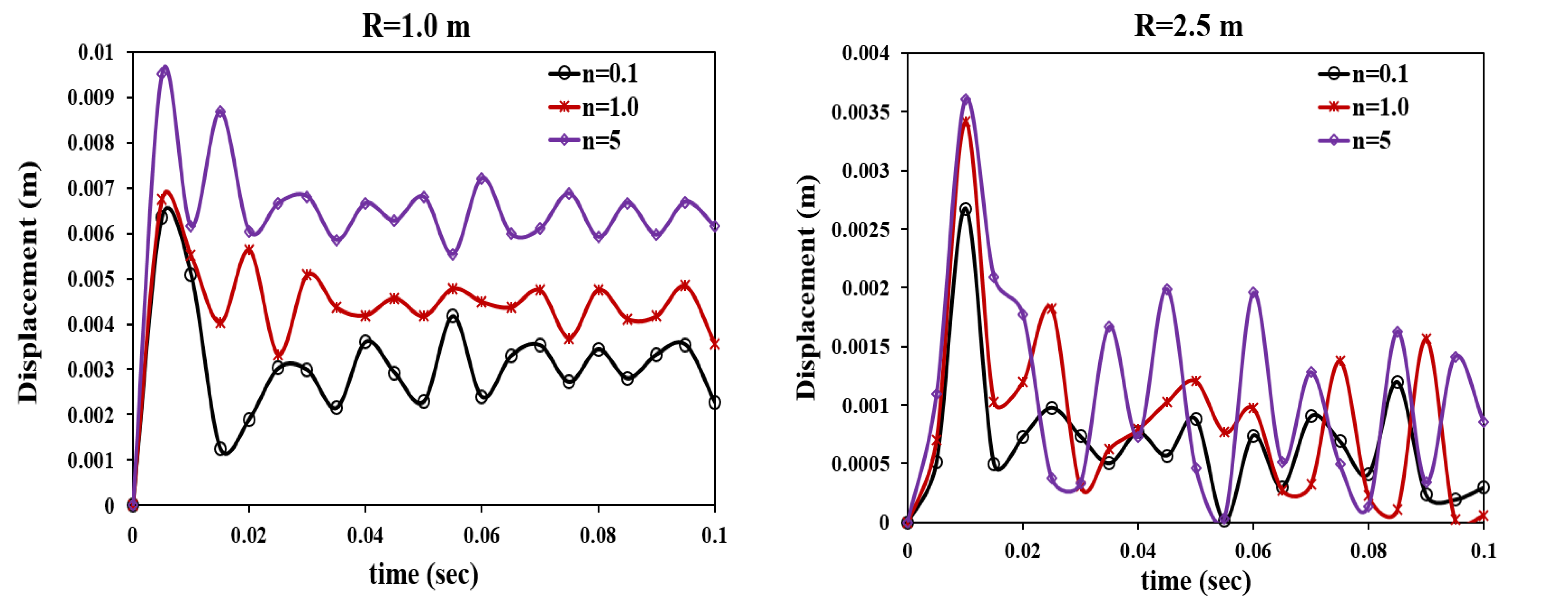
4.1. FGM Material Variation Index Sensitivity
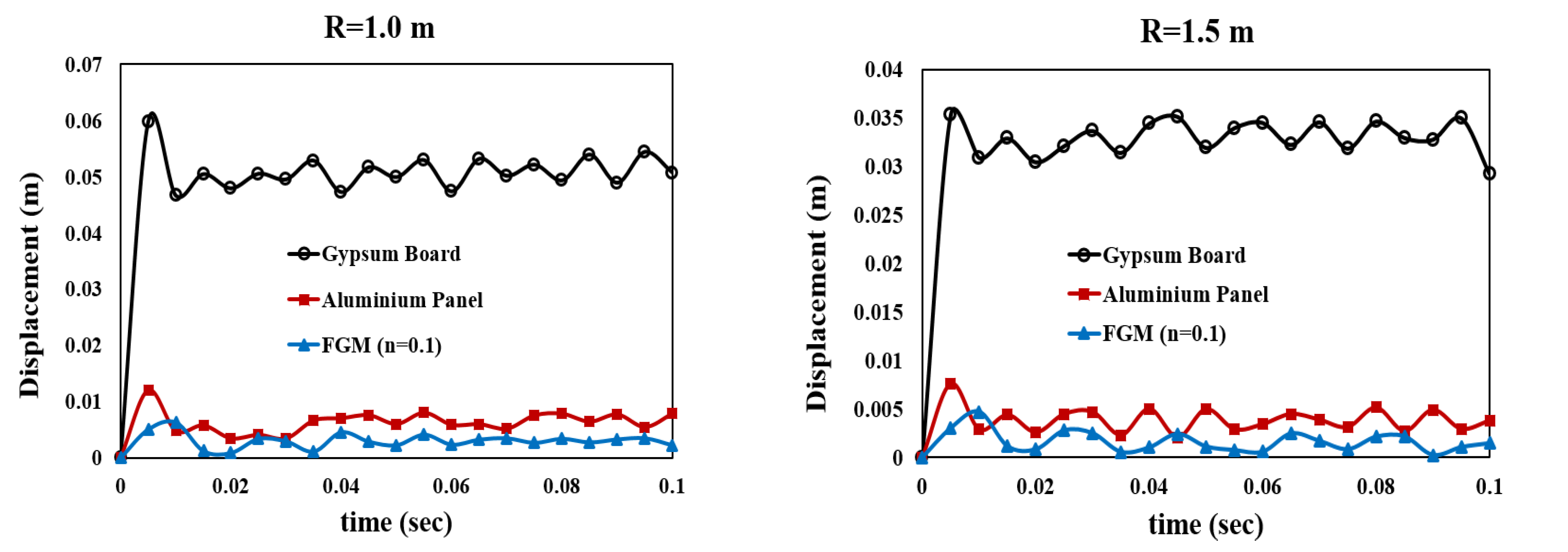
4.2. Standoff Distance Sensitivity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Stewart, L.K.; Freidenberg, A.; Hegemier, G.A. Design And Testing of A Steel Stud Wall System For Blast Mitigation. WIT Trans. Built Environ. 2014, 141, 39–49. [Google Scholar]
- Børvik, T.; Hanssen, A.G.; Langseth, M.; Olovsson, L. Response of structures to planar blast loads—A finite element engineering approach. Comput. Struct. 2009, 87, 507–520. [Google Scholar] [CrossRef]
- Bewick, B.; Williamson, E. Computational Modeling of Steel Stud Wall Systems for Applications to Blast-Resistant Design. J. Struct. Eng. 2014, 140, A4014007. [Google Scholar] [CrossRef]
- Aviram, A.; Mayes, R.L.; Hamburger, R.O. Innovative Steel Stud Walls for Blast Resistance. Structures, 29 June 2014; 22–24. [Google Scholar]
- Tao, F.; Chatterjee, A.; Moen, C.D. Monotonic and Cyclic Response of Single Shear Cold-Formed Steel-to-Steel and Sheathing-to-Steel Connections; American Iron and Steel Institute: Washington, DC, USA, 2017. [Google Scholar]
- DiPaolo, B.P.; Woodson, S.C. An Overview of Research at ERDC on Steel Stud Exterior Wall Systems Subjected to Severe Blast Loading. In Proceedings of the Stuctures Congress, St. Louis, MO, USA, 18–21 May 2006. [Google Scholar]
- Ali, E.; Woldeyes, K.; Urgessa, G. Fire performance of functionally-graded-material sheathed load bearing thin-walled structural framing. Fire Saf. J. 2021, 125, 103425. [Google Scholar] [CrossRef]
- Ali, E.; Woldeyes, K.; Urgessa, G. Influence of Non-uniform Elevated Temperature on the Structural Stability and Strength of Gypsum-Sheathed Cold-Formed Steel Beam Channel Members. J. Civ. Eng. Archit. 2021, 15, 285–293. [Google Scholar] [CrossRef]
- Padilla-Llano, D.A.; Moen, C.D.; Eatherton, M.R. Cyclic axial response and energy dissipation of cold-formed steel framing members. Thin-Walled Struct. 2014, 78, 95–107. [Google Scholar] [CrossRef]
- Aviram, A.; Mayes, R.L.; Hanburger, R.O. Blast Resistant Curtain Walls. In Modern Steel Construction; 2013; Available online: https://lsc-pagepro.mydigitalpublication.com/publication/?i=179209&article_id=1533958&view=articleBrowser&ver=html5 (accessed on 21 December 2021).
- Rezaiee-Pajand, M.; Arabi, E.; Masoodi, A.R. Nonlinear analysis of FG-sandwich plates and shells. Aerosp. Sci. Technol. 2019, 87, 178–189. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Masoodi, A.R. Analyzing FG shells with large deformations and finite rotations. World J. Eng. 2019, 16, 636–647. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Masoodi, A.R. Hygro-thermo-elastic nonlinear analysis of functionally graded porous composite thin and moderately thick shallow panels. Mech. Adv. Mater. Struct. 2020. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Masoodi, A.R.; Ali, A. Critical buckling moment of functionally graded tapered mono-symmetric I-beam. Steel Compos. Struct. 2021, 39, 599–614. [Google Scholar] [CrossRef]
- Hinman, E. Blast Safety of the Building Envelope. In National Institute of Building SCIENCES; 2017; Available online: https://www.wbdg.org/resources/blast-safety-building-envelope (accessed on 21 December 2021).
- Lane, J.W. Modeling and Design of Explosion-Resistant Steel Stud Wall Systems. Master’s Thesis, University of Missouri, Columbia, MO, USA, 2003. [Google Scholar]
- Qasrawi, Y.; Heffernan, P.J.; Fam, A. Performance of Concrete-Filled FRP Tubes under Field Close-in Blast Loading. J. Compos. Constr. 2015, 19, 04014067. [Google Scholar] [CrossRef]
- Giannaros, E.; Kotzakolios, T.; Kostopoulos, V. Blast response of composite pipeline structure using finite element techniques. J. Compos. Mater. 2016, 50, 3459–3476. [Google Scholar] [CrossRef]
- Mittal, V.; Chakraborty, T.; Matsagar, V. Dynamic analysis of liquid storage tank under blast using coupled Euler–Lagrange formulation. Thin-Walled Struct. 2014, 84, 91–111. [Google Scholar] [CrossRef]
- Zakrisson, B. Numerical and Experimental Studies of Blast Loading. Master’s Thesis, Lulea University of Technology, Luleå, Sweden, 2010. [Google Scholar]
- Chen, W.; Hao, H. Numerical Simulations of Stiffened Multi-Arch Double-Layered Panels Subjected to Blast Loading. Int. J. Prot. Struct. 2013, 4, 163–187. [Google Scholar] [CrossRef] [Green Version]
- Prueter, P.E. Using Explicit Finite Element Analysis to Simulate the Structural Damage Associated With an Internal Detonation in a Heat Exchanger. In Proceedings of the ASME 2014 Presuure Vessels and Piping, Anaheim, CA, USA, 20–24 July 2014. [Google Scholar]
- Althoey, F.; Ali, E. A Simplified Stress Analysis of Functionally Graded Beams and Influence of Material Function on Deflection. Appl. Sci. 2021, 11, 11747. [Google Scholar] [CrossRef]
- Ali, E.; Bayleyegn, Y.S. Analytical and numerical buckling analysis of rectangular functionally-graded plates under uniaxial compression. In Proceedings of the Annual Stability Conference Structural Stability Research Council, St. Louis, MO, USA, 2–5 April 2019. [Google Scholar]




| Material | Elastic Modulus (GPa) | Yield Stress (MPa) | Density (Kg/m3) |
|---|---|---|---|
| Metal (Steel) | 210 | 420 | 7850 |
| Ceramic (Al2O3) | 390 | 260 | 2130 |
| Gypsum | 4.35 | 6.20 | 727 |
| Aluminum Composite | 69 | 110 | 2640 |
| Elastic Modulus (pa) | Mass Density (kg/m3) | |||||
|---|---|---|---|---|---|---|
| Ply No. | n = 5 | n = 1 | n = 0.1 | n = 5 | n = 1 | n = 0.1 |
| 1 (metal) | 2.03395 × 1011 | 2.03395 × 1011 | 2.03395 × 1011 | 7850 | 7850 | 7850 |
| 2 | 2.89418 × 1011 | 2.25471 × 1011 | 2.05738 × 1011 | 5063.839 | 7135 | 7774.128 |
| 3 | 3.38091 × 1011 | 2.47547 × 1011 | 2.08404 × 1011 | 3487.383 | 6420 | 7687.79 |
| 4 | 3.63158 × 1011 | 2.69622 × 1011 | 2.11504 × 1011 | 2675.502 | 5705 | 7587.378 |
| 5 | 3.7869 × 1011 | 3.13773 × 1011 | 2.19895 × 1011 | 2172.418 | 4275 | 7315.602 |
| 6 | 3.79828 × 1011 | 3.35849 × 1011 | 2.26257 × 1011 | 2135.586 | 3560 | 7109.549 |
| 7 | 3.79995 × 1011 | 3.57924 × 1011 | 2.36552 × 1011 | 2130.175 | 2845 | 6776.084 |
| 8 (ceramic) | 3.8 × 1011 | 3.8 × 1011 | 3.8 × 1011 | 2130 | 2130 | 2130 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, E.; Althoey, F. Numerical Investigation on Blast Response of Cold-Formed Steel Framing Protected with Functionally Graded Composite Material. Buildings 2022, 12, 118. https://doi.org/10.3390/buildings12020118
Ali E, Althoey F. Numerical Investigation on Blast Response of Cold-Formed Steel Framing Protected with Functionally Graded Composite Material. Buildings. 2022; 12(2):118. https://doi.org/10.3390/buildings12020118
Chicago/Turabian StyleAli, Elias, and Fadi Althoey. 2022. "Numerical Investigation on Blast Response of Cold-Formed Steel Framing Protected with Functionally Graded Composite Material" Buildings 12, no. 2: 118. https://doi.org/10.3390/buildings12020118
APA StyleAli, E., & Althoey, F. (2022). Numerical Investigation on Blast Response of Cold-Formed Steel Framing Protected with Functionally Graded Composite Material. Buildings, 12(2), 118. https://doi.org/10.3390/buildings12020118






