A Novel Shear Strengthening of Existing RC Shear Walls Using Steel Wire Mesh and Polymer Mortar
Abstract
:1. Introduction
2. Experimental Program
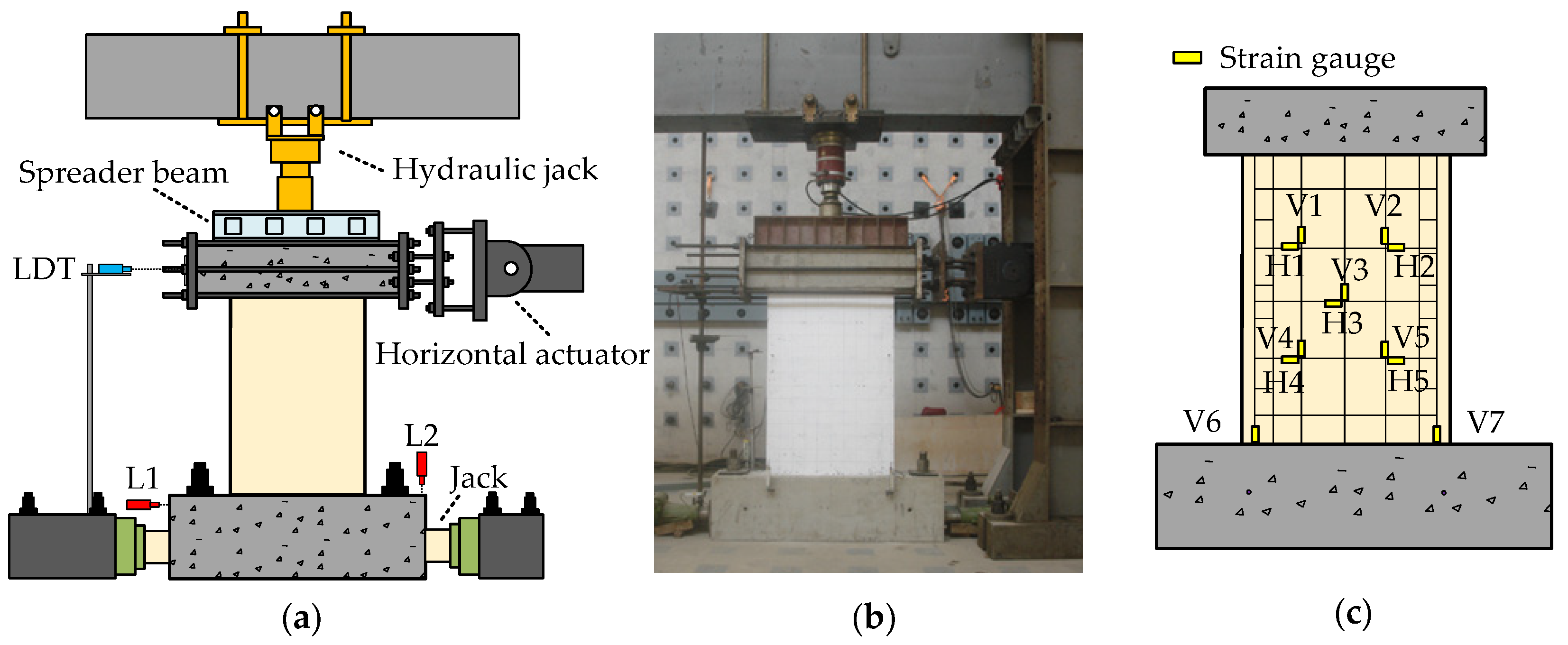
Test Setup and Instrumentation
3. Experimental Observations
4. Experimental Results and Discussion
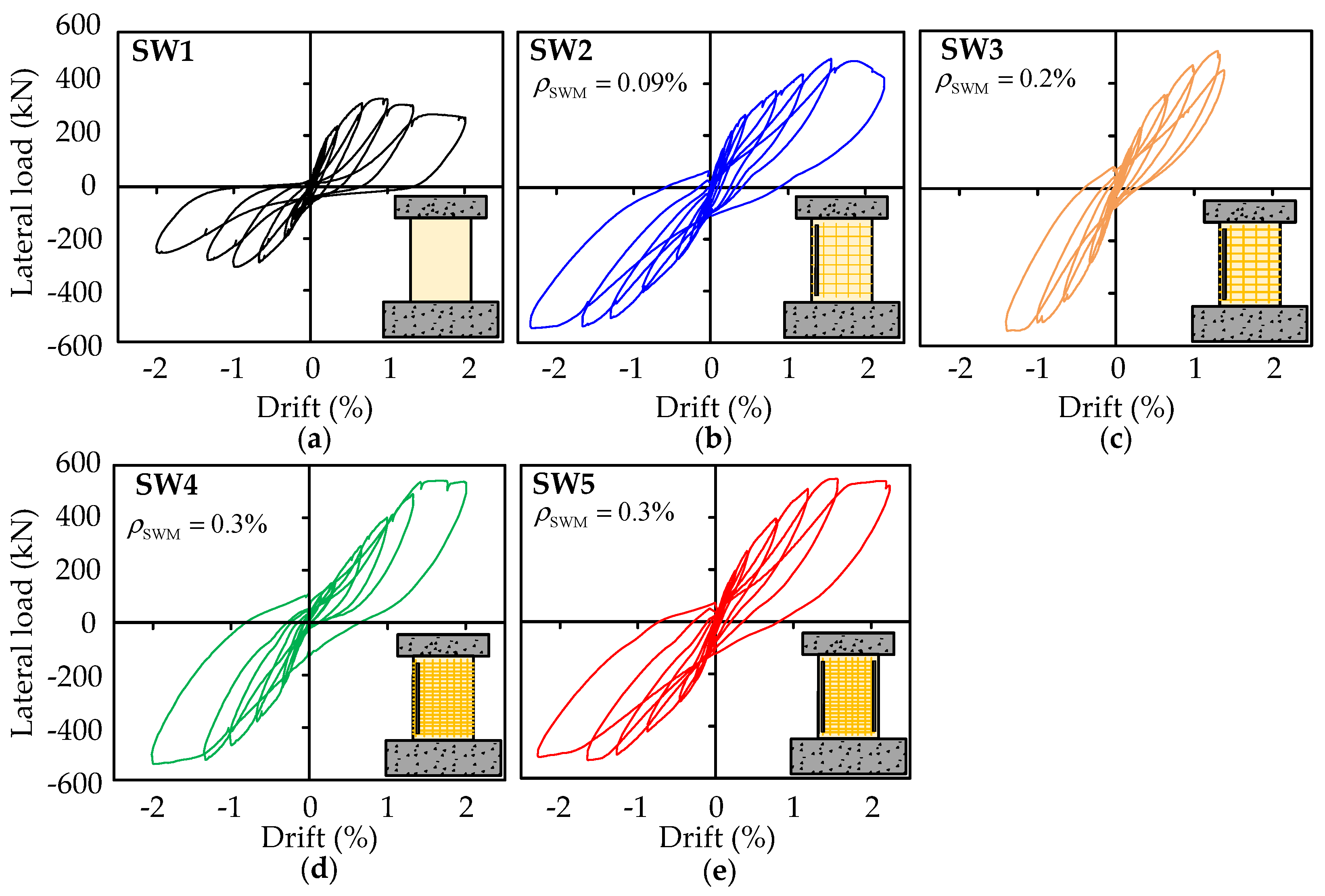
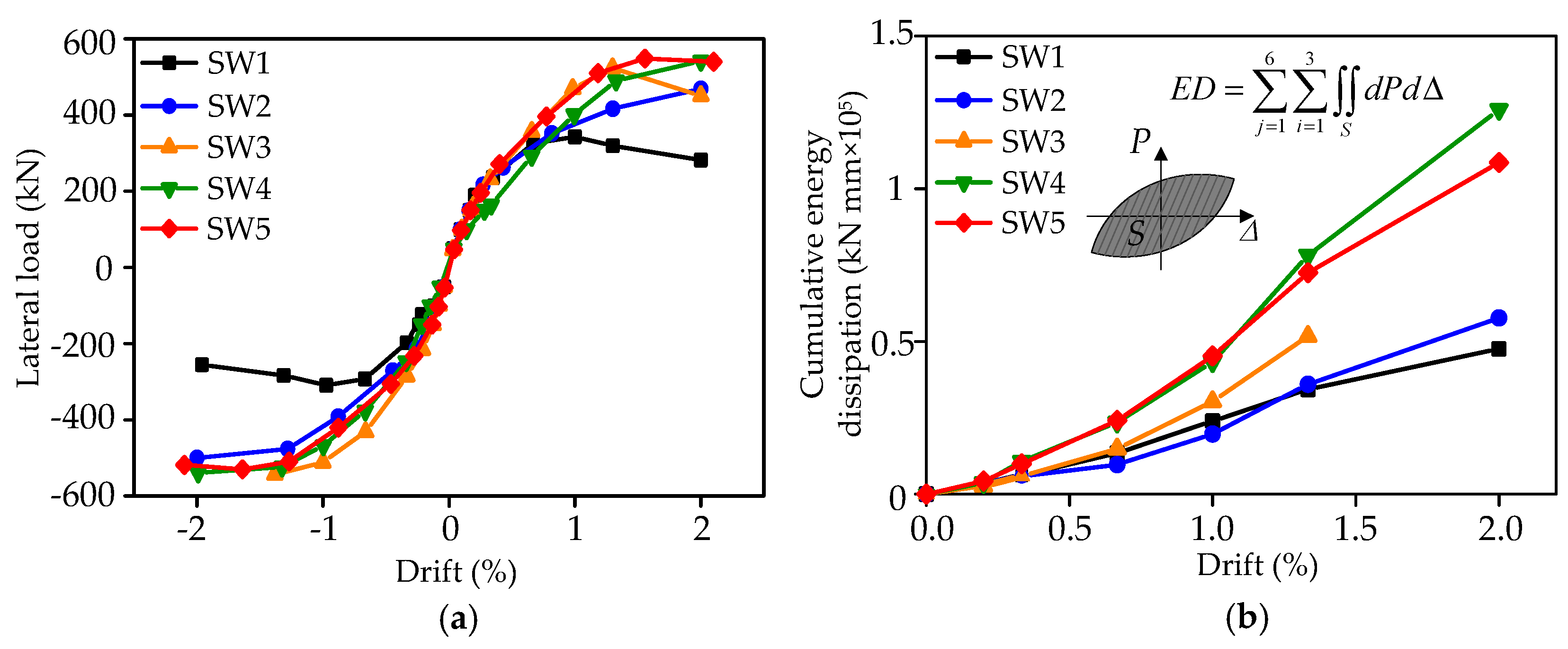
4.1. Hysteretic and Envelop Lateral Load-Drift Response
4.2. Energy Dissipation
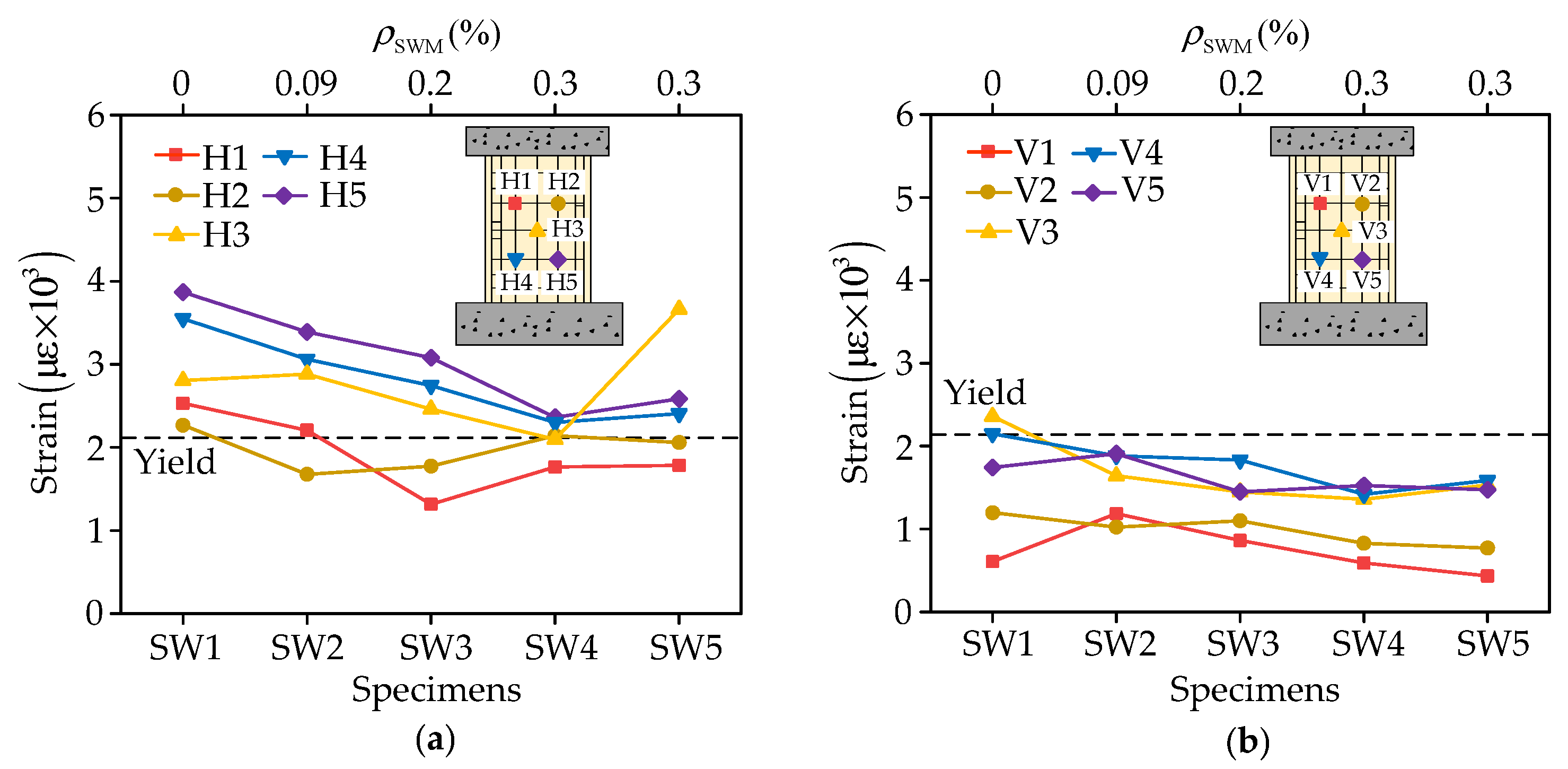
4.3. Analysis of Strain Gauge Recordings
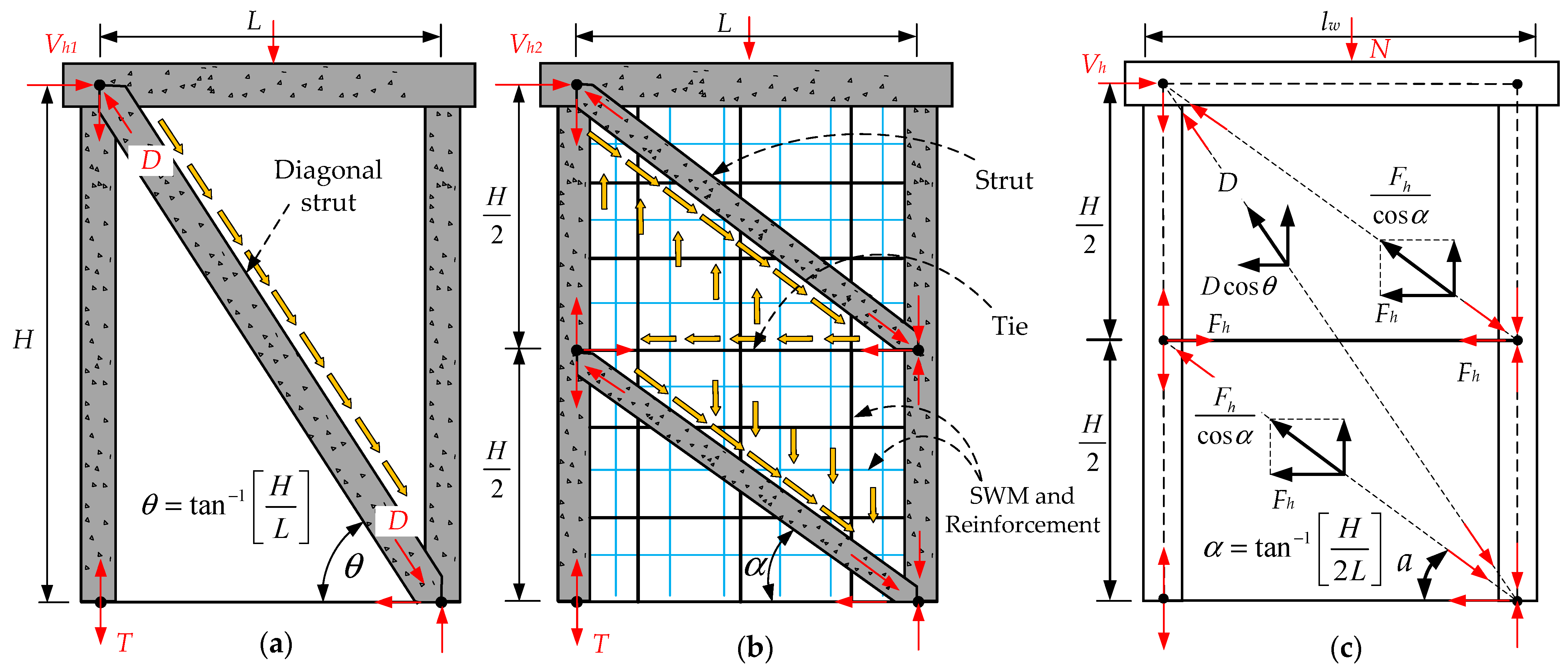
5. Estimation of Shear Capacity of Strengthened Shear Walls
6. Conclusions
- Steel wire mesh and polymer mortar strengthening method not only delayed the formation of shear cracks but also effectively restrained the crack propagation, which significantly increased the cracking load (average increase was about 79%). The capacity of the strengthened shear wall specimens increased with an increase in the reinforcement ratio of steel wire mesh. The average increase in capacity was found to be 55%, showing a favorable strengthening effect;
- The hysteretic response of strengthened specimens was found to be plumper compared to control RC specimen, which exhibited severe pinching. Wrapping of steel wire meshes around the specimen surface avoided the debonding failure of polymer mortar layers and enhanced the energy dissipation characteristics compared to wrapping only on exposed surfaces;
- The effectiveness coefficient to consider the contribution of steel wire mesh was derived to predict the capacity of strengthened shear wall specimens based on the softened strut-and-tie model. The proposed expression can be used to fairly predict the shear capacity of the strengthened specimens (present and previous experimental studies) within the scope of variables (n = 0.1–0.4, H/L = 1.62–2, and ρswm = 0.09–0.3%);
- Further from the limited theoretical investigation, it was also ascertained that the effectiveness coefficient of steel wire mesh was affected by the steel wire ratio, shear span ratio, and axial compression ratio. A steel wire mesh reinforcement ratio of about 0.1–0.2% was recommended to adopt in the strengthening of existing RC shear walls within the scope of the shear span ratio (1.62 to 2.00).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ACI Committee 318; Building Code Requirements for Structural Concrete and Commentary (ACI CODE 318-19). American Concrete Institute: Indianapolis, IN, USA, 2019.
- EN 1998-1-1; Eurocode 8: Design of Structure for Earthquake Resistance-Part 1: General Rules, Seismic Actions and Rules for Building. CEN: Brussels, Belgium, 2004.
- CMC (China Ministry of Construction). GB 50011-2010; Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2011. (In Chinese)
- Xu, P.; Huang, J.; Chen, F. Earthquake damages to shear wall structure in last fifty years and seismic design enlightenment. J. Build. Struct. 2017, 38, 1–13. (In Chinese) [Google Scholar]
- Wallace, J. Performance of structural walls in recent earthquakes and test and implications for US building codes. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Kam, W.Y.; PaMPanin, S.; Elwood, K.J. Seismic performance of reinforced concrete buildings in the 22 February Christchurch (Lyttleton) earthquake. Bull. N. Z. Nat. Soc. Earthq. Eng. 2011, 44, 239–278. [Google Scholar]
- Woods, J.E.; Lau, D.T.; Cruz-Noguez, C.A. In-Plane seismic strengthening of nonductile reinforced concrete shear walls using externally bonded CFRP sheets. J. Compos. Constr. 2016, 20, 04016052. [Google Scholar] [CrossRef]
- Marini, A.; Meda, A. Retrofitting of RC shear walls by means of high-performance jackets. Eng. Struct. 2009, 31, 3059–3064. [Google Scholar] [CrossRef]
- Altin, S.; Kopraman, Y.; Baran, M. Strengthening of RC walls using externally bonding of steel strips. Eng. Struct. 2013, 49, 686–695. [Google Scholar] [CrossRef]
- Christidis, K.I.; Vougioukas, E.; Trezos, K.G. Strengthening of non-conforming RC shear walls using different steel configurations. Eng. Struct. 2016, 124, 258–268. [Google Scholar] [CrossRef]
- Antoniades, K.K.; Salonikios, T.N.; Kappos, A.J. Tests on seismically damaged reinforced concrete walls repaired and strengthened using Fiber-Reinforced Polymers. J. Compos. Constr. 2005, 9, 236–246. [Google Scholar] [CrossRef]
- Li, B.; Lim, C.L. Tests on seismically using Fiber-reinforced Polymers. J. Compos. Constr. 2010, 14, 597–608. [Google Scholar] [CrossRef]
- Layssi, H.; Cook, W.D.; Mitchell, D. Seismic response and CFRP retrofit of poorly detailed shear walls. J. Compos. Constr. 2012, 17, 603–613. [Google Scholar] [CrossRef]
- EI-Sokkary, H.; Galal, K. Seismic Behavior of RC shear walls strengthened with Fiber-Reinforced Polymer. J. Compos. Constr. 2013, 17, 603–613. [Google Scholar] [CrossRef]
- EI-Sokkary, H.; Galal, K.; Ghorbanirenani, I.; Léger, P.; Tremblay, R. Shake table test on FRP-Rehabilitated RC shear walls. J. Compos. Constr. 2013, 17, 79–90. [Google Scholar] [CrossRef]
- Qazi, S.; Michel, L.; Ferrier, E. Seismic behaviour of RC short shear wall strengthened with externally bonded CFRP strips. Compos. Struct. 2019, 211, 390–400. [Google Scholar] [CrossRef]
- Fontanari, V.; Benedetti, M.; Monelli, B.D.; Degasperi, F. Fire behavior of steel wire ropes: Experimental investigation and numerical analysis. Eng. Struct. 2015, 84, 340–349. [Google Scholar] [CrossRef]
- Al-Kaimakchi, A.; Rambo-Roddenberry, M. Measured transfer length of 15.2-mm (0.6-in.) duplex high-strength stainless steel strands in pretensioned girders. Eng. Struct. 2021, 237, 112178. [Google Scholar] [CrossRef]
- Kumar, V.; Patel, P.V. Strengthening of axially loaded circular concrete columns using stainless SWM (SSWM)–Experimental investigations. Constr. Build. Mater. 2016, 12, 4186–4198. [Google Scholar]
- Kim, S.Y.; Yang, K.H.; Byun, H.Y.; Ashour, A.F. Tests of reinforced concrete beams strengthened with wire rope units. Eng. Struct. 2007, 29, 2711–2722. [Google Scholar] [CrossRef]
- Yang, K.; Byun, H.; Ashour, A.F. Shear strengthening of continuous reinforced concrete T-beams using wire rope units. Eng. Struct. 2009, 31, 1154–1165. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, S.; Nayak, S.; Das, S. Shear and flexural behaviour of unreinforced masonry wallets with SWM. J. Build. Eng. 2020, 30, 101254. [Google Scholar] [CrossRef]
- Sandoval, O.J.; Takeuchi, C.; Carrillo, J.; Barahona, B. Performance of unreinforced masonry panels strengthened with mortar overlays reinforced with welded wire mesh and horizontal connectors. Constr. Build. Mater. 2021, 267, 121054. [Google Scholar] [CrossRef]
- Yao, X.; Guo, Z.; Basha, S.H.; Huang, Q. Innovative seismic strengthening of historic masonry walls using polymer mortar and steel strips. Eng. Struct. 2021, 228, 111507. [Google Scholar] [CrossRef]
- Zhang, X.; Du, M.; Fang, H.; Shi, M.; Zhang, C.; Wang, F. Polymer-modified cement mortars: Their enhanced properties, applications, prospects, and challenges. Constr. Build. Mater. 2021, 299, 124290. [Google Scholar] [CrossRef]
- Shermi, C.; Dubey, R.N. Study on out-of-plane behaviour of unreinforced masonry strengthened with welded wire mesh and mortar. Constr. Build. Mater. 2017, 143, 104–120. [Google Scholar] [CrossRef]
- Shermi, C.; Dubey, R.N. In-plane behaviour of unreinforced masonry panel strengthened with welded wire mesh and mortar. Constr. Build. Mater. 2018, 178, 195–203. [Google Scholar] [CrossRef]
- CMC (China Ministry of Construction). JGJ 3-1991; Standard for Structural Design and Construction of Reinforced Concrete High-Rise Buildings. China Architecture & Building Press: Beijing, China, 1991. (In Chinese)
- CMC (China Ministry of Construction). GB/T 50081-2002; Standard for Test Method of Mechanical Properties on Ordinary Concrete. China Architecture & Building Press: Beijing, China, 2002. (In Chinese)
- CMC (China Ministry of Construction). JGJ/T70-2009; Standard for Test Method of Performance on Building Mortar. China Architecture & Building Press: Beijing, China, 2009. (In Chinese)
- CMC (China Ministry of Construction). JGJ 101-1996; Specificating of Testing Methods for Earthquake Resistant Building. China Architecture & Building Press: Beijing, China, 1996. (In Chinese)
- Basha, S.H.; Kaushik, H.B. Behavior and failure mechanisms of masonry-infilled RC frames (in low-rise buildings) subject to lateral loading. Eng. Struct. 2016, 111, 233–245. [Google Scholar] [CrossRef]
- Hwang, S.; Fang, W.; Lee, H.; Yu, H. Analytical model for predicting shear strengthof squat walls. J. Struct. Eng. 2001, 127, 43–50. [Google Scholar] [CrossRef]
- Jennewein, M.; Schafër, K. DafStb Heft 430; Standardisierte Nachweise Vonhaufigen D-Bereichen. Beuth: Berlin, Germany, 1992.
- Hwang, S.; Lee, H. Strength Prediction for discontinuity regions by softened strut-and-tie model. J. Struct. Eng. 2002, 128, 1519–1526. [Google Scholar] [CrossRef]
- Paulay, T.; Priestley, M.J.N. Seismic Design of Reinforced Concrete and Masonry Buildings; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Zhang, L.X.B.; Hsu, T.T.C. Behavior and analysis of 100 MPa concrete membrane elements. J. Struct. Eng. 1998, 124, 24–34. [Google Scholar] [CrossRef]
- Foster, S.J.; Gilbert, R.I. The design of nonflexural members with normal and high-strength concrete. ACI Struct. J. 1996, 93, 3–10. [Google Scholar]
- Liao, W.; Zhang, C.; Jia, T.; Wang, H. Experimental investigation on seismic behavior of shear wall retrofitted with pre-stressed steel wire mesh and polymer mortar. J. Build. Struct. 2017, 38, 70–77. (In Chinese) [Google Scholar]
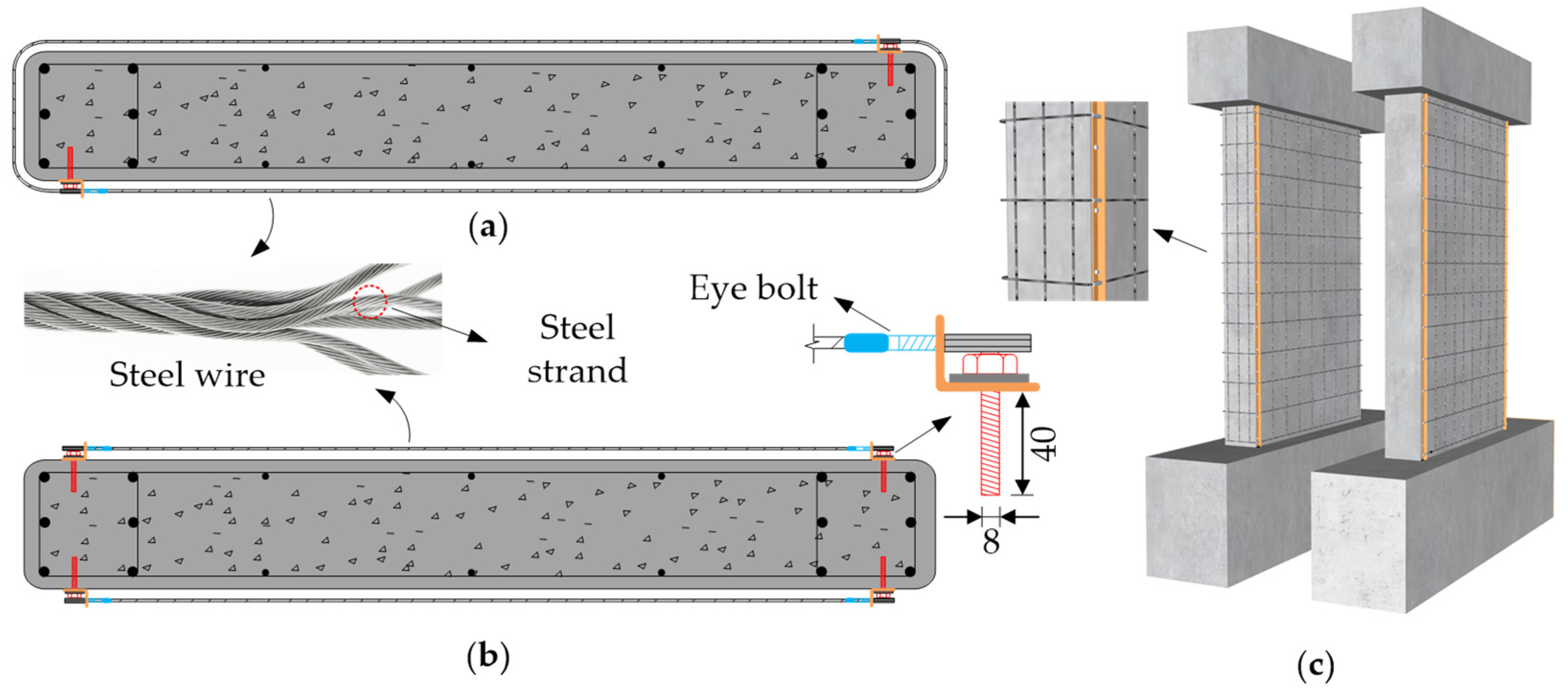







| Specimen Designation | Horizontal Steel Wire Configuration | Application of Steel Wire Mesh | |
|---|---|---|---|
| Diameter and Spacing (mm) | Steel Wire Mesh Ratio ρswm (%) | ||
| SW-1 | - | - | - |
| SW-2 | 4.0 @100 | 0.09 | Wrapping around surface |
| SW-3 | 4.5 @60 | 0.20 | Wrapping around surface |
| SW-4 | 4.5 @40 | 0.30 | Wrapping around surface |
| SW-5 | 4.5 @40 | 0.30 | Only on exposed surfaces |
| Material Properties | Number of Specimens | Average Value | COV (%) |
|---|---|---|---|
| Compression strength of concrete (MPa) | 9 | 19.6 | 5.6 |
| Compressive strength of polymer mortar (MPa) | 11 | 52.0 | 10.5 |
| Elastic modulus of concrete (MPa) | 3 | 2.55 × 104 | 12.3 |
| Elastic modulus of polymer mortar (MPa) | 3 | 3.3 × 104 | 16.1 |
| Yield strength of 8 mm diameter steel bars (MPa) | 3 | 441.0 | 2.4 |
| Yield strength of 20 mm diameter steel bars (MPa) | 3 | 448.3 | 0.6 |
| Yield strain of 8 mm diameter steel bars (με) | 3 | 2210.0 | 7.4 |
| Yield strain of 20 mm diameter steel bars (με) | 3 | 2240.0 | 3.1 |
| Ultimate tensile strength of steel wire (MPa) | 6 | 1100.0 | 6.1 |
| Specimen | Pcr (kN) | δcr (%) | Py (kN) | δy (%) | Pm (kN) | δm (%) | Ki (kN/mm) | ED (kNmm) |
|---|---|---|---|---|---|---|---|---|
| SW1 | 96 | 0.10 | 285 | 0.52 | 342 | 0.90 | 92 | 47,600 |
| SW2 | 158 | 0.17 | 383 | 0.98 | 496 | 1.30 | 106 | 57,700 |
| SW3 | 198 | 0.25 | 456 | 0.94 | 523 | 1.43 | 109 | 60,200 |
| SW4 | 212 | 0.28 | 485 | 1.31 | 541 | 1.97 | 105 | 125,800 |
| SW5 | 207 | 0.29 | 468 | 1.03 | 548 | 1.55 | 95 | 108,600 |
| Specimen | Strain (με) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| H1 | V1 | H2 | V2 | H3 | V3 | H4 | V4 | H5 | V5 | |
| SW1 | 2529 (1.14) * | 607 (0.27) | 2269 (1.03) | 1197 (0.54) | 2804 (1.27) | 2359 (1.07) | 3550 (1.61) | 2150 (0.97) | 3870 (1.75) | 1742 (0.79) |
| SW2 | 2207 (1.00) | 1187 (0.54) | 1678 (0.76) | 1024 (0.46) | 2883 (1.30) | 1641 (0.74) | 3061 (1.39) | 1884 (0.85) | 3390 (1.53) | 1910 (0.86) |
| SW3 | 1316 (0.60) | 863 (0.39) | 1774 (0.80) | 1099 (0.50) | 2462 (1.11) | 1448 (0.66) | 2743 (1.24) | 1832 (0.83) | 3080 (1.39) | 1448 (0.66) |
| SW4 | 1764 (0.80) | 589 (0.27) | 2141 (0.97) | 826 (0.37) | 2097 (0.95) | 1360 (0.62) | 2303 (1.04) | 1417 (0.64) | 2364 (1.07) | 1525 (0.69) |
| SW5 | 1784 (0.81) | 433 (0.20) | 2059 (0.93) | 770 (0.35) | 3664 (1.66) | 1529 (0.69) | 2406 (1.09) | 1585 (0.72) | 2584 (1.17) | 1473 (0.67) |
| Reference Study | Specimen | n | H/L | ρswm (%) | β | Ve (kN) | Vt (kN) | Ve/Vt |
|---|---|---|---|---|---|---|---|---|
| Present Study | SW1 | 0.1 | 1.62 | - | - | 342 | 319 | 1.07 |
| SW2 | 0.1 | 1.62 | 0.09 | 0.57 | 496 | 468 | 1.02 | |
| SW3 | 0.1 | 1.62 | 0.20 | 0.26 | 523 | 535 | 0.98 | |
| SW4 | 0.1 | 1.62 | 0.30 | 0.17 | 541 | 476 | 1.08 | |
| SW5 | 0.1 | 1.62 | 0.30 | 0.17 | 548 | 476 | 1.10 | |
| Liao et al. [39] | W2-10 | 0.2 | 2.00 | 0.10 | 0.29 | 242 | 280 | 0.86 |
| W2-20 | 0.2 | 2.00 | 0.20 | 0.15 | 271 | 274 | 0.99 | |
| W4-10 | 0.4 | 2.00 | 0.10 | 0.45 | 254 | 298 | 0.85 | |
| W4-20 | 0.4 | 2.00 | 0.20 | 0.23 | 258 | 293 | 0.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, X.; Guo, Z.; Basha, S.H.; Huang, Q. A Novel Shear Strengthening of Existing RC Shear Walls Using Steel Wire Mesh and Polymer Mortar. Buildings 2022, 12, 219. https://doi.org/10.3390/buildings12020219
Xie X, Guo Z, Basha SH, Huang Q. A Novel Shear Strengthening of Existing RC Shear Walls Using Steel Wire Mesh and Polymer Mortar. Buildings. 2022; 12(2):219. https://doi.org/10.3390/buildings12020219
Chicago/Turabian StyleXie, Xinyao, Zixiong Guo, Syed Humayun Basha, and Qunxian Huang. 2022. "A Novel Shear Strengthening of Existing RC Shear Walls Using Steel Wire Mesh and Polymer Mortar" Buildings 12, no. 2: 219. https://doi.org/10.3390/buildings12020219
APA StyleXie, X., Guo, Z., Basha, S. H., & Huang, Q. (2022). A Novel Shear Strengthening of Existing RC Shear Walls Using Steel Wire Mesh and Polymer Mortar. Buildings, 12(2), 219. https://doi.org/10.3390/buildings12020219






