Microscopical Resource Allocation for Large-Scale Apartment Foundation Work Using Queuing Systems

Abstract

Resource management can determine the success or failure of construction projects and is indispensable in frame construction owing to the numerous resources allocated. Various research methodologies have been proposed for successful resource management, but they have not been conducted from a microscopic point of view such as activity. This paper quantitatively analyzes the impact of a concrete pouring team allocation on the project from a microscopic point of view, and proposes a framework for allocating the optimal team. Firstly, a time-dependent queueing model-based method is proposed for evaluating the influence of the pouring team for foundation concrete pouring. Data from large-scale apartment project cases in South Korea were used to verify this framework. Using time and cost metrics, the impact of the pouring team on the project was quantitatively analyzed. Finally, comparative analysis was performed to compare the concrete pouring team costs, including the average server cost and waiting cost before and after optimization. The proposed method reduced the total pouring team cost by 26.27% (KRW 35,547,600); it can help determine the optimal number of concrete pouring teams required for frame construction and improve the performance of construction projects from the process planning stage itself, by ensuring appropriate resource planning. However, since a single case was used, it is necessary to apply the proposed framework to actual construction after analyzing various cases in future studies.

1. Introduction

The resource management techniques employed by construction companies play an essential role in the success or failure of construction projects owing to their competitiveness in terms of profit and project performance [1,2]. Whereas idle resources in a project can cause financial loss, a lack of resources can increase the construction period [3,4]. Many researchers have studied resource allocation and leveling in resource management [5,6,7], contributing to the development of resource management at an organizational or project level. However, these methods have certain micro-level limitations, and analyzing productivity at the micro-level can analyze the impact on other input resources [8].

Subcontractors (SubCs), employed by general contractors (GCs), work on the micro-level and can simultaneously take up several construction projects [9,10,11]. When SubCs are employed, GCs share the project-based risks with the SubCs, based on which the SubCs prepare efficient plans and schedules for the allocation and use of resources, which are analyzed objectively by the GCs [12,13]. Therefore, studying resource management at the micro-level at which SubCs perform actual work becomes necessary for successful resource management. Then, SubCs will be able to manage flexible resources such as allocating additional resources in specific sections with a high workload. In summary, microscopical resource management can increase the performance of construction projects by GCs and SubCs cooperating with each other, and the success of construction projects can be repeated to improve the competitiveness of GCs and SubCs in the industry.

Construction projects generally involve multiple interested parties [14], various materials, and many people. Large-scale construction projects have complex characteristics that are difficult to understand and hinder the achievement of the project goals [15,16]. South Korean apartments, with such complex characteristics, are the leading housing type, accounting for 63% of all types of houses as of 2019 [17]. The construction of large-scale apartments in South Korea involves simultaneous construction of multiple high-rise buildings with parking lots and community facilities in underground spaces [18] and has characteristics similar to those of large-scale construction projects. Therefore, it is essential to study resource management methods for apartment construction.

This paper quantitatively analyzed the resource allocation performance of the concrete pouring team in large-scale apartments and examined feasible resource allocation through case studies. In this paper, a simulation method was proposed to achieve cost-effective and optimized resource allocation for the daily workloads of the pouring teams to assist objective decision making during the process planning. The system of the case project was quantitatively evaluated based on the performance indicators of the queueing model. In this method, the analysis process is simple, and the optimal solution can be derived through quantitative analysis. By analyzing resource management from a microscopic point of view, this study enables finer management of input resources than previous studies that studied resource management at the company or project level.

2. Literature Review

This section describes the importance of frame construction and resource management for frame construction in apartment construction projects in South Korea by identifying the significance of related studies and the need for research in particular areas. In addition, the importance of SubCs is discussed. Furthermore, this section addresses the impact of resource management at the activity level. Finally, previous studies on the queueing model used in this study are reviewed to emphasize its merits.

2.1. Resource Management in Frame Construction

The influence of resource management and allocation on the performance of construction projects is one of the most important research subjects in construction management [2,19]. Resources such as manpower, equipment, materials, money, and space must be appropriately allocated to ensure the accomplishment of construction projects [1,20]. In addition, wastage of resources can cause excessive costs, whereas a shortage of resources can delay construction [3,4]. Therefore, a tradeoff between wastage and shortage of resources, that is, the optimization of resources, is crucial for the completion of projects within the budget and allotted time period [3].

Dabirian et al. [1], Zhong et al. [4], Anvuur and Kumaraswamy [5], Heon Jun and El-Rayes [6], Lu et al. [7], Koulinas and Anagnostopoulos [21], Brandenburg et al. [22], and Lin [23] conducted various studies to improve the performance of construction projects by solving the resource allocation problem. Although these scholars contributed to the development of resource management at both the company and project level, their works had limitations at the micro-level, such as activity limitations.

Resource management in large-scale apartment projects in South Korea is complex and difficult owing to the short construction period. Framework construction, in particular, is complex and frequently delayed considering that multiple resources are invested. Cho and Choi [24] analyzed 10 apartment projects in South Korea and found that framework construction accounted for approximately 57%, 27%, and 27% of the total construction period, construction cost, and direct construction cost, respectively. Furthermore, because large-scale apartments include multiple buildings, framework construction exhibits complex relationships between activity units [25]. Moreover, because frame construction utilizes underground spaces for parking lots and community facilities, such spaces are of high importance in South Korean apartments [18,26]. In addition, large-scale apartment construction requires a large amount of resources, and the construction period is relatively short considering the construction size. Therefore, resource allocation is essential for frame construction in large-scale apartment projects.

2.2. Microscopic Viewpoint Analysis of the Resource Planning

The performance of a construction project depends on the abilities of the selected GC and SubC [27]. Given the increasing complexity and expertise of construction projects, GCs hire more SubCs for every work type, considering that SubCs play a critical role in construction projects [13,28]. The GC shares not only the profit with the SubCs but also the risks [13,15]. Therefore, SubCs hired by the GC can account for up to approximately 90% of the total project value [11,29]. Therefore, GCs must select SubCs reasonably. The selection of SubCs requires a method of presenting an appropriate decision-making standard [30]. Because the performance of a project can vary based on the selected SubCs [28,31], risks can be reduced by objectively evaluating the schedule and resource input plan suggested by the SubCs for each work type [13,32]. Therefore, it is crucial for the GC to analyze the performance of the SubCs during selection, which requires quantification for resource planning and SubC analysis [13].

The GC and SubCs can objectively analyze and evaluate the resource allocation plan and schedule suggested by the SubCs and together perform modifications to avoid unnecessary costs [9]. The GC can effectively manage resources such as time, materials, and costs (cost reduction and compliance with construction period) suggested by the SubCs, whereas the SubCs can effectively establish and implement the resource allocation plan.

Kandil and El-Rayes [33] stated that when different resource utilization options are available at the activity level, many combinations of the resource utilization plan can be generated at the project level. McTague and Jergeas [34] claimed that 35% of the total work time is wasted by waiting, whereas only 28% is used for the preparation of tasks. Therefore, the SubCs should regulate the total work time by appropriately managing the waiting and idle times and analyze the resources that directly perform the construction work at different activity levels to control the wastage or shortage of resources.

Therefore, a quantitative evaluation method for resource allocation at the SubC planning and executing activity levels was used in this study, and the performance of equipment and human resources in actual construction scenarios was analyzed. Furthermore, a queueing model was used to analyze the resource allocation performance quantitatively and to investigate how efficiently the invested resources are used and the economic performance can be improved.

2.3. Queuing System

Halpin [35] developed a cyclic operation network (CYCLONE), which is a management tool that simulates real projects to model a work process that repeats the same process and measures productivity. Furthermore, the CYCLONE determines the logical relationships between resources, work time, and tasks using a probabilistic or deterministic approach [36]. Additionally, various simulation systems and process modeling techniques such as COOPS [37], stroboscope [38], and RESQUE [39] have been developed based on the CYCLONE method to predict the productivity and derive optimal resource combinations [40]. Although these methods optimize the production process, the need for quantitatively analyzing the effects of resource allocation on the construction performance at the micro-level, such as the activity level, has emerged.

The influence of one input variable (e.g., server) on the productivity of another (e.g., project participants) can be analyzed by measuring the workforce productivity (e.g., concrete pouring teams) from a microscopic viewpoint [8], which helps identify and improve labor productivity [41]. Therefore, when analyzing the influence of the frame construction team on other project participants, the interactions between them should be considered [42]. Workflow management (WfM) systems have been used for approximately three decades and can effectively improve the performance of business processes in terms of resource utilization, service time, waiting time, and lead time [43,44].

In WfM systems, the timing can be analyzed based on a few techniques [45,46,47,48]. Zhuge et al. [45] studied a workflow process model that combined time constraints, activity distributions, activity durations, and flow durations. Chang et al. [46] proposed a method of systematically determining a critical path based on a workflow model. Additionally, various other experiments have been conducted to evaluate the accuracy of the critical path. Li and Yang [47] analyzed the resource and time constraints of concurrent workflows and proposed a new approach for verification. Son et al. [48] proposed a method of systematically identifying the critical paths for a given workflow schema. From all such possibilities, a queueing model is most commonly used considering that it can formulate numeric values [49,50].

Figure 1 [51] demonstrates a queueing theory that describes the possible types of queueing systems. Customers arrive randomly and independently for service at the queuing system. Although more than one server provides services, customers unable to receive services immediately upon arrival are made to wait in a queue. After receiving services individually from the server, each customer moves out of the queueing system [50].

One of the main characteristics of queuing systems is that parameters such as the number of servers or arrival rate, number of call centers and agents, and air traffic are time-dependent [52], which can practically influence the performance of the queueing system. Therefore, parameter changes must be considered in the design and control stages of the queueing system.

Because the demand for medical facilities changes with time [53], the number of medical staff available in a hospital facility is time-dependent. Gillard and Knight [54] analyzed the staffing performance of a hospital facility. Emergency workers such as firefighters and police officers receive service calls over time [55]. Kolesar et al. [56] and Ingolfsson et al. [57] conducted individual studies by applying a time-limited queuing system to a patrol car scheduling algorithm. Bookbinder and Martell [58] conducted a study to minimize the damage caused by forest fires based on the available helicopter allocation, considering that air traffic and the demand for repair services are often time-dependent. Koopman [59] proposed an initial queuing model for runway analysis. Bookbinder [60] analyzed the Markovian queuing system associated with an aircraft runway used for take offs and landing. Additionally, Jung [61] analyzed the facilities providing repair services for aircraft. Chakroborty et al. [62] estimated the number of cars arriving per hour at a queuing system at a toll plaza and the number of cars that could be serviced to decide the number of toll plazas objectively. Zhang et al. [63] studied the optimal number and cost-effective number of berths for a certain period for port expansion based on the container throughput. Teknomo [64] derived the optimal number of pieces of pumping equipment, assuming that a certain amount of concrete is poured. Kim et al. [65] used a queueing model to analyze the performance of building information modeling (BIM) employees by considering the request for information (RFI) data of BIM as customers. Ham et al. [52] analyzed the performance of BIM employees through a case study and derived the optimal number of BIM employees. The above-mentioned studies prove that the queueing model is valuable for system analysis in various fields.

Therefore, a queueing model was used in this study to analyze the allocation efficiency of concrete pouring teams quantitatively, including equipment and manpower (effects on project) for frame construction. Furthermore, this paper proposes a method to determine the optimal number of servers to reduce idleness and wastage of resources in a construction project by considering both the waiting cost of the customer and the service cost of the server.

3. Preliminary Investigation of the Case Project

This paper conducted a preliminary investigation of a case project based on actual foundation concrete execution data (

Table 1. Foundation concrete daily workloads of the process plans.

Zone	Date	Workload (m3)
1	28 March 2018	456
2	3 April 2018	336
3	15 April 2018	1747
4	17 April 2018	492
5	21 April 2018	2010
6	27 April 2018	1704
7	28 April 2018	1134
8	5 May 2018	2076
9	9 May 2018	696
10 + 11	14 May 2018	2290
12	23 May 2018	1692
13 + 14 + 15	29 May 2018	2265
16 + 17	31 May 2018	1392
18	12 June 2018	792
19	14 June 2018	384
20	16 June 2018	1296
21 + 22	19 June 2018	756
23	20 June 2018	222
24	12 July 2018	552
25	18 July 2018	478
26	31 July 2018	201
27	17 October 2018	558
28	27 October 2018	322
29	2 November 2018	450

). With a total pouring volume of 24,301 m³, the foundation concrete pouring began on 28 March 2018 and was completed on 2 November 2018 after 24 rounds. Two server teams were deployed on standby to pour the daily workload. Whereas the daily workload was not constant and ranged from 201 to 2290 m³ per round, the number of input server teams, that is, the number of servers, remained the same. Furthermore, although the project staff stated that 29 zones were set to improve productivity and management efficiency (

Table 2. Description of the case project.

Category	Description
Land area	54,979 m2
Total households	1210 units
Size	12 apartment buildings having 2 basement floors and 36 floors above ground, as well as neighborhood living facilities
Resources per server team	Pump car, vibrator, 6 workers (including equipment operators)
Foundation concrete pouring areas
Total pouring volume	24,301 m3
Completion date	31 October 2018

), the objective standards, such as the technical basis for zoning, were not revealed. Therefore, the researchers in this paper assumed that the zones were set based on the empirical standards of the project manager and others involved.

The project performance can be affected significantly if process and resource input plans have no objective standards. The idleness and shortage of resources can be reduced by employing an appropriate number of servers based on the daily workload. From a practical viewpoint, it is crucial to determine the optimal number of server teams. The research method is explained in detail in the next section.

4. Research Method

As shown in Figure 2, a theoretical discussion is provided and a research method for addressing the feasibility of resource management at construction sites is presented. The researchers in this paper firstly characterized the queuing system comprising the concrete pouring team (server) and daily workload (customer) and quantitatively analyzed the system using a queueing model. Secondly, the influence of the number of input servers on the project using the performance index of a queueing model was quantitatively analyzed. Finally, the effect of waiting time, based on the customer waiting cost and server input cost, was analyzed to determine the optimal server level.

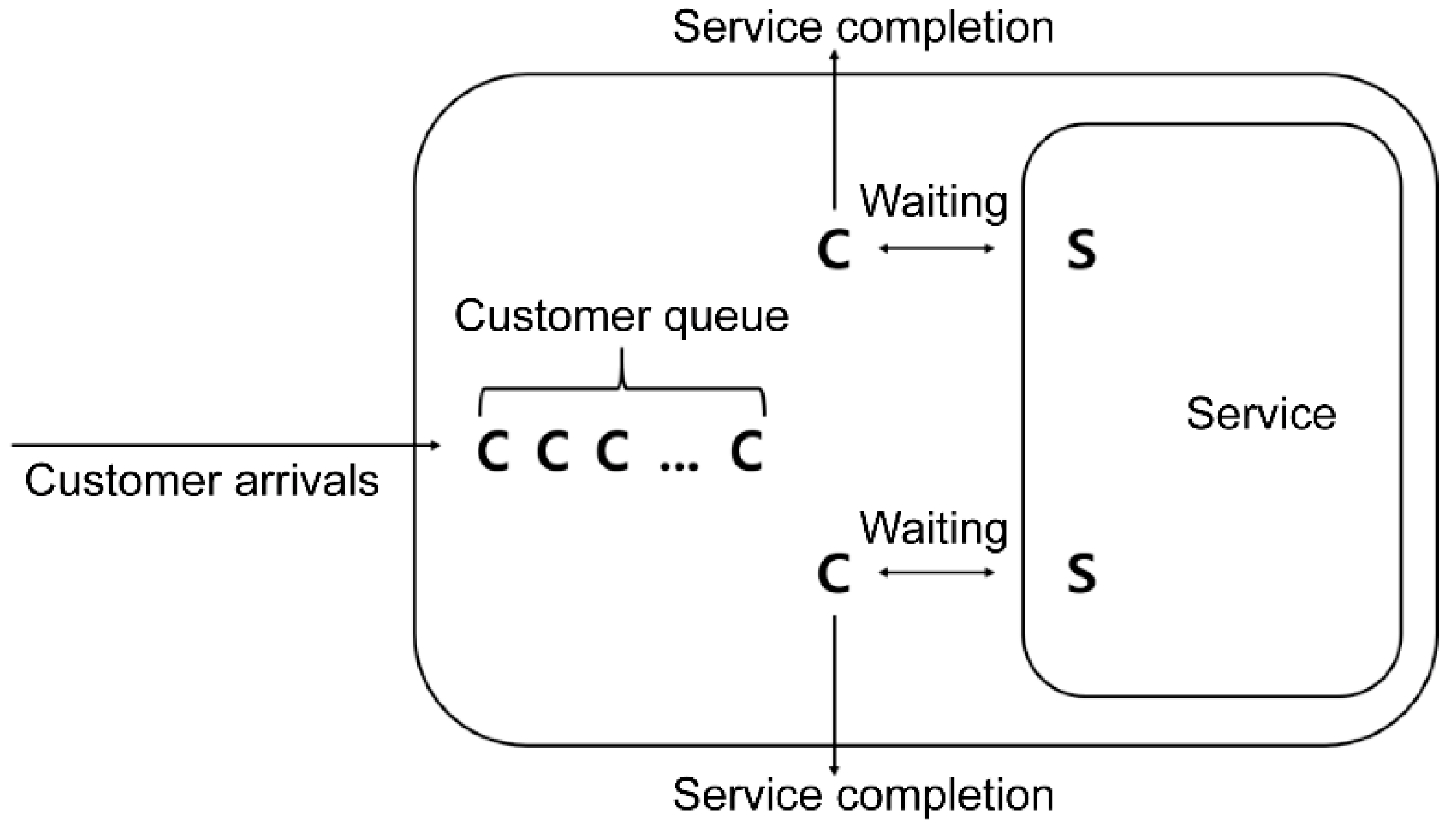
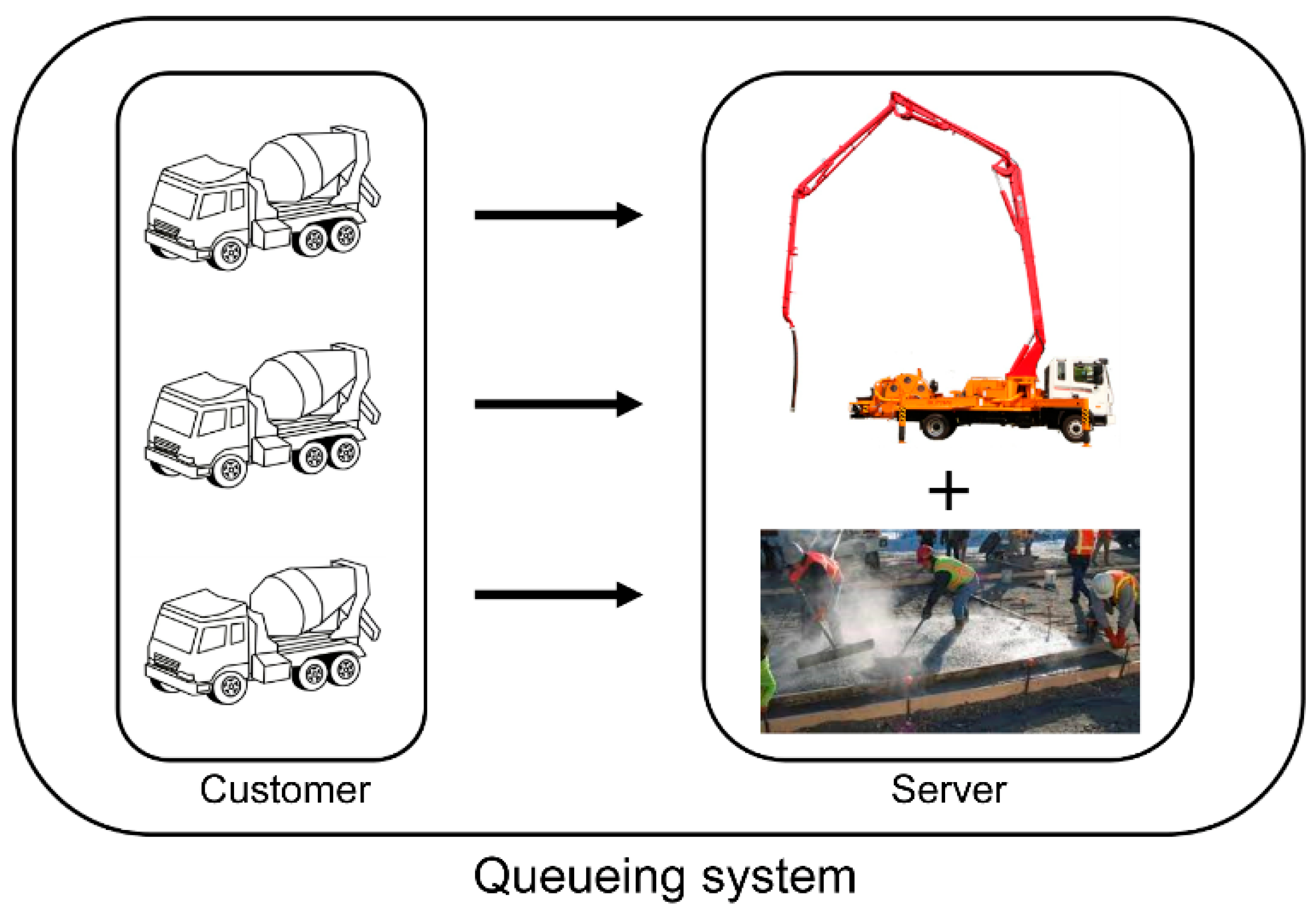
4.1. Characterization of the Queuing System

Customers and servers are always present in a queuing system. The inter-arrival time in a queuing system is the interval between the arrival of adjacent customers. Although it is difficult to predict the arrival time of the next customer accurately, if sufficient data about customers arriving at the queuing system are provided, the average number of customers arriving per unit time—the mean arrival rate (λ)—can be predicted. In addition, the probability distribution of the time between arrivals can be estimated using the mean arrival rate, and the average probability distribution for the arrival time is 1/λ. For example, if 40 customers arrived within 10 h, then λ would be 4 customers per hour. The expected average inter-arrival time is 1/4 of 1 h. The probability distribution of inter-arrivals in most queuing systems is assumed to follow an exponential distribution with Markovian characteristics. The server has no control over the customer arrivals, considering that they arrive randomly [51]. In other words, because the time elapsed since the arrival of the most recent customer does not influence the arrival time of the next customer, the arrival time of a customer is unpredictable.

In a basic queuing system, a customer is individually served by a single server. Furthermore, if multiple servers (two or more servers) provide services to one customer unit, these resources can be organized into one server team [66]. The time elapsed from the start to the completion of the service is called the service time, which varies for different customers. The average service rate (μ) is the average number of customers served by one server per unit time without interruptions. The service time is assumed to have a constant probability distribution, irrespective of the server. The average probability distribution of the service time is 1/μ. For example, if the server takes 10 min to serve one customer (1/μ is 10 min), μ will be 6 customers per hour.

The M/M/1 model includes a single server, whereas the M/M/s model has multiple servers, with the inter-arrival and service times following an exponential distribution. In the M/D/s model, M and D represent the specific probability distributions for the inter-arrival and service times, respectively, where M follows the exponential distribution and D follows a deterministic distribution (regular time).

The following are general assumptions regarding the queueing model:

• The inter-arrival time is evenly and independently distributed based on the probability.
• Every customer arriving at the queueing system waits until the service is completed.
• The number of customers is infinite, considering that there is one infinite queue in the queuing system.
• Customers in the queueing system follow the first-come, first-served rule.
• The queueing system comprises a fixed number of servers, and each server can provide services to all customers.
• One server serves each customer individually.
• The server service time is distributed evenly and independently and follows an exponential or deterministic distribution.

The service time probability distribution is determined based on the queuing system characteristics. According to the process plan, the time required for the concrete pouring team to handle the daily workload of foundation concrete pouring is short, except when more time is required. The queuing model is selected after establishing a certain probability distribution for the inter-arrival and service times. In this study, we investigated the influence of the frame construction team level on the project performance in an M/M/s queuing model, considering that two server teams are being used in this example.

4.2. Quantitative Analysis of the Server

4.2.1. Basic Performance Indicators of the M/M/S Queueing Model

The queuing system performance was analyzed based on two factors: (1) the number of customers waiting in the queue, which indicates that the customer waiting for service is an unproductive member, and (2) the customer waiting time in the queue, which is essential for customer satisfaction [51,66]. In general, customers are more interested in improving the latter [52,66]. Usually, these factors are expressed as expected average values. However, in the M/M/s queueing model, the derivation equations of $L$, $L_q$, $W$, and $W_q$ are expressed using Equations (1)–(5) [51,66], as follows

$$P_0=\frac{1}{{{\displaystyle \sum }}_{n=0}^{s-1}\frac{{\left(\lambda /\mu \right)}^n}{n!}+\frac{{\left(\lambda /\mu \right)}^s}{s!} \left(\frac{1}{1-\lambda /s\mu }\right)}$$

(1)

$$L_q=\frac{P_0{\left(\lambda /\mu \right)}^s\rho }{s!{\left(1-\rho \right)}^2}=\frac{P_0{\lambda }^{s+1}}{\left(s-1\right)!{\mu }^{s-1}{\left(s\mu -\lambda \right)}^2}$$

(2)

$$W_q=L_q/\lambda$$

(3)

$$W=W_q+\frac{1}{\mu }$$

(4)

$$L=\lambda W\left(\lambda : \mathrm{mean} \mathrm{arrival} \mathrm{rate}\right)$$

(5)

Equation (5), also called Little’s equation [67], analyzes the basic performance of the queueing model as it describes the relationship between $L$ and $W$, and $L_q$ and $W_q$. In other words, if any one of these parameters is analyzed, the others can be identified, enabling a basic analysis of the system.

4.2.2. Economic Analysis Based on the Waiting and Service Costs

It is important to determine the appropriate number of inputs for the frame construction work teams when managing the economic efficiency of frame construction work, considering the large costs involved. Whereas too many work teams can generate unnecessary service costs, insufficient work teams can generate waiting costs such as compensation for delays and additional work, as the daily pour volume on the process plan cannot be achieved. Therefore, to determine the appropriate number of frame construction work teams required, a suitable tradeoff between the service and waiting costs needs to be established [45,64]. A case study was performed to determine the number of frame construction work teams that satisfy Equation (6) [51,52,66]

$$\mathrm{Minimized} \mathrm{TC}=\mathrm{SC}+\mathrm{WC}$$

(6)

where TC is the average total cost per unit time, SC is the average service cost per unit time, and WC is the average waiting cost per unit time

In the example project, the service and waiting costs of customers when considering the average cost of the frame construction work team (manpower + equipment) are expressed using Equations (7) and (8), respectively [51,66]

$$\mathrm{SC}=C_s\times s$$

(7)

$$\mathrm{WC}=C_w\times L$$

(8)

Here, $C_s$ and $C_w$ are the service and waiting costs per unit time of the framework construction work team, respectively; s is the number of frame construction work teams (number of servers); $L$ is the average number of customers. $C_s$ and $C_w$ examine the daily input cost of the concrete pouring team and resource input cost for additional work due to delay, respectively. By determining the values of $C_s$ and $C_w$ and the tradeoff between the two, the optimal number of framing teams that satisfy Equation (9) is determined [51,52,66]

$$\mathrm{Minimized} \mathrm{TC}=C_s\times s+C_w\times L$$

(9)

4.3. Interview Design

The researchers in this paper conducted interviews with 3 employees (affiliated with SC) who managed the case project and 2 employees (affiliated with SubC) who directly performed the frame construction of the case project. The interviews were conducted one by one, questions are as follows:

• One concrete pouring team component.
• Maximum workable amount per day of one concrete pouring team and its standards (when pouring foundation concrete).
• Input cost per day for one concrete pouring team.
• In case of delay in construction period, additional work cost of pouring team
• Decision-making criteria when determining the number of pouring team.
• Concrete pouring process.
• Reasons and standards for zoning at the construction site.

5. Case Study

5.1. Project Description and Data Collection

The GC, which constructed the case project in this study, is ranked 3rd in the 2020 contract ranking in Korea. Founded in 1939, this GC has been leading South Korea’s apartment construction industry. In this study, we intend to analyze the case of one of the projects carried out by this GC. The data used in this study were prepared by drawing the foundation work part from the monthly frame construction work reports prepared by the project team (Table 2) and collected by the construction project staff. In this case study, the resources for the concrete pouring work consisted of six workers, including the pump car and vibrator operators, in one team. As shown in Figure 3, the foundation concrete daily workload was set as the customer, and the equipment, such as the pump car, vibrator, and manpower performing the pouring work, as the server. The daily work time of the servers was set to 8 h. The capacity of the ready-mixed concrete transport car was 6 m³. Because 6 m³ customer units simultaneously arrived and received service in the queue in the actual construction, one customer unit was set to 6 m³ instead of 1 m³. A stable supply of the ready-mixed concrete corresponding to the material for pouring was assumed.

The system was analyzed based on the pouring quantity of the foundation concrete in zones 1–29 using a queueing model. Furthermore, the queueing model analyzed the performance of the frame construction work teams based on the daily capability and workload of the team inputs in zones 1–29.

Table 3. Descriptions of the servers in the case project.

Zone	Server	λ	μ	ρ	1 − ρ
1	2	57.00	120.00	0.2375	0.7625
2	2	42.00	120.00	0.175	0.825
3	2	218.38	120.00	0.909896	0.090104
4	2	61.50	120.00	0.25625	0.74375
5	2	251.25	120.00	1.046875	−0.04688
6	2	213.00	120.00	0.8875	0.1125
7	2	141.75	120.00	0.590625	0.409375
8	2	259.50	120.00	1.08125	−0.08125
9	2	87.00	120.00	0.3625	0.6375
10 + 11	2	286.25	120.00	1.192708	−0.19271
12	2	211.50	120.00	0.88125	0.11875
13 + 14 + 15	2	283.13	120.00	1.179688	−0.17969
16 + 17	2	174.00	120.00	0.725	0.275
18	2	99.00	120.00	0.4125	0.5875
19	2	48.00	120.00	0.2	0.8
20	2	162.00	120.00	0.675	0.325
21 + 22	2	94.50	120.00	0.39375	0.60625
23	2	27.75	120.00	0.115625	0.884375
24	2	69.00	120.00	0.2875	0.7125
25	2	59.75	120.00	0.248958	0.751042
26	2	25.13	120.00	0.104688	0.895313
27	2	69.75	120.00	0.290625	0.709375
28	2	40.25	120.00	0.167708	0.832292
29	2	56.25	120.00	0.234375	0.765625

shows the analyzed indicators based on the number of work teams input into the case project and collected by recording actual input resources. The mean service rate (μ) and pouring flow of one server team were investigated by interviewing the experts. Assuming negligible equipment failure, one server team in foundation concrete pouring work can process 120 m³/h. Therefore, the mean service rate (μ) that one server team can pour per unit time was assumed to be 120 m³. Because two server teams were deployed in the case project, μ was estimated to be 240 m³. The mean arrival rate per hour for the total volume from zones 1–29 was estimated to be 126.57 m³ considering the total daily workloads specified according to the process plan.

In the M/M/S queuing model, the utilization rate ρ, calculated as $\lambda /s\times \mu$, for the server should be smaller than 1 under stable conditions under which services are performed normally. ρ < 1 in zones 1–4, 6, 7, 9, 12, 16 + 17, 18–20, 21 + 22, and 23–29, indicating that the specified volume can be serviced within the work time. However, ρ > 1 in zones 5, 8, 10 + 11, and 13 + 14 + 15, indicate an “overloaded” state, where all the pouring volume is not served within the work time. The server idle rate (1 − ρ) refers to the remaining time after the daily workload processing working hours, such as other task execution time, rest time, and work preparation time. Although there were idle times in zones 1–4, 6, 7, 9, 12, 16 + 17, 18–20, 21 + 22, and 23–29, the two servers in zones 5, 8, 10, 11, and 13 + 14 + 15 were busy and could only perform foundation concrete pouring. Furthermore, the daily workload (specified workload) was not processed during the specified working hours, considering that ρ was greater than 1.

5.2. Data Analysis

5.2.1. Basic Performance Analysis in the Queueing Model

The performance of the concrete pouring team was analyzed based on the performance indicators of the queueing model defined above, and the results are summarized in

Table 4. Descriptions of the servers in the example project.

Zone	Server	L	Lq	W	Wq
1	2	0.5033	0.0283	0.0529	0.0029
2	2	0.361	0.011	0.0515	0.0015
3	2	10.5875	8.7675	0.2908	0.2408
4	2	0.5485	0.036	0.0535	0.0035
5	2	N/A	N/A	N/A	N/A
6	2	8.359	6.584	0.2354	0.1854
7	2	1.8148	0.6335	0.0765	0.0268
8	2	N/A	N/A	N/A	N/A
9	2	0.8346	0.1096	0.0575	0.0075
10 + 11	2	N/A	N/A	N/A	N/A
12	2	7.8894	6.1269	0.2238	0.1738
13 +14 + 15	2	N/A	N/A	N/A	N/A
16 + 17	2	3.0566	1.6066	0.1054	0.0554
18	2	0.9941	0.1691	0.0602	0.0102
19	2	0.4166	0.0166	0.052	0.002
20	2	2.4799	1.1299	0.0918	0.0418
21 + 22	2	0.9319	0.1444	0.0591	0.0091
23	2	0.2346	0.0031	0.0506	0.0006
24	2	0.6268	0.0518	0.0545	0.0045
25	2	0.5309	0.0329	0.0533	0.0033
26	2	0.2118	0.0023	0.0505	0.0005
27	2	0.6351	0.0536	0.0546	0.0046
28	2	0.3452	0.0097	0.0514	0.0014
29	2	0.4962	0.0272	0.0529	0.0029

. The server utilization rate (ρ) of zones 5, 8, 10 + 11, and 13 + 14 + 15 are above 1.0, indicating that the server cannot provide normal services. Furthermore, the work standard of 8 h per day is breached to process the specified volume or is postponed to another day. ρ in zone 1 is 0.2375, which satisfies the condition of p < 1, indicating a stable service to the customer. The basic performance scale of zone 1 indicates that the mean waiting time for 6 m³ foundation concrete entering the queueing system is 0.0529 h (3.174 min based on an 8 h workday) until the service is completed. Moreover, the mean waiting time inside the queueing system, excluding the pouring (receiving service) time, is estimated to be 0.0029 h per 6 m³ (0.174 min based on an 8 h workday). In other words, one unit of foundation concrete in zone 1 probabilistically receives a service for 0.05 h (3 min) after a waiting time of 0.174 min per 6 m³. Because an estimated 120 m³ can be processed per hour by each server, there is sufficient room for processing the planned daily volume. Zones 2, 4, 7, 9, 18, 19, 20, 21 + 22, and 23–29, like Zone 1, comfortably allow the concrete pouring server team to handle their daily workload. ρ in zones 3, 6, and 12 is less than 1.0, indicating that stable services can be provided. However, the waiting time for customers is longer in the other zones. Furthermore, the preparation time for service provision and resting time, excluding the work processing time (foundation concrete pouring), is insufficient. The basic performance scales of zones 3, 6, and 12 show that these zones receive services per 6 m³ for 0.05 h after waiting for 0.2408 h (14.45 min), 0.1854 h (11.12 min), and 0.1738 h (10.43 min), respectively. Therefore, the researchers in this paper conclude that the customers in these three zones have longer waiting times than those in the other zones.

Thus, the work performance of the concrete pouring team can be evaluated using the performance indicators $L$, $L_q$, $W$, and $W_q$ in the queueing model and analyzing the probability of customer arrivals and waiting times in the queuing system [51,66]. The proposed method enables the quantitative evaluation of services provided by the framework construction work team in the queueing system.

5.2.2. Economic Analysis of the Input Server

When analyzing the service state of the framework from a project management perspective, determining the number of server inputs that minimize the sum of the input cost of the frame construction team and waiting cost of the ready-mixed car (as a customer) is necessary. Therefore, the researchers in this paper analyzed the economics of the system by considering the tradeoff point between the two costs.

The cost of the frame construction work team was used to calculate $C_s$ in this study. The equipment (pump car and vibrator) rental cost was KRW 1,500,000 per day, and the labor cost was KRW 230,000 per operator per day for each team, determined by interviewing expert groups. Therefore, the total input cost of one frame construction work team was KRW 2,880,000 per day. $C_w$ is the cost of additional work when waiting caused construction delays. The expert interview revealed that along with 8 h of work, 50% (KRW 1,440,000) of the daily input cost, including allowances, must be paid for an additional 3 h of work. Therefore, the waiting cost per hour of additional work was KRW 480,000. Therefore, the minimum TC based on the tradeoff point between the service and waiting costs corresponds to the number of servers that minimizes $\mathrm{KRW} 2,880,000\times s+\mathrm{KRW} 480,000\times L$.

Based on the basic performance analysis, the zones were divided into groups A, B, and C (

Table 5. Economic analysis of the optimal servers (Group A, unit: KRW).

Zone	Server 1			Server 2			Server 3
	SC, a	WC, b	TC, a + b	SC, c	WC, d	TC, c + d	SC, e	WC, f	TC, e + f
1	2,880,000	434,256	3,314,256	5,760,000	241,584	6,001,584	8,640,000	229,152	8,869,152
2	2,880,000	258,432	3,138,432	5,760,000	173,280	5,933,280	8,640,000	168,336	8,808,336
4	2,880,000	504,576	3,384,576	5,760,000	263,280	6,023,280	8,640,000	247,584	8,887,584
9	2,880,000	1,265,424	4,145,424	5,760,000	400,608	6,160,608	8,640,000	354,144	8,994,144
18	2,880,000	2,262,816	5,142,816	5,760,000	477,168	6,237,168	8,640,000	406,224	9,046,224
19	2,880,000	319,968	3,199,968	5,760,000	199,968	5,959,968	8,640,000	192,576	8,832,576
21 + 22	2,880,000	1,778,784	4,658,784	5,760,000	447,312	6,207,312	8,640,000	386,496	9,026,496
23	2,880,000	144,576	3,024,576	5,760,000	112,608	5,872,608	8,640,000	111,168	8,751,168
24	2,880,000	649,392	3,529,392	5,760,000	300,864	6,060,864	8,640,000	278,496	8,918,496
25	2,880,000	476,160	3,356,160	5,760,000	254,832	6,014,832	8,640,000	240,432	8,880,432
26	2,880,000	127,200	3,007,200	5,760,000	101,664	5,861,664	8,640,000	100,608	8,740,608
27	2,880,000	666,912	3,546,912	5,760,000	304,848	6,064,848	8,640,000	281,712	8,921,712
28	2,880,000	242,304	3,122,304	5,760,000	165,696	5,925,696	8,640,000	161,328	8,801,328
29	2,880,000	423,936	3,303,936	5,760,000	238,176	5,998,176	8,640,000	226,224	8,866,224

,

Table 6. Economic analysis of the optimal servers (Group B, unit: KRW).

Zone	Server 2			Server 3			Server 4
	SC, a	WC, b	TC, a + b	SC, c	WC, d	TC, c + d	SC, e	WC, f	TC, e + f
3	5,760,000	5,082,000	10,842,000	8,640,000	1,142,544	9,782,544	11,520,000	926,784	12,446,784
6	5,760,000	4,012,320	9,772,320	8,640,000	1,091,328	9,731,328	11,520,000	899,232	12,419,232
7	5,760,000	871,104	6,631,104	8,640,000	609,504	9,249,504	11,520,000	574,176	12,094,176
12	5,760,000	3,786,912	9,546,912	8,640,000	1,077,648	9,717,648	11,520,000	891,696	12,411,696
16 + 17	5,760,000	1,467,168	7,227,168	8,640,000	794,448	9,434,448	11,520,000	714,336	12,234,336
20	5,760,000	1,190,352	6,950,352	8,640,000	721,056	9,361,056	11,520,000	661,152	12,181,152

and

Table 7. Economic analysis of the optimal servers (Group C, unit: KRW).

Zone	Server 3			Server 4			Server 5
	SC, a	WC, b	TC, a + b	SC, c	WC, d	TC, c + d	SC, e	WC, f	TC, e + f
5	8,640,000	1,548,048	10,188,048	11,520,000	1,109,424	12,629,424	14,400,000	1,029,456	15,429,456
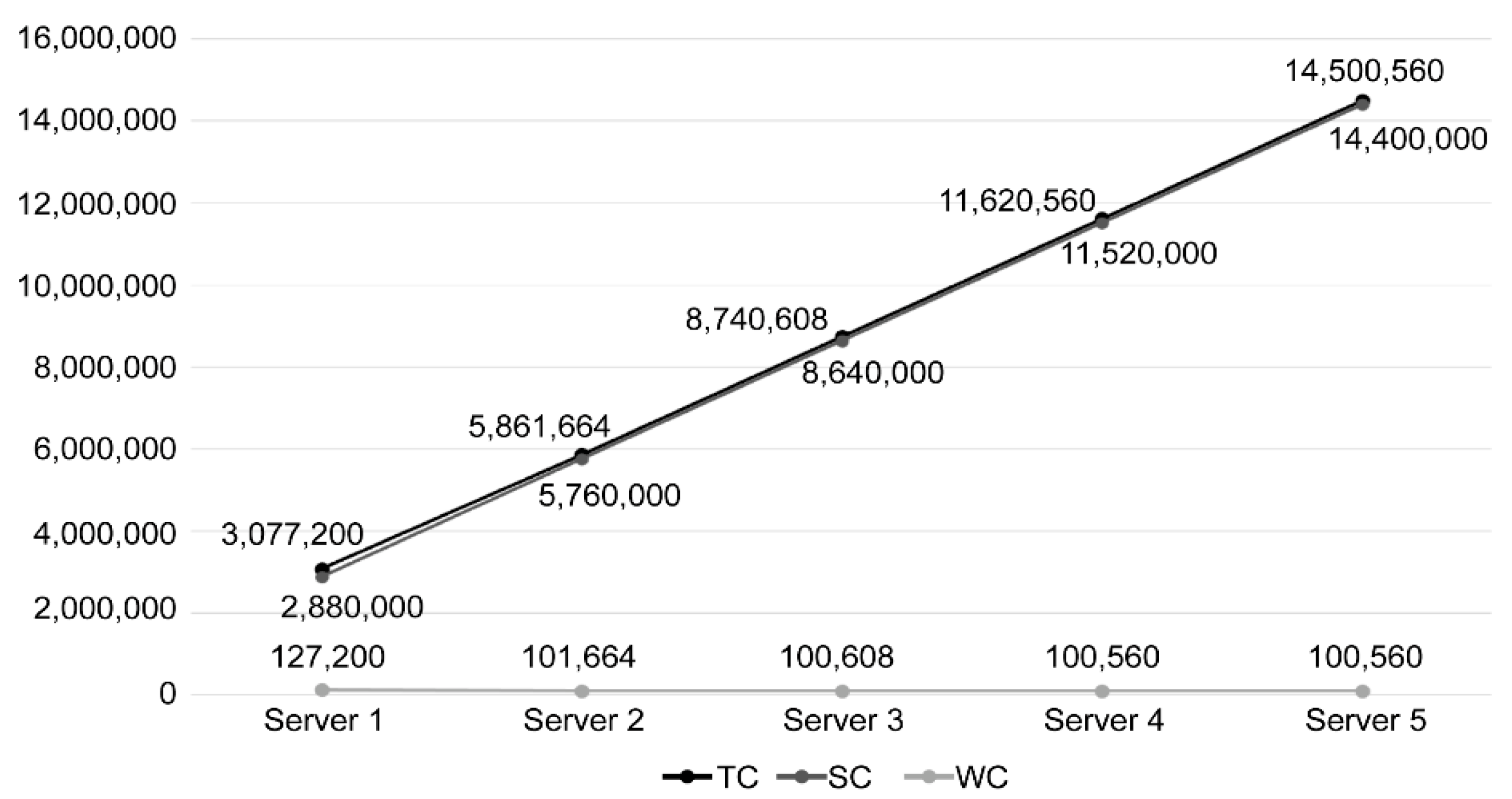
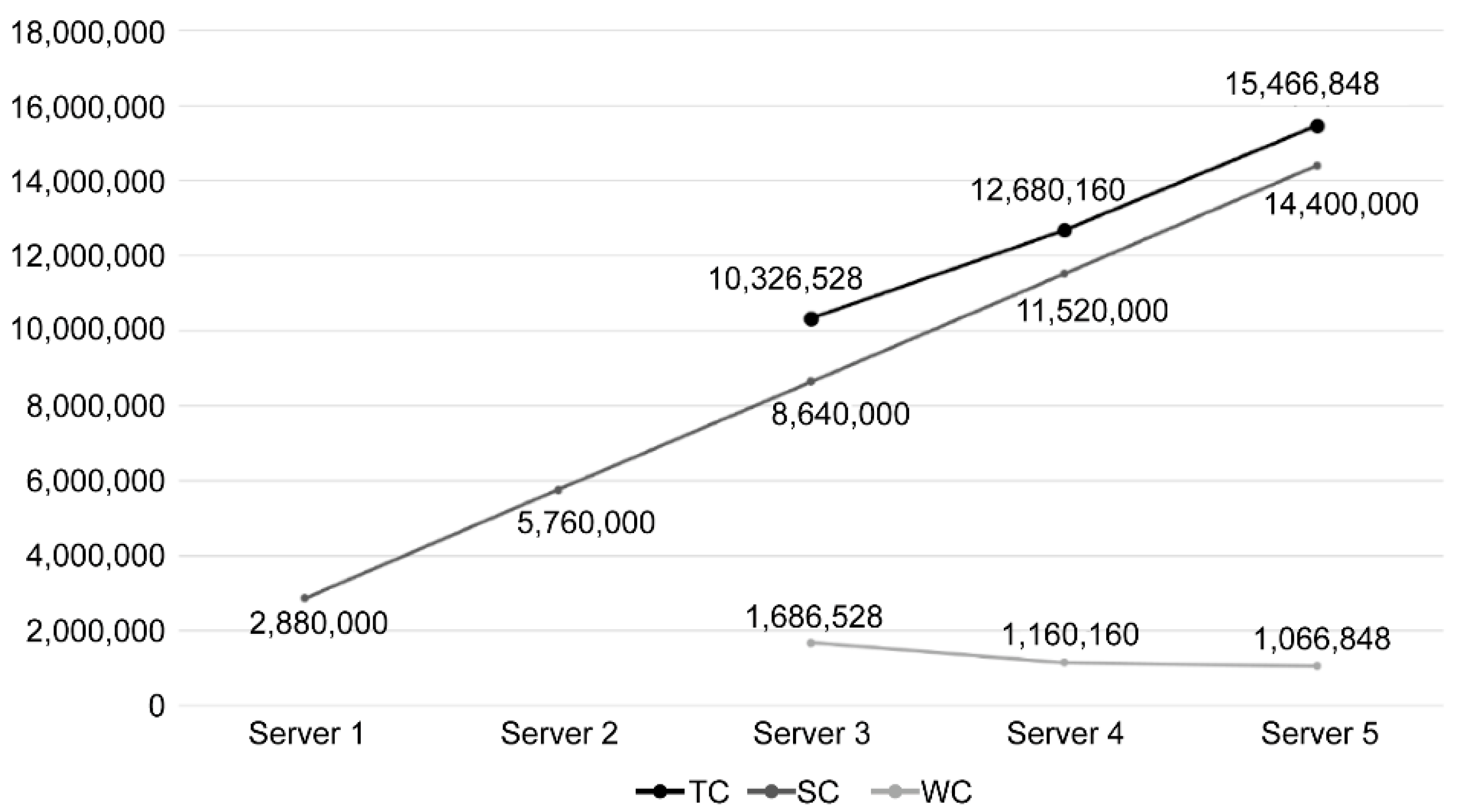
8	8,640,000	1,686,528	10,326,528	11,520,000	1,160,160	12,680,160	14,400,000	1,066,848	15,466,848
10 + 11	8,640,000	2,336,352	10,976,352	11,520,000	1,345,344	12,865,344	14,400,000	1,193,712	15,593,712
13 + 14 + 15	8,640,000	2,238,336	10,878,336	11,520,000	1,321,872	12,841,872	14,400,000	1,178,448	15,578,448

, respectively), with ρ values less than 0.5, between 0.5 and 1, and greater than 1, respectively. Considering the service and waiting costs of group A, the minimum TC refers to the number of servers that minimizes $\mathrm{KRW} 2,880,000\times s+\mathrm{KRW} 480,000\times L$. It is economically advantageous to deploy server 1 for all 14 zones in group A (Table 5), as the TC smaller than those resulting from deploying servers 2 and 3. Therefore, the existing servers are over-deployed, and deploying one server team is most efficient economically. Furthermore, deploying one server team in zone 26 of group A could save up to KRW 2,854,464 (Figure 4).

Because the server utilization rate in group B exceeds 1 in every zone for server 1, the basic performance analysis cannot be conducted, and additional servers need to be deployed in zones 3 and 6. The optimal number of servers (two) was deployed in zones 7, 12, 16 + 17, and 20 (Table 6). When comparing servers 3 and 4, the change in SC is larger than that in WC for every zone in group B. The differences in SC and WC between servers 2 and 3 in zone 3 are KRW 2,880,000 and KRW 3,939,456, respectively, indicating that the WC is higher than the cost of deploying an additional server. Similarly, the appropriate number of servers in zone 6 is 3. When additional servers are deployed in zones 7, 12, 16 + 17, and 20, the decrease in WC is smaller than the increase in SC from two to three and four servers. Furthermore, deploying three servers instead of two in zone 3 can save up to KRW 1,059,456 (Figure 5).

Because the system in group C is considered to be unstable within the specified working hours when servers 1 and 2 are deployed, the basic performance cannot be analyzed. However, for processing the volumes within working hours, every zone in group C requires additional servers. When TC is compared to the server costs, the optimal number of servers is estimated to be three in each zone (Table 7). Furthermore, as the number of servers increases, the increase in SC is larger than the decrease in WC. In zone 8, the server utilization rate is greater than 1 when the number of servers is 1 or 2, making it impossible to perform system measurements. Therefore, using three servers is economically efficient (Figure 6).

TC was optimized by compromising SC and WC based on the number of servers in each zone.

Table 8. Construction costs before and after optimization (unit: KRW).

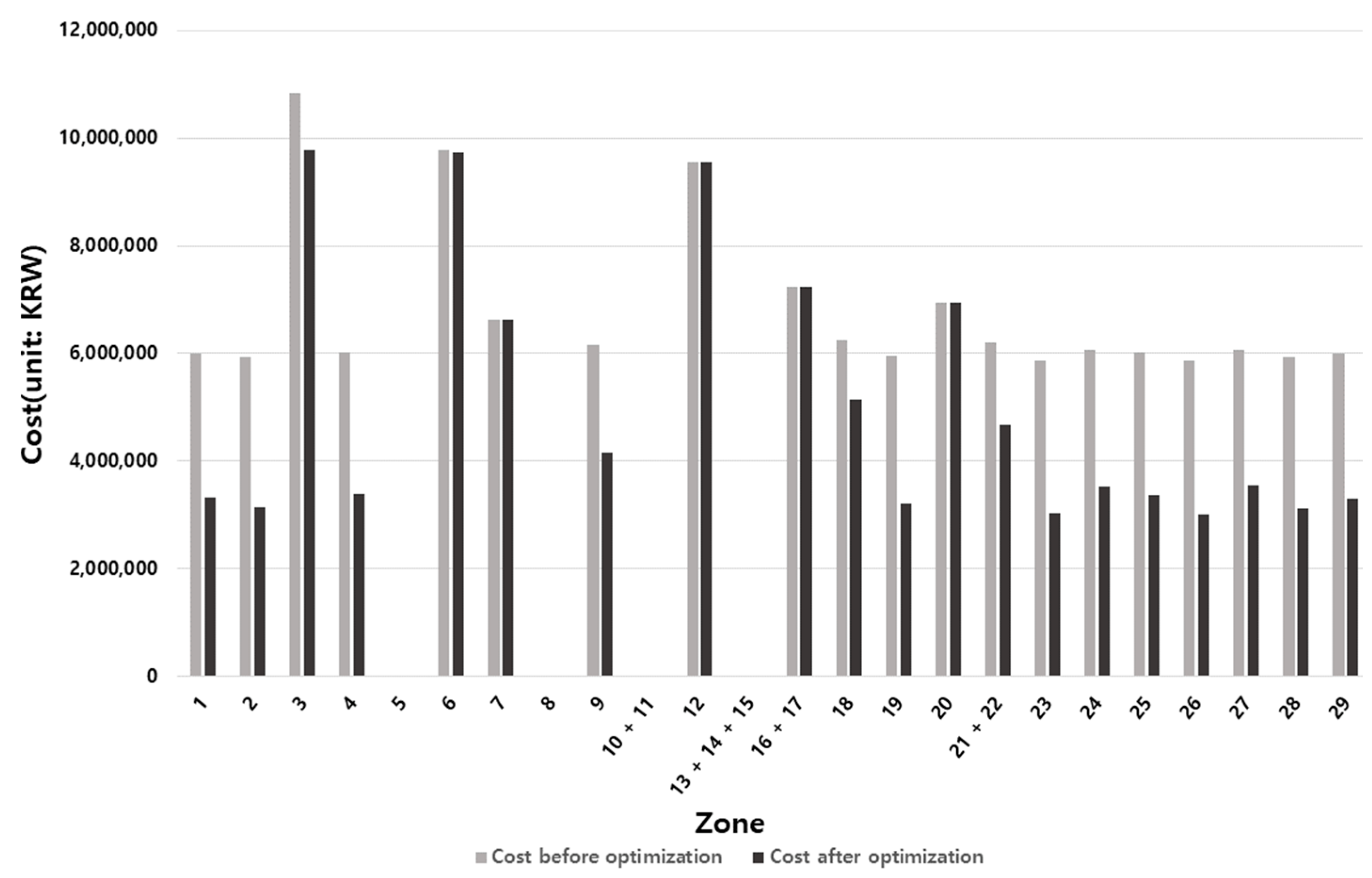
Zone	Cost before Optimization (a)	Cost after Optimization (b)	Difference in Cost (a–b)
1	6,001,584	3,314,256	2,687,328
2	5,933,280	3,138,432	2,794,848
3	10,842,000	9,782,544	1,059,456
4	6,023,280	3,384,576	2,638,704
6	9,772,320	9,731,328	40,992
7	6,631,104	6,631,104	0
9	6,160,608	4,145,424	2,015,184
12	9,546,912	9,546,912	0
16 + 17	7,227,168	7,227,168	0
18	6,237,168	5,142,816	1,094,352
19	5,959,968	3,199,968	2,760,000
20	6,950,352	6,950,352	0
21 + 22	6,207,312	4,658,784	1,548,528
23	5,872,608	3,024,576	2,848,032
24	6,060,864	3,529,392	2,531,472
25	6,014,832	3,356,160	2,658,672
26	5,861,664	3,007,200	2,854,464
27	6,064,848	3,546,912	2,517,936
28	5,925,696	3,122,304	2,803,392
29	5,998,176	3,303,936	2,694,240
Total	135,291,744	99,744,144	35,547,600 (26.27%)

compares the TCs for each zone before and after optimization. The basic performance and TC could not be measured with two server teams in zones 5, 8, 10 + 11, and 13 + 14 + 15. Therefore, they were excluded from the analysis. The queueing model estimated the TCs before and after optimization as KRW 135,291,744 and KRW 99,744,144, respectively. Therefore, 26.27% of TC (KRW 35,547,600) can be saved after optimization (Figure 7).

6. Discussion

The researchers in this paper analyzed the queueing system in management science through a case project using a queueing model by simulating the waiting and service costs. In addition, work performance was evaluated using four basic performance indicators. The analysis showed that the optimal number of servers were deployed in zones 7, 12, 16 + 17, and 20, whereas the other zones experienced wastage or shortage of servers (resources). Nearly 26.27% of the TC could be saved after optimizing the 24 zones using the queueing model. The actual server input cost was saved through the framework of this study. Since only the number of servers was adjusted without changing other factors such as construction time and daily workload during the optimization process, it is appropriate to apply the optimal number of servers derived from this study to the case. In other words, the optimized number of servers can be put in to carry out construction according to the planned schedule and workload. In addition, if only the daily workload and the service rate of the server that handles the daily workload are identified, it can be analyzed using the framework of this study. As in the case of this study, if there is a waste or shortage of resources, it will be possible to reduce the construction cost by applying the framework of this study and proceeding with the optimization process.

The findings of this study can be used in two ways. First, optimal resource allocation is possible based on the daily workload specified in the process plan generated by the SCs by deploying the optimal number of servers for the planned construction period and workload to avoid resource wastage or shortage. Second, the daily allocated workload can be evenly leveled during the process planning stage to avoid additional costs and construction delays due to resource wastage or shortage and to enable the stable employment of equipment and manpower. GCs can objectively analyze and evaluate the performance and plan put forth by the SubCs during the selection stage owing to the effective cooperation between the GCs and SubCs. Furthermore, SubCs can improve their competitiveness through objective, efficient resource scheduling and optimized resource deployment planning. Consequently, the profits of GCs and SubCs participating in construction projects can be increased. The optimization process determines the tradeoff point during the planning stage or before allocating the servers to minimize service and waiting costs of the frame construction team and additional work, respectively, using the four performance indicators.

Burgess and Killebrew [68] proposed a heuristic method for resource allocation in construction projects, but it has a disadvantage that an optimal solution cannot be obtained. Hegazy [2] proposed the Genetic Algorithm for resource allocation in construction projects, but it has a disadvantage that it is difficult to apply in large-scale construction due to the complexity of model implementation. The optimization process proposed in this paper can quantitatively analyze the system performance and can derive an optimal solution if the expected number of customers (i.e., daily workload) and performance of the servers (i.e., workload of the construction team per unit time) can be identified. Furthermore, considering that the analysis was performed at the activity level, flexible resource management, such as allocating additional servers in specific sections with large workloads, is possible.

Although this paper proposed and empirically verified an optimal resource allocation method using a queueing model, it is difficult to generalize as it was based on a single case project. Therefore, more large-scale apartments and buildings should be evaluated using the proposed method. For a stronger generalization, research that analyzes various types of work such as finishing work as well as frame work is needed. Furthermore, the cost of the pouring team before optimization is the estimated cost. Therefore, actual costs should be compared with post-optimization costs using multiple cases in future studies.

7. Conclusions

In this study, the researchers used a multi-server queueing model to analyze the performance of queuing systems, investigated the status of the services provided by construction teams, and proposed a framework to optimize the allocation of construction teams for large-scale apartment construction projects in South Korea. Furthermore, using a micro-level perspective, the researchers in this paper proposed a method of analyzing the performance of the existing frame construction work system for optimal resource allocation per unit time at the activity level. The optimal number of frame construction work teams was determined by converting the additional cost of the daily workload (considered as customer according to the queuing model) into the waiting cost. In addition, to characterize the performance and capability of the frame construction team, four basic performance indicators were derived, assuming that the inter-arrival and waiting times of customers have probabilistic Markovian properties. The proposed method could achieve approximate savings of 26.27%, that is, KRW 35,547,600. The optimal number of construction teams can be determined using the optimization method for resource allocation proposed in this study based on the waiting and service costs of the daily workload.

A combination of related services and multiple resources can enable the effective construction of large-scale projects. Effective resource management can determine the success or failure of such projects. Therefore, research should be conducted to analyze the various queueing systems in construction projects. Furthermore, automated resource allocation based on the process plan can be realized by considering different construction cases. In other words, it is necessary to study the optimal resource allocation decision-making system through the combination of the BIM containing the construction project schedule or quantity information and the framework of this paper.