Experimental Study of Infill Walls with Joint Reinforcement Subjected to In-Plane Lateral Load
Abstract
:1. Introduction
2. Experimental Program
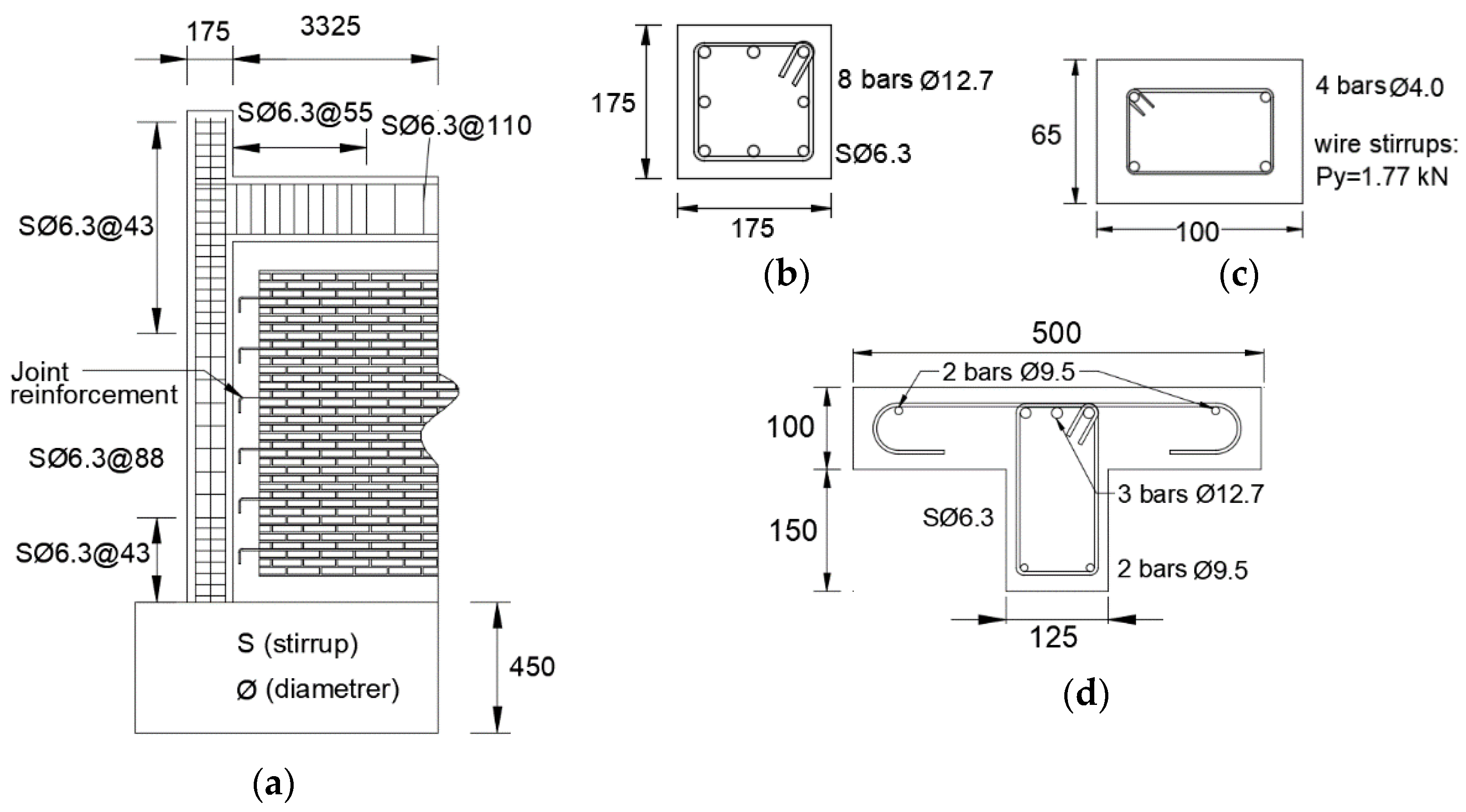
2.1. Specimens
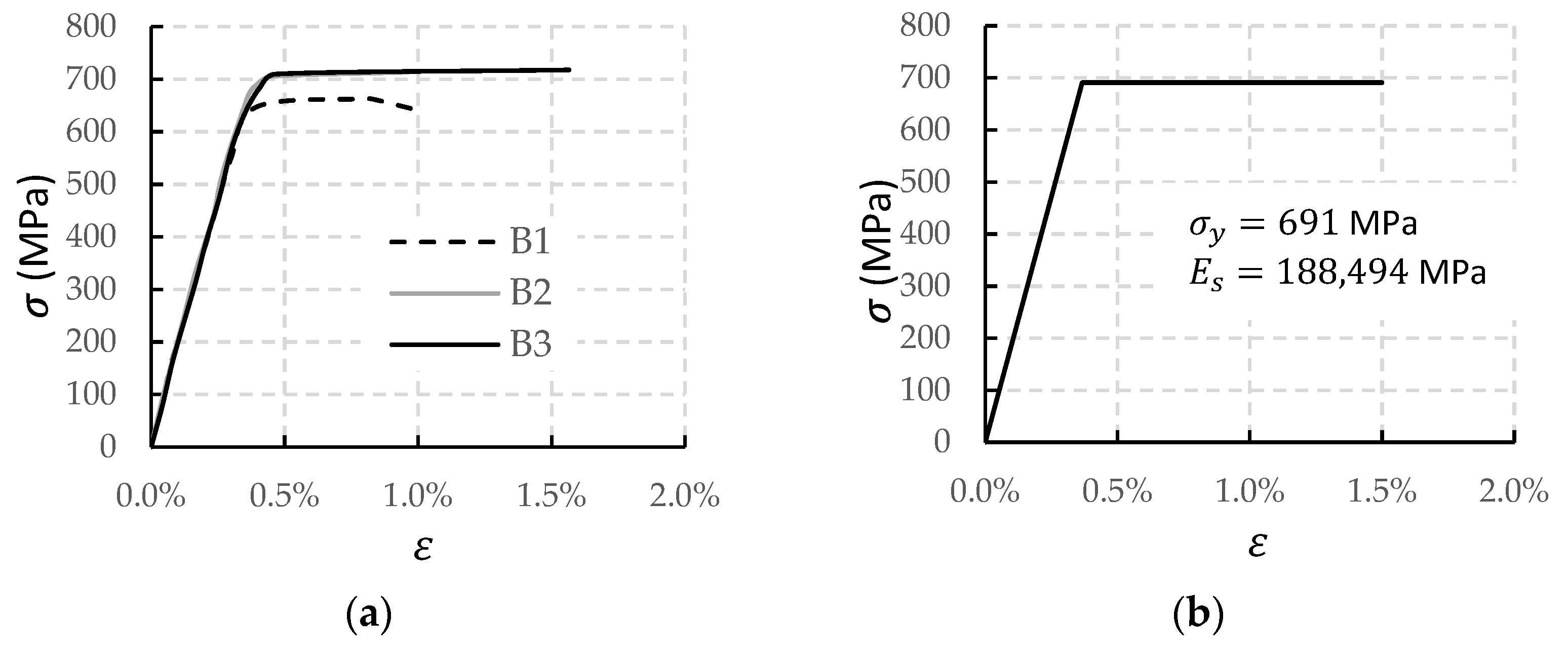
2.2. Material Properties
2.3. Reinforcement
2.3.1. Reinforcement in Reinforced Concrete Elements
2.3.2. Reinforcement in Bed-Joints
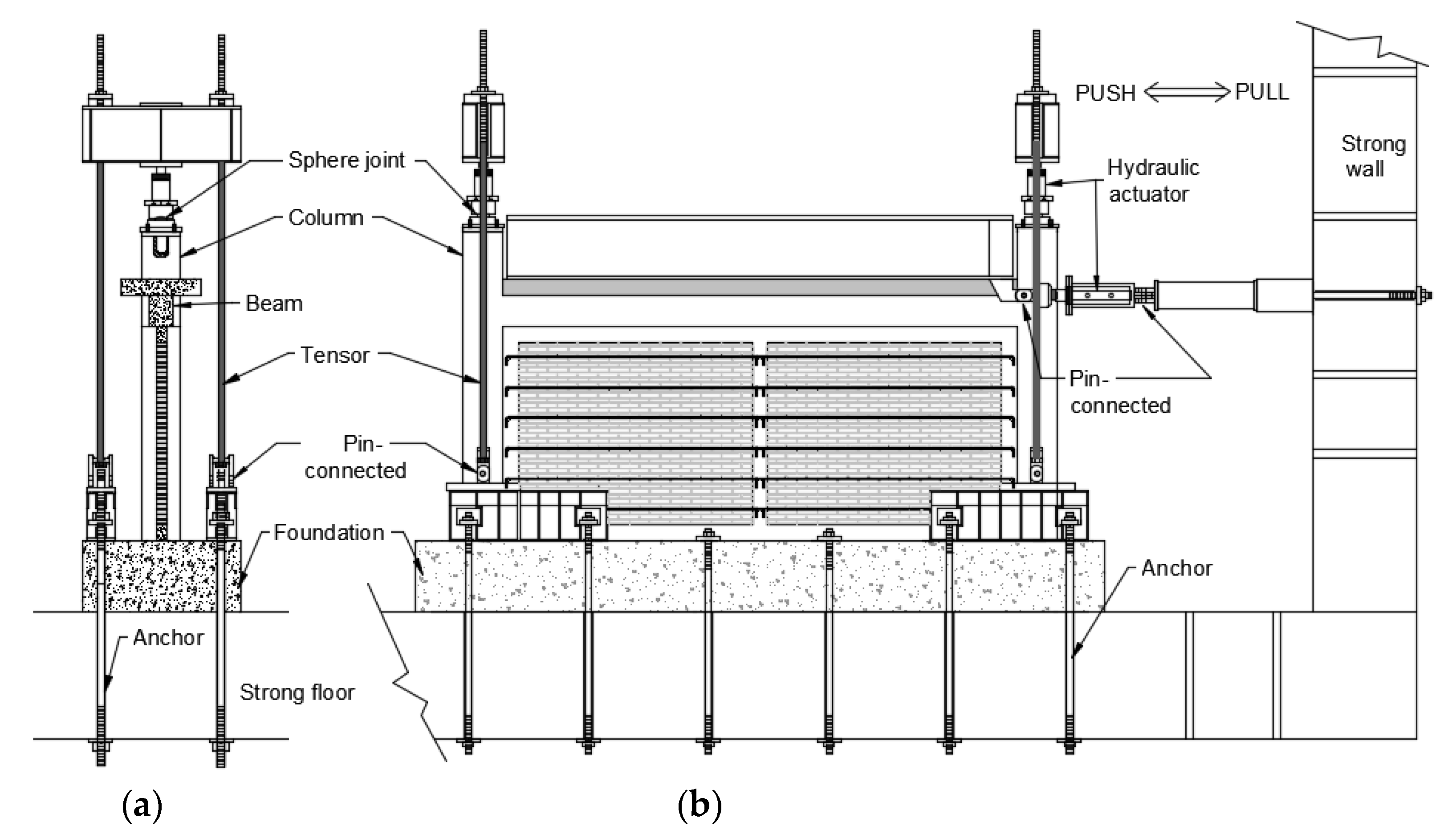
2.4. Test Setup and Load Sequence
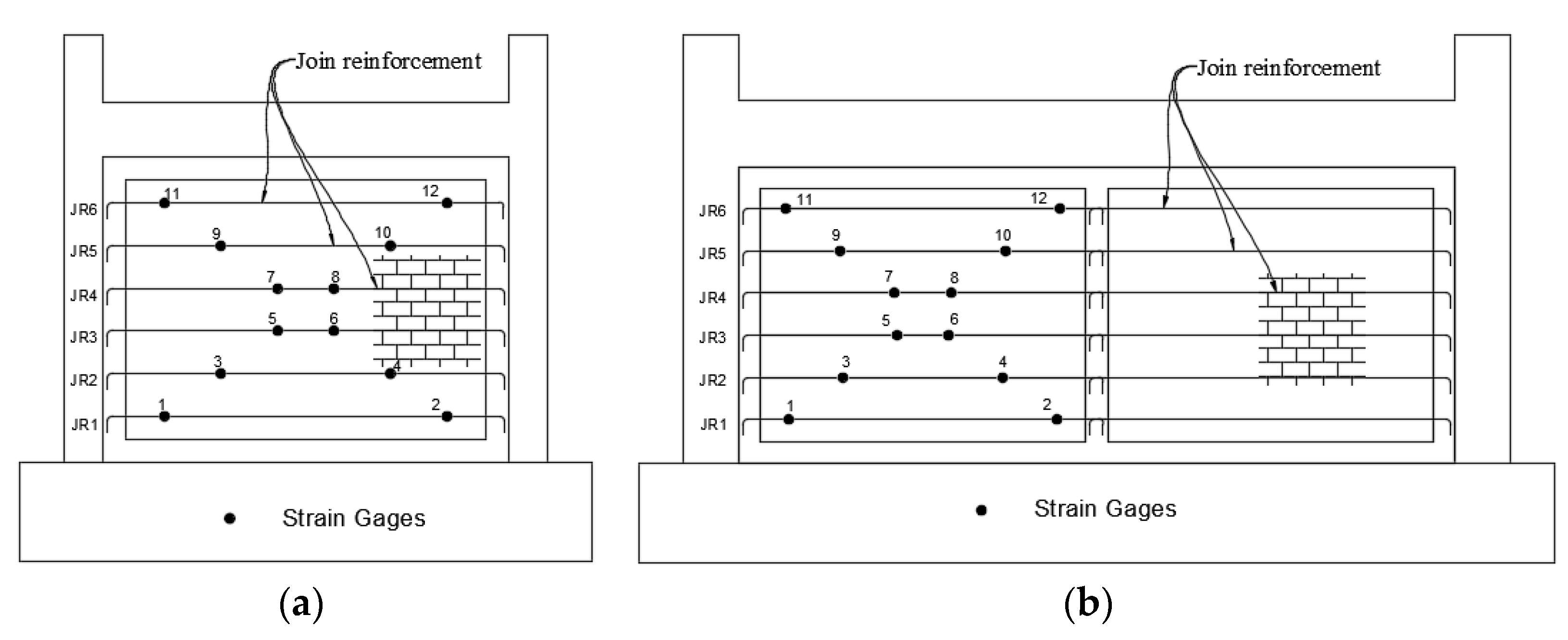
2.5. Instrumentation
3. Experimental Results
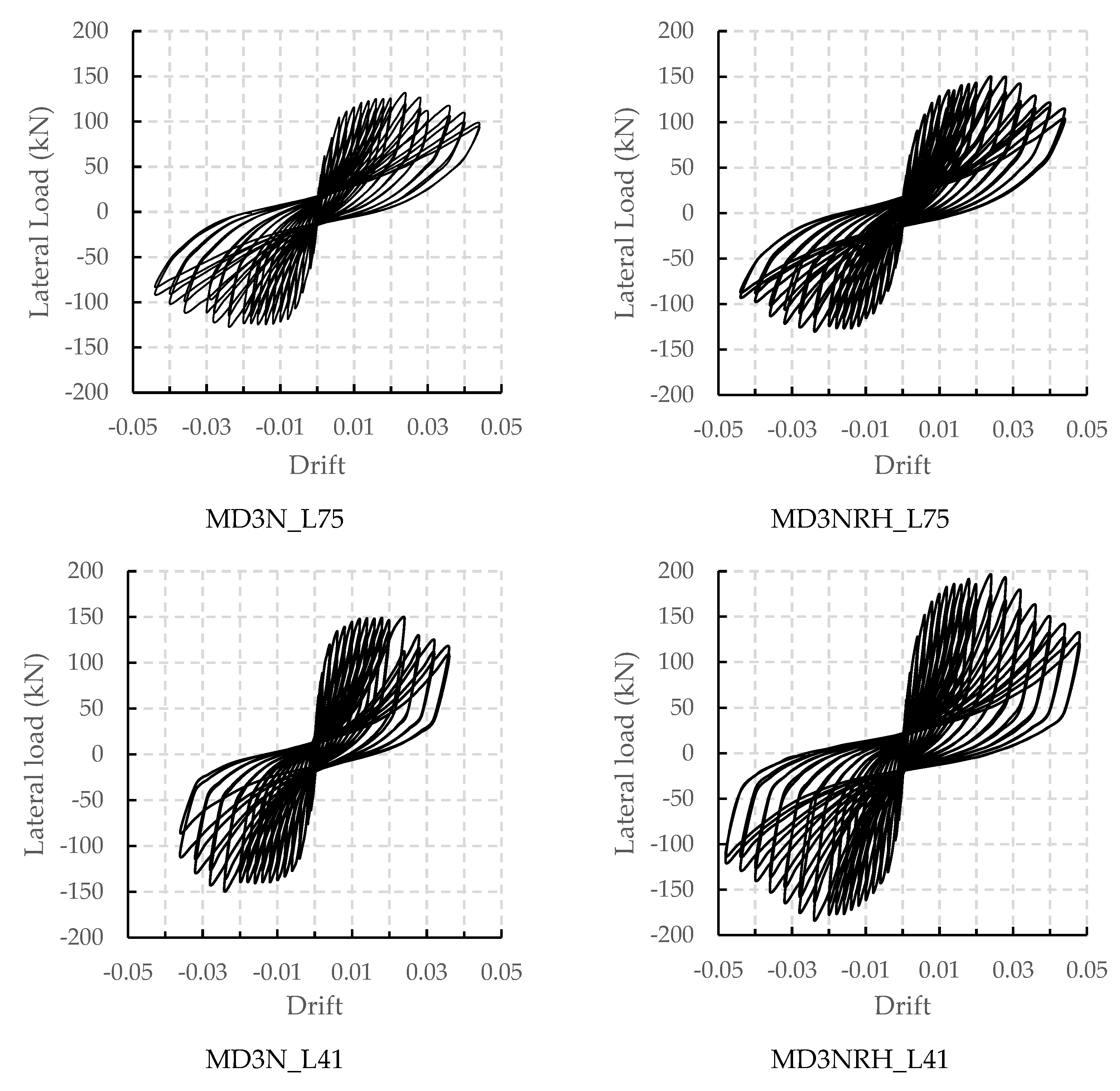
3.1. Hysteretic Curves and Crack Patterns
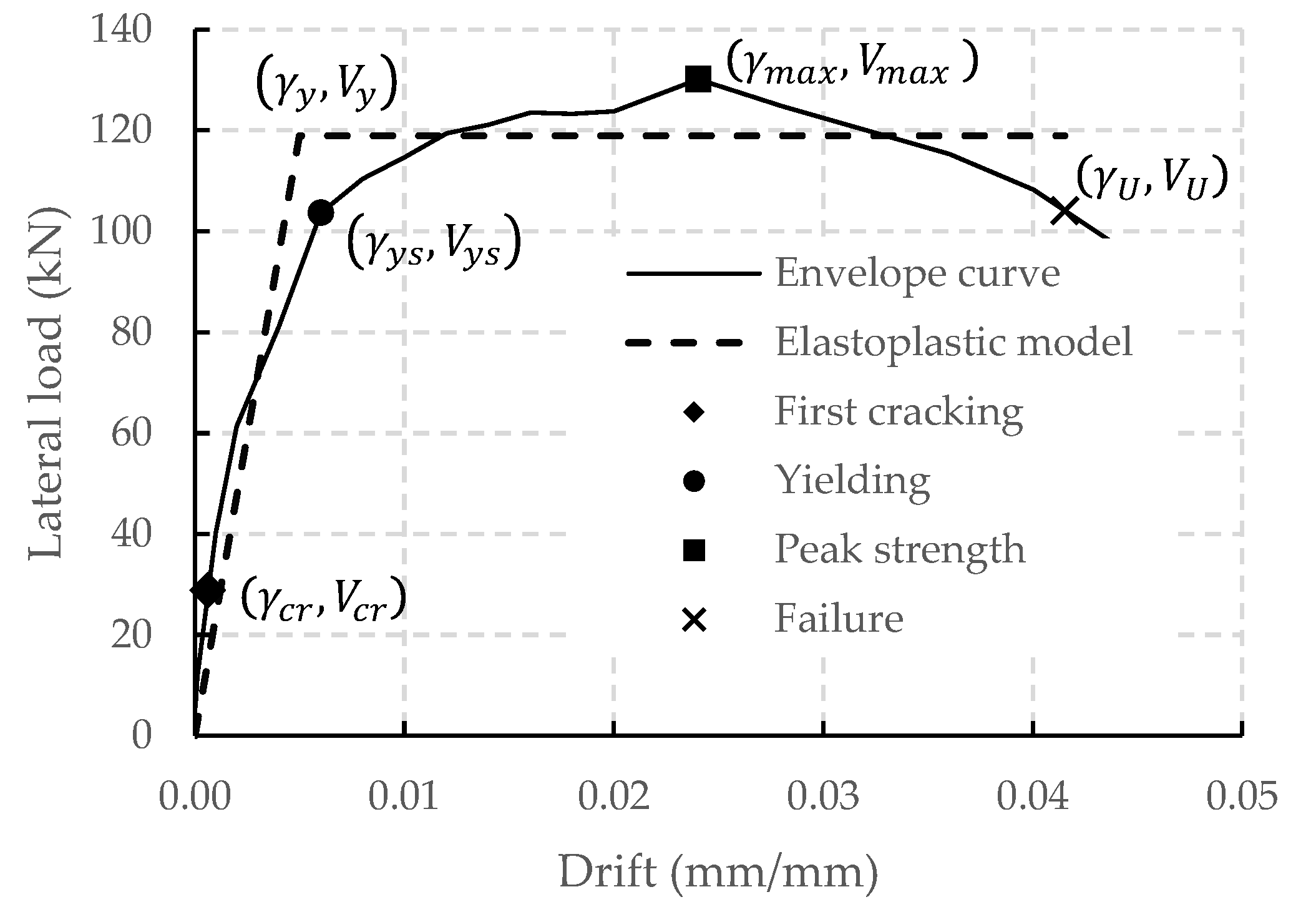
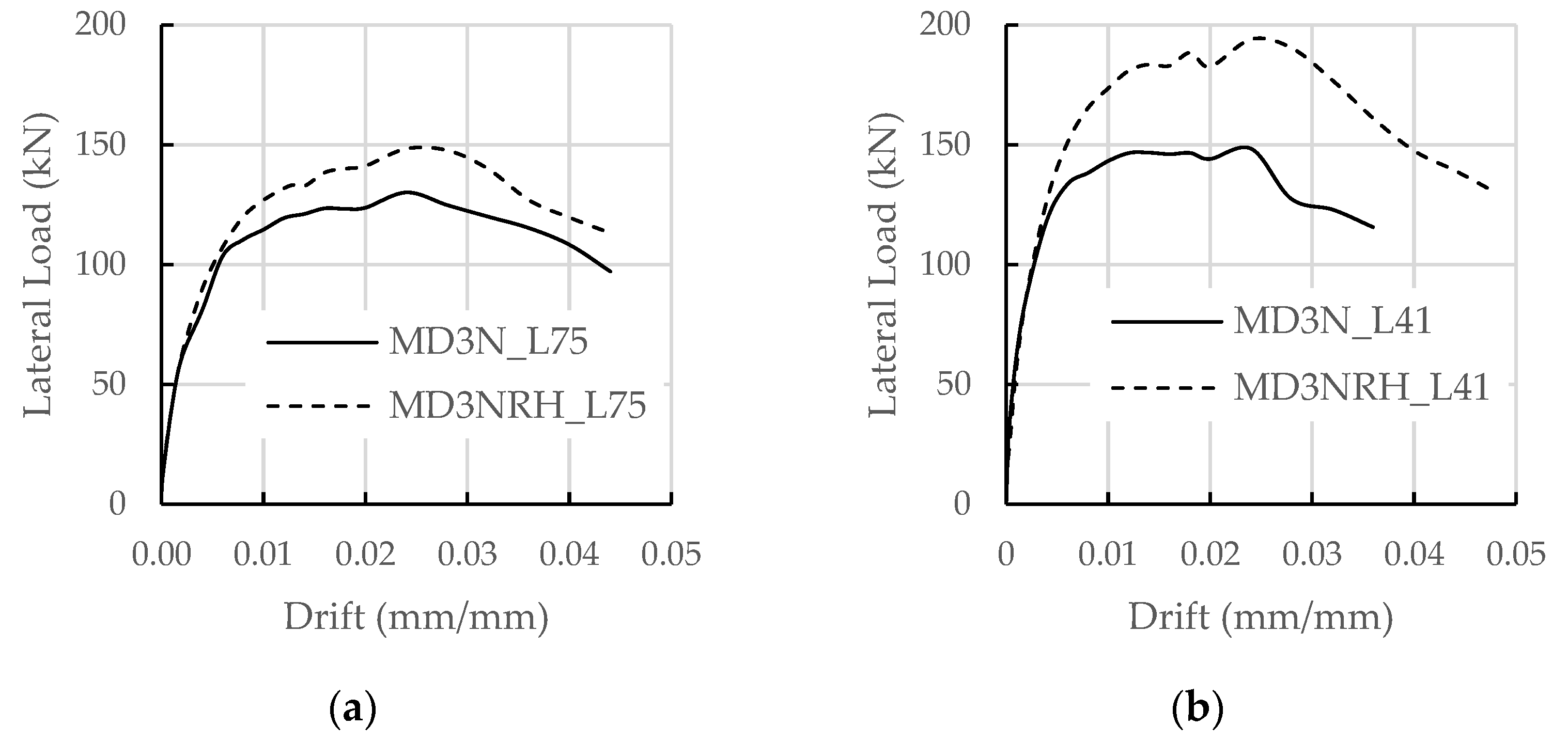
3.2. Envelope Curves
3.2.1. Cracking Strength
3.2.2. Yielding Strength
3.2.3. Peak Strength
3.2.4. Failure
3.2.5. Displacement Capacity and Ductility
3.3. Contribution of Joint Reinforcement and Infilled Frame to Lateral Load
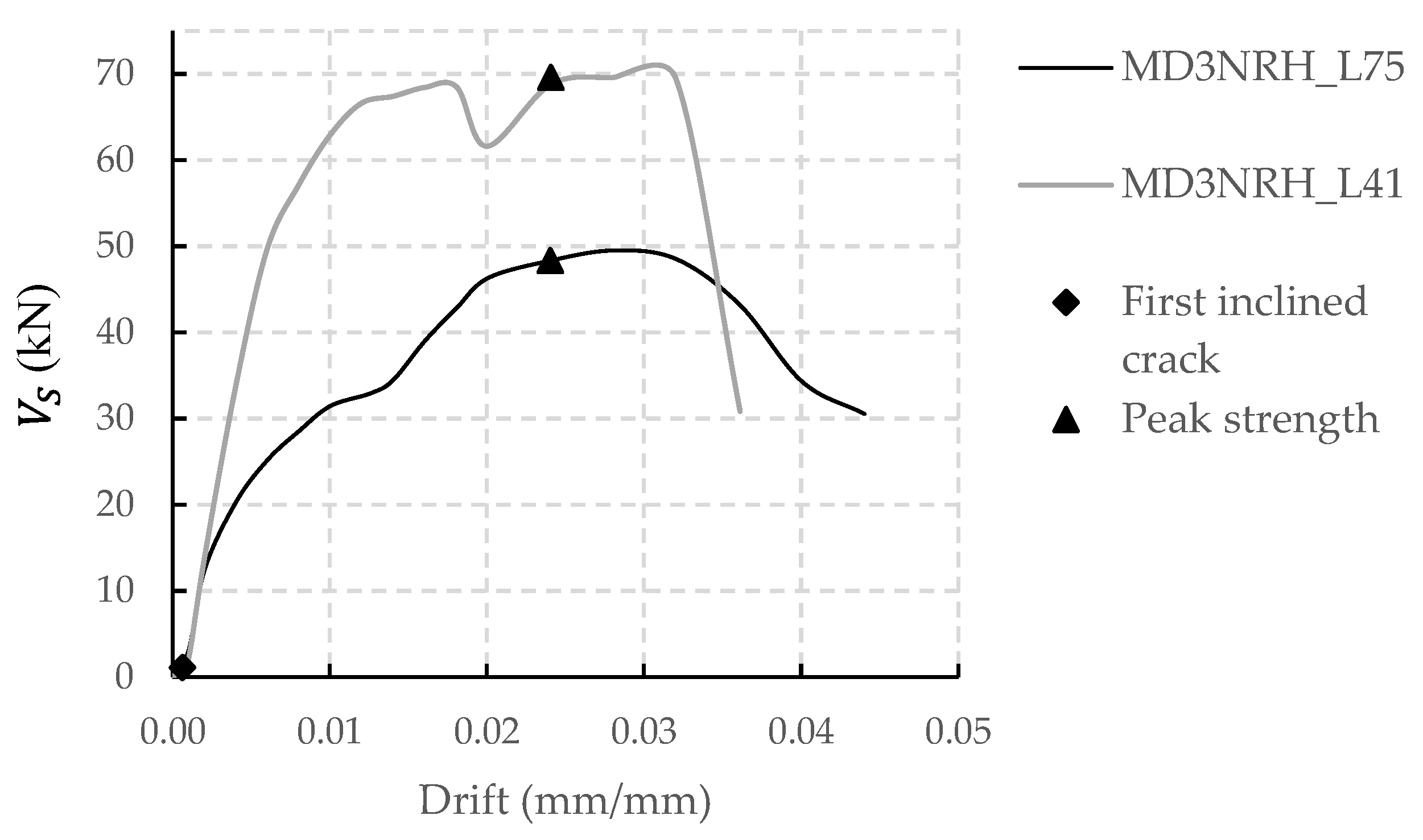
3.3.1. Contribution of the Joint Reinforcement
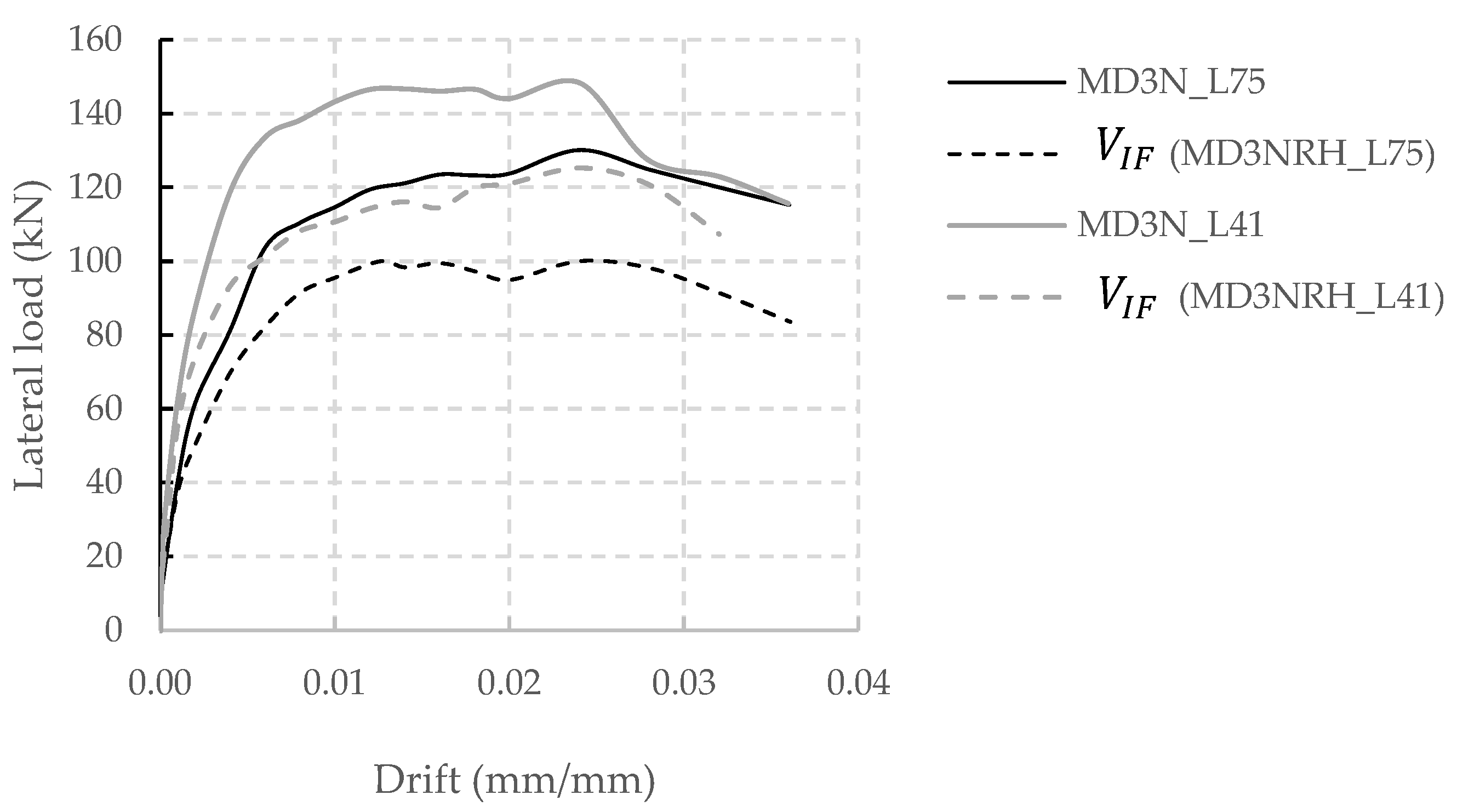
3.3.2. Contribution of Infilled Frame
4. Discussion
4.1. Cracking
4.2. Strength
4.3. Capacity of Deformation and Ductility
5. Conclusions
- (1)
- As occurs in confined walls, the joint reinforcement produces a more distributed cracking and a reduction of the cracking wide. In addition, the joint reinforcement had no effect on the initial lateral stiffness;
- (2)
- The joint reinforcement consistently increases the lateral strength of the system. However, this increase depends on the size of the wall as considered by the Mexican Code;
- (3)
- The joint reinforcement had no significant effect on the displacement capacity of the system. This result does not depend on the aspect ratio of the wall;
- (4)
- Ductility of the system is reduced with the use of joint reinforcement due to the fact that the drift at yielding of the elastoplastic model () increases with the reinforcement;
- (5)
- Sliding failure occurred after the inclined cracking. Consequently, the joint reinforcement is active, even if sliding is the dominant failure mode. A larger aspect ratio produces a greater inclined cracking;
- (6)
- The Mexican Code overestimates the join reinforcement contribution to shear strength of infill walls. For walls with H/L = 0.75 and 0.41, the prediction of the code was 2.07 and 1.49 times, respectively, larger than that of experimental results;
- (7)
- Results show that the estimation of the contribution of joint reinforcement to the shear strength in multiple panel infill walls is consistent with the current practice where the reinforcement in each panel is considered, although no previous evidence have been provided.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marques, R.; Lourenço, P.B. Structural behavior and design rules of confined masonry walls: Review and proposals. Constr. Build. Mater. 2019, 217, 137–155. [Google Scholar] [CrossRef]
- NTCM. Normas Técnicas Complementarias para el Diseño y Construcción de Estructuras de Mampostería del Gobierno de la Ciudad de México; Gaceta Oficial de la Ciudad de México: Ciudad de México, Mexico, 2017. (In Spanish) [Google Scholar]
- Leal, G.J.M.; Pérez Gavilán, J.J.; Castorena, G.J.H.; Velázquez, D.J.I. Infill walls with confining elements and horizontal reinforcement: An experimental study. Eng. Struct. 2017, 150, 153–165. [Google Scholar] [CrossRef]
- Meli, R.; Brzev, S.; Astroza, M.; Beon, T.; Crisafulli, F.J.; Farsi, M.; Hart, T.; Mebarki, A.; Moghadam, A.; Quiun, D.; et al. Seismic Design Guide for Low-Rise Confined Masonry Buildings; EERI Confined Masonry Network: Oakland, CA, USA, 2011. [Google Scholar]
- Pérez Gavilán, J.J.; Flores, L.E.; Alcocer, S.M. An experimental study of confined masonry walls with varying aspect ratio. Earthq. Spectra 2015, 31, 945–968. [Google Scholar] [CrossRef]
- Cruz, O.A.I.; Perez Gavilan, J.J.; Flores, C.L. Experimental study of in-plane shear strength of confined concrete masonry walls with joint reinforcement. Eng. Struct. 2019, 182, 213–226. [Google Scholar] [CrossRef]
- Polyakov. Masonry in Framed Buildings (Godsudarstvenoe Isdatel’stvo Literatury Po Stroidal Stvui Architecture. Moscow, 1956); Cairns, G.L., Ed.; National Lending Library for Science and Technology: Boston, MA, USA, 1956. [Google Scholar]
- Holmes, M. Steel frames with brickwork and concrete infilling. Proc. Inst. Civ. Eng. 1961, 19, 473–478. [Google Scholar] [CrossRef]
- Stafford-Smith, B. Lateral stiffness of infilled frames. ASCE J. Struct. Div. 1962, 88, 183–199. [Google Scholar] [CrossRef]
- Stafford-Smith, B. Behavior of square infilled frames. ASCE J. Struct. Div. 1966, 92, 381–403. [Google Scholar] [CrossRef]
- Stafford-Smith, B. Methods for predicting the lateral stiffness and strength of multi-storey infilled frames. Build. Sci. 1967, 2, 247–257. [Google Scholar] [CrossRef]
- Stafford-Smith, B.; Carter, C. A method of analysis for infilled frames. Proc. Inst. Civ. Eng. 1969, 44, 31–48. [Google Scholar] [CrossRef]
- Mainstone, R.J. Supplementary Note on the Stiffness and Strengths of Infilled Frames; Building Research Station: Garston, UK, 1974. [Google Scholar]
- Bazán, Z.T.E. Muros de Mampostería ante Cargas Laterales. Ph.D. Thesis, National Autonomous University of Mexico, Ciudad de México, Mexico, 1980. [Google Scholar]
- Flanagan, R.D.; Bennett, R.M. In plane analysis of masonry infills material. J. Struc. Eng. 1990, 125, 590–599. [Google Scholar] [CrossRef]
- Crisafulli, F.J. Seismic Behavior of Reinforced Concrete Structures with Masonry Infills. Ph.D. Thesis, University of Carterbury, Christchurch, New Zealand, 1997. [Google Scholar]
- Aguilar, G.; Alcocer, S.M. Efecto del Refuerzo Horizontal en el Comportamiento de Muros de Mampostería Confinada ante Cargas Laterales; Universidad Nacional Autónoma de México: Mexico City, Mexico, 2001. (In Spanish) [Google Scholar]
- Pineda, C.J.; Alcocer, S.M. Comportamiento Ante Cargas Laterales de Muros de Mampostería Confinada Reforzada con Malla Electrosoldada; Technical Report; Centro Nacional de Prevención de Desastres (CENAPRED): Ciudad de México, Mexico, 2004. (In Spanish) [Google Scholar]
- Alcocer, S.M.; Zepeda, J.A. Behavior of multi-perforated clay brick walls under earthquake-type loading. In Proceedings of the 8th North American Masonry Conference, Austin, TX, USA, 6–9 June 1999. [Google Scholar]
- NTCM. Normas Técnicas Complementarias para Diseño y Construcción de Estructuras de Mampostería; Gaceta Oficial del Distrito Federal: Ciudad de México, Mexico, 2004. (In Spanish) [Google Scholar]
- Rubio, P.L. Contribución del Refuerzo Horizontal a la Resistencia a Corte de Muros Confinados de Piezas de Arcilla Extruida. Master’s Thesis, National Autonomous University of Mexico, Ciudad de México, Mexico, 2017. (In Spanish). [Google Scholar]
- Davis, C.L. Evaluation of Design Provisions for In-Plane Shear in Masonry Walls. Master’s Thesis, Washington State University, Washington, DC, USA, 2008. [Google Scholar]
- Aguilar, G.; Meli, R.; Díaz, R.; del Mercado, A.R.V. Influence of horizontal reinforcement on the behavior of confined masonry walls. In Proceedings of the 11th World Conference Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. [Google Scholar]
- Cruz, O.A.I.; Perez Gavilan, J.J. Seismic performance of confined masonry walls with joint reinforcement and aspect ratio: An experimental study. Eng. Struct. 2021, 242, 112484. [Google Scholar] [CrossRef]
- ASCE/SEI 41-13. Seismic Evaluation and Retrofit of Existing Buildings; ASCE: Reston, VA, USA, 2014. [Google Scholar]
- Simo, J.C.; Hughes, T.J.R. Motivation. One-dimensional plasticity and viscoplasticity. In Computational Inelasticity; Marsden, J.E., Sirovich, L., Wiggins, S., Eds.; Springer: New York, NY, USA, 1997; Volume 7, pp. 1–70. [Google Scholar]
- Anderson, D.; Priestley, M. In Plane Shear Strength of Masonry Walls. In Proceedings of the 6th Canadian Masonry Symposium, Sasketoon, SK, Canada, 15–17 June 1992. [Google Scholar]





| Pairs | Specimens | Joint Reinforcement | H/L of the Infill Wall |
|---|---|---|---|
| 1 | MD3N_L75 | - | 0.75 |
| MD3NRH_L75 | 0.6 MPa | 0.75 | |
| 2 | MD3N_L41 + | - | 0.41 |
| MD3NRH_L41 + | 0.6 MPa | 0.41 |
| Specimens | Units | Mortar | Concrete of Frame | Concrete of Tie-Elements | Masonry | ||||
|---|---|---|---|---|---|---|---|---|---|
| MD3N_L75 | 9.36 | 12.80 | 32.51 | 24773 | 22.62 | 21998 | 1.6 | 0.29 | - |
| MD3NRH_L75 | 9.36 | 12.80 | 32.51 | 24773 | 22.62 | 21998 | 1.6 | 0.29 | - |
| MD3N_L41 | 9.36 | 15.01 | 19.03 | 19490 | 15.07 | 17220 | 3.40 | 0.53 | 703 |
| MD3NRH_L41 | 9.36 | 8.01 | 19.95 | 19719 | 13.30 | 15661 | 3.34 | 0.59 | 693 |
| Specimen | Cycle of First Cracking | Cycle of Peak Strength | Cycle of Failure | |||
|---|---|---|---|---|---|---|
| MD3N_L75 | 0.00042 | 0.906 | 0.0064 | 0.908 | 0.0160 | 0.963 |
| MD3NRH_L75 | 0.00045 | 0.928 | 0.0054 | 0.907 | 0.0153 | 0.907 |
| MD3N_L41 | 0.00092 | 0.891 | 0.0091 | 0.747 | 0.0154 | 0.925 |
| MD3NRH_L41 | 0.00097 | 0.913 | 0.0071 | 0.881 | 0.0149 | 0.882 |
| Specimen | |||||||
|---|---|---|---|---|---|---|---|
| MD3N_L75 | 118.9 | 28.8 | 103.7 | 130.1 | 104.1 | 3.60 | 1.26 |
| MD3NRH_L75 | 135.0 | 31.5 | 120.1 | 148.3 | 118.7 | 3.81 | 1.24 |
| MD3N_L41 | 137.1 | 76.9 | 119.4 | 148.2 | 118.6 | 1.55 | 1.24 |
| MD3NRH_L41 | 178.4 | 68.6 | 150.9 | 194.0 | 155.2 | 2.20 | 1.29 |
| Specimen | |||||||
|---|---|---|---|---|---|---|---|
| MD3N_L75 | 0.0050 | 0.0006 | 0.006 | 0.024 | 0.042 | 4.8 | 8.3 |
| MD3NRH_L75 | 0.0057 | 0.0006 | 0.008 | 0.024 | 0.041 | 4.2 | 7.2 |
| MD3N_L41 | 0.0030 | 0.0014 | 0.004 | 0.024 | 0.034 | 8.0 | 11.4 |
| MD3NRH_L41 | 0.0050 | 0.0014 | 0.006 | 0.024 | 0.038 | 4.8 | 7.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leal-Graciano, J.M.; Pérez-Gavilán, J.J.; Reyes-Salazar, A.; Valenzuela-Beltrán, F.; Bojórquez, E.; Bojórquez, J. Experimental Study of Infill Walls with Joint Reinforcement Subjected to In-Plane Lateral Load. Buildings 2022, 12, 259. https://doi.org/10.3390/buildings12030259
Leal-Graciano JM, Pérez-Gavilán JJ, Reyes-Salazar A, Valenzuela-Beltrán F, Bojórquez E, Bojórquez J. Experimental Study of Infill Walls with Joint Reinforcement Subjected to In-Plane Lateral Load. Buildings. 2022; 12(3):259. https://doi.org/10.3390/buildings12030259
Chicago/Turabian StyleLeal-Graciano, Jesús Martin, Juan J. Pérez-Gavilán, Alfredo Reyes-Salazar, Federico Valenzuela-Beltrán, Edén Bojórquez, and Juan Bojórquez. 2022. "Experimental Study of Infill Walls with Joint Reinforcement Subjected to In-Plane Lateral Load" Buildings 12, no. 3: 259. https://doi.org/10.3390/buildings12030259
APA StyleLeal-Graciano, J. M., Pérez-Gavilán, J. J., Reyes-Salazar, A., Valenzuela-Beltrán, F., Bojórquez, E., & Bojórquez, J. (2022). Experimental Study of Infill Walls with Joint Reinforcement Subjected to In-Plane Lateral Load. Buildings, 12(3), 259. https://doi.org/10.3390/buildings12030259








