Numerical Investigation of the Post-Fire Performance of Steel Columns
Abstract
:1. Introduction
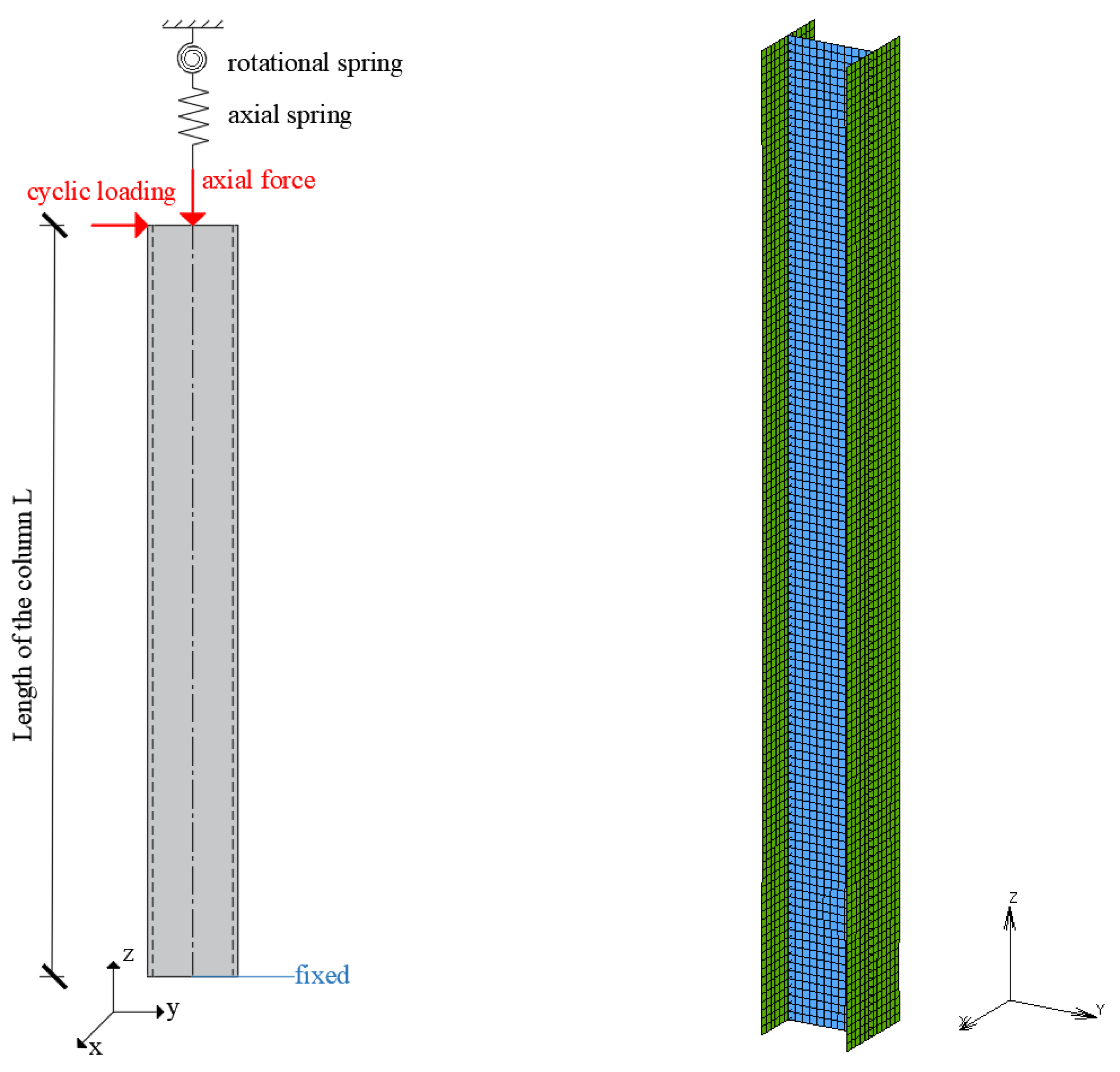
2. Computational Modelling
2.1. Numerical Models
2.2. Numerical Analyses
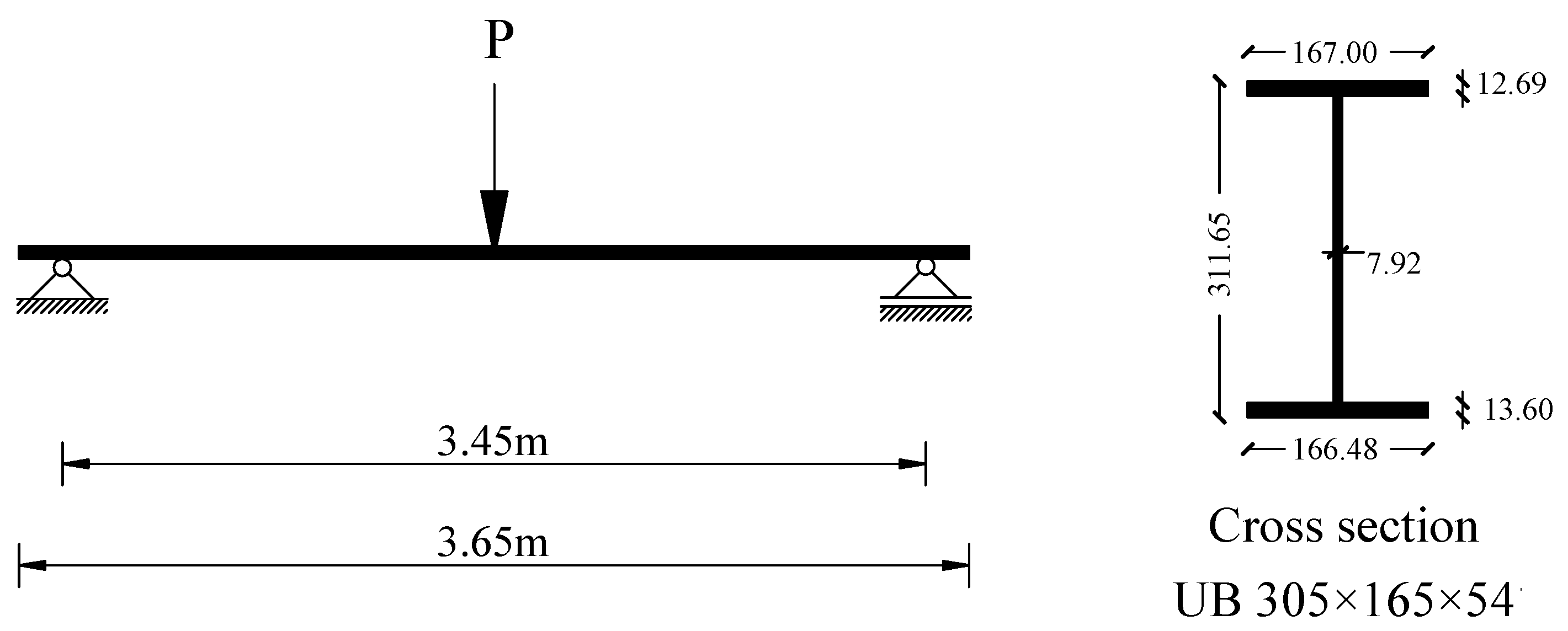
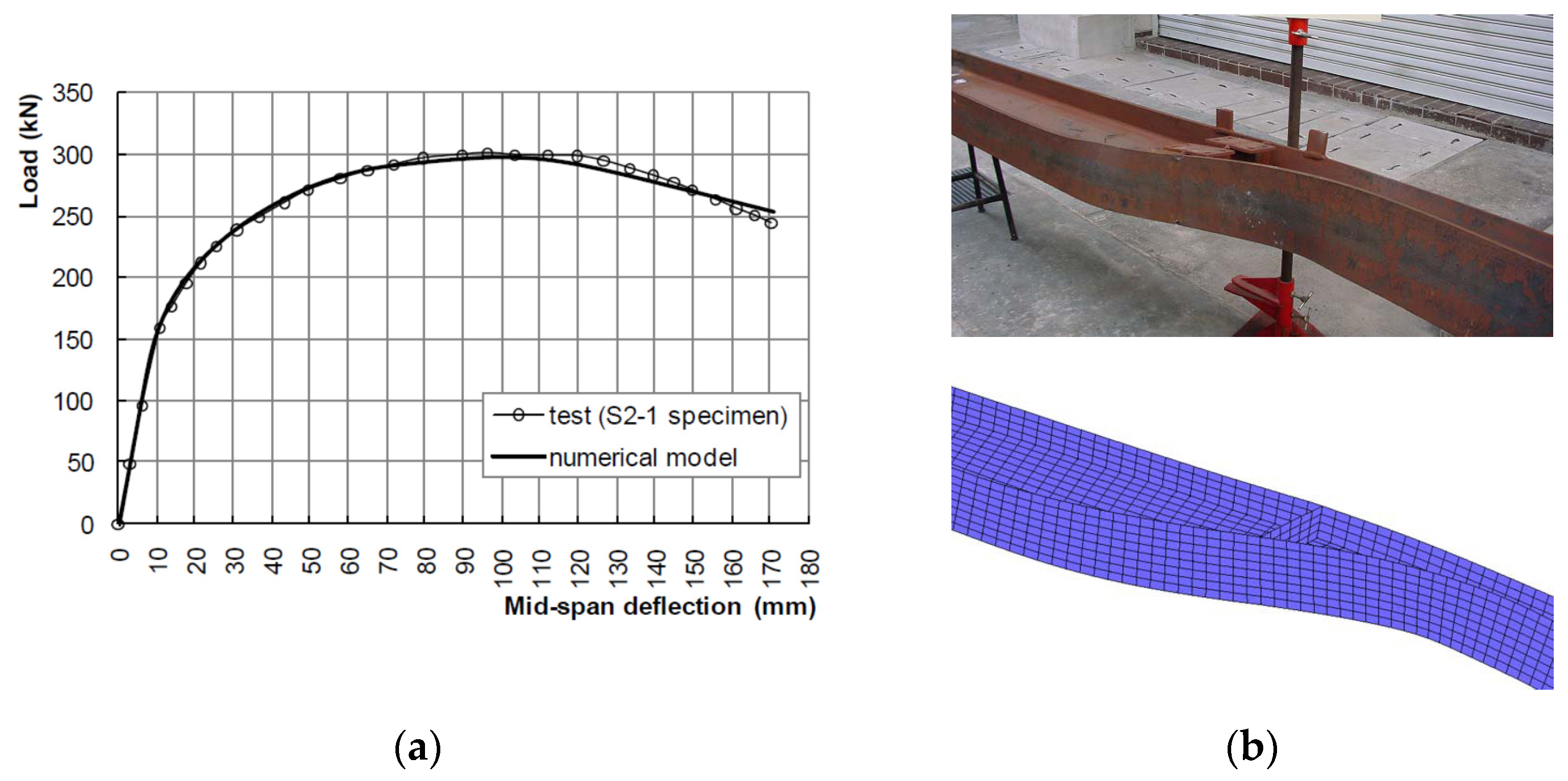
2.3. Finite Element Model Validation
3. Columns with Simplified Boundary Conditions
3.1. Behaviour during the Fire Stage
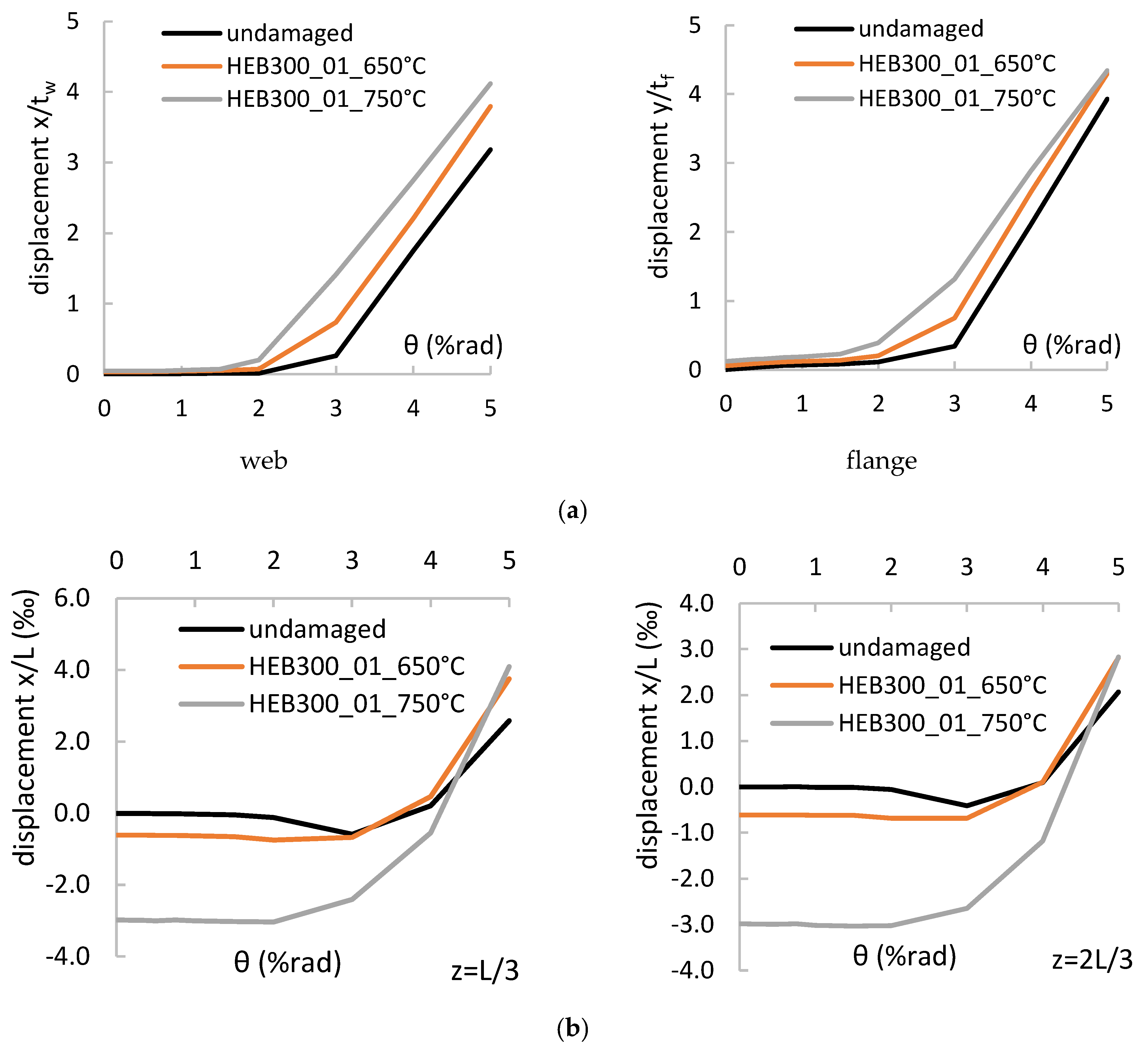
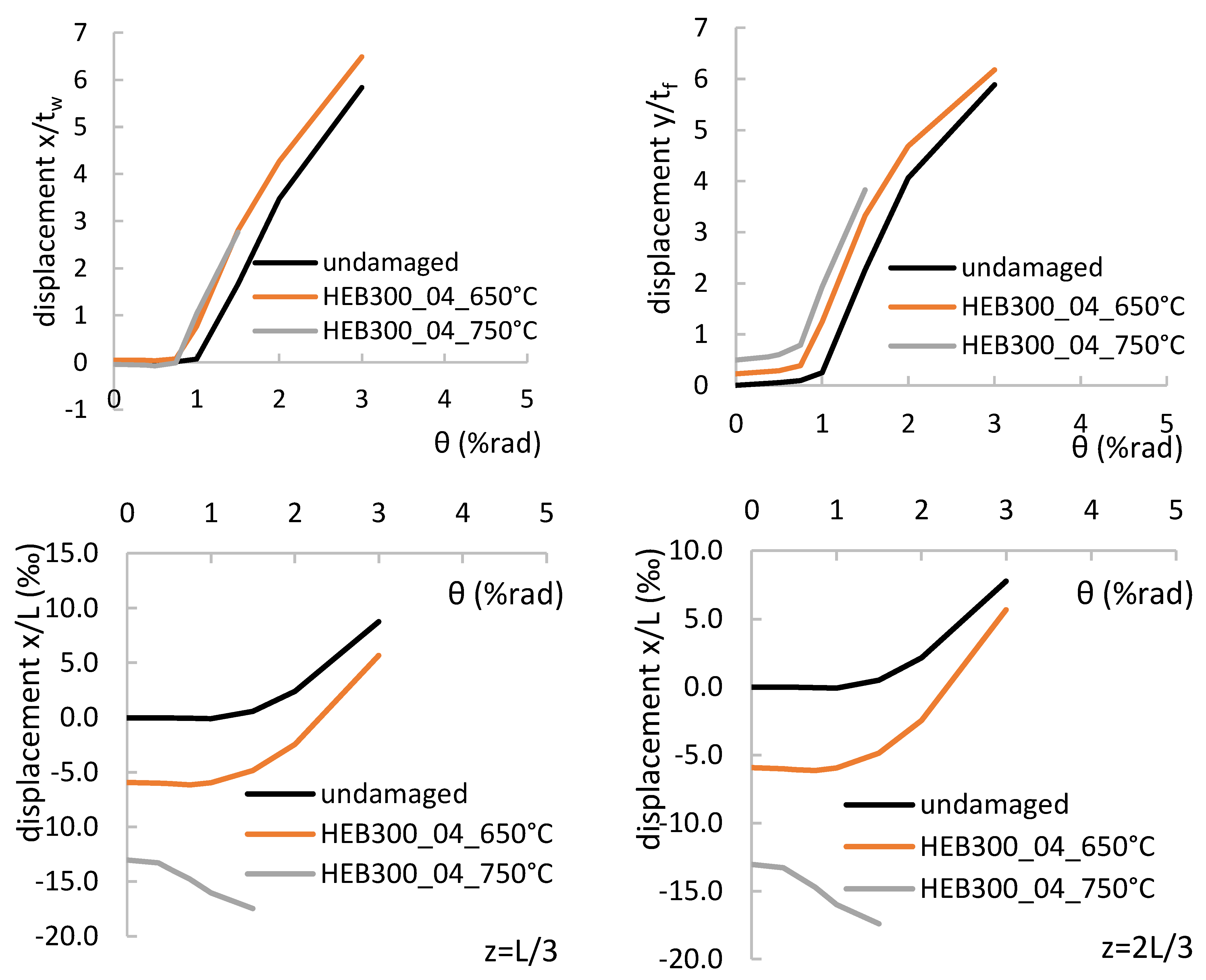
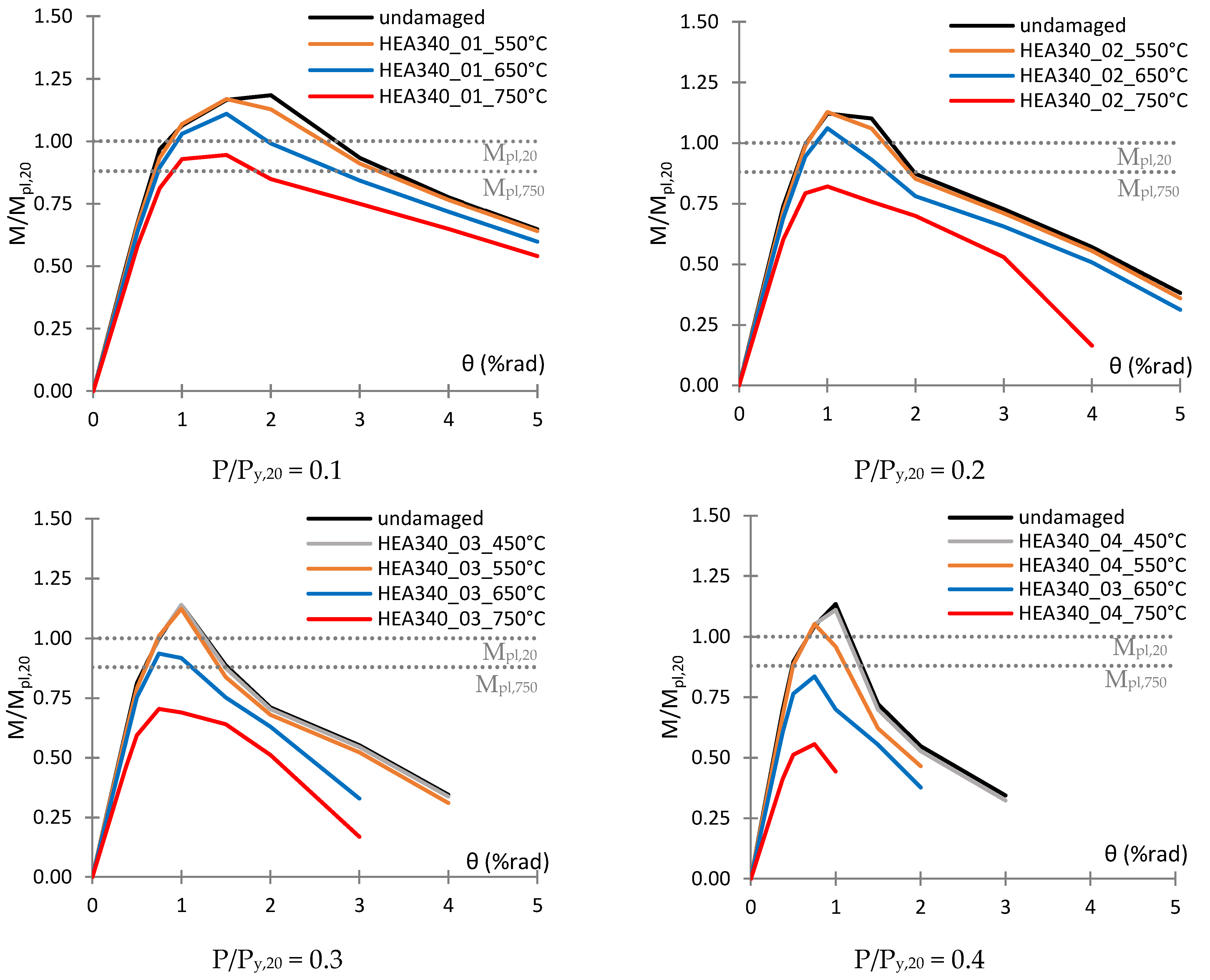
3.2. Behaviour during Cyclic Loading
4. Column with Realistic Boundary Conditions
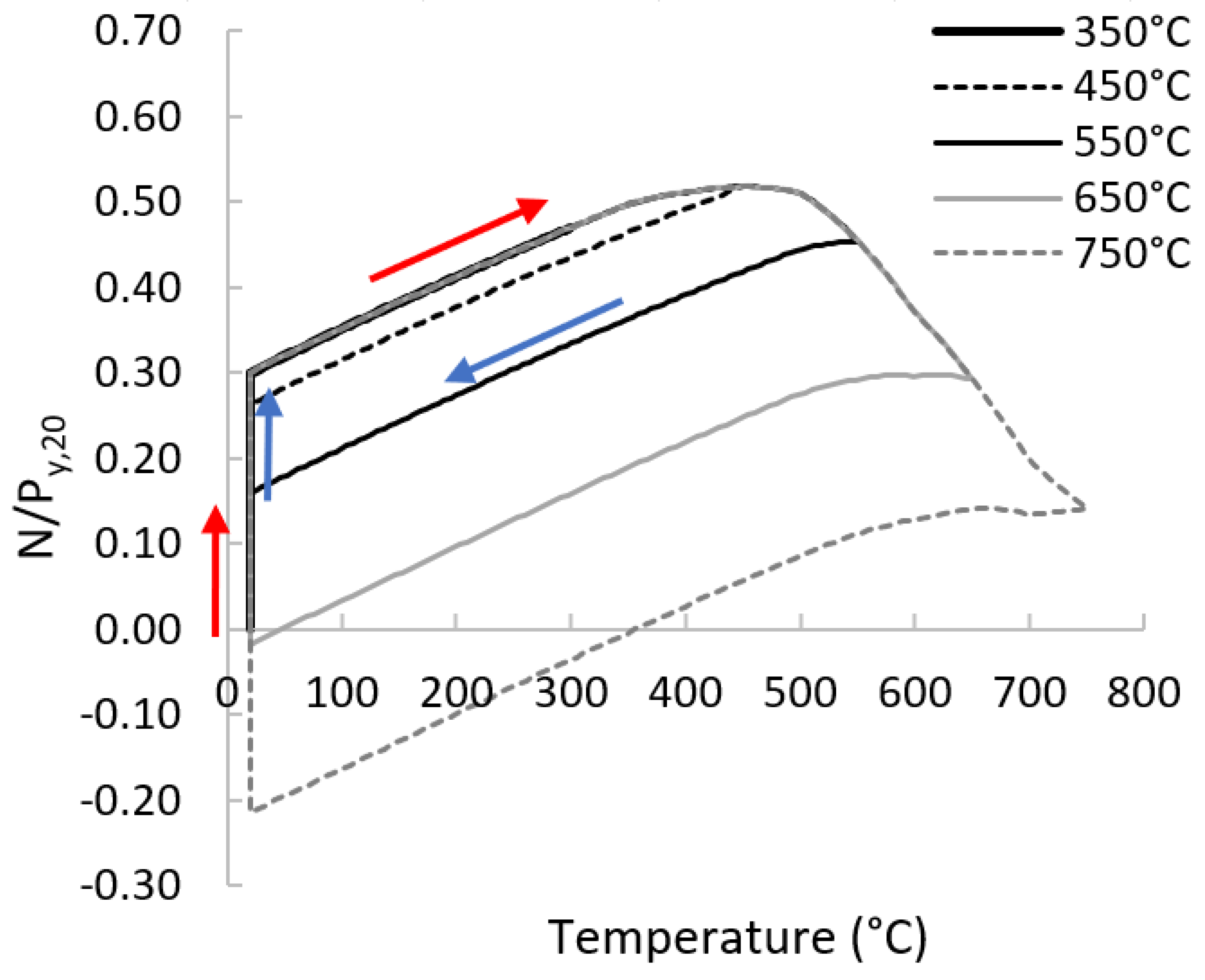
4.1. Behaviour during the Fire Stage
4.2. Behaviour during Cyclic Loading
5. Summary and Conclusions
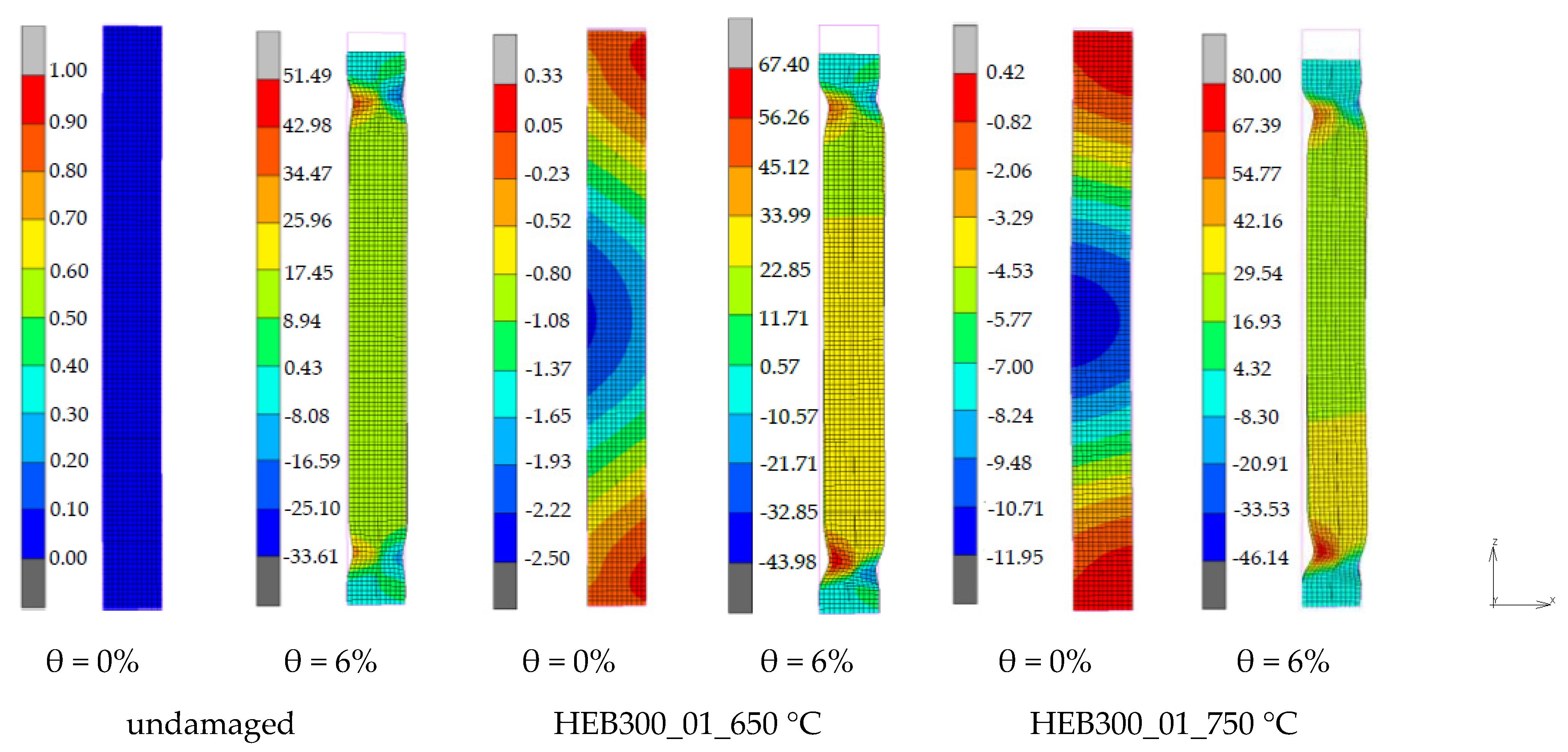
- At the end of the fire stage, global out-of-plane displacements are coupled with local buckling of web and flanges. Their magnitude escalates with the load level and the maximum recorded temperature.
- Slight residual local displacements (approximately 1 mm) did not affect the behaviour of the columns during the cyclic loading for maximum recorded temperatures less or equal to 550 °C.
- Larger amplitude of local out-of-pane displacements near their base may affect their cyclic behaviour by triggering premature local buckling phenomena and subsequent loss of the flexural capacity. This was more obvious as the load level increases and for temperature levels more than 550 °C.
- The global out-of-plane residual displacements (less than 1% L) did not affect the cyclic behaviour of the columns and did not activate any global instabilities.
- The failure of the columns was mainly attributed to the plastic hinge formulation and the local buckling mechanism which triggers global out-of-plane displacements.
- Another failure mode was also detected which couples local and global instabilities. For these columns, the maximum moment is less than the full plastic moment of the cross section, and the plastic hinges are not formed. Nevertheless, the excessive local buckling deformations trigger global instability about the weak axis.
- Only the heavily damaged columns (magnitude of global out-of-plane displacements more than 1% L) failed due to lateral buckling.
- During the cyclic loading, the flexural capacity of all the columns was reduced, mainly due to the deterioration of material properties.
- The rotation capacity of the damaged columns is reduced due to both the residual displacements and the deterioration of the mechanical properties.
- The flexural deterioration is detected earlier for the damaged columns, and this triggers earlier local buckling and subsequent flexural deterioration at the top end.
- Although the fire-damaged columns can survive at high temperatures (750 °C) without significant damage, their behaviour will be more vulnerable during an upcoming earthquake.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Karavasilis, T.; Bazeos, N.; Beskos, D. Maximum displacement profiles for the performance based seismic design of plane steel moment resisting frames. Eng. Struct. 2006, 28, 9–22. [Google Scholar] [CrossRef]
- Karavasilis, T.; Bazeos, N.; Beskos, D. A New Seismic Design Method for Steel Structures. Adv. Struct. 2010, 13, 161–171. [Google Scholar]
- Kariniotakis, K.; Karavasilis, T. Limits for the interstorey drift sensitivity coefficient θ of steel MRFs with viscous dampers designed according to Eurocode 8. Soil Dyn. Earthq. Eng. 2019, 117, 203–215. [Google Scholar] [CrossRef]
- Dimopoulos, A.; Karavasilis, T.; Vasdravellis, G.; Uy, B. Seismic design, modelling and assessment of self-centering steel frames using post-tensioned connections with web hourglass shape pins. Bull. Earthq. Eng. 2013, 11, 1797–1816. [Google Scholar] [CrossRef]
- Beer, Μ.; Kougioumtzoglou, Ι.A.; Patelli, Ε.; Au, S.-K. Encyclopedia of Earthquake Engineering; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Wang, Y.; Burgess, Ι.; Wald, F.; Gillie, M. Performance-Based Fire Engineering of Structures; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Franssen, J.-M.; Kodur, V.; Zaharia, R. Designing Steel Structures for Fire Safety; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Wang, Y.C. Steel and Composite Structures, Behaviour and Design for Fire Safety; Spon Press: London, UK, 2002. [Google Scholar]
- Porcari, G.F.; Zalok, E.; Mekky, W. Fire induced progressive collapse of steel building structures: A review of the mechanisms. Eng. Struct. 2015, 82, 261–267. [Google Scholar] [CrossRef]
- Wald, F.; da Silva, L.S.; Moore, D.B.; Lennon, T.; Chladná, M.; Santiago, A.; Beneš, M.; Borges, L. Experimental behaviour of a steel structure under natural fire. Fire Saf. J. 2006, 41, 509–522. [Google Scholar] [CrossRef]
- EN 1991-1-2; Eurocode 1: Actions on Structures Exposed to Fire—Part 1–2. General Actions—Structural Fire Design. European Committee for Standardization: Brussels, Belgium, 2002.
- EN 1993-1-2; Eurocode 3: Design of Steel Structures—Part 1–2. General Rules—Structural Fire Design. European Committee for Standardization: Brussels, Belgium, 2005.
- SCI. Structural Fire Engineering. In Investigation of Broadgate Phase 8 Fire; The Steel Construction Institute: Ascot, UK, 1991. [Google Scholar]
- Outinen, J.; Makelainen, P. Mechanical properties of structural steel at elevated temperatures and after cooling down. Fire Mater. 2004, 28, 237–251. [Google Scholar] [CrossRef]
- Tao, Z.; Wang, X.Q.; Uy, B. Stress-strain curves of structural and reinforcing steel after exposure to elevated temperatures. J. Mater. Civ. Eng. 2013, 9, 1306–1316. [Google Scholar] [CrossRef]
- Lee, J.; Engelhardt, M.D.; Taleff, E.M. Mechanical properties of ASTM A992 steel after fire. Eng. J. 2012, 49, 33–44. [Google Scholar]
- BS 5950-8; Structural Use of Steelwork in Building, Part 8: Code of Practice for Fire Resistant Design. BS Institution: London, UK, 2003.
- Li, G.Q.; Jiang, S.C.; Yin, Y.Z.; Chen, A.K.; Li, M.F. Experimental Studies on the Properties of Constructional Steel at Elevated Temperatures. J. Struct. Eng. 2003, 129, 1717–1721. [Google Scholar] [CrossRef]
- Kirby, B.R.; Preston, R.R. High temperature properties of hot-rolled, structural steels for use in fire engineering design studies. Fire Saf. J. 1988, 13, 27–37. [Google Scholar] [CrossRef]
- Maraveas, C.; Fasoulakis, Z.; Tsavdaridis, K.D. Post-fire assessment and reinstatement of steel structures. J. Struct. Fire Eng. 2017, 8, 181–201. [Google Scholar] [CrossRef]
- Tide, R.H. Integrity of structural steel after exposure to fire. Eng. J. AISC 1998, 35, 26–38. [Google Scholar]
- Smith, C.I.; Kirby, B.R.; Lapwood, D.G.; Cole, K.J.; Cunningham, A.P.; Preston, R.R. The reinstatement of fire damaged steel framed structures. Fire Saf. J. 1981, 4, 21–62. [Google Scholar] [CrossRef]
- Kirby, B.R.; Lapwood, D.G.; Thompson, G. The Reinstatement of Fire Damaged Steel and Iron Framed Structures; British Steel Corporation Swinden Laboratories: Rotherham, UK, 1986. [Google Scholar]
- Lou, G.B.; Zhu, M.C.; Li, M.; Zhang, C.; Li, G.Q. Experimental research on slip-resistant bolted connections after fire. J. Constr. Steel Res. 2015, 104, 1–8. [Google Scholar] [CrossRef]
- Yu, L. Behavior of Bolted Connections during and after a Fire. Ph.D. Thesis, University of Texas, Austin, TX, USA, 2006. [Google Scholar]
- Liu, H.; Tan, Z.; Chen, Z.; Liu, Z.; Liu, D. Experimental Study on Residual Mechanical Properties of Bolt-Sphere Joints After a Fire. Int. J. Steel Struct. 2018, 18, 802–820. [Google Scholar] [CrossRef]
- Liu, H.; Liu, D.; Chen, Z.; Yu, Y. Post-fire residual slip resistance and shear capacity of high-strength bolted connection. J. Constr. Steel Res. 2017, 138, 65–71. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, M.-C.; Kodur, V.; Li, G.-Q. Behavior of welded connections after exposure to elevated temperature. J. Constr. Steel Res. 2017, 130, 88–95. [Google Scholar] [CrossRef]
- Liu, H.; Liao, X.; Chen, Z.; Huang, S.-S. Post-fire residual mechanical properties of steel butt weld—Experimental study. J. Constr. Steel Res. 2017, 129, 156–162. [Google Scholar] [CrossRef]
- Zhu, M.-C.; Li, G.-Q. Behavior of beam-to-column welded connections in steel structures after fire. Procedia Eng. 2017, 210, 551–556. [Google Scholar] [CrossRef]
- Rodrigues, D.M.; Leitão, C.; Balakrishnan, M.; Craveiro, H.D.; Santiago, A. Tensile properties of S355 butt welds after exposure to high temperatures. Constr. Build. Mater. 2021, 302, 124374. [Google Scholar] [CrossRef]
- Sagiroglu, M. Experimental evaluation of the post-fire behavior of steel T-component in the beam-to-column connection. Fire Saf. J. 2018, 96, 153–164. [Google Scholar] [CrossRef]
- Molkens, T.; Rossi, B. Reliability-based structural response of single-bay steel frames in case of fire and in post-fire conditions. Struct. Saf. 2021, 93, 102132. [Google Scholar] [CrossRef]
- He, K.; Chen, Y.; Han, S. Experimental investigation of square stainless steel tubular stub columns after elevated temperatures. J. Constr. Steel Res. 2019, 159, 397–414. [Google Scholar] [CrossRef]
- EN 1998-1-1; Eurocode 8: Design of Structures for Earthquake Resistance—Part 1. General Rules Seismic Actions and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- Quayyum, S.; Hassan, T. Seismic Performance of a Fire-Exposed Moment-Resisting Frame. J. Struct. Eng. 2018, 144, 04018206. [Google Scholar] [CrossRef]
- MSC Software Corp. MSC MARC v. 2018, Theory and User Information; MSC Software Corp.: Santa Ana, CA, USA, 2018. [Google Scholar]
- Shepherd, P.G.; Burgess, I.W. On the buckling of axially restrained steel columns in fire. Eng. Struct. 2011, 33, 2832–2838. [Google Scholar] [CrossRef] [Green Version]
- Tan, K.H.; Yuan, W.F. Buckling of elastically restrained steel columns under longitudinal non-uniform temperature distribution. J. Constr. Steel Res. 2008, 64, 51–61. [Google Scholar]
- Pournaghshband, A.; Afshan, S.; Foster, A.S.J. Structural fire performance of axially and rotationally restrained stainless steel columns. Thin Walled Struct. 2019, 137, 561–572. [Google Scholar] [CrossRef]
- EN 10025–2:2019; Hot Rolled Products of Structural Steels, Technical Delivery Conditions for Non-Alloy Structural Steels. European Committee for Standardization: Brussels, Belgium, 2019.
- Von Mises, R. Mechanik der festen Körper im plastischdeformablen Zustand. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen. Math. Phys. Kl. 1913, 1, 582–592. [Google Scholar]
- Lemaitre, J.; Chaboche, J.L. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Mohabeddine, A.; Koudri, Y.W.; Correia, J.A.F.O.; Castro, J.M. Rotation capacity of steel members for the seismic assessment of steel buildings. Eng. Struct. 2021, 244, 112760. [Google Scholar] [CrossRef]
- Elkady, A.; Lignos, D. Improved Seismic Design and Nonlinear Modeling Recommendations for Wide-Flange Steel Columns. J. Struct. Eng. 2018, 144, 04018162. [Google Scholar] [CrossRef]
- Dharma, R.; Tan, K.H. Rotational capacity of steel I-beams under fire conditions Part I: Experimental study. Eng. Struct. 2007, 29, 2391–2402. [Google Scholar] [CrossRef]
- Poh, K.W. Stress-strain temperature relationship for structural steel. J. Mater. Civil Eng. 2001, 13, 371–379. [Google Scholar] [CrossRef]
- Kodur, V.; Dwaikat, M. Response of steel beam-columns exposed to fire. Eng. Struct. 2009, 31, 369–379. [Google Scholar] [CrossRef]
- Pantousa, D.; Karavasilis, T. Numerical Assessment of the Fire Behavior of Steel Posttensioned Moment-Resisting Frames. J. Struct. Eng. 2020, 146, 04020032. [Google Scholar] [CrossRef]
- EN 1990; Basis of Structural Design. European Committee for Standardization: Brussels, Belgium, 2002.
- Cadorin, J.; Franssen, J. A tool to design steel elements submitted to compartment fires—Ozone v2. Part 1: Pre-and post-flashover compartment fire model. Fire Saf. J. 2003, 38, 395–427. [Google Scholar] [CrossRef]















| Case Study | Cross Section | Length (m) | b/2tf | h/tw | P/Py,20 | Class at Room Temp. | Class at High Temp. | aA | aR | Maximum Temperature (°C) |
|---|---|---|---|---|---|---|---|---|---|---|
| HEB300_01_Tmax | HEB300 | 4000 | 7.9 | 24 | 0.1 | 1 | 1 | 0.1 | fixed | 350–750 |
| HEB300_02_Tmax | 0.2 | 1 | 1 | 0.1 | fixed | 350–750 | ||||
| HEB300_03_Tmax | 0.3 | 1 | 1 | 0.1 | fixed | 350–750 | ||||
| HEB300_04_Tmax | 0.4 | 1 | 1 | 0.1 | fixed | 350–750 | ||||
| HEA340_01_Tmax | HEA340 | 4000 | 9.1 | 31 | 0.1 | 1 | 3 | 0.1 | fixed | 350–750 |
| HEA340_02_Tmax | 0.2 | 1 | 3 | 0.1 | fixed | 350–750 | ||||
| HEA340_03_Tmax | 0.3 | 1 | 3 | 0.1 | fixed | 350–750 | ||||
| HEA340_04_Tmax | 0.4 | 1 | 3 | 0.1 | fixed | 350–750 |
| Cross Section | Load Level | Maximum Temperature during Heating | Tcr (°C) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 450 °C | 550 °C | 650 °C | 750 °C | |||||||||||
| Global | Web | Flange | Global | Web | Flange | Global | Web | Flange | Global | Web | Flange | |||
| HEB300 | 0.1 | 0.0 | 0.4 | 0.1 | 0.2 | 2.2 | 0.3 | 1.0 | 11.3 | 0.4 | 2.2 | 509 | ||
| 0.2 | 1.0 | 0.2 | 0.6 | 5.4 | 0.3 | 1.7 | 21.1 | 1.4 | 3.8 | 493 | ||||
| 0.3 | 0.5 | 0.2 | 0.3 | 2.0 | 0.3 | 0.9 | 12.3 | 0.4 | 2.2 | 31.6 | 3.0 | 6.0 | 447 | |
| 0.4 | 0.9 | 0.2 | 0.5 | 4.5 | 0.4 | 1.4 | 22.7 | 1.5 | 3.8 | 39.9 | 5.7 | 8.3 | 375 | |
| HEA340 | 0.1 | 0.0 | 0.4 | 0.2 | 0.2 | 2.3 | 1.2 | 1.2 | 10.8 | 4.9 | 4.1 | 509 | ||
| 0.2 | 1.0 | 0.4 | 0.5 | 5.7 | 2.4 | 2.1 | 19.0 | 10.0 | 12.5 | 492 | ||||
| 0.3 | 0.5 | 0.2 | 0.3 | 2.1 | 0.9 | 1.1 | 12.2 | 4.7 | 4.0 | 41.6 | 10.4 | 16.4 | 446 | |
| 0.4 | 0.9 | 0.4 | 0.6 | 4.9 | 1.7 | 1.8 | 25.6 | 8.6 | 10.9 | 55.3 | 12.4 | 22.4 | 375 | |
| Loading Level | Undamaged | 450 °C | 550 °C | 650 °C | 750 °C | |
|---|---|---|---|---|---|---|
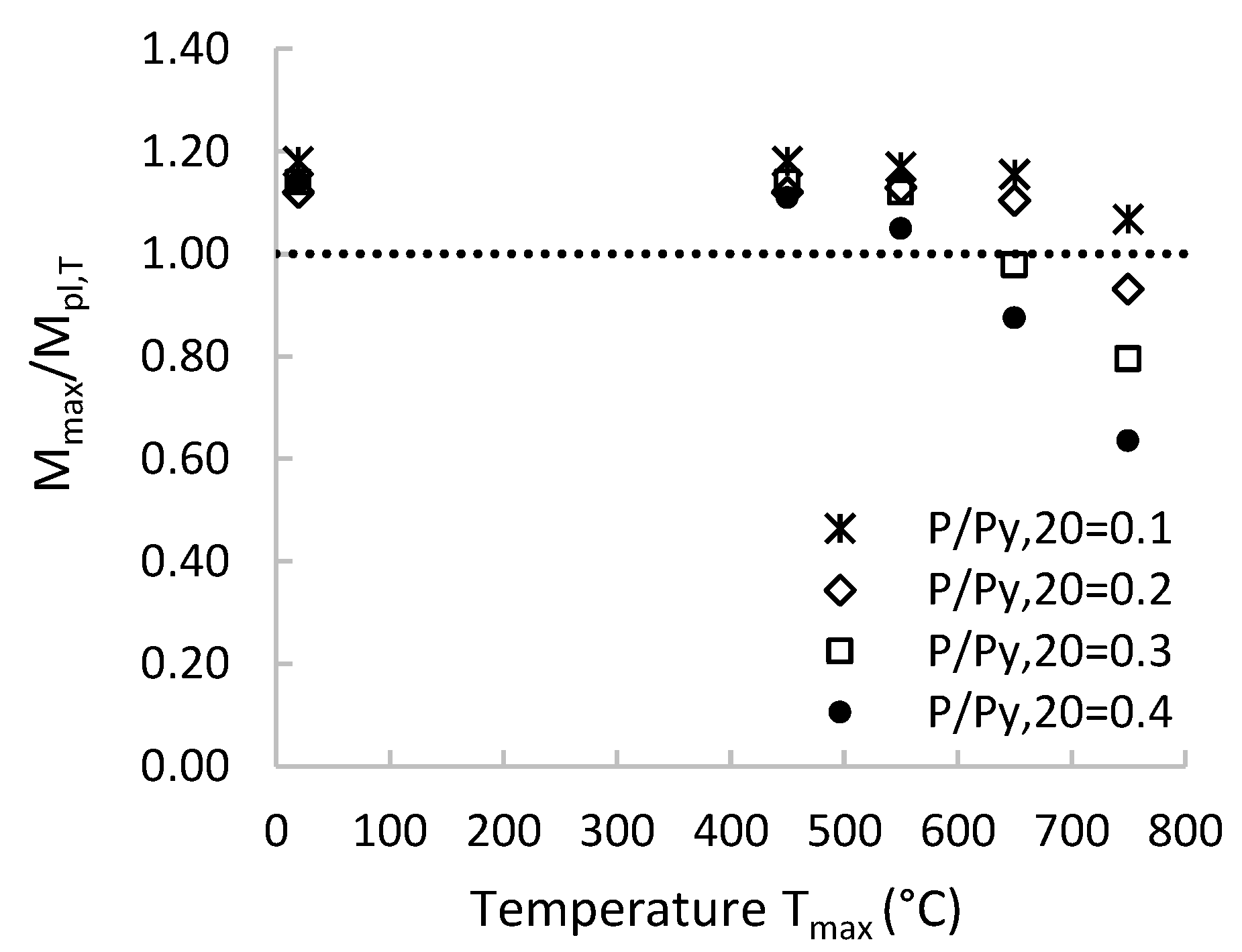
| overstrength factor Mmax/Mpl, 20 | P/Py,20 = 0.1 | 1.29 | 1.29 | 1.28 | 1.19 | 1.08 |
| P/Py,20 = 0.2 | 1.28 | 1.28 | 1.25 | 1.19 | 1.01 | |
| P/Py,20 = 0.3 | 1.26 | 1.24 | 1.20 | 1.09 | 0.93 | |
| P/Py,20 = 0.4 | 1.23 | 1.23 | 1.23 | 1.06 | 0.81 | |
| θMmax | P/Py,20 = 0.1 | 3.0 | 3.0 | 3.0 | 2.0 | 2.0 |
| P/Py,20 = 0.2 | 2.0 | 2.0 | 1.5 | 1.5 | 1.5 | |
| P/Py,20 = 0.3 | 1.5 | 1.5 | 1.5 | 1.0 | 1.0 | |
| P/Py,20 = 0.4 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| Rotation capacity | P/Py,20 = 0.1 | 4.40 | 4.40 | 4.33 | 3.96 | 3.09 |
| P/Py,20 = 0.2 | 3.07 | 3.07 | 3.15 | 2.51 | 1.56 | |
| P/Py,20 = 0.3 | 2.04 | 1.98 | 1.94 | 1.56 | 0.00 | |
| P/Py,20 = 0.4 | 1.71 | 1.64 | 1.53 | 1.15 | 0.00 |
| Loading Level | Undamaged | 450 °C | 550 °C | 650 °C | 750 °C | |
|---|---|---|---|---|---|---|
| overstrength factor Mmax/Mpl, 20 | P/Py,20 = 0.1 | 1.18 | 1.18 | 1.17 | 1.11 | 0.94 |
| P/Py,20 = 0.2 | 1.12 | 1.12 | 1.13 | 1.06 | 0.82 | |
| P/Py,20 = 0.3 | 1.14 | 1.14 | 1.12 | 0.94 | 0.70 | |
| P/Py,20 = 0.4 | 1.14 | 1.11 | 1.05 | 0.84 | 0.56 | |
| θMmax | P/Py,20 = 0.1 | 2.00 | 2.00 | 1.50 | 1.50 | 1.50 |
| P/Py,20 = 0.2 | 1.50 | 1.50 | 1.00 | 1.00 | 1.00 | |
| P/Py,20 = 0.3 | 1.0 | 1.0 | 1.0 | 1.0 | 0.75 | |
| P/Py,20 = 0.4 | 1.0 | 1.0 | 0.75 | 0.75 | 0.75 | |
| Rotation capacity | P/Py,20 = 0.1 | 2.73 | 2.73 | 2.59 | 1.96 | 0.00 |
| P/Py,20 = 0.2 | 1.72 | 1.72 | 1.64 | 1.24 | 0.00 | |
| P/Py,20 = 0.3 | 1.28 | 1.27 | 1.22 | 0.00 | 0.00 | |
| P/Py,20 = 0.4 | 1.16 | 1.13 | 0.89 | 0.00 | 0.00 |
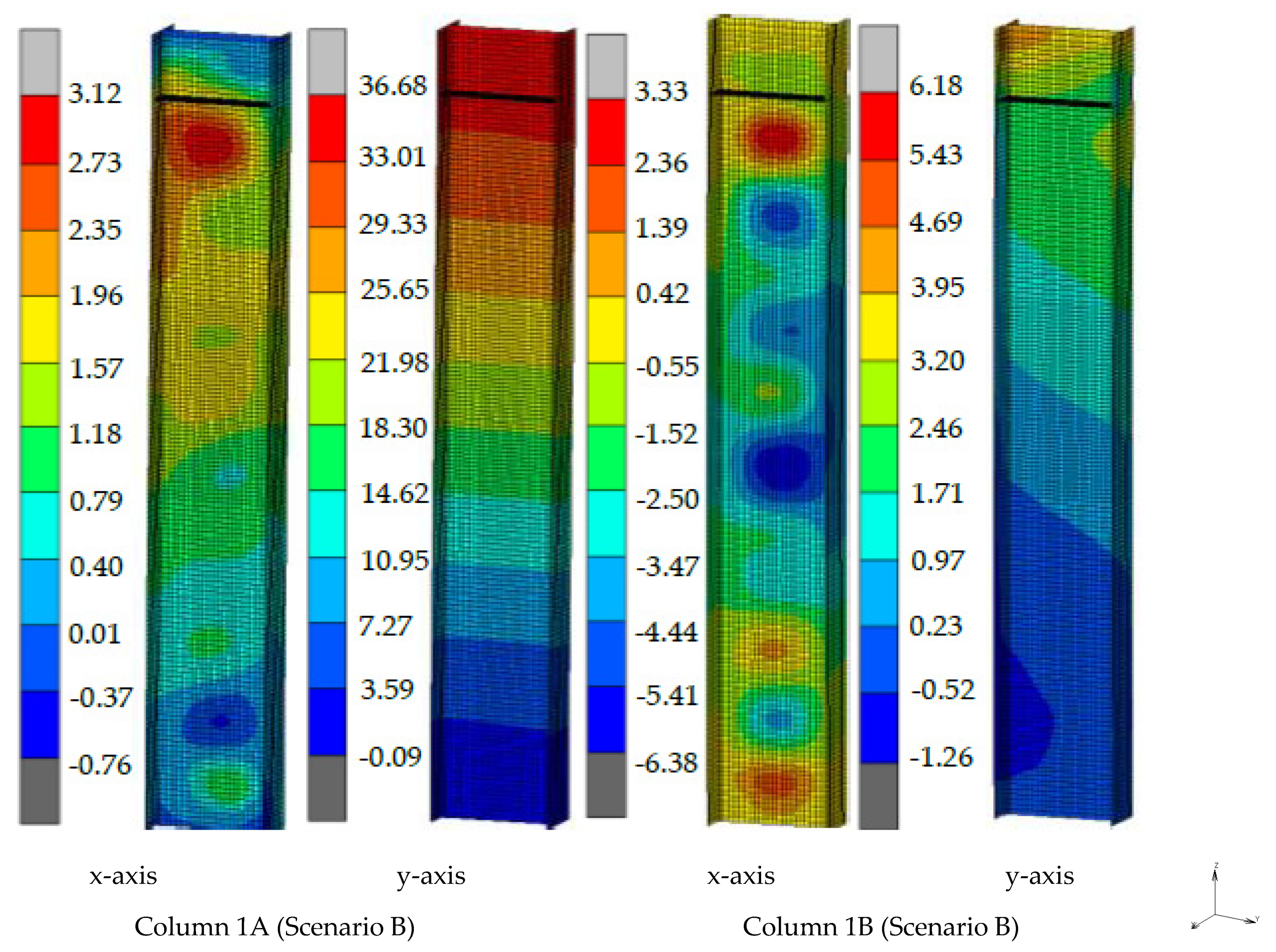
| Scenario A | Scenario B | ||||
|---|---|---|---|---|---|
| Undamaged | Column 1A | Column 1Β | Column 1A | Column 1B | |
| overstrength factor | 1.29 | 1.11 | 1.13 | 1.10 | 1.10 |
| θMmax | 2.00 | 1.75 | 1.75 | 1.60 | 1.80 |
| Rotation capacity | 3.92 | 2.16 | 3.84 | 2.92 | 3.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pantousa, D.; Karavasilis, T.; Maraveas, C. Numerical Investigation of the Post-Fire Performance of Steel Columns. Buildings 2022, 12, 288. https://doi.org/10.3390/buildings12030288
Pantousa D, Karavasilis T, Maraveas C. Numerical Investigation of the Post-Fire Performance of Steel Columns. Buildings. 2022; 12(3):288. https://doi.org/10.3390/buildings12030288
Chicago/Turabian StylePantousa, Dafni, Theodoros Karavasilis, and Chrysanthos Maraveas. 2022. "Numerical Investigation of the Post-Fire Performance of Steel Columns" Buildings 12, no. 3: 288. https://doi.org/10.3390/buildings12030288






