Behavior of One-Way Reinforced Concrete Slabs with Polystyrene Embedded Arched Blocks
Abstract
:1. Introduction
2. Experimental Work
2.1. Material Specifications
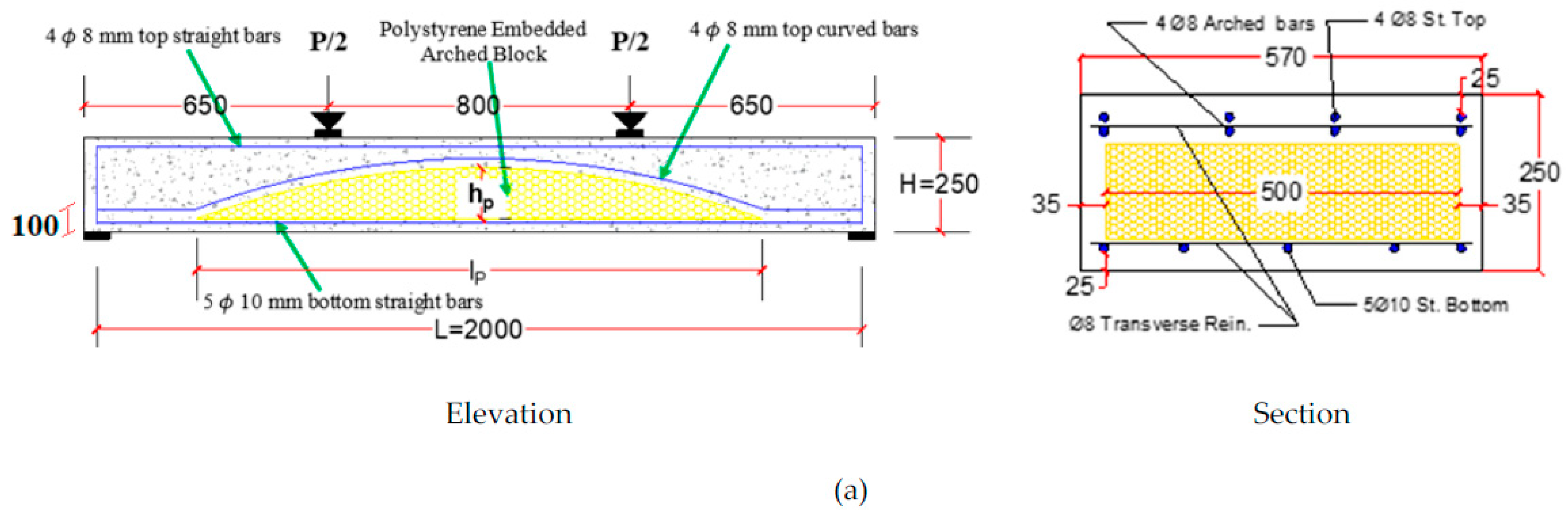
2.2. Description of the Specimens’ Parameters
2.3. Details of the Tested Specimens
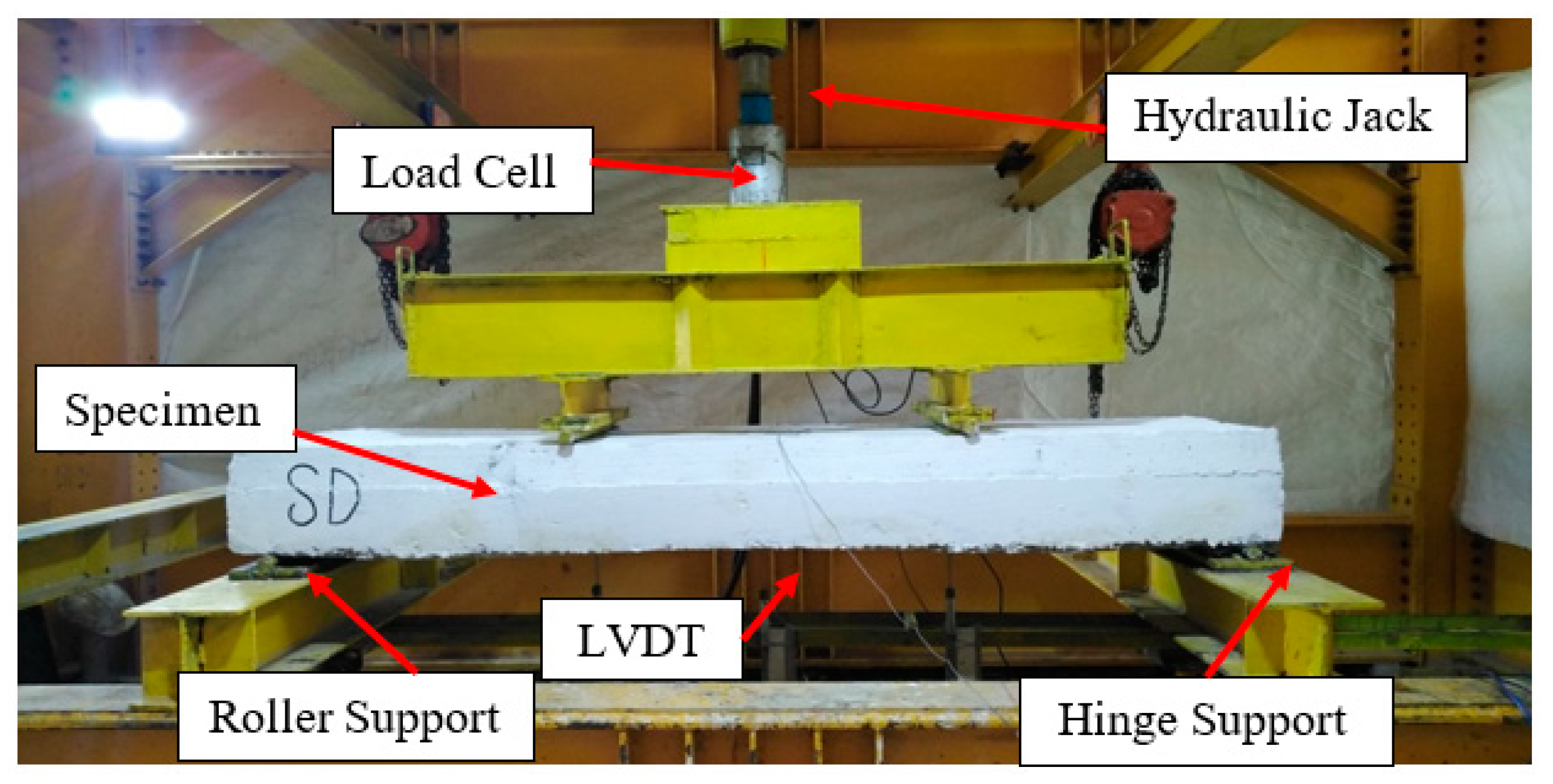
2.4. Testing Setup and Instrumentations
3. Findings of the Test Results and Discussions
3.1. Ultimate Load Capacities and Modes of Failure
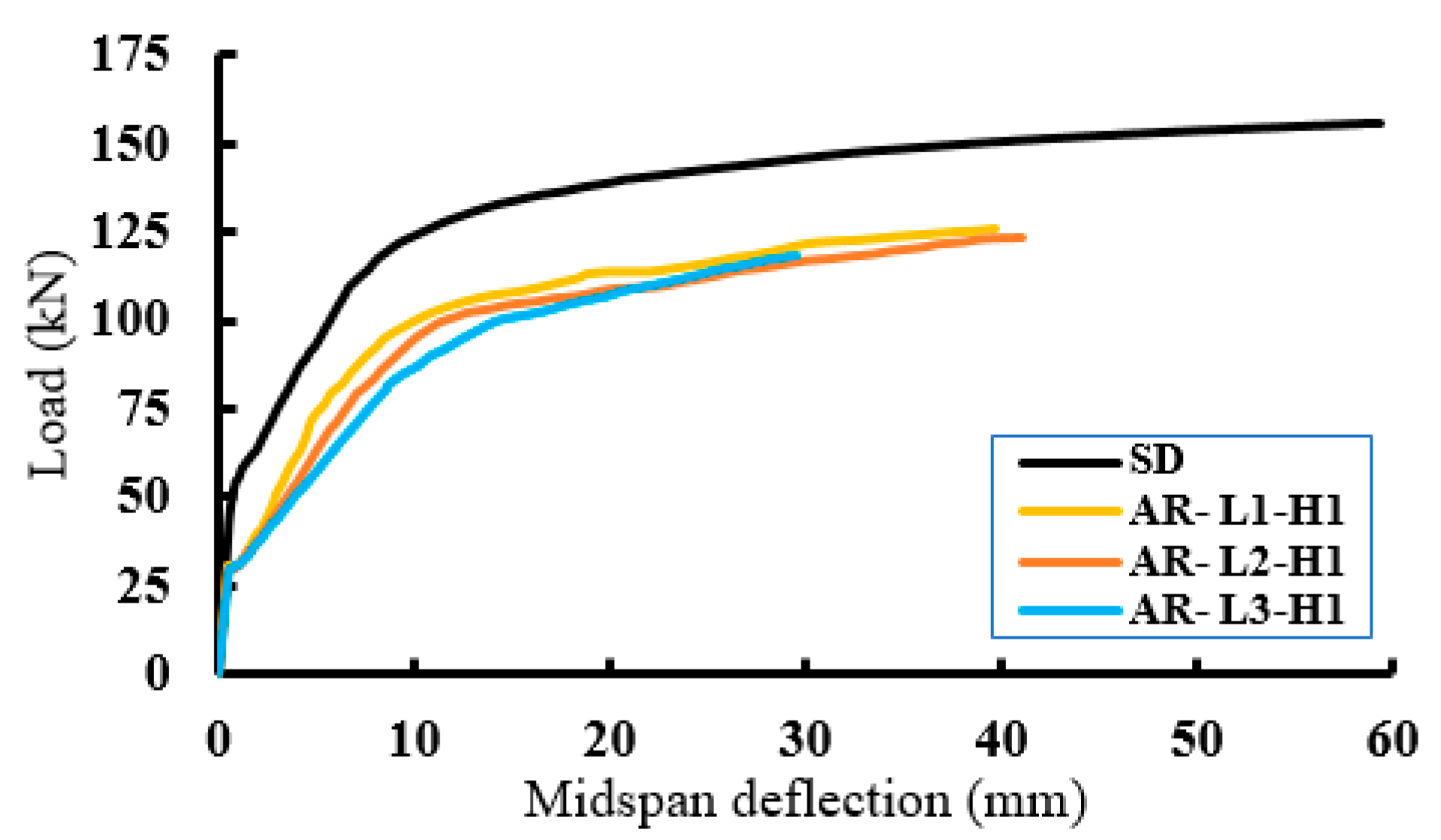
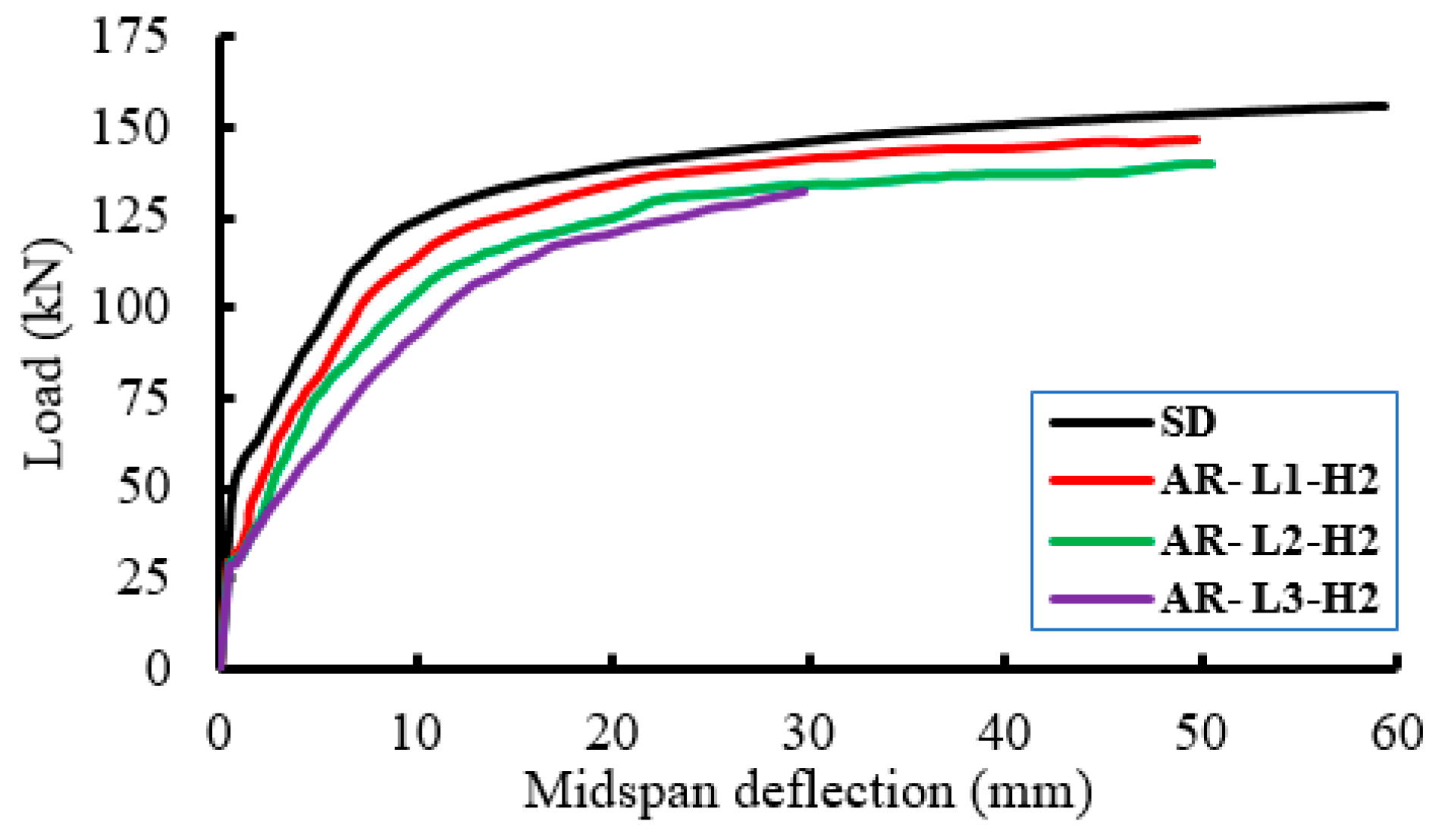
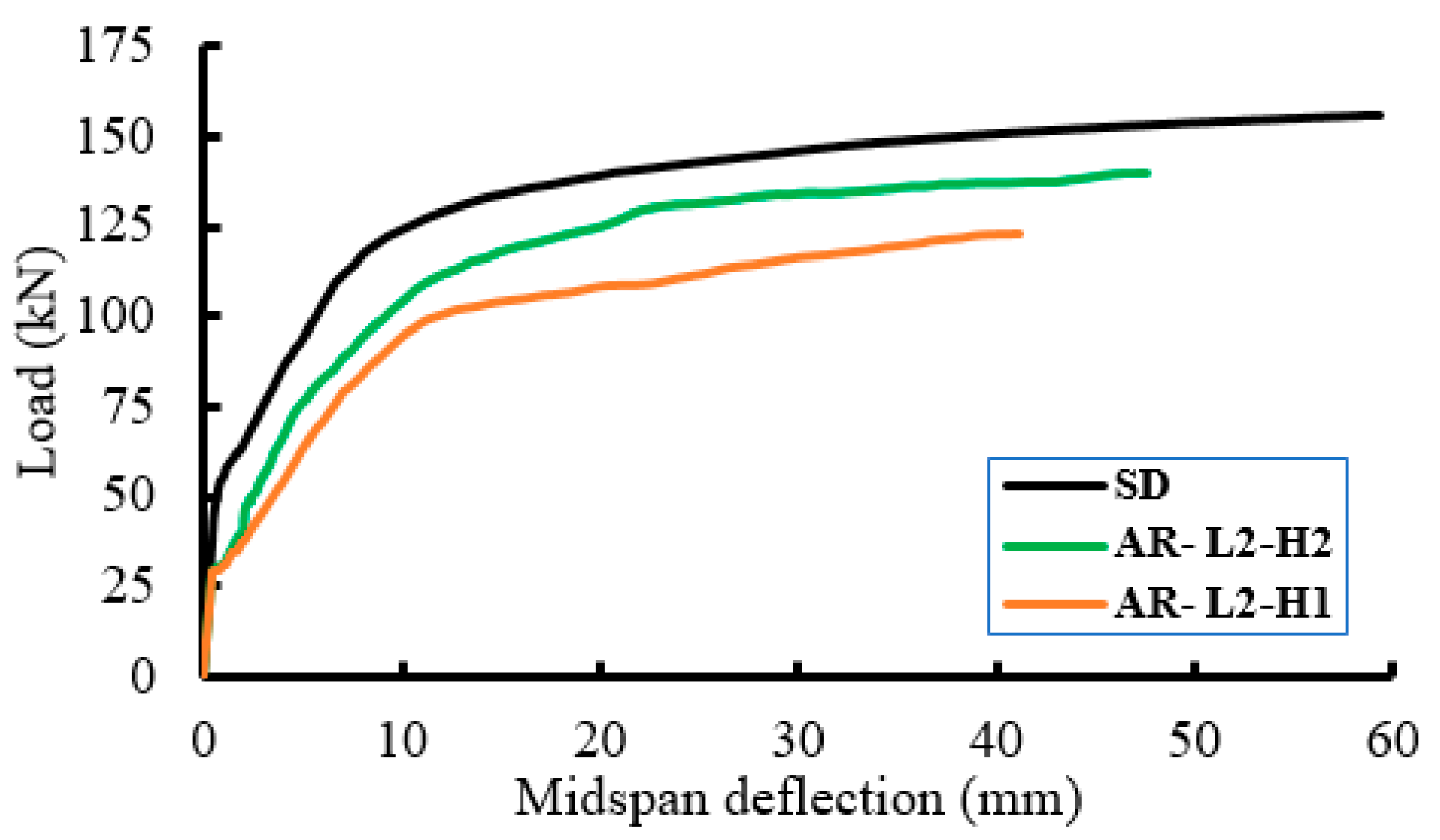
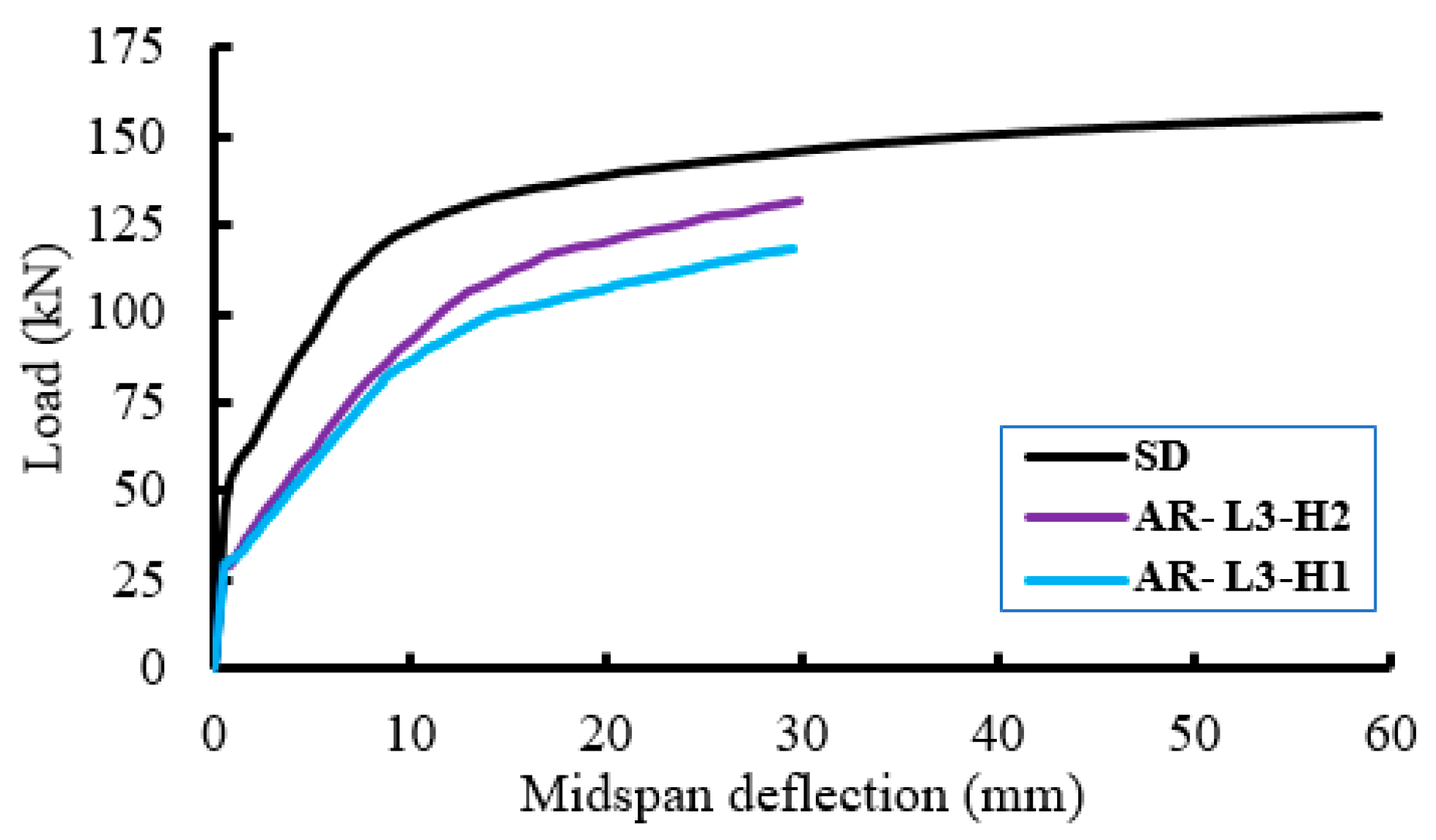
3.2. Load–Deflection Response
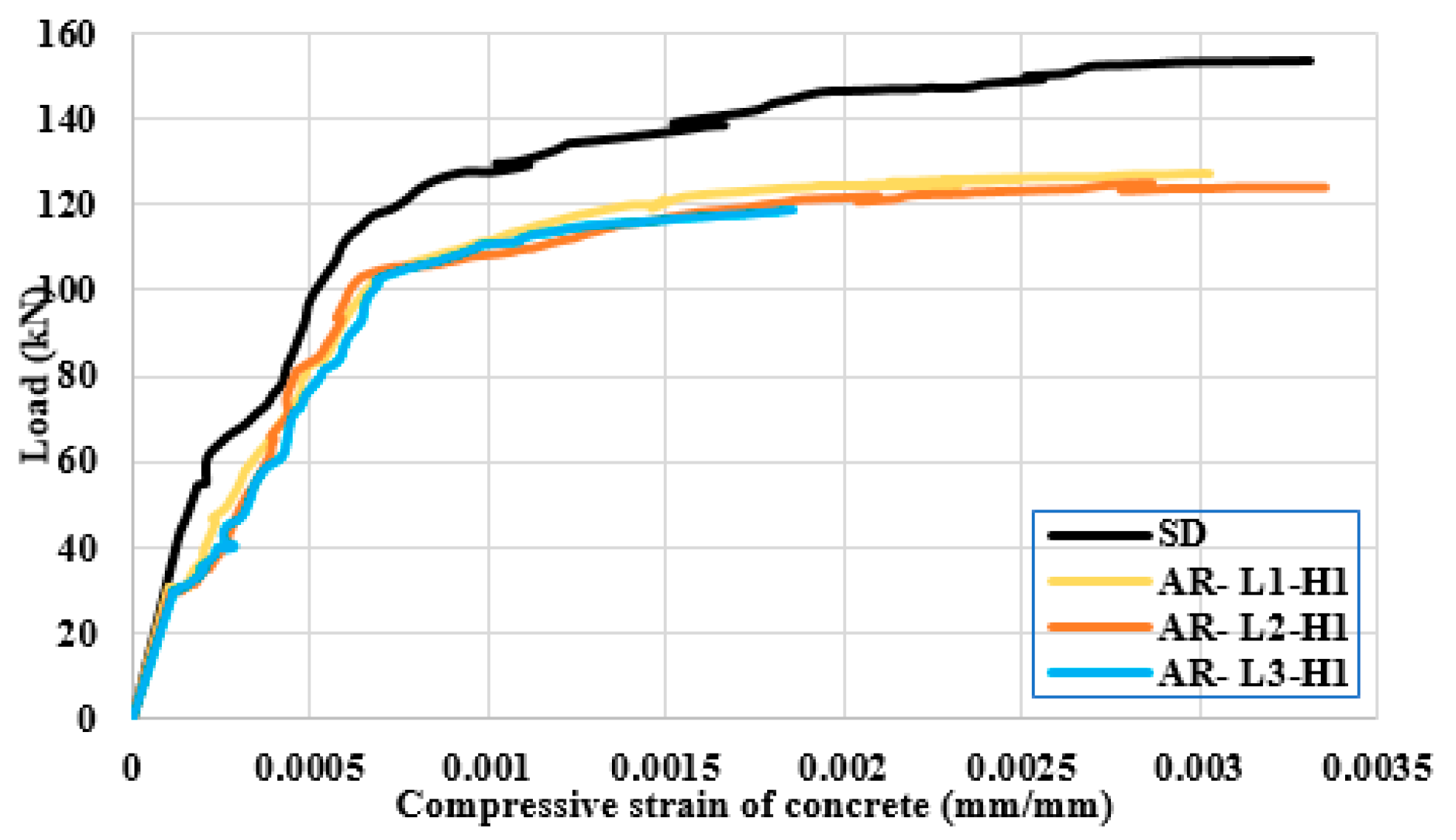
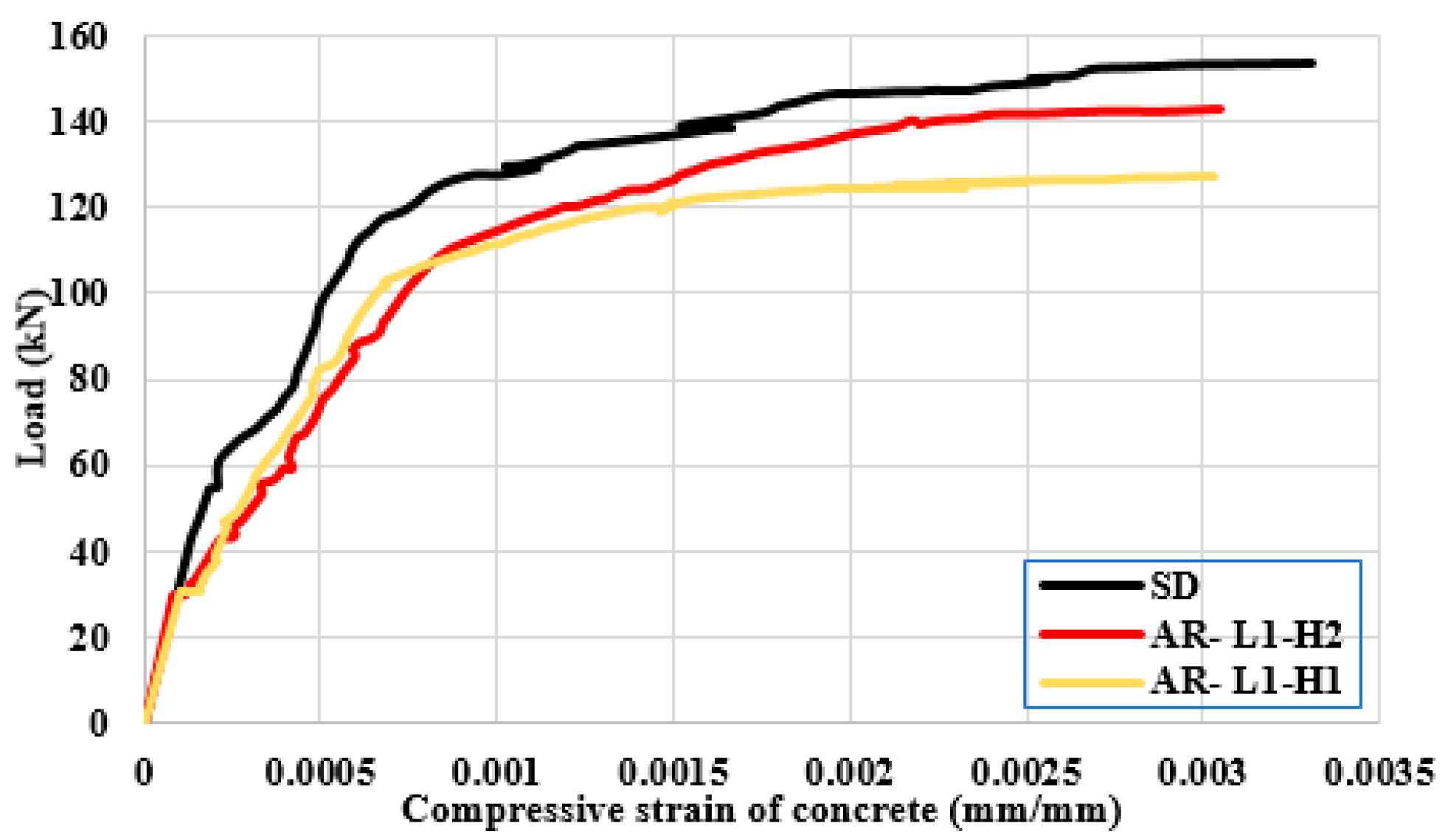
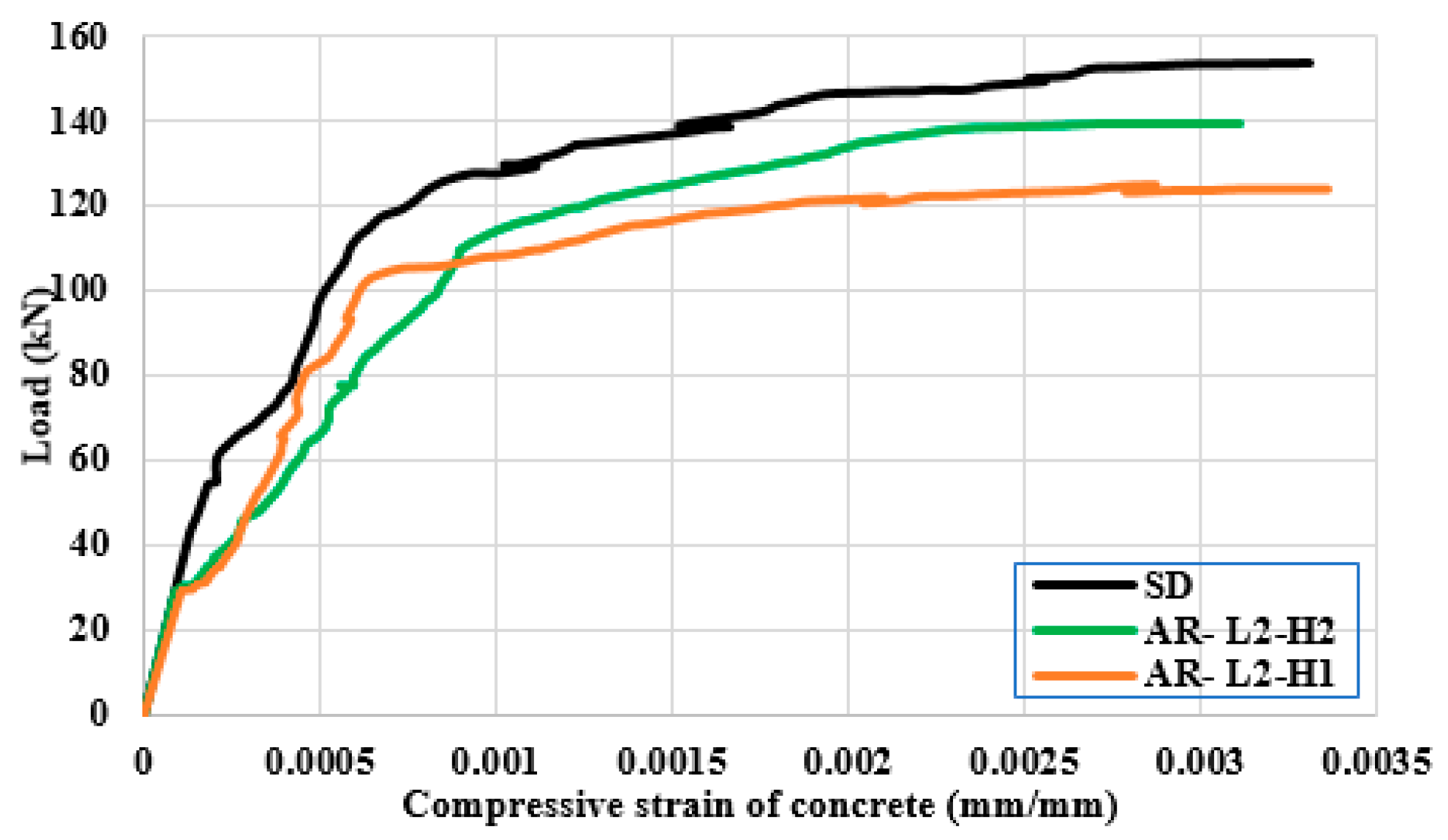
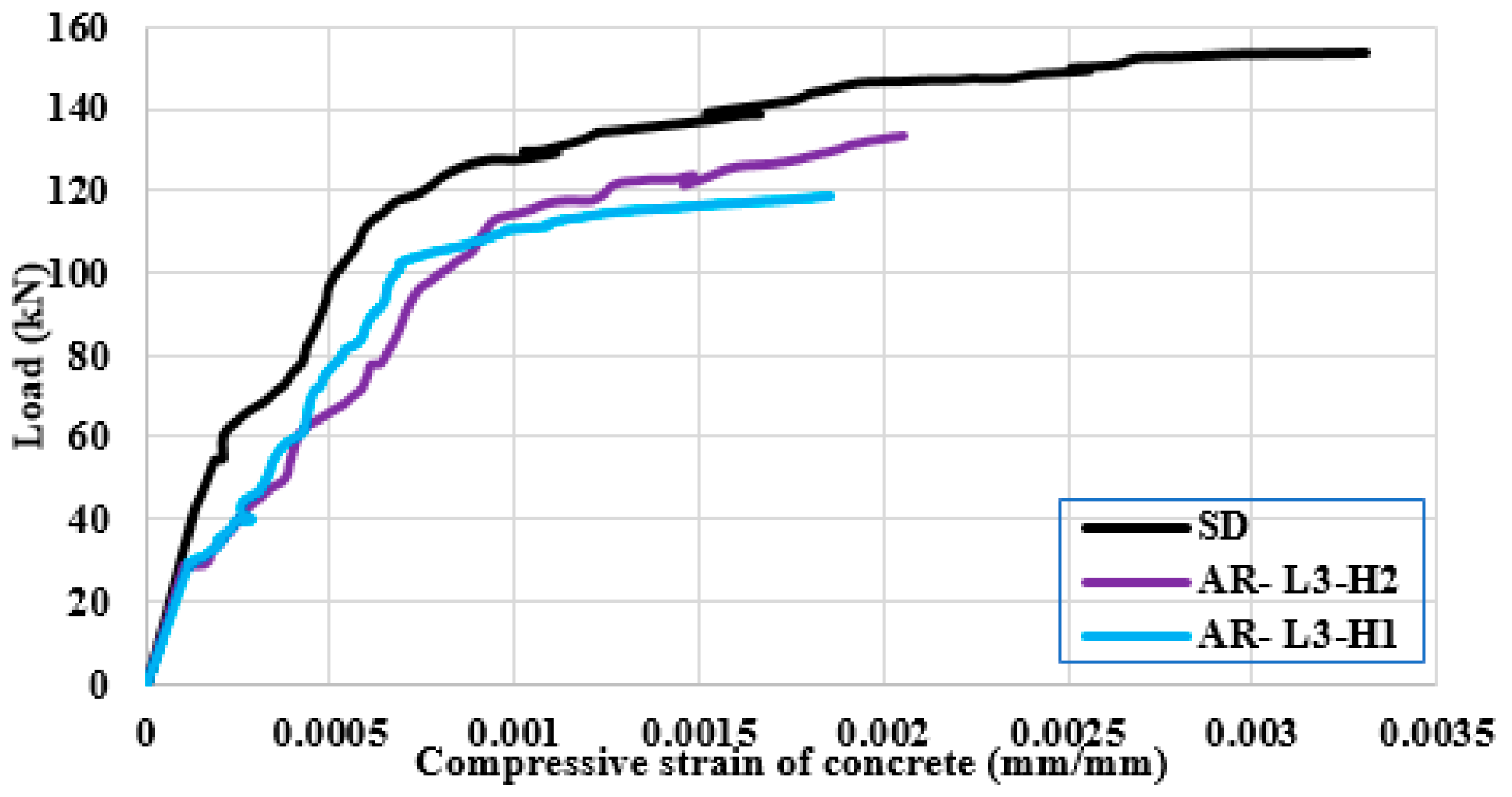
3.3. Strains in the Concrete
4. Finite Element Simulation
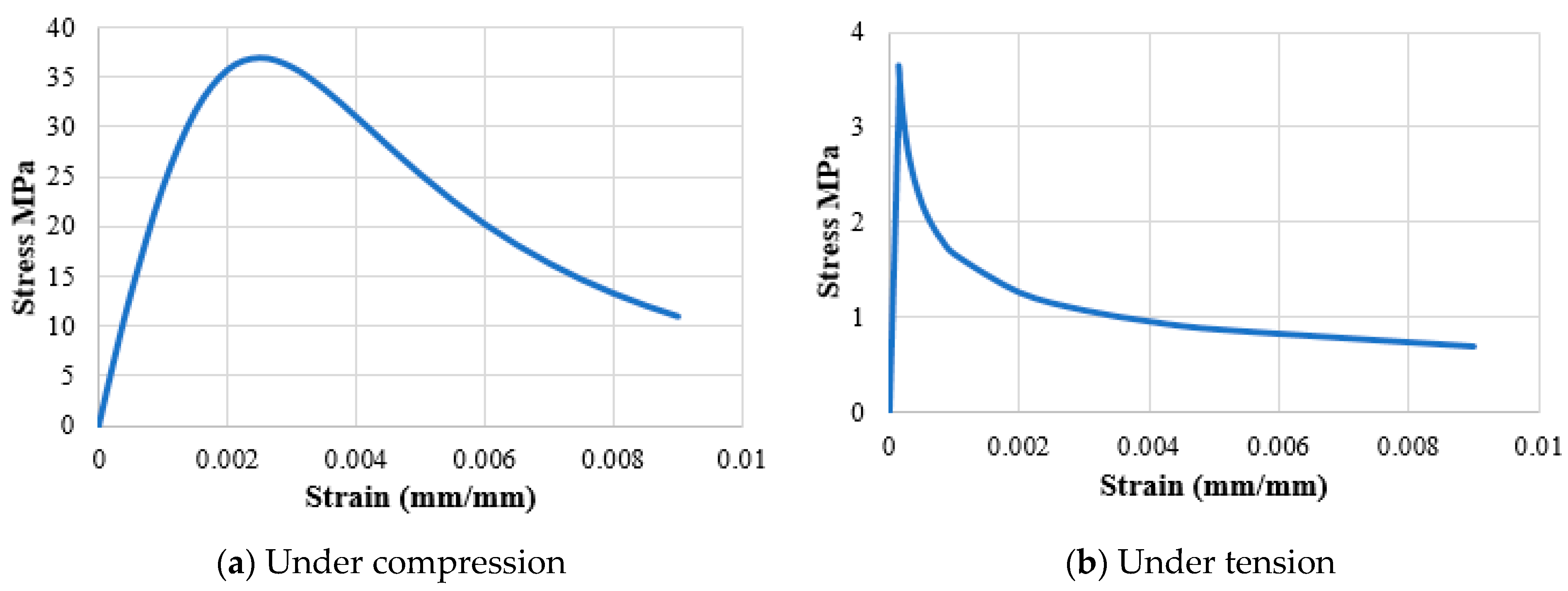
4.1. Constitutive Models of Materials
4.2. FE Mesh and Discretization
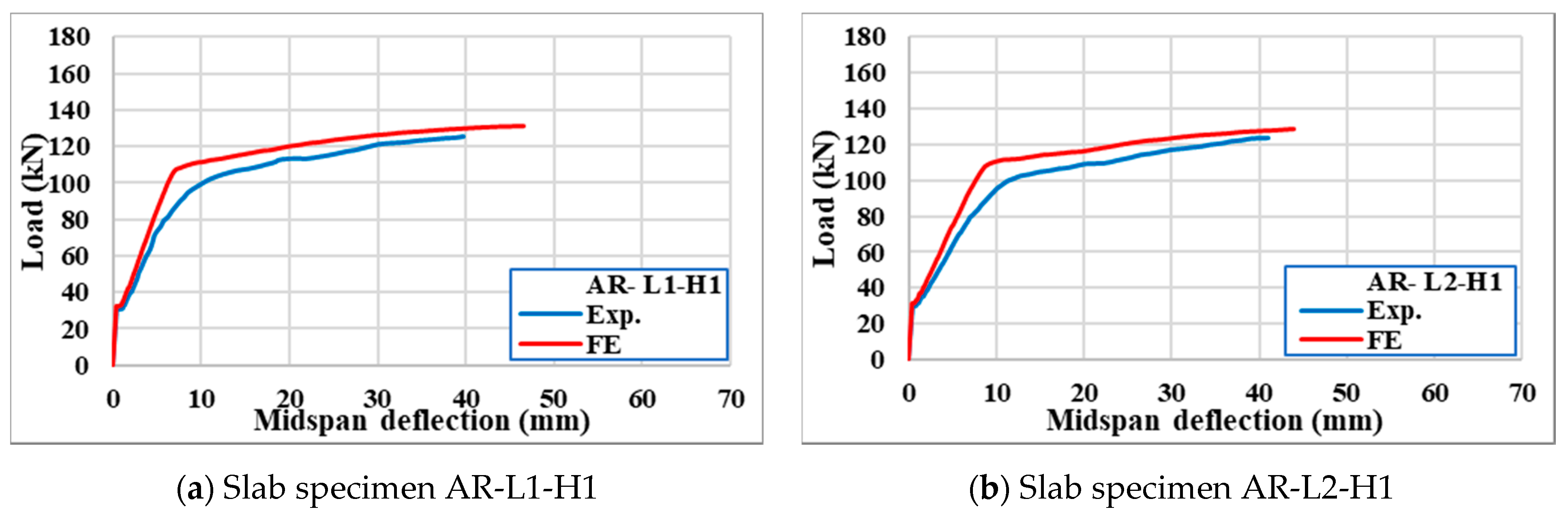
4.3. Verification of the FE Results
4.3.1. Load–Deflection Relationships
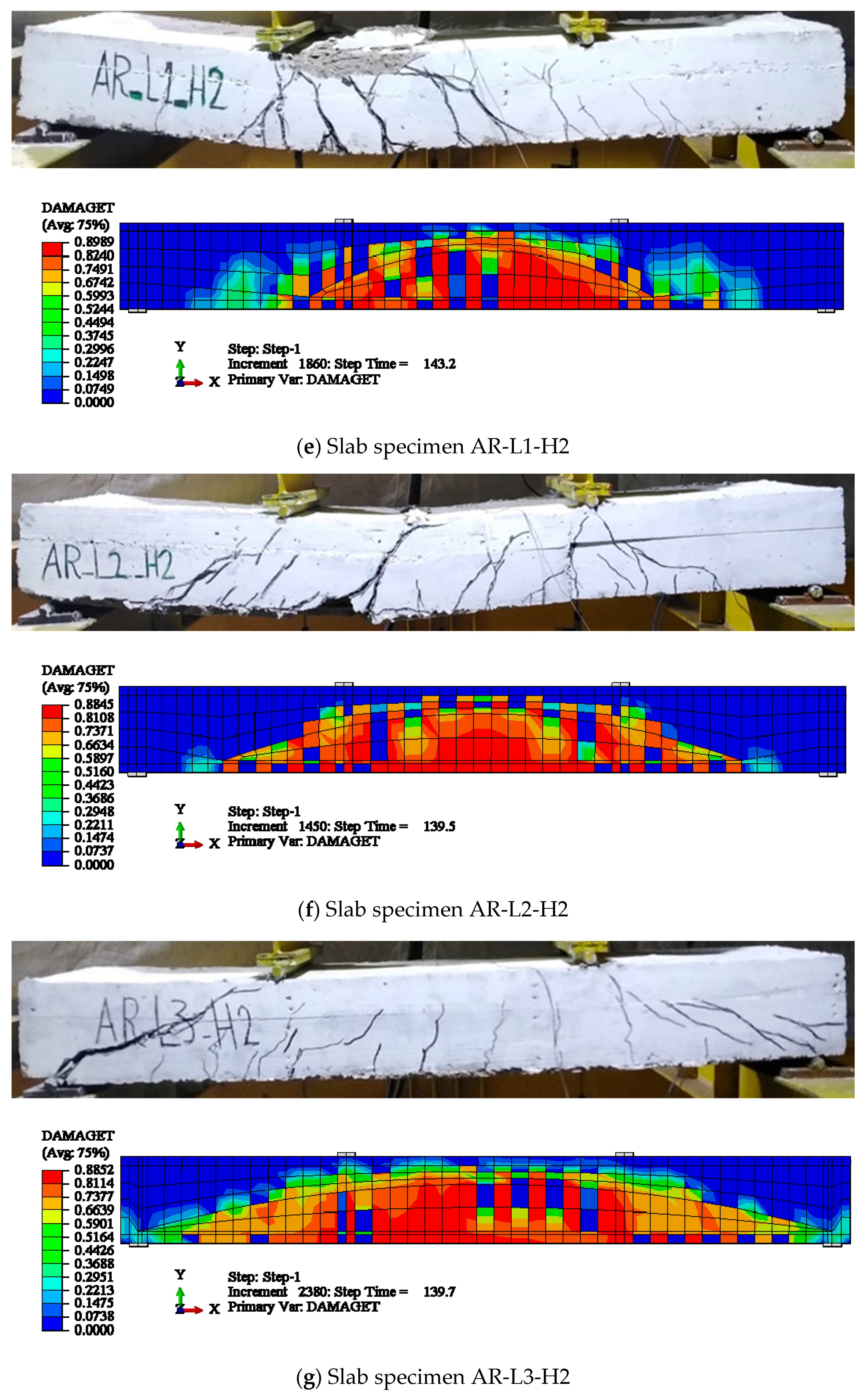
4.3.2. Damage of the Analyzed Beams
5. Conclusions
- Inserting the polystyrene arched blocks into the slab core significantly reduced the self-weight of the slab. On the other hand, this reduced the slab stiffness and led to strength degradations. The minimum decrease in the ultimate load capacity was about 6% with a minimum reduction in the slab weight of 15%. In contrast, the maximum decrease in ultimate load capacity was about 24% with a maximum reduction in the slab weight of about 40%.
- The mode of failure of the slabs with the polystyrene arched blocks was affected by the ratio of the length of the PEABs to the length of the slab (lP/L). When the lP/L ratio was more than 0.5, the failure mode gradually changed from flexural failure to shear failure, and complete shear failure occurred when the lP/L ratio was equal to one.
- At a certain ratio of the height of the PEABs to the total slab depth (hP/H), the ultimate strength was reduced by increasing the length of the PEABs. For the slabs with hP/H = 0.7, the decreases in the ultimate loads were about 19%, 21%, and 24% for slabs with lP/L = 0.5, 0.75, and 1.0, respectively. For the slabs with hP/H = 0.54, these percentages were 6%, 10%, and 15%, respectively.
- At a certain lP/L ratio, the ultimate load was reduced by increasing the depth of the PEABs. For the slabs with lP/L = 0.5, the decreases in the ultimate loads were about 19% and 6% for slabs with hP/H = 0.7 and 0.54, respectively. For the slabs with lP/L = 0.75, the decreases in the ultimate loads were about 21% and 10% for the slabs with hP/H = 0.7 and 0.54, respectively.
- Increasing the lP/L ratio had an insignificant effect on the concrete compressive strain except for the case of lP/L = 1, where the mode of failure changed to be shear failure. This might be attributed to the constant compression zone of concrete at the mid-span. In contrast, increasing the hP/H ratio had a significant effect on increasing the concrete compressive strain.
- To increase the ultimate strength of slabs with PEABs, the shear resistance of the slab must be increased effectively by using higher compressive strength of concrete and/or using shear reinforcement within the shear zone.
- During the elastic stage, the slab responses from the FE and experimental were fairly similar. The FE findings stiffened slightly as the applied load approached the yielding load. The supposed complete contact between the concrete and reinforcement was attributed to the disparity in response. However, there were good agreements between the experimental and FE results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chung, J.-H.; Choi, H.-K.; Lee, S.-C.; Choi, C.-S. One-way shear strength of circular voided reinforced concrete floor slabs. Proc. Inst. Civ. Eng.-Struct. Build. 2015, 168, 336–350. [Google Scholar] [CrossRef]
- Valivonis, J.; Jonaitis, B.; Zavalis, R.; Skuturna, T.; Šneideris, A. Flexural capacity and stiffness of monolithic biaxial hollow slabs. J. Civ. Eng. Manag. 2014, 20, 693–701. [Google Scholar] [CrossRef] [Green Version]
- Al-Gasham, T.S.S. Structural performance of reinforced concrete bubble slabs after exposing to fire flame. Eng. Sustain. Dev. 2015, 19, 1–14. [Google Scholar]
- Al-Gasham, T.S.; Mhalhal, J.M.; Jabir, H.A. Improving punching behavior of interior voided slab-column connections using steel sheets. Eng. Struct. 2019, 199, 109614. [Google Scholar] [CrossRef]
- Hashemi, S.S.; Sadeghi, K.; Vaghefi, M.; Siadat, S.A. Evaluation of ductility of RC structures constructed with bubble deck system. Int. J. Civ. Eng. 2018, 16, 513–526. [Google Scholar] [CrossRef]
- Schnellenbach-Held, M.; Pfeffer, K. Punching behavior of biaxial hollow slabs. Cem. Concr. Compos. 2002, 24, 551–556. [Google Scholar] [CrossRef]
- Fiala, C.; Hájek, P. Environmentally based optimization of RC slab floor structures. In CESB 07 Conference Proceedings; Citeseer: Prague, Czech Republic, 2007. [Google Scholar]
- Yang, W.; Yang, Y.; Han, B.; Jiang, P. Experimental study on mechanical property of corner columns supported reinforced concrete honeycombed-core girderless floor. Open Civ. Eng. J. 2013, 7, 179–188. [Google Scholar] [CrossRef] [Green Version]
- Chung, J.; Choi, H.K.; Lee, S.C.; Choi, C.S. Shear capacity of biaxial hollow slab with donut type hollow sphere. Procedia Eng. 2011, 14, 2219–2222. [Google Scholar] [CrossRef] [Green Version]
- Fanella, D.A.; Mahamid, M.; Mota, M. Flat plate–voided concrete slab systems: Design, serviceability, fire resistance, and construction. Pract. Period. Struct. Des. Constr. 2017, 22, 04017004. [Google Scholar] [CrossRef]
- Boyd, T.D. The Arch and the Vault in Greek Architecture. Am. J. Archaeol. 1978, 82, 83–100. [Google Scholar] [CrossRef]
- Chebo, K.A.; Temsah, Y.; Abou Saleh, Z.; Darwich, M.; Hamdan, Z. Experimental investigation on the structural performance of single span hollow core slab under successive impact loading. Materials 2022, 15, 599. [Google Scholar] [CrossRef] [PubMed]
- Sarvaiya, D.M.; Jivani, D. An experimental study on spherical voided slab. Int. J. Emerg. Technol. Innov. Res. 2022, 9, 226–230. [Google Scholar]
- Bhamare, V.P.; Jadhao, P.D.; Pawar, A.J. Design and experimental study of voided slab with proposed new shape of void former. In Smart Technologies for Energy, Environment and Sustainable Development; Springer: Singapore, 2019. [Google Scholar] [CrossRef]
- Singh, M.; Saini, B. Analytical and experimental study of voided slab. In International Conference on Sustainable Waste Management through Design; ICSWMD 2018, Lecture Notes in Civil Engineering; Singh, H., Garg, P., Kaur, I., Eds.; Springer: Cham, Switzerland, 2019; Volume 21. [Google Scholar] [CrossRef]
- Sagadevan, R.; Rao, B.N. Effect of void former shapes on one-way flexural behaviour of biaxial hollow slabs. Int. J. Adv. Struct. Eng. 2019, 11, 297–307. [Google Scholar] [CrossRef] [Green Version]
- Abaqus, A. Computer Software for Finite Element Analysis; Dassault Systems Simulia: Johnston, RI, USA, 2020. [Google Scholar]
- Hafezolghorani, M.; Hejazi, F.; Vaghei, R.; Bin Jaafar, M.S.; Karimzade, K. Simplified damage plasticity model for concrete. Struct. Eng. Int. 2017, 27, 68–78. [Google Scholar] [CrossRef]
- SANEZ, L. Discussion of “Equation for the stress-strain curve of concrete”, by Desayi, P. and Krishnan, S. ACI J. 1964, 61, 1227–1239. [Google Scholar]
- Belarbi, A.; Hsu, T.T. Constitutive laws of concrete in tension and reinforcing bars stiffened by concrete. Struct. J. 1994, 91, 465–474. [Google Scholar]














| Specimens | Height of PEABs hP (mm) | hP/H | Length of PEABs lP (mm) | lP/L | Reduction of Weight (%) |
|---|---|---|---|---|---|
| SD | - | - | - | - | - |
| AR-L1-H1 | 175 | 0.70 | 1000 | 0.50 | 19.97 |
| AR-L2-H1 | 1500 | 0.75 | 29.56 | ||
| AR-L3-H1 | 2000 | 1.00 | 39.63 | ||
| AR-L1-H2 | 135 | 0.54 | 1000 | 0.50 | 15.27 |
| AR-L2-H2 | 1500 | 0.75 | 22.73 | ||
| AR-L3-H2 | 2000 | 1.00 | 30.64 |
| Specimens | hP/H | lP/L | Ultimate Load (kN) | Decrease in the Ultimate Load (%) | Mode of Failure |
|---|---|---|---|---|---|
| SD | - | - | 156 | - | Flexure |
| AR-L1-H1 | 0.70 | 0.50 | 126 | 19.23 | Flexure |
| AR-L2-H1 | 0.75 | 123 | 21.15 | Shear-Flexure | |
| AR-L3-H1 | 1.00 | 119 | 23.72 | Shear | |
| AR-L1-H2 | 0.54 | 0.50 | 147 | 5.77 | Flexure |
| AR-L1-H2 | 0.75 | 140 | 10.26 | Shear-Flexure | |
| AR-L1-H2 | 1.00 | 132 | 15.38 | Shear |
| Parameter | Value |
|---|---|
| φ | 39° |
| ε | 0.1 |
| fbo/fco | 1.16 |
| K | 0.667 |
| μ | 0.001 |
| Slab Designation | Ultimate Load Exp. (kN) | Ultimate Load FE (kN) | Exp./FE |
|---|---|---|---|
| SD | 156 | 165 | 0.95 |
| AR-L1-H1 | 126 | 131 | 0.96 |
| AR-L2-H1 | 123 | 129 | 0.95 |
| AR-L3-H1 | 119 | 125 | 0.95 |
| AR-L1-H2 | 147 | 157 | 0.94 |
| AR-L2-H2 | 140 | 148 | 0.95 |
| AR-L3-H2 | 132 | 144 | 0.92 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Ahmed, A.H.A.; Ibrahim, F.H.; Allawi, A.A.; El-Zohairy, A. Behavior of One-Way Reinforced Concrete Slabs with Polystyrene Embedded Arched Blocks. Buildings 2022, 12, 331. https://doi.org/10.3390/buildings12030331
Al-Ahmed AHA, Ibrahim FH, Allawi AA, El-Zohairy A. Behavior of One-Way Reinforced Concrete Slabs with Polystyrene Embedded Arched Blocks. Buildings. 2022; 12(3):331. https://doi.org/10.3390/buildings12030331
Chicago/Turabian StyleAl-Ahmed, Ali Hussein Ali, Falah Hasan Ibrahim, Abbas AbdulMajeed Allawi, and Ayman El-Zohairy. 2022. "Behavior of One-Way Reinforced Concrete Slabs with Polystyrene Embedded Arched Blocks" Buildings 12, no. 3: 331. https://doi.org/10.3390/buildings12030331
APA StyleAl-Ahmed, A. H. A., Ibrahim, F. H., Allawi, A. A., & El-Zohairy, A. (2022). Behavior of One-Way Reinforced Concrete Slabs with Polystyrene Embedded Arched Blocks. Buildings, 12(3), 331. https://doi.org/10.3390/buildings12030331








