Vibration Test and Control of Factory a Building under Excitation of Multiple Vibrating Screens
Abstract
:1. Introduction
2. Field Vibration Monitoring and Modal Analysis of Factory Buildings
2.1. Engineering Background
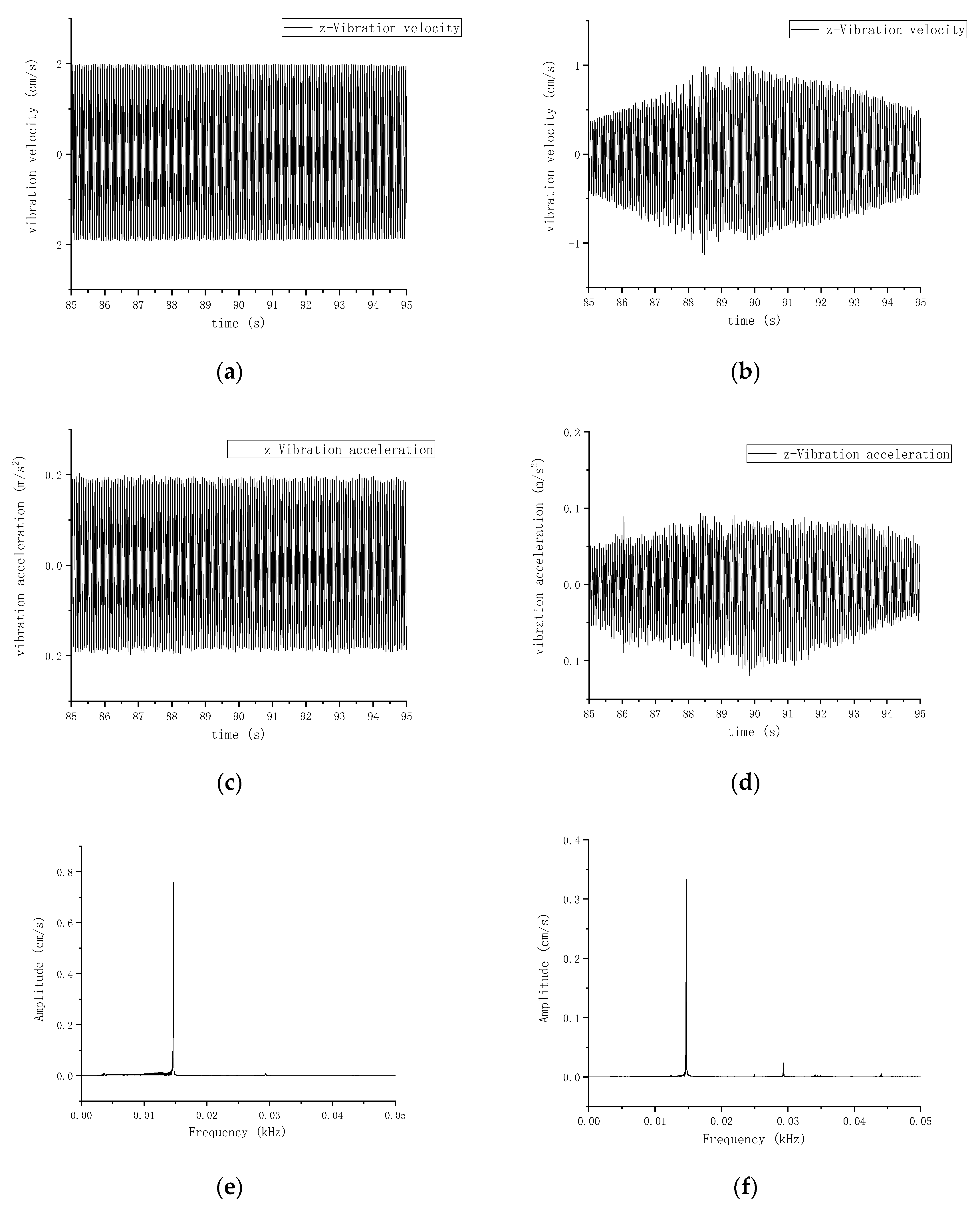
2.2. Field Vibration Monitoring
2.3. Modal Testing
3. Numerical Simulation of Vibration Response
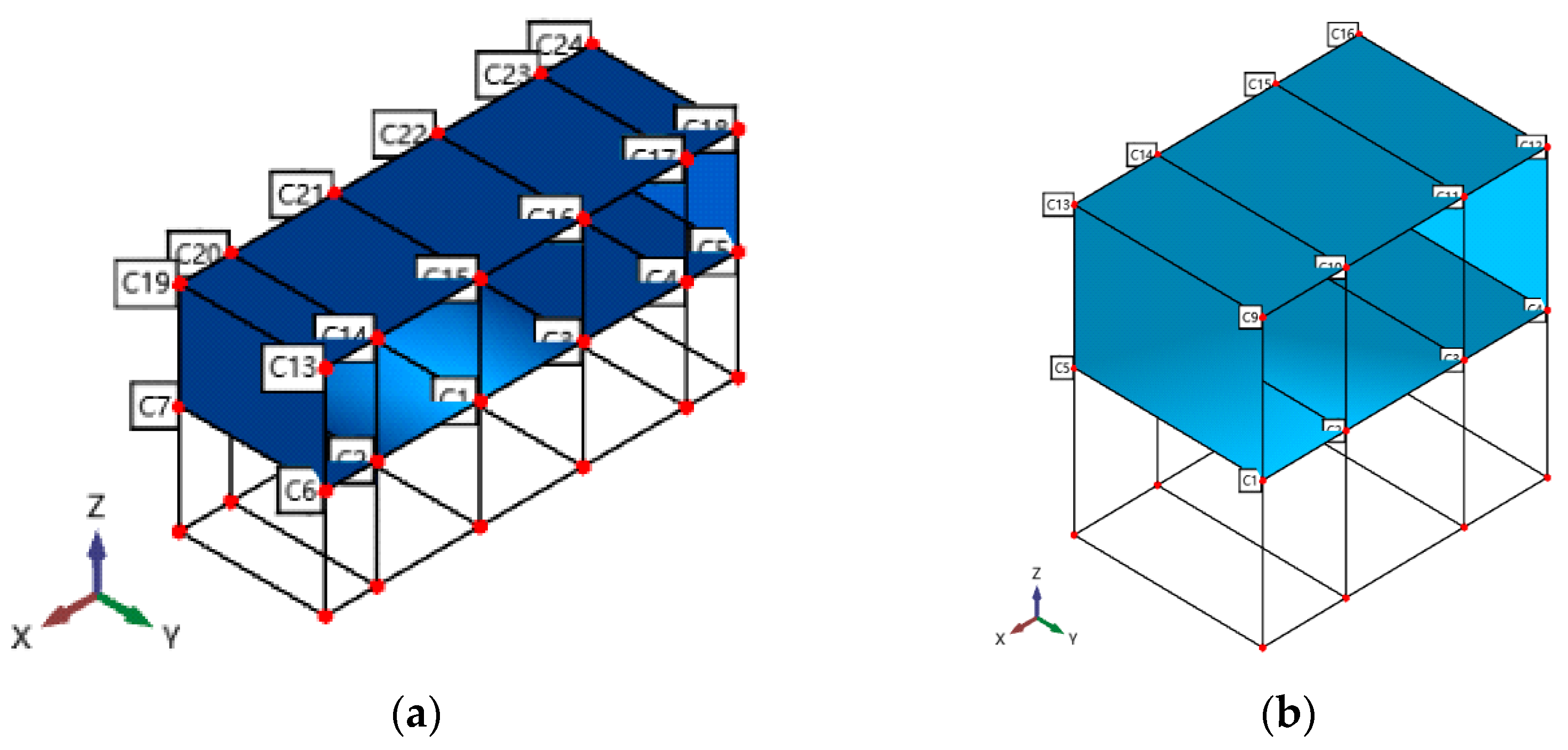
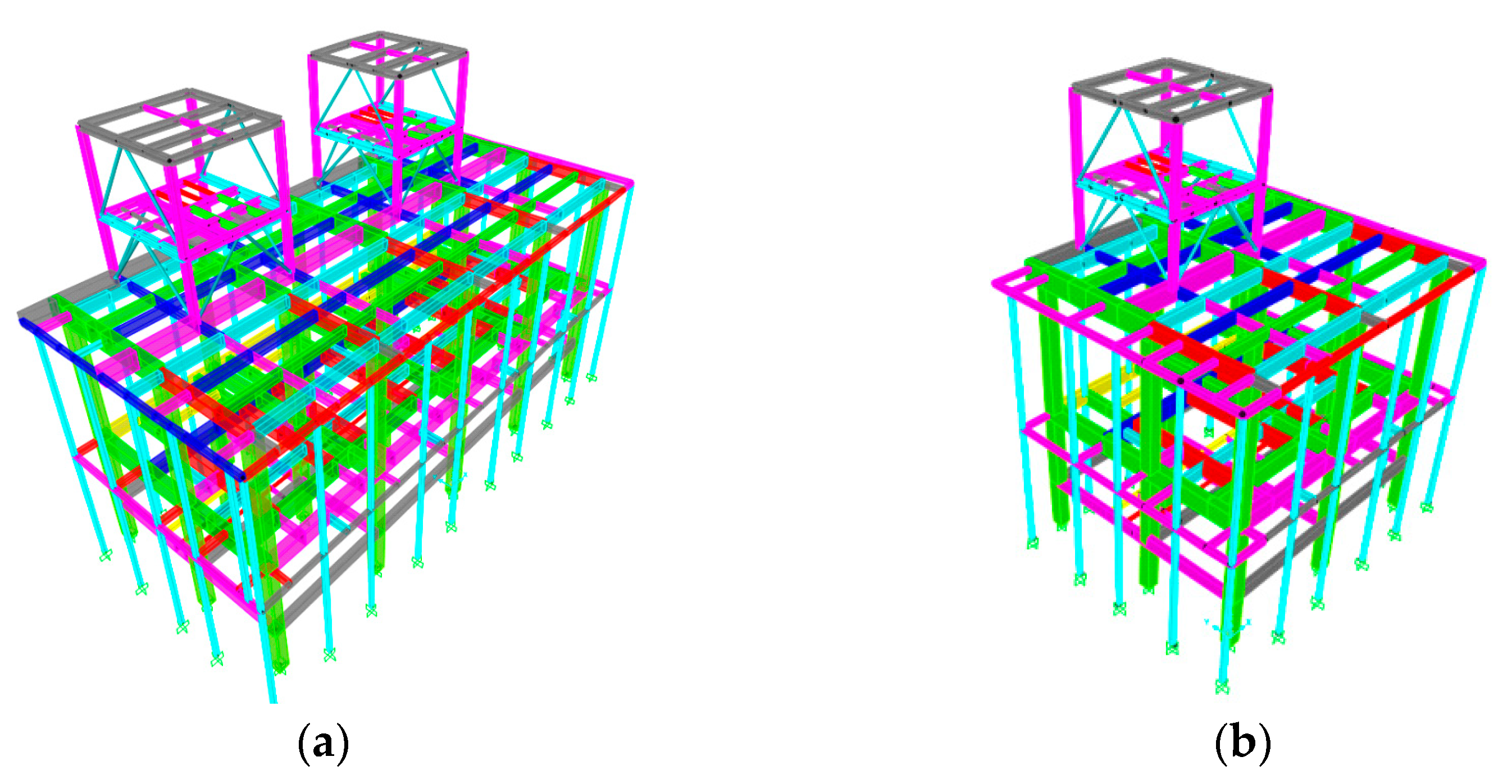
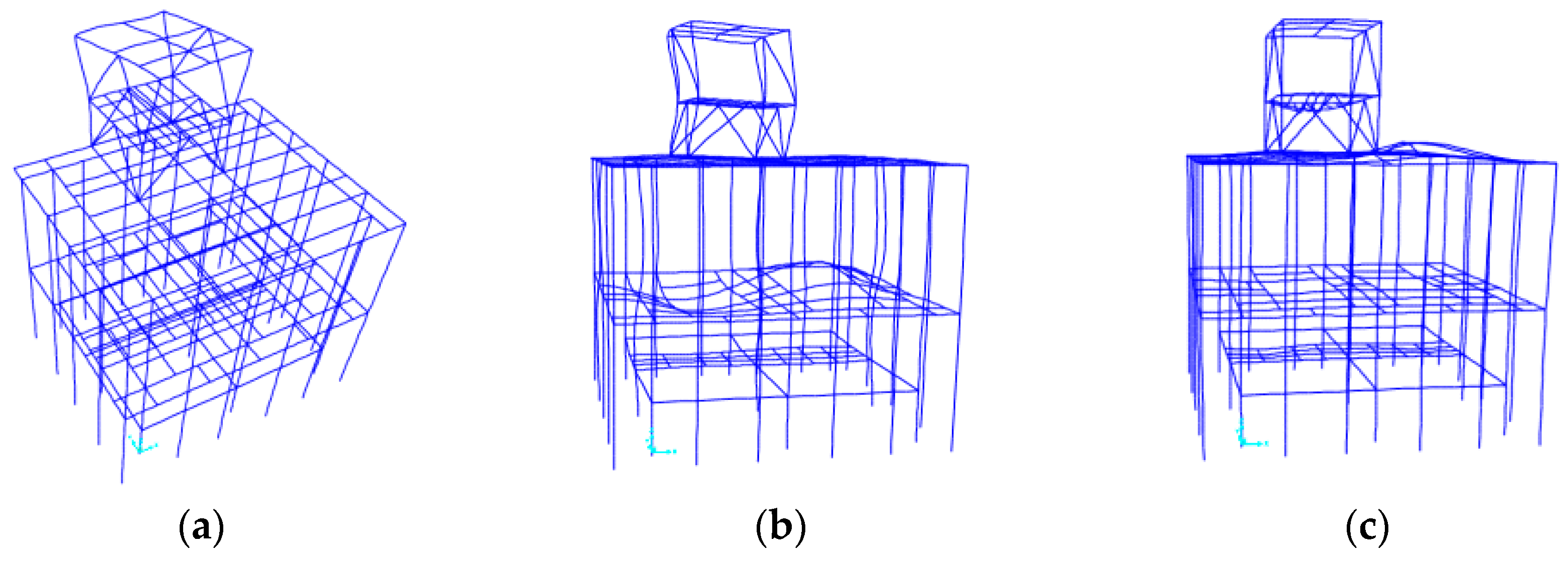
3.1. Model Building
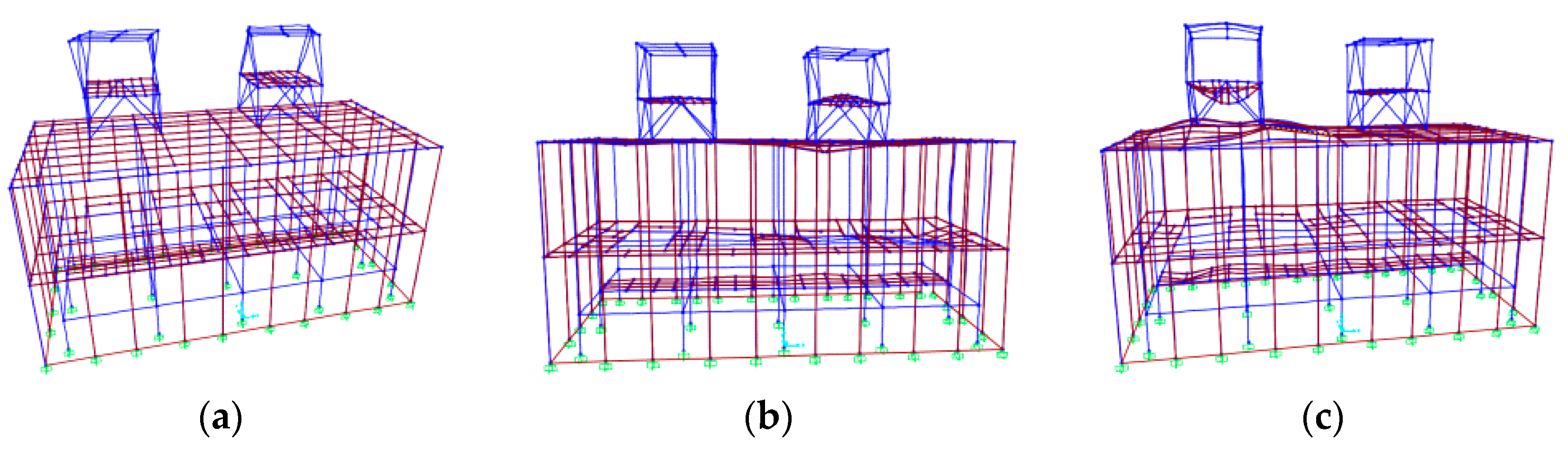
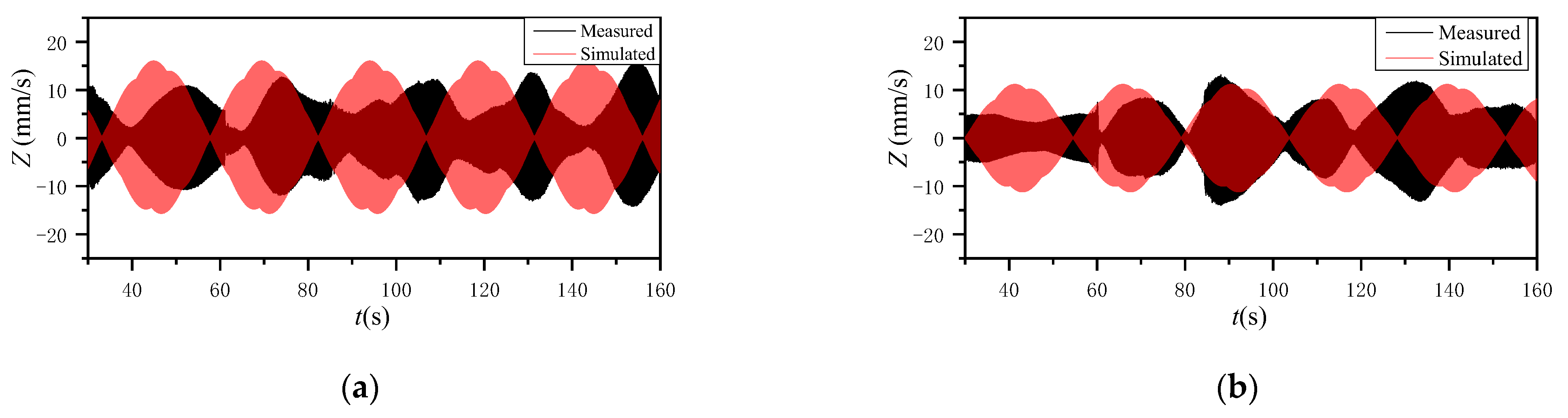
3.2. Finite Element Model Verification
4. Vibration Control of the Structure
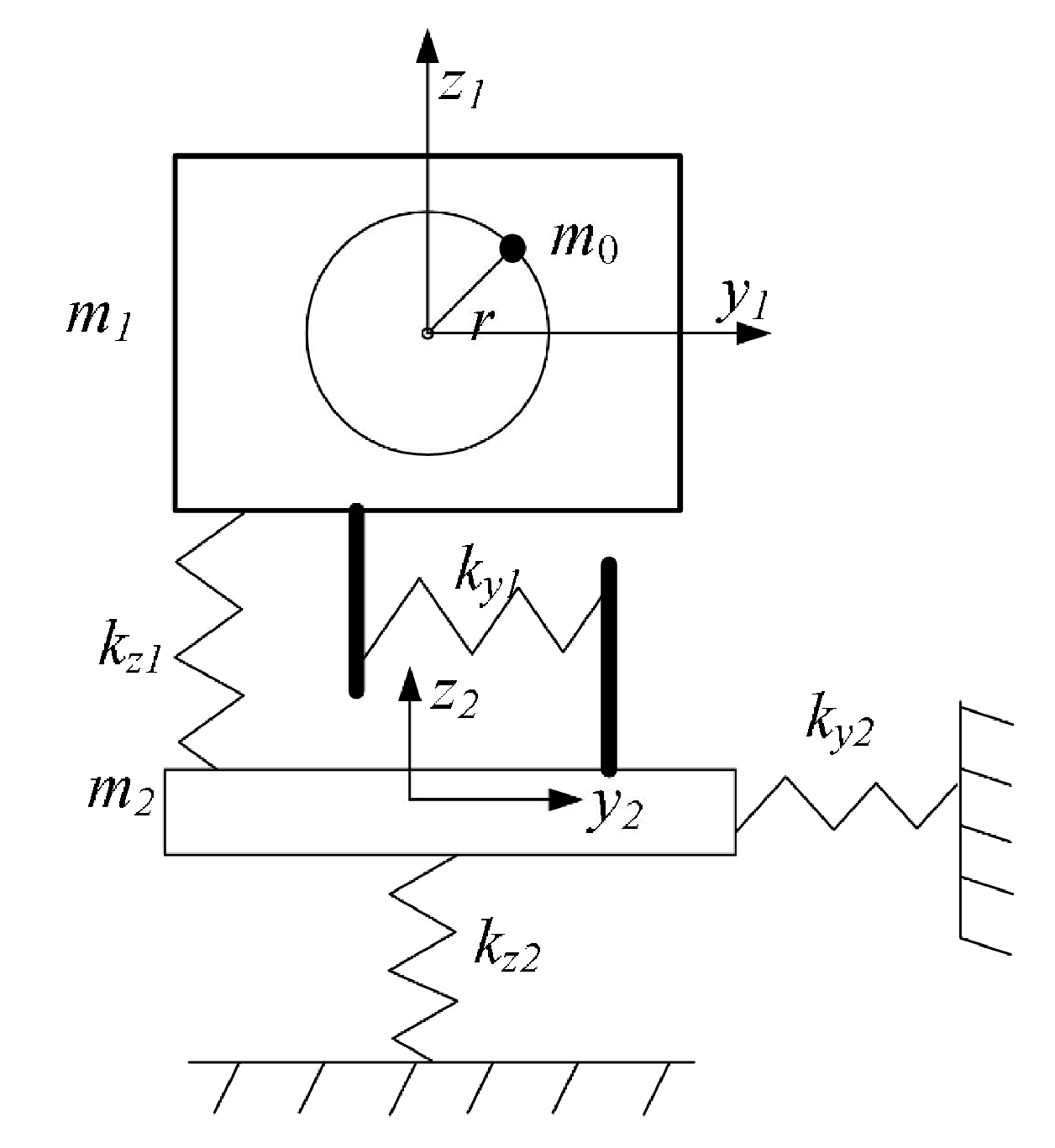
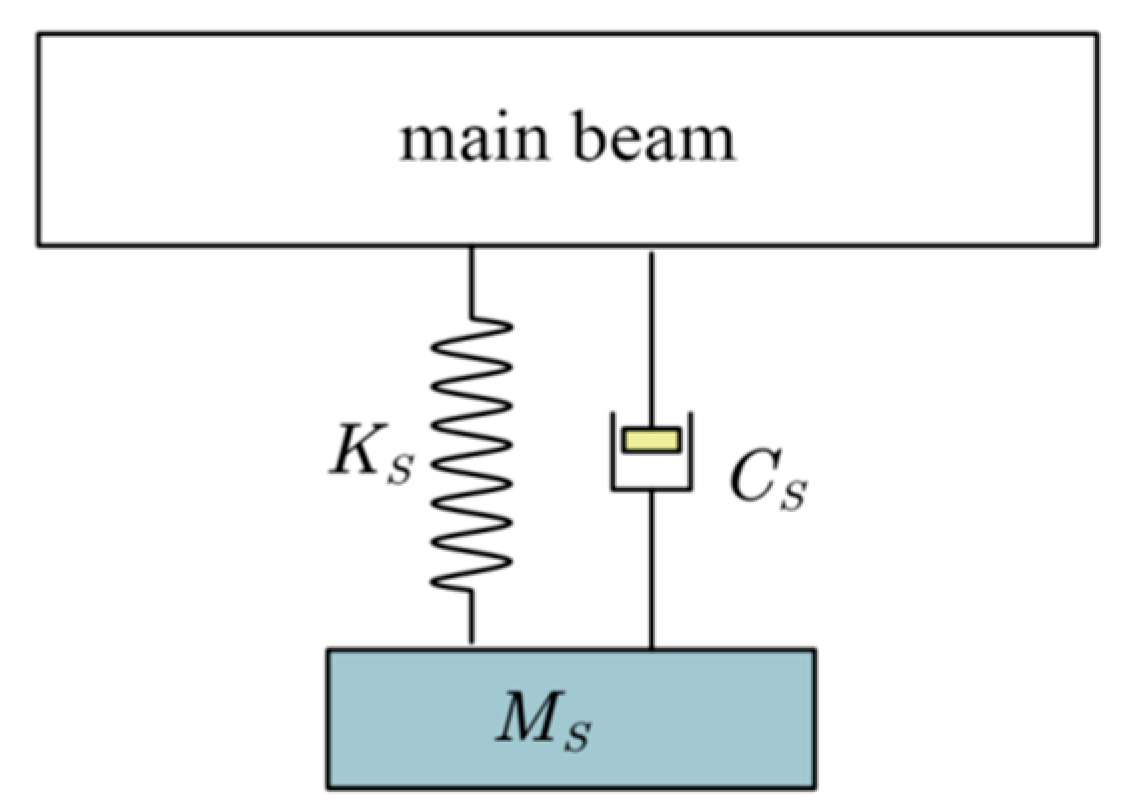
4.1. Vibration Reduction Scheme
4.2. Analysis of Vibration Reduction Effect
5. Discussion
6. Conclusions
7. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ren, W. Research on diagnosis system for abnormal vibration of mine vibrating screen. Mech. Manag. Dev. 2021, 36, 167–169. [Google Scholar]
- Li, J.W.; Gu, Z.F.; Zhu, H.F.; Yu, J.X. Study on intense vibration of local structures of Zhanghewan pumped-storage powerhouse. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 8. [Google Scholar] [CrossRef]
- Fujino, Y.; Siringoringo, D.M.; Ikeda, Y.; Nagayama, T.; Mizutani, T. Research and Implementations of Structural Monitoring for Bridges and Buildings in Japan—A Review. Engineering 2019, 5, 1093–1119. [Google Scholar] [CrossRef]
- Wyjadlowski, M. Methodology of dynamic monitoring of structures in the vicinity of hydrotechnical works—Selected case studies. Studia Geotech. Mech. 2017, 39, 121–129. [Google Scholar] [CrossRef] [Green Version]
- Clemente, P.; Bongiovanni, G.; Buffarini, G.; Saitta, F. Structural health status assessment of a cable-stayed bridge by means of experimental vibration analysis. J. Civ. Struct. Health Monit. 2019, 9, 655–669. [Google Scholar] [CrossRef]
- Ponzo, C.F.; Di Cesare, A.; Telesca, A.; Pavese, A.; Furinghetti, M. Advanced Modelling and Risk Analysis of RC Buildings with Sliding Isolation Systems Designed by the Italian Seismic Code. Appl. Sci. 2021, 11, 1938. [Google Scholar] [CrossRef]
- Bergamo, E.; Fasan, M.; Bedon, C. Efficiency of Coupled Experimental–Numerical Predictive Analyses for Inter-Story Floors Under Non-Isolated Machine-Induced Vibrations. Actuators 2020, 9, 87. [Google Scholar] [CrossRef]
- Czech, K.; Gosk, W. Impact of the operation of a Tri-Band Hydraulic Compactor on the Technical Condition of a Residential Building. Appl. Sci. 2019, 9, 336. [Google Scholar] [CrossRef] [Green Version]
- Golik, V.I.; Kongar-Syuryun, C.B.; Michałek, A.; Pires, P.; Rybak, A. Ground transmitted vibrations in course of innovative vinyl sheet piles driving. J. Phys. Conf. Ser. 2021, 1921, 012083. [Google Scholar] [CrossRef]
- Ekanayake, S.; Liyanapathirana, D.; Leo, C. Influence zone around a closed-ended pile during vibratory driving. Soil Dyn. Earthq. Eng. 2013, 53, 26–36. [Google Scholar] [CrossRef]
- Oliveto, G.; Decanini, L.D. Repair and retrofit of a six story reinforced concrete building damaged by The earthquake in south-east Sicily on The 13th December 1990. Soil Dyn. Earthq. Eng. 1998, 17, 57–71. [Google Scholar] [CrossRef]
- Durucan, C.; Dicleli, M. Analytical study on seismic retrofitting of reinforced concrete buildings using steel braces with shear link. Eng. Struct. 2010, 32, 2995–3010. [Google Scholar] [CrossRef]
- De la Cruz, S.T.; López-Almansa, F.; Oller, S. Numerical simulation of the seismic behavior of building structures equipped with friction energy dissipators. Comput. Struct. 2007, 85, 30–42. [Google Scholar] [CrossRef]
- Caetano, E.; Cunha, Á.; Magalhães, F.; Moutinho, C. Studies for controlling human-induced vibration of the Pedro e Inês footbridge, Portugal. Part 1. Assess. Dyn. Behav. 2010, 32, 1069–1081. [Google Scholar]
- Živanović, S.; Pavic, A.; Reynolds, P. Modal testing and FE model tuning of a lively footbridge structure. Eng. Struct. 2006, 28, 857–868. [Google Scholar] [CrossRef] [Green Version]
- Zhi, B.; Ma, Z. Disturbance analysis of hydropower station vertical vibration dynamic characteristics: The effect of dual disturbances. Struct. Eng. Mech. 2015, 53, 297–309. [Google Scholar] [CrossRef]
- Fischer, O. Wind-excited vibrations-Solution by passive dynamic vibrating screens of different types. J. Wind. Eng. Ind. Aerodyn. 2007, 95, 1028–1039. [Google Scholar] [CrossRef]
- Li, Y.; Duan, Y.; Xiang, Y.; Luo, W.; Zhu, J. Vibration test and crack analyses on multi-story industrial factory buildings. Vib. Impact 2010, 29, 199–206. [Google Scholar]
- Okumura, K. Statistical analysis of field data of railway noise and vibration collected in an urban area. Appl. Acoust. 1991, 33, 263–280. [Google Scholar] [CrossRef]
- Ding, Y.; Fu, H.; Wang, Z.; Wang, Y.; Xie, W. Vibration test and comfort analysis of wooden building floor structure under environmental and impact excitation. Build. Struct. 2020, 50, 100–106. [Google Scholar]
- Saurenman, H. In-service tests of the effectiveness of vibration control measures on the BART rail transit system. J. Sound Vib. 2006, 293, 888–900. [Google Scholar] [CrossRef]
- Lombact, G.; Degrand, G. The control of ground-boune vibrations from railway traffic by means of continuous floating slab. J. Sound Vib. 2006, 297, 946–961. [Google Scholar] [CrossRef]
- Chen, J.; Wei, S.; Xin, L. Vibration analysis and treatment of the main building structure of a workshop of a coal preparation plant. Eng. Constr. Des. 2019, 10, 1–2. [Google Scholar]
- Zhou, J.; Fang, X.; Liang, Z. Evaluation of long-period seismic spectrum based numerical simulation and shaking-table test of assembly structures. J. Build. Struct. 2018, 39, 88–98. [Google Scholar]
- Xu, J. Numerical simulation analysis of structure optimization design on different beam of vibrating screen. Coal Technol. 2017, 36, 286–288. [Google Scholar]
- Lin, S. New equipment for blasting safety assessment TC-4850 blasting vibration meter. Blasting 2008, 4, 33. [Google Scholar]
- GB50868-2013; Standard for Allowable Vibration of Building Engineering. Nation Standard of the People’s Republic of China, China Planning Press: Beijing, China, 2014.
- Xu, J. Structure Vibration Engineering Manual; China Architecture & Building Press: Beijing, China, 2002; p. 55. [Google Scholar]
- Meng, W.; Feng, Y.; Shen, J.; An, X. Vibration test and reinforcement and design of beam and plate in Matou coal preparation plant. Coal Eng. 2018, 50, 133–136. [Google Scholar]
- Wang, X.; Bai, J.; Hu, Y.; Wang, S.; Han, Y. Determination of damping ratio in secondary vibration isolation design of vibration machinery. Coal Min. Mach. 2014, 35, 25–27. [Google Scholar]
- ISO 4866:2010; Mechanical Vibration and Shock—Vibration of Fixed Structures—Guidelines for the Measurement of Vibrations and Evaluation of Their Effects on Structures. International Organization for Standardization: Geneve, Switzerland, 2010.
- DIN 4150-3:1999; Structural Vibration. Part 3: Effects of Vibration on Structures. DIN Deutsches Institut für Normung: Berlin, Germany, 1999.
- BS 7385-2:1993; Evaluation and Measurement for Vibration in Buildings—Part 2: Guide to Damage Levels from Groundborne Vibration. British Standard Institution: London, UK, 1993.
- BS 5228-4:1992; Code of Practice for Noise and Vibration Control Applicable to Piling Operations. British Standard Institution: London, UK, 1992.
- VSS-SN640-312a:1992; Effects of Vibration on Construction. Swiss Consultants for Road Construction Association: Zurich, Switzerland, 1992.

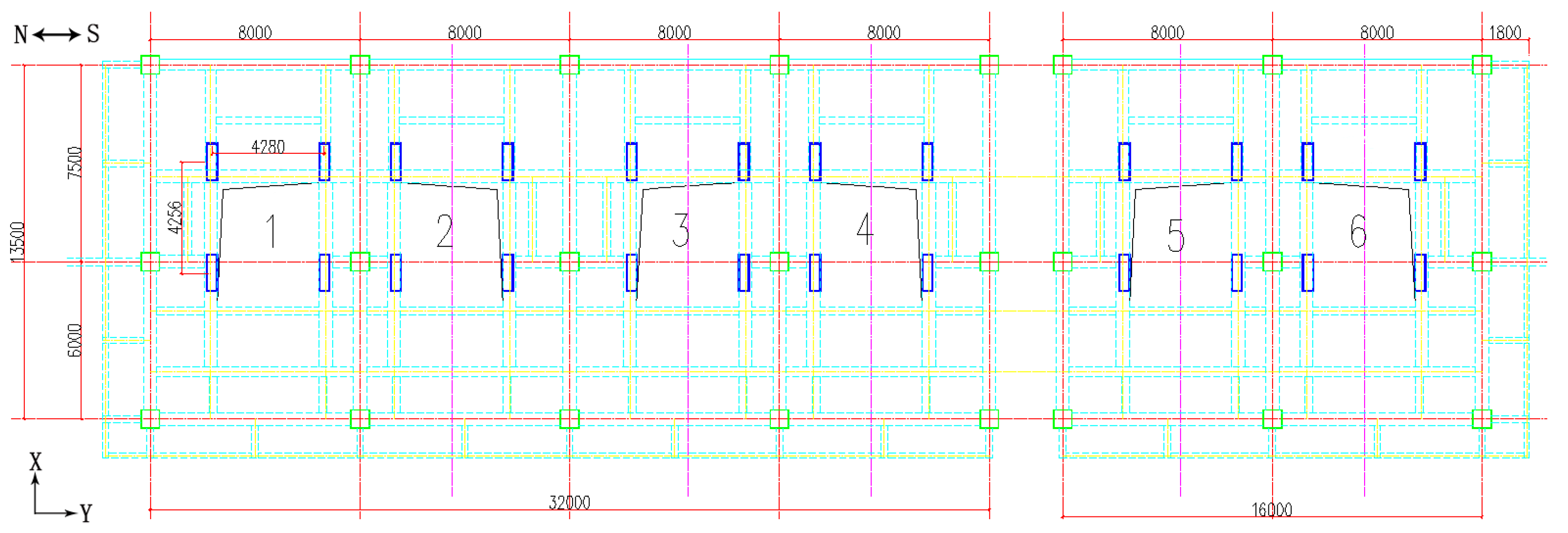
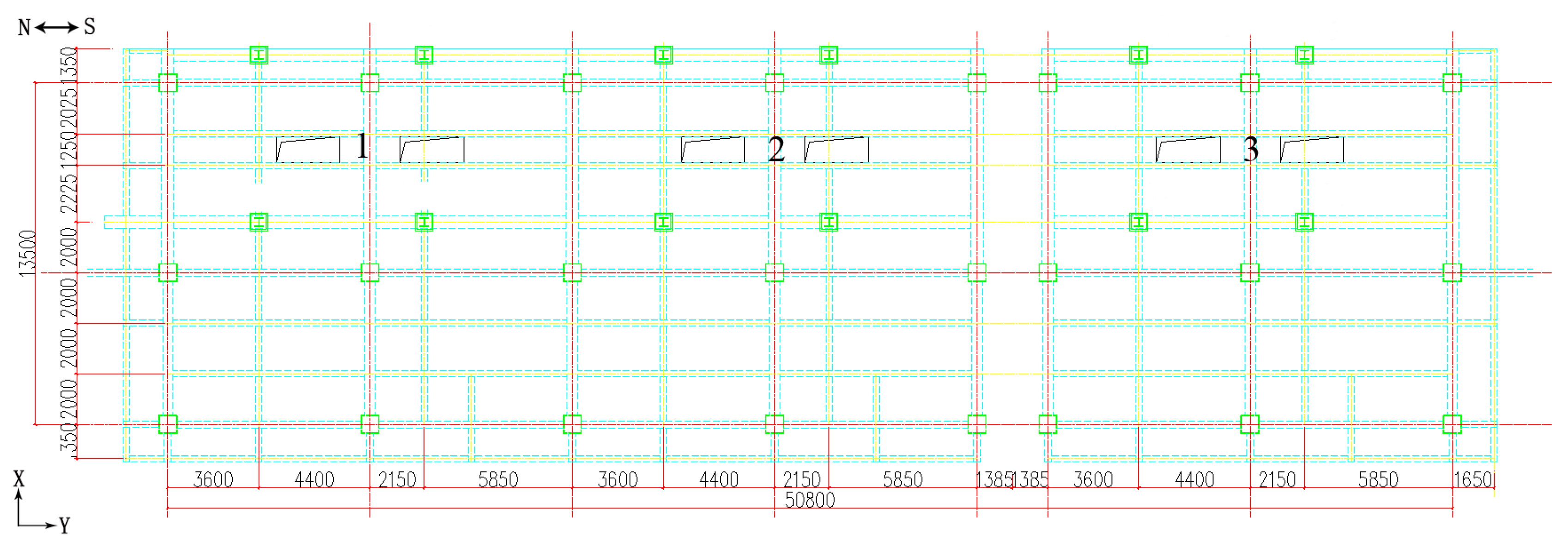
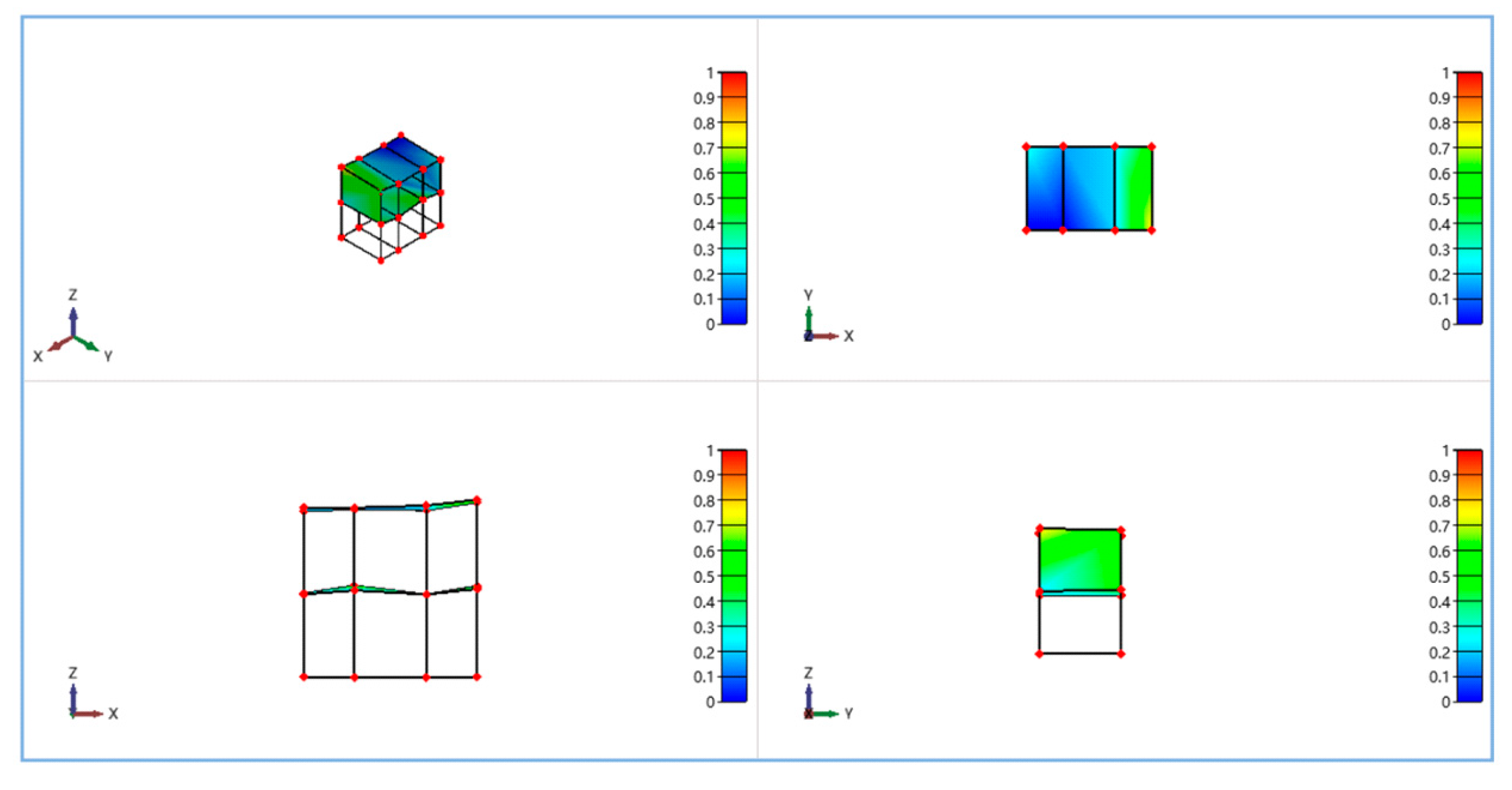
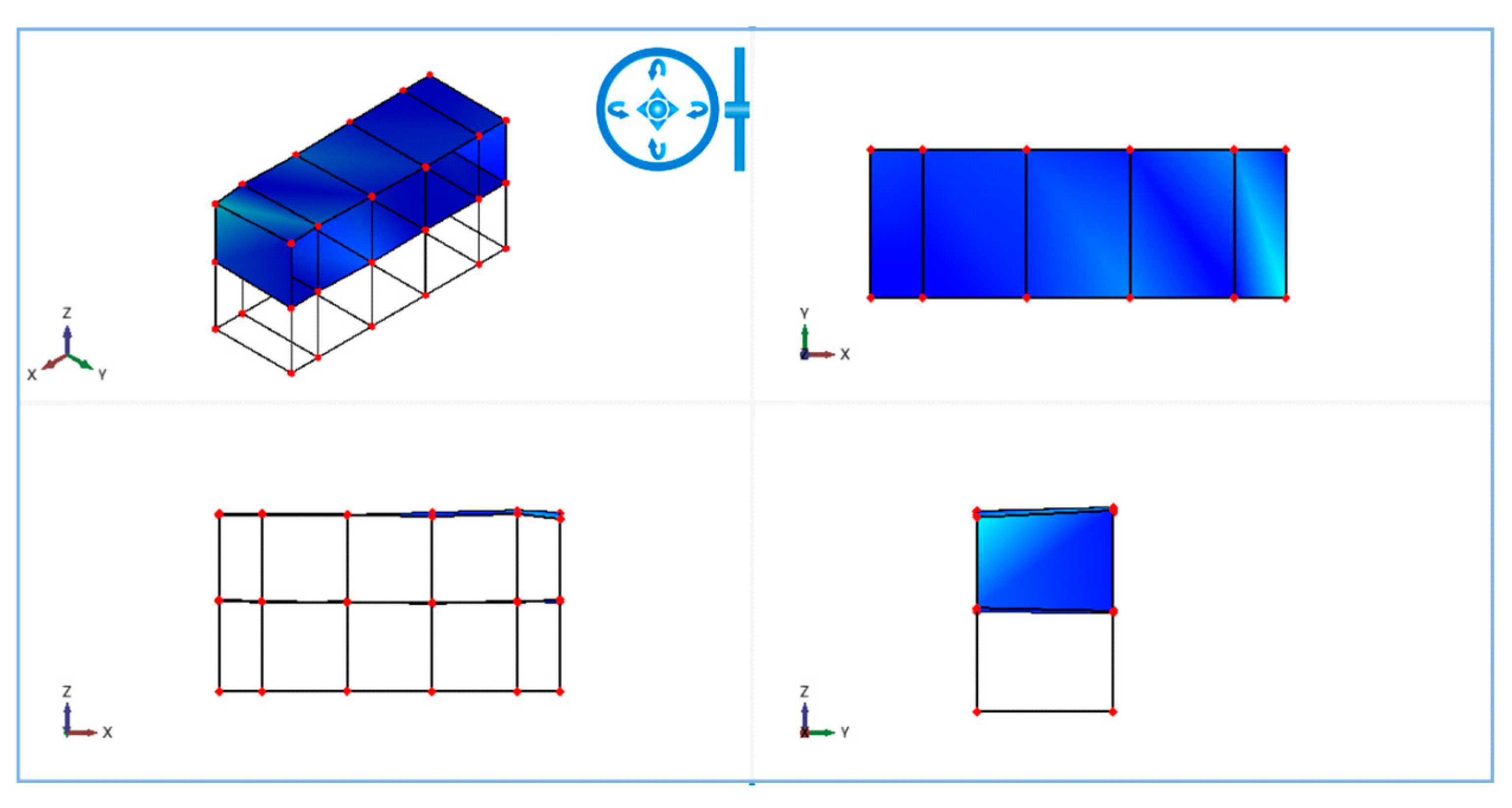

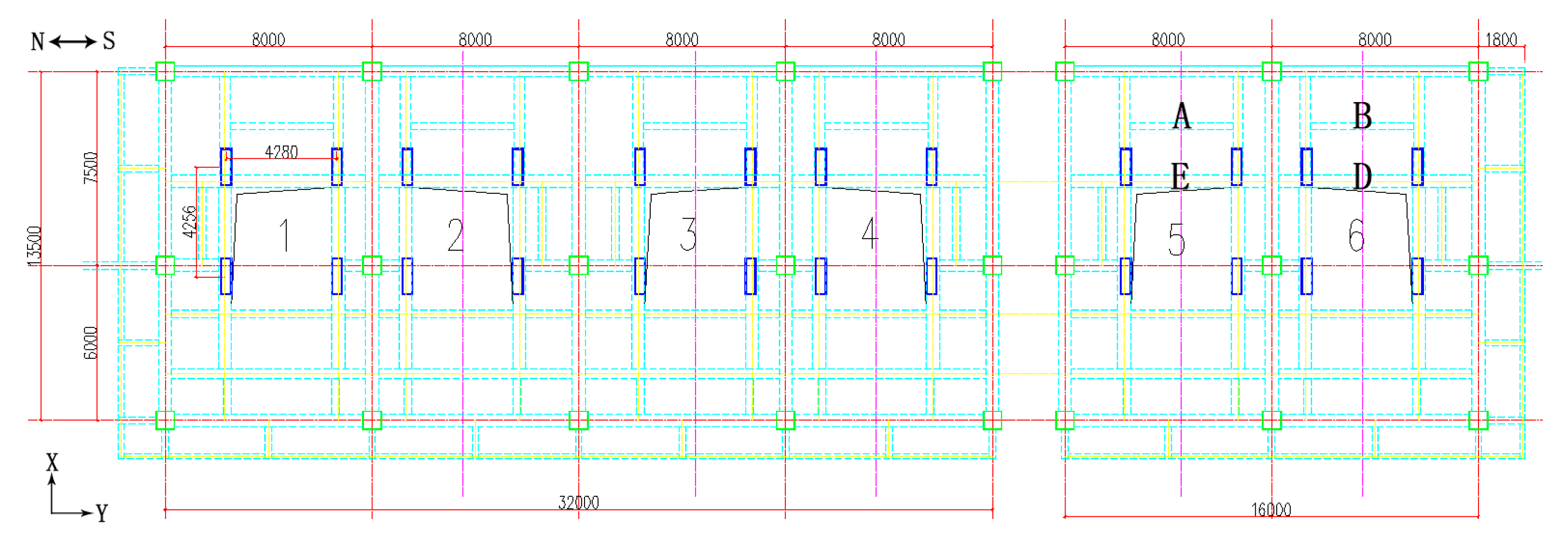

| Number | Details of Monitoring |
|---|---|
| 1 | The peripheral beam–plate of single vibrating screen under no-load state |
| 2 | The peripheral beam–plate of single vibrating screen under heavy-load state |
| 3 | The peripheral beam–plate of multiple vibrating screens under no-load state |
| 4 | The steel frame supports on the third floor of multiple vibrating screens under no-load state |
| 5 | The west-half beam on the third floor of multiple vibrating screens under no-load state |
| 6 | The longitudinal beam on the third floor of multiple vibrating screens under no-load state |
| 7 | The east longitudinal beam on the second floor of multiple vibrating screens under no-load state |
| 8 | Vibrating screen support of multiple vibrating screens under heavy-load state |
| 9 | The east longitudinal beam–plate of multiple vibrating screens under heavy-load state |
| 10 | Longitudinal beam–plate on the west side of the third floor of multiple vibrating screens under heavy-load state |
| Number | Details of Monitoring |
|---|---|
| 11 | Vibrating screen support of single vibrating screen under no-load state |
| 12 | The peripheral beam–plate of single vibrating screens under no-load state |
| 13 | The peripheral beam–plate of multiple vibrating screens under no-load state |
| 14 | The steel frame supports on the third floor of multiple vibrating screens under no-load state |
| 15 | The west-half beam on the third floor of multiple vibrating screens under no-load state |
| 16 | The north–south longitudinal beam of the third floor of multiple vibrating screens under heavy-load state |
| Number | Measuring Points (North Part) | Measuring Direction | Number | Measuring Points (South Part) | Measuring Direction | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | Z+/Y+ | 1 | 1 | 2 | 3 | 4 | 5 | 6 | Z+/X+ |
| 2 | 1 | 2 | 3 | 4 | 5 | 6 | Z+/X+ | 2 | 1 | 2 | 3 | 4 | 5 | 6 | Z+/Y+ |
| 3 | 1 | 7 | 8 | 9 | 10 | 11 | Z+/Y+ | 3 | 1 | 7 | 8 | 9 | 10 | 11 | Z+/X+ |
| 4 | 1 | 7 | 8 | 9 | 10 | 11 | Z+/X+ | 4 | 1 | 7 | 8 | 9 | 10 | 11 | Z+/Y+ |
| 5 | 1 | 12 | Z+/X+/Y+ | 5 | 1 | 12 | 13 | 14 | 15 | 16 | Z+/X+ | ||||
| 6 | 1 | 13 | 14 | 15 | 16 | 17 | Z+/Y+ | 6 | 1 | 12 | 13 | 14 | 15 | 16 | Z+/Y+ |
| 7 | 1 | 13 | 14 | 15 | 16 | 17 | Z+/X+ | ||||||||
| 8 | 1 | 18 | 19 | 20 | 21 | 22 | Z+/Y+ | ||||||||
| 9 | 1 | 18 | 19 | 20 | 21 | 22 | Z+/X+ | ||||||||
| 10 | 1 | 23 | 24 | Z+/X+/Y+ | |||||||||||
| Modality | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Frequency (Hz) | 0.738 | 2.673 | 3.179 | 9.948 | 12.467 | 15.748 | 16.591 |
| Damping ratio (%) | 4.953 | 1.704 | 0.186 | 1.438 | 0.730 | 0.379 | 0.101 |
| Modality | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Frequency (Hz) | 1.987 | 3.729 | 4.449 | 5.644 | 6.359 | 10.944 | 12.553 | 14.837 |
| Damping ratio (%) | 0.056 | 1.173 | 1.045 | 2.596 | 1.502 | 1.158 | 0.442 | 0.424 |
| Mode | Mode Description | Frequency (Hz) | Error (%) | |
|---|---|---|---|---|
| Measured | Simulation | |||
| 1 | Bending in Y-direction | 1.96 | 1.97 | 0.10 |
| 2 | Bending in X-direction | 1.97 | 2.00 | 1.73 |
| 3 | Torsion in the X-Y plane | 2.64 | 2.80 | 5.99 |
| 4 | Second-order bending in Y-direction | 4.48 | 4.38 | −2.12 |
| 5 | Second-order bending in X-direction | 4.62 | 4.57 | −1.00 |
| 6 | First-order bending of steel frame in X-direction on the third floor | 5.64 | 5.50 | −2.53 |
| 7 | Second-order bending in X-direction of the concrete/steel frame | 5.81 | 5.78 | −0.48 |
| 8 | Second-order torsion in X-Y plane of the concrete/steel frame | 6.36 | 6.30 | −0.90 |
| 9 | Torsion in X-Y plane of steel frame | 10.94 | 10.51 | −3.97 |
| 10 | First-order bending beam–plate in Z-direction | 12.55 | 11.84 | −5.68 |
| 11 | Second-order bending of beam–plate in Z-direction | 14.84 | 14.94 | 0.69 |
| Mode | Mode Description | Frequency (Hz) | Error (%) | |
|---|---|---|---|---|
| Measured | Simulation | |||
| 1 | Bending in Y-direction | 1.99 | 1.97 | −1.01 |
| 2 | Bending in X-direction | 1.99 | 2.1 | 5.53 |
| 3 | Torsion in the X-Y plane | 2.62 | 2.97 | 13.36 |
| 4 | Second-order bending in Y-direction | 4.85 | 4.65 | −4.12 |
| 5 | Second-order bending in X-direction | 5.06 | 4.77 | −5.73 |
| 6 | First-order bending of steel frame in X-direction of the third floor | 5.76 | 5.75 | −0.17 |
| 7 | Second-order torsion in X-direction of the concrete-steel frame | 6.42 | 6.97 | 8.57 |
| 8 | Bending of steel frame in X-direction of the second floor | 7.66 | 7.40 | −3.39 |
| 9 | Torsion in the X-Y plane of steel frame | 9.95 | 10.55 | 6.03 |
| 10 | Bending in Z-direction of beam–plate of the second floor | 12.47 | 12.05 | −3.37 |
| 11 | Bending in Z-direction of beam–plate of the third floor | 15.74 | 14.69 | −6.67 |
| Directions | Damping Coefficient (kN/(mm/s)) | Velocity Index |
|---|---|---|
| X | 10 | 1 |
| Y | 10 | 1 |
| Z | 28 | 1 |
| Scheme | Vibrating Screens Number | Structure Location |
|---|---|---|
| 1 | 2, 3 | Under the beam of the east support of the vibrating screens |
| 2 | 1, 4 | |
| 3 | 1, 2, 3, 4 |
| Point | Acceleration Vibration Reduction Rate (%) | Velocity Vibration Reduction Rate (%) | Displacement Vibration Reduction Rate (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Damping | Isolation | Absorption | Damping | Isolation | Absorption | Damping | Isolation | Absorption | |
| 56 | 82.50 | 80.98 | 84.75 | 83.12 | 80.92 | 81.28 | 83.55 | 80.99 | 77.03 |
| 60 | 64.22 | 80.98 | 94.49 | 66.60 | 80.94 | 94.76 | 68.79 | 80.99 | 94.00 |
| 96 | 74.62 | 80.98 | 84.01 | 74.39 | 80.98 | 80.67 | 75.54 | 81.03 | 77.58 |
| ⋯ | |||||||||
| 490 | 82.71 | 80.95 | 92.14 | 83.88 | 80.96 | 92.64 | 84.35 | 80.95 | 91.85 |
| 491 | 78.52 | 80.97 | 92.82 | 78.77 | 80.97 | 92.57 | 78.53 | 80.97 | 90.37 |
| 492 | 82.62 | 80.95 | 92.10 | 83.79 | 80.94 | 92.59 | 84.26 | 80.95 | 91.62 |
| Scheme | Cost | Construction Period | Comprehensive | Vibration Reduction Rate |
|---|---|---|---|---|
| Vibration damping | The purchase of dampers and the design and construction of support columns | Need to consider the design of the support column, the construction period and the purchase period of the damper | Moderate cost and long construction period | More than 70% |
| Vibration isolation | Procurement and installation of vibration isolation frame | Purchase and installation cycle of vibration isolation frame | Moderate cost and short construction period | More than 80% |
| Vibration absorption | Design and processing of vibration absorber (needs to be customized) | Vibration absorber design, custom processing and installation cycle | High cost and long construction period | More than 90% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Li, Z.; Zhang, Z.; Zhao, W.; Niu, Z.; Cheng, J. Vibration Test and Control of Factory a Building under Excitation of Multiple Vibrating Screens. Buildings 2022, 12, 607. https://doi.org/10.3390/buildings12050607
Yu J, Li Z, Zhang Z, Zhao W, Niu Z, Cheng J. Vibration Test and Control of Factory a Building under Excitation of Multiple Vibrating Screens. Buildings. 2022; 12(5):607. https://doi.org/10.3390/buildings12050607
Chicago/Turabian StyleYu, Jianxin, Zhenzhen Li, Zhenhua Zhang, Wusheng Zhao, Zhiwei Niu, and Jingji Cheng. 2022. "Vibration Test and Control of Factory a Building under Excitation of Multiple Vibrating Screens" Buildings 12, no. 5: 607. https://doi.org/10.3390/buildings12050607






