Bearing Capacity of Annular Foundations on Rock Mass with Heterogeneous Disturbance by Finite Element Limit Analysis

Abstract

Estimating the performance of foundations on rock mass is essential in designing buildings. Stability assessment of weathered rocks under foundation load is a complicated task if there is an internal opening within the foundation. This study applies finite element limit analysis to evaluate the bearing capacity of annular foundations resting on medium to highly weathered rocks following the modified Hoek–Brown rock mass. Special attention is focused on the effect of rock mass disturbance. The level and heterogeneity of rock mass disturbance are considered as constant or linearly varying disturbance factors with depth, which capture the damage level and zones due to construction and blasting. The results obtained from the analysis compare well with the existing solutions. The numerical results are presented in the familiar form of bearing capacity factors as a function of the dimensionless parameters related to foundation perforation and rock mass properties as well as the foundation-rock interface. The failure patterns of annular foundations are also investigated for a few cases with different levels of disturbance and foundation roughness.

1. Introduction

High-rise buildings constructed in urban areas are often placed on weathered rocks with uninform disturbance. Rock mass in its in situ medium has heterogenous and anisotropic properties, and several classification systems of the rock mass have been developed [1]. A good understanding of the stability of rock mass is of great significance to the design of buildings and infrastructure.

Ring footings are commonly used to support axisymmetric structures such as liquid storage tanks, radar stations, chimneys, and silos. The stability of such footings is significantly affected by the mere presence and geometry of perforation. Annular foundations are commonly used to support the silo structure. Many studies have been devoted to estimating the bearing capacity of annular foundations resting on soil mass based on the physical model tests [2,3], the in situ tests [4,5], the limit equilibrium method [6], the method of characteristic [7,8,9], the finite element method [10,11,12], the finite difference method [13,14,15], and the finite element limit analysis [16,17]. In contrast, limited studies have been carried out to determine the bearing capacity of annular foundations over rock mass, though numerous studies have been carried out by researchers [18,19,20]. In their research, results were presented for the perforation ratio as well as the rock mass properties, although the significance of rock mass disturbance is not discussed.

Rock masses consist of rock materials and discontinuities such as joints, fractures, and bedding planes. The strength of such rock media can be quantified by the Hoek–Brown failure criterion, where the rock mass disturbance induced by blasting and/or construction is taken into account by using the disturbance factor D. Several numerical studies on the bearing capacity of rock mass have been reported and most of generally assumed a condition of D = 0. These results can be found in the works of Merifield et al. [21], Saada et al. [22], Clausen [23], Keshavarz and Kumar [24], Chakarborty and Kumar [25], Yang [26], Mansouir et al. [27], and Keawsawasvong et al. [28]. However, a constant D applied to an entire rock mass will not be appropriate, as pointed out by Hoek and Brown [29]. Li et al. [30] reported the stability numbers of heterogenous rock slopes with the variation of D with distance from the face significantly differs from those of the undisturbed and homogenous disturbed rock slopes.

This paper applied finite element limit analysis to estimate the bearing capacity of annular foundations resting on rock mass obeying the modified Hoek–Brown failure criterion and associated flow rule. The obtained solutions are presented in the familiar form of bearing capacity factors and compared with the numerical solutions reported in the literature. The effect of rock mass disturbance on the stability of annular foundation is highlighted.

2. Background

To estimate the non-linear strength envelope of intact rock and jointed rock masses, the original Hoek–Brown (HB) failure criterion was proposed in 1980 and has been subsequently updated. The last version, used here, is expressed as [31]:

$${\sigma }_1={\sigma }_3+{\sigma }_{ci}{\left(m_b\frac{{\sigma }_3}{{\sigma }_1}+s\right)}^a$$

(1)

where σ_ci is the uniaxial compressive strength of the intact rock. σ₁ and σ₃ are the major and minor principal stresses, respectively, which are considered as positive when tensile in nature. m_b, s, and a are the dimensionless material parameters, defined as:

$$m_b=m_i \exp \left(\frac{GSI-100}{28-14D}\right)$$

(2)

$$s=\exp \left(\frac{GSI-100}{9-3D}\right)$$

(3)

$$a=\frac{1}{2}+\frac{1}{6}\left(e^{-\mathrm{GSI}/16}-e^{-20/3}\right)$$

(4)

where m_i is the value of m_b for intact rock. The value of m_i is related to the minerology and texture of the intact rock, varying from 4 for very fine weak rock (e.g., claystone) to 33 for coarse igneous light-colored rocks (e.g., granite). GSI is the geological strength index which features the quality of the rock mass [32]. The value of GSI ranges from approximately 10 for extremely poor rock masses to 100 for intact rock. D is the disturbance factor which depends on the extent of weathering and blast damage of the rock mass. The value of D varies from 0 for the undisturbed in situ rock masses to 1 for extremely disturbed rock masses. One may recognize that rock mass foundations subjected to less weathering and good blasting attain greater rock mass strength compared to severely disturbed rock mass foundations, indicating that the application of a constant D to an entire rock mass underlying foundation can underpredict the stability of the rock-foundation system. Thus, the heterogeneous disturbance of rock mass should be taken into account in rock foundations.

Using the modified Hoek–Brown failure criterion, the ultimate bearing capacity of surface spread foundations on rock mass q_u can be expressed in terms of a dimensionless bearing capacity factor N_σ:

$$q_u= {\sigma }_{ci}{N}_{\sigma }$$

(5)

For weightless rock mass, the bearing capacity factor $N_{\sigma }$ is denoted by $N_{\sigma 0}$.

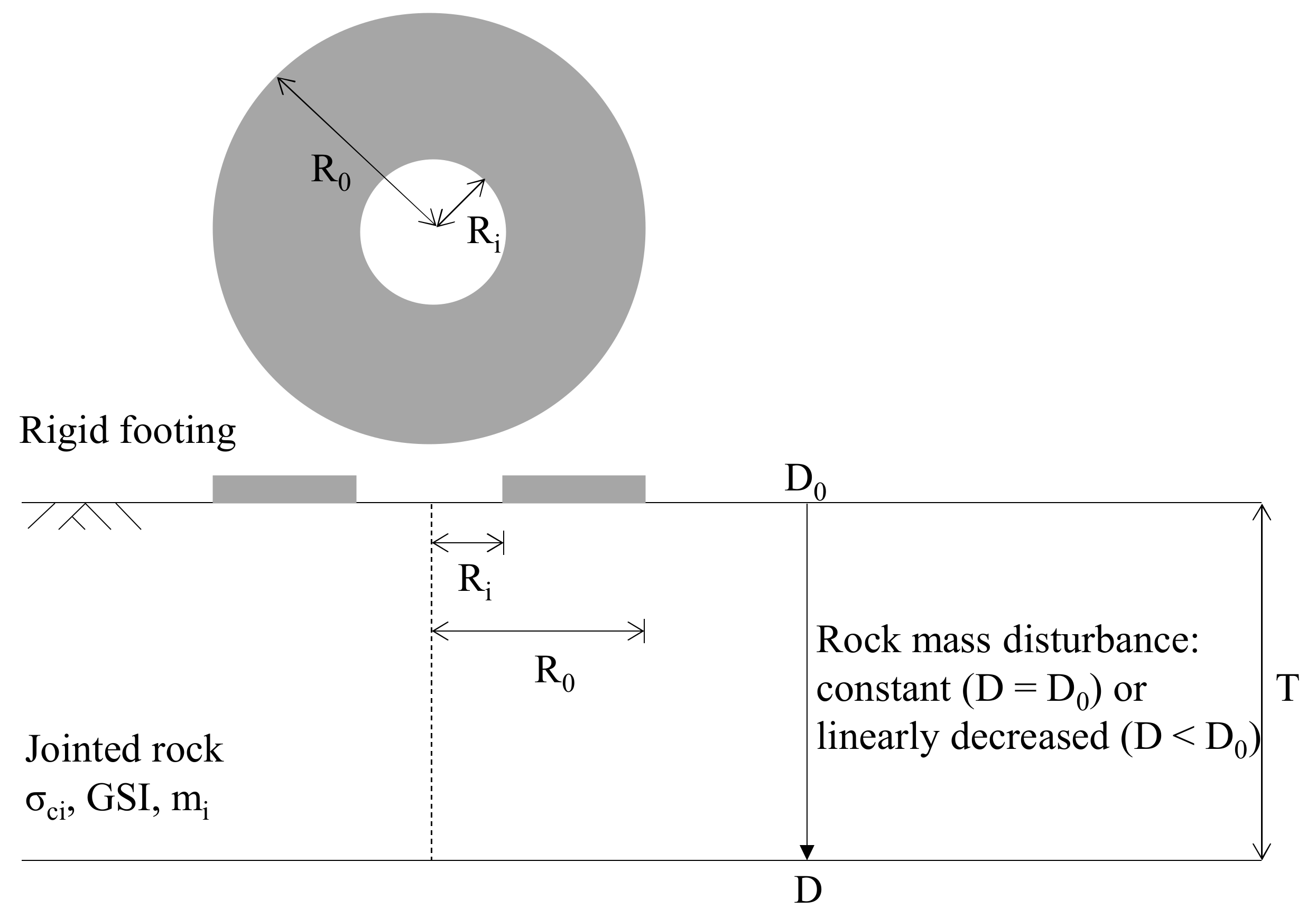
3. Problem Definition

Figure 1 illustrates the geometry and parameters of the rock-foundation system considered. A rigid annular foundation is placed on a rock mass medium with horizontal ground surface. The annular foundation is specified with external and internal radii R₀ and R_i, respectively. The base of the foundation is assumed to be perfectly smooth and perfectly rough. The interface between the soil and foundation is prescribed as bonded (i.e., no separation allowed) for rough and frictionless for smooth. A similar assumption is used by Keshavarz and Kumar [8] for circular foundations. The disturbance of rock mass is considered to be homogeneous or heterogeneous. For the homogeneous condition, the disturbance factor D is constant with depth. For the heterogeneous condition, the disturbance factor on the ground surface D₀ decreases linearly with depth and becomes zero at the damage depth from the ground surface T.

For convenience in analysis, dimensionless parameters for geometry and materials are introduced. The perforation of annular foundations is presented as the external-to-internal radius ratios R_i/R₀. The value of R_i/R₀ ranges from 0 to 0.75, which covers most problems of practical interest [11,12]. The unit weight of rock γ was quantified as σ_ci/γR₀, varying from 250 to ∞. The infinite value of σ_ci/γR₀ indicates the weightless rock mass. The values of GSI and m_i are within the range of 10–100 and 5–35, respectively. The damage depth of heterogeneous disturbance is quantified as T/R₀, which ranges from 1 to 5.

4. Finite Element Limit Analysis

All of the calculations in this study were carried out using the commercial software OptumG2 [33], which enables calculations of the collapse loads for geotechnical stability problems using the finite element limit analysis (FELA). This numerical technique combines the discretization of finite elements for handling intricate soil properties, loadings, and boundary conditions, with the plastic bound theorems of limit analysis to obtain the exact limit load by upper bound (UB) and lower bound (LB) solutions. The LB solution aims for the lower bound of the ultimate load in the static admissible stress field, while the UB solution considers that there exists an upper bound of the true bearing capacity based on the kinematically allowable velocity field [34]. All numerical results from the present study are described by using an average (AVG) solution:

$$\mathrm{AVG}=\left(\mathrm{UB}+\mathrm{LB}\right)/2$$

(6)

Figure 2 shows the problem domain and boundary conditions. The foundation is adopted as a weightless and perfectly rigid element. To achieve a perfectly smooth and perfectly rough interface between the rock mass and foundation, the interface factors are set as 0 and 1. Due to an axisymmetric distribution of the stress about a vertical line passing through the center of the foundation, only half of the problem domain was considered. To avoid the boundary effect, the horizontal boundary was placed 20R₀ away from the edge of the foundation, and the vertical boundary was placed at a depth of 15R₀ from the surface. Both horizontal and vertical boundaries were modeled to prevent radial displacement, and the bottom boundary was modeled as fully fixed to prevent radial and vertical displacement. Adaptive meshing in FELA is used to decrease the gap between the upper and lower bound estimates of the failure load to a minimum. This technique is normally based on an error determination of some control parameters.

5. Results and Comparison

Figure 3 provides the obtained N_σ0 values of a circular foundation (R_i/R₀ = 0) on undisturbed weightless rock mass (D = 0 and σ_ci/γR₀ = ∞), together with other numerical analyses for equivalent conditions. This result indicates the variation of N_σ0 values with m_i for the case of GSI = 10, 50 and 100. As shown in the Figure 3, the results of the numerical analysis are very close to those obtained with the finite element method of Clausen [23] and method of characteristics of Keshavarz and Kumar [24]. For example, the N_σ0 values of 1.61 for m_i =10 and GSI = 50 is obtained, which are <4% in error compared with those from Clausen [23] and Keshavarz and Kumar [24], i.e., 1.65 and 1.67, respectively. The expression from the lower bound finite element method of Chakarborty and Kumar [24] gives values that are consistent with the present numerical analysis results, except for N_σ0 values of GSI = 10. Furthermore, even under conditions other than given GSI values, N_σ0 values are consistent with comparable numerical analysis results.

The variation of the bearing capacity factors N_σ for different combinations of R_i/R₀ and GSI is shown in Figure 4 for the case of m_i = 15, D₀ = 0 and σ_ci/γR₀ = 1000, 10,000 and infinite (=weightless soil). For each GSI at a given value of σ_ci/γR₀, there is little effect on the N_σ values due to the increase in R_i/R₀. This indicates that the unit weight of the rock mass has little influence on the value of N_σ. Figure 4 also shows an increase in the value of N_σ as the GSI increases, and compares the N_σ values obtained from the present analysis to the results of Xiao et al. [18] when GSI = 10 and 100 of weightless soil. It can be observed that the present solutions compare reasonably well with the results of Xiao et al. [18].

The variation of the bearing capacity factors N_σ for different combinations of R_i/R₀ and σ_ci/γR₀ is shown in Figure 5 for the case of GSI = 50, D₀ = 0, and m_i = 5, 15, 25, and 35. The result shows that as R_i/R₀ increases from 0 to 0.25 the value of N_σ increases, reaching the peak of bearing capacity. However, when R_i/R₀ becomes a value higher than 0.25 the value of N_σ decreases as R_i/R₀ increases. Figure 5a,b show that for low intact rock parameters (m_i ≤ 15). When R_i/R₀ ≤ 0.25, the variation in the value of N_σ increases as σ_ci/γR₀ increases, which is greater when m_i is 15 rather than 5. It is also noted that for all annular foundations, except where R_i/R₀ is 0.25, there is less N_σ than the circular foundation (R_i/R₀ = 0). On the other hand, Figure 5c,d demonstrate this for high intact rock parameters (m_i ≥ 25). Different from Figure 5a,b described earlier, σ_ci/γR₀ exhibits almost the same tendency due to it not affecting the N_σ values. In addition, when mi is greater than 25, the range of R_i/R₀ where the value of N_σ is greater than the circular foundation of 0.25 to 0.33.

The variation of the bearing capacity factors N_σ of rock mass with homogeneous disturbance factor D for different combinations of R_i/R₀ and m_i is shown in Figure 6 for the case of σ_ci/γR₀ = 1000, GSI = 50, D = 0, and m_i = 5, 15, 25, and 35. As expected, the value of N_σ decreases as disturbance factor D increases. Furthermore, the variation in N_σ values due to the increase in R_i/R₀ decreases as D increases. This implies that the larger D, the less influence on the external-to-internal radius ratios R_i/R₀. It is also noticed that, for a given each value of m_i, the tendency for N_σ values to peak at R_i/R₀ = 0.25 becomes more pronounced as m_i increases. In addition, it can be seen that when m_i is less than 15, the N_σ value remains almost constant because the increase in R_i/R₀ does not affect the N_σ value.

The variation of the bearing capacity factor N_σ of rock mass with heterogeneous disturbed regions T/R₀ for different combinations of R_i/R₀ and D₀ is shown in Figure 7 for the case of σ_ci/γR₀ = 1000, GSI = 50, m_i = 15, D = 0, and D₀ = 0, 0.5, and 1.0. It is observed that as the heterogeneous disturbed region T/R₀ increases, the N_σ values of D₀ = 0.5 and D₀ = 1.0, excluding undisturbed (D₀ = 0), decrease. In addition, a larger T/R₀ diminishes the rate of decrease in the value of N_σ as increases in R_i/R₀. Furthermore, as the values of D₀ increase, the peak of bearing capacity becomes the circular foundation (R_i/R₀ = 0) rather than the value of R_i/R₀ = 0.25 in the annular foundation. Additionally, when T/R₀ is greater than 4, the value of heterogenous rock mass N_σ is approximately equal to that N_σ value of the rock mass of homogenous. This is described in more detail in the following Figure 8.

The variation of the bearing capacity factor N_σ of rock mass with linear decrease disturbance factor D₀ for different combinations of T/R₀ and R_i/R₀ is shown in Figure 8 for the case of σ_ci/γR₀ = 1000, GSI = 50, m_i = 15, and D = 0. As expected, the value of N_σ decreases as D₀ increases. However, it can be seen that the N_σ value of each R_i/R₀, due to the increase in T/R₀, has the same trend because the rate of diminishing is almost identical. It is also noticed that the N_σ values decrease the most in the circular foundation (R_i/R₀ = 0), and the N_σ values rate of decrease diminishes with the increase in R_i/R₀. Furthermore, it can be seen that for the given values of D₀, the value of N_σ decreases to an increase in T/R₀ up to T/R₀ ≈ 4, and, thereafter, the value of N_σ becomes almost constant.

The variation of bearing capacity factor N_σ of unit wight, GSI, m_i, and D of rock mass with smooth and rough bases for different combinations of R_i/R₀ is shown in Figure 9. The results indicate that for an annular foundation with a smooth base, the peak of bearing capacity occurs at the circular foundation (R_i/R₀ = 0). It can also be seen that for all parameters, the N_σ values are smaller than the annular foundation of the rough base, and the N_σ value decreases continuously as R_i/R₀ increases. Figure 9a shows that the variation of N_σ values at a smooth and rough bases for the unit weights of rock mass. The largest difference in N_σ values due to roughness is a R_i/R₀ value of 0.25, and the difference in N_σ values is expected to increase as is the peak of bearing capacity significantly in the case of rough bases. Figure 9b shows that the variation of N_σ values at smooth and rough bases for GSI of rock mass. It can be seen that the difference in N_σ values due to roughness are not significant for given values of GSI. Figure 9c shows that the variation of N_σ values at smooth and rough bases for the m_i of rock mass. The difference in N_σ values due to roughness is the largest difference when the R_i/R₀ value is 0.25, such as in Figure 9a. In addition, the decrease in m_i indicates a difference in N_σ values due to roughness decreasing. Figure 9d shows that the variation of N_σ values at a smooth and rough base for D of rock mass. It can be seen that the difference in N_σ values due to roughness decrease as D decreases. This shows that the m_i in Figure 9c has the same tendency to decrease.

Since the failure mechanisms obtained from UB and LB methods are slightly different, only failure mechanisms obtained from the UB method are used to portray the effects of HB parameters as well as the condition of loading. Figure 10 shows the cases of the rough base annular foundations on the rock masses for different homogeneous disturbed with R_i/R₀ = 0.5, σ_ci/γR₀ = 1000, GSI = 50, and m_i = 15. It is found that the size of the failure mechanism depends on the disturbance factor D, where the failure mechanism for the cases of D = 1 values are smaller than that of D = 0 values. In other words, the smaller the disturbance factor D, the greater the N_σ values, but the wider the failure mechanism. It is also noticed that the largest failure mechanism corresponds to 6.2R₀ at the edge of the annular foundation and the smallest failure mechanism corresponds to 4.3R₀ at the edge of the annular foundation.

Figure 11 shows the cases of the smooth and rough bases annular foundations on the rock masses with R_i/R₀ = 0.5, σ_ci/γR₀ = 1000, GSI = 50, m_i = 15, and D = 0. In the case of Figure 11a, which is a rough base annular foundation, the failure mechanism is formed by intersecting under the annular foundation. On the other hand, in the case of Figure 11b, which is a smooth base annular foundation, the failure mechanism of the external radius is not included in the internal radius region because the failure mechanism does not intersect. It is also noticed that the rough base annular foundation failure mechanism has a larger region compared to the smooth base annular foundation failure mechanism.

6. Conclusions

The following conclusions can be drawn from the present study:

• The bearing capacity factors N_σ obtained from the finite element limit analysis are in good agreement with those from analytical methods reported in literature for weightless undisturbed rock mass.
• As R_i/R₀ increases, the value of N_σ increases first and then decreases: the peak value of N_σ is achieved at R_i/R₀ = 0.25, indicating the optimal opening ratio such that the bearing capacity of annular foundations against the vertical loading is maximum. The N_σ value increases continuously with increasing GSI and m_i. However, an increase in σ_ci/γR₀ leads to a decrease in N_σ and the effect of σ_ci/γR₀ on N_σ is more predominant for smaller value of R_i/R₀.
• The rock mass disturbance has significant effect on the value of N_σ. For constant D, the N_σ value decreases with increasing D, implying that for poor quality rock masses, no consideration of disturbance (D = 0) will overestimate the bearing capacity of rock foundations. For heterogeneous D (which decreases linearly with depth), the N_σ value decreases with an increase in T/R₀. This means that the larger thickness of rock disturbance zone gives rise to the lower stability of annular foundations.
• The values of N_σ for a rough foundation for all values of GSI, m_i, σ_ci/γR₀ and D are always larger than those for a smooth foundation. In general, the maximum difference between the N_σ values occurs at R_i/R₀ = 0.25.
• In the failure mechanism of annular foundations, the extent of failure surface for an undisturbed rock mass is greater than that for a disturbed rock mass. In terms of internal plastic zone, a smooth foundation provides a local soil failure near ground surface, but its region is small compared with the corresponding rough foundation.