Defect Identification of Concrete Piles Based on Numerical Simulation and Convolutional Neural Network
Abstract
:1. Introduction
2. Method
2.1. Low-Strain Pile Integrity Test
2.2. Wavelet Packet Decomposition
2.3. Finite Element Analysis of Pile
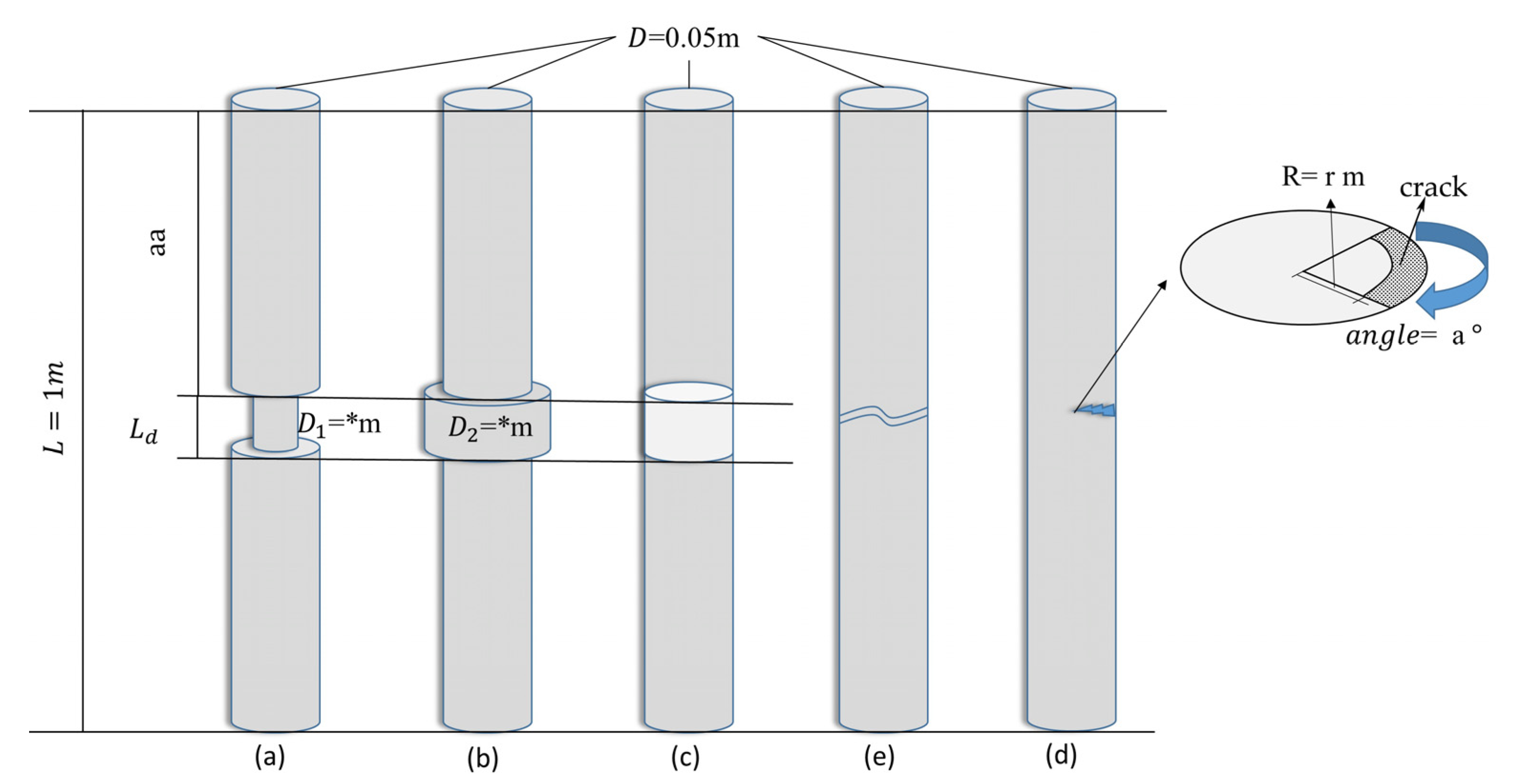
2.3.1. Basic Theory and Modeling Parameters
2.3.2. Specific Modeling Method
2.4. Experimental Validation
2.5. Batch Modeling Using Python Scripts
2.6. Convolution Neural Network
2.7. Data Enhancement and WPT
3. Result
4. Conclusions
- (1)
- The application of LSPIT is affected by many complex situations, such as the influence of environmental noise on low-strain data and the influence of rebound waves superimposed on each other in concrete piles, but these influences will not destroy the information contained in low-strain data. Therefore, signal processing by computer technology can help to extract the characteristic indexes of the signal and eliminate the influence of complex conditions on the signal.
- (2)
- After feature extraction and signal structure reconstruction of the signal, a CNN can be used as an auxiliary tool for defect identification of concrete pile defects by the low-strain reflection wave method.
- (3)
- The complex noise in the original signal has a negative impact on the performance of the CNN classifier. The performance and robustness of the CNN classifier were increased by WPT and data enhancement. Using WPT and data enhancement can improve the accuracy of signal recognition compared with using only velocity signals as a defect index.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rausche, F. Non-destructive evaluation of deep foundations. In Proceedings of the 5th International Conference on Case Histories in Geotechnical Engineering, New York, NY, USA, 13–17 April 2004; pp. 1–9. [Google Scholar]
- Chow, Y.K.; Phoon, K.K.; Chow, W.F. Low strain integrity testing of piles: Three-dimensional effects. J. Geotech. Geoenvironmental Eng. 2003, 129, 1057–1062. [Google Scholar] [CrossRef]
- Luo, W.; Chen, F.; Hu, J. Improvement of Low Strain Pile Integrity Test. In Proceedings of the ASEE (American Society of Engineering Education) Conference, Boston, MA, USA, 7–8 May 2010; pp. 583–589. Available online: https://monolith.asee.org/documents/zones/zone1/2008/student/ASEE12008_0082_paper.pdf (accessed on 11 April 2022).
- Liu, W.; Tian, S. Classification of pile integrity based on convolutional neural network. J. Nanchang Univ. (Eng. Ed. ) 2021, 43, 263–268. [Google Scholar] [CrossRef]
- Bao, L.S.; Ye, X.F.; Li, Q.; Wang, H. Research on the application of neural network based on genetic algorithm in pile foundation detection. Highw. Transp. Technol. (Appl. Technol. Version) 2017, 13, 228–231. [Google Scholar]
- Tam, C.M.; Tong, T.K.L.; Lau, T.C.T. Diagnosis of prestressed concrete pile defects using probabilistic neural networks. Eng. Struct. 2004, 26, 1155–1162. [Google Scholar] [CrossRef]
- Cui, D.M.; Yan, W.; Wang, X.Q. Towards intelligent interpretation of low strain pile integrity testing results using machine learning techniques. Sensors 2017, 17, 2443. [Google Scholar] [CrossRef] [Green Version]
- Yan, T.N.; Wang, S.; Li, S.J. The application of artificial neural network method in pile foundation detection. Geol. Sci. Technol. Inf. 1999, (Suppl. S1), 38–41. [Google Scholar]
- Cai, Q.Y.; Lin, J.H. Diagnosis of pile defects based on wavelet analysis and neural network. Vib. Impact 2002, 3, 13–16. [Google Scholar] [CrossRef]
- Cai, Q.Y. Diagnosis of Pile Defects Based on Wavelet Analysis and Neural Network. Master’s Thesis, Huaqiao University, Quanzhou, China, 2001. [Google Scholar]
- Wang, C.H.; Zhang, W. Neural network model for pile integrity identification based on reflection wave method. Geotech. Mech. 2003, 6, 952–956. [Google Scholar] [CrossRef]
- Liu, M.G.; Yue, X.H.; Yang, Y.B.; Li, Q. Intelligent identification of pile defects based on Sym wavelet and BP neural network. J. Rock Mech. Eng. 2007, 192 (Suppl. S1), 3484–3488. [Google Scholar]
- Zhang, G.; Jiang, X.L.; Liu, Z.J. Pile defect intelligent identification based on wavelet analysis and neural networks. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Frienbach, Switzerland, 2014; Volume 608–609, pp. 899–902. [Google Scholar] [CrossRef]
- Protopapadakis, E.; Schauer, M.; Pierri, E. A genetically optimized neural classifier applied to numerical pile integrity tests considering concrete piles. Comput. Struct. 2016, 162, 68–79. [Google Scholar] [CrossRef]
- Kang, W.; Zhao, Y.; Liu, L. Pile defect identification based on multi-higher order moment feature. J. GeoEng. 2018, 13, 69–77. [Google Scholar]
- Vu, G.; Timothy, J.J.; Singh, D.S. Numerical simulation-based damage identification in concrete. Modelling 2021, 2, 355–369. [Google Scholar] [CrossRef]
- Xie, Y.; Xiao, Y.; Liu, X. Time-frequency distribution map-based convolutional neural network (CNN) model for underwater pipeline leakage detection using acoustic signals. Sensors 2020, 20, 5040. [Google Scholar] [CrossRef]
- Zhuo, D.B.; Cao, H. Joint damage identification based on wavelet time-frequency diagram and lightweight convolutional neural network. Eng. Mech. 2021, 38, 228–238. [Google Scholar]
- Ritto, T.G.; Rochinha, F.A. Digital twin, physics-based model, and machine learning applied to damage detection in structures. Mech. Syst. Signal Processing 2021, 155, 107614. [Google Scholar] [CrossRef]
- Karvelis, P.; Georgoulas, G.; Kappatos, V. Deep machine learning for structural health monitoring on ship hulls using acoustic emission method. Ships Offshore Struct. 2021, 16, 440–448. [Google Scholar] [CrossRef]
- Rautela, M.; Senthilnath, J.; Moll, J. Combined two-level damage identification strategy using ultrasonic guided waves and physical knowledge assisted machine learning. Ultrasonics 2021, 115, 106451. [Google Scholar] [CrossRef]
- Perry, B.J.; Guo, Y. Atadero, R. Streamlined bridge inspection system utilizing unmanned aerial vehicles (UAVs) and machine learning. Measurement 2020, 164, 108048. [Google Scholar] [CrossRef]
- Li, Z.; Li, D.; Chen, Y. Deep learning-based guided wave method for semi-grouting sleeve detection. J. Build. Eng. 2022, 46, 103739. [Google Scholar] [CrossRef]
- Rausche, F.; Moses, F.; Goble, G.G. Soil resistance predictions from pile dynamics. J. Soil Mech. Found. Div. 1972, 98, 917–937. [Google Scholar] [CrossRef]
- Kim, H.J.; Mission, J.L.; Dinoy, P.R. Guidelines for impact echo test signal interpretation based on wavelet packet transform for the detection of pile defects. Appl. Sci. 2020, 10, 2633. [Google Scholar] [CrossRef] [Green Version]
- Smith, E.A.L. Pile-driving analysis by the wave equation. J. Soil Mech. Found. Div. 1960, 86, 35–61. [Google Scholar] [CrossRef]
- ASTM D5882-07; Standard Test Method for Low Strain Impact Integrity Testing of Deep Foundations. ASTM International: West Conshohocken, PA, USA, 2007.
- Dai, Y.W. Reliability Method for Damage Identification of Solid Concrete Piles Based on Low Strain Reflection Wave Method. Ph.D. Thesis, South China University of Technology, Guangzhou, China, 2018. [Google Scholar]
- Yuan, Q.; Zhou, W.; Zhang, L. Epileptic seizure detection based on imbalanced classification and wavelet packet transform. Seizure 2017, 50, 99–108. [Google Scholar] [CrossRef] [PubMed]
- Han, J.G.; Ren, W.X.; Sun, Z.S. Wavelet packet based damage identification of beam structures. Int. J. Solids Struct. 2005, 42, 6610–6627. [Google Scholar] [CrossRef] [Green Version]
- Bettayeb, F.; Haciane, S.; Aoudia, S. Improving the time resolution and signal noise ratio of ultrasonic testing of welds by the wavelet packet. NDT E Int. 2005, 38, 478–484. [Google Scholar] [CrossRef]
- Yen, G.G.; Lin, K.C. Wavelet packet feature extraction for vibration monitoring. IEEE Trans. Ind. Electron. 2000, 47, 650–667. [Google Scholar] [CrossRef] [Green Version]
- Schauer, M.; Langer, S. Numerical simulations of pile integrity tests using a coupled FEM SBFEM approach. PAMM 2012, 12, 547–548. [Google Scholar] [CrossRef]
- Huang, Y.H.; Ni, S.H.; Lo, K.F. Assessment of identifiable defect size in a drilled shaft using sonic echo method: Numerical simulation. Comput. Geotech. 2010, 37, 757–768. [Google Scholar] [CrossRef]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review. Available online: https://www.osti.gov/biblio/249299 (accessed on 11 April 2022).
- Liao, S. Nondestructive Testing of Piles. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 1994. [Google Scholar]
- Kim, H.J.; Mission, J.L.C.; Park, I.S. Analysis of static axial load capacity of single piles and large diameter shafts using nonlinear load transfer curves. KSCE J. Civ. Eng. 2007, 11, 285–292. [Google Scholar] [CrossRef]
- ABAQUS User’s Manual-Version 6.7; SIMULIA Dassault Systemes: Vélizy-Villacoublay, France, 2007.
- Li, J.B. Numerical Simulation and Application of Elastic Wave Method for Bridge Pile Detection in South Sichuan Intercity Railway. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2020. [Google Scholar]
- Ni, S.H.; Lo, K.F.; Lehmann, L. Time–frequency analyses of pile-integrity testing using wavelet transform. Comput. Geotech. 2008, 35, 600–607. [Google Scholar] [CrossRef]
- Lu, Z.T.; Wang, Z.L.; Liu, D.J. Study on low-strain integrity testing of pipe-pile using the elastodynamic finite integration technique. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 536–550. [Google Scholar] [CrossRef]
- Cooke, R.W.; Price, G.; Tarr, K. Jacked piles in London clay: Interaction and group behaviour under working conditions. Geotechnique 1980, 30, 97–136. [Google Scholar] [CrossRef]
- Gschossmann, S.; Oberascher, T.; Schagerl, M. Quantification of subsurface cracks in a thin aluminium beam by the use of nonlinear guided wave theory–a numerical and model-based approach. In Proceedings of the 9th EWSHM, Manchester, UK, 10–13 July 2018; pp. 10–13. [Google Scholar]
- Sun, Y.; Ma, S.; Sun, S. Partial discharge pattern recognition of transformers based on mobilenets convolutional neural network. Appl. Sci. 2021, 11, 6984. [Google Scholar] [CrossRef]
- Cao, K. Research on pile defects based on low strain reflection wave method. Master’s Thesis, Hebei University, Baoding, China, 2018. [Google Scholar]
- Dozat, T. Incorporating Nesterov Momentum into Adam. Available online: https://openreview.net/pdf?id=OM0jvwB8jIp57ZJjtNEZ (accessed on 11 April 2022).
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the ICML, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Zhang, B.; Muradov, K.; Dada, A. Principal component analysis-assisted selection of optimal denoising method for oil well transient data. J. Pet. Explor. Prod. 2021, 11, 509–530. [Google Scholar] [CrossRef]

















| Parts | Length (m) | Radius (m) | Material | Density (kg/m3) | Elastic Modulus (Pa) | Poisson Ratio |
|---|---|---|---|---|---|---|
| Pile | 1 | 0.05 | C30 concrete | 2500 | 3.0 × 1010 | 0.18 |
| Soil around pile | 1 | 0.5 | clay | 2100 | 5.0 × 107 | 0.25 |
| Bottom soil of the pile | 0.5 | 0.5 | clay | 2100 | 5.0 × 107 | 0.25 |
| Types | Length (m) | Radius (m) | Length of Defect (m) | Position of Defect (m) | Radius of Defect (m) |
|---|---|---|---|---|---|
| Neck defect | 1 | 0.05 | 0.08 | 0.5 | 0.03 |
| Bulge imperfection | 1 | 0.05 | 0.08 | 0.5 | 0.08 |
| Weak concrete | 1 | 0.05 | 0.08 | 0.5 | 0.05 |
| Crack | 1 | 0.05 | 0 | 0.5 | 0.05 |
| Broken | 1 | 0.05 | 0 | 0.5 | 0.05 |
| Parts | * (Radius) | Aa (Position) | Material (Pa) | Angle (°) | Amount | |
|---|---|---|---|---|---|---|
| Neck defect | 0.12 → 0.02 m | 0.05 → 0.1 m | 0.2–0.8 m | 3 × 1010 | None | 400 |
| Bulge imperfection | 0.12 → 0.02 m | 0.02 → 0.05 m | 0.2–0.8 m | 3 × 1010 | None | 400 |
| Weak concrete | 0.12 → 0.02 m | 0.05 m | 0.2–0.8 m | 3 × 109 →3 × 1010 | None | 400 |
| Crack | 0 | 0.01–0.045 m | 0.2–0.8 m | - | 10° → 270° | 400 |
| Broken | 0 | 0.05 m | 0.2–0.8 m | - | None | 400 |
| Stage | Layers | Stride | Output Shape |
|---|---|---|---|
| 0 | Conv3 × 3 | 1 | 18 × 18 × 6 |
| 1 | Pooling | 1 | 9 × 9 × 6 |
| 2 | Conv2 × 2 | 1 | 7 × 7 × 16 |
| 3 | Pooling | 1 | 3 × 3 × 16 |
| 4 | Conv3 × 3 | 1 | 1 × 1 × 120 |
| 6 | Flatten | 1 | 120 |
| 7 | Dense | - | 84 |
| 8 | Dropout | - | - |
| 9 | Dense | - | 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.-S.; Zhang, J.-Q.; Qi, L.-L.; Zhuo, D.-B. Defect Identification of Concrete Piles Based on Numerical Simulation and Convolutional Neural Network. Buildings 2022, 12, 664. https://doi.org/10.3390/buildings12050664
Wu C-S, Zhang J-Q, Qi L-L, Zhuo D-B. Defect Identification of Concrete Piles Based on Numerical Simulation and Convolutional Neural Network. Buildings. 2022; 12(5):664. https://doi.org/10.3390/buildings12050664
Chicago/Turabian StyleWu, Chuan-Sheng, Jian-Qiang Zhang, Ling-Ling Qi, and De-Bing Zhuo. 2022. "Defect Identification of Concrete Piles Based on Numerical Simulation and Convolutional Neural Network" Buildings 12, no. 5: 664. https://doi.org/10.3390/buildings12050664





