Evaluation of Residual Lateral Capacities of Impact-Damaged Reinforced Concrete Members
Abstract
:1. Introduction
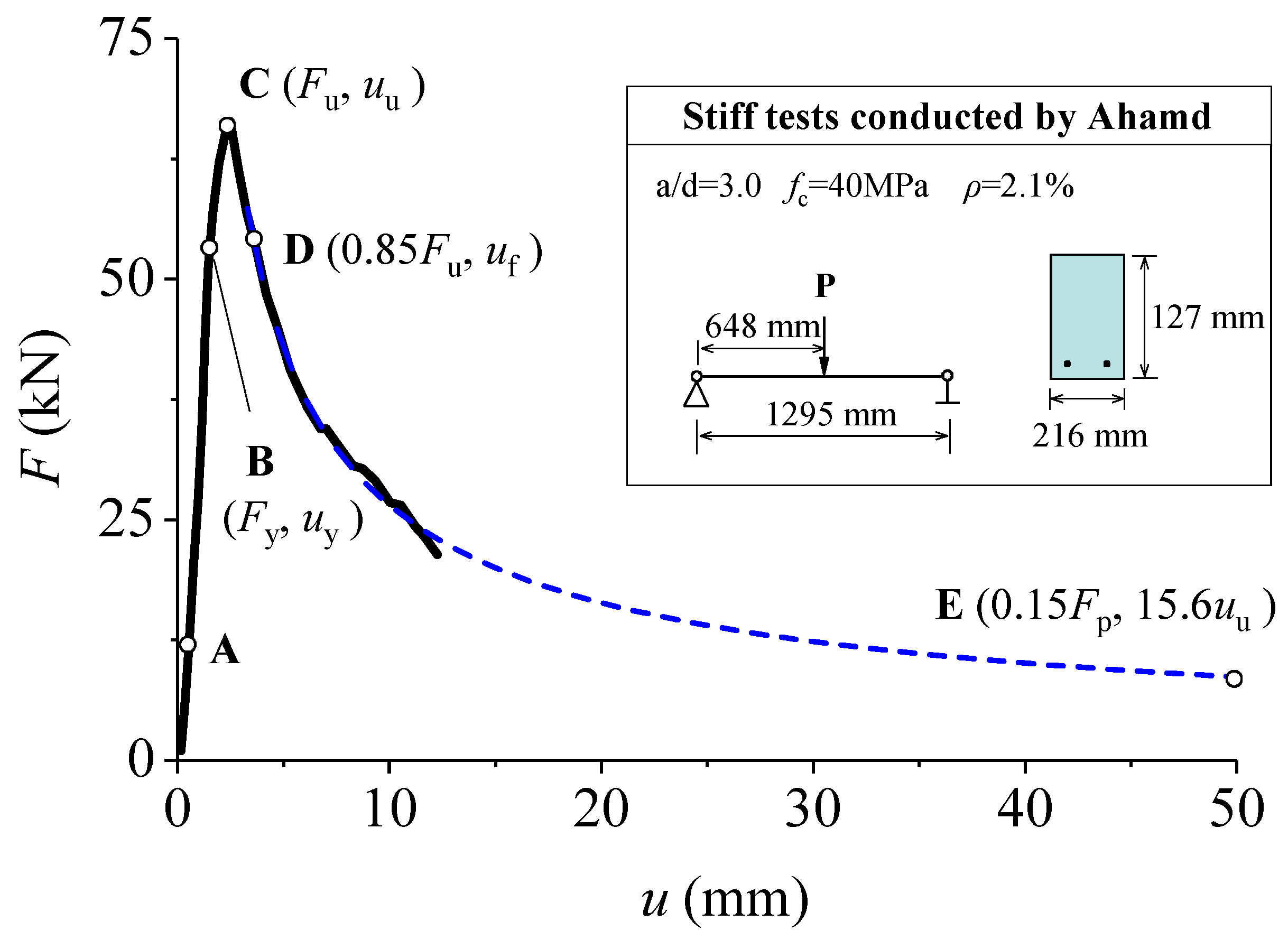
2. Previous Experimental Work
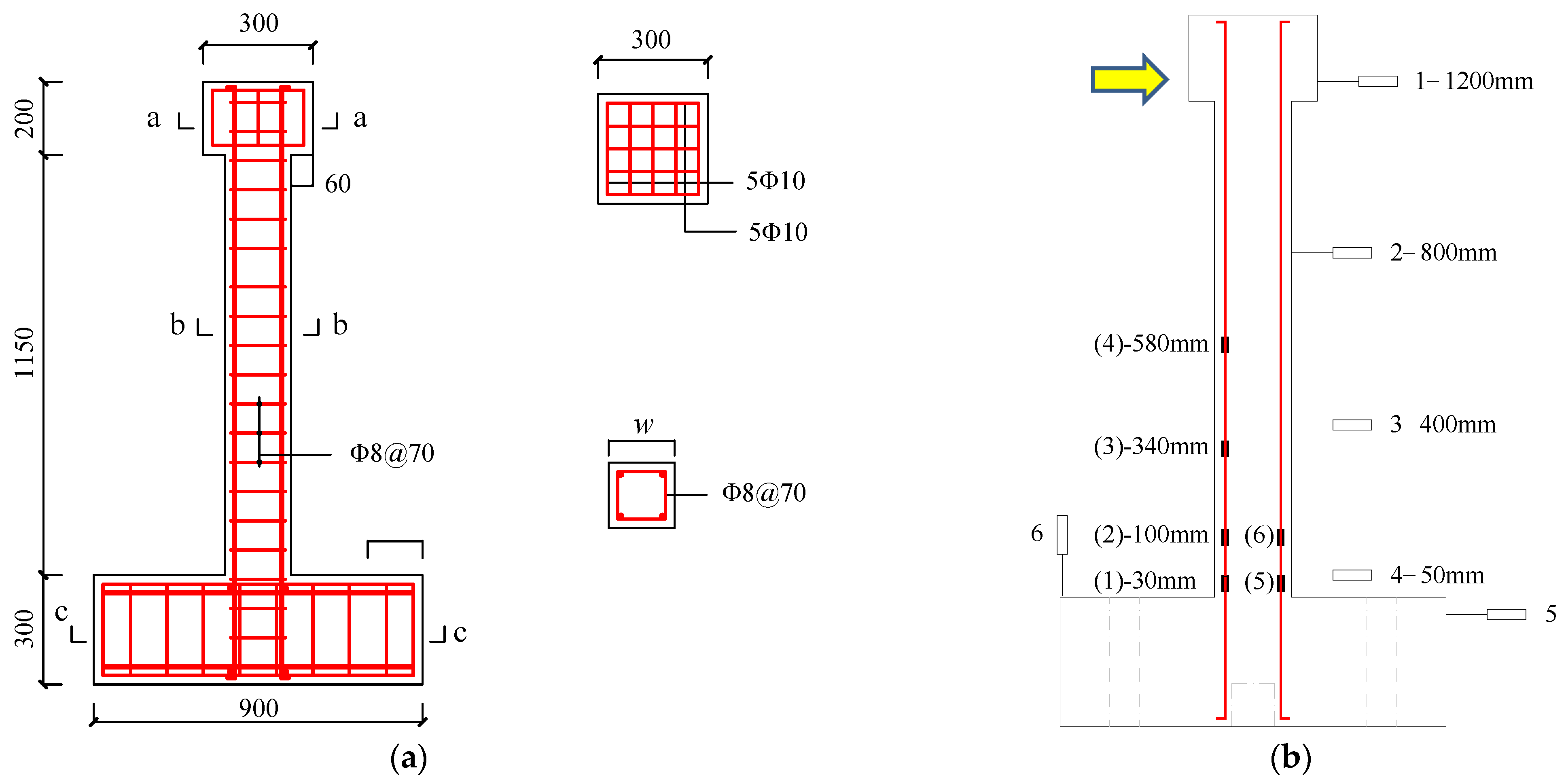
2.1. Tested Specimens
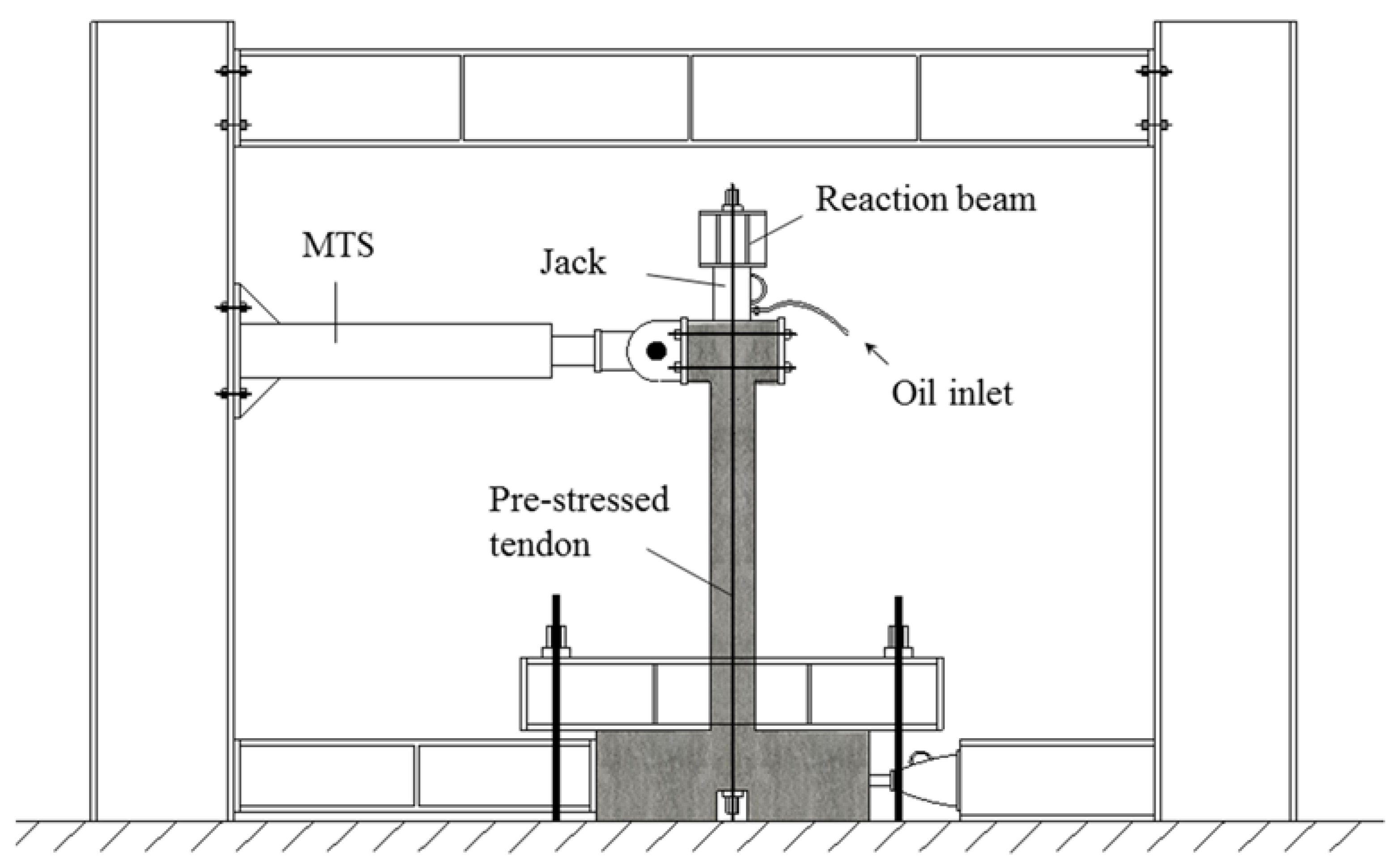
2.2. Static Test
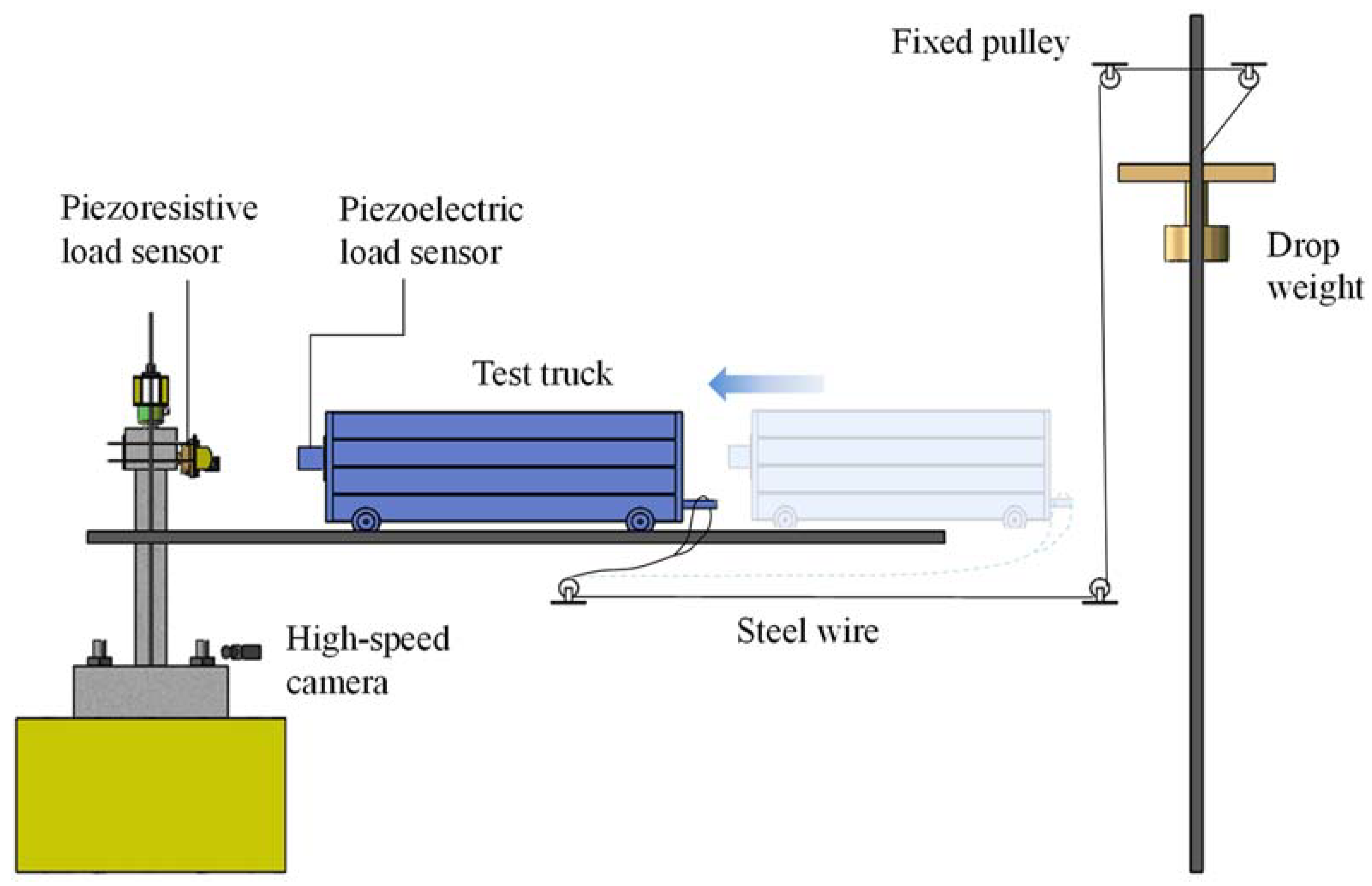
2.3. Impact Test
3. Overview of Experimental Results
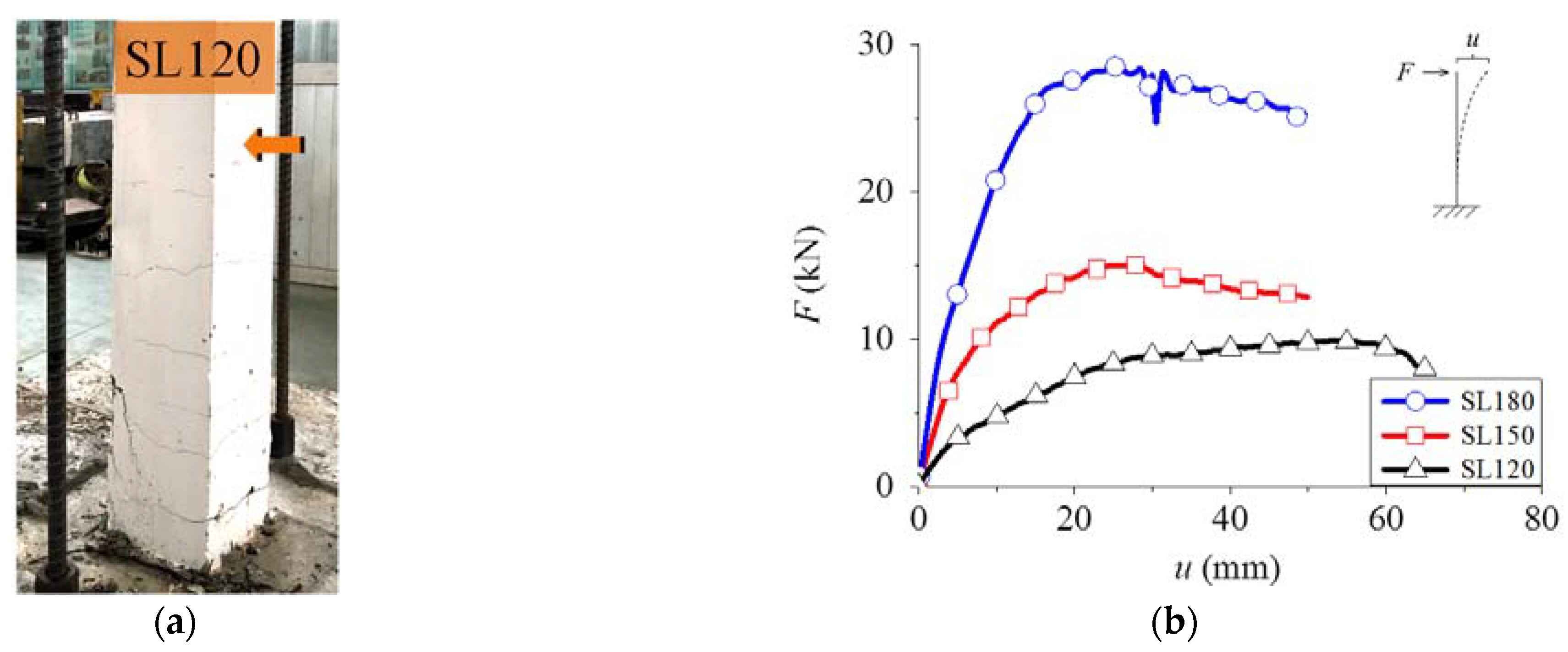
3.1. Static Test Results
3.2. Impact Test Results
3.2.1. Crack Development
3.2.2. Load–Displacement Relationship
3.3. Residual Strength Test Results
4. Damage Assessment and Residual Bearing Capacity Evaluation
4.1. Modified Park–Ang Damage Model
4.2. Calculation Method of Residual Bearing Capacity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fan, W.; Sun, Y.; Yang, C.; Sun, W.; He, Y. Assessing the response and fragility of concrete bridges under multi-hazard effect of vessel impact and corrosion. Eng. Struct. 2020, 225, 111279. [Google Scholar] [CrossRef]
- AASHTO-LRF; LRFD Bridge Design Specifications. American Association of State Highway and Transportation Official: Washington, DC, USA, 2007.
- JTG D60-2015; General Specification for Design of Highway Bridges and Culverts. China Communication Press: Beijing, China, 2015. (In Chinese)
- Saatci, S.; Vecchio, F.J. Effects of shear mechanisms on impact behavior of reinforced concrete beams. ACI Struct. J. 2009, 106, 78–86. [Google Scholar]
- Fu, Y.; Yu, X.; Dong, X.; Zhou, F.; Ning, J.; Li, P.; Zheng, Y. Investigating the failure behaviors of RC beams without stirrups under impact loading. Int. J. Impact Eng. 2020, 137, 103432. [Google Scholar] [CrossRef]
- Kani, G.N.J. Basic facts concerning shear failure. ACI Struct. J. 1966, 63, 675–692. [Google Scholar]
- JTS 144-1-2010; Load Code for Harbour Engineering. China Communication Press: Beijing, China, 2010. (In Chinese)
- Dok, G.; Caglar, N.; Ilki, A.; Yilmaz, C. Effect of impact loading on residual flexural capacity of high-strength reinforced concrete beams. Structures 2020, 27, 2466–2480. [Google Scholar] [CrossRef]
- Esfahani, M.; Hoseinzade, M.; Shakiba, M.; Arbab, F.; Yekrangnia, M.; Pachideh, G. Experimental investigation of residual flexural capacity of damaged reinforced concrete beams exposed to elevated temperatures. Eng. Struct. 2021, 240, 112388. [Google Scholar] [CrossRef]
- Adhikary, S.D.; Li, B.; Fujikake, K. Residual resistance of impact damaged reinforced concrete beams. Mag. Concr. Res. 2014, 67, 364–378. [Google Scholar] [CrossRef]
- Fujikake, K. Impact Performance of ultra-high performance fiber reinforced concrete beam and its analytical evaluation. Int. J. Prot. Struct. 2014, 5, 167–186. [Google Scholar] [CrossRef]
- Peng, T.; Chen, L.; Liu, T.; Demartino, C.; Xu, J. Static shear performance and residual axial capacity of rectangular RC bridge piers under near-ground lateral loads. J. Struct. Eng. 2021, 147, 04021219. [Google Scholar] [CrossRef]
- Tian, L.; Zhu, C. Damage evaluation and protection technique of RC columns under impulsive load. Eng. Mech. 2013, 30, 144–150. [Google Scholar] [CrossRef]
- Pei, C. Experimental Studies and Simulation Analysis on Dynamic Response and Residual Strength of H-Shaped Steel Member under Lateral Impact. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2013. (In Chinese). [Google Scholar]
- Tran, T.T.; Pham, T.M.; Huang, Z.; Chen, W.; Hao, H.; Elchalakani, M. Impact response of fibre reinforced geopolymer concrete beams with BFRP bars and stirrups. Eng. Struct. 2021, 231, 111785. [Google Scholar] [CrossRef]
- Hao, H.; Tran, T.T.; Li, H.; Pham, T.M.; Chen, W. On the Accuracy, Reliability and Controllability of Impact Tests of RC Beams. Int. J. Impact Eng. 2021, 157, 103979. [Google Scholar] [CrossRef]
- Tran, T.T.; Pham, T.M.; Huang, Z.; Chen, W.; Ngo, T.T.; Hao, H.; Elchalakani, M. Effect of fibre reinforcements on shear capacity of geopolymer concrete beams subjected to impact load. Int. J. Impact Eng. 2022, 159, 104056. [Google Scholar] [CrossRef]
- Demartino, C.; Wu, J.G.; Xiao, Y. Response of shear-deficient reinforced circular RC columns under lateral impact loading. Int. J. Impact Eng. 2017, 109, 196–213. [Google Scholar] [CrossRef]
- Xiao, Y. Development of structural testing equipment for impact and complex loading. J. Struct. Integr. Maint. 2021, 6, 1–15. [Google Scholar] [CrossRef]
- Cai, J.; Ye, J.-B.; Chen, Q.-J.; Liu, X.; Wang, Y. Dynamic behaviour of axially-loaded RC columns under horizontal impact loading. Eng. Struct. 2018, 168, 684–697. [Google Scholar] [CrossRef]
- Ye, J.-B.; Cai, J.; Chen, Q.-J.; Liu, X.; Tang, X.-L.; Zuo, Z.-L. Experimental investigation of slender RC columns under horizontal static and impact loads. Structures 2020, 24, 499–513. [Google Scholar] [CrossRef]
- Park, Y.J.; Ang, A.H.S.; Wen, Y.K. Seismic Damage Analysis of Reinforced Concrete Buildings. J. Struct. Eng. 1987, 111, 740–757. [Google Scholar] [CrossRef]
- Chen, L.; Jiang, H.; Lv, X. Modified Park-Ang damage model for reinforced concrete structures. J. Tongji Univ. (Nat. Sci.) 2010, 38, 1103–1107. (In Chinese) [Google Scholar]
- Kishi, N.; Mikami, H.; Matsuoka, K.; Ando, T. Impact behavior of shear-failure-type RC beams without shear rebar. Int. J. Impact Eng. 2002, 27, 955–968. [Google Scholar] [CrossRef]
- Ahmad, S.H.; Hino, S.; Chung, W.; Xie, Y. An experimental technique for obtaining controlled diagonal tension failure of shear critical reinforced concrete beams. Mater. Struct. 1995, 28, 8–15. [Google Scholar] [CrossRef]
- Adhikary, S.D.; Li, B.; Fujikake, K. Low velocity impact response of reinforced concrete beams: Experimental and numerical investigation. Int. J. Prot. Struct. 2015, 6, 81–111. [Google Scholar] [CrossRef]



| Reinforcement | Φ8 | Φ10 | Φ12 | Φ15 |
|---|---|---|---|---|
| fy (MPa) | 408.8 | 424.6 | 470.4 | 886.2 |
| fu (MPa) | 541.1 | 642.3 | 685.7 | 1135.7 |
| Specimen | v0 (m/s) | Fp (kN) | td (s) | umax (mm) | ures (mm) | Eab,d (kJ) | Damage State |
|---|---|---|---|---|---|---|---|
| DL150-1.5-0.4 | 0.329 | 8.899 | 0.142 | 7.803 | 0.53 | 0.035 | ○ |
| DL150-1.5-0.8 | 0.767 | 44.463 | 0.211 | 40.12 | 7.51 | 0.307 | ○ |
| DL150-1.5-1.2 | 1.191 | 59.003 | 0.238 | 56.01 | 5.16 | 0.872 | ● |
| DL150-1.2-0.8 | 1.083 | 63.943 | 0.149 | 43.16 | - | 0.638 | ○ |
| DL150-1.8-0.8 | 0.891 | 56.878 | 0.214 | 58.08 | - | 0.696 | ○ |
| DL120-1.2-0.8 | 0.802 | 37.139 | 0.221 | 54.37 | 0.17 | 0.364 | ○ |
| DL120-1.5-0.8 | 0.794 | 34.978 | 0.228 | 67.3 | 1.81 | 0.402 | ○ |
| DL120-1.8-0.8 | 0.869 | 50.419 | 0.385 | 77.25 | - | 0.645 | ● |
| DL180-1.5-0.4 | 0.503 | 24.325 | 0.095 | 11.24 | - | 0.153 | ○ |
| DL180-1.5-0.8 | 0.743 | 36.025 | 0.124 | 20.1 | 0.65 | 0.335 | ○ |
| DL180-1.5-1.2 | 1.291 | 80.309 | 0.124 | 39.26 | - | 0.925 | ○ |
| DL180-1.2-0.8 | 0.791 | 30.131 | 0.122 | 15.84 | - | - | ○ |
| DL180-1.8-0.8 | 0.907 | 71.901 | 0.114 | 27.64 | 1.29 | 0.708 | ○ |
| Static Tested Specimen | Fu (kN) | uu (mm) | Eab,s (kJ) |
|---|---|---|---|
| SL120 | 9.92 | 53 | 0.708 |
| SL150 | 15.05 | 27.79 | 0.321 |
| SL180 | 28.5 | 25.23 | 0.406 |
| Specimen | uu (mm) | Fres,ex (kN) | Fres,eq (kN) |
|---|---|---|---|
| SDL180-1.5-0.8 | 27.24 | 25.65 (0.90) | 26.38 (0.93) |
| SDL180-1.8-0.8 | 30.90 | 25.07 (0.88) | 25.10 (0.88) |
| SDL150-1.5-0.8 | 36.61 | 13.25 (0.88) | 13.11 (0.87) |
| SDL150-1.8-0.8 | 30.91 | 13.94 (0.93) | 11.78 (0.78) |
| SDL120-1.2-0.8 | 50.82 | 8.92 (0.96) | 8.93 (0.90) |
| SDL120-1.5-0.8 | 49.94 | 8.52 (0.86) | 8.73 (0.88) |
| Specimen | b × h (mm) | Fu (kN) | Fy (kN) | uu (mm) | h0 (m) | umax (mm) | Eab,d (J) | Fres,ex (kN) | Dres,eq | Fres,eq (kN) | Fres,ex/ Fres,p | Post-Impact Failure Mode | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DR3.3-2.4 | 150 × 250 | 120.35 | 108.8 | 2.76 | 0.15 | 3.8 | 264.6 | 116.74 | 0.13 | 104.44 | 1.13 | Shear- compression |  |
| 0.3 | 6.9 | 529.2 | 78.23 | 0.25 | 90.49 | 0.88 |  | ||||||
| 0.6 | 12.7 | 1058.4 | 63.79 | 0.47 | 63.70 | 1.04 |  | ||||||
| DR3.3-2.4-0.12 | 150 × 250 | 136.88 | 130.49 | 7.31 | 0.3 | 6.4 | 529.2 | 146.46 | 0.08 | 125.41 | 1.19 | Shear- compression |  |
| 0.6 | 11.5 | 1058.4 | 102.66 | 0.16 | 115.50 | 0.91 |  | ||||||
| 0.9 | 18.2 | 1587.6 | 106.77 | 0.24 | 103.68 | 1.08 |  | ||||||
| 1.2 | 21.6 | 2116.8 | 102.66 | 0.30 | 95.81 | 1.14 |  | ||||||
| DR3.3-2.4-0.56 | 150 × 250 | 243.73 | 233.26 | 19.04 | 0.6 | 9.0 | 1058.4 | 231.54 | 0.04 | 233.45 | 0.97 | Flexure |  |
| 0.9 | 13.4 | 1587.6 | 212.04 | 0.06 | 228.40 | 0.90 |  | ||||||
| 1.2 | 15.7 | 2116.8 | 194.98 | 0.19 | 197.73 | 0.90 |  | ||||||
| 1.6 | 19.2 | 2822.4 | 182.80 | 0.23 | 186.83 | 0.88 |  | ||||||
| SR3.8-0.8 | 160 × 240 | 73.28 | 73.28 | 5.67 | 0.3 | 10.8 | 529.2 | 81.34 | 0.06 | 68.61 | 1.19 | Shear |  |
| 0.6 | 20.2 | 1058.4 | 76.21 | 0.13 | 63.95 | 1.19 |  | ||||||
| 0.9 | 29.5 | 1587.6 | 58.63 | 0.19 | 59.28 | 0.99 |  | ||||||
| DR3.8-0.8-0.11 | 160 × 240 | 80.25 | 67.35 | 27.78 | 0.6 | 18.6 | 1058.4 | 86.67 | 0.07 | 74.54 | 1.19 | Flexure |  |
| 0.9 | 34.5 | 1587.6 | 72.22 | 0.12 | 70.47 | 1.07 |  | ||||||
| 1.2 | 41.0 | 2116.8 | 41.73 | 0.35 | 52.02 | 1.01 |  | ||||||
| DR3.8-0.8-0.15 | 160 × 240 | 91.86 | 68.75 | 27.09 | 0.6 | 19.6 | 1058.4 | 84.51 | 0.07 | 85.00 | 1.02 | Flexure |  |
| 0.9 | 28.8 | 1587.6 | 81.76 | 0.11 | 81.69 | 1.05 |  | ||||||
| 1.2 | 39.2 | 2116.8 | 74.41 | 0.15 | 78.13 | 1.01 |  | ||||||
| SR5.7-1.6 | 120 × 170 | 52.11 | 47.51 | 22.57 | 0.3 | 20.0 | 529.2 | 47.32 | 0.08 | 47.87 | 0.96 | Flexure |  |
| 0.45 | 28.8 | 793.8 | 35.36 | 0.29 | 36.88 | 0.86 |  | ||||||
| 0.6 | 37.1 | 1058.4 | 24.96 | 0.38 | 32.41 | 0.66 |  | ||||||
| DR5.7-1.6-0.15 | 120 × 170 | 49.43 | 45.98 | 12.09 | 0.3 | 20.0 | 529.2 | 43.50 | 0.15 | 41.84 | 0.96 | Flexure |  |
| 0.45 | 30.0 | 793.8 | 39.54 | 0.23 | 38.05 | 0.92 |  | ||||||
| 0.6 | 39.1 | 1058.4 | 30.65 | 0.30 | 34.49 | 1.08 |  | ||||||
| DR5.7-1.6-0.2 | 120 × 170 | 48.93 | 41.78 | 19.41 | 0.3 | 19.1 | 529.2 | 46.46 | 0.10 | 44.25 | 1.00 | Flexure |  |
| 0.45 | 28.8 | 793.8 | 41.57 | 0.14 | 41.89 | 0.93 |  | ||||||
| 0.6 | 37.9 | 1058.4 | 34.23 | 0.46 | 26.63 | 0.96 |  | ||||||
| Mean | 1.01 | ||||||||||||
| COV | 0.11 | ||||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, J.; Wang, Y.; Cai, J.; Chen, Q.; He, A. Evaluation of Residual Lateral Capacities of Impact-Damaged Reinforced Concrete Members. Buildings 2022, 12, 669. https://doi.org/10.3390/buildings12050669
Ye J, Wang Y, Cai J, Chen Q, He A. Evaluation of Residual Lateral Capacities of Impact-Damaged Reinforced Concrete Members. Buildings. 2022; 12(5):669. https://doi.org/10.3390/buildings12050669
Chicago/Turabian StyleYe, Jiabin, Yingtao Wang, Jian Cai, Qingjun Chen, and An He. 2022. "Evaluation of Residual Lateral Capacities of Impact-Damaged Reinforced Concrete Members" Buildings 12, no. 5: 669. https://doi.org/10.3390/buildings12050669
APA StyleYe, J., Wang, Y., Cai, J., Chen, Q., & He, A. (2022). Evaluation of Residual Lateral Capacities of Impact-Damaged Reinforced Concrete Members. Buildings, 12(5), 669. https://doi.org/10.3390/buildings12050669






