Abstract
Digital green innovation management activities are the core of low-carbon intelligent development of prefabricated construction enterprises (PCEs) for sustainable urban development. PCEs have to seek joint venture partners to avoid the financial risk of digital green innovation projects. The purpose of this study is to develop a conceptual partner selection framework for the digital green innovation management of prefabricated construction towards urban building 5.0. In this study, first, symbiosis theory and six analysis methods were integrated to innovatively build a 3W1H-P framework system for the joint venture capital partner selection of digital green innovation projects. Second, the dual combination weighting method was innovatively proposed to avoid subjective and objective deviation in attribute weight and time weight. Finally, empirical research was carried out to verify the scientific nature, reliability, and practicability of the framework system and selection model. The results of this study show that the framework system and selection model proposed can be used to assist PCEs to select joint investment partners of digital green and innovative projects for sustainable urban development.
1. Introduction
In 2020, China announced at the UN Climate Conference that its carbon dioxide emissions would peak by 2030 and become carbon neutral by 2060. The carbon emissions from buildings account for more than 40% of the total carbon emissions in the whole cycle [1,2,3]. Housing is one of the top four sources of carbon emissions in Europe, accounting for a significant share of the total carbon emissions in society [4]. Carbon emissions run through all aspects of the construction industry. There is plenty of room to reduce carbon emissions in building materials and construction [5,6]. In the context of carbon peak and carbon neutral, it is very important to reduce the carbon emissions of the construction industry. Prefabricated construction enterprises (PCEs) need to transfer a large number of operations in traditional construction methods from the construction site to the construction factory. These constructs and fittings are installed to construct the building through reliable connections [7]. The goal of carbon peak and carbon neutrality promotes the development of PCEs towards green digital innovation [8].
The construction industry can be developed by accelerating the transformation of traditional construction methods. First, the traditional construction industry is based on on-site manual work. This approach has problems, such as low resource utilization efficiency and construction safety [9]. The parts of prefabricated buildings are made in a factory and assembled on site with reliable connections. As a result, this approach has the characteristics of standardized design, factory production, construction and prefabricated, integration of decoration, management information, intelligent application, and so on [10]. Second, in the past few decades, the progress of the cast-in-place concrete building model has benefitted from China’s abundant labor resources. However, with the gradual disappearance of the demographic dividend and the rapid increase in labor costs, labor-intensive production mode will be unsustainable. At the same time, it not only accelerated the upgrading of the traditional construction industry to the industrialization of construction but also promoted the overall progress of the construction industry [11,12]. Third, the traditional construction industry has caused great damage to the ecology and environment, mainly reflected in the carbon emissions [13]. The modular, industrial production of prefabricated components can also minimize the discharge of construction waste, save consumables, and reduce air, noise, and other pollution. Therefore, it can reduce carbon emissions over the life of the building [14,15,16,17,18]. If prefabricated buildings can replace conventional buildings on a large scale in the future, carbon emissions will be greatly reduced.
However, the development of PCEs in China is still facing great challenges. The first is that PCEs are increasingly demanding carbon reduction [19]. At present, many developed countries have decoupled carbon emissions from economic development, but China is still in the stage of increasing carbon emissions and has not reached the peak [20]. As one of the industries with high carbon emissions, carbon emission reduction means that the production mode, technological level, material selection, and business model in the industry will face innovation. The goal of carbon peak and carbon neutrality puts forward new requirements for the traditional construction industry. It also means that PCEs have higher requirements for carbon reduction [21,22]. The second is the low degree of intelligent PCEs [23]. In the prefabricated building industry, chain technology, prefabricated shear wall structure connection, site installation and construction and acceptance methods, and other key technologies are not yet mature. In addition, related technical standards, norms, and construction methods cannot keep up, resulting in varying degrees of constraints on its development [24]. In the degree of standardization, the modular production and standardization of building components are relatively low. General components are used less. These conditions result in low construction efficiency and a high cost of prefabricated buildings. It is difficult to give full play to the advantages of industrialization [25].
In the face of the above problems, PCEs solve them through green digital innovation projects. In recent years, promoting the development of PCEs through research and development projects has become a hot spot of scholars’ research [26,27,28,29]. Many companies are also carrying out this activity. In April 2021, the Yunnan Kunming Steel Construction Group Co., Ltd. Green Prefabricated Building Innovation Studio was established. The green prefabricated building design research and development innovation group, green and intelligent manufacturing innovation group, and green building construction and installation method innovation group were set up. They promote advanced concepts and technology to solve the technical bottleneck of production and operation. In May of the same year, the Hubei Provincial Intelligent Construction Science and Technology Innovation Consortium was established. In addition, in order to empower the transformation and upgrading of the construction industry in Hubei Province, all the member units will jointly summarize and form a list of key technologies of intelligent construction.
As the spillover effect of technological innovation becomes more and more prominent, how to effectively conduct digital green innovation activities has become a very important problem in the development of PCEs. In the process of promoting the development of PCEs, they have to face huge financial and risk pressure. In addition, other PCEs are also searching for methods. In the market, there is more cooperation between PCEs, which provides a way to solve this dilemma. However, it also involves the issue of partner selection [30]. At present, many systematic approaches provide ideas for choosing joint investment partners, but there are still some shortcomings.
In recent years, many scholars have studied partner selection in terms of the methods and index system [31,32,33,34,35,36,37,38,39]. The research methods mainly include the partner evaluation method, the attribute weighting method, and the weighting method. As for the partner evaluation method, analytic hierarchy process (AHP) and data envelopment analysis (DEA) methods were adopted before, while some new methods and combined methods were adopted in recent years [31,32,33,34,35]. This research is mainly committed to considering all kinds of complex factors. With respect to the attribute weighting method, there are mainly linear programming models, methods for minimum and maximum entropy values, membership, and non-membership methods. Regarding the weighting method, there are mainly techniques for the order preference by similarity to an ideal solution (TOPSIS) method, coefficient of variation method, and ideal point method [36,37,38,39]. In terms of the index system, some scholars proposed that innovation has an important impact on partner selection [31,32,33]. Some scholars believed that technology plays a non-negligible role in partner selection [34,35,36]. Many scholars expressed their views in choosing methods and systems, but there are still some shortcomings [37,38,39]. In the selection of methods, most previous studies have focused on a single subjective or objective weight. However, there are fewer studies of intuitive fuzzy weights and their combination with objective weights. There is a lack of a certain degree of combing and summary in the construction of the system, which cannot explain the level of digital green innovation projects carried out by PCEs under the goal of double-carbon. It is not conducive to the evaluation of the implementation and a full grasp of its situation.
To solve the above problems, the purpose of this research is to build a research system to select joint investment partners and select scientific methods to promote the digital green innovation development of PCEs. Firstly, a new fuzzy entropy comprehensive evaluation formula is proposed based on the entropy method and TOPSIS method. Second, combined with the existing research index system, this paper divides the joint venture capital partners of PCEs into risk indicators and resource indicators under the dual-carbon goal. This study builds a research system of PCEs choosing joint investment partners in the investment activities of digital green innovation projects. This study expounds the relevant theory and proposes the fusion method.
2. Literature Review and Theoretical Framework
2.1. Literature Review
2.1.1. Digital Green Innovative and Joint Venture Investment
(i) Digital green innovation. In recent years, some scholars have conducted in-depth research on digital green innovative management. They thought that digital green innovative management of enterprises is particularly important [40,41]. Khin & Ho (2018) put forward that digital technology can significantly improve the sales revenue and reduce the operating cost rate of enterprises [40]. Li et al. (2020) believed that, in the era of the digital economy, the application of digital technology can significantly promote the improvement of enterprises’ capabilities. The capability improvement effect of digital technology application can be more fully reflected in enterprises with a poor resource base and high dynamic capability [41]. Meanwhile, many scholars put forward their views on green innovation management [42,43,44]. Kaluarachchi (2021) believed that ecological and green development in the field of architectural design in China are promoted through the integration of digital technology and green building design [42]. Jiang (2021) believed that it is necessary to achieve high-quality fusion of digital economy and green economy development. The research of the green economy sustainable paradigm shift must consider the digital tools in environmental sustainability. Changing the thinking mode of environmental governance should not only attach great importance to the use of digital solutions but also cannot ignore the digital economy accountability of the carbon footprint [43]. Chaker et al. (2022) believed that the value of digital technology capability is beyond doubt, but its value potential is conditional. Digital technology enterprises must make further use of business model innovation to give full play to the potential value of digital technology [44].
(ii) Joint venture investment. Many scholars have discussed the motivations of joint venture investment [45,46,47,48,49,50,51,52,53,54,55,56,57]. Pence [45] (1982) and Perez [46] (1986) argued that venture capitalists are motivated to co-invest by obtaining a second opinion, which double-checks their investments using the views of other investment partners. It can not only prevent the deficiency of their own screening and management skills but also prevent the adverse selection problem caused by information asymmetry. This is supported by the empirical study conducted by Lerner [47]. The empirical results of Altintig et al. (2013) also supported both drivers [48]. Tykvova and Schertler (2014) examined the joint drivers of multinational venture capital. They found that joint investment was more conducive to obtain investment opportunities, improve risk allocation, and reduce information costs, thus indirectly proving both drivers [49]. Manigart and Lockett (2006) argued that risk diversification drivers and access to trade flow factors are more important than screening and appreciation drivers. In the early investment stage, there will be a stronger value-added motivation, and the motivation of joint investment with investors is to obtain the screening and value-added skills of leaders [50]. Lockett and Wright (2001) formally classified previous studies into risk diversification and resource accumulation. Resource accumulation motivation is more important for early-stage investment at least [51]. Brander et al. (2002) summarized joint venture capital factors as risk dispersion hypotheses for diversification of the portfolio, screening hypotheses for acquiring pre-investment screening skills, and value-added assumptions for managing post hoc investments. The study found more support for the value-added hypothesis [52]. Verwaal et al. (2010) tended to support access to transaction flow factors [53]. Ferrary (2010) believed that the motivation of a joint venture is the accumulation of resources [54]. Hopp and Rieder (2011) believed that the motive of venture capital association is not to diversify the asset portfolio but to disperse risks [55]. Lerner (1991) believed that venture capital institutions would engage in window dressing. Window dressing is the practice of quarterly performance reviews of fund managers in which market performance is a noisy indicator and investors also look at portfolios at the end of each quarter. As a result, fund managers are likely to buy shares in companies with good quarterly results and sell shares in companies with poor quarterly results [56]. Admati and Pfleiderer (1994) believed that the lead investor may deliberately overestimate the security price of the follow-up financing by using this information advantage to seek the interests of the co-investor. To prevent this opportunistic behavior, co-investors often invest together so that the lead investor must maintain a constant share [57].
(iii) Based on the above literature review, it is summarized as follows. Many scholars only conducted research on digital innovation management or green innovation management. Few scholars put forward opinions on the integration of digital innovation management and green innovation management. According to the existing literature, the motivations of joint venture investment can be divided into risk dispersion motivation, resource accumulation motivation, and collusion motivation. Venture capital institutions have the need to reduce investment risk. Co-investing in one area can diversify a portfolio away from systemic risk. More importantly, it possesses the specific nature of a syndicate to improve the ability of investment against risk. Much of the literature supports the idea of risk diversification drivers [45,46,47,48,49,50]. According to the research of resource accumulation motivation, the main motivation of joint venture investment lies in the acquisition of pre-investment screening resources and post-investment management resources, as well as the acquisition and exchange of transaction flows [51,52,53,54,55]. The main motivation of venture capitalists’ association is to prevent the opportunistic behavior and window dressing behavior of leading investors [56,57]. It can be seen from the above literature that the existing studies tend to support the motivation of resource accumulation.
2.1.2. Criteria for Venture Capital Partner Selection and Characteristics of Preference
(i) Criteria for venture capital partner selection. In much of the literature on partner selection, different scholars have proposed different criteria for partner selection [58,59,60,61,62,63]. Zhu et al. (2010) built the green technology innovation of the enterprise environmental evaluation index system from the two dimensions of the enterprise internal environment and the external environment [58]. Bi et al. (2013) built an evaluation index system of green process innovation performance from the three aspects of economic performance, social performance, and ecological performance [59]. Ghisetti and Rennings (2014) measured green innovation efficiency, selected 92 indicators of energy consumption and environmental pollution, and made a distinction between energy efficiency innovation and environmental beneficial innovation based on the two aspects [60]. Salamat et al. (2018) established a partner selection index system for the international strategic alliance [61]. Dedehayir et al. (2018) studied the role of innovation leadership, direct value creation, value creation support, and the entrepreneurial ecosystem in the innovation ecosystem. They point out that organizational culture, partners, and technological level are important factors for the long-term development of the innovation ecosystem [62]. Yin et al. (2020) measured the four dimensions of regional green innovation input capacity, green innovation output capacity, green innovation environment capacity, and green diffusion input capacity [63].
(ii) Characteristics of preference. As for the characteristics of co-investment partners that venture capital institutions should or prefer to choose, scholars have studied as follows [64,65,66,67]. Du (2016) found that venture capital institutions are more inclined to unite with investment partners with similar experience [64]. Gompers et al. (2016) examined the impact of the individual-level characteristics of venture capitalists on the selection of joint investment partners. The study found that venture capitalists preferred to choose partners who had attended the same university and were of the same race and gender [65]. In terms of experience level, Lerner (1994) believed that experienced venture capitalists in the first round of investment tend to associate with investors with a similar experience level and generally do not choose smaller or junior partners. Casamatta and Haritchabalet (2007) theoretically believed that experienced venture capitalists would choose more experienced partners to unite [66]. In terms of capital scale and heterogeneous resource endowment, Hochberg et al. (2015) conducted a combined study and believed that risk diversification is not the main driving force for joint investment partner selection. By selecting partners with much resource endowment and specific heterogeneous resources, resource superposition and complementarity can be realized [67].
(iii) Based on the above literature review, it is summarized as follows. Many scholars expressed their opinions on the selection of evaluation indicators. However, the lack of a certain degree of summary is not conducive to the evaluation and implementation and a comprehensive grasp of the situation [58,59,60,61,62,63]. Based on the existing literature, there are two views on what characteristics venture capital institutions prefer to select as co-investment partners. The first view holds that venture capital institutions tend to form syndicates with partners with similar characteristics or types. The reason is that this type of syndicate also has lower agency costs and information asymmetry, making the investment risk lower. There is much literature supporting the selection of similarity partners [64,65]. The second view holds that venture capital institutions tend to form syndicates with partners with different characteristics or types and the same level of resource endowment. The reason is that joint investment with venture capital institutions with the same level of heterogeneity or resource endowment can obtain the heterogeneous resources of the other side, which is conducive to resource superposition, complementarity, and exchange to achieve cumulative advantages. There are two ways to combine venture capital to accumulate resources. One is to select partners with the same level of resource endowment for resource superposition. The other is to select partners with different characteristics or types for resource complementarity and exchange. With regard to supporting the view of selecting resource accumulation partners, the existing literature examines the effects of experience level, capital size, and heterogeneous resource endowment [66,67].
2.1.3. Approaches for Venture Capital Partner Selection
In terms of partner selection methods, Nikghadam et al. (2016) have proposed partner selection methods based on fuzzy target optimization [68]. Chen and Han (2018) constructed linear planning models for the case of incomplete attribute information [69]. For the case where the weight information is completely unknown, Gao et al. (2016) proposed methods based on minimum and maximum entropy values [70]. Yin et al. (2018) proposed methods that considered membership and non-membership [71]. Liang & Chong (2019) proposed the gray model and the DEA method [72]. In terms of the weighting method, Zhang et al. (2021) used the TOPSIS method to solve the optimal capacity configuration of the system [73]. Zhao and Yu (2021) used the coefficient of variation method to comprehensively evaluate the indicators through the corresponding weight combination [74]. Liu et al. (2021) used the ideal point method to construct the evaluation model [75]. Liu (2021) used the ideal point method to optimize the hierarchical analysis method, entropy weight method, and excessive weighting method [76]. Lin and Bai (2021) used the TOPSIS method to construct a weighted standard matrix and evaluated the advantages and disadvantages of each power plant [77]. Chen et al. (2021) established a combined weight optimization method based on the Gini coefficient method and excessive weighting method [78]. Chou et al. (2022) proposed a combined weight method based on MOEAD [79].
Numerous studies provide methods and ideas for partner selection. On the level of partner selection and weighting, many opinions and ideas have been provided by predecessors [68,69,70,71,72,73,74,75,76,77,78,79]. In terms of evaluation methods, there are methods such as the comprehensive index method, grey correlation method, grey fuzzy comprehensive evaluation method, AHP, combination weight, and so on. However, the combination evaluation and in-depth analysis with other evaluation methods are rarely carried out, and there are some problems, such as a lack of consistency in the evaluation results. Regarding the determination of weights, the subjective weighting method may be highly subjective and arbitrary, influenced by the decision-maker’s lack of knowledge or experience. Objective weighting ignores the subjective information of decision-makers. The algorithm complexity of the combination weighting method is generally high. Each of these methods has advantages and disadvantages.
2.2. Theoretical Framework
2.2.1. Theoretical Model of Joint Investment Partner Selection
Digital green innovation projects usually occur in the process of enterprise change. Digital green innovation plays an important role in improving the performance of PCEs. It is regarded as one of the key factors affecting the green competitive advantage and strategic selection of PCEs. However, PCEs have to face significant investment pressure for innovative activities in many digital green R&D projects. More and more PCEs are choosing joint partners to spread risks and share resources when conducting digital green innovation activities. This practice has helped the construction industry to some extent. Problems related to the selection of joint partners by prefabricated construction firms can be solved by constructing joint venture capital networks. The specific theoretical model is shown in Figure 1.
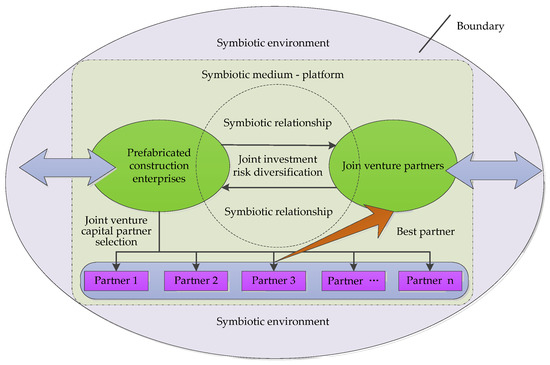
Figure 1.
Theoretical model of PCEs choosing joint venture capital partners.
In the joint venture network, PCEs and joint venture partners are the two main subjects of digital green innovation projects. The exchange of green knowledge and digital innovation technologies between construction firms and joint venture partners helps to promote business development and technological progress because this kind of cooperation not only combines heterogeneous partners but also combines heterogeneous knowledge. In the process of knowledge and technology exchange, PCEs and joint venture partners gradually form a mutually beneficial symbiotic relationship. The two share more and more complementary resources on digital green innovation. Whether PCEs can choose appropriate joint venture partners is directly related to the development of mutualistic symbiosis. In the joint venture capital network, it is particularly important to select one or more joint venture partners for PCEs to carry out digital green innovation activities. However, this selection is a complex decision-making process. This paper addresses this issue.
2.2.2. Framework System of Joint Investment Partner Selection
By systematically sorting out and summarizing the five aspects of the knowledge of alliance motivation (why), partner selection (who), situation influence on alliance (where), alliance process (how), and alliance investment influence on the performance of PCEs, it can be found that there is a certain logical relationship between them.
First, motivation affects partner selection, which, in turn, affects firm performance. Namely, PCEs choose joint venture partners based on the risk diversification motivation to carry out digital green innovation projects to promote the enterprise venture investment performance. In this mechanism, PCEs are in different situations, leading to different joint motivations and partner selection behaviors. The impact on performance will be different, and the play of the mechanism will present heterogeneity.
Secondly, partner selection and the impact on the performance of PCEs is to analyze the process of the black box of joint venture investment. PCEs carry out digital green innovation projects to carry out joint venture investment, which is the process of joint venture capital partners investing in PCEs. In this process, joint venture partners and PCEs will play against each other based on the principle of maximizing their own interests.
Finally, it can be seen that PCEs’ selection of joint investment partners is a process of investment behavior. The motivations of joint venture, partner selection, and game behavior in the process of a joint venture are bound to be affected by the situation of joint venture partners and PCEs.
Based on the above analysis and the idea of six analysis methods, this paper integrated the above logical relations. The activity of PCEs choosing joint venture partners in digital green innovation projects innovatively puts forward a research framework of joint venture capital, 3W1H-P, as shown in Figure 2.
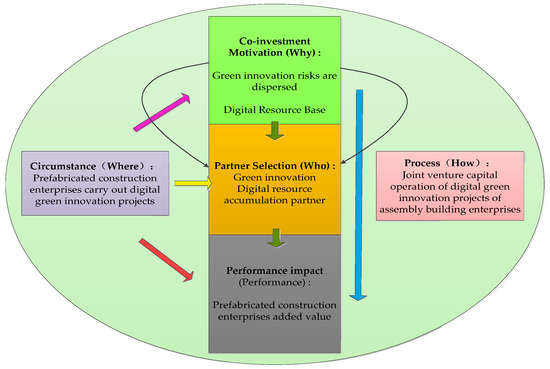
Figure 2.
PCEs choose the joint investment partner 3W1H-P research framework.
Many scholars have emphasized the importance of partner selection criteria [58,59,60,61,62,63]. Partner selection should be based on the level of environmental protection [60,63]. Innovative leadership, direct value creation, and value creation support are considered when selecting strategic alliance partners [62]. Scholars have put forward their own views on the environmental, economic, social, and ecological aspects [59]. At the same time, organizational culture, partners, and other factors cannot be ignored [62]. This paper established a research system for PCEs to select joint venture partners when carrying out digital green innovation projects, as shown in Figure 3.
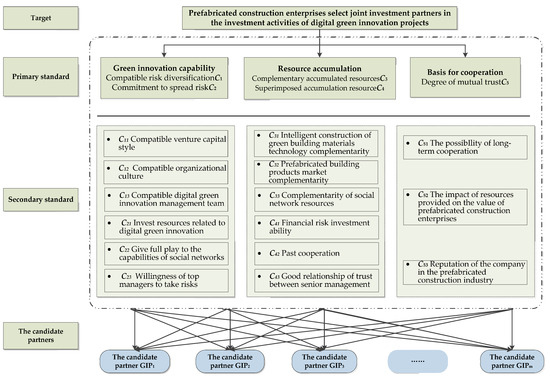
Figure 3.
Criterion framework for PCEs to select joint venture partners when carrying out digital green innovation projects.
3. Methodology
3.1. Methodological Framework
In this study, a selection method was proposed. It is an integrated approach based on fuzzy prospect theory and vise kriterijumska optimizacijai kompromisno resenje (VIKOR). The running logic of this method is shown in Figure 4.
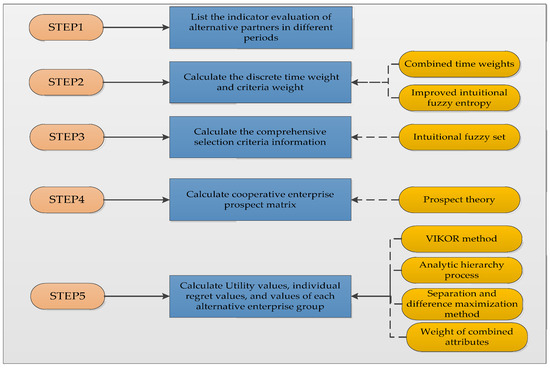
Figure 4.
Methodological framework of choosing digital green innovation partner for PCEs.
Figure 4 illustrates the process used by PCEs to dynamically select digital green innovation partners. The main steps are as follows. Step 1: List the indicator evaluation of alternative partners in different periods. Step 2: Calculate the discrete time weight and criteria weight. Step 3: Calculate the comprehensive selection criteria information. Step 4: Calculate cooperative enterprise prospect matrix. Step 5: Use VIKOR and attribute weight method to calculate utility values, individual regret values, and values of each alternative enterprise group.
3.2. Preliminary
3.2.1. Intuitional Fuzzy Set
3.2.2. AHP
AHP is a subjective weighting method with strong applicability and operability. This method can better represent each factor and their correlation degree [83]. AHP method is adopted in this study. First of all, each element under the same criterion layer is compared in pairs with the expert consultation method and the relevant literature using 1–9 scale method, and the judgment matrix is constructed. Secondly, the consistency of the judgment matrix is tested. Finally, , the weights of each factor layer and criterion layer, are calculated. The specific decision-making process of AHP is shown in Appendix B.
3.2.3. Separation and Difference Maximization Method
The deviation maximization method is an objective method, which has the characteristics of focusing on the relationship between the information while ignoring the relationship between the information itself [84]. Appendix C shows the specific calculation steps.
3.2.4. Weight of Combined Attributes
Index weight under the comprehensive AHP method and index weight under the deviation maximization method are introduced to determine the comprehensive weight of the index [85,86].
The distance between the two was determined by the Euclidean distance. The result is as follows:
The actual weight after correction is represented by two parameters. The result is as follows:
In Formula (A2), and represent the weight preference coefficient of AHP method and deviation maximization method, respectively, and the following constraints are satisfied:
3.2.5. Prospect Theory
The prospect theory was proposed in 1979 and expanded by Tversky and Kahneman in 1992. Prospect theory is an effective tool to reflect the utility of intuitive perception and has been widely used to solve various decision-making problems. In this study, fuzzy prospect theory is introduced to help PCEs to avoid similar risks blindly and make the decision more reasonable and effective. Based on the above analysis, the following definitions are made in this paper. Definitions related to prospect theory are given in Appendix D.
3.3. Fusion Approaches
3.3.1. Combined Time Weights
In the process of PCEs choosing joint investment partners in the investment activities of digital green innovation projects, the weight vector of time series reflects the preference degree of PCEs to time, and time degree is crucial to obtain the weight of time and the selection result.
Subjective time weight based on time degree and ideal solution. Let be a time vector, where . Time degree represents the attention degree and preference degree of decision-makers to different time information. When , is called the positive ideal time weight vector, and the decision-maker only pays attention to the current information. As increases, decision-makers shift from focusing only on current information to focusing on past information. When , then is called the negative ideal time weight vector, indicating that decision-makers only pay attention to the past information. Let be the Euclidean distance and between the time weight vectors, and the distance can be expressed as:
Therefore, the Euclidean distance between the time weight vector and the positive ideal time weight vector and negative ideal time weight vector can be expressed as:
The ideal time weight vector is expressed as:
The model is then optimized based on the TOPSIS idea and the ideal solution. The model (M-1) is expressed as:
Objective time weight can be shown as follows:
Then, the maximum entropy principle was used to solve the time weight of the information entropy to establish a nonlinear planning model. It is as follows:
Based on subjective and objective comprehensive time weight. According to the principle of enriching the present and thinning the past, the greater the degree of relationship, the greater the degree of attention to the current decision information. It considers the influence of subjective preference and objective criterion information of PCEs and can make the results of joint investment partner selection more comprehensive, accurate, and reliable when PCEs carry out digital green innovation project investment activities. The model can be expressed as:
where is the equilibrium coefficient, .
3.3.2. Improved Intuitional Fuzzy Entropy
Let be an intuitionistic fuzzy set on domain , and let
be the entropy of intuitionistic fuzzy set .
Theorem 1.
is intuitional fuzzy entropy .
Proof.
First prove because , , so . Let , where , with respect to ; take the partial derivative with respect to and there is
Equals if . So, is decreasing with respect to . When , the minimum value is 0. is true.
To illustrate the rationality and superiority of the entropy formula proposed in this paper in measuring intuitive fuzzy information and fuzzy information, two classical intuitionistic fuzzy entropy formulas are selected as follows:
□
Example 1.

Suppose , , and are the three intuitionistic fuzzy sets in domain and calculate intuitionistic fuzzy set by entropy formula , , and , respectively. The calculated results are shown in Table 1.

Table 1.
Comparison of the calculation results.
The new intuitionistic fuzzy entropy shows that, when the hesitancy degree is the same, the smaller the absolute deviation between membership degree and non-membership degree, the larger the intuitionistic fuzzy entropy is . When the absolute deviation between membership degree and non-membership degree is the same, the greater the hesitation degree, the greater the intuitive fuzzy entropy, such as , which is consistent with the actual situation. However, although the hesitancy of element belonging to and is the same, the absolute deviation between the membership degree of belonging to and the non-membership degree is greater than that of belonging to , so the uncertainty of should be less than that of . Using entropy formulas and , , can be obtained, which is not true.
Example 1 shows that and cannot accurately capture the difference of intuitionistic fuzzy entropy caused by absolute deviation of membership degree and non-membership degree (fuzzy information) in intuitionistic fuzzy set with the same hesitation degree (intuitive information). The formula proposed in this paper considers intuitionistic information and fuzzy information contained in intuitionistic fuzzy sets more comprehensively. Therefore, when describing the entropy of intuitionistic fuzzy sets, formula proposed in this paper is more reasonable.
Set as the target attribute weight of periods and establish the optimization model of the target attribute weight of a sequence as follows:
The Lagrangian function was constructed according to the above formula:
Take the partial derivative of and , respectively, and make the partial derivative function equal to 0; then:
Solving the above formula, the target attribute weight is
3.3.3. VIKOR Method
The methodological steps for the VIKOR method are shown in Appendix E.
4. Empirical Study
4.1. Empirical Background
Tianfeng Green Prefabricated Group was founded in 1997. It has been committed to the green intelligent prefabricated industry, building an industrial ecological chain of steel structure prefabricated buildings, cluster intelligent prefabricated buildings, modular prefabricated houses, energy-saving plates, intelligent equipment, new energy, steel logistics, and distribution. The company has undertaken a number of torch programs of the Ministry of Science and Technology, major provincial and municipal science and technology projects, and obtained more than 200 national patents. Therefore, how to reduce the carbon emissions of building materials, improve green competitiveness, and profit are important issues. Therefore, Tianfeng will be committed to the development and practice of digital green and innovative projects to innovate green products and provide green building materials as the development goal.
Tianfeng is about to launch a digital green innovation project. The main body of the project is a cluster intelligent prefabricated building. A cluster intelligent prefabricated building is a prefabricated steel structure with an ultra-low energy consumption building system that adopts new construction technology and green building materials. Moreover, the cluster prefabricated building structure system has the characteristics of light weight, manual handling, convenient installation, and strong and durable structure, which is very suitable for application in mountainous areas and scenic spots. Tianfeng customized the program design and housing construction and committed to close cooperation with a number of enterprises, gathering wisdom development, creating a win–win situation. At present, the enterprise needs to select a matching joint venture partner from some enterprises to carry out the project.
In recent years, seven enterprises have carried out digital green and innovative activities. Prefab construction company Tianfeng needs to select one of them as a partner to carry out digital green innovation activities, and these companies are willing to work with them. Tianfeng has some experience in the selection of partners, but how to choose the best digital green innovation partner from multiple enterprises is still a difficult problem.
4.2. Empirical Elements
4.2.1. Development of Evaluation Criteria
In different scenarios, enterprises choose different methods for partners. In view of the current situation, PCEs need to develop in the direction of digitalization, greening, and innovation. The current systems and methods cannot satisfy Tianfeng to choose the best risk joint investment partner. In order to evaluate the suitability of joint investment partners for PCEs to carry out digital green innovative project investment activities, this paper innovatively proposes a research framework of joint venture investment 3W1H-P in the evaluation index system. This theory has a solid theoretical basis, and the research system of PCEs to choose joint investment partners in the investment activities of digital green innovative projects is constructed. This system can meet the requirements of Tianfeng to select joint investment partners. The evaluation criteria of the research system for enterprises to choose joint investment partners usually come from the green innovation ability, resource accumulation, and degree of overlap of cooperation foundation. In the digital green innovation system of enterprise cooperation and collaboration, green innovation capability is divided into compatible risk diversification and commitment risk diversification, including compatible venture investment style, organizational culture, digital green innovation management team, investment in digital green innovation resources, social network capability, and risk investment willingness of senior managers. Resource accumulation can be divided into complementary accumulation resources and superposition accumulation resources, including technological complementarity, market complementarity, social network resource complementarity, financial risk investment ability, past cooperation, and good mutual trust between senior managers. The basis of cooperation is the mutual trust degree of both parties, including whether the cooperative enterprise has the possibility of long-term cooperation with the PCEs, the influence of the resources provided by the cooperative enterprise on the value of the PCEs, and the reputation of the cooperative enterprise in the prefabricated construction industry. The established evaluation system is shown in Figure 3.
4.2.2. Data and Scenarios
Tianfeng is a construction enterprise with professional construction qualifications. At present, the concept of green building is gradually being taken seriously, and the government has set carbon emission reduction targets for PCEs. Construction companies face hefty fines if their total carbon emissions exceed the limits set by the government. How to reduce the carbon emissions of construction projects and improve green competitiveness and profits is an important issue. In this case, Tianfeng needs to select the best joint investment partner from a large number of alternative enterprises in the construction project. The standards and methods proposed in this paper are suitable for PCEs to select joint investment partners in the development of digital green innovative project investment activities. The reason is that managers and participants understand that the weight of partner selection criteria for digital green innovation is in a vague state. After preliminary screening, seven digital green innovation initiatives have been shortlisted by co-investment partner .
4.3. Results and Discussion
4.3.1. Results
Step 1: List the indicator evaluation of alternative partners in different periods. Tianfeng needs to select the best partner from the seven major co-investment partners according to the suggested standards and methods. The potential co-investment partners mentioned above are evaluated according to the compiled co-investment partner selection criteria, as shown in Figure 3, including five main criteria and fifteen sub-criteria. In this process, this paper selects time series set of different periods in recent 4 years. For the sake of simplicity, this paper only gives the calculation of five main criteria, denoted as attribute set . Table 2, Table 3, Table 4 and Table 5 list the evaluation of indicators of seven alternative partners in four different periods.

Table 2.
Original evaluation criteria information matrix at the moment t1.

Table 3.
Original evaluation criteria information matrix at the moment t2.

Table 4.
Original evaluation criteria information matrix at the moment t3.

Table 5.
Original evaluation criteria information matrix at the moment t4.
Step 2: Calculate the discrete time weight and criteria weight. It is according to the original evaluation criteria information matrix of joint venture capital partner selection, which contains only venture capital partner . Based on consultation with relevant experts, we take . is the time vector; . According to Equations (4)–(11), it can be known that the weight of comprehensive time degree based on subjective and objective can be solved. According to Equation (12), the criterion weight based on improved intuitionistic fuzzy entropy can be obtained. Specific values can be seen from Table 6.

Table 6.
Discrete time weight and criteria weight.
Step 3: Calculate the comprehensive selection criteria information. According to Appendix A, the weighted IFNs’ decision matrices of different periods are assembled by using dynamic intuitionistic fuzzy weighted geometric operators. These five criteria are combined into a set of criteria information of cooperative enterprise selection matrix of four periods, as shown in Table 7.

Table 7.
Comprehensive selection criteria information.
Step 4: Calculate cooperative enterprise prospect matrix. This study can make the enterprise decision-making more reasonable and effective. It helps PCEs to blindly avoid similar risks. Using the Appendix D of prospect value function, the prospect matrix is obtained, as shown in Table 8.

Table 8.
Cooperative enterprise prospect matrix.
Step 5: Use VIKOR and attribute weight method to calculate utility values, individual regret values, and values. Based on Appendix B and Appendix C, Equations (1)–(3) and combination weight method , this paper obtains the combination weight. VIKOR method and Equation (A18) were used to obtain positive ideal points and negative ideal points of attributes. By using Equation (A19), group utility value and individual regret value are calculated. Take the compromise coefficient and use Equation (A20) to calculate the value . Specific values are shown in Table 9.

Table 9.
Utility values, individual regret values, and values.
Finally, the value of each potential partner in the construction project is determined as follows:
The seven potential partners were rated as worthy in order of priority . Therefore, the joint venture investment partner of digital innovation activities of Tianfeng is determined as . Based on the above evaluation and selection, the joint venture partner is the best joint venture partner of Tianfeng. In fact, has become a preferred co-venture partner. In addition, joint venture partner is recommended as a reserved venture partner.
Based on the case of Tianfeng’s selection of joint venture investment partners in carrying out digital green and innovative activities, the above study indicates the selection process of joint venture investment partners from the perspective of digital green innovation customers. This process is also for the PCEs to carry out the digital green innovation process. The above analysis further verifies that the key influencing factors for PCEs to choose joint venture investment partners in digital green and innovative activities include compatible risk diversification, commitment to risk diversification, complementary accumulation of resources, overlapping accumulation of resources, and mutual trust degree. In addition, the time preference of cooperative enterprises also has an important impact on the digital green innovation activities of PCEs.
4.3.2. Discussion
(i) Managerial implications. This study has two important management implications for PCEs in the selection of joint investment partners. The practical management significance of this study is as follows:
This paper constructs a theoretical model of a joint venture capital network. PCEs and joint venture partners are two main bodies of digital green and innovative projects. The exchange of green knowledge and digital innovation technologies between construction firms and joint venture partners helps to promote business development and technological progress. In the process of knowledge and technology exchange, PCEs and joint venture partners gradually form a mutually beneficial symbiotic relationship. The two share more and more complementary resources on digital green innovation. Whether PCEs can choose appropriate joint venture partners is directly related to the development of mutualistic symbiosis. The theoretical model based on the joint venture capital network can be applied to the selection of partners in PCEs, which can make the decision more theoretical and scientific.
In this study, the logical relationship is integrated with the idea of six analysis methods. This study innovatively proposes a 3W1H-P research framework of joint venture capital. First, motivation affects partner selection, which, in turn, affects firm performance. PCEs choose joint venture partners based on risk diversification motivation to carry out digital green innovative projects to promote enterprise venture investment performance. Secondly, this study comprehensively analyzes the motivations, partner selection, and the impact on performance. The joint venture investment behavior of PCEs in carrying out digital green innovation projects is the process of joint venture investment partners to invest in PCEs under certain motivation. In this process, joint venture partners and PCEs will play against each other based on the principle of maximizing their own interests. Finally, the selection of joint venture partners by PCEs is a process of investment behavior, and its joint motivation, partner selection, and game behavior in the process of joint venture partners are bound to be affected by the situation of joint venture partners and PCEs. Based on the research framework of 3W1H-P, the research system is constructed in this study, which can meet the requirements of PCEs to select joint investment partners in the investment activities of digital green innovation projects. The evaluation criteria of research systems for enterprises to choose joint investment partners usually come from green innovation ability, resource accumulation, and the degree of overlap of the cooperation foundation. Green innovation capability is divided into compatible risk diversification and commitment risk diversification, including the compatible venture investment style, organizational culture, digital green innovation management team, investment in digital green innovation resources, social network capability, and risk investment willingness of senior managers. Resource accumulation can be divided into complementary accumulation resources and superposition accumulation resources, including technological complementarity, market complementarity, social network resource complementarity, financial risk investment ability, past cooperation, and good mutual trust between senior managers. The basis of cooperation is the mutual trust degree of both parties, including whether the cooperative enterprise has the possibility of long-term cooperation with the PCEs, the influence of the resources provided by the cooperative enterprise on the value of the PCEs, and the reputation of the cooperative enterprise in the prefabricated construction industry. For managers, the use of the 3W1H-P research framework and the newly built research system can enable PCEs to select joint investment partners in the development of digital, green, and innovative project investment activities, which is more efficient and accurate, thus reducing the management costs and promoting the efficient operation of enterprises.
(ii) Theoretical implications. This study is based on the case of Tianfeng’s joint venture investment partner in digital green and innovative activities. This study first listed the time series set , attribute set , alternative partner set in different periods, and the evaluation of indicators of seven alternative partners in four different periods. Secondly, this study used the combined time weight to solve the subjective and objective comprehensive time weight and obtained the criterion weight according to the improved intuitionistic fuzzy number entropy. Then, this study used dynamic intuitionistic fuzzy weighted geometric operators to assemble the weighted intuitionistic fuzzy decision matrices of different time periods and combined these five criteria into a set of criteria information of a cooperative enterprise selection matrix including four time periods. Furthermore, this study helps PCEs to blindly avoid similar risks, making decision-making more reasonable and effective. Using the formula of prospect value function, the prospect matrix is obtained. The combined weight set is obtained by using the combined weight method. The VIKOR method was adopted to obtain the positive ideal points and negative ideal points of attributes and calculate the group utility value and individual regret value and value . Finally, the evaluation value of partners is prioritized to obtain the best partner. The theoretical process can be applied to other PCEs in the process of choosing joint venture capital partners. In this way, enterprises have sufficient theoretical support when choosing partners and can produce more realistic and effective selection results.
5. Conclusions and Enlightenment
5.1. Conclusions
With the background of carbon peak and carbon neutrality, it is very necessary for the construction industry to carry out digital green and innovative activities. It has gradually become an inevitable trend for PCEs to adapt to the new era, create new models, and develop healthily and long-term by choosing joint investment partners in the development of digital green innovative project investment activities. First, in this study, a theoretical model for PCEs to select joint investment partners in digital green innovative project investment activities was constructed. Second, with the help of the idea of six analysis methods, this study innovatively proposed a research framework of joint venture capital 3W1H-P by integrating logical relations. Third, on this basis, the research system of selecting joint investment partners was constructed. Fourth, intuitionistic fuzzy set, intuitionistic fuzzy number aggregation operator, and intuitionistic fuzzy entropy were expounded. The combined theoretical knowledge of combined time weight, improved intuitionistic fuzzy number entropy, and the VIKOR method is proposed. This practice brings positive enlightenment to other PCEs when they choose joint investment partners to make decisions in the investment activities of digital green innovative projects.
The results are drawn as follows. This study constructed a theoretical model of PCEs selecting joint investment partners. This study proposed the research framework of 3W1H-P. This study constructed a research system for the selection of joint investment partners. The research system includes green innovation capacity indicators, cooperation basic indicators, resource accumulation indicators, etc. This study indicates that the joint venture investment network theoretical model, the joint venture investment 3W1H-P research framework, research system, and applied theory can enable Tianfeng to select the optimal partner. Further, this approach can be applied to the selection of joint investment partners by global PCEs in the development of digital green innovative project investment activities.
5.2. Implications
This study has important management implications. This study not only constructed a theoretical model in the joint venture investment network but also innovatively proposed a 3W1H-P research framework of joint venture investment by integrating logical relations with the idea of six analysis methods. On this basis, a research system for PCEs to select joint investment partners in the investment activities of digital green innovative projects was constructed. The theoretical model, research framework, and research system can be used to assist PCEs to select joint investment partners in the investment activities of digital green innovative projects. This study has important theoretical implications. In this study, intuitionistic fuzzy set, intuitionistic fuzzy number aggregation operator, intuitionistic fuzzy entropy, AHP, deviation maximization method, combinatorial attribute weight, and prospect theory were theoretically expounded, and the theoretical knowledge of combination time weight, improved intuitionistic fuzzy number entropy, and the VIKOR method was proposed.
5.3. Deficiencies and Future Prospects
There are still some limitations in this study that deserve further attention. Artificial intelligence (AI) technology is gradually applied to decision-making problems, and the combination of resource complementarity and AI plays an important role in future enlightenment. In addition, only one case study was conducted in this study, and future studies may include large sample sizes from many PCEs to verify the correctness of the theoretical models, frameworks, systems, and use of theoretical knowledge. PCEs can be classified according to the scale of R&D or enterprise size.
Author Contributions
Conceptualization, S.Y. and T.D.; methodology, S.Y.; software, S.Y.; validation, T.D. and S.Y.; writing—original draft preparation, T.D.; writing—review and editing, S.Y., B.L., and S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Philosophy and Social Sciences Planning Project of the Ministry of Education grant number [21YJCZH203], Soft Science Special Project of Hebei Innovation Capability Enhancement Program grant number [21557635D], Social Science Fund project of Hebei Province grant number [HB21YJ003], Top Young Talents Scientific Research Project of Higher Education in Hebei Province grant number [BJ2021084], Baoding Philosophy and Social Science Planning Project grant number [2020047], Teaching and Research Project of Hebei Agricultural University grant number [2021C-39], and Scientific Research Foundation for the Talents of Hebei Agricultural University grant number [YJ2020017], Basic Scientific Research Funds for Universities in Heilongjiang Province, Heilongjiang University Special Fund Project (2020-KYYWF-0969), Philosophy and Social Science research Planning project of Heilongjiang Province (20JYB030), Hebei Agricultural Industry System Project [HBCT2021230301], and Henan Key Research and Development and Promotion Special (Soft Science Research) grant number [222400410126].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Definition A1.
Let X be a non-empty-theoretic domain, and the intuitive fuzzy set on X be defined as , where is the membership function of the element for the set . is a non-membership function for the element x for the set . relative to ,. is called the intuitionistic ambiguity of the set , . Intuitionistic fuzzy sets over a non-empty field X are collectively denoted as . is an intuitionistic fuzzy number (IFN).
Definition A2.
Set as a group of IFNs; then:
is called intuitionistic fuzzy weighted average operator, and its calculation formula is
Definition A3.
Set as a group of intuitionistic fuzzy numbers, and then is called intuitionistic fuzzy weighted geometric operators, and its calculation formula is
Definition A4.
Let and be two intuitionistic fuzzy sets, and call function intuitionistic fuzzy entropy if it satisfies the following criteria.
Criterion A1.
if and only if is a clear set for ; there is or, .
Criterion A2.
if and only if ; there is .
Criterion A3.
.
Criterion A4.
for . When , there are and ; when , there are and
Criterion A5.
For , when and , there is .
Appendix B
(i) Construct the comparative judgment matrix. Using AHP method, the comparative judgment matrix of digital green innovation development level evaluation index of PCEs is constructed as follows:
In the evaluation index system of digital green innovation of PCEs, is the importance of the index relative to the j index. , and, obviously, ; ; . As for the value of in the comparative judgment matrix, saaty1–9 contrast scale is used in this paper to measure the comparison of importance among indicators. The contrast scale is shown in Table A1.

Table A1.
Saaty’s contrast ruler.
Table A1.
Saaty’s contrast ruler.
| Contrast Scale | Implication |
|---|---|
| 1 | The evaluation index Ci has the same importance as the evaluation index Cj |
| 3 | The evaluation index Ci is slightly more important than the evaluation index Cj |
| 5 | The evaluation index Ci is significantly more important than the evaluation index Cj |
| 7 | The evaluation index Ci is strongly more important than the evaluation index Cj |
| 9 | The evaluation index Ci is absolutely more important than the evaluation index Cj |
| 2, 4, 6, 8 | The results of evaluation index Ci and evaluation index Cj are in the middle position |
| Count backwards | The importance comparison result of evaluation index Ci and evaluation index Cj is the reciprocal of evaluation index Cj and evaluation index Ci |
(ii) Calculate the weight set and conduct consistency test.
The weight set is calculated by the weight judgment matrix of the development level evaluation index of digital green innovation of prefabricated building enterprises, and the consistency test is carried out.
Multiply the elements in each row of the comparison judgment matrix, namely:
where is the element in row and column of the weight comparison judgment matrix of the development level evaluation index of digital green innovation of PCEs. is the weight of the first indicator to the upper indicator in the development level evaluation system of digitalization, greening, and innovation of PCEs. It is concluded that is the relative importance of the next layer to the upper layer, that is, the weight value of the index of the next layer to the upper layer. Consistency check is as follows:
where is the largest characteristic root of the judgment matrix of the development level evaluation index of digital green innovation of PCEs. CI is the consistency index of the index weight comparison and judgment matrix in the digital, green, and innovative development level evaluation system of PCEs. In n, the larger the CI, the worse the consistency (and vice versa). Since CI is an error of randomness, it is compared to the stochastic consistency index RI. CR is the random consistency ratio of index weight comparison judgment matrix in the evaluation system of digital green innovation development level of prefabricated building enterprises. RI values are shown in Table A2.

Table A2.
RI values table.
Table A2.
RI values table.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| RI | 0 | 0 | 0.58 | 0.96 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 |
The basis of consistency test is that, when , it means that the judgment matrix of development level risk evaluation of digital green innovation of prefabricated building enterprises is consistent. Otherwise, it is necessary to readjust the judgment matrix to meet the requirements of .
Appendix C
Under the condition that normalization and weight constraint principles are satisfied, is set to represent the deviation between partner and other partners for indicator . and are the -th index value of the -th and -th partner, respectively. is the weight of the first evaluation index of . The deviation maximization method was used to calculate its weight, and the objective function was calculated as follows:
The determination of index weight is based on the principle of maximizing the total deviation of all partner evaluation indexes, and the following linear programming model is established . The result is as follows:
It is solved using the Lagrangian function . The result is as follows:
The partial derivatives of and were taken, respectively, to obtain the optimal solution of the model. The result is as follows:
Norm-normalized is as follows:
Appendix D
If the candidate partner is odd, the median is used as the reference point. If it is an even number of alternative partners, the mean of the two middle fuzzy numbers is used as the reference point. Assume that the reference point of the criterion value of in the state of criterion is , and the prospect value function can be determined based on the distance formula of the two fuzzy numbers and the comparison results:
Among them, is the risk attitude coefficient. . The higher the value, the more likely it is to take risks. When , the decision-maker is regarded as risk neutral. Here, define , as loss avoidance coefficient, and define . Since the decision weight is closely related to the objective probability, the ratio of the weight of probability to the deterministic weight is taken as the decision weight of gain and loss, which are, respectively:
Among them, is the risk–return attitude coefficient; is the risk–loss attitude coefficient, and and are defined here. Then, the comprehensive prospect value is as follows:
Appendix E
(i) Set as the positive ideal point of the attribute, as the negative ideal point of the attribute; then:
(ii) Calculate group utility value and individual regret value ; then:
(iii) The value is calculated by the following formula:
where is the decision-making mechanism coefficient.
References
- Cheng, M.; Lu, Y.; Zhu, H.; Xiao, J. Measuring CO2 emissions performance of China’s construction industry: A global Malmquist index analysis. Environ. Impact Assess. Rev. 2022, 92, 106673. [Google Scholar] [CrossRef]
- Cheekatamarla, P.; Sharma, V.; Shen, B. Sustainable Energy Solutions for Thermal Load in Buildings—Role of Heat Pumps, Solar Thermal, and Hydrogen-Based Cogeneration Systems. J. Eng. Sustain. Build. Cities 2021, 2, 034501. [Google Scholar] [CrossRef]
- Mostafavi, F.; Tahsildoost, M.; Zomorodian, Z. Energy efficiency and carbon emission in high-rise buildings: A review (2005–2020). Build. Environ. 2021, 206, 108329. [Google Scholar] [CrossRef]
- Reisinger, J.; Kugler, S.; Kovacic, I.; Knoll, M. Parametric Optimization and Decision Support Model Framework for Life Cycle Cost Analysis and Life Cycle Assessment of Flexible Industrial Building Structures Integrating Production Planning. Buildings 2022, 12, 162. [Google Scholar] [CrossRef]
- Lu, N.; Feng, S.; Liu, Z.; Wang, W.; Lu, H.; Wang, M. The Determinants of Carbon Emissions in the Chinese Construction Industry: A Spatial Analysis. Sustainability 2020, 12, 1428. [Google Scholar] [CrossRef]
- Cang, Y.; Yang, L.; Luo, Z.; Zhang, N. Prediction of embodied carbon emissions from residential buildings with different structural forms. Sustain. Cities Soc. 2020, 54, 101946. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Gao, W.; Kuroki, S. Life cycle environmental and cost performance of prefabricated buildings. Sustainability 2020, 12, 2609. [Google Scholar] [CrossRef]
- Jiang, W.; Huang, Z.; Peng, Y.; Fang, Y.; Cao, Y. Factors affecting prefabricated construction promotion in China: A structural equation modeling approach. PLoS ONE 2020, 15, e0227787. [Google Scholar] [CrossRef]
- Li, J.; Greenwood, D.; Kassem, M. Blockchain in the built environment and construction industry: A systematic review, conceptual models and practical use cases. Autom. Constr. 2019, 102, 288–307. [Google Scholar] [CrossRef]
- Xiao, Y.; Bhola, J. Design and optimization of prefabricated building system based on BIM technology. Int. J. Syst. Assur. Eng. Manag. 2021, 13, 111–120. [Google Scholar] [CrossRef]
- Panteleeva, M.; Borozdina, S. Sustainable Urban Development Strategic Initiatives. Sustainability 2021, 14, 37. [Google Scholar] [CrossRef]
- Li, Y.; Song, Y.; Wang, J.; Li, C. Intellectual capital, knowledge sharing, and innovation performance: Evidence from the Chinese construction industry. Sustainability 2019, 11, 2713. [Google Scholar] [CrossRef]
- Du, Q.; Zhou, J.; Pan, T.; Sun, Q.; Wu, M. Relationship of carbon emissions and economic growth in China’s construction industry. J. Clean. Prod. 2019, 220, 99–109. [Google Scholar] [CrossRef]
- Huang, B.; Gao, X.; Xu, X.; Song, J.; Geng, Y.; Sarkis, J.; Nakatani, J. A Life Cycle Thinking Framework to Mitigate the Environmental Impact of Building Materials. One Earth 2020, 3, 564–573. [Google Scholar] [CrossRef]
- Hertwich, E.G.; Ali, S.; Ciacci, L.; Fishman, T.; Heeren, N.; Masanet, E.; Wolfram, P. Material efficiency strategies to reducing greenhouse gas emissions associated with buildings, vehicles, and electronics—A review. Environ. Res. Lett. 2019, 14, 043004. [Google Scholar] [CrossRef]
- Wu, G.; Yang, R.; Li, L.; Bi, X.; Liu, B.; Li, S.; Zhou, S. Factors influencing the application of prefabricated construction in China: From perspectives of technology promotion and cleaner production. J. Clean. Prod. 2019, 219, 753–762. [Google Scholar] [CrossRef]
- Jain, S.; Singhal, S.; Pandey, S. Environmental life cycle assessment of construction and demolition waste recycling: A case of urban India. Resour. Conserv. Recycl. 2020, 155, 104642. [Google Scholar] [CrossRef]
- Yu, S.; Liu, Y.; Wang, D.; Bahaj, A.S.; Wu, Y.; Liu, J. Review of thermal and environmental performance of prefabricated buildings: Implications to emission reductions in China. Renew. Sustain. Energy Rev. 2021, 137, 110472. [Google Scholar] [CrossRef]
- Chang, R.D.; Zuo, J.; Zhao, Z.Y.; Soebarto, V.; Lu, Y.; Zillante, G.; Gan, X.L. Sustainability attitude and performance of construction enterprises: A China study. J. Clean. Prod. 2018, 172, 1440–1451. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, F. The effects of trade openness on decoupling carbon emissions from economic growth–Evidence from 182 countries. J. Clean. Prod. 2021, 279, 123838. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, K.; Liu, Q.; Tao, Z.; Lin, L. Carbon footprint and eco-efficiency of China’s regional construction industry: A life cycle perspective. J. Oper. Res. Soc. 2020, 72, 2704–2719. [Google Scholar] [CrossRef]
- Atanda, J.O.; Olukoya, O.A. Green building standards: Opportunities for Nigeria. J. Clean. Prod. 2019, 227, 366–377. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Song, X.; Han, Y. IoT-Based Intelligent Construction System for Prefabricated Buildings: Study of Operating Mechanism and Implementation in China. Appl. Sci. 2020, 10, 6311. [Google Scholar] [CrossRef]
- Li, S.; Wu, C.; Kong, F. Shaking table model test and seismic performance analysis of a high-rise RC shear wall structure. Shock Vib. 2019, 2019, 1–17. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, J.; Wu, J.; Shi, W.; Ji, D.; Wang, X.; Zhao, X. Constraints hindering the development of high-rise modular buildings. Appl. Sci. 2020, 10, 7159. [Google Scholar] [CrossRef]
- Chen, G.; Liu, J.C.; Ma, Y.F. Application of digital technology in the whole process of prefabricated building design, production and construction: A case study of the National Synthetic Biotechnology Innovation Center project. Civ. Eng. Inf. Technol. 2021, 14, 1–11. [Google Scholar]
- Chen, Z.L.; Niu, C.L.; Liu, F.J.; Wei, H.L.; Wu, X.R. Research on prefabricated building design method based on BIM technology. Technol. Mark. 2021, 10, 60–63. [Google Scholar]
- Li, Y.D.; Zhao, J.H. Quality and safety management of prefabricated buildings based on Internet of Things technology. Bulk Cement. 2021, 5, 63–65. [Google Scholar]
- Sun, Y.Q.; Zhang, Y. Thinking and innovation research on intelligent construction of prefabricated buildings. China Hous. Facil. 2021, 8, 47–48. [Google Scholar]
- Zhong, B.; Hei, Y.; Li, H.; Rose, T.; Luo, H. Patent cooperative patterns and development trends of Chinese construction enterprises: A network analysis. J. Civ. Eng. Manag. 2019, 25, 228–240. [Google Scholar] [CrossRef]
- Maskuriy, R.; Selamat, A.; Maresova, P.; Krejcar, O.; David, O.O. Industry 4.0 for the construction industry: Review of management perspective. Economies 2019, 7, 68. [Google Scholar] [CrossRef]
- Allmendinger, M.P.; Berger, E.S. Selecting corporate firms for collaborative innovation: Entrepreneurial decision making in asymmetric partnerships. Int. J. Innov. Manag. 2020, 24, 2050003. [Google Scholar] [CrossRef]
- Tetik, M.; Peltokorpi, A.; Seppänen, O.; Holmström, J. Direct digital construction: Technology-based operations management practice for continuous improvement of construction industry performance. Autom. Constr. 2019, 107, 102910. [Google Scholar] [CrossRef]
- Kim, H.C.; Yoon, W. Study on types of technology cooperation partner and innovation performance: Focusing on incremental and radical innovation. Int. J. Innov. Manag. 2019, 23, 1950005. [Google Scholar] [CrossRef]
- Ran, C.; Song, K.; Yang, L. An improved solution for partner selection of industry-university cooperation. Technol. Anal. Strateg. Manag. 2020, 32, 1478–1493. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J. A Cooperative Partner Selection Study of Military-Civilian Scientific and Technological Collaborative Innovation Based on Interval-Valued Intuitionistic Fuzzy Set. Symmetry 2021, 13, 553. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Rezaei, G.; Liao, H.; Mardani, A. Extended Pythagorean fuzzy TOPSIS method based on similarity measure for sustainable recycling partner selection. Int. J. Fuzzy Syst. 2020, 22, 735–747. [Google Scholar] [CrossRef]
- Uren, V.; Miller, T.; Da Campo, R.; Dadzie, A.S. A model for partner selection criteria in energy from waste projects. J. Clean. Prod. 2021, 279, 123582. [Google Scholar] [CrossRef]
- Badulescu, Y.; Hameri, A.P.; Cheikhrouhou, N. Sustainable partner selection for collaborative networked organisations with risk consideration in the context of COVID-19. J. Glob. Oper. Strateg. Sourc. 2021, 15, 197–218. [Google Scholar] [CrossRef]
- Khin, S.; Ho, T.C. Digital technology, digital capability and organizational performance: A mediating role of digital innovation. Int. J. Innov. Sci. 2018, 8, 256–269. [Google Scholar] [CrossRef]
- Li, Y.; Dai, J.; Cui, L. The impact of digital technologies on economic and environmental performance in the context of industry 4.0: A moderated mediation model. Int. J. Prod. Econ. 2020, 229, 107777. [Google Scholar] [CrossRef]
- Kaluarachchi, Y. Potential advantages in combining smart and green infrastructure over silo approaches for future cities. Front. Eng. Manag. 2021, 8, 98–108. [Google Scholar] [CrossRef]
- Jiang, J.H. Sustainable digital era: High-quality integrated development of digital economy and green economy. Enterp. Econ. 2021, 7, 23–30. [Google Scholar]
- Chaker, N.N.; Nowlin, E.L.; Pivonka, M.T.; Itani, O.S.; Agnihotri, R. Inside sales social media use and its strategic implications for salesperson-customer digital engagement and performance. Ind. Mark. Manag. 2022, 100, 127–144. [Google Scholar] [CrossRef]
- Pence, C.C. How Venture Capitalists Make Investment Decisions; UMI Research Press: New York, NY, USA, 1982. [Google Scholar]
- Perez, R.C. Inside Venture Capital: Past, Present, and Future; Praeger Pub Text: Westport, CT, USA, 1986. [Google Scholar]
- Lerner, J. Venture capitalists and the decision to go public. J. Financ. Econ. 1994, 35, 293–316. [Google Scholar] [CrossRef]
- Altintig, Z.A.; Chiu, H.H.; Goktan, M.S. How does uncertainty resolution affect VC syndication? Financ. Manag. 2013, 42, 611–646. [Google Scholar] [CrossRef]
- Tykvova, T.; Schertler, A. Does syndication with local venture capitalists moderate the effects of geographical and institutional distance? J. Int. Manag. 2014, 20, 406–420. [Google Scholar] [CrossRef]
- Manigart, S.; Lockett, A.; Meuleman, M.; Wright, M.; Landström, H.; Bruining, H.; Hommel, U. Venture capitalists’ decision to syndicate. Entrep. Theory Pract. 2006, 30, 131–153. [Google Scholar] [CrossRef]
- Lockett, A.; Wright, M. The syndication of venture capital investments. Omega 2001, 29, 375–390. [Google Scholar] [CrossRef]
- Brander, J.A.; Amit, R.; Antweiler, W. Venture-capital syndication: Improved venture selection vs. the value-added hypothesis. J. Econ. Manag. Strategy 2002, 11, 423–452. [Google Scholar] [CrossRef]
- Verwaal, E.; Bruining, H.; Wright, M.; Manigart, S.; Lockett, A. Resources access needs and capabilities as mediators of the relationship between VC firm size and syndication. Small Bus. Econ. 2010, 34, 277–291. [Google Scholar] [CrossRef]
- Ferrary, M. Syndication of venture capital investment: The art of resource pooling. Entrep. Theory Pract. 2010, 34, 885–908. [Google Scholar] [CrossRef]
- Hopp, C.; Rieder, F. What drives venture capital syndication? Appl. Econ. 2011, 43, 3089–3102. [Google Scholar] [CrossRef]
- Lerner, J. The Syndication of Venture Capital Investments. Financ. Manag. 1994, 23, 16–27. [Google Scholar] [CrossRef]
- Admati, A.R.; Pfleiderer, P. Robust financial contracting and the role of venture capitalists. J. Financ. 1994, 49, 371–402. [Google Scholar] [CrossRef]
- Zhu, Y.Y.; Ma, Z.Q.; Chen, Y.Q. Multi-stage fuzzy comprehensive evaluation of enterprise green technology innovation environment. Sci. Technol. Prog. Countermeas. 2010, 9, 102–105. [Google Scholar]
- Bi, K.X.; Yang, Z.J.; Huang, P. Regional differences and influencing factors of green process innovation performance in China. China Ind. Econ. 2013, 10, 57–69. [Google Scholar]
- Ghisetti, C.; Rennings, K. Environmental innovations and profitability: How does it pay to be green? An empirical analysis on the German innovation survey. J. Clean. Prod. 2014, 75, 106–117. [Google Scholar] [CrossRef]
- Salamat, V.; Aliahmadi, A.; Pishvaee, M.; Hafeez, K. A robust fuzzy possibilistic AHP approach for partner selection in international strategic alliance. Decis. Sci. Lett. 2018, 7, 481–502. [Google Scholar] [CrossRef]
- Dedehayir, O.; Mäkinen, S.J.; Ortt, J.R. Roles during innovation ecosystem genesis: A literature review. Technol. Forecast. Soc. Chang. 2018, 136, 18–29. [Google Scholar] [CrossRef]
- Yin, S.; Zhang, N.; Li, B. Enhancing the competitiveness of multi-agent cooperation for green manufacturing in China: An empirical study of the measure of green technology innovation capabilities and their influencing factors. Sustain. Prod. Consum. 2020, 23, 63–76. [Google Scholar] [CrossRef]
- Du, Q. Birds of a feather or celebrating differences? The formation and impacts of venture capital syndication. J. Empir. Financ. 2016, 39, 1–14. [Google Scholar] [CrossRef]
- Gompers, P.A.; Mukharlyamov, V.; Xuan, Y. The cost of friendship. J. Financ. Econ. 2016, 119, 626–644. [Google Scholar] [CrossRef]
- Casamatta, C.; Haritchabalet, C. Experience, screening and syndication in venture capital investments. J. Financ. Intermed. 2007, 16, 368–398. [Google Scholar] [CrossRef]
- Hochberg, Y.V.; Lindsey, L.A.; Westerfield, M.M. Resource accumulation through economic ties: Evidence from venture capital. J. Financ. Econ. 2015, 118, 245–267. [Google Scholar] [CrossRef]
- Nikghadam, S.; Sadigh, B.L.; Ozbayoglu, A.M.; Unver, H.O.; Kilic, S.E. A survey of partner selection methodologies for virtual enterprises and development of a goal programming–Based approach. Int. J. Adv. Manuf. Technol. 2016, 85, 1713–1734. [Google Scholar] [CrossRef]
- Chen, S.M.; Han, W.H. A new multiattribute decision making method based on multiplication operations of interval-valued intuitionistic fuzzy values and linear programming methodology. Inf. Sci. 2018, 429, 421–432. [Google Scholar] [CrossRef]
- Gao, M.M.; Sun, T.; Zhu, J.J. Interval-intuitionistic fuzzy multi-attribute decision making based on improved entropy and new score function. Control Decis. 2016, 10, 1757–1764. [Google Scholar]
- Yin, S.; Yang, Z.; Chen, S.Y. Interval intuitionistic fuzzy multi-attribute decision making based on improved fuzzy entropy. Syst. Eng. Electron. 2018, 5, 1079–1084. [Google Scholar]
- Liang, R.; Chong, H.Y. A hybrid group decision model for green supplier selection: A case study of megaprojects. Eng. Constr. Archit. Manag. 2019, 26, 1712–1734. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, B.; Zhang, R.; An, Z.J. Optimal configuration of multi-energy complementary cosupply systems based on entropy-weight TOPSIS. J. Huazhong Univ. Sci. Technol. 2021, 10, 1–8. [Google Scholar]
- Zhao, Y.G.; Yu, Z. Evaluation of influencing factors of satisfaction of different automobile brands based on entropy-weight variation method. China Automob. 2021, 10, 4–9. [Google Scholar]
- Liu, Y.; Xiong, S.J.; Wang, F.Q.; Wei, H.F.; Wang, Y. Evaluation of heavy equipment manufacturing resources based on entropy-ideal point method. Heavy Mach. 2021, 5, 49–56. [Google Scholar]
- Liu, J. Application of fuzzy mathematical model based on combined weights in water quality assessment of Jinghe River reach in Pingliang City. Gansu Sci. Technol. 2021, 16, 33–36. [Google Scholar]
- Lin, Y.J.; Bai, Q.F. Operation index evaluation of thermal power plant based on combined weight and TOPSIS method. Shandong Electr. Power Technol. 2021, 8, 61–65. [Google Scholar]
- Chen, W.Q.; Yang, R.Z.; Zhao, Y.F.; Liu, L.P. Evaluation of rock slope stability based on combination-weighted TOPSIS. J. Saf. Environ. 2021, 3, 1–12. [Google Scholar]
- Chou, J.S.; Truong, D.N. Multiobjective forensic-based investigation algorithm for solving structural design problems. Autom. Constr. 2022, 134, 104084. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Xu, Z.S. Intuitionistic fuzzy aggregation operators. Trans. Fuzzy Syst. 2008, 14, 1179–1187. [Google Scholar]
- Song, Y.; Wang, J.; Guo, F.; Lu, J.; Liu, S. Research on Supplier Selection of Prefabricated Building Elements from the Perspective of Sustainable Development. Sustainability 2021, 13, 6080. [Google Scholar] [CrossRef]
- Awad, J.; Jung, C. Extracting the Planning Elements for Sustainable Urban Regeneration in Dubai with AHP (Analytic Hierarchy Process). Sustain. Cities Soc. 2022, 76, 103496. [Google Scholar] [CrossRef]
- Venkatesan, C.; Kannadasan, R.; Alsharif, M.H.; Kim, M.K.; Nebhen, J. A novel multiobjective hybrid technique for siting and sizing of distributed generation and capacitor banks in radial distribution systems. Sustainability 2021, 13, 3308. [Google Scholar] [CrossRef]
- Yin, S.; Zhang, N.; Xu, J. Information fusion for future COVID-19 prevention: Continuous mechanism of big data intelligent innovation for the emergency management of a public epidemic outbreak. J. Manag. Anal. 2021, 8, 391–423. [Google Scholar] [CrossRef]
- Yin, S.; Zhang, N.; Dong, H. Preventing COVID-19 from the perspective of industrial information integration: Evaluation and continuous improvement of information networks for sustainable epidemic prevention. J. Ind. Inf. Integr. 2020, 19, 100157. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).