Risk Assessment and Prevention Strategy of Virus Infection in the Context of University Resumption

Abstract

The risk assessment system of virus infection probability and the prevention measures for virus transmission are keys to controlling epidemics. In the context of university resumption, this study identifies the risk elements in terms of the mechanism of virus transmission. The effect of two recognized effective measures, i.e., occupancy constraints and ventilation intervention, on the infection risk are quantified and compared using the improved Wells–Riley model. Considering the priority of these two measures, the controlling quantity are determined, and the optimal schemes are proposed based on the targeted infection risk. The results show that the effect of reducing infection risk by constraining occupancy within 25% of all public campus buildings is better than that achieved by increasing the ventilation rate alone. If the ventilation system of the building type is operated by occupiers, it is a priority to prevent the risk of virus infection by restricting occupancy and ensuring the distance between occupants, while if the ventilation system of the building type is centrally controlled, it is a priority to increase the ventilation rate and then limit the occupancy rate during peak periods to 75%.

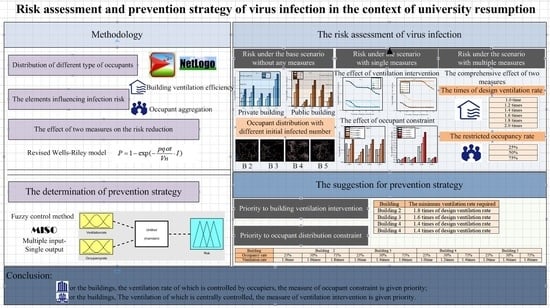
1. Introduction

The outbreak of coronavirus disease 2019 (COVID-19) has attracted worldwide attention. It was the most serious public health event in the 21st century so far and has seriously affected the security, economic development, and national stability of the populations in all countries worldwide. The severity of the epidemic varies between countries and cities due to their different emphases and prevention measures. According to the latest reported data from the WHO, the cumulative death toll was 5.57 million worldwide by 21 January 2022 [1]. The global pandemic situation is still in a trend of obvious harm. The wide spread of COVID-19 has brought huge challenges to the ability to deal with major public health events. Exploring technologies of accurate prediction, dynamic monitoring, and effective prevention is urgently needed in the interdisciplinary fields of public health, clinical medicine, geographic science and public management. The virus transmission depends on the contact between the source of infection and the infected populations. The risk of infection is closely related to the basic disease of an individual, and the mortality of an infected individual differs between genders. Although temperature, precipitation, and climate may also affect the spread of an epidemic, the impact of the natural factors is limited. Therefore, besides the differences of medical conditions, the population aggregation and ventilation efficiency have been proved to produce a significant effect on the airborne virus infection [2].

The differences in outbreak site, population density, population flow characteristics, and prevention policy each affect epidemic situation at the scale of community, city, and country [3]. At the community scale, the spatial distribution of the epidemic is mainly affected by the aggregation mode of the populations and the community type [4]. At the city scale, the spatial distribution of the epidemic is mainly affected by the population density and the intensity of population flow [5]. At the country scale, cities with large populations are always the hot spots for epidemic outbreaks [6]. Therefore, reducing the aggregation and flow of population is fundamental to epidemic prevention and control. Relevant studies have shown that the spread of an epidemic is closely related to the flow of the population at the earliest outbreak site [7]. At the scale of space, the flow of the population can be referred to as ‘occupancy’. Occupancy represents the occupied status or number of occupants at four different levels: (1) the number of occupants in buildings, (2) the occupancy status of a space, (3) the number of occupants in a space, and (4) the location of each occupant in the space [8]. Based on the exploration of the temporal and spatial transmission mode of the infectious virus, it was found that the epidemic spreads from the aggregation of the population and then spreads to other sites due to the flow of population [9]. Sari [10] examined the factors affecting virus spread in buildings and concluded that the occupant density is one of the most important factors in virus transmission. Kovesi [11] examined the effect of the population of pupils on respiratory infections in Canadian schools and demonstrated the importance of occupant distribution. Sun [12] proposed a prediction model for infection risk in confined spaces considering occupant density, ventilation rate, and exposure time; the results showed that social distancing is a great approach to decreasing the infection risk, and it also minimizes the required ventilation rate in buildings. Considering infection risk assessment and pandemic control in built environments, the existing literature primarily focuses on the level of the number of occupants in an enclosed space. The word ‘occupancy’ mentioned below refers to the number of occupants.

In recent years, the study of occupancy and its impact on building ventilation and energy performance has gained momentum and is also promoted by ASHARE. However, Anand [13] pointed out that supplying ASHARE a specified minimum required ventilation based on occupancy level is not suitable at the current time since the minimum required ventilation may not be sufficient to mitigate the COVID-19 virus’s spread in confined spaces. Morawska [14] proposed that increasing existing ventilation rates and enhancing ventilation effectiveness may be key elements in limiting the spread of the virus. Srivastava [15] assessed the influence of ventilation on the infection risk based on numerical simulation and pointed out that the use of 100% outdoor air would sharply reduce the infection risk from 27% to only 3.1%, though the effort would significantly increase energy costs for handling the air. Especially for some high-metabolic venues (e.g., indoor exercise arenas such as gyms, dance studios, boxing studios, etc.), occupants exhale and inhale at much higher rates than in sedentary or office scenarios, and the corresponding risks of infection increase exponentially with the metabolic rate, where there is an urgent need to improve ventilation control systems to reduce the risk of respiratory infection [16]. Since the outbreak of the pandemic, the guidelines for the operation of the air conditioning and ventilation system in public places during the pandemic period have been issued by HVAC associations. The recommended strategies regarding the operation of the HVAC system to mitigate COVID-19 infection were reviewed and are presented in

Table 1. The recommended strategies for ventilation system [17,18,19].

Association	Operating Time Point	Running Time in Length	Supplying Fresh Air
ASHARE	Operate 2 h before and post occupied	Run for 24 h a day; Run for 7 days a week	As high as 100% if possible
REHVA	Run at the nominal speed for at least 2 h before occupied and at a lower speed 2 h after occupied.	Run toilet ventilation system for 24 h a day; Run toilet ventilation system for 7 days a week
SHASE	Run continuously for 24 h if possible	Run the exhaust system in toilets continuously

.

The international guidelines all put forward strict requirements for reducing the spread of epidemics. However, all guidelines emphasize the importance of ventilation, but the specific ventilation rate that can eliminate the risk of transmission of airborne particulate matter has not been established [20]. Ventilation control is closely related to the transmission of influenza diseases (such as influenza, measles, tuberculosis, SARS, etc.) [21]. In the face of the huge demand for ventilation during the epidemic, a determined increasing amount of ventilation efficiency and volume is of great significance to protect the health and safety of indoor occupants. However, only the ventilation control measure adopted in places with high occupant metabolic rates often cannot satisfy the requirement of infection prevention during the COVID-19 outbreak [22]. The simultaneous use of multiple measures enhancing ventilation and limiting occupant number may be encouraged.

The simulation and quantitative assessment of infection risk with the consideration of the uncertainty of occupant distribution and the ventilation condition could provide a reference for risk management in the post-pandemic period [23]. At present, there are four kinds of risk-assessment models in the field of disaster science at home and abroad, including historical data statistics [24], the comprehensive index system [25], GIS-based modeling [26], and scenario-based simulations [27]. Among these, the modeling and assessment based on simulations refers to the simulation of the possible trend of development and consequences of the events under different scenarios. In view of the risk at different stages throughout an epidemic, scholars have carried out scenario simulations in terms of four aspects, including early traffic restriction, medium-term community prevention, and the medical resource allocation, later followed by resumption of work, classes, and production [28]. Chinazzi [29] simulated a scenario in which the virus spread all over the world without the ‘city closure’ policy of Wuhan, China. It was estimated that the closure policy reduced the number of international cases by nearly 80%. Zhang [30] built a model to simulate the impact of social distancing and school closure on virus transmission based on contact survey data of Wuhan and Shanghai before and during the outbreak. The results showed that social distancing alone, as implemented in China during the outbreak, is sufficient to control COVID-19. In contrast, proactive school closure cannot completely interrupt transmission, but the measure could reduce the peak incidence by 40–60% and delay the epidemic. By the end of the year 2020, intense control measures of prolonged school closure and work holidays reduced the cumulative infections while also delaying the peak of the outbreak [31]. A study on the containment effect of social distancing and school closure on COVID-19 transmission suggested that the social distancing should be earlier in the process of the implementation of measure [32].

The resumption of work, classes, and production is an inevitable trend for maintaining the normal order of the economy and sustainable development in the post-epidemic period. However, the resumption also increases the degree of population aggregation, resulting in the second outbreak of the epidemic. Therefore, it is necessary to pre-assess the risk of virus infection in the context of its resumption and formulate corresponding strategies so as to ensure the orderly development of the resumption. The risk assessment of COVID-19 in the context of business resumption received a high level of concern; however, the risk assessment in the context of university resumption is still in its primary stage. In the face of major public health events, universities will experience huge pressure owing to their wide range of occupant sources, large occupant density, and greater number of gathering activities. The disastrous consequences may include an outbreak if prevention and control measures are not in place. In the premise of considering the uncertainty of the pandemic and the particularity of the university, it is of great significance for orderly recovery of all of society to establish a risk assessment and prevention system in the context of university resumption. Unlike other social systems, the resumption of universities means large-scale population migration. After the interweaving of populations in various types of transportation, universities will provide a destination that brings about new locations for occupants gathering and living on campus. Based on the analysis of the interaction mechanism among risk factors in terms of pressure, state, and response of the PSR (Pressure–State–Response) model, Wang [33] established a comprehensive index system for COVID-19 risk assessment to assist universities in the organizing decisions relating to the resumption of classes. Ding [34] established a scientific index system for risk assessment in the context of class resumption to analyze the weakness of prevention and control measures, which could provide theoretical support for scientific decisions, prevention material to allocate, and instructions on orderly development. However, most of these studies assessed the risk of virus infection in the context of the resumption of universities from the macro perspective and rarely quantitatively evaluated and analyzed the effect of concrete prevention and control measures on the reduction in virus infection. In addition, the occupant distribution at the time point of typical events, even for the same building, was different due to the large mobility of campus occupants, which caused different risks to virus infection. On this basis, the risk of virus infection brought about by the uncertainty of typical events and occupant distribution could not be better simulated by only evaluating only one campus building and situation.

Therefore, this study proposes a set of risk-assessment and prevention methods for virus infection under different scenarios in the context of university resumption. The selected buildings used as cases basically represent all types of functional campus buildings. With the consideration of the priority of the two measures as building ventilation intervention and occupant flow constraints, the optimal schemes of prevention measures that could meet the requirements of an extremely low risk of virus infection were put forward. Compared with previous studies, this study evaluates the effect of prevention measures on the reduction in infection risk from the quantitative perspective. In addition, the selection of different scenarios for risk assessment could provide more targeted opinions and guidelines for the epidemic prevention and control in the post-pandemic era.

The rest of this study was organized as follows: Section 2 introduces the methodology regarding to the identification of risk elements, the risk assessment, and the determination of prevention measures. Section 3 introduces the selection of case buildings and objects. Section 4 provides detailed research results and corresponding discussion, including the effect of infected proportion on the infection risk and the effect of single and multiple measures on the reduction of infection risk. The determination of prevention measures is presented in Section 5. Finally, the conclusion and limitations of the current research study are discussed in Section 6.

2. Methodology

In this study, the research framework was mainly established according to the following four steps: (1) identifying of risk elements based on the mechanism of virus transmission and expert experience; (2) applying Netlogo to simulate the change in the distribution of infected and healthy occupants with exposure duration in space to explore the effect of initial percentage of infectious occupants on the transmission of the virus; (3) evaluating and comparing the effect of building ventilation intervention and occupancy constraint on the reduction of infection risk; (4) quantifying the risk element, controlling based on the targeted risk by fuzzy control method; (5) proposing prevention schemes in terms of the priority of building ventilation interventions and the priority of occupancy constraints using an optimization algorithm. A detailed framework of the methodology adopted in this study is graphically depicted as Figure 1.

2.1. The Identification of Risk Elements

The system of COVID-19 transmission includes three parts: potential source, transmission route, and susceptible occupants. For campus buildings, the virus spread mainly through droplet and contact. The droplet transmission can be blocked by restricting the aggregation of occupant or enhancing the building ventilation efficiency. The contact transmission can be blocked by enhancing the disinfection intensity. Although the transmission mode of the virus, which is mainly by droplets and contact, has been recognized by the World Health Organization (WHO) [14], and more and more evidence has proved that the transmission through aerosol cannot be ignored. Ventilation, as an important intervention measure of virus infection, plays an important role in the process of epidemic prevention. Therefore, this study intends to assess the effect of occupancy constraints and building ventilation interventions on decreasing the risk of infection, and the effect of other uncertain and uneven factors on research results should also be eliminated as much as possible. The location of occupants in the building exhibits randomness, and this will lead to differences in the degree occupant aggregation and indoor air distribution in different areas; however, these factors are outside the research scope of this study. In addition, in order to simplify the research process, it is assumed that the virus in the space will not disappear or die. Therefore, in the process of risk assessment, the following assumptions are made to create a relatively ideal environment:

(1)

Suppose the probability of being infected anywhere in the targeted buildings is equal;

(2)

Suppose the occupants are evenly distributed in the buildings to make the contact probability of each individual the same;

(3)

Ignore the inhomogeneity of ventilation in the buildings;

(4)

Ignore the number of pathogens removed through leakage, filtration, sedimentation, and mortality from the buildings.

The element ventilation rate or volume affects the dilution effect of indoor air. Generally, a higher ventilation efficiency can better dilute the pathogen concentration and reduce the risk of indoor virus transmission [35]. Within the allowable operation range of the original ventilation system, the air supply volume shall be increased as much as possible to reduce the risk of virus infection. In this study, based on the design ventilation rate of the case buildings, an additional five scenarios—1.2 times, 1.4 times, 1.6 times, 1.8 times, and 2.0 times the designs’ ventilation rate–will be assumed to evaluate the effect of the increased ventilation rate on the reduce of infection risk. In contrast, another element, occupancy, will directly affect the aggregation of occupants, which presents extreme randomness. The differences in the arrangement of classes and behavior habits will lead to the variety of transfer behaviors even for students of the same grade. However, the behavioral habits of one occupant will be not easily change for a long period. In addition, limited by fixed class time, the occupant transfer follows certain regularity. The transfer of occupants from one moment to the next only depends on the positions of the current moment and not on all previous moments. In terms of data collection, GPS trackers (introduced in detail in Section 3.2) are issued to the testers to record their tracks for a period of time and obtain the proportion of their transfers between time points of adjacent typical events, which will be applied as a training set to predict the occupancy rate based on the stationary distribution. Taking the prediction results obtained by stationary distribution, the effects of 25%, 50%, and 75% occupancy restriction on the reduction of virus infection were evaluated.

Suppose that X = {t₀, t₁, t₂,…} represents a random time series; the set of states corresponding to variable x is called state space and defined as S = {i₁,…, i_n−1, i_n, j}. Then, the transition probability between different states can be expressed as Equation (1).

$$P\{X(t_{n+1})=j|X(t_n)=i_n,X(t_{n-1})=i_{n-1},\dots X(t_1)=i_1,X(t_0)=i_0\}$$

(1)

where TS = t_n+1 − t_n represents given time step and the values of 0.5, 1.0, and 2.0 were selected as TS to describe and compare the k-step transfer probability between adjacent event points in this study. According to the results shown in Section 2.1, all position states can be valued as {State0 = outside, State 1 = dormitory building, State 2 = lecture building, State 3 = office building, State 4 = canteen, State 5 = library}. The probability that an occupant located at state i at time t_n but transferred to state j at time t_n+1 after k steps can be expressed as Equation (2).

$$P_{ij}^k(t_n)=P\{X(t_{n+1})=j|X(t_n)=i\}$$

(2)

When k = 1, the one-step transfer probability can be calculated using Equation (3). When k > 1, the multi-step transfer probability can be calculated using Equation (4).

$$P_{ij}=\frac{N_{ij}}{{\displaystyle \sum _{j=1}^n{N}_{ij}}}$$

(3)

$$P_{ij}^k=P_{il1}{P}_{il2}\dots P_{lk-1j}$$

(4)

When Markov chain is applied to describe the random movement of occupants between campus buildings in this study, the state space I = {1,2,3,4,5} is finite. In addition, there always exists a positive integer k such that $P_{ij}^k>0$ for any i, j ∈ I. Therefore, the Markov chain is irreducible and ergodic, and a unique stationary distribution exists. The stationary distribution sequence is defined as {π_j}, where for each j ∈ I, π_j = P{X(t_n) = j}. This represents the probability that an occupant is in state j after a long enough time. The non-negative sequence {π_j} satisfies Equation (5).

$$\begin{array}{l}{\pi }_j={\displaystyle \sum _{i=0}^{\infty }{\pi }_i{p}_{ij}},j=0,1,2;\\ {\displaystyle \sum _{j=0}^{\infty }{\pi }_j=1}\end{array}$$

(5)

After the transfer probability has been obtained based on the Markov matrix, the occupant number of different buildings at time points of typical events can be calculated using Equation (6).

$$occ(i,t_m)=occ(i,t_o)P_{ij}^k$$

(6)

where occ(i,t_o) represents the building occupant number at original time point and occ(i,t_m) represents the building occupant number at target time point. Their matrix form is expressed as follows:

$$occ(i,t_o)=[occ(0,t_o),occ(1,t_o),occ(2,t_o),occ(3,t_o),occ(4,t_o)]$$

(7)

$$occ(i,t_m)=[occ(0,t_m),occ(1,t_m),occ(2,t_m),occ(3,t_m),occ(4,t_m)]$$

(8)

2.2. Distribution of Occupants in Space

Netlogo is pre-loaded with a relatively large library consisting of models that help researchers run simulations to address problems and explore various aspects [36]. By simulating the interaction between multiple individuals, many complex phenomena, such as ant colony, bird colony, ecosystems, apartheids, and virus transmission can emerge [37]. The simulated world is composed of subjects, which can accept commands and then carry out corresponding behaviors, and the behaviors of all subjects occur in parallel. Netlogo has three types of subjects, namely ‘turtles’, ‘patches’, and ‘observer’. Among these, ‘turtles’ refers to the agents that can move in the simulated world; they can be regarded as the observed objects with the attributes of individuals. ‘Patches’ refers to a network composed of patches, and each patch occupies a rectangular block. It cannot move but still has its own properties and behavior. ‘Observer’ refers to the global agent, observing the simulated world composed of turtles and patches [38]. It can execute instructions to obtain all or part of the state of the world, so as to realize the control of the world [39].

In this study, Netlogo was applied to simulate the difference in the distribution of healthy and infected occupants caused by the spread of the virus under a certain exposure duration in space. ‘Turtles’ refers to the occupants, who could move randomly and freely, including infected occupants, susceptible occupants, and non-susceptible occupants. ‘Patches’ refers to the simulated space of campus buildings. Each space is divided into several subspaces, each of which is occupied by one occupant. As introduced above, the transmission routes of this virus were mainly droplet transmission and contact transmission, and many cases can be traced to the close contact with confirmed cases. Therefore, it was assumed the contact transmission is the main route when simulating the spread of virus between different types of occupants. In order to simplify the model, it was assumed that the infectious occupants will not die during the simulation; instead, they can only be cured or infect other susceptible occupants and will not be infected with the same virus once cured. Targeted at the campus buildings in this study, the initial percentage of infected occupants was taken as variable in order to study the influence of the variable on the spread of virus and the distribution difference of healthy and infected occupants with a certain duration of exposure.

2.3. Risk Assessment of Virus Infection

Virus researcher Wells put forward the concept of ‘quanta’ in 1955, which was defined as the minimum number of pathogens required to cause an occupant illness. The average infection probability of an occupant inhaling a quanta of virus generally obeys the Poisson distribution, that is 63.2% (1 − e⁻¹). Based on the theory proposed by Wells, Riley further considered the intake dose of airborne pathogens in terms of the quanta number to evaluate the probability of infection and successfully predicted the measles outbreak in a suburban primary school located in New York [40]. Combined with the Poisson distribution of the random motion of discrete particles, the Wells–Riley model was derived as Equation (9).

$$P=\frac{C}{S}=1-\exp (-\frac{Ipqt}{Vn})$$

(9)

where P represents the probability of infection; C represents the number of new infections for an outbreak; S represents susceptible occupant number; I represents infected occupant number; p represents the respiratory ventilation and has a value of 0.6 m³/h; q represents the production rate of ‘quanta’ for an infected occupant and has a value of 13; t represents the exposure duration; V represents the volume of targeted space (m³); n represents the ventilation rate (h⁻¹).

The denominator shown in Equation (9) in the brackets indicates the influence of building volume and building ventilation efficiency on the infection risk in the space, and the numerator in the brackets indicates the influence of the distribution of infected and uninfected occupants and the aggregation degree of occupants on the infection risk. Equation (9) regards all occupants in the space as a whole, and the situation without any prevention measures can be defined as the base scenario. When considering the effect of occupancy constraints on the decrease in infection risk, the numerator in the brackets will be corrected by occupancy rate α. When considering the effect of ventilation intervention on the decrease in infection risk, the denominator in the brackets will be corrected by the increasing times of ventilation rate, which will be multiplied by the original design ventilation rate of n′. When the two measures are considered simultaneously, the risk of virus infection can be evaluated as Equation (10).

$$P=1-\exp (-\frac{pq\alpha t}{V{n}^{\prime }}·I)$$

(10)

where α represents the occupancy rate of targeted buildings.

2.4. Determination of Prevention Measures

The relationship between risk elements and probability of infection needs to be further determined. The risk elements of occupant aggregation level, building ventilation rate, and building disinfection level were adopted as the variables to evaluate the risk of virus infection under different scenarios. Therefore, the network structure for risk assessment within a campus unit can be constructed. The nodes of the network structure were divided into M-type nodes and N-type nodes. Generally, the value of M-type nodes was obtained by simulation or calculation, while the value of N-type nodes was obtained by empirical value or logical judgement. In this study, the ‘occupant aggregation’ belongs to the M-type node, which was mainly reflected by the indicator ‘occupancy rate’, and its value was calculated by Stable Distribution, while the ‘building ventilation rate’ belongs to N-type nodes, the value of which were judged by empirical values or architectural design standards. It was assumed that the probability of occurrence of each value for the same node was equal. The risk of virus infection R was divided into five levels, as shown in

Table 2. The risk classification of virus infection.

Probability of Virus Infection	0%	<25%	25–50%	50%	50–75%	>75%
Risk level of virus infection	No-risk	Extreme low-risk	Low-risk	Medium-risk	High-risk	Extreme high-risk

.

The risk of virus infection R can be determined by multiple fuzzy rules. However, the traditional modeling method cannot adequately deal with fuzzy systems. Therefore, the rule-based modeling method was applied to evaluate the risk of virus infection under different scenarios, and fuzzy control was applied to obtain the minimum control quantity of the risk elements based on the targeted risk value in this study. The fuzzy input space consisted of linguistic variables as premises, and the output space consisted of linguistic variables as conclusions. The input space and output space need to be fuzzily divided to make the value of each linguistic variable correspond to a specific domain. In this study, the input space M and N and output space R were fuzzily divided as follows,

(1)

Input 1: M = {0, 25% occupancy, 50% occupancy, 75% occupancy, 100% occupancy};

(2)

Input 2: N = {1.0 time of design ventilation rate, 1.2 times of design ventilation rate, 1.4 times of design ventilation rate, 1.6 times of design ventilation rate, 1.8 times of design ventilation rate, 2.0 times of design ventilation rate};

(3)

Output: R = {Extremely low, Low, Medium, High, Extremely high}

The qualitative indexes M and N, after fuzzy segmentation, were quantified as matrix A = (a_n)^T, which was then transformed into a fuzzy membership matrix B = (b_n)^T using the maximum membership method. The proposed node N belongs to benefit indicators; that is, larger indicators have an effect on the achievement of the goal. The node N was divided into six levels, i.e., n₁ = 6. The membership degree of N was solved using Equation (11), while the proposed node M belongs to the cost indicator; that is, smaller indicators mean fewer obstacles to the achievement of the goal. M was divided into five levels, i.e., n₂ = 5, and its membership degree was solved using Equation (12).

$$b_n=\frac{(a_n-\underset{1\le n\le 5}{\inf }\{a_n\})}{(\underset{1\le n\le 5}{\sup }\{a_n\}-\underset{1\le n\le 5}{\sup }\{a_n\})}$$

(11)

$$b_n=\frac{(\underset{1\le n\le 6}{\sup }\{a_n\}-a_n)}{(\underset{1\le n\le 6}{\sup }\{a_n\}-\underset{1\le n\le 6}{\inf }\{a_n\})}$$

(12)

Based on the above division rules of input space, 30 (5 × 6) multiple input and single output (MISO) rules can be established to form a rule base. The fuzzy implication relation R_i corresponding to each rule is defined by Equations (13) and (14):

R_i = (N_i and M_i)→R_i, i.e.,

(13)

$$\mu R_i=\mu (N_{1i} and M_{2i})\to R_i(x,\nu ,r)=[\mu N_i(x) and \mu M_i(z)]\to \mu R_i(r)$$

(14)

where x and y represent the linguistic variables of system state and r represents the linguistic variable of control state. N_i, M_i, and R_i (i = 1, 2,…, n) represent the value of linguistic variables x, y, and r in their own domains X, Y, and R.

On the premise of determined targeted control variable r, the corresponding input variables x and y can be obtained based on the fuzzy control. However, as for MISO fuzzy control system, a determined control variable r can correspond to multiple combinations of x and y. The most optimal schemes for reducing risk of virus infection will be discussed according to the priority of the two prevention measures in Section 5.

3. Case Study

3.1. Selection of Case Buildings

This study was conducted in a campus in Tianjin, China. The areas of the campus are shown in Figure 2. The campus was constructed in the form of teaching groups; that is, some basic facilities, such as teaching zone, office zone, living zone, meal zone, library zone, and other activity centers, were built within a certain range. Occupants in the campus generally transferred between five types of buildings: dormitory buildings, lecture buildings, office buildings, canteens, and libraries. The five types of buildings are determined as the targeted objects and assigned codes: ‘B1’, ‘B2’, ‘B3’, ‘B4’, and ‘B5’, respectively. The basic building information is listed in

Table 3. Basic information for target buildings.

Building Type	Code	Total Floor Area (m2)	Maximum Capacity of Occupant	Maximum Capacity for Each Room	Opening Time	Room Functions
Dormitory building	B1	3400	500	6	00:00–24:00	For living/ studying
Lecture building	B2	12,670	3000	100	06:30–22:30	For class/ self-studying
Office building	B3	3690	1000	30	06:30–22:30	For official business/ scientific research
Canteen	B4	4210	500	300	06:30–22:00	For meal/ communication
Library	B5	13,100	1000	100	06:30–22:00	For self-studying

.

The design ventilation rates of buildings B1–B5 are 4 times/h, 6 times/h, 6 times/h, 10 times/h, and 10 times/h, respectively. The volume of each room of buildings B1–B5 are 35 m², 200 m², 100 m², 1200 m², and 320 m², respectively. The per-capita occupied area of each room in the dormitory building is relatively crowded, generally no more than 7 per m². In comparison, the volume of rooms in other four buildings are relatively spacious, and the per-capita occupied area will vary with the occupancy rate.

3.2. Selection of Objects

The occupants of colleges and universities mainly belong to three types of groups: students, teachers, and other staff. The on-campus students can be further divided into two stages: undergraduates and postgraduates. Due to the variety of course arrangements, accommodation conditions, and nature of learning, the regularity of transfer of students may be extremely different. When exploring the transfer regularity of students, it is necessary to distinguish student groups by undergraduates and postgraduates. One hundred thirty students, with an 8:5 proportion of undergraduates to postgraduates, volunteered the for tracking test from 14 June to 14 July 2019, when all buildings within the campus unit were under normal operation. Compared with campus students, the activities of teachers within the campus were relatively fixed and uniform. Except for special circumstances, they generally transferred between the lecture building/office building and canteen, limited by the work time and lunch/dinner time. Their transfer regularity could be obtained through the questionnaires targeted at the hourly positioning in a day, 100 samples of which was selected to represent the overall. However, the other staff accounted for merely about 2% of the total number of occupants within campus. This group of occupants had a tiny influence on the degree of occupant aggregation, which can be considered negligible in this study.

The data collection was conducted before the outbreak of epidemic to predict the occupancy schedule at the typical time points of targeted campus buildings without any interference measures. Based on the prediction results, the effects of different degrees of occupancy restriction on the reduction of infection risk under can be evaluated. The selected GPS (Global Positioning System) trackers in this study are shown in Figure 3. The trackers can receive satellite signals from GPS from the United States and GLONASS (Global Navigation Satellite System) from Russia at the same time. Combined with three other signals, Wi-Fi, base station, and gravity induction, GPS trackers can lock on the positions of carriers more quickly and accurately. The positioning accuracy is a radius of 5 m for open sites outdoors. However, in the actual testing process, it was found that the tracker could accurately judge which building occupants are located in, but it could not identify their specific locations in the buildings. Therefore, this study only distinguishes the building difference, ignoring the specific locations of occupants in the buildings. In addition, the tracker could withstand a wider temperature range of −10–50 °C, and it could retain power for at least one week with a long standby function. During the test, it was required that 130 volunteers carried trackers for not less than two weeks to obtain a more universal transfer regularity within campus units. In order to avoid data loss due to insufficient power of the trackers, volunteers were required to charge their trackers every week.

3.3. Definition of Typical Events

The process of occupant transfer within campus is usually driven by events such as being at work or in class, being off work or out of class, meals, sleep, and other activities. These events occur in a time sequence, and the probability of these events’ occurrence at adjacent time nodes can be reflected by the probability of the occupant transfer between the execution position of these events. The change in occupant position generally means the occurrence of transfer events. A complete transfer process can be characterized by a series of transfer events. Based on the working schedule and habits of occupants, the typical events are defined as {Event 1 = morning work time (8:30–12:00); Event 2 = lunch time (12:00–13:30); Event 3 = afternoon work time (13:30–17:00); Event 4 = dinner time (17:00–20:00); Event 5 = night time (20:00–8:00)}.

By uploading the longitude and latitude coordinates of each occupant at the time points of typical events obtained by GPS trackers, the position of all occupants at the same time points can be shown in the form of a thermal diagram to realize the visualization of occupancy. The regularity of occupancy corresponding to time points of typical events barely changed for the various testing days. Therefore, the results of occupancy within the campus unit obtained in this test mostly reflect the movement regularity of the occupants.

Occupants usually transferred between campus buildings for living, studying, meals, or other basic activities. The main differences between universities nationally and internationally lie in the climate, teaching characteristics, activity categories, number of building groups, and the behavior habits of occupants. The differences between the climate, teaching characteristics, and activity categories do not affect the results of this study. The differences in habits are embodied in the occurring time points of typical events. The earliest starting time points, the latest ending time points, and the course duration of different universities may vary due to the diversity of sunrise and sunset times in different regions. Influenced by the regional culture, the dining time also varies, especially for dinner time. This paper intends to propose effective prevention and control suggestions to decrease risk of virus infection based on the occupancy characteristics and exposure durations at typical events. Therefore, in the actual process of risk prediction and prevention management, the occurring time points corresponding to the above typical events can be moved forward or backward in accordance with the region. The case buildings of this study represent the typical functional buildings in colleges and universities. The selected case campus represents the distribution of multiple functional buildings of the general university nationally and internationally.

4. Risk Assessment of Virus Infection

4.1. Prediction Results of Occupant Aggregation Degree

Based on the GPS tracking results, the transfer probability between adjacent events was obtained using Stationary Distribution, as shown in Figure 4. The depth of color corresponding to Π_j reflects the variety of transfer probability, and a darker color represents greater transfer probability.

As seen in the figure, occupants tend to transfer to B3 and B4 from event 1 to event 2 and tend to transfer to B3 from event 2 to event 3. In comparison, occupants tend to transfer to B1 from event 3 to event 4 and from event 4 to event 5. The transfer probability obtained by Stationary Distribution only reflects the potential transferring regularity of occupants between campus buildings. The concrete occupancy rate corresponding to the typical time periods is determined by the initial occupancy rate of different buildings. Suppose that the initial occupancy rate of each building is occ(i,t_o) and the occupancy rate corresponding to the typical periods of different buildings is calculated according to Equation (8); the prediction results are shown as Figure 5.

The results obtained will be used as a benchmark to assess the infection risk without any prevention measures and compare the effect of different occupancy levels on the decrease in risk, which will be discussed in Section 4.2.1 and Section 4.2.2, respectively.

4.2. Risk Assessment of Virus Infection under Different Scenarios

4.2.1. Probability of Virus Infection under the Base Scenario without Any Measures

After obtaining the occupancy rate corresponding to the typical periods, the probability of virus infection without any prevention measures can be calculated according to Equation (9), and the results are shown in Figure 6. IP (Infectious Proportion) refers to the percentage of the number of infectious occupants to the maximum number of occupants in the space. The scenarios of IP valuing 1/max, 25%, 50%, and 75% were assumed, respectively.

Combining the results shown in Figure 5 and Figure 6, the comprehensive influence of occupancy rate and exposure duration on the risk of virus infection can be analyzed. Figure 6 intuitively expresses the influence of IP on the infection risk without any prevention measures. The risk of virus infection was affected by multiple factors. Besides the occupancy rate and exposure duration, the volume of the building itself, the distance between adjacent occupants, and the ventilation condition will also affect the risk. For private buildings with relatively crowded spaces such as B1, the risk during the periods with a higher occupancy rate and exposure duration is always higher no matter how high the IP value is. As long as one infected occupant appears, the transmission speed and scope of the virus will spread rapidly. For buildings with uncontrolled distance between occupants such as B2 and B3, a lower occupancy rate and exposure duration make the risk extremely low, even if IP exceeds 75%; however, typical periods with higher occupancy rate significantly increase the risk once IP exceeds 25%. In comparison, for large spaces providing meals for occupants such as B4, the risk of virus infection will significantly increase to a low level until IP exceeds 75%. In addition, time periods with a relatively lower occupancy but higher exposure duration need to be given special attention. For example, Figure 6d shows a higher risk of virus infection during event 3 than event 2. The exposure duration corresponding to event 3 was four times that of other typical events, though with lower occupancy, causing a higher level of risk no matter how high the IP value was. For large spaces providing learning or communication, such as B5, the risk is maintained at low-risk level until IP exceeds 75%.

Then, Netlogo was applied to simulate the change in the distribution of infected and healthy occupants with the exposure durations under the conditions of different initial percentage of infectious occupants. The results are shown in the figures and listed in

Table 4. The distribution of occupants under different initial percentage of infectious occupants.

Building	The Initial Percentage of the Infectious Occupants
	25%	50%	75%
B2
B3
B4
B5

The red dots—the infected occupants; the gray dots—the susceptible occupants; the blue dots—the non-susceptible occupants. The susceptible occupants and non-susceptible occupants all belong to the category of healthy occupants.

. One room of four case buildings are used for simulation, respectively and the legend of the figures are 1:3. Three scenarios, assume 25%, 50%, and 75% initial percentage of the infectious occupants. After the designated exposure duration (the longest exposure duration at typical events for different buildings), the distributions of different types of occupants are shown as figures and listed in Table 3.

“Susceptible occupants” refers to a group of occupants who lack immunity to the virus and are easily infected by it. The proportion coupled with that of infected occupants is the overall probability of being infected in space. As seen in the figures, for B2 and B3, the proportion exceeds than that of uninfected occupants with the increase in exposure duration when the initial IP was 25%. However, for B4 and B5, the proportions are both relatively lower when the initial percentage was 25% or 50%. Until the initial percentage is over 75%, the proportion exceeds than that of uninfected occupants. Based on the above analysis, for the buildings with crowded space per capita such as B1–B3, the risk of virus infection and the percentage of the infectious occupants both significantly increase once IP exceeds 25%. In contrast, the spacious and open spaces in B4 and B5 provide larger average occupied space, causing the a significantly increased risk until IP exceeds 75%. Based on the above analysis, in the subsequent research, the scenario with 25% IP of B1–B3 and the scenario with 75% IP of B4 and B5 will be selected for further analysis.

4.2.2. Influence of a Single Prevention Measure on the Probability of Virus Infection

By taking the building ventilation rate and occupancy rate as variables, respectively, the effect of single prevention measure on the infection risk are evaluated as follows.

(1)

Influence of increasing ventilation rate on the probability of virus infection.

The effect of increasing the ventilation rate on the infection risk are analyzed, respectively, and the results are shown in Figure 7a–e. The occupancy rate during the typical events can be seen to be within a certain lower range, and the increase in ventilation rate has a significant effect on the decrease in risk, though the increase is limited. In particular, for the space where occupants inevitably gather, such as B4 during lunch and dinner time, multiplying the design ventilation rate by 1.4 has a significant effect on the decrease in risk, and a minimum per-capita quantity of fresh air of 56 m³/h is required. Once the occupancy rate exceeds the upper limit of the lower range, the simple increase in the ventilation rate will not work. Specially, the occupancy rate during typical events such as the event 5 of B1 is higher than 75%, and multiplying the design ventilation rate by 1.8 could produce an obvious downward trend of risk, and the minimum per capita quantity of fresh air of 57.6 m³/h is required. However, an unlimited increase in ventilation rate will lead to excessive selection of equipment, resulting in higher operation energy consumption and maintenance costs. When only an increase in ventilation rate cannot achieve the goal of decreasing infection risk, other measures need to be simultaneously considered.

(2)

Influence of restricting occupancy on the probability of virus infection.

The effect of restricting occupancy on the risk of virus infection in space of all buildings are analyzed, respectively, and the results are shown in Figure 8a–d. The occupancy rates during event 5 of B2–B5 are predicted to lower than 25% and will be not discussed in this section.

The effect of restricting occupancy on the decrease of infection risk will be more obvious with a greater predicted occupancy. Additionally, the effect of continuing to restrict occupancy rate will be weakened when the predicted occupancy rate is reduced lower than 25%. Based on the results of the effect of building ventilation intervention and occupancy constraint on reducing infection risk obtained in Section 4.2.2 (1) and (2), the quantitative effect of increasing the ventilation rate and restricting occupancy is compared in

Table 5. Comparison of quantitative effect of the two measures on the risk reduction.

State	Event	ΔRisk (%)
		Constraining Occupancy			Increasing Ventilation Rate
		25%	50%	75%	1.2	1.4	1.6	1.8	2.0
B2	Event 1	23.98	11.23	0.39	5.24	9.25	12.42	14.98	17.09
	Event 2	-	-	-	1.07	1.84	2.42	2.88	3.24
	Event 3	21.14	8.39	-	4.96	8.73	11.70	14.09	16.05
	Event 4	11.80	-	-	3.91	6.82	9.06	10.89	12.36
B3	Event 1	22.52	11.82	2.42	4.81	1.92	3.42	4.55	5.38
	Event 2	4.75	-	-	1.75	1.02	1.92	2.72	3.42
	Event 3	19.75	0.90	-	4.51	1.92	3.42	4.55	5.38
	Event 4	14.99	4.29	-	3.95	1.92	3.42	4.55	5.38
B4	Event 1	3.71	0.80	-	1.09	0.49	0.96	1.40	1.82
	Event 2	7.71	4.80	1.98	1.70	0.49	0.96	1.40	1.82
	Event 3	11.32	-	-	4.62	3.25	5.20	6.24	6.66
	Event 4	5.85	2.93	0.11	1.42	0.49	0.96	1.40	1.82
B5	Event 1	-	-	-	0.34	0.36	0.70	1.03	1.35
	Event 2	5.02	-	-	2.10	1.35	2.49	3.45	4.24
	Event 3	11.50	-	-	4.00	2.49	4.24	5.42	6.15
	Event 4	4.58	-	-	3.12	2.49	4.24	5.42	6.15

.

The measure of restricting occupancy is more effective than that of increasing ventilation rate to reduce the risk. Especially during the lunch and dinner periods of B4, the measure of staggering the peak for meals and restricting the occupancy rate of each batch within 25% could effectively prevent virus spread and infection. A larger design ventilation rate of B4 makes the effect of a continued increase in ventilation rate on the reduction of infection risk relatively weaker. Similarly, the risk-reduction effect of restricting the occupancy rate within 25% during event 1 and event 3 of B2 is even more significant than that of increasing the ventilation rate to 2.0 times the design value, and the effect during event 4 is equal to that of increasing the ventilation rate to 1.8 times design value. In contrast, the effect of restricting the occupancy rate within 50% during event 1 of B3 could have an obvious effect on decreasing the risk. However, for the typical events with longer exposure duration, the two measures both have an effect on the reduction. The comparison of the effect of ventilation and occupant constraint on the reduction in infection risk is reviewed in

Table 6. The review and comparison of the effect of ventilation and occupant constraint on the reduction of infection risk.

Building Type	Controlling Measures	Effect	Reference
Inpatient department	Reducing the ratio of attendant-to-patient	Reducing 15–22% of infection risk.	[41]
University building	Changing the occupant distribution pattern	Reducing the number of infected occupants by up to 56%.	[42]
Outpatient department	Increasing ventilation rates by 2 times of the Chinese standard	Reducing infection risk to 1.92–5.64 with the infector proportion of 5%, 10%, and 15%.	[43]
School building	Securing ventilation rate of 6.51 h−1, restricting exposure time to less than 3 h.	Maintaining infection risk to less than 1%.	[44]
Weekdays: workplace, public transport Weekends: markets, shopping centers	Increasing ventilation rate to 50 m3/h/p	Maintaining R0 no more than 1.0.	[45]
Classroom	Adopting active ventilation strategy	Reducing average 66% concentration of virus.	[46]
University building	Constraining occupant number	Reducing infection risk maximum to 23.98%.	This study
	Increasing ventilation rate	Reducing infection risk maximum to 17.09%

.

In the Wells–Riley model, the infection risk of occupants in an enclosed space is directly related to the ventilation, occupant exposure duration, and the ratio of infected individuals in the space. Based on the quantitative assessment results of the Wells–Riley model, multiple measures have been proposed and adopted to prevent infection. Among these, increasing the ventilation rate has been proved to reduce virus transmission, and this approach has been recommended by several organizations and governments. The exposure duration of the susceptible occupant is a predominant factor that influences the infection risk, which is directly associated with the occupancy status. Large gatherings have been prohibited in several public places, as controlling the number of occupants in enclosed spaces can reduce the probability of infection through close contact and long-range virus transmission. Compared with other studies, two controlling measures of constraining occupant number and increasing ventilation rate are further quantified and divided into different levels in this study. The effect of different controlling levels of two measures on the decrease of infection risk are evaluated. Only constraining occupancy to 25% was able to reduce the infection probability to 3.71–23.98%. Only increasing ventilation rate to maximum as able to reduce the probability to 1.35–17.09%. The comprehensive influence of different groups of two measures on the infection probability are further evaluated and compared as follows:

4.2.3. Influence of Multiple Prevention Measures on the Probability of Virus Infection

For the public campus buildings such as B2–B5, increasing the ventilation rate and restricting occupancy can be jointly taken to prevent the spread of virus. The comprehensive effect of the two measures on the reduction of infection risk was quantified as shown in

Table 7. The comprehensive effect of the measures on the risk reduction.

State	Event	ΔRisk (%)
		n = 1.0 Time			n = 1.2 Times			n = 1.4 Times			n = 1.6 Times			n = 1.8 Times			n = 2.0 Times
		Occ = 25%	Occ = 50%	Occ = 75%	Occ = 25%	Occ = 50%	Occ = 75%	Occ = 25%	Occ = 50%	Occ = 75%	Occ = 25%	Occ = 50%	Occ = 75%	Occ = 25%	Occ = 50%	Occ = 75%	Occ = 25%	Occ = 50%	Occ = 75%
B2	Event 1	23.9	11.2	0.39	26.3	15.3	5.6	28.0	18.3	9.6	29.3	20.6	12.7	30.4	22.5	15.3	31.1	23.9	17.4
	Event 2	-	-	-	0.05	-	-	0.96	-	-	1.7	-	-	2.2	-	-	2.6	-	-
	Event 3	21.1	8.4	-	23.5	12.4	2.8	25.2	15.4	6.7	26.5	17.8	9.9	27.5	19.6	12.4	28.3	21.1	14.5
	Event 4	11.8	-	-	14.1	3.08	-	15.8	6.09	-	17.2	8.4	0.54	18.2	10.3	3.08	18.9	11.8	5.2
B3	Event 1	22.5	11.8	2.4	24.4	15.2	6.9	25.8	17.8	10.4	26.9	19.7	13.1	27.7	21.3	15.2	28.4	22.5	16.9
	Event 2	4.7	-	-	5.8	0.8	-	6.5	2.2	-	7.1	3.2	-	7.5	4.1	0.8	7.8	4.7	1.8
	Event 3	19.8	9.0	-	21.7	12.5	-	23.1	14.9	-	24.1	16.9	-	24.9	18.5	-	25.6	19.8	-
	Event 4	14.9	4.3	-	16.9	7.7	-	18.3	10.2	2.9	19.4	12.2	5.5	20.2	13.7	7.7	20.9	14.9	9.5
B4	Event 1	3.7	0.8	-	4.2	1.8	-	0.46	2.45	0.39	4.83	2.9	1.2	5.0	3.4	1.8	5.2	3.7	2.2
	Event 2	7.7	4.8	1.9	8.2	5.8	3.4	8.6	6.5	4.4	8.8	6.9	5.2	9.0	7.4	5.8	9.2	7.7	6.2
	Event 3	11.3	-	-	14.6	-	-	16.9	3.5	-	18.8	6.9	-	20.3	9.2	-	21.5	11.3	2.3
	Event 4	5.8	2.9	0.11	6.4	3.9	1.5	6.7	4.6	2.5	6.9	5.1	3.3	7.2	5.5	3.9	7.3	5.8	4.4
B5	Event 1	-	-	-	0.27	-	-	0.53	-	-	0.72	-	-	0.87	-	-	0.99	-	-
	Event 2	5.0	-	-	6.4	-	-	7.3	1.6	-	8.1	3.0	-	8.6	4.1	-	9.1	5.0	1.1
	Event 3	11.5	-	-	13.9	2.2	-	15.8	5.4	-	17.2	7.9	-	18.3	9.9	2.2	19.2	11.5	4.5
	Event 4	4.6	-	-	7.1	-	-	8.9	-	-	10.3	0.98	-	11.4	2.9	-	12.3	4.6	-

.

The results show that when the occupancy during typical events is higher than 50%, the effect of 25% occupancy rate restriction alone on reducing infection risk is equal to that of increasing the ventilation rate to 2.0 times the design value with a 50% occupancy rate restriction. When the occupancy rate during typical events is higher than 75%, the effect of increasing ventilation rate to 1.2 times the design value with 50% occupancy rate restriction is equal to that of increasing the ventilation rate to 1.8 times the design value with 75% occupancy rate restriction. The measure of simultaneously increasing the ventilation rate and restricting occupancy rate is the most effective. However, when the ventilation rate increases over 1.4 times the design value for B2 and B3 and 1.2 times the design value for B4 and B5, the effect of restricting the occupancy rate on the reduction will gradually weaken. Especially during event 1 and event 3 of B2; event 4 of B3; and event 1, event 2, and event 4 of B4, the effect of increasing ventilation rate to 1.6 times the design value with 75% occupancy rate restriction is more than that of 50% occupancy rate restriction alone.

5. Determination of Optimal Prevention Measures

5.1. Priority to Building Ventilation Intervention

A series of combinations of ventilation rate and occupancy that which could meet the demand extremely low risk can be obtained based on the fuzzy control method, as shown in the scattered points in Figure 9a–d. On the premise of not disturbing the movement of campus occupants, the measure of building ventilation intervention is given priority to reduce the risk of infection. Based on the results shown in Figure 9, the upper limit of the occupancy rate during typical events under different ventilation conditions can be obtained and is shown in

Table 8. The upper limit of occupancy rate during typical events under different ventilation rates.

Building	The Times of Design Ventilation Rate	The Upper Limit of Occupancy Rate during Typical Events
		Event 1	Event 2	Event 3	Event 4
B2	1.0 times	0.50	0.56	0.48	0.52
	1.2 times	0.56	0.63	0.52	0.60
	1.4 times	0.62	0.67	0.57	0.65
	1.6 times	0.67	0.74	0.63	0.70
	1.8 times	0.72	0.78	0.68	0.74
	2.0 times	0.76	0.84	0.72	0.87
	Reference	0.72	0.21	0.67	0.48
B3	1.0 times	0.53	0.65	0.58	0.59
	1.2 times	0.59	0.72	0.63	0.66
	1.4 times	0.64	0.77	0.70	0.72
	1.6 times	0.69	0.74	0.76	0.77
	1.8 times	0.75	0.90	0.80	0.82
	2.0 times	0.79	1.0	0.85	0.87
	Reference	0.68	0.45	0.74	0.61
B4	1.0 times	0.53	0.50	0.43	0.61
	1.2 times	0.58	0.52	0.48	0.68
	1.4 times	0.64	0.63	0.53	0.74
	1.6 times	0.70	0.65	0.55	0.80
	1.8 times	0.75	0.70	0.60	0.85
	2.0 times	0.78	0.75	0.65	0.91
	Reference	0.57	0.63	0.41	0.76
B5	1.0 times	0.42	0.50	0.60	0.66
	1.2 times	0.47	0.55	0.62	0.73
	1.4 times	0.52	0.61	0.73	0.80
	1.6 times	0.57	0.67	0.78	0.87
	1.8 times	0.60	0.70	0.85	1.0
	2.0 times	0.64	0.75	0.90	1.0
	Reference	0.24	0.41	0.66	0.33

, where ‘reference’ represents the occupancy rate predicted by the stationary distribution based on the historical data.

Taking the predicted results as a reference, the minimum ventilation rates that can meet the occupancy during the whole periods for B2–B5 are 1.8 times, 1.6 times, 1.4 times, and 1.4 times the design ventilation rate, and the required minimum per-capita quantities of fresh air are 21.6 m³/h, 32 m³/h, 56 m³/h, and 44.8 m³/h, respectively (As shown in the lines with bold words of Table 8). A higher ventilation rate promotes the circulation of indoor air and decreases the risk of infection. However, excessively high ventilation rate will not only increase the fan power consumption but also result in the excessive equipment capacity. Under this condition, the upper limit-of-occupancy rates during event 1 to event 4 are 0.72, 0.78, 0.67, and 0.74, respectively, for B2; the upper limit-of-occupancy rates are 0.69, 0.74, 0.76, and 0.77, respectively, for B3; the upper limit-of-occupancy rates are 0.64, 0.61, 0.53, and 0.74, respectively, for B4; and the upper limits are 0.52, 0.61, 0.73, and 0.80, respectively, for B5. The upper limit-of-occupancy rates during the typical events based on the minimum ventilation rate required above are marked as the shading parts with corresponding colors in Figure 9a–d.

5.2. Priority to Occupancy Constraint

On the premise of changing the building ventilation rate with minimum effort, the measure of occupancy constraints is given priority to reduce the infection risk. The distributions of the infection risks under different limit of occupancy rates during typical events of B2–B5 are shown as Figure 10a–d.

As shown, the design ventilation rate with 25% occupancy rate restriction during the entire periods of B2–B5 could meet the demand of reducing the risk of infection to extremely low levels. When the occupancy rate is controlled within 50% during the whole periods, the required minimum per-capita quantities of fresh air are 19.2 m³/h, 28 m³/h, 48 m³/h, and 44.8 m³/h, respectively. When the occupancy rate is controlled within 75% during the whole periods, the required minimum per-capita quantities of fresh air are 21.6 m³/h, 32 m³/h, 56 m³/h, and 51.2 m³/h, respectively. If the occupancy rate cannot be restricted within 75%, only the infection risk during certain periods can be controlled under the condition of higher ventilation volume. However, it will be meaningless to only control the risk during a certain period; instead, it is necessary to ensure that the infection risk during the whole periods can be held to an extremely low level. When the occupancy rate is controlled, the ventilation rate required for a space with a small per-capita occupied area is higher than that with a larger per-capita occupied area.

Comparing the results obtained in Section 5.1 and Section 5.2, for B2 and B3, if the priority is given to controlling the risk of infection without affecting occupant movement, the ventilation volume required may be excessively large. For this kind of building with crowded space, increased ventilation rate can better dilute the indoor air to make the indoor cleanliness reach this standard. However, if the indoor air of each area must be circulated and purified, a certain delay in time will be inevitable. Especially for building types such as B2 and B3, the HVAC (Heating, Ventilation, and Air-conditioning) system of each room is independently controlled by the occupier. Therefore, the ventilation system will generally be turned on only when the occupant arrives. If the indoor air cannot be purified in time before occupants arrive, the priority should be given to restricting the occupancy and ensuring a certain distance between the occupants entering the space, on the basis of which another measure of increasing ventilation rate appropriately simultaneously is also necessary in order to control the transmission of the virus. In comparison, for building types such as B4 and B5, their space is relatively open, and the HVAC system is always centrally controlled. That is, before the arrival of typical events with a larger occupancy rate, the ventilation system is turned on to pre-purify the indoor air to make the air of each breathing area reaching this standard. However, it is not reasonable to accommodate occupants without any restrictions. It is still necessary to limit occupancy rates within 75% during peak periods, which is easy to achieve in reality. In addition, original design ventilation rates of such buildings are more larger than other buildings; thus, a slight increase in ventilation rate could bring the risk of virus infection during typical events to a low level. Therefore, for this building type, it is preferred to control the risk of virus infection by increasing the ventilation rate and ensuring the occupancy rate during the peak periods within 75%.

The evaluation system proposed in this study fuzzifies the input items of the Wells–Riley model and determines the fuzzy subset of each input item expressed by language variables. After determining the fuzzy subset, the fuzzy output item is obtained by introducing the quantization function, and then the fuzzy output is mapped to the practical significance through the defuzzification process. The risk levels proposed are obtained by mapping the domains to language variables, and the division of the risk level depends on the quantitative distribution characteristics of infection risk. REHVA recommends that the evaluation of risk be based on the basic regeneration index R₀ and real-time regeneration index R_t. The regeneration index refers to the average number of new infections caused by a case. R₀ is usually used to evaluate the transmission intensity of the virus during the early outbreak of the epidemic, and R_t is usually used to evaluate the transmission intensity at the stage of the middle or late development of the epidemic. When R_t is less than 1, this indicates that the epidemic can be controlled based on the current prevention measures. When R_t is greater than 1, this indicates that the epidemic will continue to spread and that optimized and strengthened prevention measures are needed. The method of risk assessment is based on the scope of the community, city, or country, which is used to predict and evaluate the risk trend to adjust the corresponding prevention measures. The corresponding division of low-risk, medium-risk, and high-risk areas are based on the currently cumulative case and the epidemic situation during a period of time.

The definition is different from the risk level divided in this study. The proposed risk value in this study refers to the distribution of susceptible and infected occupants and uninfected occupants, which is used to quantitatively evaluate the prevention effect of controlling measures on the decrease in infection probability. In the Wells–Riley model, the droplet nuclei are assumed to be evenly distributed in space so that the probability of being infected anywhere is equal, and the quanta during the exposure time are assumed to be stable. Each individual is taken as research object to evaluate the average probability of being infected by the aerosol transmission, contact transmission, and other means when there infections appear in the space. Though the Wells–Riley model has been widely adopted to evaluate the infection risk of airborne transmission, the dynamic transmission and evolution processes of pathogen are not all involved, which can be further improved and enhanced.

The risk of virus infection of selected campus buildings was evaluated, the results of which could provide theoretical support for the management of epidemics in the context of campus-resumption. However, only several representative buildings were selected for research, and other types of buildings within the same unit were ignored. In addition, the activities of volunteers selected in this study were limited between target buildings; actually, some of the campus occupants were still distributed in other buildings. Besides the five typical time periods selected in this study, other periods with a sharp increase in occupancy rates due to special activities were also not considered. These may cause errors in the predicted occupancy rates and lead to deviation of the determination of schemes for prevention measures. In future research, the distribution regularity of campus occupants closer to the actual situation will be explored, and more specific measures for the prevention of epidemics will be uncovered. In addition, the exposure duration and the mask efficiency, as another predominant factor that can influence the airborne infection risk, were not involved in this study. The influence of the factors on the risk can be evaluated to provide a reference for the class duration of university in the future.

6. Conclusions

This study takes a university as a case, and several typical buildings representing the living, learning, working, and dining are selected. Based on the mechanism of the virus transmission through droplets and contact, the risk elements influencing the virus infection under the background of university resumption are identified. The effects of the two measures of occupancy constraints and ventilation interventions on the decrease in infection risk were quantified and compared based on the Wells–Riley model. Based on the targeted risk of virus infection, the controlling quantity of prevention measures are proposed considering the priority of occupancy constraints and ventilation interventions. The main conclusions are as follows.

(1) For the private space providing living and accommodation for campus occupants, only the measure of building ventilation intervention is mainly considered and implemented to reduce the risk. However, for the public spaces providing meals, communication, learning, and working for campus occupants, the two measures need to be considered simultaneously. In quantitatively comparing the separate effects of the two measures on the degree of risk reduction, the measure of constraining occupancy is generally considered more effective than that of enhancing ventilation. Especially during the typical lunch and dinner periods in the buildings providing meals for campus occupants, the measure of staggering peaks for meals and restricting the occupancy of each batch within 25% could effectively prevent the spread and infection of the virus.

(2) When the two measures can be considered simultaneously for public buildings, maximizing restricting occupancy on the basis of increasing ventilation rate has the best effect. However, the restriction and increase also have certain limits; otherwise, the strength of the risk reduction is weakened. When the occupancy is predicted to be more than 50%, the effect of constraining the occupancy within 50% on the basis of increasing the ventilation rate to 2.0 times the design value is equal to that of only constraining the occupancy within 25%. When the occupancy rate is predicted to be more than 75%, the effect of constraining the occupancy within 50% on the basis of increasing the ventilation rate to 1.2 times the design value is equal to that of constraining the occupancy within 75% on the basis of increasing the ventilation rate to 1.8 times the design value.

(3) When the building ventilation system is independently controlled by the occupants, the priority is suggested to be given to constraining occupancy and ensuring the distance between occupants to make up for the difference between the time of indoor air being thoroughly purified by the ventilation system and the time of the occupant arriving, the operation of which is mainly independently controlled by the arriving occupants. In comparison, when the building ventilation system is centrally controlled, it is preferred that the infection risk be controlled by increasing the ventilation rate and ensuring the occupancy rate during the peak periods within 75%.