1. Introduction
Standard practice for seismic requirements is defined through a design-level earthquake for which a structure must meet life safety conditions. This requires that occupants evacuate a structure during a seismic event, but it does not imply that the structure can return to normal operational activities or even be reoccupied after the earthquake [
1]. In other words, the seismic design and assessment of buildings focus only on protecting the lives of building occupants, but significant damage to the structure, nonstructural components, and building contents is allowed as long as the code objective is met [
1]. Current building codes adopt performance-based design (PBD), which establishes seismic performance objectives characterized by limit state target displacements [
2] and evaluates the structural response of both existing and new structures to ensure that particular deformation-based criteria are met [
3,
4]. Even though this is seen as a long and complex process, as discussed in [
5], unifying each performance level and the corresponding probabilities of failure leads to a better overall seismic behavior since less frequent events are also examined, helping to control serviceability limit states. Even though PBD can limit damage, high expected losses may result from seismic events, affecting a building’s functionality [
2]. For example, direct economic losses for new, code-designed frame buildings can reach more than 20% of their total replacement value (e.g., Terzic et al. [
6] and Mayes et al. [
7]), which leave them unusable for more than a year [
6]. A similar conclusion was drawn by Ramirez and Miranda [
8], who observed that 4- and 12-story reinforced concrete (RC) frame buildings in Los Angeles can attain, respectively, 42% and 34% of direct financial losses for the design-level earthquake as a result of substantial residual drifts. These permanent deformations are considered an important indicator of reparability, meaning that excessive deformations would lead to the total loss of a building [
1] although it had not collapsed. Furthermore, existing seismically deficient buildings pose high vulnerability and thus higher direct losses and result also in longer downtimes (i.e., indirect losses), which is much more difficult to quantify [
1]. These considerations highlight the importance of improving the performance of existing deficient buildings to reduce seismic consequences and increase the ability to regain functionality as promptly as possible [
9].
As described by Cimellaro et al. [
10], seismic resilience is considered an effective method for assessing the seismic performance of buildings for which repair, rehabilitation, and retrofitting are foreseen to improve their performance. Bruneau et al. [
11] describe resilience as the capacity of a system to reduce the chances of perturbations, to absorb them, or recover quickly after a shock. Within a seismic context, seismic resilience aims to maintain the functionality of structures and provide livable conditions after strong ground motions [
10]. In particular, downtime, a component associated with seismic resilience, could be used to evaluate retrofit alternatives through an assessment methodology by incorporating a sequence of repairs, impeding factors, and the availability utility [
9]. In other words, special attention or preference would be granted to a retrofit alternative with the lowest downtime. Consequently, the recovery time is a key input in any seismic resilience assessment method and is related to the building’s performance levels. Additionally, it requires integrated multidisciplinary design and contingency planning, together with performance-based assessments to ensure that resilience objectives are met [
9]. In this sense, it is necessary to select a proper metric for resilience (e.g., indicator within a scoring method or resilience index) that can be used by decision makers [
12] to evaluate the seismic resilience of buildings.
In seismic-prone regions such as Italy, characterized by a long history of moderate–high intensity earthquakes [
13,
14], PBD is the current approach adopted for the design and assessment of earthquake-resistant structures (i.e., Eurocode 8 [
15,
16] and NTC 2018 [
17]). At the same time, there are no specific local guidelines addressing the seismic resilience of buildings, which is a critical issue due to the seismic vulnerability of existing buildings in such contexts [
18]. Following the 2002 Molise earthquake, the government issued the Ordinance 3274/2003 that required the seismic verification of many existing structures. These included important buildings (e.g., schools and museums), strategic buildings (e.g., hospitals and police stations), both public and private. These works were to be carried out by the building owner or manager within 5 years in the zones of highest seismicity. For what specifically concerns school buildings, the 2003 governmental ordinance stated that these critical facilities had to be assessed providing a funding plan, an assessment study, and a retrofit scheme, if applicable (Gazzetta Ufficiale 2003 [
19]). What transpired was a series of deadline extensions up until 2013 and a lack of uniform implementation. This was also aided by the lack of adequate funding to execute the works, meaning that only those who had the financial capacity to carry out the works were required to do so, and those who did not, faced no explicit penalties for failing to do so. In addition to the relevancy of school building as critical facilities, these buildings are used as emergency shelters; hence, it is vital to quantify the immediate postearthquake reduction and recovery of the shelter-in-place housing capacity. Even though several studies have examined the seismic risk of Italian school buildings (e.g., O’Reilly et al. [
20] and Perro et al. [
21]) and explored seismic retrofit techniques and preferences (e.g., Carofilis et al. [
22], Caruso et al. [
23], Gentile and Galasso [
24], Leone and Zuccaro [
25], and Caterino et al. [
26]), they have not addressed seismic resilience. Yet, this relevant topic influences the reactivation of a region’s regular activities after earthquake disasters. For instance, the reconstruction and recovery of Amatrice’s Capranica Elementary School, led the recovery efforts of the region affected by the 2016 Amatrice earthquake, becoming a symbol of rebirth (Il Corriere della Sera 2016 [
27]). Another example is reported by Fiorentino et al. [
28] for an RC frame school building seismically retrofitted with passive dampers in Norcia, a region also affected by the same aforementioned earthquake. The passive dampers were effective in preventing structural damage and minimizing nonstructural damage. As reported by Mazzoni et al. [
18], Norcia had suffered damaging earthquakes in the past; therefore, it specified stronger seismic criteria in its reconstruction policy. On the other hand, Amatrice had not experienced significant earthquakes in recent history and hence had a much more vulnerable building stock [
18]. For this reason, Norcia began to repopulate much faster, while much of the buildings in Amatrice were still in ruins. Additionally, special civil engineering structures require, in turn, not only seismic retrofit but also strict and constant monitoring, especially those considered as essential facilities, to guarantee high stability to any external vibration [
29].
Furthermore, many buildings are not only prone to suffer from damage during seismic events but also have deficient energy performance throughout the year, highlighting the importance of exploring energy retrofitting techniques as well. In this sense, integrating seismic and energy retrofitting techniques ensures that these two concerns are addressed, contributing as well to enhanced building resilience. From an economic perspective, integrated retrofitting often results in more cost-effective retrofitting, when compared to treating each seismic or energy-efficient retrofitting alone [
30]. Such an integrated framework has been significantly addressed for the Italian context where buildings are both seismically vulnerable and energy inefficient (Menna et al. [
31]). Accordingly, recent studies have focused on retrofitting buildings to simultaneously improve their seismic and energy performance (Caruso et al. [
23], Formisano et al. [
32], Passoni et al. [
33], and Pohoryles et al. [
34]). While these studies use a single metric or few decision variables to evaluate the combined retrofitting strategies, Clemett et al. [
30] also explored the combination of seismic and energy-efficient retrofitting adopting the multicriteria decision-making (MCDM) analysis to select the most beneficially integrated retrofitting option. The MCDM procedure enabled the so-called “three pillars” of sustainability (i.e., economic, social, and environmental, WCED 1987 [
35]) to be easily incorporated into the decision assessment. When looking at this from a resilience perspective, in a broader sense, resilience could succeed sustainability in what concerns city development [
36,
37]. The approach of sustainable development is to meet society’s needs by wisely using current resources without compromising the demands of future generations, whereas resilience lessens the impact of possible hazards [
36]. The main objective of resilience-based design (RBD) is to make communities more resilient by developing actions and technologies that allow a structure and/or community to recover its function as promptly as possible whenever a disaster occurs [
2]. Consequently, an optimally integrated retrofitting approach can be achieved by incorporating a seismic resilience metric into the MCDM of combined seismic and energy retrofitting schemes.
With the above considerations in mind, this study proposes a framework to identify an optimally combined seismic and energy retrofitting strategy for existing buildings, which also includes seismic resilience as an evaluation metric. Several seismic resilience approaches are revised and critically analyzed to subsequently assess a case study school building with four distinct retrofitting configurations. Finally, the most suitable seismic resilience metric is integrated within an MCDM framework, used to identify the optimally combined retrofitting option. A detailed discussion is also provided, focusing on the relevance and impact of considering resilience as a parameter, when choosing and designing an integrated retrofitting scheme.
2. Seismic Resilience of Buildings
Resilience has often been defined as the degree of recovery from a damaged state to a fully operational state [
11]. Accordingly, several studies [
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39] have quantified resilience through a recovery function that represents how a building restores its original functionality over time. In particular, Li et al. [
38] found it challenging to quantify the optimum recovery process of substations in China due to the dynamic interrelations among components, thus identifying three major properties that affect a recovery function: the definition of system functionality, the system model (which considers the interrelations among components), and the recovery strategy to restore system functionality.
Figure 1a illustrates the general concept of a recovery function. Initially, the system, which can be an individual building or a community, is operating normally (i.e., 100% functionality or normal operation activities) until it is disturbed by a seismic event (i.e., earthquake happens at time T0E). The functionality of a building then drops to a certain amount—this portion is associated with the seismic vulnerability, which depends on the earthquake intensity and seismic performance of the structural and nonstructural elements. This seismic vulnerability is expressed as the loss ratio caused by that seismic event [
10]. The horizontal axis represents the recovery time of the building, where any time after T0E indicates the period in which the building is unable to fully operate (i.e., downtime). Once the functionality of a building drops, there is a period in which it remains constant, while the building does not regain any functionality. This period refers to the delay time (DT), which accounts for all external activities that need to be carried out before repairs in the building begin. This includes structural inspections, permits, financing to utility restoration (i.e., lifelines, such as electricity, water, road, and any other external components that enable the building to restore normal operations). The components of the delay are further detailed and explored in the subsequent subsections. Once the delays have been estimated, the repair process begins, i.e., repair time (TRE). The recovery path will likely have an irregular shape, but it can be idealized by different recovery functions, as illustrated in
Figure 1a, such as linear [
10], exponential [
40], or trigonometric [
41]. The expressions in Equation (1) mathematically describe these three functions.
Resilience can be evaluated during an observation period or the life cycle of the building (TLC), meaning that the system would be evaluated for all seismic events that affect the building’s functionality for which different recovery processes and actions would be foreseen. Furthermore, according to Bruneau et al. [
11] and Cimellaro et al. [
10], resilience has four main properties, known as 4R—robustness, redundancy, resourcefulness, and rapidity—which are defined as follows:
Robustness: refers to any measure of analysis (e.g., strength and losses) to withstand a given level of stress or demand, without suffering degradation or loss of function. It is evaluated as the residual functionality level following an extreme event, represented in
Figure 1b by one minus the loss ratio [
10].
Figure 1b also displays a worthless limit, implying that it is impractical to conduct any repair action in a building with robustness under this threshold since it refers to partial collapse or irreparable damage;
Rapidity: relates to meeting priorities and achieving goals promptly to contain losses, recover functionality, and avoid future disruption. In
Figure 1b, rapidity is represented as the slope of the functionality curve, mathematically expressed as the derivative of the loss function with respect to time. As such, rapidity varies according to the shape of the recovery function. For instance, the rapidity is constant in the case of linear recovery function; on the other hand, an exponential function presents a greater rapidity (faster recovery actions) at the beginning, while it decelerates at the end of the recovery path. Conversely, a trigonometric function presents a lower rapidity (lower recovery rate) at the beginning with respect to the linear one, but then it increases and surpasses the rate of the linear function. Therefore, for the sake of simplicity, an average estimation of rapidity is defined by knowing the total losses and the total recovery time to reach 100% functionality (expressed in percentage/time) regardless of the type of recovery function [
10]. However, rapidity does not include the delay time, which considerably affects the rate of recovery in a building;
Resourcefulness: is the capacity to apply material (i.e., monetary, physical, technological, and informational) and human resources in the process of recovery to meet established priorities and achieve goals [
10]. It is, therefore, primarily an ad hoc action, which requires momentary decisions to engage additional and alternative resources [
11]. Its quantification is better illustrated graphically in
Figure 1c, where the third axis illustrates that added resources can be used to reduce time to recovery. In theory, if infinite resources were available, the time to recovery would asymptotically approach zero, but practically, even in the presence of enormous financial and labor capabilities, human limitations will dictate a practical minimum time to recovery [
10].
Redundancy: is the extent to which measures are replaceable and capable of satisfying functional requirements in the event of disruption, degradation, or loss of functionality [
10].
Figure 1d presents the resilience of all components of a system. However, it is important to note that buildings depend on lifelines (e.g., highway and street networks, bridges, electrical systems, piping systems, etc.), meaning that if these are not operative, the building will not be functional, even if all repairs have been concluded. It can be assumed that the performance of a network of elements can be established by a simple aggregation of the performance of individual elements [
11]. Moreover, for the case of school buildings and other learning facilities, redundancy can be considered as excess space and classrooms available in the building.
Robustness and rapidity are essentially the desired ends that are accomplished through resilience-enhancing measures and are the outcomes that more deeply affect decisions by stakeholders [
10]. On the other hand, redundancy and resourcefulness are measures that define how resilience can be increased, e.g., by adding redundant elements to a system or concentrating damage in replaceable components. All the elements of resilience are important, but robustness and rapidity are seen as the key elements for resilience [
11]. In contrast, resourcefulness and redundancy are strongly coupled, but difficult or more complex to quantify [
10], as they depend on human factors and available resources; therefore, an analytical function is not provided for these two quantities at this stage. However, changes in resourcefulness and redundancy affect the shape and the slope of the recovery curve, the repair time (TRE), and the robustness. Moreover, resilience is also correlated with four dimensions known as TOSE (i.e., technical, organization, social, and economic) [
11]. However, the analysis and review of these four dimensions is beyond the scope of this study.
2.1. Assessment Methodologies
As described, the most common approach to estimate resilience is through a functionality curve that represents the recovery process of a system. However, there are other methodologies and studies that evaluate resilience from different perspectives and parameters. The methods presented in this subsection have been grouped according to similar frameworks, resulting in three groups, detailed as follows:
2.1.1. Index-Based Methods
As mentioned previously, the functionality is estimated from a mathematical function. The complexity of each model is specific to the problem at hand, where different recovery functions may not be able to capture the actual recovery path, but at least are used to approximate it. Many assumptions and interpretations must be made in the quantification of the seismic resilience when diverse factors or fields are considered (e.g., engineering, economics, operations, etc.) into a unique parameter, leading to results that are unbiased by uninformed intuition or preconceived notions of risk. For example,
Figure 2 illustrates how the area under the recovery function is used as a resilience index [
10].
The commonly employed resilience index is defined in a simplified manner as the percentage rate between two functionality areas. The first one corresponds to the area under the curve of the recovery function, which is integrated from the earthquake occurrence to the end of the repairs (when the building has restored its normal conditions). The second area corresponds to the rectangle measured within the same limits, with a height corresponding to full functionality (total replacement cost of a building) and a length of the total recovery time. If the expected losses are considered as a loss ratio (full functionality equals one), the former area is simply normalized by the examination period.
Carofilis et al. [
42] examined a seismic resilience-based assessment method applied to school buildings with different retrofitting options. The method was based on Cimellaro et al. [
10], assuming a linear recovery function but without considering the delay time. The seismic resilience was estimated using Equation (2), and, as Cimellaro et al. [
10] did not consider any type of delays,
t1 was set as the T0E (moment when the earthquake happens), and
t2 was taken as the repair time TRE. However, the integration limits can be modified to include delays or even integrate the recovery function with respect to an observation period (TLC), which considers resilience with respect to the life cycle of a building. This means that if a delay time is considered,
t2 is defined as DT + TRE if T0E is set as zero. This equation has also been used by other authors in resilience assessment studies (Anwar and Dong [
9]).
The seismic resilience index is used to evaluate both hypothetical and real cases. For example, this evaluation parameter was used to assess Iranian school buildings, including post-recovery and retrofitting processes [
43]. Immediately after the occurrence of the 2017 Ezgeleh earthquake and in the following three years, the recovery process of the school buildings was monitored, and the gathered information was used to extract the seismic resilience indices. School buildings that had been retrofitted before the 2017 Ezgeleh earthquake demonstrated a high level of resilience with full functionality. Moreover, those schools that had not been retrofitted before the earthquake had the lowest resilience indices with zero robustness [
43]. Similarly, the seismic resilience of another Iranian school building was evaluated with four hazard levels, namely, 50%, 20%, 10%, and 2% probability of exceedance in 50 years [
44]. The results indicated that moment-resisting frames retrofitted with base isolation have a higher resilience index and lower repair costs compared to the conventional fixed-base system. Conventional engineering judgement suggests that if the structural damage exceeds 35% of a building reconstruction cost [
44], retrofitting is no longer a feasible repair alternative, and the structure should be reconstructed immediately. Moreover, it is also assumed that if the school’s functionality decreases by more than 50%, the school must be evacuated until the retrofitting operations are completed, meaning that the utilization process does not take place before the retrofitting operations are completed [
44]. Similar criteria were used by O’Reilly and Sullivan [
45] to evaluate the seismic vulnerability of Italian school buildings, assuming that when the expected economic losses exceed 60% of the replacement cost of the building, the stakeholder would decide to demolish rather than repair the existing building. On the other hand, Elwood et al. [
46] reported a much lower ratio following the Canterbury earthquakes of 2011 and 2012 in New Zealand, noting that over 50% of the structures presented a damage ratio ranging from 2 to 10% were demolished. This peculiar threshold is a result of a severe legislative decision that penalized old RC buildings by labeling them as seismically vulnerable regardless of their real damage condition. In this study, for the Italian context, the demolition threshold of 0.6 adopted by O’Reilly et al. [
20] was used to estimate robustness through Equation (3), thereby leading to the robustness threshold of 0.4 (1–0.6). This means that for an expected loss ratio equal or higher than 60% of the total replacement cost of a building, or for a robustness lower or equal to 40%, it is more practical to demolish the structure rather than spending resources to restore its original configuration/use.
Rapidity, in turn, is modified to account for the delays. As observed in
Figure 2, if delays are considerably long, the rapidity of the system decreases (
θ’). Conversely, if delays are short, the rapidity of the system increases (
θ). In this study, Equation (4) is proposed to compute rapidity, whether accounting for the delay time or not (i.e.,
T corresponds to the recovery time that may or may not include delays).
It is clear that the seismic resilience of buildings is estimated by different metrics. For example, the assessment is based solely on the four main components of resilience: rapidity, robustness, redundancy, and resourcefulness of which only the first two are numerically quantified. Even though redundancy and resourcefulness influence rapidity and robustness, they cannot be numerically quantified and depend on monetary or human resources. Given that redundancy and resourcefulness cannot be estimated analytically, these two dimensions of resilience are not evaluated in this study.
2.1.2. Methods Based on Recovery States
The approaches within this group address postearthquake functionality and recovery states, including a sequence of damage states that a building undergoes before regaining normal operation activities. The Resilience-based Earthquake Design Initiative (REDi) Rating System developed by Almufti and Willford [
1] provides to owners and other stakeholders a framework for implementing resilience-based earthquake design according to the PEER PBEE methodology [
47]. It is a holistic beyond-code design method that integrates planning and assessment for achieving a much higher performance [
1]. The REDi framework assigns a building a rating class from its three-tiered system (i.e., Platinum, Gold, or Silver). To assign a rating class, it is necessary to satisfy mandatory criteria of the baseline resilience objectives defined in the REDi guidelines [
1]. Even though the method considers only the design earthquake level, the framework can be implemented for other demand levels or performance states. Given their usefulness, the REDi guidelines are used in this study to determine the recovery states and their features (e.g., delay time, repair time, element repair states, functionality level, etc.) for the seismic resilience assessment of existing buildings, when no rating classes are evaluated and assigned.
REDi is a practical framework to estimate influential aspects, such as long lead-time, delays due to utility downtimes and impeding factors, to result in three possible recovery states:
Reoccupancy. A building is safe enough to be occupied (e.g., as a shelter). If damage is apparent, this typically requires an inspection. Any damage to structural and nonstructural components is minor and does not pose a threat to life safety.
Functional Recovery. Condition to regain the facility’s primary function. This would require restoring power, water, fire sprinklers, lighting, and HVAC systems, while also ensuring that elevators return operational. It also indicates the time required for the resumption of specific functions particular to a certain occupancy type. Examples include emergency services and typical services in hospitals or classes in educational facilities.
Full Recovery. Repairs are required primarily for aesthetic purposes (such as painting cracked partitions) to restore the building to its original pre-earthquake condition.
All of these recovery states depend on an average damage state reported for each building element after conducting a loss assessment (PACT [
48]). The REDi guidelines provide average repair classes for most structural and nonstructural components based on their average damage state. These repair classes (1, 2, and 3) are related to the recovery states. For instance, components in repair class 1 are expected to experience minimal or minor cosmetic damage. An element in repair class 2 has a certain level of damage that does not pose a life safety risk. Finally, an element in repair class 3 has a heavily damaged component that represents a life safety risk or it is not operative. To achieve a certain recovery state, the components influencing that state must be repaired. The reoccupancy recovery state requires the repair of components in repair class 3 only. Similarly, the functional recovery state requires the repair of the elements in repair classes 2 and 3. For full recovery, all elements must be repaired.
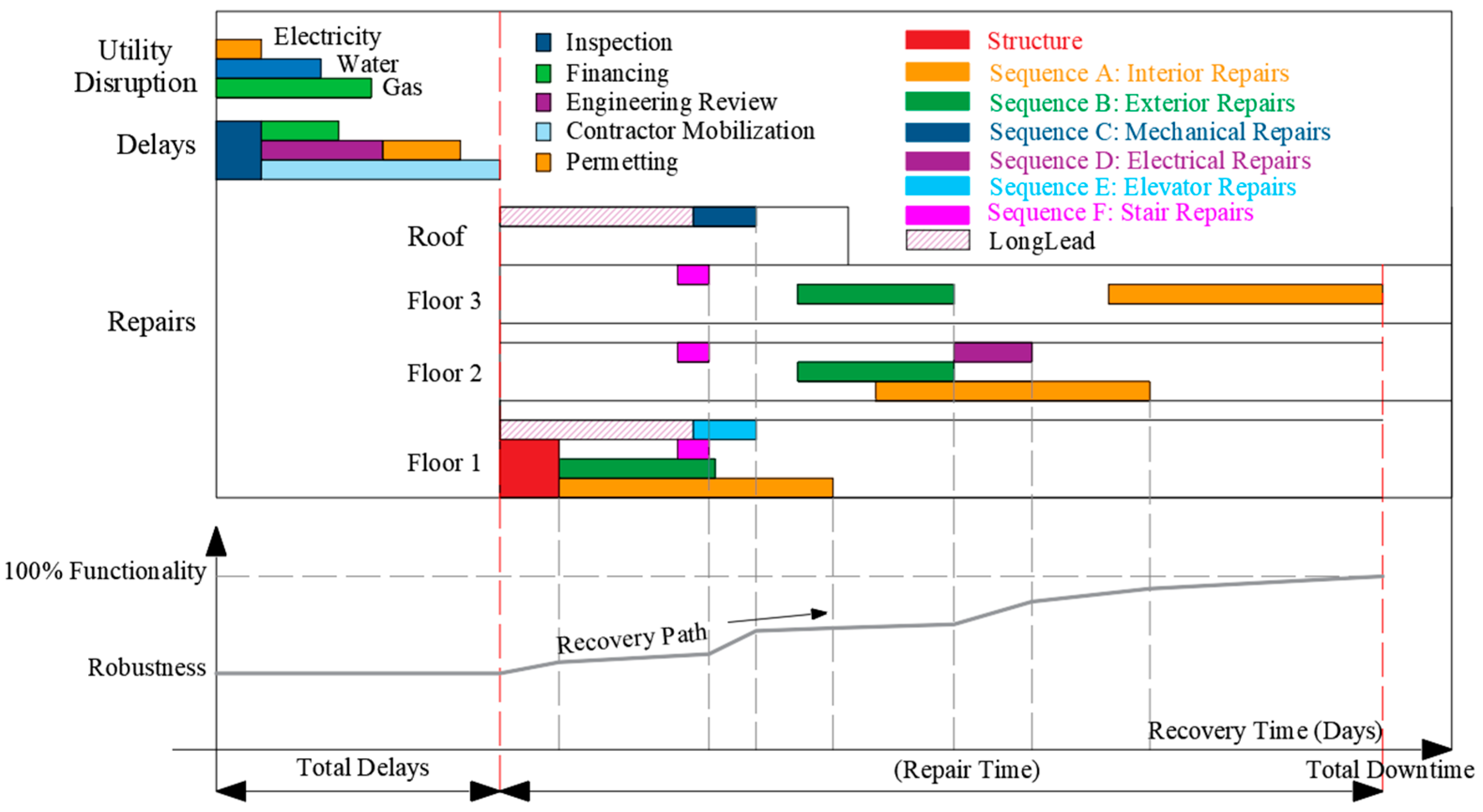
Figure 3a exemplifies the recovery paths for the three aforementioned recovery states. For reoccupancy, the building regains a certain level of functionality after the seismic event; the recovery time needed to reach such states is much less than that of the other two states. Additionally, the delays are shorter since the building does not require that all services are operative and reoccupied. The functional recovery has a much higher functionality and thereby a longer recovery time. Finally, the full recovery state represents the conditions where the building has regained normal operation activities. Furthermore,
Figure 3b displays the sequence of repairs followed by each recovery state depending on the damage reported by each repair group (Tables 4 and 5 of the REDi guidelines [
1]). The sequence starts with the structural repairs that must be completed before proceeding with any other repair component. These repair groups (e.g., interior repairs, exterior repairs, and mechanical repairs) can be addressed in parallel as long as the maximum number of workers is not exceeded [
1].
The delays between the earthquake event and the initiation of repairs, which are significant, are referred to as impeding factors and include the time it takes to complete postearthquake building inspections, secure financing for repairs, mobilize engineering services, obtain permitting, mobilize a contractor and necessary equipment, and for the contractor to order and receive the required components including long lead-time items [
1]. The utility disruption is another component of the delay times, which is likely to occur for a design-level earthquake and must be considered for buildings attaining a full recovery state, including lifelines, such as electricity, gas, and water lines.
The REDi framework is also very practical for a good estimate of the downtime, which is determined in a more rigorous fashion from a loss assessment using the software PACT [
48]. Despite acknowledging the US-specific limitations of this software for conducting a loss assessment in regions outside of the US, the outputs that this tool generates can be used to carry out a comparison among strategies.
Figure 4 lists the steps involved to obtain the recovery time. The recovery time framework for the reoccupancy state includes impeding factors and any building components classified as repair class 3. On the other hand, the recovery time framework for functional recovery integrates utilities and impeding factors as delays, and then all components defined as repair classes 2 and 3 are considered. Similarly, the downtime framework for full recovery includes utilities and impeding factors and considers all repair classes (i.e., 1, 2, and 3). The sequence of delays due to impeding factors is initiated by the postearthquake inspections, followed by the financing, engineering mobilization and review, and contractor mobilization. Contractor mobilization leads to permitting and any long lead-time components.
Furthermore,
Figure 5 illustrates the repair sequence to reach full recovery for a four-story building. REDi presents a reasonable sequence to conduct repairs; therefore this repair schedule is used to estimate the recovery function or path as displayed at the bottom of
Figure 5. The recovery path is determined by adding the cost associated with each repair sequence (regaining of functionality) and by adding the total delays with the time associated with each repair sequence (total downtime). It is also important to notice the availability of financial resources, which, when lacking, considerably lengthen the time due to delays. In that case, other sources of financing, such as credits or loans, need to be explored. Eghbali et al. [
43] revealed that the most noticeable factors causing delays to the start of the renovation of Iranian school buildings after the 2017 Ezgeleh earthquake were lack of sufficient funding by the government and/or donors, time-consuming procedures for the selection of contractors, use of school buildings as temporary shelters for local residents, and delays in the removal of school equipment by the Ministry of Education. Similarly, the time representing the long lead is followed after the contractor mobilization, indicating that if financing exceeds contractor mobilization, one does not have to wait until the repair tasks begin to consider the long lead. As such, the repair of components depending on long lead will not delay the repair activities.
Overall, the REDi guidelines provide a comprehensive framework to evaluate different resilience parameters. Even though the framework is challenging and time-consuming, due to the level of analysis to carry out and subsequent postprocessing of outputs, it yields relevant aspects, such as delays, total downtime, repair classes, and resilience category, among others, that can evaluate seismic resilience in a more precise way. However, one may argue that, given the context in which the REDi guidelines were developed, they should be applied only to case studies in the United States. While it is evident that the resilience measures are not fully representative of the region where the assessment is conducted, for comparative purposes, the framework can be still used as illustrated in subsequent sections through the comparative analysis of retrofitting solutions, including resilience as an evaluation parameter.
2.1.3. Performance-Based Multicriteria-Based Methods
Anwar et al. [
49] introduced a performance-based multicriteria decision-making (PB–MCDM) approach to assess the seismic resilience of buildings from a long-term perspective. The PB–MCDM integrates the performance assessment with the MCDM framework [
26], and the seismic resilience is evaluated for a range of intensities and includes several consequences (i.e., economic, social, and environmental consequences) [
49]. Therefore, to implement the PB–MCDM, three types of analyses need to be carried out: (1) performance assessment module—PAM (loss assessment), (2) sustainability assessment module—SAM (expected consequences: social and environmental), and (3) resilience assessment module—RAM. These three metrics are then integrated into an annualized value, and through an MCDM analysis, the most convenient retrofitting option is selected (
Figure 6). This section is divided by subheadings. It provides a concise and precise description of the experimental results, their interpretation, and the experimental conclusions that are drawn.
At a first glance, the PB–MCDM framework appears as an extensive methodology (i.e., four modules have to be evaluated); however, the method is simplified by using the software PACT [
48], from which the three first modules (PAM, SAM, and RAM) can be quickly obtained. Each module is evaluated for different intensities, and then all the PAM, SAM, and RAM parameters are integrated into a single metric. The integration procedure, illustrated in
Figure 7, combines the mean annual frequency of occurrence and the total consequence curves, considering hazard scenarios converted to expected annual consequences (EACs). Finally, the MCDM [
26] is applied to the parameters obtained from these modules.
Anwar et al. [
49] evaluated three different earthquake intensities: FLE (Frequent-Level Earthquake), DLE (Design-Level Earthquake), and MCE (Maximum Considered Earthquake) when analyzing a 4-story RC building with three retrofitting alternatives. Five parameters were considered for the MCDM evaluation: seismic loss (economic losses), sustainability, through three parameters (casualties, equivalent carbon emissions, and embodied energy), and resilience. The repair time, sequence of repairs, and total repair time were determined using the REDi methodology [
1]. The alternative with the highest relative closeness [
26] was considered as the best retrofit option among the considered alternatives.
Furthermore, Anwar et al. [
49] found that long-term consequences result in different closeness coefficients, and thereby long-term consequences greatly influence the rank preference. As such, the expected long-term economic losses and environmental consequences (embodied carbon emissions and embodied energy) are also contemplated in this study and determined through Equations (5) and (6), respectively:
where
L accounts for the expected economic losses for a given intensity;
λ is the frequency of the earthquake for a given intensity determined from a hazard curve;
r is the financial discount rate;
tmax is the investigated period;
S is a parameter that represents an environmental consequence (i.e., embodied carbon emissions or embodied energy).
The PB–MCDM adopted by Anwar et al. [
49] focuses on sustainability and resilience aspects. However, the versatility of the MCDM allows it to incorporate many additional aspects, such as social, technical, and environmental ones. For a more comprehensive evaluation, PB–MCDM should incorporate other important variables, such as cost, duration of work, architectural impacts, etc., which have been demonstrated to control and alter the selection of the most favorable strategy (Carofilis et al. [
42]).
Table 1 summarizes the main features of the reviewed methodologies highlighting the main advantages and disadvantages for each approach.
4. Integrated MCDM-Based Optimal Retrofitting Selection
As a further step with respect to the resilience-based PB–MCDM approach described in
Section 2.1.3 and applied in
Section 3.4, this section defines an extended MCDM framework that integrates the estimated seismic resilience with several other relevant evaluation parameters, building upon the work carried out by Clemett et al. [
30]. In this work, the authors designed a number of seismic and energy-efficient retrofitting schemes and applied the MCDM framework to select the optimal combination of those schemes, conditioned on the adopted decision variables and weight vector. The seismic retrofitting strategies correspond to the ones already presented in
Section 4 (i.e., A1 to A4), while the energy retrofit measures adopted in such a study [
30] consisted of: E1—external roof insulation with EPS panels; E2—external wall insulation with EPS panels combined with the interventions of E1; and E3—replacement of windows with new double glazing with PVC frames with internal venetian blinds, floor insulation, along with the E2 interventions. The label S and E indicate the seismic (S1–S4 are equivalent to A1–A4 defined in
Section 4) and energy retrofit schemes, respectively, that comprise the combined alternative. The different retrofit combination alternatives (considering both energy and seismic retrofitting) were analyzed across the DVs listed in
Table 5 [
30].
The integrated MCDM-based optimal retrofitting selection follows the procedure illustrated in the flowchart shown in
Figure 15. The two first steps relate to designing the energy and seismic retrofitting separately. Then, the alternatives are combined to obtain a set of integrated energy and seismic retrofitting options. This new set of different retrofit combinations is evaluated in terms of energy efficiency, seismic performance, and seismic resilience. Finally, the MCDM is applied to the set of combined alternatives considering all the DVs of
Table 5.
Regarding the weight vector (w) that is required for the MCDM implementation, one of many possible acceptable vectors was determined using the analytical hierarchy process (AHP) and engineering judgment. The same assumptions of Clemett et al. [
30] guided the selection of the values for the pairwise comparison of the variables.
Figure 16 illustrates three possible cases; w1 gives equal importance to the seismic resilience and LCEI (expected life cycle environmental impacts of retrofitted structure); w2 considers the seismic resilience as the most important parameter; w3 assumes seismic resilience as the fifth most important variable, with lower importance when compared to the annual probability of collapse but higher with respect to the duration of works.
Table 6 represents the decision matrix used for conducting the MCDM analysis. The decision matrix was filled according to the results reported for the case study location (Isola del Gran Sasso, Italy), described in the study of Clemett et al. [
30] (i.e., values for C
1 to C
8). The calculation of each DV value is described in detail by Clemett et al. [
30]. To represent the seismic resilience DV (C
9), three parameters were considered, namely, the annualized resilience index (EARe), the resilience index at SLV (Re_SLV), and the ratio of all the building elements categorized with a repair class of 1 at SLD (R1_SLD).
The ranking representing the preference of all nine combined retrofitting strategies is reported in
Table 7 when the weight vector w1 is used. Different tones of gray are used to distinguish the four seismic retrofitting options. On the other hand,
Table 8 reports the cases for weight vectors w2 and w3 for the EARe and R1_SLD resilience DVs, since these are the seismic resilience DVs that alter the ranking preference of the second and third alternatives. All the tested options for weight vector and resilience DV resulted in S
4E
3 as the most beneficial strategy, which coincides with the selection reported in Clemett et al. [
30]. However, the subsequent three preference positions follow the same pattern as in Clement et al. [
30] just when Re_SLV is adopted as the seismic resilience parameter. For EARe and RI_SLD, S
3E
3, S
4E
2, and S
3E
2 are ranked as the second, third, and fourth best alternatives.
Furthermore, adopting different weight vectors slightly alters the rank positions of the alternatives with higher relative closeness, yet S4E3 is still granted the top position, i.e., as the most convenient solution. It is evident that by combining the strategy with CFRP and viscous dampers (seismic retrofitting) with the E3 energy retrofitting level, the most favorable outcome is obtained.