Identification of Wind Loads on Structures Based on Modal Kalman Filter with Unknown Inputs
Abstract
:1. Introduction
2. Improved Identification Method of Wind Loads
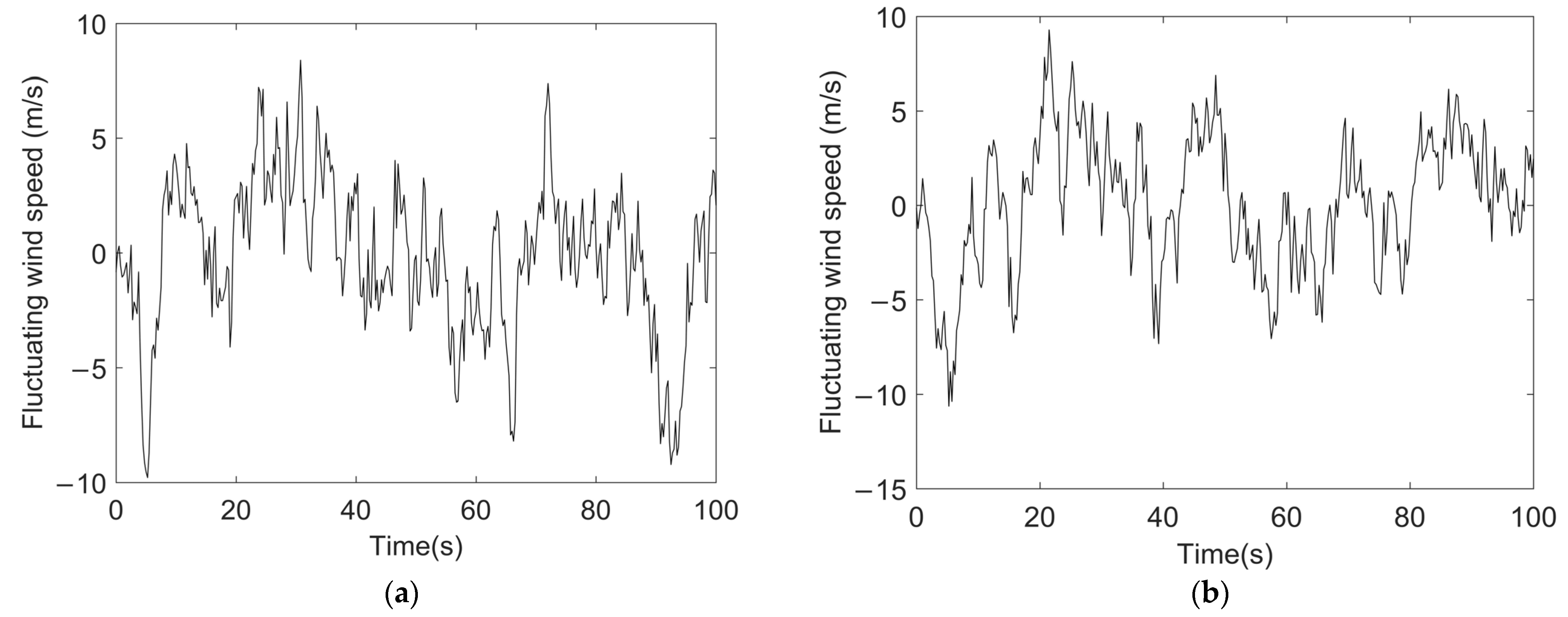
2.1. Simulation of Wind Loads on Structures
2.2. Wind Loads Decomposition and Modal Transformation
2.2.1. Identification of Wind Loads on Continuous Structural Systems
2.2.2. Identification of Wind Loads on Discrete Structural Systems
2.3. Wind Loads Identification Based on MKF-UI
3. Numerical Identification Examples
3.1. Identification of Wind Loads on Continuous Structure of Wind Tower
3.2. Identification of Wind Loads on a Discrete 20-Story Shear Frame
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Xia, Y. The Identification for Vibration Loads of Launch Vehicle in Ground-Winds. Struct. Environ. Eng. 1998, 1998, 1–7. [Google Scholar]
- Chen, J.; Li, J. Study on Wind Load Inverse of Tall Building. Chin. Q. Mech. 2001, 2001, 72–77. [Google Scholar]
- Kang, C.C.; Lo, C.Y. An inverse vibration analysis of a tower subjected to wind drags on a shaking ground. Appl. Math. Model. 2002, 26, 517–528. [Google Scholar] [CrossRef]
- Law, S.S.; Bu, J.Q.; Zhu, X.Q. Time-varying wind load identification from structural responses. Eng. Struct. 2005, 27, 1586–1598. [Google Scholar] [CrossRef]
- Luigi, C.; Giovanni, S.; Federica, T. Proper orthogonal decomposition in wind engineering. Part 2: Theoretical aspects and some applications. Wind Struct. 2007, 10, 177–208. [Google Scholar] [CrossRef]
- Federica, T.; Giovanni, S. Double Proper Orthogonal Decomposition for Representing and Simulating Turbulence Fields. J. Eng. Mech. 2005, 131, 1302–1312. [Google Scholar] [CrossRef]
- Hwang, J.S.; Kareem, A.; Kim, H. Wind load identification using wind tunnel test data by inverse analysis. J. Wind Eng. Ind. Aerod. 2011, 99, 18–26. [Google Scholar] [CrossRef]
- Kang, N.; Kim, H.; Choi, S.; Seongwoo Jo, S.; Hwang, J.S.; Yu, E. Performance Evaluation of TMD under Typhoon Using System Identification and Inverse Wind Load Estimation. Comput.-Aided. Civ. Inf. 2012, 27, 455–473. [Google Scholar] [CrossRef]
- Zhi, L.H.; Chen, B.; Fang, M.X. Wind load estimation of super-tall buildings based on response data. Struct. Eng. Mech. 2015, 56, 625–648. [Google Scholar] [CrossRef]
- Zhi, L.H.; Yu, P.; Li, Q.S.; Chen, B.; Fang, M.X. Identification of wind loads on super-tall buildings by Kalman filter. Comput. Struct. 2018, 208, 105–117. [Google Scholar] [CrossRef]
- Zhi, L.H.; Li, Q.S.; Fang, M.X.; Yi, J. Identification of Wind Loads on Supertall Buildings Using Kalman Filtering–Based Inverse Method. J. Struct. Eng.-ASCE. 2016, 143, 06016004. [Google Scholar] [CrossRef]
- Niu, Y.; Fritzen, C.; Jung, H.; Buethe, I.; Ni, Y.-Q.; Wang, Y.-W.W. Online Simultaneous Reconstruction of Wind Load and Structural Responses—Theory and Application to Canton Tower. Comput.-Aided. Civ. Inf. 2015, 30, 666–681. [Google Scholar] [CrossRef]
- Xu, A.; Xie, Z.N.; Fu, J.Y.; Wu, J.R.; Tuan, A. Evaluation of wind loads on super-tall buildings from field-measured wind-induced acceleration response. Struct. Des. Tall Spec. 2014, 23, 641–663. [Google Scholar] [CrossRef]
- Li, K.; Liu, J.; Han, X.; Sun, X.; Jiang, C. A novel approach for distributed dynamic load reconstruction by space–time domain decoupling. J. Sound Vib. 2015, 348, 137–148. [Google Scholar] [CrossRef]
- Wu, S.Q.; Zhu, J. Reconstruction of distributed with load on structures from response samples. In Mechanics of Structures and Materials: Advancements and Challenges, Hao, H., Zhang, C., Eds.; 1st ed.; CRC Press: London, UK, 2016. [Google Scholar]
- Xue, H.L.; Lin, K.; Luo, Y.; Liu, H.J.; Marc, T. Time-Varying Wind Load Identification Based on Minimum-Variance Unbiased Estimation. Shock Vib. 2017, 2017, 9301876. [Google Scholar] [CrossRef] [Green Version]
- Xue, H.L.; Liu, H.J.; Peng, H.Y.; Luo, Y.; Lin, K. Wind Load and Structural Parameters Estimation from Incomplete Measurements. Shock Vib. 2019, 2019, 4862983. [Google Scholar] [CrossRef]
- Petersen, Ø.W.; Øiseth, O.; Lourens, E. Investigation of dynamic wind loads on a long-span suspension bridge identified from measured acceleration data. J. Wind Eng. Ind. Aerod. 2020, 196, 104045. [Google Scholar] [CrossRef]
- Petersen, Ø.W.; Øiseth, O.; Lourens, E. Wind load estimation and virtual sensing in long-span suspension bridges using physics-informed Gaussian process latent force models. Mech. Syst. Signal. Processing 2022, 170, 108742. [Google Scholar] [CrossRef]
- Nasrabad, V.S.; Hajnayeb, A.; Sun, Q. Effective wind speed estimation based on a data-driven model of wind turbine tower deflection. Proc. Inst. Mech. Eng. CJ. Mech. Eng. Sci. 2021, 236, 795–810. [Google Scholar] [CrossRef]
- Charisi, S.; Thiis, T.K.; Aurlien, T. Full-Scale Measurements of Wind-Pressure Coefficients in Twin Medium-Rise Buildings. Buildings 2019, 9, 63. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, C.H.; Nguyen, D.T. Predicted aerodynamic damping of slender single beam structures in across-wind vibrations. Acta Mech. Sinica.-Prc. 2020, 36, 990–998. [Google Scholar] [CrossRef]
- Macdonalda, J.H.G.; Larose, G.L. A unified approach to aerodynamic damping and drag/lift instabilities, and its application to dry inclined cable galloping. J. Fluid. Struct. 2006, 22, 229–252. [Google Scholar] [CrossRef]
- Nguyen, C.H.; Macdonald, J.H.G.; Cammelli, S. Non-across-wind galloping of a square-section cylinder. Meccanica 2020, 55, 1333–1345. [Google Scholar] [CrossRef]
- Amiria, A.K.; Bucher, C. A procedure for in situ wind load reconstruction from structural response only based on field testing data. J. Wind Eng. Ind. Aerod. 2017, 167, 75–86. [Google Scholar] [CrossRef]
- Liu, L.J.; Zhu, J.J.; Lei, Y. A Generalized Identification of Joint Structural State and Unknown Inputs Using Data Fusion MKF-UI. J. Appl. Comput. Mech. 2021, 7, 1198–1204. [Google Scholar] [CrossRef]
- Simiu, E.; Scanlan, R.H. Wind effects on structures: Fundementals and applications to design. Choice Rev. Online 1997, 34, 34–3889. [Google Scholar] [CrossRef]
- Shinozuka, M. Simulation of Multivariate and Multidimensional Random Processes. J. Acoust. Soc. Am. 1971, 49, 357–368. [Google Scholar] [CrossRef]
- Piccardo, G.; Solari, G. Generalized equivalent spectrum technique. Wind Struct. 1998, 1, 161–174. [Google Scholar] [CrossRef]
- Shinozuka, M.; Jan, C.M. Digital simulation of random processes and its applications. J. Sound. Vib. 1972, 25, 111–128. [Google Scholar] [CrossRef]
- Kuhar, E.J.; Stahle, C.V. Dynamic transformation method for modal synthesis. AIAA J. 1974, 12, 672–678. [Google Scholar] [CrossRef]
- Feng, C.D.; Chen, X.Z. Evaluation and Characterization of Probabilistic Alongwind and Crosswind Responses of Base-Isolated Tall Buildings. J. Eng. Mech-Asce. 2019, 145, 04019097. [Google Scholar] [CrossRef]
- GB 50009-2012; Load Code for the Design of Building Structures. China Architecture & Building Press: Beijing, China, 2012.








| Height (m) | RMS Error (%) | Height (m) | RMS Error (%) |
|---|---|---|---|
| 5 | 14.51 | 35 | 5.29 |
| 10 | 6.64 | 40 | 5.18 |
| 15 | 7.93 | 45 | 5.01 |
| 20 | 5.87 | 50 | 6.24 |
| 25 | 6.08 | 55 | 5.43 |
| 30 | 6.83 | 60 | 5.82 |
| Floor Number | RMS Error (%) | Floor Number | RMS Error (%) |
|---|---|---|---|
| 1 | 10.15 | 11 | 5.88 |
| 2 | 6.95 | 12 | 5.70 |
| 3 | 7.50 | 13 | 3.36 |
| 4 | 3.94 | 14 | 5.27 |
| 5 | 8.05 | 15 | 5.05 |
| 6 | 7.08 | 16 | 3.10 |
| 7 | 3.91 | 17 | 5.11 |
| 8 | 6.73 | 18 | 5.13 |
| 9 | 6.37 | 19 | 4.62 |
| 10 | 3.55 | 20 | 4.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, P.; Liu, L.; Lei, Y. Identification of Wind Loads on Structures Based on Modal Kalman Filter with Unknown Inputs. Buildings 2022, 12, 1003. https://doi.org/10.3390/buildings12071003
Zhao P, Liu L, Lei Y. Identification of Wind Loads on Structures Based on Modal Kalman Filter with Unknown Inputs. Buildings. 2022; 12(7):1003. https://doi.org/10.3390/buildings12071003
Chicago/Turabian StyleZhao, Pingnan, Lijun Liu, and Ying Lei. 2022. "Identification of Wind Loads on Structures Based on Modal Kalman Filter with Unknown Inputs" Buildings 12, no. 7: 1003. https://doi.org/10.3390/buildings12071003
APA StyleZhao, P., Liu, L., & Lei, Y. (2022). Identification of Wind Loads on Structures Based on Modal Kalman Filter with Unknown Inputs. Buildings, 12(7), 1003. https://doi.org/10.3390/buildings12071003








