Seismic Fragility Assessment of Cable-Stayed Bridges Crossing Fault Rupture Zones
Abstract
:1. Introduction
2. Seismic Fragility Methodology
3. Simulation of the Ground Motions
3.1. Ground-Motion Models
- (1)
- The equation of the pulse indicator (larger than 0.85) is given as:where the PGV ratio is defined as the PGV of the residual record divided by the original record’s PGV and the energy ratio with a similar definition.
- (2)
- The pulse occurs at the early stage of the motion, as indicated by the time when the original record reaches 20% of its total cumulative squared velocity (CSV) and is greater than the time at which the pulse reaches 10% of its CSV.
- (3)
- The PGV of the motion is larger than 30 cm/s.
3.2. Determination of the Input Parameters of the Models
4. Vulnerability Analysis of a Fault-Crossing Bridge
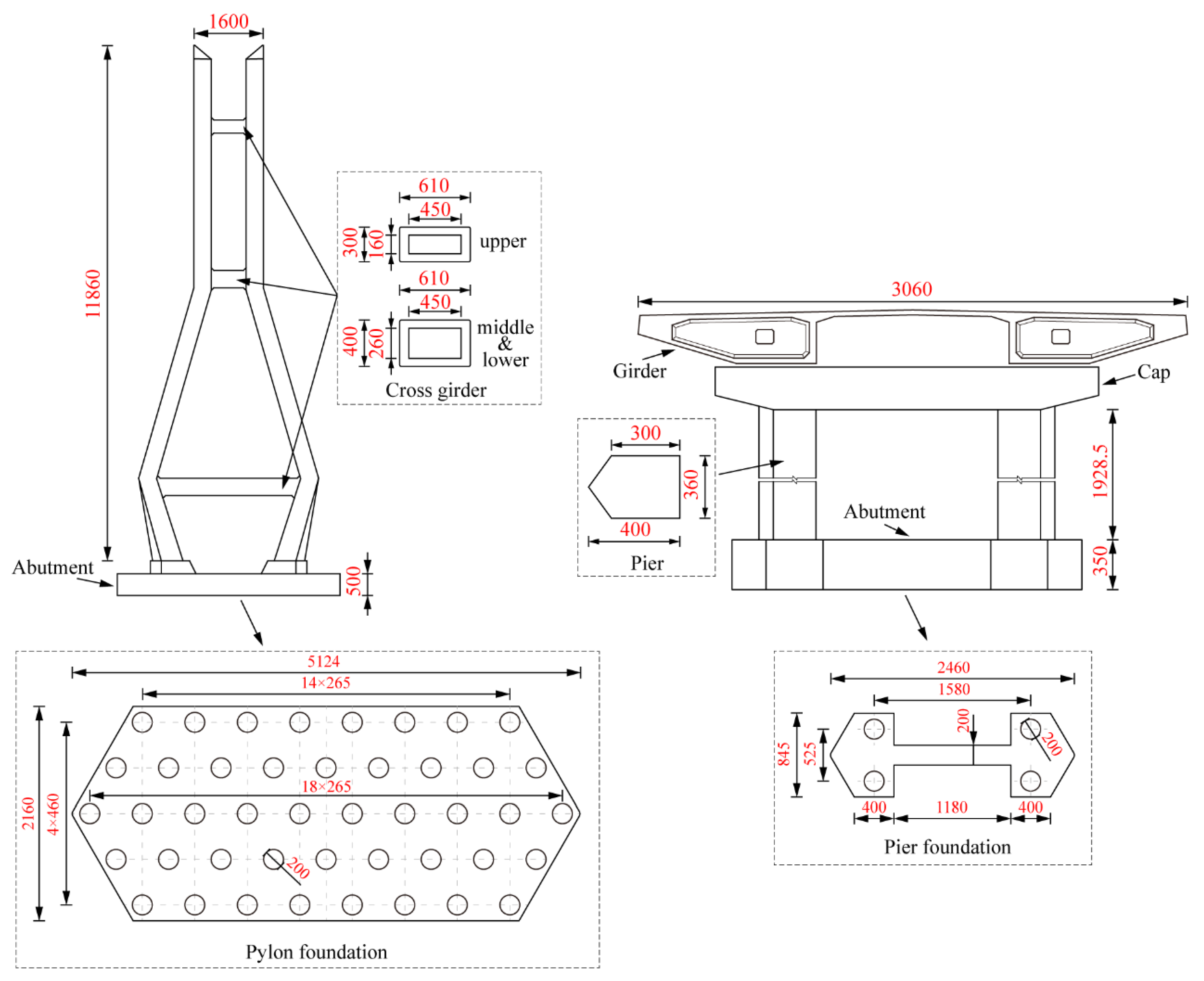
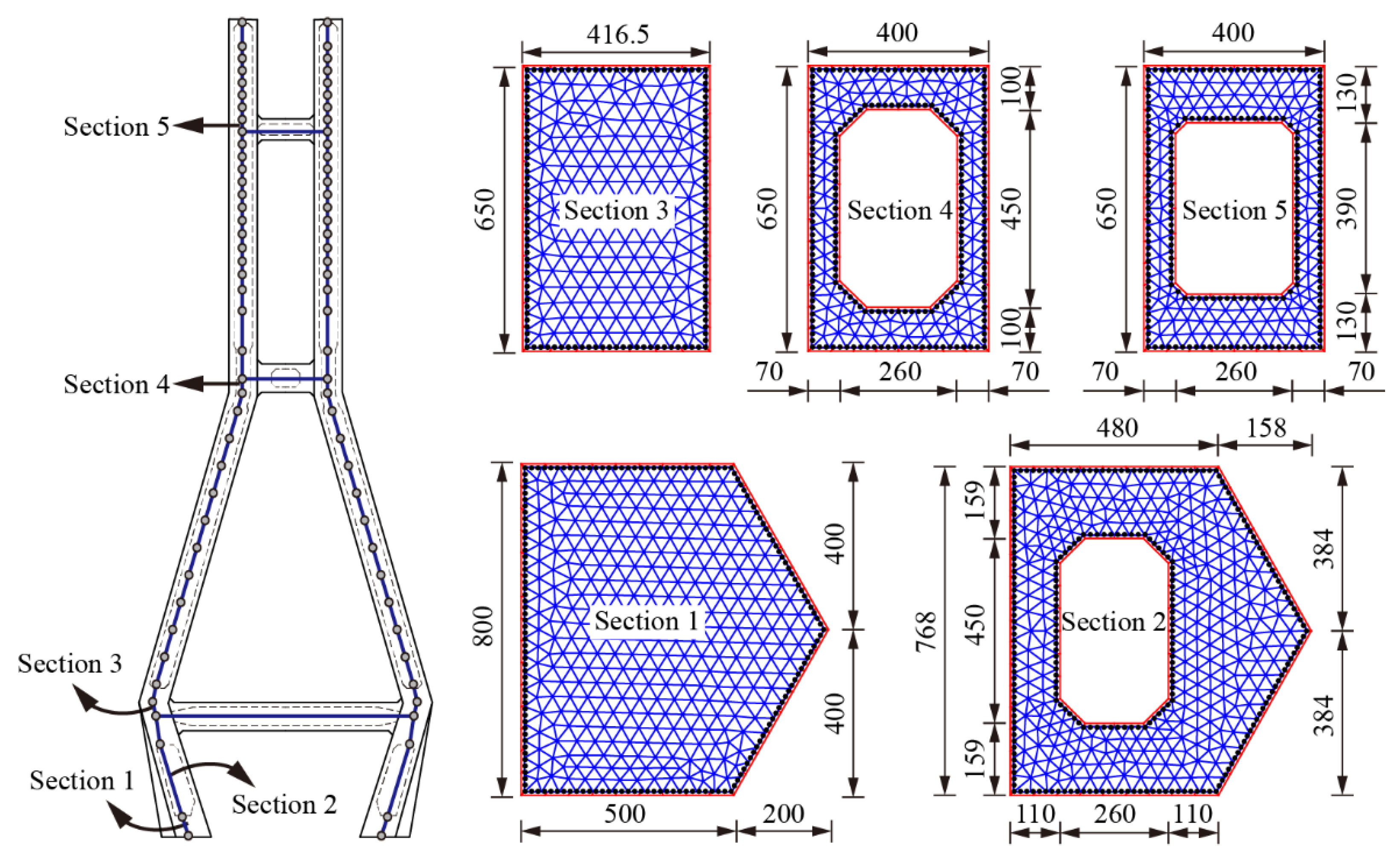
4.1. Depiction of the Analysis Model
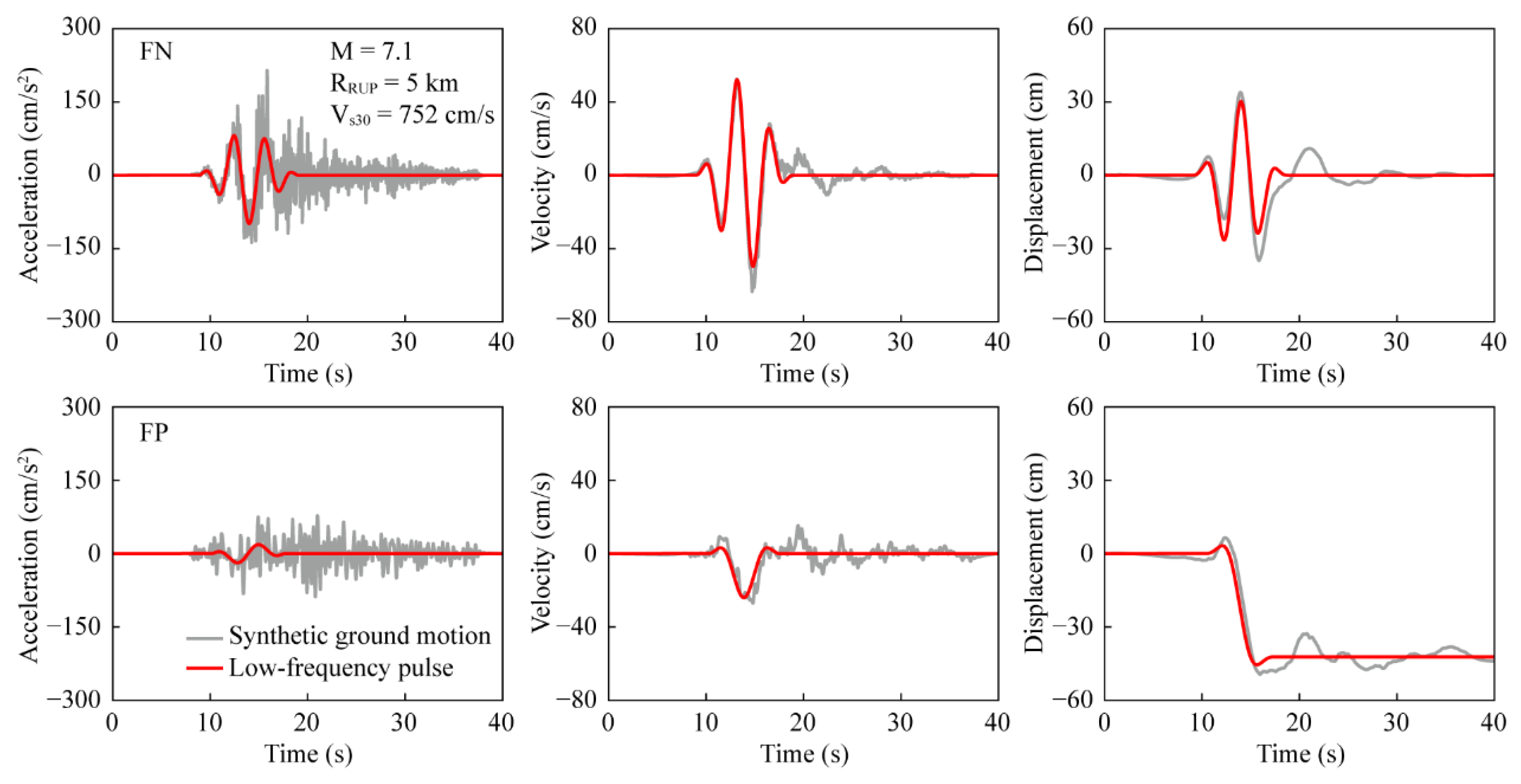
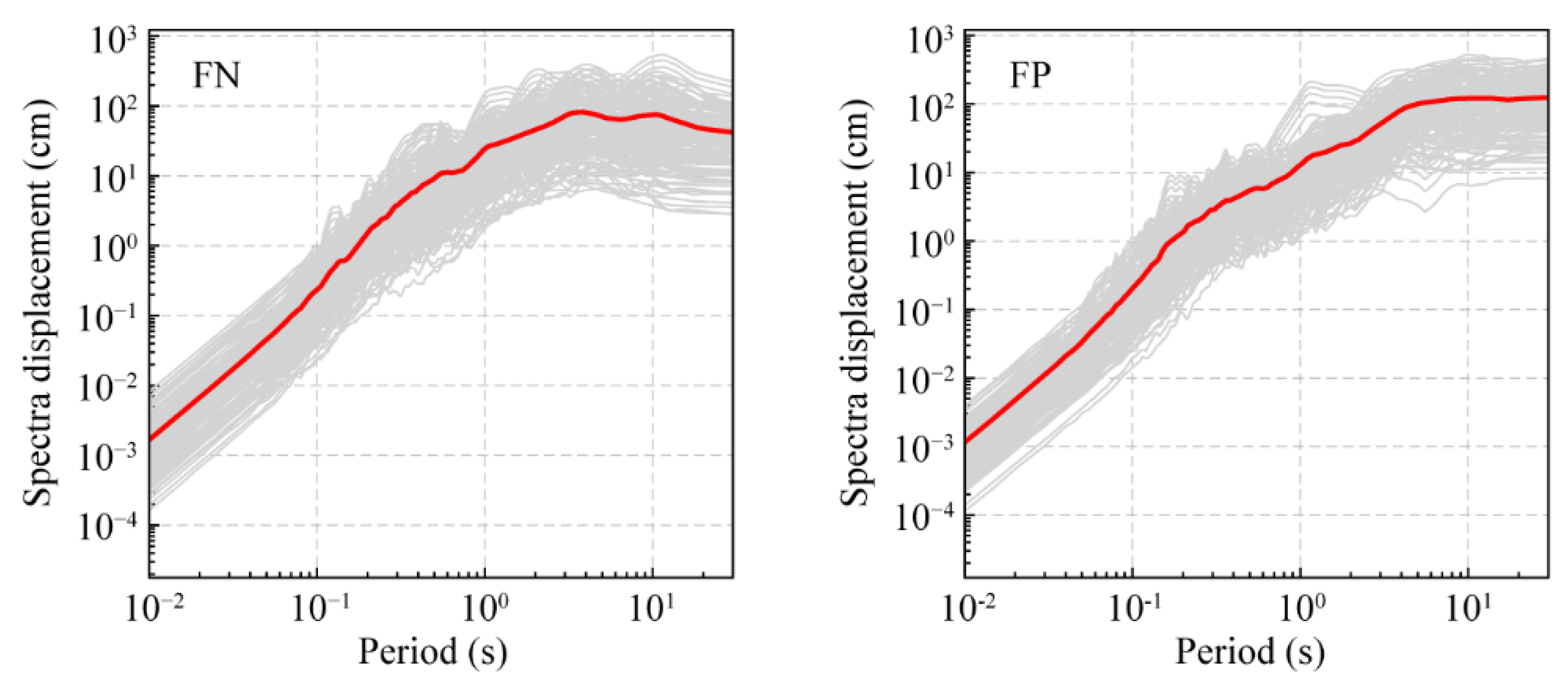
4.2. Ground Motions
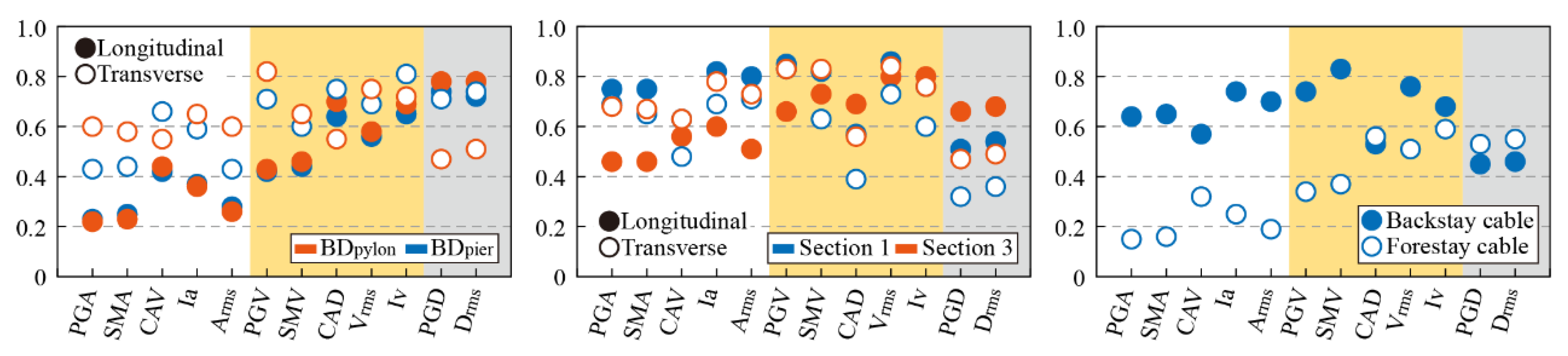
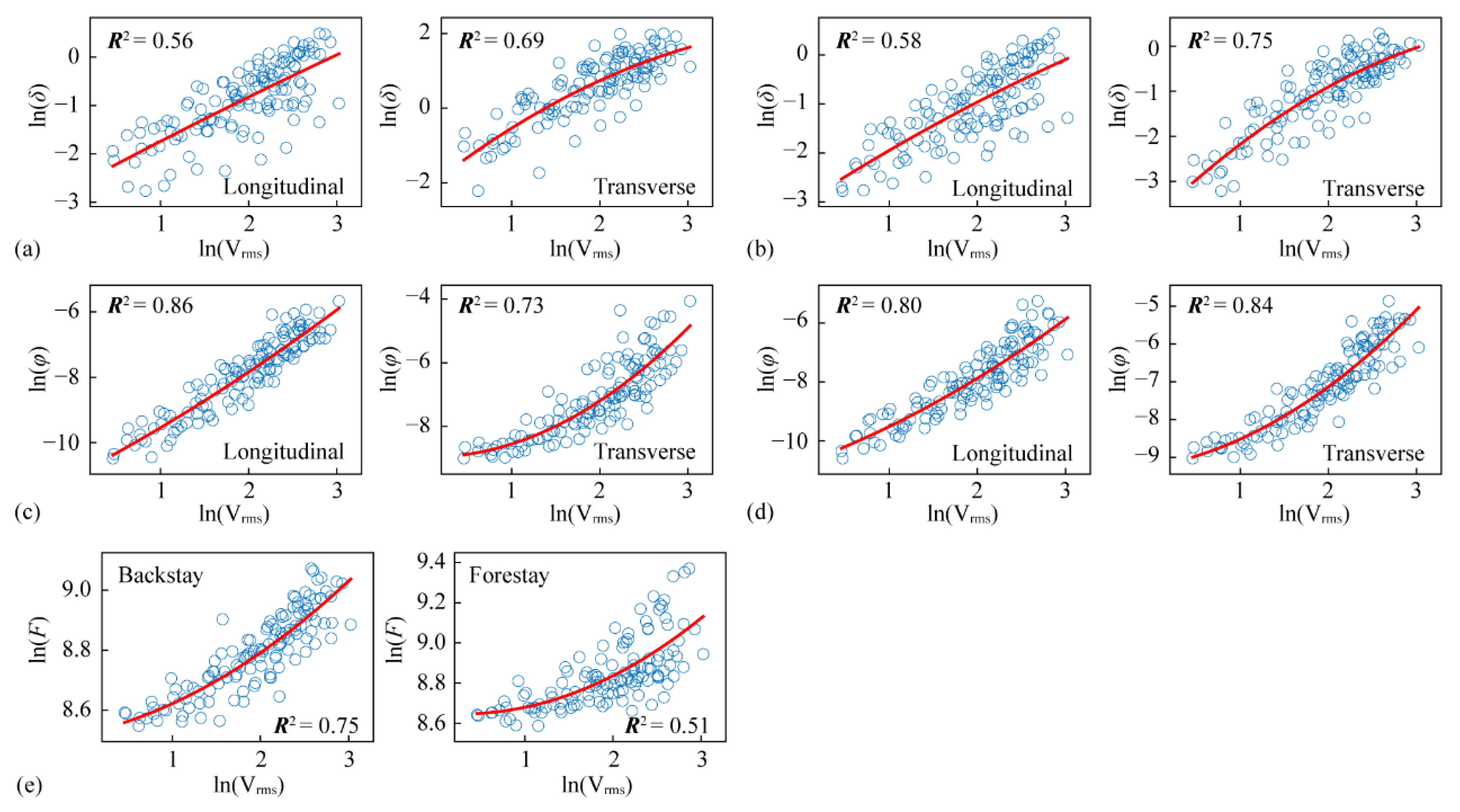
4.3. Optimal IM Determination and PSDMs Establishment
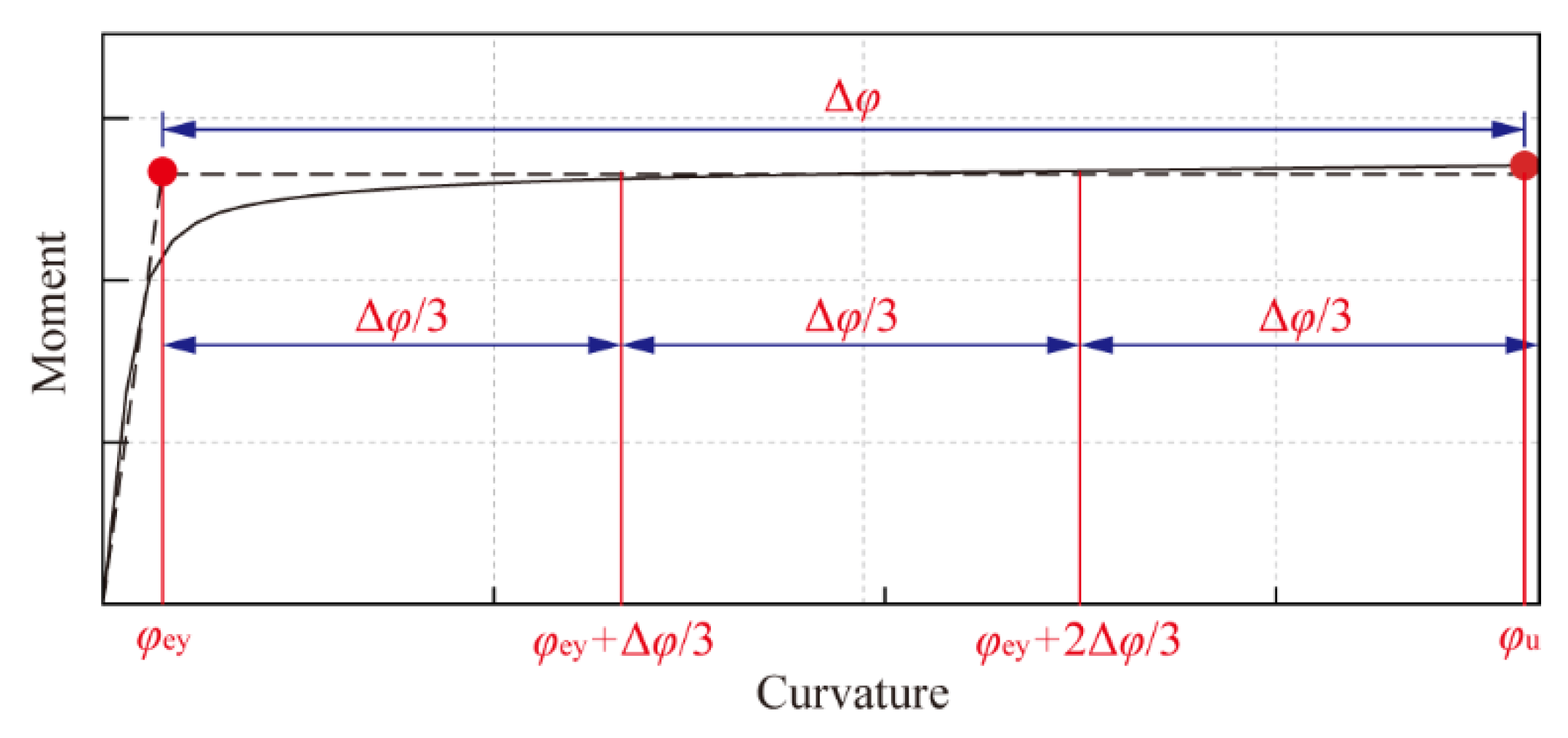
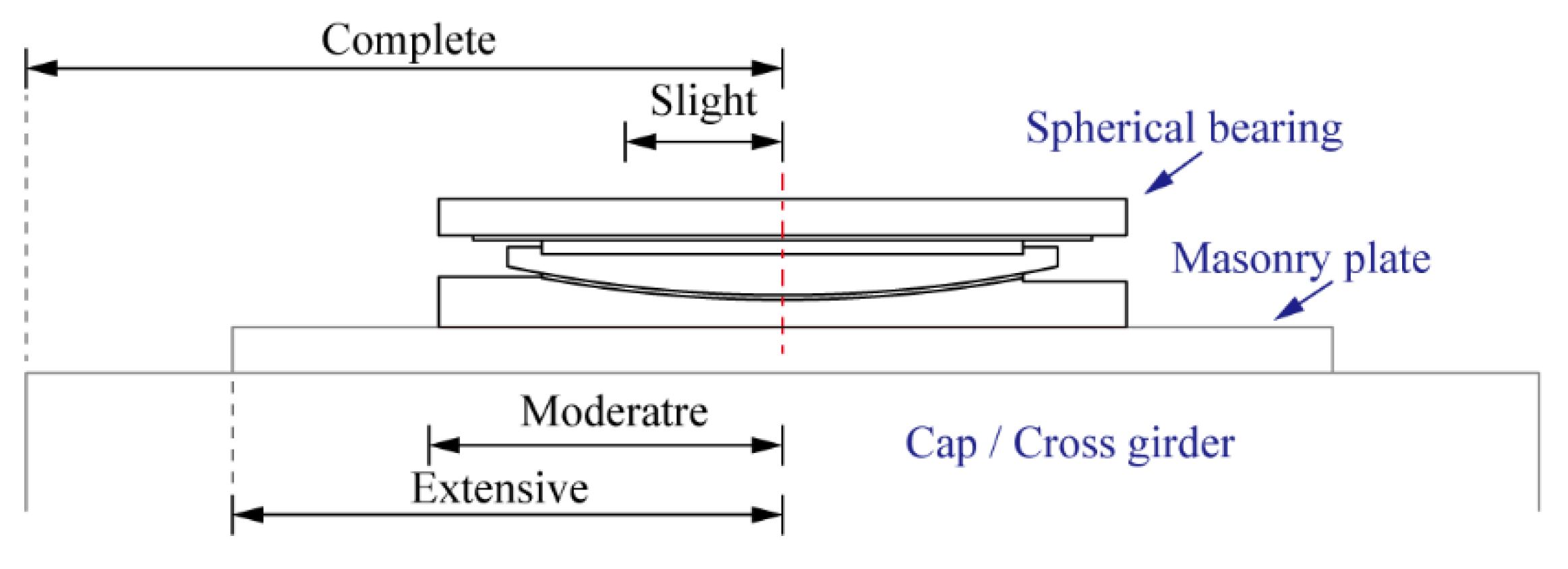
4.4. Definition of the Damage Index
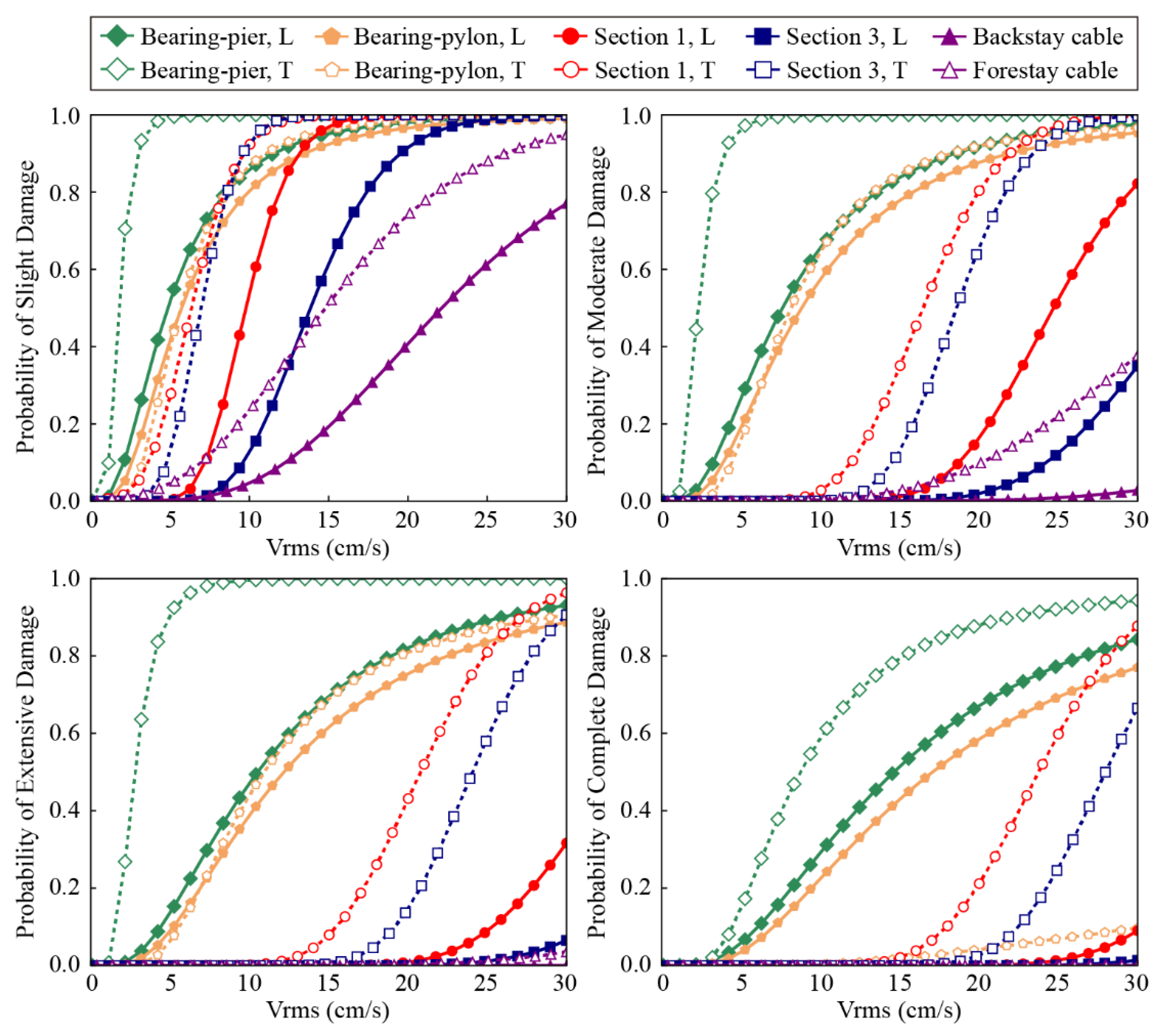
4.5. Component Fragility Curves
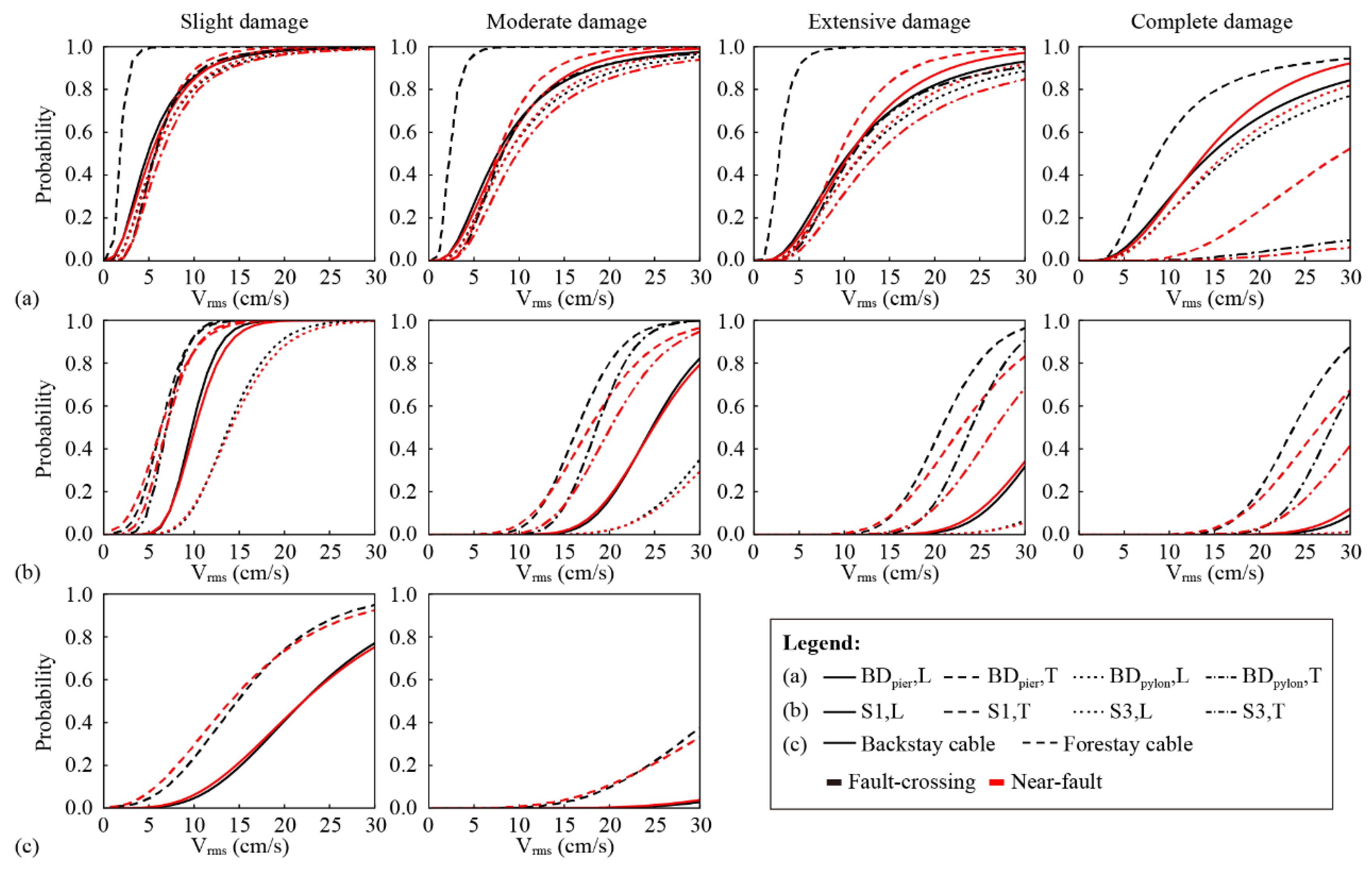
5. Comparison of the Fragility of the Bridge Subjected to Fling-Step and Near-Faults Motions
6. Conclusions
- (1)
- According to the coefficient of determination R2 and the multicriteria decision-making (MCDM) method, the root-mean-square velocity (Vrms) is identified as the optimal IM for the cable-stayed bridge crossing faults.
- (2)
- Bearings are the most fragile components for the fault-crossing bridge, especially in the transverse direction of those on transition piers. The pylon bottom is more vulnerable than the connection zone between the pylon and cross-girder. In contrast, the cables are not likely to suffer severe damage.
- (3)
- Compared with the bridge subjected to near-fault motions, the vulnerability of pylons and bearings of the fault-crossing bridge becomes higher in the transverse direction. However, the vulnerability of the cables is comparable.
- (4)
- This study limits the fragility analysis of cable-stayed bridges subjected to vertical strike-slip faults with a fault crossing angle of 90°. The vulnerability of cable-stayed bridges crossing dip-slip and oblique-slip faults or existing bridges with other fault crossing angles needs further investigation.
Author Contributions
Funding
Conflicts of Interest
References
- Hui, Y.; Wang, K.; Wu, G.; Li, C. Seismic responses of bridges crossing faults and their best crossing angles. J. Vib. Shock 2015, 34, 6–11. (In Chinese) [Google Scholar]
- Yang, S.; Mavroeidis, G.P. Bridges crossing fault rupture zones: A review. Soil Dyn. Earthq. Eng. 2018, 113, 545–571. [Google Scholar] [CrossRef]
- Yang, S.; Mavroeidis, G.P.; Tsopelas, P. Seismic response study of ordinary and isolated bridges crossing strike-slip fault rupture zones. Earthq. Eng. Struct. Dyn. 2021, 50, 2841–2862. [Google Scholar] [CrossRef]
- Park, S.W.; Ghasemi, H.; Shen, J.; Somerville, P.G.; Yen, W.P.; Yashinsky, M. Simulation of the seismic performance of the Bolu Viaduct subjected to near-fault ground motions. Earthq. Eng. Struct. Dyn. 2004, 33, 1249–1270. [Google Scholar] [CrossRef]
- Goel, R.K.; Asce, F.; Chopra, A.K.; Asce, M. Role of Shear Keys in Seismic Behavior of Bridges Crossing Fault-Rupture Zones. J. Bridg. Eng. 2008, 13, 398–408. [Google Scholar] [CrossRef] [Green Version]
- Goel, R.K.; Chopra, A.K. Nonlinear analysis of ordinary bridges crossing fault-rupture zones. J. Bridg. Eng. 2009, 14, 216–224. [Google Scholar] [CrossRef] [Green Version]
- Goel, R.K.; Chopra, A.K. Linear analysis of ordinary bridges crossing fault-rupture zones. J. Bridg. Eng. 2009, 14, 203–215. [Google Scholar] [CrossRef] [Green Version]
- Ucak, A.; Mavroeidis, G.P.; Tsopelas, P. Assessment of Fault Crossing Effects on a Seismically Isolated Multi-Span Bridge. In Proceedings of the 15th World Conference on Earthquake Engineering (15WCEE), Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Ucak, A.; Mavroeidis, G.P.; Tsopelas, P. Behavior of a seismically isolated bridge crossing a fault rupture zone. Soil Dyn. Earthq. Eng. 2014, 57, 164–178. [Google Scholar] [CrossRef]
- Yang, H.; Li, J. Response analysis of seismic isolated bridge under influence of fault-crossing ground motions. J. Tongji Univ. (Nat. Sci.) 2015, 43, 1144–1152. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, F.; Li, S.; Wang, J.; Zhang, J. Effects of fault rupture on seismic responses of fault-crossing simply-supported highway bridges. Eng. Struct. 2020, 206, 110104. [Google Scholar] [CrossRef]
- Sharabash, A.M.; Andrawes, B.O. Application of shape memory alloy dampers in the seismic control of cable-stayed bridges. Eng. Struct. 2009, 31, 607–616. [Google Scholar] [CrossRef]
- Zhong, J.; Jeon, J.-S.; Yuan, W.; DesRoches, R. Impact of Spatial Variability Parameters on Seismic Fragilities of a Cable-Stayed Bridge Subjected to Differential Support Motions. J. Bridg. Eng. 2017, 22, 04017013. [Google Scholar] [CrossRef]
- Zeng, C.; Song, G.; Jiang, H.; Huang, L.; Guo, H.; Ma, X. Nonliear Seismic Response Characteristics of Fault-crossing Single-tower Cable-stayed Bridge. China J. Highw. Transp. 2021, 34, 230–245. (In Chinese) [Google Scholar]
- Gu, Y.; Guo, J.; Dang, X.; Yuan, W. Seismic performance of a cable-stayed bridge crossing strike-slip faults. Structures 2022, 35, 289–302. [Google Scholar] [CrossRef]
- Wu, Y.M.; Wu, C.F. Approximate recovery of coseismic deformation from Taiwan strong-motion records. J. Seismol. 2007, 11, 159–170. [Google Scholar] [CrossRef]
- Iwan, W.D.; Moser, M.A.; Peng, C.-Y. Some observations on strong-motion earthquake measurement using a digital accelerograph. Bull. Seismol. Soc. Am. 1985, 75, 1225–1246. [Google Scholar] [CrossRef]
- Boore, D.M. Effect of baseline corrections on displacements and response spectra for several recordings of the 1999 Chi-Chi, Taiwan, earthquake. Bull. Seismol. Soc. Am. 2001, 91, 1199–1211. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Zong, Z.; Tian, S.; Lin, J. A new baseline correction method for near-fault strong-motion records based on the target final displacement. Soil Dyn. Earthq. Eng. 2018, 114, 27–37. [Google Scholar] [CrossRef]
- Charles, M. An Analytical Model for Near-Fault Ground Motions and the Response of SDOF Systems. In Proceedings of the 7th U.S. National Conference on Earthquake Engineering, Boston, MA, USA, 21–25 July 2002. [Google Scholar]
- Mavroeidis, G.P.; Papageorgiou, A.S. A mathematical representation of near-fault ground motions. Bull. Seismol. Soc. Am. 2003, 93, 1099–1131. [Google Scholar] [CrossRef]
- Makris, N.; Black, C.J. Dimensional Analysis of Rigid-Plastic and Elastoplastic Structures under Pulse-Type Excitations. J. Eng. Mech. 2004, 130, 1006–1018. [Google Scholar] [CrossRef]
- Hoseini Vaez, S.R.; Sharbatdar, M.K.; Ghodrati Amiri, G.; Naderpour, H.; Kheyroddin, A. Dominant pulse simulation of near fault ground motions. Earthq. Eng. Eng. Vib. 2013, 12, 267–278. [Google Scholar] [CrossRef]
- Kamai, R.; Abrahamson, N.; Graves, R. Adding fling effects to processed ground-motion time histories. Bull. Seismol. Soc. Am. 2014, 104, 1914–1929. [Google Scholar] [CrossRef]
- Burks, L.S.; Baker, J.W. A predictive model for fling-step in near-fault ground motions based on recordings and simulations. Soil Dyn. Earthq. Eng. 2016, 80, 119–126. [Google Scholar] [CrossRef]
- Yadav, K.K.; Gupta, V.K. Near-fault fling-step ground motions: Characteristics and simulation. Soil Dyn. Earthq. Eng. 2017, 101, 90–104. [Google Scholar] [CrossRef]
- Hamidi, H.; Khosravi, H.; Soleimani, R. Fling-step ground motions simulation using theoretical-based Green’s function technique for structural analysis. Soil Dyn. Earthq. Eng. 2018, 115, 232–245. [Google Scholar] [CrossRef]
- Yang, S.; Mavroeidis, G.P.; Ucak, A. Analysis of bridge structures crossing strike-slip fault rupture zones: A simple method for generating across-fault seismic ground motions. Earthq. Eng. Struct. Dyn. 2020, 49, 1281–1307. [Google Scholar] [CrossRef]
- Papageorgiou, A.S.; Aki, K. A specific barrier model for the quantitative description of inhomogenous faulting and the prediction of strong ground motion. Bull. Seismol. Soc. Am. 1983, 73, 693–722. [Google Scholar] [CrossRef]
- Rezaeian, S.; Kiureghian, A. Der A stochastic ground motion model with separable temporal and spectral nonstationarities. Earthq. Eng. Struct. Dyn. 2008, 37, 1565–1584. [Google Scholar] [CrossRef]
- Rezaeian, S.; Kiureghian, A. Der Simulation of synthetic ground motions for specified earthquake and site characteristics. Earthq. Eng. Struct. Dyn. 2010, 39, 1155–1180. [Google Scholar] [CrossRef]
- Dabaghi, M.; Der Kiureghian, A. Stochastic Modeling and Simulation of Near-Fault Ground Motions for Performance-Based Earthquake Engineering; University of California: Berkeley, CA, USA, 2014. [Google Scholar]
- Dabaghi, M.; Der Kiureghian, A. Stochastic model for simulation of near-fault ground motions. Earthq. Eng. Struct. Dyn. 2016, 46, 963–984. [Google Scholar] [CrossRef]
- Dabaghi, M.; Der Kiureghian, A. Simulation of orthogonal horizontal components of near-fault ground motion for specified earthquake source and site characteristics. Earthq. Eng. Struct. Dyn. 2018, 47, 1369–1393. [Google Scholar] [CrossRef]
- Pang, Y.; Wu, X.; Shen, G.; Yuan, W. Seismic Fragility Analysis of Cable-Stayed Bridges Considering Different Sources of Uncertainties. J. Bridg. Eng. 2014, 19, 04013015. [Google Scholar] [CrossRef]
- Zhong, J.; Pang, Y.; Jeon, J.S.; Desroches, R.; Yuan, W. Seismic fragility assessment of long-span cable-stayed bridges in China. Adv. Struct. Eng. 2016, 19, 1797–1812. [Google Scholar] [CrossRef]
- Zhong, J.; Jeon, J.S.; Ren, W.X. Risk assessment for a long-span cable-stayed bridge subjected to multiple support excitations. Eng. Struct. 2018, 176, 220–230. [Google Scholar] [CrossRef]
- Zhong, J.; Jeon, J.-S.; Shao, Y.-H.; Chen, L. Optimal Intensity Measures in Probabilistic Seismic Demand Models of Cable-Stayed Bridges Subjected to Pulse-Like Ground Motions. J. Bridg. Eng. 2019, 24, 04018118. [Google Scholar] [CrossRef]
- Wu, W.; Li, L.; Shao, X. Seismic Assessment of Medium-Span Concrete Cable-Stayed Bridges Using the Component and System Fragility Functions. J. Bridg. Eng. 2016, 21, 04016027. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.; Zhang, F. Seismic fragility analyses of long-span cable-stayed bridge isolated by SMA Wire-based Smart Rubber Bearing in near-fault regions. China J. Highw. Transp. 2017, 30, 30–39. (In Chinese) [Google Scholar] [CrossRef]
- Li, C.; Li, H.N.; Hao, H.; Bi, K.; Chen, B. Seismic fragility analyses of sea-crossing cable-stayed bridges subjected to multi-support ground motions on offshore sites. Eng. Struct. 2018, 165, 441–456. [Google Scholar] [CrossRef]
- Wei, B.; Hu, Z.; He, X.; Jiang, L. Evaluation of optimal ground motion intensity measures and seismic fragility analysis of a multi-pylon cable-stayed bridge with super-high piers in Mountainous Areas. Soil Dyn. Earthq. Eng. 2020, 129, 105945. [Google Scholar] [CrossRef]
- Zhu, M.; McKenna, F.; Scott, M.H. OpenSeesPy: Python library for the OpenSees finite element framework. SoftwareX 2018, 7, 6–11. [Google Scholar] [CrossRef]
- Mangalathu, S.; Jeon, J.-S.; Padgett, J.E.; DesRoches, R. Performance-based grouping methods of bridge classes for regional seismic risk assessment: Application of ANOVA, ANCOVA, and non-parametric approaches. Earthq. Eng. Struct. Dyn. 2017, 46, 2587–2602. [Google Scholar] [CrossRef]
- Pan, Y.; Agrawal, A.K.; Ghosn, M. Seismic Fragility of Continuous Steel Highway Bridges in New York State. J. Bridg. Eng. 2007, 12, 689–699. [Google Scholar] [CrossRef]
- Baker, J.W. Quantitative classification of near-fault ground motions using wavelet analysis. Bull. Seismol. Soc. Am. 2007, 97, 1486–1501. [Google Scholar] [CrossRef]
- Somerville, P.G.; Smith, N.F.; Graves, R.W.; Abrahamson, N.A. Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity. Seismol. Res. Lett. 1997, 68, 199–222. [Google Scholar] [CrossRef]
- Abrahamson, N. Velocity pulses in near-fault ground motions. In Proceedings of the UC Berkeley—CUREE Symposium in Honor of Ray Clough and Joseph Penzien, Berkeley, CA, USA, 9–11 May 2002; pp. 40–41. [Google Scholar]
- Guo, J.; Yuan, W.; Dang, X.; Alam, M.S. Cable force optimization of a curved cable-stayed bridge with combined simulated annealing method and cubic B-Spline interpolation curves. Eng. Struct. 2019, 201, 109813. [Google Scholar] [CrossRef]
- Stefanidou, S.P.; Kappos, A.J. Methodology for the development of bridge-specific fragility curves. Earthq. Eng. Struct. Dyn. 2017, 46, 73–93. [Google Scholar] [CrossRef]
- Nielson, B.G.; DesRoches, R. Analytical seismic fragility curves for typical bridges in the central and southeastern United States. Earthq. Spectra 2007, 23, 615–633. [Google Scholar] [CrossRef]
- Wang, X.; Shafieezadeh, A.; Ye, A. Optimal intensity measures for probabilistic seismic demand modeling of extended pile-shaft-supported bridges in liquefied and laterally spreading ground. Bull. Earthq. Eng. 2018, 16, 229–257. [Google Scholar] [CrossRef]
- Dreger, D.; Hurtado, G.; Chopra, A.; Larsen, S. Near-Fault Seismic Ground Motions; Report No. UCB/EERC-2007/03; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2007. [Google Scholar]
- Nuttli, O.W. The Relation of Sustained Maximum Acceleration and Velocity to Earthquake Intensity and Magnitude; Report No. S-73-1; U.S. Army Engineer Waterways Experiment Station: Vicksburg, MI, USA, 1979. [Google Scholar]
- Reed, J.W.; Kassawara, R.P. A criterion for determining exceedance of the operating basis earthquake. Nucl. Eng. Des. 1990, 123, 387–396. [Google Scholar] [CrossRef] [Green Version]
- Arias, A. A Measure of Earthquake Intensity; MIT Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Padgett, J.E.; Nielson, B.G.; Desroches, R. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios. Earthq. Eng. Struct. Dyn. 2008, 37, 711–725. [Google Scholar] [CrossRef]
- Hedayati Dezfuli, F.; Alam, M.S. Multi-criteria optimization and seismic performance assessment of carbon FRP-based elastomeric isolator. Eng. Struct. 2013, 49, 525–540. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, J.; Zhou, Z.; Yan, X.; Xu, L.; Lin, J. Lateral seismic fragility assessment of cable-stayed bridge with diamond-shaped concrete pylons. Shock Vib. 2021, 2021, 2847603. [Google Scholar] [CrossRef]
- Bradley, B.A. Empirical correlations between cumulative absolute velocity and amplitude-based ground motion intensity measures. Earthq. Spectra 2012, 28, 37–54. [Google Scholar] [CrossRef] [Green Version]
- Feng, R.; Yuan, W.; Sextos, A. Probabilistic loss assessment of curved bridges considering the effect of ground motion directionality. Earthq. Eng. Struct. Dyn. 2021, 50, 3623–3645. [Google Scholar] [CrossRef]
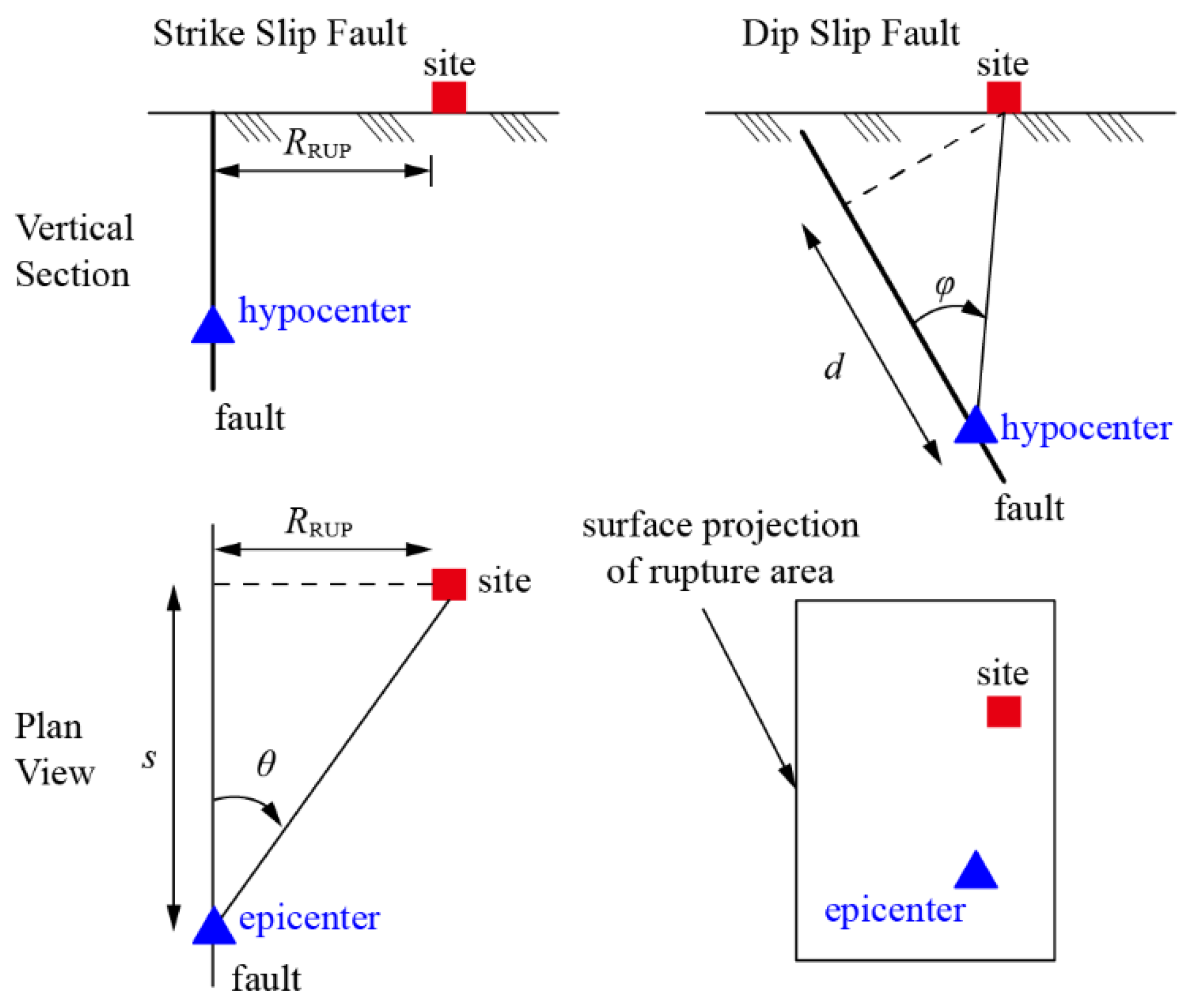



| Model | Predictive Equation | Reference |
|---|---|---|
| MFW model | α, β, c, tmax,q, fmid, f’ = F(F, M, ZTOR, RRUP, Vs30, s, θ) t0,q = 0 | [32,33,34] |
| Directivity pulse model | Vp, Tp, γ, ν, tmax,p = F(F, M, ZTOR, RRUP, Vs30, s, θ) | [32,33,34] |
| Fling model | Vp = 2Dsite/[Tp/(2 + ε)], ε ∈ (0,0.1] log(Tp) = log(2 + ε) − 3.00 + 0.50M, ε ∈ (0,0.1] log(Dsite)avg = −1.70 + 0.50M, (Dsite)max ≈ (Dsite)avg/λ, λ ∈ [0.2,0.8] γ = 1 + ε, ε ∈ (0,0.1] ν ≈ 0 or π t0 ≥ γTp/2 | [28] |
| Variable | Distribution * | Reference |
|---|---|---|
| fc,pylon | Normal (C50, μ = 32.35 MPa, cov = 0.18) | [50] |
| fc,pier | Normal (C40, μ = 26.75 MPa, cov = 0.18) | [50] |
| fy | Lognormal (HRB400, μ = 400 MPa, cov = 0.08) | [51] |
| E | Lognormal (μ = 2 × 108 MPa, cov = 0.033) | [52] |
| b | Lognormal (μ = 0.005, cov = 0.2) | [35,52] |
| R | Uniform (μ = 1, σ = 0.1) | / |
| GM | M | RRUP (km) | Vs30 (m/s) | GM | M | RRUP (km) | Vs30 (m/s) |
|---|---|---|---|---|---|---|---|
| 1 | 6 | 10 | 702 | 14 | 7.3 | 5.1 | 873 |
| 2 | 7 | 18.9 | 446 | 15 | 7.2 | 6.5 | 508 |
| 3 | 7.1 | 5 | 752 | 16 | 7.2 | 8.2 | 524 |
| 4 | 6.7 | 15.1 | 642 | 17 | 7 | 7.9 | 691 |
| 5 | 7.3 | 7.8 | 993 | 18 | 6.7 | 9 | 651 |
| 6 | 7.1 | 5.8 | 954 | 19 | 7.5 | 23.4 | 445 |
| 7 | 6.3 | 14.2 | 691 | 20 | 6 | 15.9 | 588 |
| 8 | 6.9 | 8.2 | 846 | 21 | 6.7 | 10.8 | 630 |
| 9 | 7.1 | 20.3 | 882 | 22 | 7.1 | 8.2 | 675 |
| 10 | 6.1 | 7 | 542 | 23 | 6.3 | 14.3 | 947 |
| 11 | 7.3 | 7.2 | 622 | 24 | 6.9 | 5.8 | 455 |
| 12 | 6.2 | 12.4 | 905 | 25 | 6.9 | 15.1 | 587 |
| 13 | 6.8 | 5.9 | 903 |
| Type | IM | Definition | Reference |
|---|---|---|---|
| Acceleration-related | PGA | Peak ground acceleration , a(t) is the acceleration time history | / |
| SMA | Sustained maximum acceleration third largest peak in a(t) | [54] | |
| CAV | Cumulative absolute velocity , ttot is the total duration | [55] | |
| Ia | Arias intensity , | [56] | |
| Arms | Root-mean-square of acceleration | / | |
| Velocity-related | PGV | Peak ground velocity , v(t) is the velocity–time history | / |
| SMV | Sustained maximum acceleration third largest peak in v(t) | [54] | |
| CAD | Cumulative absolute displacement , ttot is the total duration | [55] | |
| Vrms | Root-mean-square of velocity | / | |
| Iv | Velocity intensity | [57] | |
| Displacement-related | PGD | Peak ground displacement , d(t) is the displacement–time history | / |
| Drms | Root-mean-square of displacement | / |
| Attribute Evaluation | Value |
|---|---|
| Extremely unimportant | 0 |
| Very unimportant | 1 |
| Unimportant | 3 |
| Average | 5 |
| Important | 7 |
| Very important | 9 |
| Extremely important | 10 |
| Weight of Criteria | Rank of the Optimal IMs | ||||
|---|---|---|---|---|---|
| Pylons | Cables | Bearings | 1st | 2nd | 3rd |
| 10 | 10 | 7 | Vrms | Iv | PGV |
| 10 | 10 | 5 | Vrms | Iv | PGV |
| 10 | 10 | 3 | Vrms | Iv | PGV |
| EDP | Longitudinal | EDP | Transverse | EDP | / | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | a | b | c | a | b | c | |||
| σb,pier | −0.022 | 0.979 | −2.696 | σb,pier | −0.196 | 1.864 | −2.202 | Fbc | 0.035 | 0.065 | 8.522 |
| σb,pylon | −0.059 | 1.165 | −3.054 | σb,pylon | −0.203 | 1.883 | −3.856 | Ffc | 0.065 | −0.038 | 8.652 |
| φS1 | 0.099 | 1.408 | −11.050 | φS1 | 0.471 | −0.058 | −8.963 | ||||
| φS3 | 0.183 | 1.091 | −10.791 | φS3 | 0.326 | 0.408 | −9.252 | ||||
| EDP | Slight | Moderate | Extensive | Complete | ||||
|---|---|---|---|---|---|---|---|---|
| SC | βC | SC | βC | SC | βC | SC | βC | |
| φS1, longitudinal | 1 | 0.04 | 6.1 | 0.05 | 11.2 | 0.05 | 16.3 | 0.06 |
| φS1, transverse | 1 | 0.04 | 7.6 | 0.04 | 14.3 | 0.04 | 20.9 | 0.04 |
| φS3, longitudinal | 1 | 0.15 | 6.7 | 0.06 | 12.5 | 0.06 | 18.2 | 0.06 |
| φS3, transverse | 1 | 0.13 | 7.1 | 0.04 | 13.2 | 0.04 | 19.3 | 0.04 |
| σb, longitudinal (mm) | 300 | 0.35 | 450 | 0.35 | 600 | 0.35 | 800 | 0.35 |
| σb, transverse (mm) | 300 | 0.35 | 450 | 0.35 | 600 | 0.35 | 2500 | 0.35 |
| Fbc (kN) | 8586 | 0.10 | 11,785 | 0.10 | 14,987 | 0.10 | 18,188 | 0.10 |
| Ffc (kN) | 8279 | 0.10 | 11,196 | 0.10 | 14,114 | 0.10 | 17,031 | 0.10 |
| EDP | Slight | Moderate | Extensive | Complete | ||||
|---|---|---|---|---|---|---|---|---|
| FC | NF | FC | NF | FC | NF | FC | NF | |
| σb,pier, longitudial | 4.86 | 5.24 | 7.62 | 8.00 | 10.56 | 10.63 | 14.71 | 13.95 |
| σb,pier, transverse | 1.77 | 5.70 | 2.28 | 7.63 | 2.76 | 9.43 | 8.73 | 29.02 |
| σb,pylon, longitudial | 5.71 | 5.75 | 8.81 | 8.76 | 12.17 | 11.90 | 17.08 | 16.27 |
| σb,pylon, transverse | 5.65 | 6.37 | 8.15 | 9.76 | 10.97 | 13.62 | / | / |
| φS1, longitudial | 9.77 | 10.12 | 24.67 | 24.88 | 33.08 | 32.93 | 39.49 | 38.97 |
| φS1, transverse | 6.34 | 6.33 | 16.45 | 17.80 | 20.76 | 22.91 | 23.72 | 26.49 |
| φS3, longitudial | 13.85 | 14.12 | 32.82 | 34.64 | 42.35 | 45.30 | 49.31 | 53.18 |
| φS3, transverse | 6.96 | 6.96 | 18.61 | 20.13 | 24.10 | 26.75 | 28.00 | 31.57 |
| Fbc | 22.04 | 21.73 | 59.95 | 59.08 | / | / | / | / |
| Ffc | 14.80 | 14.02 | 33.76 | 36.57 | / | / | / | / |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Gu, Y.; Wu, W.; Chu, S.; Dang, X. Seismic Fragility Assessment of Cable-Stayed Bridges Crossing Fault Rupture Zones. Buildings 2022, 12, 1045. https://doi.org/10.3390/buildings12071045
Guo J, Gu Y, Wu W, Chu S, Dang X. Seismic Fragility Assessment of Cable-Stayed Bridges Crossing Fault Rupture Zones. Buildings. 2022; 12(7):1045. https://doi.org/10.3390/buildings12071045
Chicago/Turabian StyleGuo, Junjun, Yitong Gu, Weihong Wu, Shihyu Chu, and Xinzhi Dang. 2022. "Seismic Fragility Assessment of Cable-Stayed Bridges Crossing Fault Rupture Zones" Buildings 12, no. 7: 1045. https://doi.org/10.3390/buildings12071045
APA StyleGuo, J., Gu, Y., Wu, W., Chu, S., & Dang, X. (2022). Seismic Fragility Assessment of Cable-Stayed Bridges Crossing Fault Rupture Zones. Buildings, 12(7), 1045. https://doi.org/10.3390/buildings12071045






