Influence of Morphology Characteristics on Shear Mechanical Properties of Sawtooth Joints
Abstract
:1. Introduction
2. Specimen Preparation and Test Scheme
3. Test Results and Analysis
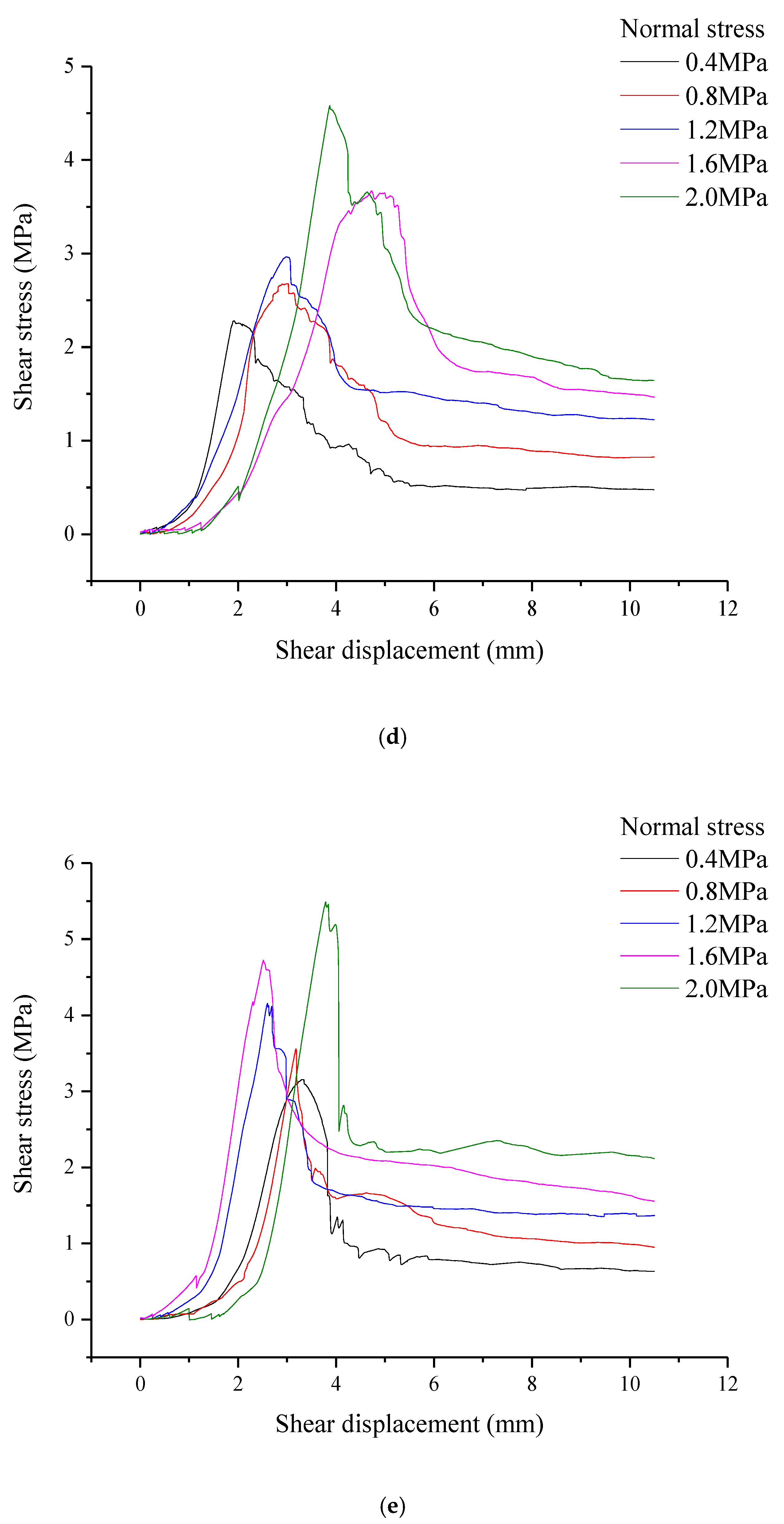
3.1. Shear Stress–Shear Displacement Curve
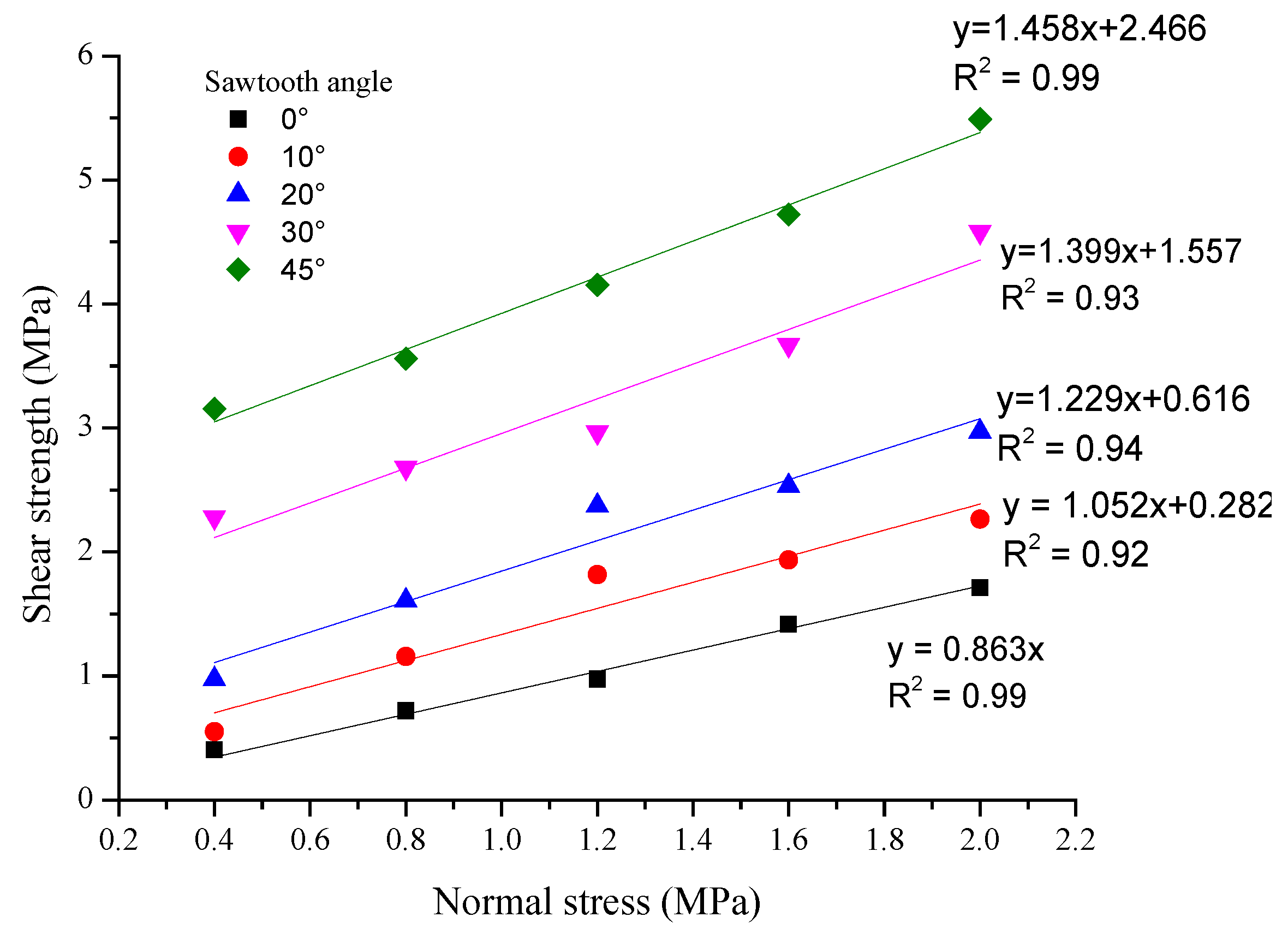
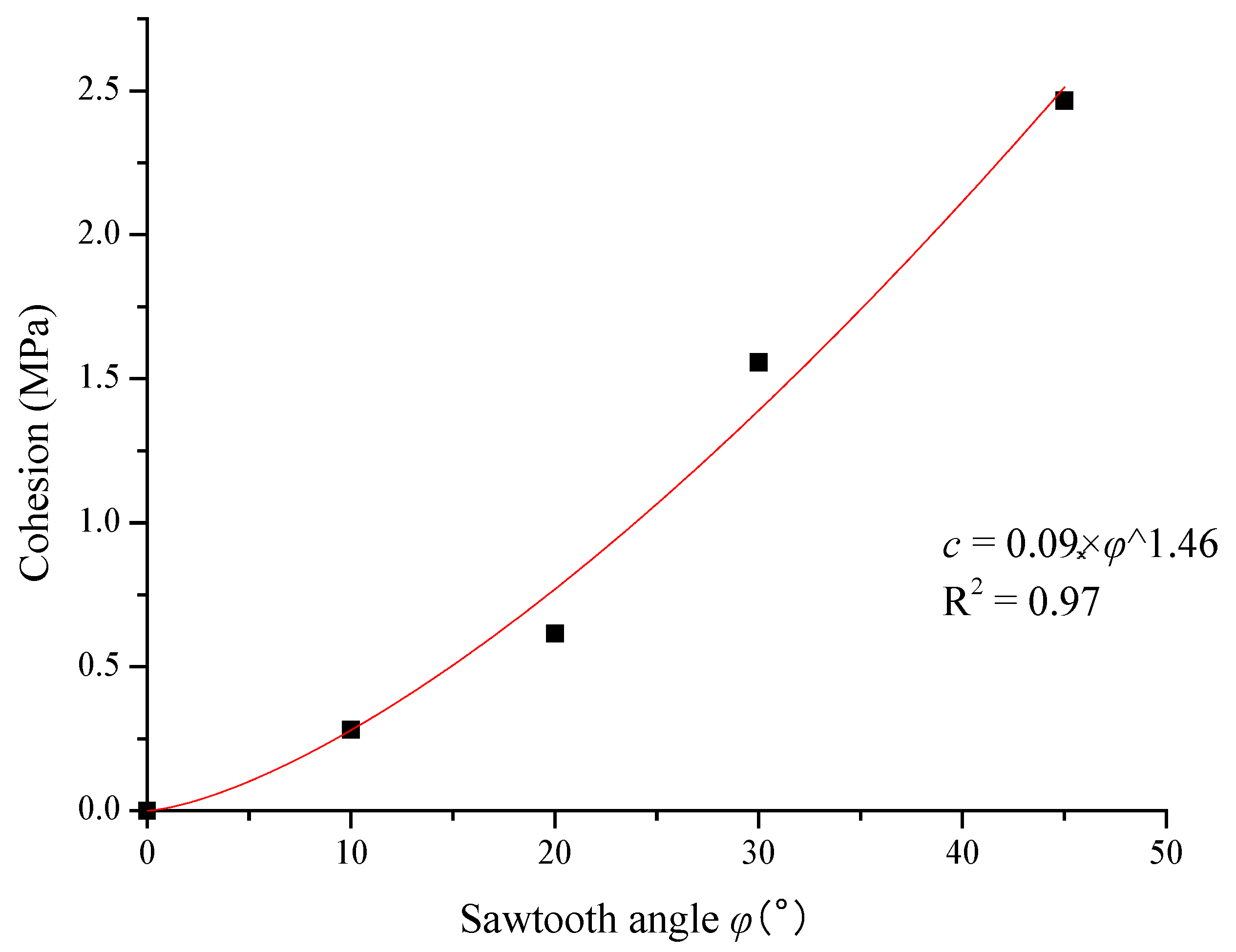
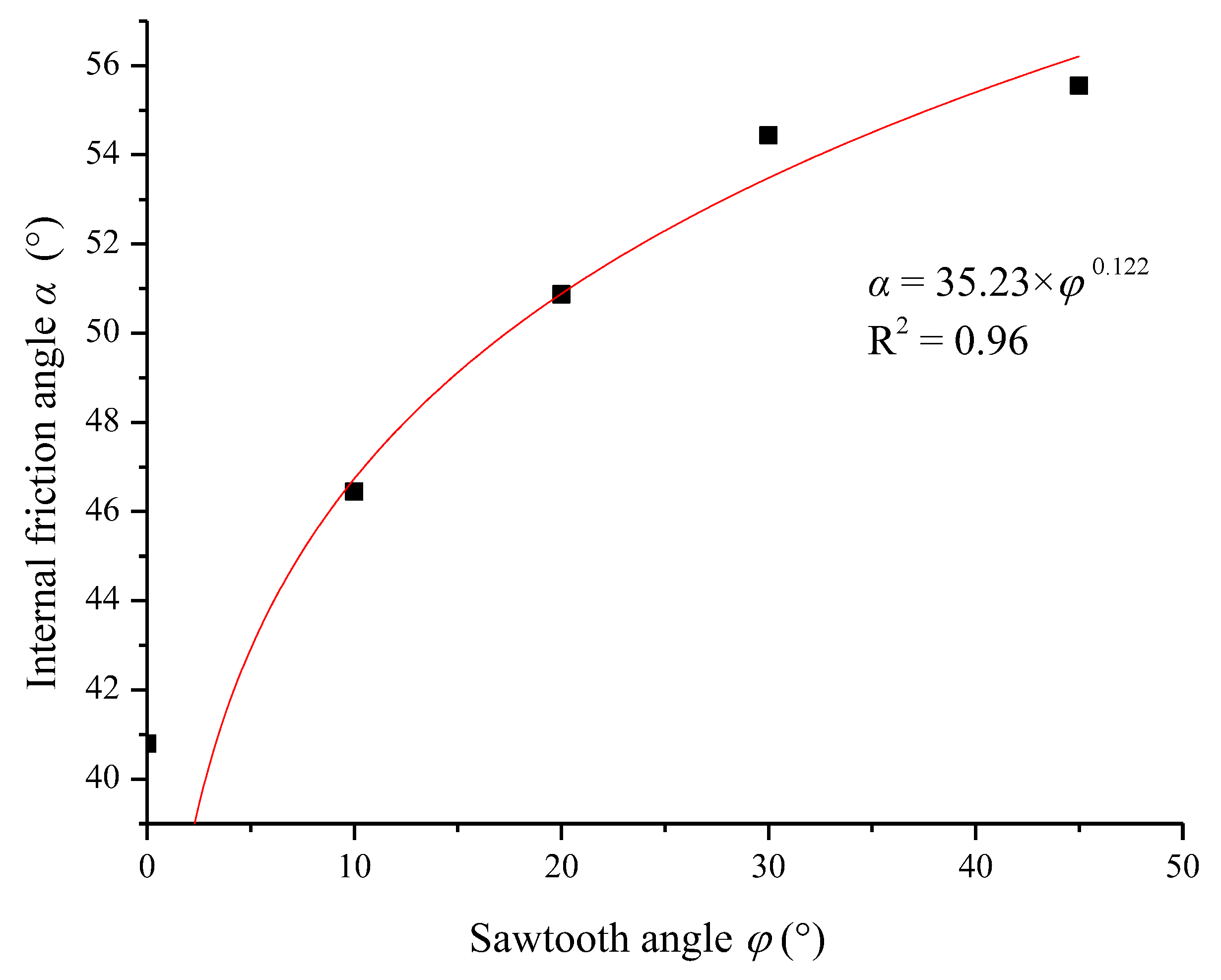
3.2. Shear Characteristics Analysis Based on Mohr–Coulomb Criterion
3.3. Empirical Equation for Shear Strength of Joints
3.4. Analysis of Failure Mechanism
4. Conclusions
- (1)
- The shear stress under each sawtooth angle increased with increasing shear displacement. When the sawtooth angle of the joints was small, there was not a significant decrease between the shear strength and the residual shear strength, and the size of the drop was also smaller. The peak shear displacement showed a trend of first increasing and then decreasing with increasing normal stress, but the normal stress corresponding to the transition at different sawtooth angles was different.
- (2)
- The shear strength of joints at each sawtooth angle increased with the increase of the normal stress. The Mohr–Coulomb criterion was used to analyze the shear strength of the joints. It was found that the cohesion c and the internal friction angle α both increased nonlinearly with increasing sawtooth angle, but the increasing trend was different.
- (3)
- By introducing the function relation between cohesion and the internal friction angle and sawtooth angle into the shear strength formula of joints, an empirical equation for shear strength considering sawtooth angle was established.
- (4)
- The shear failure of sawtooth joints can be divided into two modes: the “saw-toothed sliding gnawing failure mechanism” (SSG) and the “tensile fracture mechanism” (TFM). With increasing sawtooth angle and normal stress, the shear failure mode ranges from slipping to slip gnawing to complete gnawing. The tensile fracture mechanism mainly occurs at high sawtooth angles.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ghazvinian, A.H.; Azinfar, M.J.; Vaneghi, R.G. Importance of Tensile Strength on the Shear Behavior of Discontinuities. Rock Mech. Rock Eng. 2012, 45, 349–359. [Google Scholar] [CrossRef]
- Lin, H.; Sun, P.H.; Chen, Y.F.; Zhu, Y.Y.; Fan, X.; Zhao, Y.L. Analytical and experimental analysis of the shear strength of bolted saw-tooth joints. Eur. J. Environ. Civ. Eng. 2022, 26, 1639–1653. [Google Scholar] [CrossRef]
- Du, S.-G.; Lin, H.; Yong, R.; Liu, G.-J. Characterization of Joint Roughness Heterogeneity and Its Application in Representative Sample Investigations. Rock Mech. Rock Eng. 2022, 55, 1–25. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, C.; Wang, Y.; Lin, H. Shear-related roughness classification and strength model of natural rock joint based on fuzzy comprehensive evaluation. Int. J. Rock Mech. Min. Sci. 2021, 137, 104550. [Google Scholar] [CrossRef]
- Antronico, L.; Borrelli, L.; Coscarelli, R.; Gulla, G. Time evolution of landslide damages to buildings: The case study of Lungro (Calabria, southern Italy). Bull. Eng. Geol. Environ. 2015, 74, 47–59. [Google Scholar] [CrossRef]
- Luo, H.Y.; Zhang, L.M.; Wang, H.J.; He, J. Process of building collapse caused by the Po Shan Road landslide in Hong Kong on 18 June 1972. Landslides 2021, 18, 3769–3780. [Google Scholar] [CrossRef]
- Parisi, F.; Sabella, G. Flow-type landslide fragility of reinforced concrete framed buildings. Eng. Struct. 2017, 131, 28–43. [Google Scholar] [CrossRef]
- Du, S.-G.; Saroglou, C.; Chen, Y.; Lin, H.; Yong, R. A new approach for evaluation of slope stability in large open-pit mines: A case study at the Dexing Copper Mine, China. Environ. Earth Sci. 2022, 81, 102. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Q.; Zhang, C.; Liao, J.; Lin, H.; Wang, Y. Coupled seepage-damage effect in fractured rock masses: Model development and a case study. Int. J. Rock Mech. Min. Sci. 2021, 144, 104822. [Google Scholar] [CrossRef]
- Wang, F.; Cao, P.; Cao, R.; Gao, Q.; Xiong, X.; Wang, Z. Influence of parallel joint interaction on mechanical behavior of jointed rock mass. J. Central South Univ. 2018, 49, 2498–2507. [Google Scholar]
- Liu, J.; Zhao, Y.; Tan, T.; Zhang, L.; Zhu, S.; Xu, F. Evolution and modeling of mine water inflow and hazard characteristics in southern coalfields of China: A case of Meitanba mine. Int. J. Min. Sci. Technol. 2022, 32, 513–524. [Google Scholar] [CrossRef]
- Kazerani, T.; Yang, Z.Y.; Zhao, J. A Discrete Element Model for Predicting Shear Strength and Degradation of Rock Joint by Using Compressive and Tensile Test Data. Rock Mech. Rock Eng. 2012, 45, 695–709. [Google Scholar] [CrossRef] [Green Version]
- Lei, D.; Lin, H.; Wang, Y. Damage characteristics of shear strength of joints under freeze–thaw cycles. Arch. Appl. Mech. 2022, 92, 1615–1631. [Google Scholar] [CrossRef]
- Fan, X.; Yang, Z.; Li, K. Effects of the lining structure on mechanical and fracturing behaviors of four-arc shaped tunnels in a jointed rock mass under uniaxial compression. Theor. Appl. Fract. Mech. 2021, 112, 102887. [Google Scholar] [CrossRef]
- Huang, C.C.; Yang, W.D.; Duan, K.; Fang, L.D.; Wang, L.; Bo, C.J. Mechanical behaviors of the brittle rock-like specimens with multi-non-persistent joints under uniaxial compression. Constr. Build. Mater. 2019, 220, 426–443. [Google Scholar] [CrossRef]
- Jang, H.S.; Jang, B.A. New Method for Shear Strength Determination of Unfilled, Unweathered Rock Joint. Rock Mech. Rock Eng. 2015, 48, 1515–1534. [Google Scholar] [CrossRef]
- Oh, J.; Li, Y.; Mitra, R.; Canbulat, I. A Numerical Study on Dilation of a Saw-Toothed Rock Joint Under Direct Shear. Rock Mech. Rock Eng. 2017, 50, 913–925. [Google Scholar] [CrossRef]
- Xie, S.; Lin, H.; Cheng, C.; Chen, Y.; Wang, Y.; Zhao, Y.; Yong, W. Shear strength model of joints based on Gaussian smoothing method and macro-micro roughness. Comput. Geotech. 2022, 143, 104605. [Google Scholar] [CrossRef]
- Barton, N.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. Rock Eng. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Li, K.-H.; Cao, P.; Zhang, K.; Zhong, Y.-F. Macro and meso characteristics evolution on shear behavior of rock joints. J. Central South Univ. 2015, 22, 3087–3096. [Google Scholar] [CrossRef]
- Shi, J.C.; Li, J.C.; Li, X.; He, L. Effect of joint surface roughness on normal stiffness and morphology in rock masses under cyclic impact. J. Central South Univ. 2021, 52, 2661–2668. [Google Scholar] [CrossRef]
- Lee, Y.K.; Park, J.W.; Song, J.J. Model for the shear behavior of rock joints under CNL and CNS conditions. Int. J. Rock. Mach. Min. Sci. 2014, 70, 252–263. [Google Scholar] [CrossRef]
- Singh, H.K.; Basu, A. Evaluation of existing criteria in estimating shear strength of natural rock discontinuities. Eng. Geol. 2018, 232, 171–181. [Google Scholar] [CrossRef]
- Xia, C.C.; Tang, Z.C.; Xiao, W.M.; Song, Y.L. New Peak Shear Strength Criterion of Rock Joints Based on Quantified Surface Description. Rock Mech. Rock Eng. 2014, 47, 387–400. [Google Scholar] [CrossRef]
- Sanei, M.; Faramarzi, L.; Fahimifar, A.; Goli, S.; Mehinrad, A.; Rahmati, A. Shear strength of discontinuities in sedimentary rock masses based on direct shear tests. Int. J. Rock. Mach. Min. Sci. 2015, 75, 119–131. [Google Scholar] [CrossRef]
- Li, S.; Lin, H.; Feng, J.; Cao, R.; Hu, H. Mechanical Properties and Acoustic Emission Characteristics of Anchored Structure Plane with Different JRC under Direct Shear Test. Materials 2022, 15, 4169. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, H.; Xie, S.; Ding, X.; He, D.; Yong, W.; Gao, F. Effect of joint microcharacteristics on macroshear behavior of single-bolted rock joints by the numerical modelling with PFC. Environ. Earth Sci. 2022, 81, 276. [Google Scholar] [CrossRef]
- Tang, Z.C.; Zhang, Q.Z.; Peng, J.; Jiao, Y.Y. Experimental study on the water-weakening shear behaviors of sandstone joints collected from the middle region of Yunnan province, P.R. China. Eng. Geol. 2019, 258, 105161. [Google Scholar] [CrossRef]
- Kong, W.; Li, Y.; Nie, L.; Dong, Z.; Cai, W.; Wang, Z.; Wang, K. Experimental and numerical investigations on crack propagation characteristics of rock-like specimens with preexisting flaws subjected to combined actions of internal hydraulic pressure and shear force. Arch. Appl. Mech. 2022, 92, 221–239. [Google Scholar] [CrossRef]
- Zhao, Y.; Chang, L.; Wang, Y.; Lin, H.; Liao, J.; Liu, Q. Dynamic response of cylindrical thick-walled granite specimen with clay infilling subjected to dynamic loading. Arch. Appl. Mech. 2022, 92, 643–648. [Google Scholar] [CrossRef]
- Shen, Y.; Yang, H.; Xi, J.; Yang, Y.; Yongzhi, W.; Wei, X. A novel shearing fracture morphology method to assess the influence of freeze–thaw actions on concrete–granite interface. Cold Reg. Sci. Technol. 2019, 169, 102900. [Google Scholar] [CrossRef]
- Fan, X.; Yu, H.; Deng, Z.; He, Z.; Zhao, Y. Cracking and deformation of cuboidal sandstone with a single nonpenetrating flaw under uniaxial compression. Theor. Appl. Fract. Mech. 2022, 119, 103284. [Google Scholar] [CrossRef]
- Xie, S.J.; Lin, H.; Chen, Y.F.; Wang, Y.X. A new nonlinear empirical strength criterion for rocks under conventional triaxial compression. J. Central South Univ. 2021, 28, 1448–1458. [Google Scholar] [CrossRef]
- Tang, W.; Lin, H.; Chen, Y.; Feng, J.; Hu, H. Mechanical Characteristics and Acoustic Emission Characteristics of Mortar-Rock Binary Medium. Buildings 2022, 12, 665. [Google Scholar] [CrossRef]
- Liu, B.; Lin, H.; Chen, Y. Deformation Characteristics of Bolted Rock Joints under Compression-Shear Load. Appl. Sci. 2022, 12, 5226. [Google Scholar] [CrossRef]
- Zhou, K.; Liu, C.; Li, S.; Cheng, Y. Size Effect on the Rheological Shear Mechanical Behaviors of Different Joints: A Numerical Study. Geofluids 2022, 2022, 7484209. [Google Scholar] [CrossRef]
- Han, L.; Lin, H.; Chen, Y.; Lei, D. Effects of strength property difference on shear strength of joint of binary media. Environ. Earth Sci. 2021, 80, 1–10. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Ruan, H.; Ke, B.; Lin, H. The strain characteristics and corresponding model of rock materials under uniaxial cyclic load/unload compression and their deformation and fatigue damage analysis. Arch. Appl. Mech. 2021, 91, 2481–2496. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Jiang, T. The propagation mechanism of an oblique straight crack in a rock sample and the effect of osmotic pressure under in-plane biaxial compression. Arab. J. Geosci. 2020, 13, 736. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, H.; Cao, R.; Zhang, C. Slope Stability Analysis Considering Different Contributions of Shear Strength Parameters. Int. J. Geomech. 2021, 21, 04020265. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, L.; Wang, W.; Liu, Q.; Tang, L.; Cheng, G. Experimental Study on Shear Behavior and a Revised Shear Strength Model for Infilled Rock Joints. Int. J. Geomech. 2020, 20, 0402014. [Google Scholar] [CrossRef]







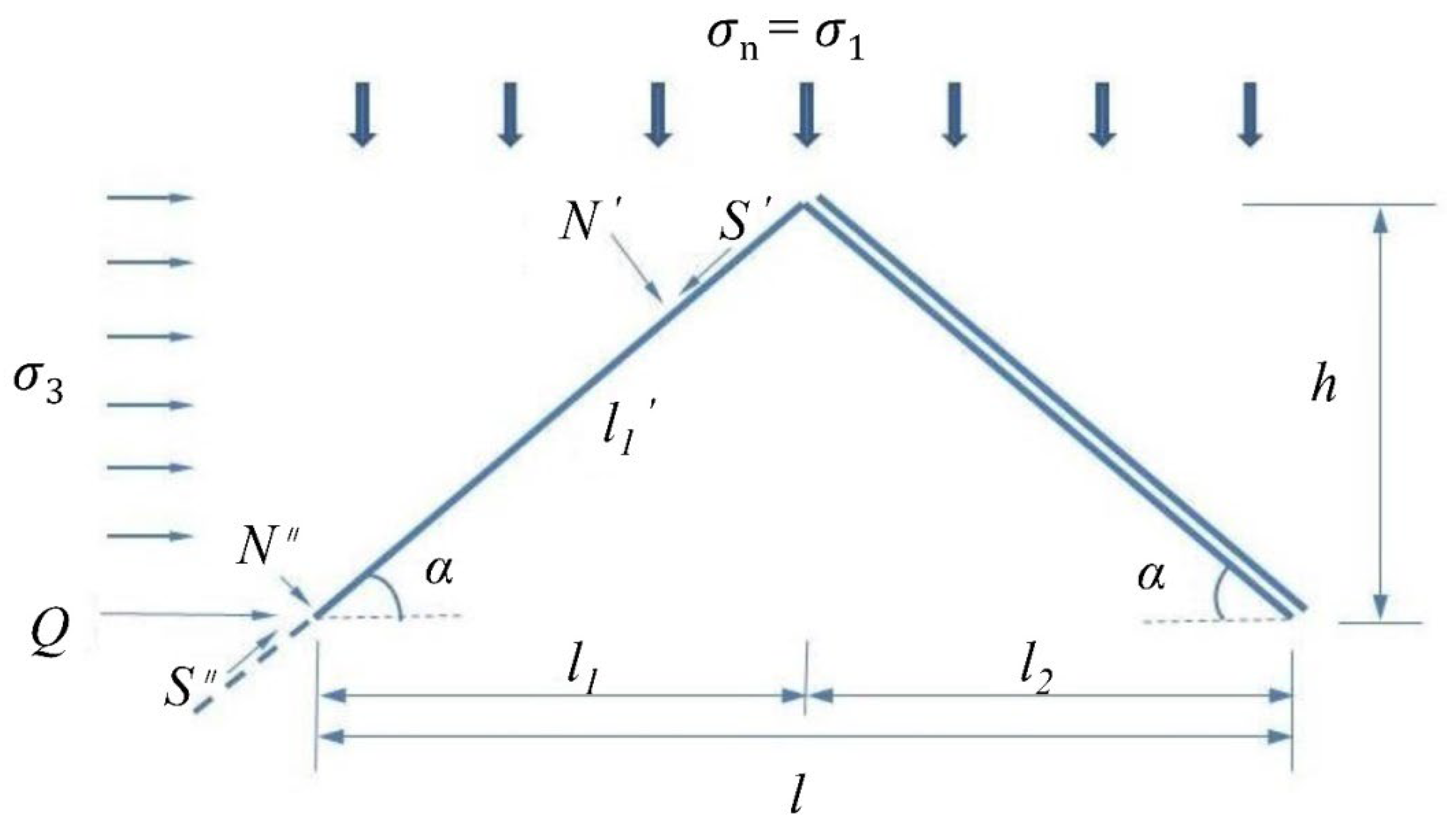

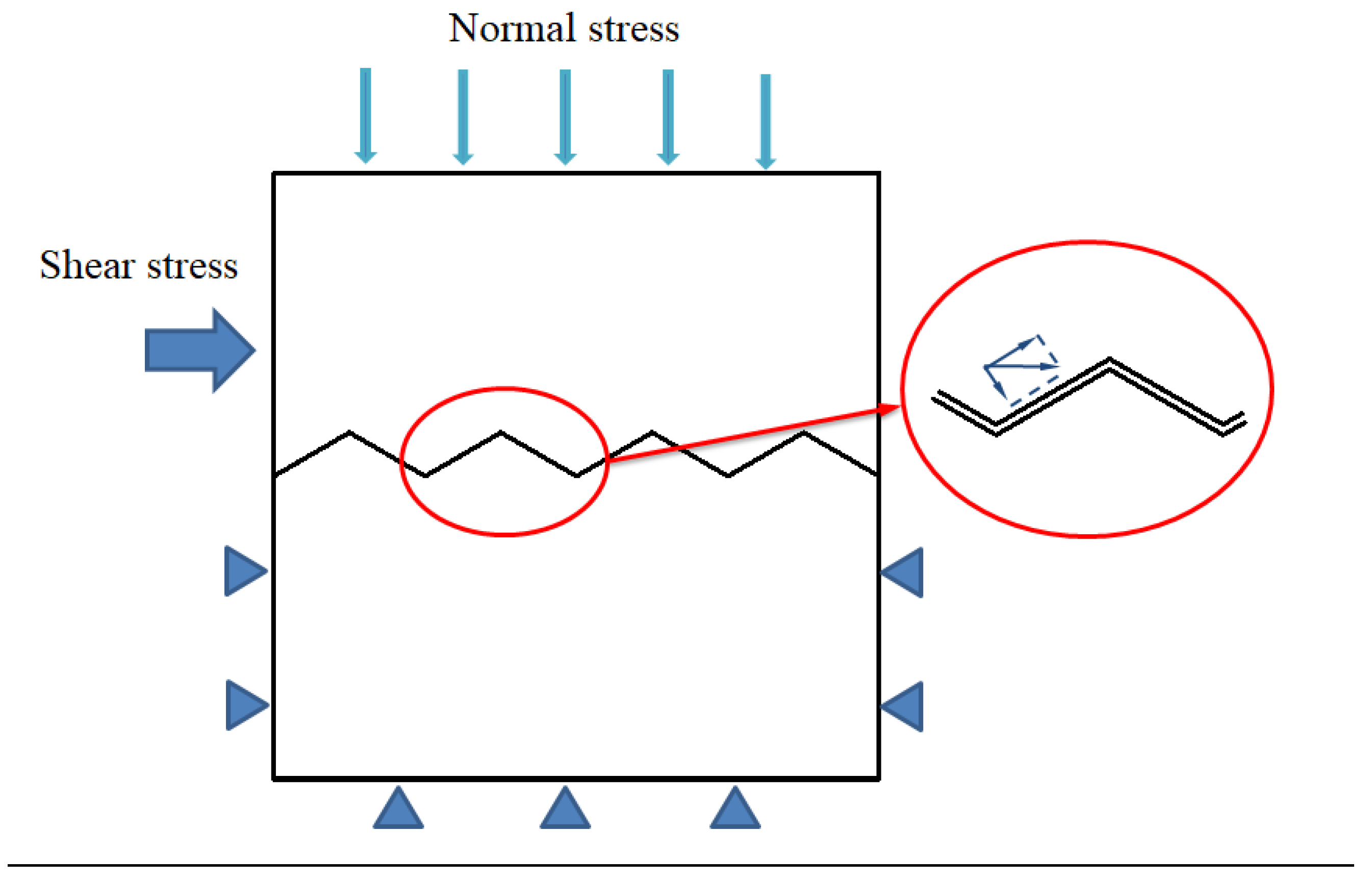
| Sawtooth Angle/° | Normal Stress/MPa | Loading Rate | Number of Samples |
|---|---|---|---|
| 0 | 0.4, 0.8, 1.2, 1.6, 2.0 | 1 mm/min | 15 |
| 10 | 15 | ||
| 20 | 15 | ||
| 30 | 15 | ||
| 45 | 15 |
| Sawtooth Angle φ (°) | Cohesion c (Mpa) | Internal Friction Angle α (°) |
|---|---|---|
| 0 | 0 | 40.79 |
| 10 | 0.282 | 46.45 |
| 20 | 0.616 | 50.87 |
| 30 | 1.557 | 54.44 |
| 45 | 2.466 | 55.55 |
| Sawtooth Angle (°) | Normal Stress (MPa) | ||||
|---|---|---|---|---|---|
| 0.4 | 0.8 | 1.2 | 1.6 | 2.0 | |
| 10 | Slipping | Slip gnawing | |||
| 20 | Slipping | Slip gnawing | |||
| 30 | Slip gnawing | Complete gnawing | |||
| 45 | Slip gnawing | Complete gnawing | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Zhang, X.; Qin, J.; Lin, H. Influence of Morphology Characteristics on Shear Mechanical Properties of Sawtooth Joints. Buildings 2022, 12, 886. https://doi.org/10.3390/buildings12070886
Hu H, Zhang X, Qin J, Lin H. Influence of Morphology Characteristics on Shear Mechanical Properties of Sawtooth Joints. Buildings. 2022; 12(7):886. https://doi.org/10.3390/buildings12070886
Chicago/Turabian StyleHu, Huihua, Xing Zhang, Jianxin Qin, and Hang Lin. 2022. "Influence of Morphology Characteristics on Shear Mechanical Properties of Sawtooth Joints" Buildings 12, no. 7: 886. https://doi.org/10.3390/buildings12070886
APA StyleHu, H., Zhang, X., Qin, J., & Lin, H. (2022). Influence of Morphology Characteristics on Shear Mechanical Properties of Sawtooth Joints. Buildings, 12(7), 886. https://doi.org/10.3390/buildings12070886







