Plastic Deformation Analysis of a New Mega-Subcontrolled Structural System (MSCSS) Subjected to Seismic Excitation
Abstract
:1. Introduction
2. Scope
3. Generation of Ground Motion
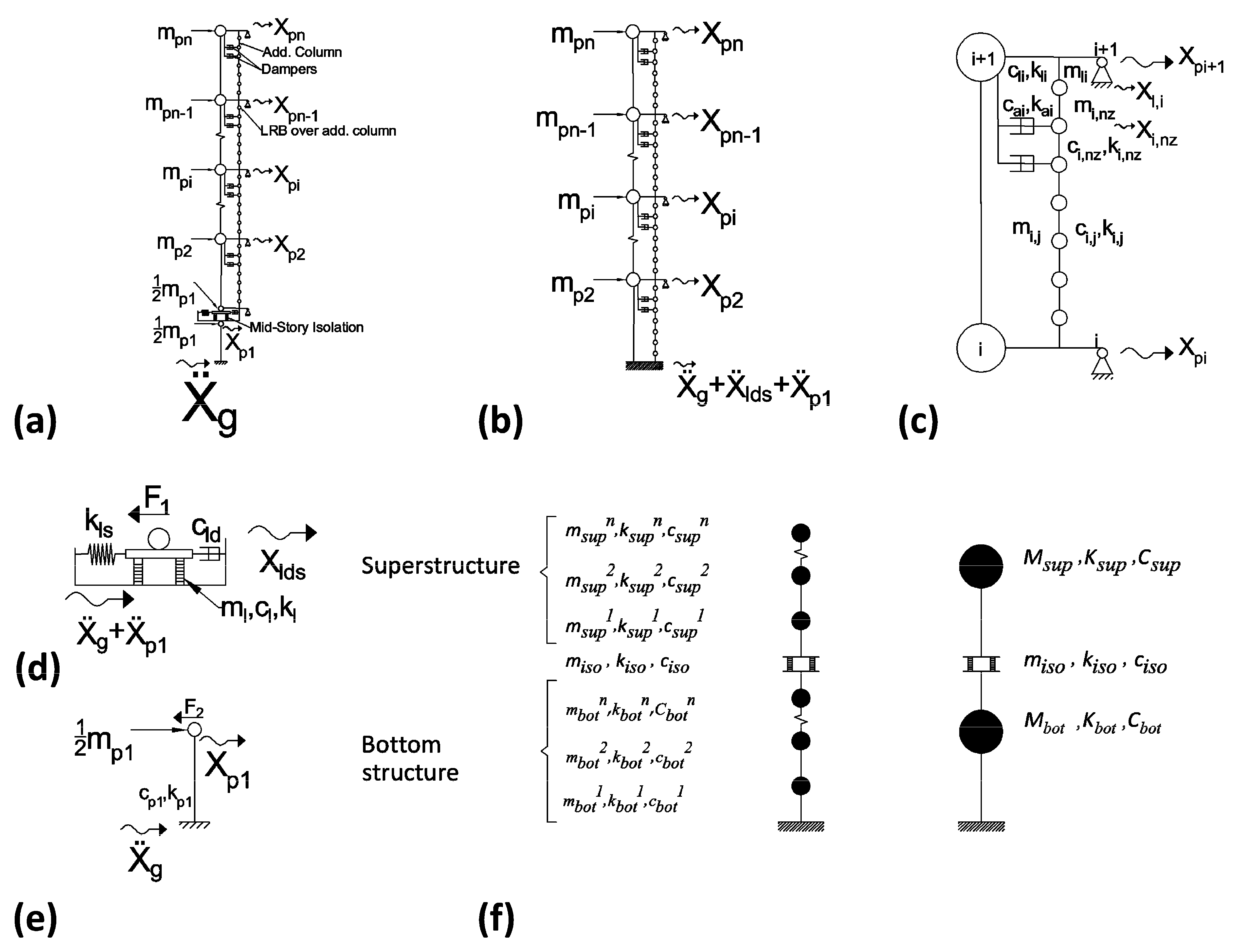
4. Computation Model
- The mass matrix MTPS in Equation (1) can be expressed as:where MP, Ms, and Msi are diagonal mass matrices of super mega-structure, substructures, and ith substructure, respectively. Mass of shear wall infill panels at the at jth floor of ith substructure is represented by .
- The damping matrix CTPS of the superstructure in Equation (1) can be expressed as:where Cp and Cs are damping matrices of the super mega-structure and substructures. The [(n − 1)] × [(n − 1) (nz + 1)] matrix Cc in Equation (3) is the coupling damping matrix between the super mega-structure and substructures. Cli is damping coefficient of LRB placed over additional column of ith substructure and adCi is damping coefficient of additional column of ith substructure. It can be expressed as:
- The stiffness matrix KTPS of the superstructure in Equation (1) can be expressed as:where Kp and Ks are stiffness matrices of the super mega-structure and substructures. The [(n − 1)] × [(n − 1) (nz + 1)] matrix Kc in Equation (5) is the coupling damping matrix between the super mega-structure and substructures. It can be expressed as:
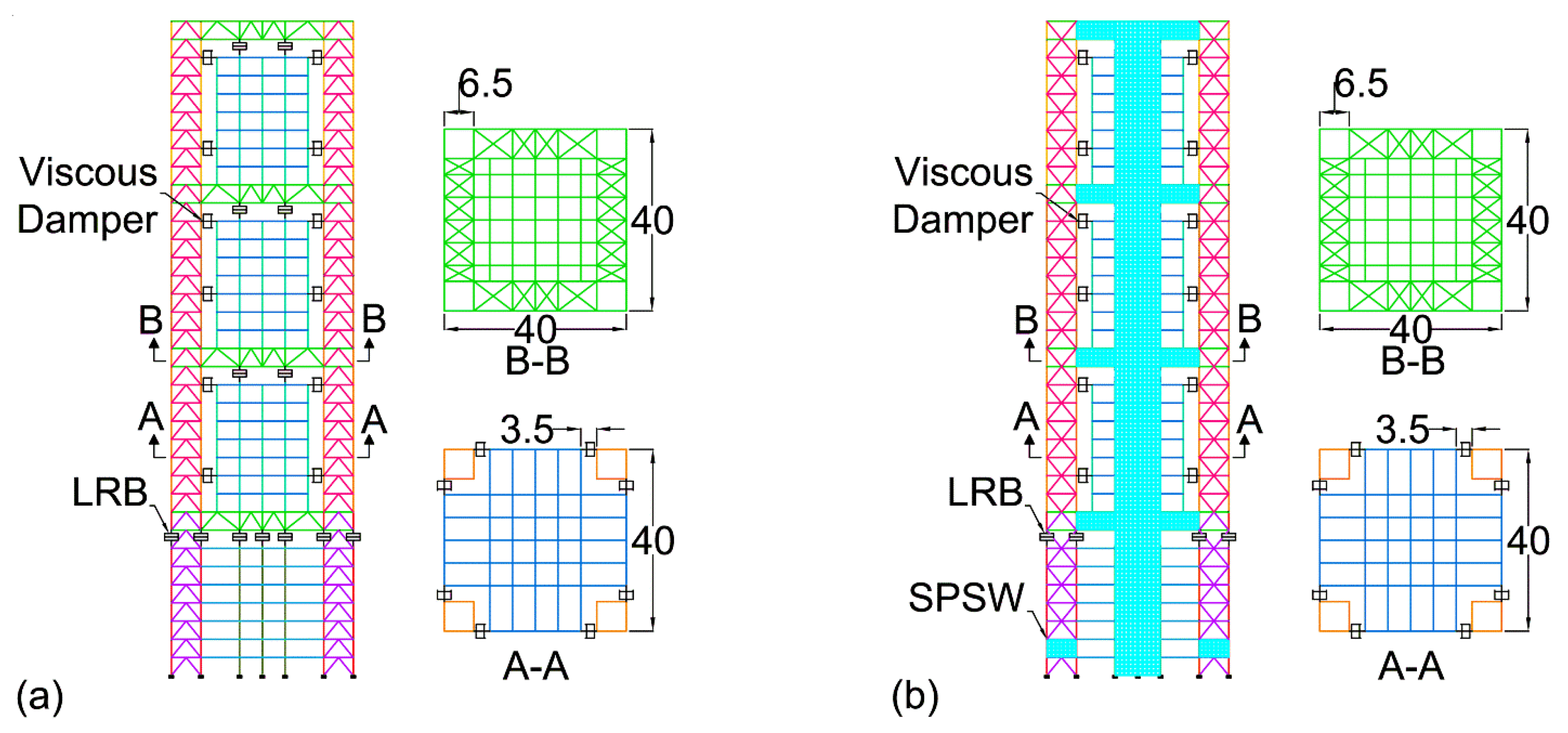
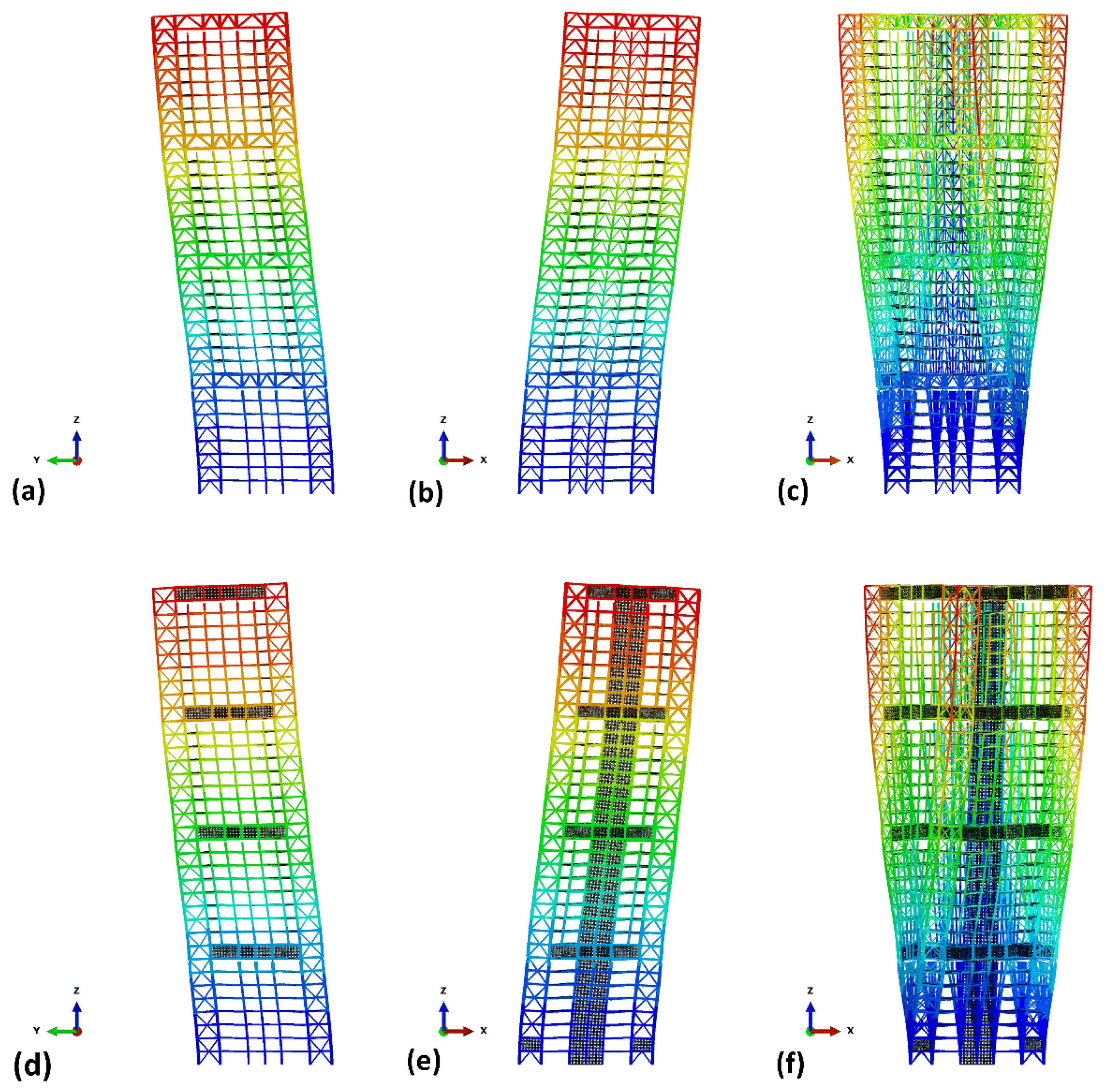
4.1. Development of the Finite Element Model
4.2. Reasons for the Preference of the Dynamic Explicit Solver
- (a)
- Calculations for stress wave propagation are more accurate when using the dynamic explicit solver.
- (b)
- In the dynamic implicit, the time and computational costs exponentially increase with the number of DOFs.
- (c)
- Although the central difference method becomes unstable if , it is preferable to take . For this reason, very small time increments are taken to attain the desired precision.
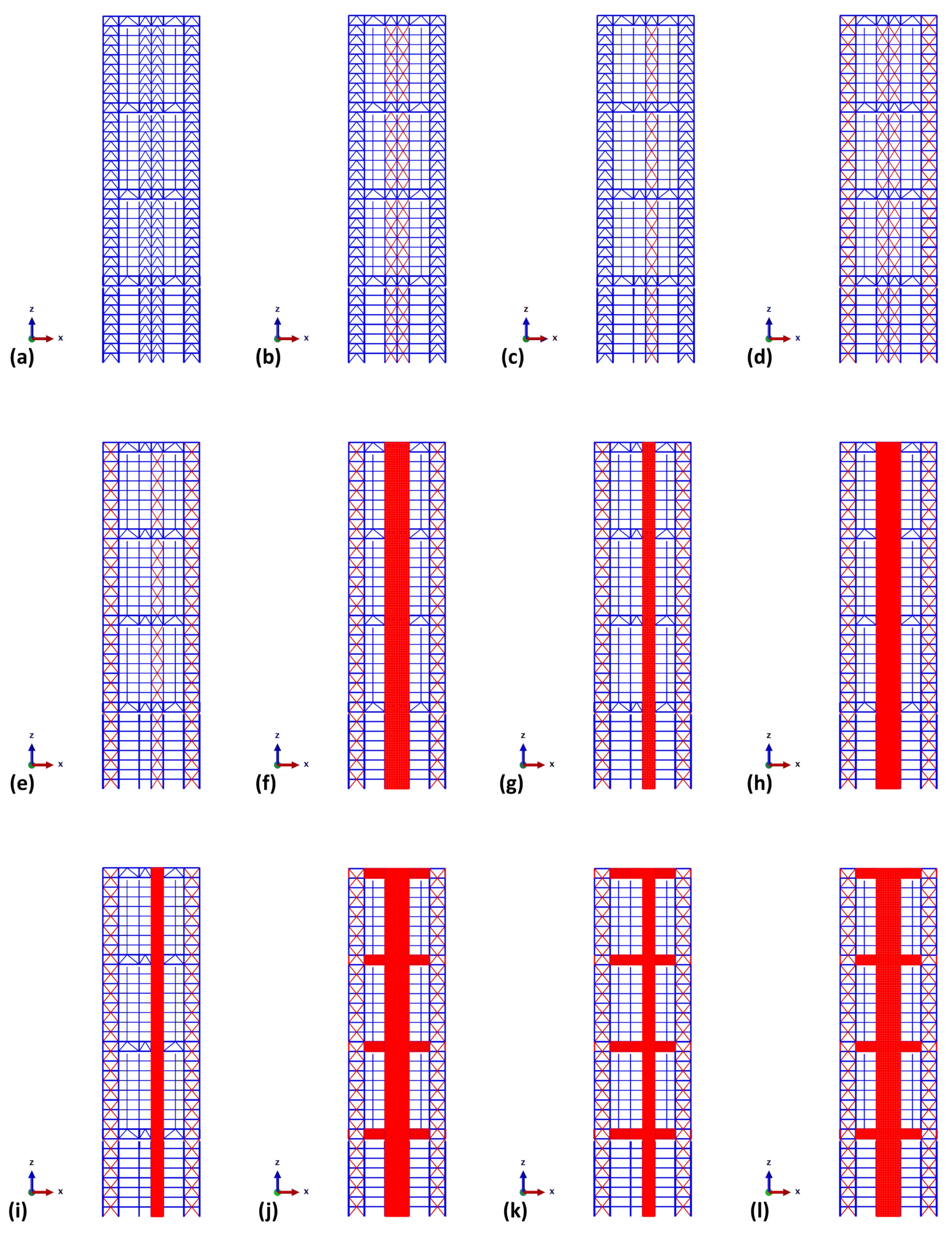
4.3. MSCSS Configurations
- i.
- Configuration 1 which was proposed by Muhammad et al. [21], is an improved configuration initially proposed by Abdulhadi et al. [16]. This configuration has 49 lead rubber bearings beneath the first mega-beam and inverted V-bracing (Chevron) in the middle of the structure across its whole height. This Chevron bracing is present at 15 m to 25 m in the X-axis and 20 m in the Y-axis.
- ii.
- Configuration 2 is the same as configuration 1, but Chevron bracing is replaced by X-bracing.
- iii.
- Configuration 3 is the same as configuration 2, but the X-bracing location is changed from configuration 2; that is, X-bracing is present at 20 m to 25 m in both the X and Y axes.
- iv.
- Configuration 4 is the same as configuration 2, but X-bracing is also used between the mega-columns, which have also been previously used for Chevron bracing.
- v.
- Configuration 5 is the same as configuration 3, but X-bracing is also used between mega-columns, which were before also Chevron bracing.
- vi.
- vii.
- Configuration 7 is the same as configuration 5, but the X-bracing, which is used in the center of the structure, is replaced by ring-shaped infill panels of the SPSW. The dimensions of the ring-shaped infill panels are the same as those in configuration 6.
- viii.
- Configuration 8 is the same as configuration 4, but the X-bracing, which is used in the center of the structure, is replaced by unstiffened infill panels of the SPSW with a thickness of 6 mm.
- ix.
- Configuration 9 is the same as configuration 5, but the X-bracing, which is used in the center of the structure, is replaced by unstiffened infill panels of the SPSW with a thickness of 6 mm.
- x.
- Configuration 10 is the same as configuration 8 along with steel infill panels. This configuration replaces mega-beam bracings.
- xi.
- Configuration 11 is the same as configuration 9 along with steel infill panels. This configuration replaces mega-beam bracings.
- xii.
- Configuration 12 is the same as configuration 6 except for the addition of steel infill panels. Mega-beam bracings are replaced by infill panels in this configuration. Appendix B Table A1 shows the dimensions of the ring-shaped infill panels.
- xiii.
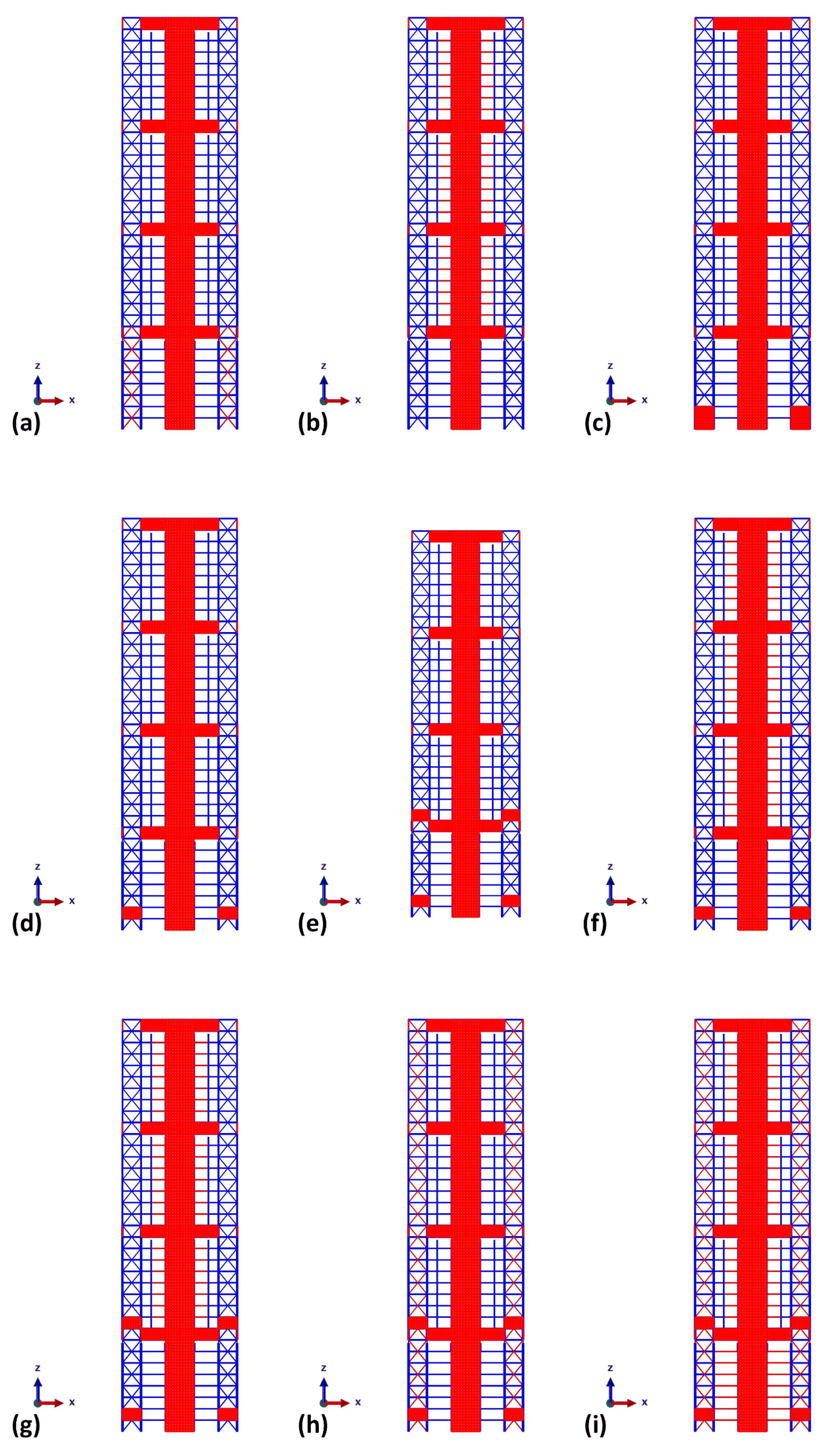
- Configuration 13 is the same as configuration 12, but the infill panel’s thickness is revised to 5 mm.
- xiv.
- Configuration 14 is the same as configuration 7 along with steel infill panels. This configuration replaces mega-beam bracings. The dimensions of the ring-shaped infill panels are the same as those in configuration 12.
- xv.
- Configurations 15 and 16 are identical to configurations 12 and 14, respectively, but the steel infill panel properties have changed, as shown in Table A2 of Appendix B.
- xvi.
- Configurations 17 and 18 are identical to configurations 15 and 16, respectively, but the dimensions of ring-shaped infill panels are shown in Table A1 of Appendix B, and mega-column 1 (MC1) and substructure column 1 (SSC1) are revised, with details shown in Table A3 of Appendix B.
- xvii.
- Configurations 19 and 20 are the same as configurations 17 and 18, respectively, but the thickness of the infill panels of the SPSW is increased from 6 mm to 8 mm.
- xvii.
- Configuration 21 is identical to configuration 12, but the thickness of the SPSW infill panels has been increased from 6 mm to 10 mm. In addition, section members’ profiles have been updated, and Appendix B Table A4 illustrates the changes.
- xix.
- Configuration 22 is the same as configuration 21, but the infill panel’s thickness is revised to 5 mm.
- xx.
- Configuration 23 is the same as configuration 12, but the infill panel’s thickness is revised to 10 mm, and the section members are also modified, and Table A5 of Appendix B illustrates its details.
- xxi.
- Configuration 24 is the same as configuration 12, but the infill panel’s thickness is revised to 8 mm, and the section members are also modified in configuration 23.
- xxii.
- Configuration 25 is the same as configuration 24, but the bracing between the first substructure mega-columns (MC Bracing 1) and the first three mega-beams (MB 1~3) is revised, as illustrated in Table A6 of Appendix B.
- xxiii.
- Configuration 26 is identical to configuration 24, but the lead rubber bearing (LRB) parameters and substructure beams (SB) of substructures 2 to 4 are revised, as shown in Appendix B Table A7 and Table A8.
- xxiv.
- Configuration 27 is identical to configuration 24, except that the first three mega-beams (MB 1~3) are revised, and infill panels are added in the mega-column of the first substructures on floors 1 and 2. Appendix B Table A9 and Table A10 contain information on revised section members and infill panels.
- xxv.
- Configuration 28 is the same as configuration 27, but the infill panels are only added in the mega-column of the first substructures on the second floor.
- xxvi.
- Configuration 29 is identical to configuration 28, but infill panels are also added on the first floor of the second substructure at the mega-column (MC 2) above the first mega-beam (MB 1).
- xxvii.
- Configuration 30 is the same as configuration 28, but the lead rubber bearing (LRB) parameters and substructure beams (SB) of substructures 2–4 have been revised, as shown in Appendix B Table A7 and Table A8. Table 3 lists the section members in detail.
- xxviii.
- Configuration 31 is the same as configuration 29, but substructure beams (SB) of substructures 2–4 and LRB parameters are revised as shown in Appendix B Table A7 and Table A8.
- xxix.
- Configuration 32 is the same as configuration 29, but the LRB parameters have been revised as shown in Appendix B Table A7. Furthermore, the bracing in mega-columns for the entire structure (MC Bracing 1 and 2~4) has been revised, as shown in Appendix B Table A11.
- xxx.
- Configuration 33 is the same as configuration 32, but substructural beams (SB 1 and SB 2~4) of the entire structure are revised, and Appendix B Table A12 illustrates its details.
5. Comparative Analyses
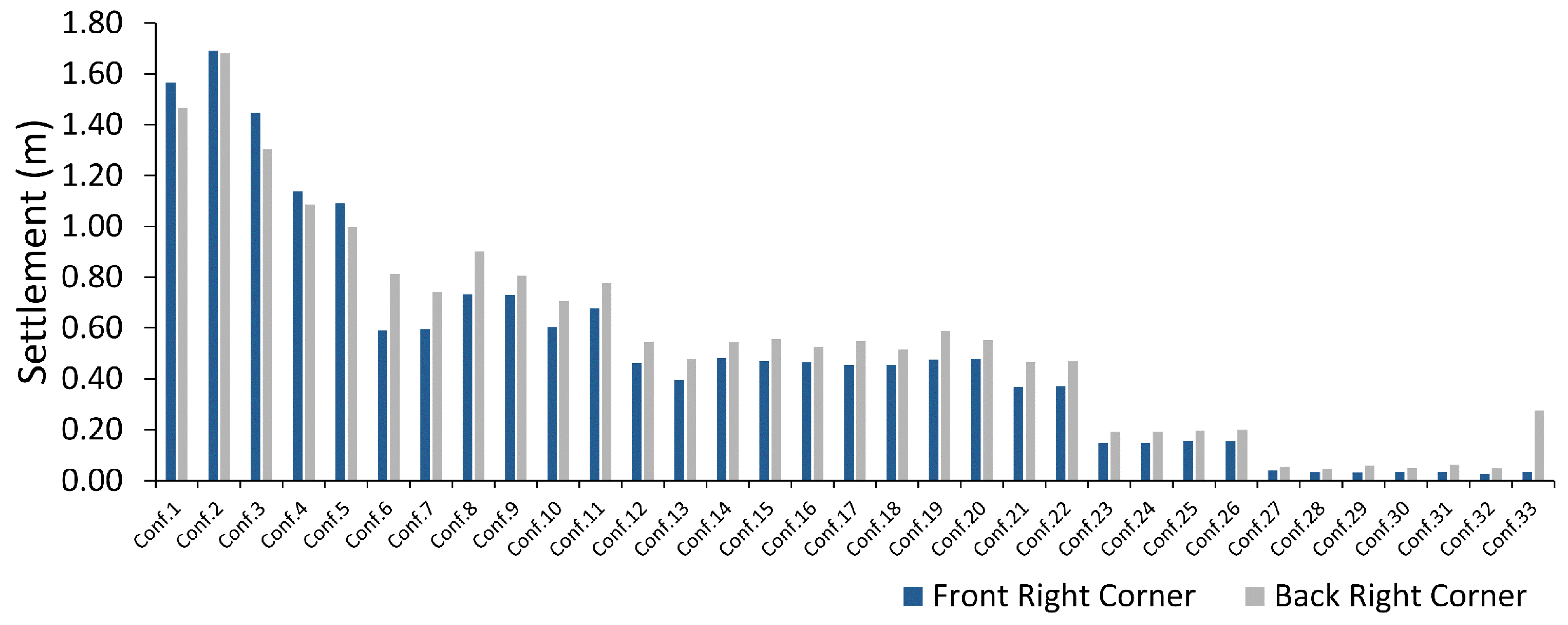
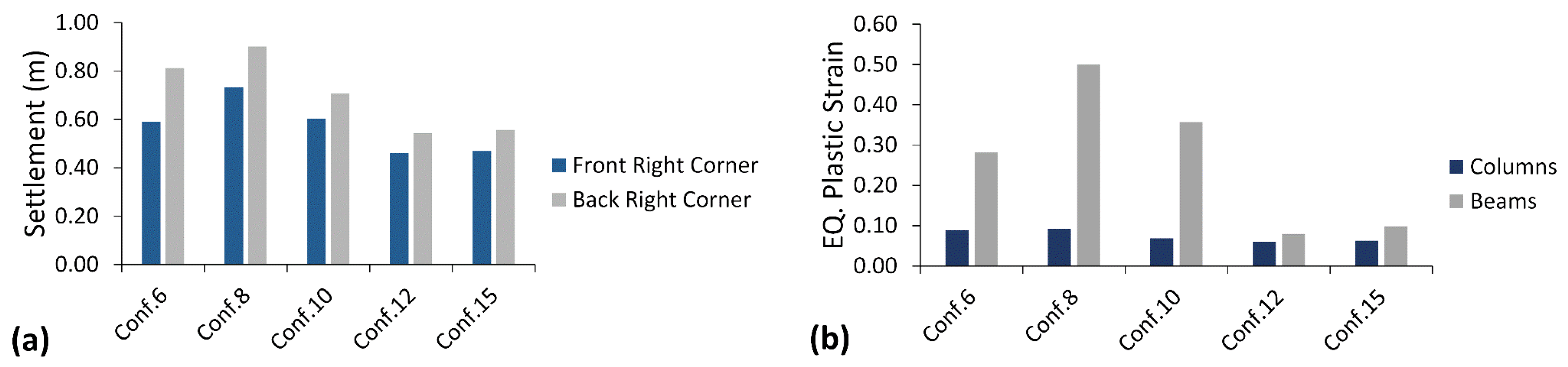
5.1. Settlement at the Top of the Structure
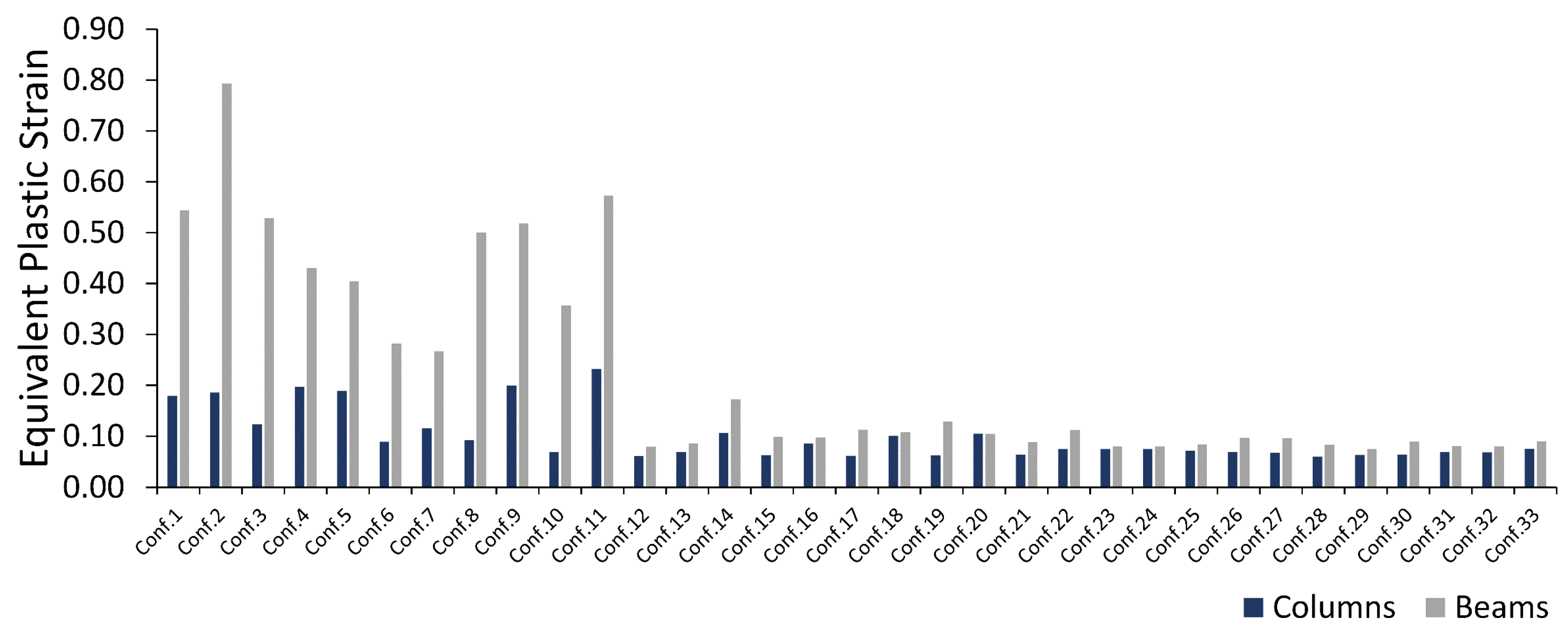
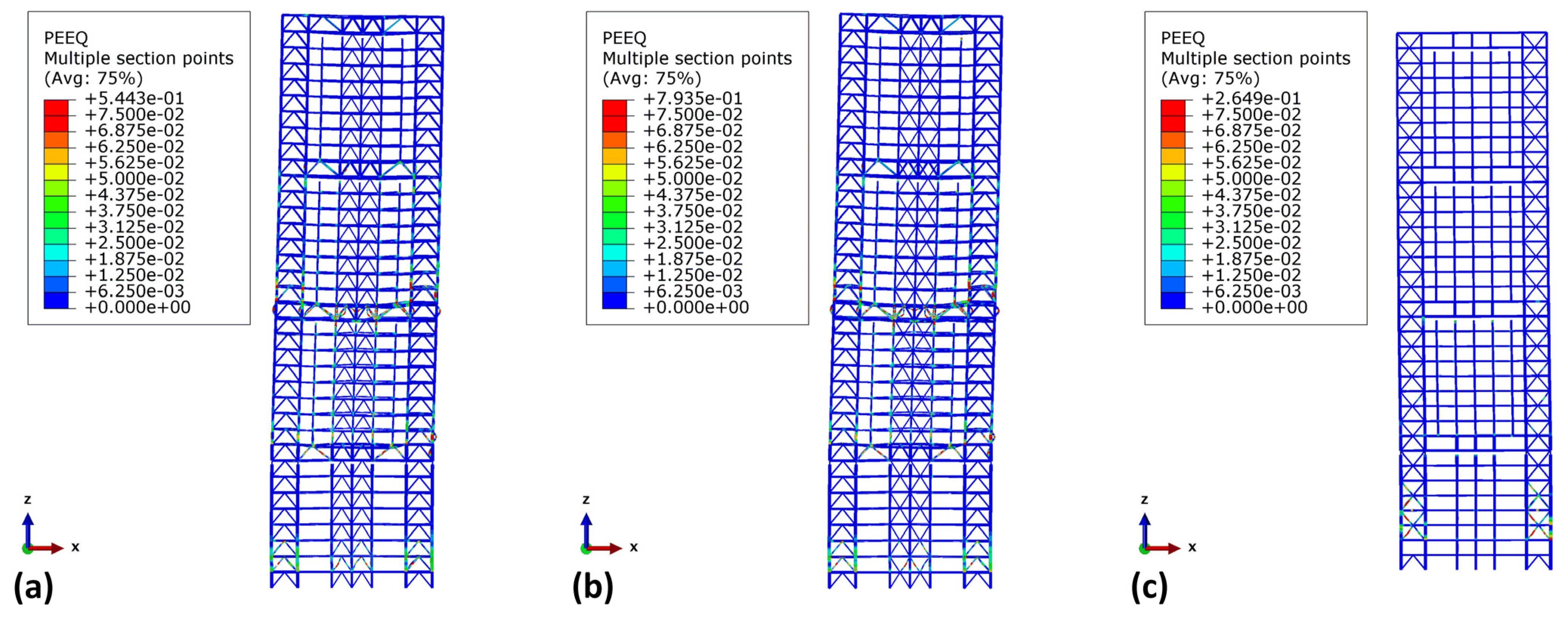
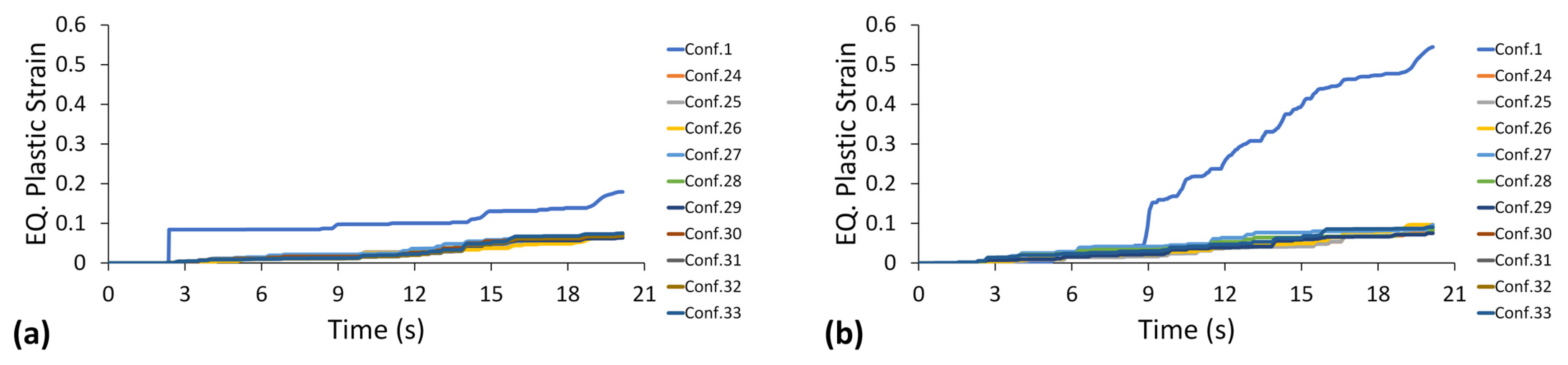
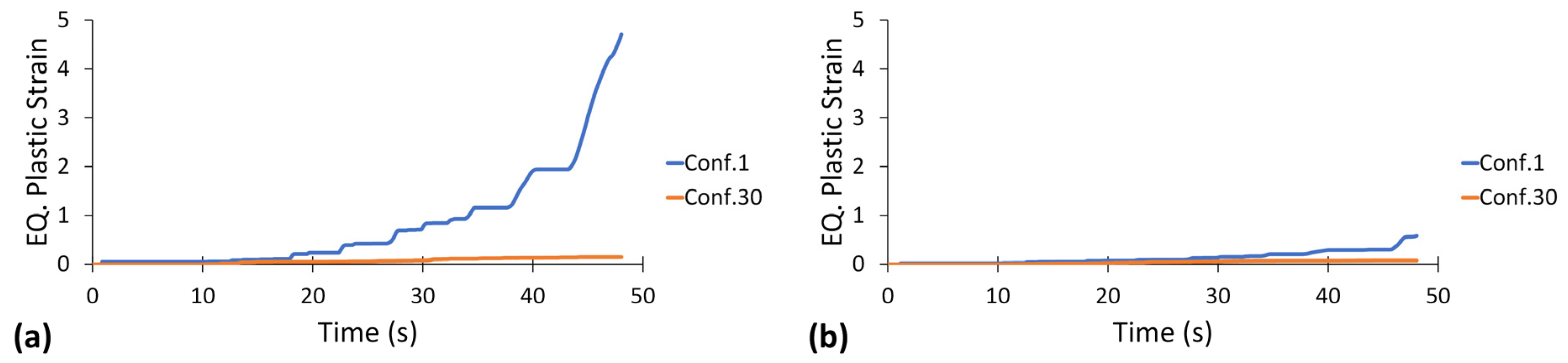
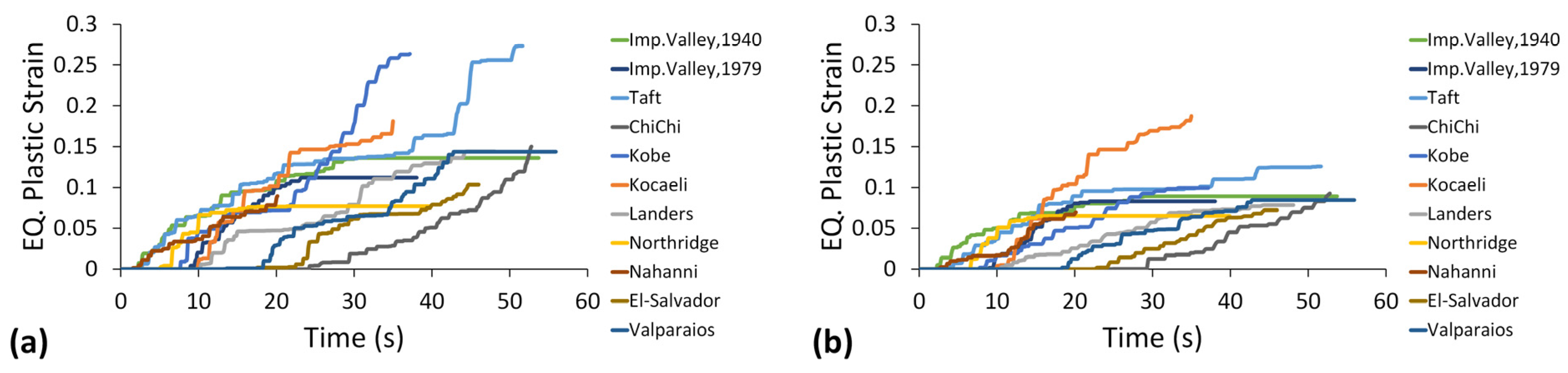
5.2. Equivalent Plastic Strain
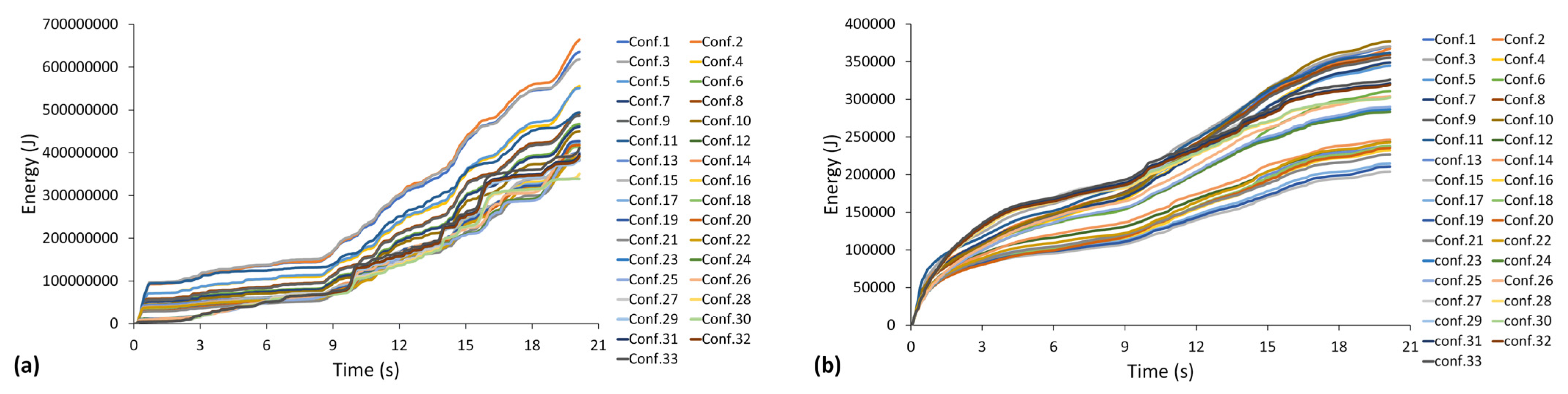
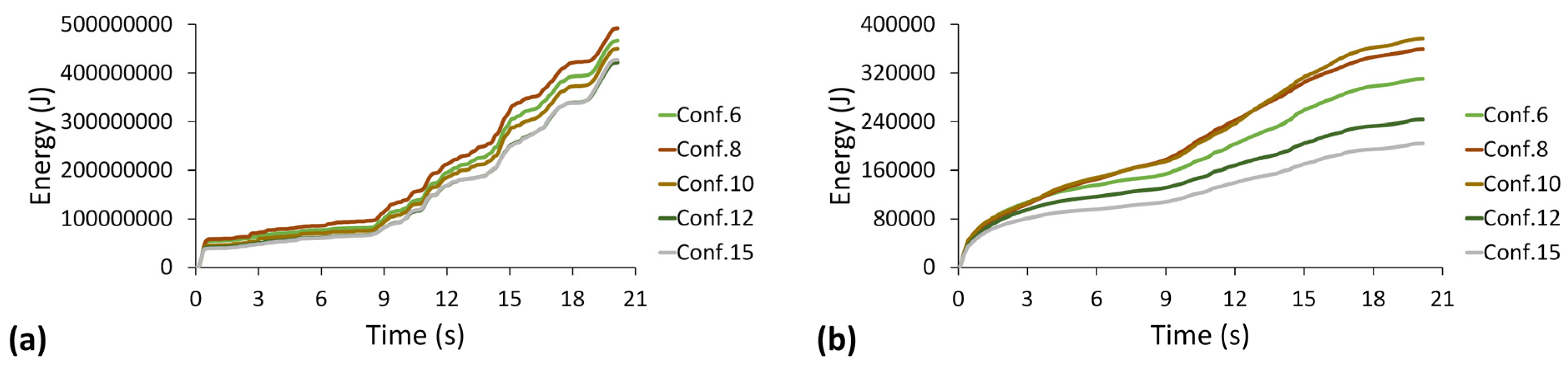
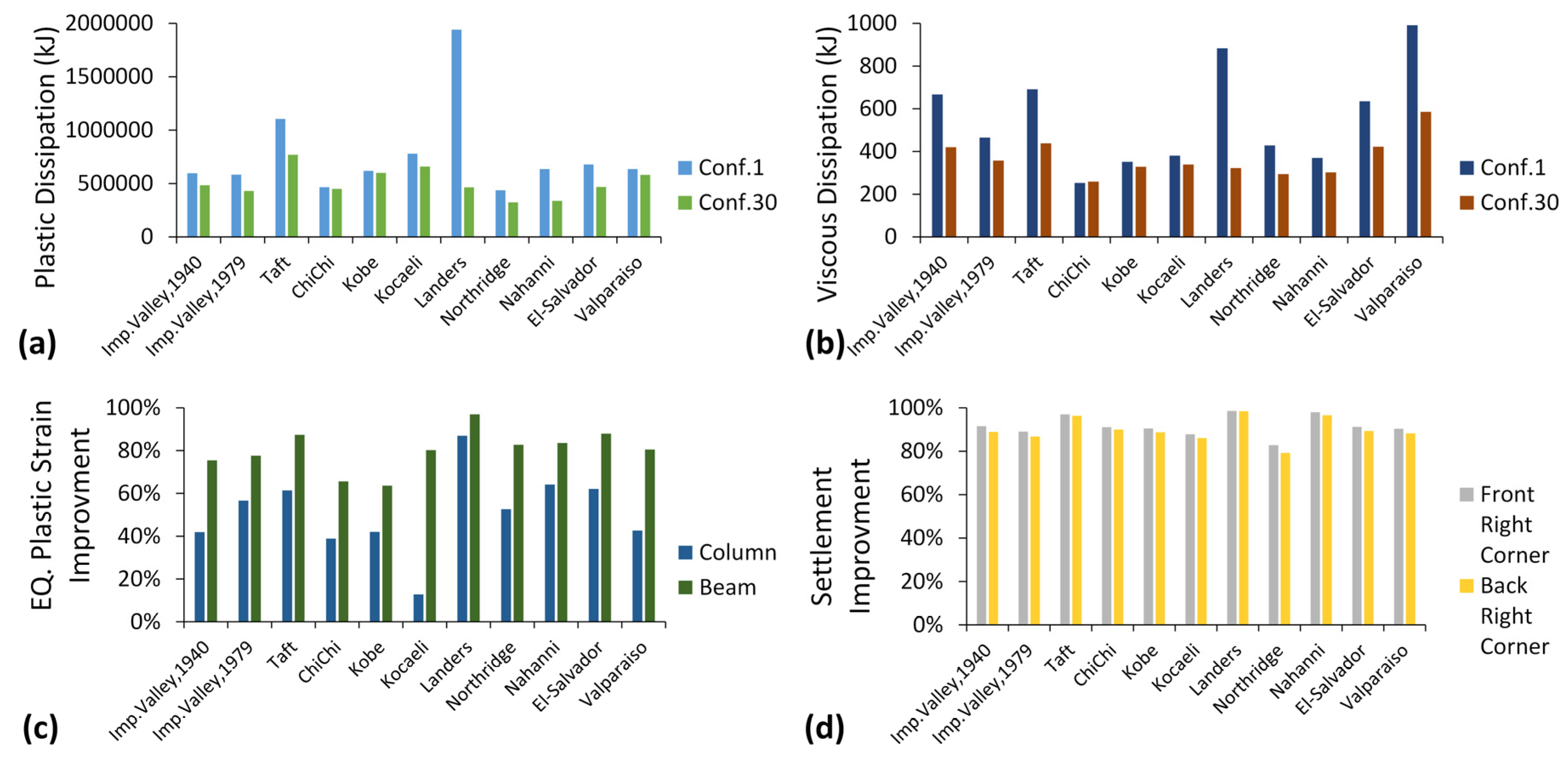
5.3. Energy Dissipation
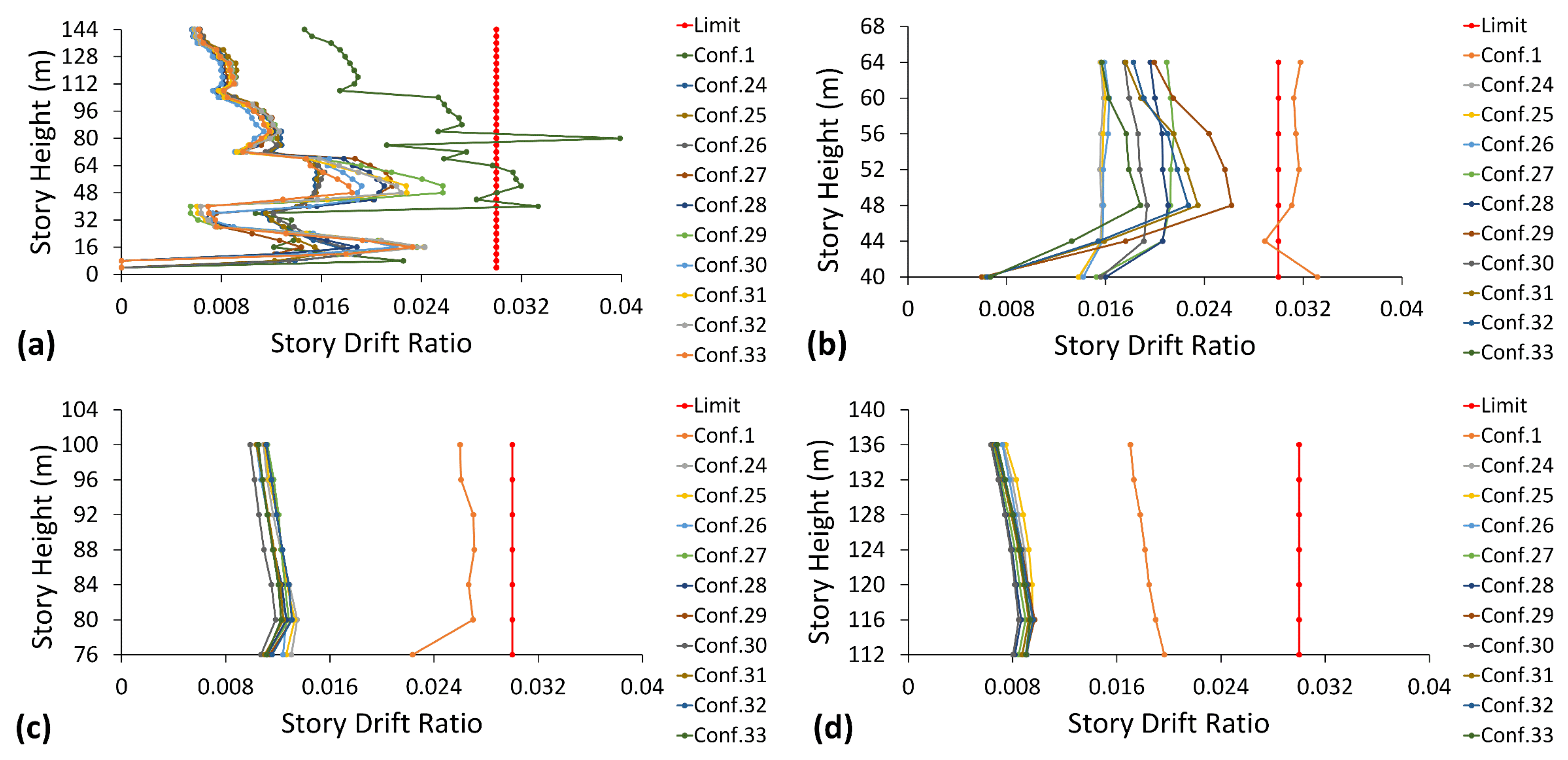
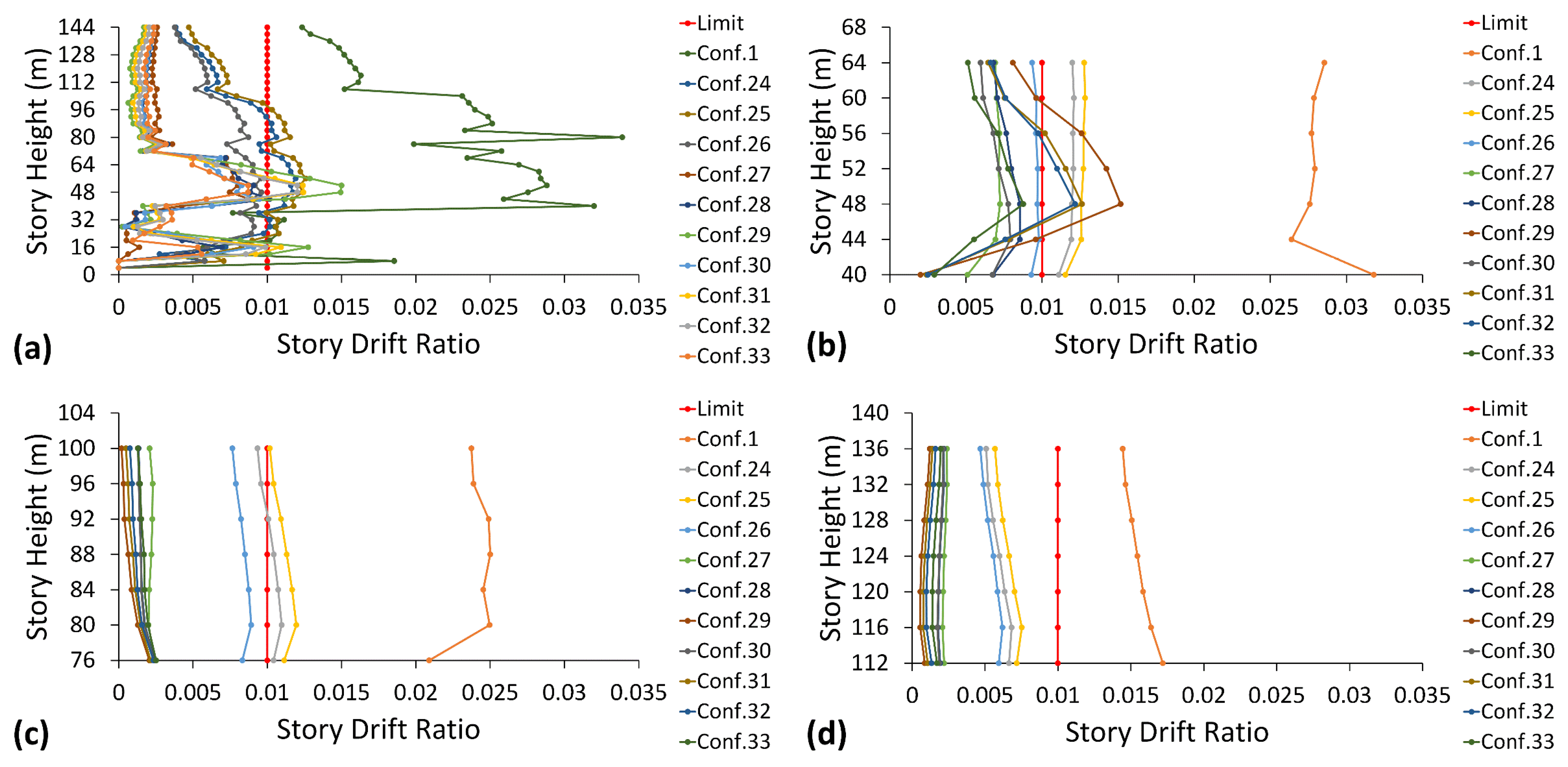
5.4. Peak Transient Story Drift
5.5. Residual Story Drift
6. Selection of the Optimized Design
Selection of Optimized Infill Panels
7. Nonlinear Dynamic Analysis
8. Conclusions
- Configuration 30 is proposed as a novel configuration for the MSCSS, as it has minimum plastic dissipation with medium-to-high viscous dissipation among all other tentative configurations. The maximum equivalent plastic strains are 64% and 83.6% less in the column and beam, respectively, in configuration 30 than in configuration 1.
- Compared to configuration 1, configuration 30 showed the most control structural response, as the minimum residual story drift improvement was 70%, 88.73%, and 85.25% in the first, second, and third substructures, respectively.
- Compared to conventional infill panels, ring-shaped infill panels showed improved seismic performance and a 44% decrease in maximum equivalent plastic strain in beam where ring-shaped infills were used. Large radius ring-shaped infill panels cut-outs showed slightly better performance. The SPSW provides strength and stability to the whole structure even under extensive exposure to strong earthquakes.
- Ring-shaped infill panels exhibit improved stiffness, as they have less buckling effect because of deformation ring properties, which increase energy dissipation.
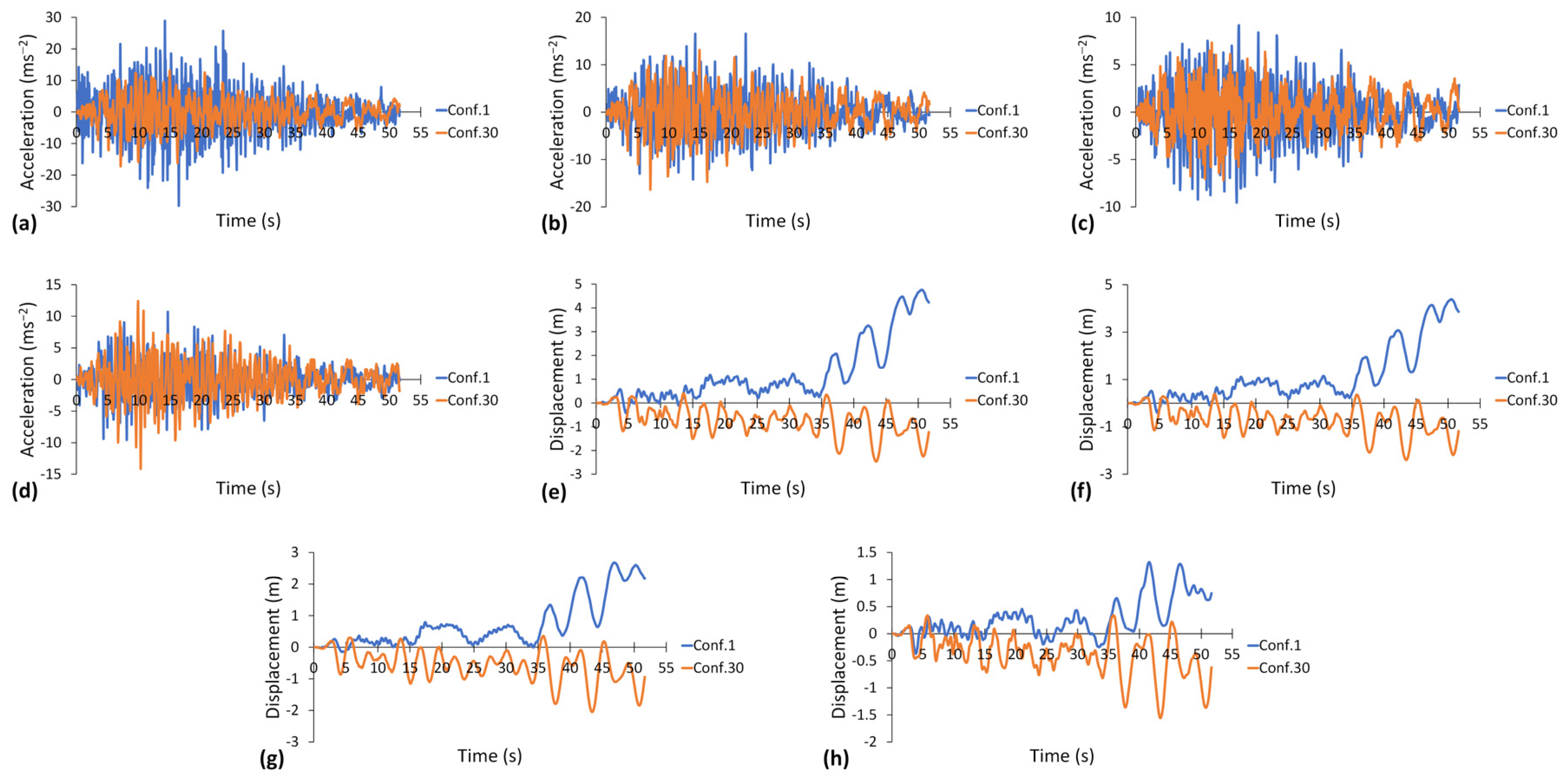
- Configuration 30 showed a more consistent seismic structural response, as the maximum COV was 16% and 32% in the acceleration and displacement responses, respectively.
- Compared to configuration 1, configuration 30 showed a mean improvement of 51% in plastic strain in columns, while in beams, it was 80%. The equivalent plastic strain in columns of configuration 30 never crossed the failure limits, but in beams, section failure occurred only under Taft and Kobe ground motions. Under Taft, the structure leans toward the left side because of plastic deformation in the mega-columns, which causes severe damage to the mega-frame of a structure.
- Under Taft, configuration 30 dissipated 770 MJ of energy in the form of plastic deformation, which is approximately 30% less than that under configuration 1, and under the Kobe earthquake, plastic dissipation is 21.9% less than that under Taft. Configuration 1 shows catastrophic damage under the Landers and Taft earthquakes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
Appendix B
| Steel Infill Panel Properties (5 m × 4 m) | Steel Infill Panel Properties (8.5 m × 4 m) | ||
|---|---|---|---|
| Parameters | Dimensions | Parameters | Dimensions |
| Thickness | 6 mm | Thickness | 6 mm |
| Ro | 0.44 m | Ro | 0.4 m |
| wc | 0.11 m | wc | 0.1 m |
| Wi | 0.15 m | Wi | 0.14 m |
| Broader at the top and bottom | 0.08 m | Broader at the top and bottom | 0.2 m |
| Broader at the right and left sides | 0.1 m | Broader at the right and left sides | 0.2 m |
| Steel Infill Panel Properties (5 m × 4 m) | Steel Infill Panel Properties (8.5 m × 4 m) | ||
|---|---|---|---|
| Parameters | Dimensions | Parameters | Dimensions |
| Thickness | 6 mm | Thickness | 6 mm |
| Ro | 0.42 m | Ro | 0.42 m |
| wc | 0.11 m | wc | 0.11 m |
| Wi | 0.15 m | Wi | 0.15 m |
| Broader at the top and bottom | 0.12 m | Broader at the top and bottom | 0.2 m |
| Broader at the right and left sides | 0.15 m | Broader at the right and left sides | 0.2 m |
| Sections | Old | Revised |
|---|---|---|
| MC1 | 800 × 800 × 34 × 34 mm | 900 × 900 × 34 × 34 mm |
| SSC1 | 600 × 600 × 20 × 20 mm | 600 × 600 × 34 × 34 mm |
| Sections | Old (mm) | Revised (mm) |
|---|---|---|
| Substructural beams up to the 1st mega-beam | 500 × 250 × 18 × 10 | 500 × 250 × 18 × 12 |
| Substructural beams between the 1st and 4th mega-beam | 350 × 250 × 10 × 10 | 350 × 250 × 12 × 12 |
| Sections | Old (mm) | Revised (mm) |
|---|---|---|
| MC 1 | 800 × 800 × 34 × 34 | 900 × 900 × 34 × 34 |
| MC 2 | 600 × 600 × 34 × 34 | 800 × 800 × 34 × 34 |
| MC 3 | 600 × 600 × 20 × 20 | 700 × 700 × 34 × 34 |
| MC 4 | 600 × 600 × 20 × 20 | 600 × 600 × 34 × 34 |
| MB 1~3 | 600 × 350 × 25 × 16 | 650 × 450 × 25 × 25 |
| MB 4 | 582 × 300 × 17 × 12 | 600 × 300 × 18 × 18 |
| MC Beam 1~2 | 582 × 300 × 17 × 12 | 582 × 350 × 20 × 20 |
| MC Beam 3~4 | 500 × 250 × 18 × 10 | 500 × 300 × 18 × 18 |
| SC 1 | 600 × 600 × 20 × 20 | 700 × 700 × 34 × 34 |
| SC 2~4 | 400 × 400 × 20 × 20 | 600 × 600 × 34 × 34 |
| SB 1 | 500 × 250 × 18 × 12 | 500 × 350 × 25 × 25 |
| SB 2~4 | 350 × 250 × 12 × 12 | 500 × 300 × 18 ×18 |
| MC Bracing 1 | 350 × 300 × 25 × 25 | 400 × 350 × 25 × 25 |
| MC Bracing 2~4 | 350 × 300 × 19 × 12 | 350 × 350 × 25 × 25 |
| Add Column | 400 × 400 × 20 × 20 | 600 × 600 × 34 × 34 |
| Sections | Old (mm) | Revised (mm) |
|---|---|---|
| MC Bracing 1 | 400 × 350 × 25 × 25 | 450 × 350 × 30 × 30 |
| MB 1~3 | 650 × 450 × 25 × 25 | 650 × 550 × 30 × 30 |
| Sections | Old (mm) | Revised (mm) |
|---|---|---|
| SB 2~4 | 500 × 300 × 18 ×18 | 500 × 350 × 25 × 25 |
| Main LRB | Small LRB | ||||
|---|---|---|---|---|---|
| Old | Revised | Old | Revised | ||
| Bearing horizontal stiffness, Kh | 9.26 × 103 kNm−1 | 2.32 × 103 kNm−1 | Bearing horizontal stiffness, Kh | 4.17 × 103 kNm−1 | 1.27 × 103 kNm−1 |
| Bearing vertical stiffness, Kv | 3.59 × 107 kNm−1 | 4.10 × 107 kNm−1 | Bearing vertical stiffness, Kv | 2.59 × 107 kNm−1 | 3.16 × 107 kNm−1 |
| Rotation Linear Elastic, stiffness | 1.63 × 1010 kNm.rad | 1.75 × 1010 kNm.rad | Rotation Linear Elastic, stiffness | 4.84 × 109 kNm.rad | 7.74 × 109 kNm.rad |
| Torsion Linear Elastic, stiffness | 1.32 × 106 kPa | 6.83 × 105 kPa | Torsion Linear Elastic, stiffness | 1.07 × 106 kPa | 6.12 × 105 kPa |
| Sections | Old (mm) | Revised (mm) |
|---|---|---|
| MB 1~3 | 650 × 450 × 25 × 25 | 650 × 550 × 30 × 30 |
| Parameters | Dimensions |
|---|---|
| Thickness | 8 mm |
| Ro | 0.4 m |
| wc | 0.1 m |
| Wi | 0.15 m |
| Broader at the top and bottom | 0.2 m |
| Broader at the right and left sides | 0.1 m |
| Sections | Old (mm) | Revised (mm) |
|---|---|---|
| MC Bracing 1 | 400 × 350 × 25 × 25 | 450 × 350 × 30 × 30 |
| MC Bracing 2~4 | 350 × 350 × 25 × 25 | 350 × 350 × 30 × 30 |
| Sections | Old (mm) | Revised (mm) |
|---|---|---|
| SB 1 | 500 × 350 × 25 × 25 | 500 × 350 × 30 × 30 |
| SB 2~4 | 500 × 300 × 18 ×18 | 500 × 350 × 30 × 30 |
Appendix C
References
- CTBUH. The Global Tall Buildings Database of the CTBUH. Available online: http://www.skyscrapercenter.com/ (accessed on 23 March 2020).
- Ali, M.M.; Moon, K.S. Structural Developments in Tall Buildings: Current Trends and Future Prospects. Arch. Sci. Rev. 2007, 50, 205–223. [Google Scholar] [CrossRef]
- Gunel, M.H.; Ilgin, H.E. Tall Buildings—Structural Systems and Aerodynamic Form; Routledge: Oxfordshire, UK, 2014. [Google Scholar] [CrossRef]
- Zhang, Z.; Nielsen, S.R.K.; Blaabjerg, F.; Zhou, D. Dynamics and Control of Lateral Tower Vibrations in Offshore Wind Turbines by Means of Active Generator Torque. Energies 2014, 7, 7746–7772. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Adhikari, S. Experimental validation of soil–structure interaction of offshore wind turbines. Soil Dyn. Earthq. Eng. 2011, 31, 805–816. [Google Scholar] [CrossRef]
- Feng, M.Q.; Mita, A. Vibration Control of Tall Buildings Using Mega SubConfiguration. J. Eng. Mech. 1995, 121, 1082–1088. [Google Scholar] [CrossRef] [Green Version]
- Chai, W.; Feng, M.Q. Vibration control of super tall buildings subjected to wind loads. Int. J. Non-Linear Mech. 1997, 32, 657–668. [Google Scholar] [CrossRef] [Green Version]
- Lan, Z.; Fang, L.; Wang, X. Multifunctional shock-absorption system of RC megaframe structures. Ind. Constr. 2002, 32, 1–4. [Google Scholar]
- Xun’An, Z.; Dong, W.; Jiesheng, J. The controlling mechanism and the controlling effectiveness of passive mega-sub-controlled frame subjected to random wind loads. J. Sound Vib. 2005, 283, 543–560. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, J.; Wang, D.; Jiang, J. Controlling Characteristics of Passive Mega-Subcontrolled Frame Subjected to Random Wind Loads. J. Eng. Mech. 2005, 131, 1046–1055. [Google Scholar] [CrossRef]
- Lian, Y.; Zhang, X.; Sheldon, C. Damping characteristics of friction damped braced frame and its effectiveness in the mega-sub controlled structure system. Earthq. Eng. Eng. Vib. 2007, 6, 171–181. [Google Scholar] [CrossRef]
- Qin, X.; Zhang, X.; Sheldon, C. Study on semi-active control of mega-sub controlled structure by MR damper subject to random wind loads. Earthq. Eng. Eng. Vib. 2008, 7, 285–294. [Google Scholar] [CrossRef]
- Zhang, X.; Qin, X.; Cherry, S.; Lian, Y.; Zhang, J.; Jiang, J. A New Proposed Passive Mega-Sub Controlled Structure and Response Control. J. Earthq. Eng. 2009, 13, 252–274. [Google Scholar] [CrossRef]
- Li, T.; Zhang, X.A.; Wang, Q. Control characteristics of mega-sub controlled structure system with friction damper under rare earthquake. In Proceedings of the World Congress on Engineering 2012, London, UK, 4–6 July 2012; International Association of Engineers: Hong Kong, China, 2010; Volume 2189, pp. 791–796. [Google Scholar]
- Li, T.; Zhang, X.A.; Limazie, T. Viscous Dampers Installation Arrangement and Hysteresis Curve Characteristics Research on the Mega-Sub Controlled Structure System. Appl. Mech. Mater. 2011, 71–78, 1687–1690. [Google Scholar] [CrossRef]
- Abdulhadi, M.; Xun’an, Z.; Fan, B.; Moman, M. Design, Optimization and Nonlinear Response Control Analysis of the Mega Sub-Controlled Structural System (MSCSS) Under Earthquake Action. J. Earthq. Tsunami 2020, 14, 2050013. [Google Scholar] [CrossRef]
- Abdulhadi, M.; Xun’An, Z.; Fan, B.; Moman, M. Evaluation of Seismic Fragility Analysis of the Mega Sub-Controlled Structural System (MSCSS). J. Earthq. Tsunami 2020, 14, 2050025. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Shahzad, M.M.; Shi, X. Research on the disaster prevention mechanism of mega-sub controlled structural system by vulnerability analysis. Structures 2021, 33, 4481–4491. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Shahzad, M.M.; Wang, T. Research on dynamic response characteristics and control effect of mega-sub controlled structural system under long-period ground motions. Structures 2020, 29, 225–234. [Google Scholar] [CrossRef]
- Abdulhadi, M.; Xun’an, Z.; Fan, B.; Moman, M. Substructure design optimization and nonlinear responses control analysis of the mega-sub controlled structural system (MSCSS) under earthquake action. Earthq. Eng. Eng. Vib. 2021, 20, 687–704. [Google Scholar] [CrossRef]
- Shahzad, M.M.; Zhang, X.; Wang, X.; Abdulhadi, M.; Wang, T.; Xiao, Y. Response control analysis of a new mega-subcontrolled structural system (MSCSS) under seismic excitation. Struct. Des. Tall Spéc. Build. 2022, 31, e1935. [Google Scholar] [CrossRef]
- Bruneau, M.; Bhagwagar, T. Seismic retrofit of flexible steel frames using thin infill panels. Eng. Struct. 2002, 24, 443–453. [Google Scholar] [CrossRef]
- Berman, J.; Bruneau, M. Plastic Analysis and Design of Steel Plate Shear Walls. J. Struct. Eng. 2003, 129, 1448–1456. [Google Scholar] [CrossRef] [Green Version]
- Berman, J.W. Seismic behavior of code designed steel plate shear walls. Eng. Struct. 2010, 33, 230–244. [Google Scholar] [CrossRef]
- Daniel, J.B.; Larry, A.F. Seismic Design and Analysis of Steel Plate Shear Walls with Coupling. J. Struct. Eng. 2013, 139, 1263–1273. [Google Scholar] [CrossRef]
- Shahzad, M.M.; Zhang, X.; Wang, X.; Abdulhadi, M. Comparative response assessment of different steel plate shear walls (SPSWs) under near-field ground motion. J. Constr. Steel Res. 2022, 190, 107147. [Google Scholar] [CrossRef]
- Sabelli, R.; Bruneau, M. Design Guide 20: Steel Plate Shear Walls; American Institute of Steel Construction: Chicago, IL, USA, 2007. [Google Scholar]
- Qureshi, R.; Bruneau, M. Behavior of Steel Plate Shear Walls Subjected to Long Duration Earthquakes; State University of New York: Buffalo, NY, USA, 2016. [Google Scholar]
- Lv, Y.; Li, Z.-X. Influences of the gravity loads on the cyclic performance of unstiffened steel plate shear wall. Struct. Des. Tall Spéc. Build. 2016, 25, 988–1008. [Google Scholar] [CrossRef]
- Maurya, A. Computational Simulation and Analytical Development of Buckling Resistant Steel Plate Shear Wall (BR-SPSW). Master’s Thesis, Department of Civil and Environmental Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2012. [Google Scholar]
- Egorova, N.; Eatherton, M.R.; Maurya, A. Experimental study of ring-shaped steel plate shear walls. J. Constr. Steel Res. 2014, 103, 179–189. [Google Scholar] [CrossRef] [Green Version]
- ASCE/SEI 7–16; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2016.
- Kawashima, K.; Aizawa, K. Bracketed and normalized durations of earthquake ground acceleration. Earthq. Eng. Struct. Dyn. 1989, 18, 1041–1051. [Google Scholar] [CrossRef]
- ASCE/SEI 41-17; Seismic Evaluation and Retrofit of Existing Buildings. American Society of Civil Engineers: Reston, VA, USA, 2017.
- Lilhanand, K.; Tseng, W. Generation of synthetic time histories compatible with multiple-damping design response spectra. In Proceedings of the 9th International Conference on Structural Mechanics in Reactor Technology, Lausanne, Switzerland, 17–21 August 1987; Volume K1. [Google Scholar]
- Lilhanand, K.; Tseng, W.S. Development and application of realistic earthquake time histories compatible with multiple-damping design spectra. In Proceedings of the 9th World Conference on Earthquake Engineering, Tokyo-Kyoto, Japan, 2–9 August 1988; Japan Association for Earthquake Disaster Prevention: Tokyo, Japan, 1989; Volume 2, pp. 819–824. [Google Scholar]
- Abrahamson, N. Non-stationary spectral matching. Seismol. Res. Lett. 1992, 63, 30. [Google Scholar]
- Hancock, J.; Watson-Lamprey, J.; Abrahamson, N.A.; Bommer, J.J.; Markatis, A.; McCOYH, E.; Mendis, R. An improved method of matching response spectra of recorded earthquake ground motion using wavelets. J. Earthq. Eng. 2006, 10, 67–89. [Google Scholar] [CrossRef]
- Al Atik, L.; Abrahamson, N. An Improved Method for Nonstationary Spectral Matching. Earthq. Spectra 2010, 26, 601–617. [Google Scholar] [CrossRef] [Green Version]
- Kelly, J.M. Base Isolation: Linear Theory and Design. Earthq. Spectra 1990, 6, 223–244. [Google Scholar] [CrossRef]
- Kelly, J.M. Earthquake-Resistant Design with Rubber; Springer: London, UK, 1993. [Google Scholar]
- Wang, S.-J.; Chang, K.-C.; Hwang, J.-S.; Lee, B.-H. Simplified analysis of mid-story seismically isolated buildings. Earthq. Eng. Struct. Dyn. 2011, 40, 119–133. [Google Scholar] [CrossRef]
- Wang, S.-J.; Chang, K.-C.; Hwang, J.-S.; Hsiao, J.-Y.; Lee, B.-H.; Hung, Y.-C. Dynamic behavior of a building structure tested with base and mid-story isolation systems. Eng. Struct. 2012, 42, 420–433. [Google Scholar] [CrossRef]
- Driver, R.G. Seismic Behaviour of Steel Plate Shear Walls. Ph.D. Thesis, Department of Civil and Environmental Engineering, University of Alberta Edmonton, Edmonton, AB, Canada, 1997. [Google Scholar]



| Event | Year | Station | Mw | Mechanism | Rjb (km) | Rrup (km) | Arias Intensity (m/s) |
|---|---|---|---|---|---|---|---|
| Imperial Valley | 1940 | El Centro Array # 9 | 6.95 | Strike Slip | 6.09 | 6.09 | 1.6 |
| Imperial Valley | 1979 | El Centro Array # 13 | 6.53 | Strike Slip | 21.98 | 21.98 | 0.3 |
| Chi-Chi | 1999 | TCU045 | 7.62 | Reverse Oblique | 26 | 26 | 1.4 |
| Kobe | 1995 | Kakogawa | 6.9 | Strike Slip | 22.5 | 22.5 | 1.7 |
| Kocaeli | 1999 | Yarimca | 7.51 | Strike Slip | 1.38 | 4.83 | 1.3 |
| Kern County | 1952 | Taft Lincoln School | 7.36 | Reverse | 38.42 | 38.89 | 0.6 |
| Landers | 1992 | Lucerne | 7.28 | Strike Slip | 2.19 | 2.19 | 7 |
| Northridge | 1994 | Canoga Park | 6.69 | Reverse | 0 | 14.7 | 2.8 |
| Nahanni | 1985 | Site 1 | 6.76 | Reverse | 2.48 | 9.6 | 3.9 |
| El Salvador | 2001 | Santiago de Maria | 7.6 | Strike Slip | Epicenter 52.2 km | 11.7 | |
| Valparaiso | 1985 | San Isidro | 8 | Reverse Oblique | Epicenter 33 km | 16 | |
| Parameters | Dimensions |
|---|---|
| Thickness | 6 mm |
| Ro | 0.44 m |
| wc | 0.11 m |
| Wi | 0.15 m |
| Broader at the top and bottom | 0.08 m |
| Broader at the right and left sides | 0.1 m |
| Member | Section Shape | Section Size (mm) | Area (m2) | Moment of Inertia | Section Modulus | Radius of Gyration | |||
|---|---|---|---|---|---|---|---|---|---|
| Ix (m4) | Iy (m4) | Wx (m3) | Wy (m3) | Rgx (m) | Rgy (m) | ||||
| Mega-columns up to the 1st mega-beam |  | 900 × 900 × 34 × 34 | 0.1178 | 0.0147 | 0.0147 | 0.0328 | 0.0328 | 0.3538 | 0.3538 |
| Mega-columns between the 1st and 2nd mega-beams |  | 800 × 800 × 34 × 34 | 0.1042 | 0.0102 | 0.0102 | 0.0255 | 0.0255 | 0.313 | 0.313 |
| Mega-columns between the 2nd and 3rd mega-beams |  | 700 × 700 × 34 × 34 | 0.0906 | 6.713 × 10−3 | 6.713 × 10−3 | 0.0192 | 0.0192 | 0.2722 | 0.2722 |
| Mega-columns between the 3rd and 4th mega-beams |  | 600 × 600 × 34 × 34 | 0.077 | 6.165 × 10−3 | 6.165 × 10−3 | 0.0137 | 0.0137 | 0.2315 | 0.2315 |
| Substructural columns up to the 1st mega-beam |  | 700 × 700 × 34 × 34 | 0.0906 | 6.713 × 10−3 | 6.713 × 10−3 | 0.0192 | 0.0192 | 0.2722 | 0.2722 |
| Substructural columns between the 1st and 4th mega-beams |  | 600 × 600 × 34 × 34 | 0.077 | 6.165 × 10−3 | 6.165 × 10−3 | 0.0137 | 0.0137 | 0.2315 | 0.2315 |
| Additional columns |  | 600 × 600 × 34 × 34 | 0.077 | 6.165 × 10−3 | 6.165 × 10−3 | 0.0137 | 0.0137 | 0.2315 | 0.2315 |
| Mega-beams 1, 2 and 3 | H | 650 × 550 × 30 × 30 | 0.0507 | 3.687 × 10−3 | 8.332 × 10−3 | 0.0113 | 3.030 × 10−3 | 0.2697 | 0.1282 |
| Mega-beam 4 | H | 600 × 300 × 18 × 18 | 0.0219 | 1.426 × 10−3 | 8.13 × 10−5 | 4.388 × 10−3 | 5.42 × 10−4 | 0.2555 | 0.061 |
| Beams between the mega-columns up to the 2nd mega-beam | H | 582 × 350 × 20 × 20 | 0.0248 | 1.371 × 10−3 | 1.433 × 10−4 | 4.712 × 10−3 | 8.187 × 10−4 | 0.235 | 0.0759 |
| Beams between the mega-columns from the 2nd to 4th mega-beam | H | 500 × 300 × 18 × 18 | 0.0192 | 7.774 × 10−4 | 8.123 × 10−5 | 3.11 × 10−3 | 5.415 × 10−4 | 0.2015 | 0.0651 |
| Bracing in the mega-columns up to mega-beam 1 | H | 450 × 350 × 30 × 30 | 0.0327 | 1.076 × 10−3 | 2.153 × 10−4 | 4.782 × 10−3 | 1.23 × 10−3 | 0.1814 | 0.0811 |
| Bracing in the mega-columns above mega-beam 1 | H | 350 × 350 × 25 × 25 | 0.025 | 5.193 × 10−4 | 1.79 × 10−4 | 2.967 × 10−3 | 1.023 × 10−3 | 0.1441 | 0.0846 |
| Substructural beams | H | 500 × 350 × 25 × 25 | 0.0288 | 1.178 × 10−3 | 1.792 × 10−4 | 4.711 × 10−3 | 1.024 × 10−3 | 0.2024 | 0.079 |
| Configuration Name | Modal Time Period (s) | Modal Frequency (Hz) | ||||
|---|---|---|---|---|---|---|
| Mode 1 | Mode 2 | Mode 3 | Mode 1 | Mode 2 | Mode 3 | |
| Conf.1 | 4.320 | 4.171 | 2.650 | 0.231 | 0.240 | 0.377 |
| Conf.2 | 4.334 | 4.197 | 2.651 | 0.231 | 0.238 | 0.377 |
| Conf.3 | 4.281 | 4.266 | 2.622 | 0.234 | 0.234 | 0.381 |
| Conf.4 | 4.377 | 4.235 | 2.686 | 0.228 | 0.236 | 0.372 |
| Conf.5 | 4.339 | 4.287 | 2.686 | 0.230 | 0.233 | 0.372 |
| Conf.6 | 4.606 | 4.606 | 4.402 | 0.217 | 0.217 | 0.227 |
| Conf.7 | 4.606 | 4.606 | 4.400 | 0.217 | 0.217 | 0.227 |
| Conf.8 | 4.515 | 4.515 | 4.316 | 0.221 | 0.221 | 0.232 |
| Conf.9 | 4.515 | 4.515 | 4.314 | 0.221 | 0.221 | 0.232 |
| Conf.10 | 4.427 | 4.427 | 4.231 | 0.226 | 0.226 | 0.236 |
| Conf.11 | 4.427 | 4.427 | 4.229 | 0.226 | 0.226 | 0.236 |
| Conf.12 | 5.135 | 5.135 | 4.519 | 0.195 | 0.195 | 0.221 |
| Conf.13 | 5.529 | 5.529 | 4.968 | 0.181 | 0.181 | 0.201 |
| Conf.14 | 5.235 | 5.152 | 4.600 | 0.191 | 0.194 | 0.217 |
| Conf.15 | 5.083 | 5.014 | 4.365 | 0.197 | 0.199 | 0.229 |
| Conf.16 | 5.078 | 5.017 | 4.364 | 0.197 | 0.199 | 0.229 |
| Conf.17 | 4.984 | 4.913 | 4.365 | 0.201 | 0.204 | 0.229 |
| Conf.18 | 4.978 | 4.919 | 4.364 | 0.201 | 0.203 | 0.229 |
| Conf.19 | 4.961 | 4.888 | 3.275 | 0.202 | 0.205 | 0.305 |
| Conf.20 | 4.953 | 4.896 | 3.275 | 0.202 | 0.204 | 0.305 |
| Conf.21 | 4.809 | 4.730 | 2.977 | 0.208 | 0.211 | 0.336 |
| Conf.22 | 5.529 | 5.529 | 4.855 | 0.181 | 0.181 | 0.206 |
| Conf.23 | 3.916 | 3.865 | 2.769 | 0.255 | 0.259 | 0.361 |
| Conf.24 | 3.923 | 3.874 | 3.459 | 0.255 | 0.258 | 0.289 |
| Conf.25 | 3.842 | 3.794 | 3.459 | 0.260 | 0.264 | 0.289 |
| Conf.26 | 3.741 | 3.699 | 3.459 | 0.267 | 0.270 | 0.289 |
| Conf.27 | 3.877 | 3.827 | 2.742 | 0.258 | 0.261 | 0.365 |
| Conf.28 | 3.884 | 3.835 | 3.424 | 0.257 | 0.261 | 0.292 |
| Conf.29 | 3.804 | 3.756 | 3.424 | 0.263 | 0.266 | 0.292 |
| Conf.30 | 3.704 | 3.663 | 3.424 | 0.270 | 0.273 | 0.292 |
| Conf.31 | 3.839 | 3.789 | 2.715 | 0.260 | 0.264 | 0.368 |
| Conf.32 | 3.846 | 3.797 | 3.391 | 0.260 | 0.263 | 0.295 |
| Conf.33 | 3.766 | 3.719 | 3.391 | 0.266 | 0.269 | 0.295 |
| Top of the Structure | Top of the 4th Substructure | Top of the 3rd Substructure | Top of the 2nd Substructure | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Max. Acc. (ms−2) | Acc. RMS. (ms−2) | Max. Acc. (ms−2) | Acc. RMS. (ms−2) | Max. Acc. (ms−2) | Acc. RMS. (ms−2) | Max. Acc. (ms−2) | Acc. RMS. (ms−2) | ||
| Configuration 1 | Imperial Valley, 1940 | 26.80 | 6.92 | 13.69 | 4.43 | 9.61 | 2.79 | 9.58 | 2.70 |
| Imperial Valley, 1979 | 27.51 | 5.89 | 15.23 | 3.60 | 10.10 | 2.39 | 10.90 | 2.39 | |
| Taft | 29.78 | 6.87 | 16.56 | 4.25 | 9.54 | 2.75 | 10.72 | 2.51 | |
| Chi-Chi | 22.23 | 3.40 | 13.79 | 2.03 | 7.66 | 1.12 | 7.90 | 1.33 | |
| Kobe | 25.49 | 5.04 | 15.30 | 3.05 | 12.45 | 1.91 | 7.80 | 1.88 | |
| Kocaeli | 23.30 | 5.68 | 15.00 | 3.58 | 9.74 | 2.12 | 8.61 | 2.15 | |
| Landers | 36.13 | 5.07 | 14.06 | 3.02 | 8.79 | 1.86 | 8.64 | 1.90 | |
| Northridge | 31.64 | 5.85 | 14.74 | 3.51 | 9.64 | 2.27 | 8.72 | 2.08 | |
| Nahanni | 25.56 | 7.01 | 14.08 | 4.40 | 9.31 | 2.76 | 11.40 | 2.68 | |
| El Salvador | 34.93 | 6.37 | 16.02 | 4.19 | 11.33 | 2.77 | 12.23 | 2.65 | |
| Valparaiso | 25.25 | 7.62 | 19.35 | 4.88 | 10.06 | 2.72 | 10.52 | 3.01 | |
| Mean (µ) | 28.06 | 5.97 | 15.26 | 3.72 | 9.84 | 2.31 | 9.73 | 2.30 | |
| Variance, σ2 | 18.86 | 1.28 | 2.43 | 0.61 | 1.41 | 0.26 | 2.05 | 0.21 | |
| SD, σ | 4.34 | 1.13 | 1.56 | 0.78 | 1.19 | 0.51 | 1.43 | 0.46 | |
| CoV, % | 15% | 19% | 10% | 21% | 12% | 22% | 15% | 20% | |
| Configuration 30 | Imperial Valley, 1940 | 18.59 | 4.16 | 17.64 | 3.79 | 8.41 | 2.11 | 10.51 | 2.70 |
| Imperial Valley, 1979 | 19.65 | 3.80 | 17.61 | 3.48 | 8.62 | 1.88 | 11.17 | 2.53 | |
| Taft | 17.23 | 4.25 | 16.35 | 3.92 | 7.34 | 2.21 | 14.15 | 2.93 | |
| Chi-Chi | 13.92 | 2.48 | 12.45 | 2.34 | 5.75 | 1.53 | 10.04 | 1.48 | |
| Kobe | 19.26 | 3.99 | 17.95 | 3.69 | 7.80 | 2.22 | 13.97 | 2.61 | |
| Kocaeli | 15.39 | 4.16 | 13.63 | 3.83 | 6.33 | 1.94 | 11.78 | 2.87 | |
| Landers | 17.68 | 3.16 | 15.63 | 2.94 | 6.64 | 1.78 | 12.02 | 2.09 | |
| Northridge | 16.18 | 3.35 | 14.87 | 3.05 | 7.63 | 1.79 | 11.92 | 2.22 | |
| Nahanni | 17.80 | 5.04 | 16.65 | 4.60 | 9.90 | 2.38 | 11.98 | 3.53 | |
| El Salvador | 16.98 | 4.11 | 16.27 | 3.73 | 10.05 | 2.17 | 12.80 | 2.74 | |
| Valparaiso | 17.86 | 4.62 | 16.16 | 4.16 | 8.23 | 2.75 | 12.32 | 2.95 | |
| Mean (µ) | 17.32 | 3.92 | 15.93 | 3.59 | 7.88 | 2.07 | 12.06 | 2.61 | |
| Variance, σ2 | 2.56 | 0.45 | 2.66 | 0.35 | 1.69 | 0.10 | 1.45 | 0.26 | |
| SD, σ | 1.60 | 0.67 | 1.63 | 0.59 | 1.30 | 0.32 | 1.21 | 0.51 | |
| CoV, % | 9% | 17% | 10% | 17% | 16% | 15% | 10% | 20% | |
| Top of the Structure | Top of the 4th Substructure | Top of the 3rd Substructure | Top of the 2nd Substructure | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Max. Disp. (m) | Disp. RMS. (m) | Max. Disp. (m) | Disp. RMS. (m) | Max. Disp. (m) | Disp. RMS. (m) | Max. Disp. (m) | Disp. RMS. (m) | ||
| Configuration 1 | Imperial Valley, 1940 | 1.09 | 0.62 | 1.03 | 0.58 | 0.77 | 0.39 | 0.50 | 0.25 |
| Imperial Valley, 1979 | 2.02 | 0.84 | 1.97 | 0.82 | 1.68 | 0.69 | 1.22 | 0.49 | |
| Taft | 4.76 | 1.79 | 4.39 | 1.66 | 2.68 | 1.05 | 1.32 | 0.44 | |
| Chi-Chi | 1.63 | 0.56 | 1.56 | 0.54 | 1.19 | 0.46 | 1.04 | 0.36 | |
| Kobe | 1.41 | 0.58 | 1.32 | 0.54 | 0.93 | 0.37 | 0.79 | 0.27 | |
| Kocaeli | 2.62 | 1.25 | 2.44 | 1.17 | 1.56 | 0.79 | 1.20 | 0.43 | |
| Landers | 18.26 | 4.01 | 16.46 | 3.62 | 7.83 | 1.87 | 1.30 | 0.48 | |
| Northridge | 1.03 | 0.60 | 0.98 | 0.57 | 0.68 | 0.42 | 0.49 | 0.30 | |
| Nahanni | 2.66 | 0.77 | 2.54 | 0.73 | 1.89 | 0.54 | 1.00 | 0.34 | |
| El Salvador | 1.94 | 0.61 | 1.82 | 0.58 | 1.11 | 0.38 | 0.76 | 0.21 | |
| Valparaiso | 1.67 | 0.73 | 1.59 | 0.70 | 1.10 | 0.50 | 0.63 | 0.24 | |
| Mean (µ) | 3.55 | 1.12 | 3.28 | 1.05 | 1.95 | 0.68 | 0.93 | 0.35 | |
| Variance, σ2 | 22.61 | 0.96 | 18.17 | 0.77 | 3.76 | 0.18 | 0.09 | 0.01 | |
| SD, σ | 4.76 | 0.98 | 4.26 | 0.88 | 1.94 | 0.43 | 0.30 | 0.10 | |
| CoV, % | 134% | 87% | 130% | 84% | 100% | 63% | 32% | 28% | |
| Configuration 30 | Imperial Valley, 1940 | 0.78 | 0.32 | 0.75 | 0.31 | 0.61 | 0.24 | 0.43 | 0.16 |
| Imperial Valley, 1979 | 1.23 | 0.46 | 1.20 | 0.45 | 0.96 | 0.41 | 0.88 | 0.37 | |
| Taft | 2.46 | 0.93 | 2.39 | 0.90 | 2.05 | 0.74 | 1.56 | 0.52 | |
| Chi-Chi | 1.63 | 0.49 | 1.59 | 0.48 | 1.35 | 0.42 | 1.02 | 0.33 | |
| Kobe | 1.73 | 0.55 | 1.69 | 0.53 | 1.45 | 0.44 | 1.13 | 0.32 | |
| Kocaeli | 1.70 | 0.59 | 1.69 | 0.58 | 1.63 | 0.52 | 1.52 | 0.44 | |
| Landers | 1.46 | 0.53 | 1.43 | 0.53 | 1.26 | 0.46 | 1.00 | 0.37 | |
| Northridge | 1.38 | 0.52 | 1.34 | 0.50 | 1.08 | 0.42 | 0.73 | 0.27 | |
| Nahanni | 1.93 | 0.61 | 1.88 | 0.60 | 1.63 | 0.53 | 1.25 | 0.44 | |
| El Salvador | 1.32 | 0.39 | 1.29 | 0.38 | 1.12 | 0.32 | 0.86 | 0.25 | |
| Valparaiso | 1.18 | 0.33 | 1.15 | 0.32 | 0.98 | 0.26 | 0.74 | 0.19 | |
| Mean (µ) | 1.53 | 0.52 | 1.49 | 0.51 | 1.28 | 0.43 | 1.01 | 0.33 | |
| Variance, σ2 | 0.18 | 0.03 | 0.17 | 0.02 | 0.14 | 0.02 | 0.11 | 0.01 | |
| SD, σ | 0.42 | 0.16 | 0.41 | 0.15 | 0.38 | 0.13 | 0.32 | 0.11 | |
| CoV, % | 28% | 31% | 28% | 30% | 30% | 30% | 32% | 32% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahzad, M.M.; Zhang, X.; Wang, X.; Abdulhadi, M.; Xiao, Y.; Fan, B. Plastic Deformation Analysis of a New Mega-Subcontrolled Structural System (MSCSS) Subjected to Seismic Excitation. Buildings 2022, 12, 987. https://doi.org/10.3390/buildings12070987
Shahzad MM, Zhang X, Wang X, Abdulhadi M, Xiao Y, Fan B. Plastic Deformation Analysis of a New Mega-Subcontrolled Structural System (MSCSS) Subjected to Seismic Excitation. Buildings. 2022; 12(7):987. https://doi.org/10.3390/buildings12070987
Chicago/Turabian StyleShahzad, Muhammad Moman, Xun’an Zhang, Xinwei Wang, Mustapha Abdulhadi, Yanjie Xiao, and Buqiao Fan. 2022. "Plastic Deformation Analysis of a New Mega-Subcontrolled Structural System (MSCSS) Subjected to Seismic Excitation" Buildings 12, no. 7: 987. https://doi.org/10.3390/buildings12070987
APA StyleShahzad, M. M., Zhang, X., Wang, X., Abdulhadi, M., Xiao, Y., & Fan, B. (2022). Plastic Deformation Analysis of a New Mega-Subcontrolled Structural System (MSCSS) Subjected to Seismic Excitation. Buildings, 12(7), 987. https://doi.org/10.3390/buildings12070987






