Influence of Non-Constant Hygrothermal Parameters on Heat and Moisture Transfer in Rammed Earth Walls

Abstract

As environment-friendly building materials, earth materials are attracting significant attention because of their favorable hygrothermal properties. In this study, the earth materials in northwest Sichuan were tested and curves of thermal conductivity and water vapor permeability with relative humidity were obtained. The function curves and constants of the two coefficients were substituted into the verified nonstationary model of heat and moisture transfer in rammed earth walls and indoor air for calculation. The difference in the calculation results when the hygrothermal parameters are functions and constants were analyzed, and the influence of the non-constant hygrothermal parameters on the heat and moisture transfer in rammed earth walls, was obtained. The test results show that thermal conductivity is linearly related to moisture content, and water vapor permeability has a small variation in the relative humidity range of 0–60% and increases exponentially above 60%. The calculation results indicate that the non-constant hygrothermal parameters have little influence on the internal surface temperature of the rammed earth walls and Mianyang City’s indoor air temperature and humidity during the summer and winter. The heat transfer on the internal surface will be underestimated by using a non-constant for the hygrothermal parameter when the moisture content of the wall is low, and vice versa. In hot-humid areas or seasons with large differences in temperature and humidity between indoors and outdoors, non-constant hygrothermal parameters have a more obvious effect on heat transfer on the internal surface of the wall. The results of this study demonstrate the necessity of parameter testing.

1. Introduction

The rapid economic development of modern society is based on a large amount of energy consumption, leading to severe environmental issues. Therefore, sustainable development has become crucial to society. Owing to rapid urbanization, the total building area in China is increasing at a rate of over 1 billion m² per year [1]. Building energy consumption accounts for approximately one-third of the total social energy consumption. Studies show that 40% of the building energy consumption originated from the material preparation stage [2]. In this context, materials that can effectively reduce the energy consumption in buildings, such as earth materials, are beginning to gain attention.

Compared with modern building materials, traditionally used earth materials have various advantages, such as local availability, reusability, and low cost. They lead to sustainable development [3,4], resulting in energy conservation. In addition, earth materials have good climatic suitability. They can provide superior indoor heat comfort owing to their excellent heat storage performance. When the outdoor climate changes, the indoor thermal environment can be adjusted by absorbing and releasing heat [5]. Meanwhile, they exhibit good moisture absorption and release characteristics. With a change in the environmental relative humidity, they absorb and release water vapor from the air to regulate and stabilize the indoor environmental humidity [6,7]. Although China has a long history of using rammed earth buildings, systematic research on earth materials is lacking. Research on improving the mechanical properties of earth materials is relatively common. Sabbà, M. F et al. [8] carried out preliminary sensory and qualitative analysis of the straw iber earth material and tested its properties. In recent years, researchers have focused on studying the hygrothermal properties and parameters of earth materials. He [9] measured and analyzed the effective thermal conductivity of sand with different moisture contents using a thermal constant analyzer. Nikiforova T et al. [10] used the MIT-1 m to determine the thermal conductivity of various types of earth materials and analyzed the variation in their thermal conductivity with the moisture content. Loam has a thermal conductivity change of up to 380%, with moisture content from 0% to 40%. Jin et al. [11,12] used the thermal probe method to study the variation in thermal conductivity of the various types of earth materials with moisture content. The results show that the change rate of thermal conductivity of sand commonly used in engineering exceeds 400% (moisture content from 0% to 30%), while the change rate of clay is even higher. In [13], experiments were designed to study and analyze the relationship between the water vapor permeability and relative humidity of four materials. In [14], the water vapor permeability of different building materials at different relative humidity values was measured using the desiccant method. The integral average value of the vapor permeability coefficient of various building materials between 60% and 100% has increased by more than 1000% compared with that between 0% and 60%. In addition, to improve the hygrothermal properties of the earth materials, researchers have studied earth modification [15,16,17]. Giada, G et al. [18] summarized the research on the hydrothermal performance of modified earth materials with different base materials (such as inorganic soil, natural fibers, minerals or recycled aggregates, and chemical stabilizers). Various studies have shown that humidity has a significant influence on the thermal conductivity and water vapor permeability of earth materials.

In the study of heat and moisture transfer in porous media, the material hygrothermal parameters are generally assumed constant for convenience [19,20], whereas the hygrothermal parameters of the material are influenced by the changes in temperature and humidity [21,22,23]. Accurate calculation of the heat and moisture transfer process in the building wall is the basis for HVAC system designs and building energy consumption analysis. The cooling and heating loads formed on the wall structure are related to the heat and moisture transfer inside the wall. Ignoring the influence of temperature and humidity on the hygrothermal parameters of the wall material can lead to a lack of accuracy in the calculation of the thermal and moisture transfer process, which inevitably leads to errors in the calculation of cooling and heating loads. The literature [24] shows that moisture content has a significant impact on the heat consumption of rammed earth buildings. Therefore, in this study, earth materials from Northwest Sichuan were used as the test object to explore the variation law of its thermal conductivity and water vapor permeability under different humidity values. Simulation calculations and analyses were conducted to determine the effect of hygrothermal parameters on the hygrothermal performance of the rammed earth walls, which was simulated using commercial software with an established numerical model.

2. Testing of Hygrothermal Parameters of Earth Materials

2.1. Thermal Conductivity

2.1.1. Specimen Preparation

The chemical composition of the earth materials from Northwestern Sichuan, based on X-ray fluorescence spectrometry analysis, is presented in

Table 1. Chemical composition of earth materials.

Compound Name	SiO2	Al2O3	Fe2O3	K2O	MgO	Na2O	TiO2	CaO	SO3
Mass fraction (%)	71.79	17.01	5.22	1.96	0.97	0.94	0.91	0.80	0.09

.

The earth materials were crushed and passed through a 2 mm sieve. The treated earth materials were dried in a constant temperature blast drying oven (DGG-9140A, accuracy: ± 0.1 °C) until the change in the mass was less than 0.1%, within 24 h. A precision electronic balance (JJ324BC, range: 0–320 g, accuracy: ±0.1 mg) was used to weigh the adequately dried earth materials. In accordance with the specification of the earth test [25], 13% water was added to the earth materials, mixed and stirred well, poured into a mold, and pressed into a cylinder (R = 0.078 m, L = 0.021 m) using a hydraulic press. Based on relevant specifications, Shang Jianli determined the standard value of compressive strength of the earth materials as 2.0 Mpa [26]. The density of the specimen in this experiment was 2100 kg/m³, which meets this requirement. Finally, the pressed specimens were placed at 20 ± 1 °C and 60 ± 1% RH for 28 d of curing (shown in Figure 1). The cured specimens were used for parameter testing.

2.1.2. Thermal Conductivity Test

The moisture content of the rammed earth specimens was controlled using the weight moisture method. The expression for the moisture content is given by Equation (1). Water, with the corresponding moisture content of 2%, 4%, 6%, 8%, 10%, 12%, and 14% in sequence, was sprayed on the surface of the specimen after curing and drying. The specimen reached its plastic limit when its moisture content reached 16%; therefore, the data recorded thereafter was not considered [24]. Then, the specimen was wrapped fully with a plastic cling film, sealed, and cured for 12 h to ensure permeation of water evenly in the specimen. Finally, a thermal conductivity tester (TC-3000E, range: 0.001–10 W/mK, accuracy: ±3%) was used to measure the thermal conductivities of the specimens (Figure 2). Each specimen was measured three times to obtain the average values, which were recorded.

$$w=\frac{m_1-m_0}{m_0}$$

(1)

where $w$ is the moisture content of the rammed earth specimen (%), $m_1$ is the mass of the specimen after spraying it with water (kg), and $m_{0 }$ is the mass of the specimen after adequate drying (kg).

2.1.3. Results

The results of the thermal conductivity tests are presented in

Table 2. Thermal conductivity of rammed earth specimens at different moisture contents.

Moisture Content (%)	Thermal Conductivity (W/mK)
0	0.528
2	0.601
4	0.644
6	0.716
8	0.782
10	0.843
12	0.904
14	0.967

.

By fitting the experimental data, the functional relationship between the thermal conductivity of the earth materials and the moisture content was obtained as

$$\lambda =0.529+3.126w$$

(2)

where $\lambda$ is the thermal conductivity (W/mK).

Thermal conductivity was linearly related to moisture content, with an R² greater than 0.98.

2.2. Water Vapor Permeability

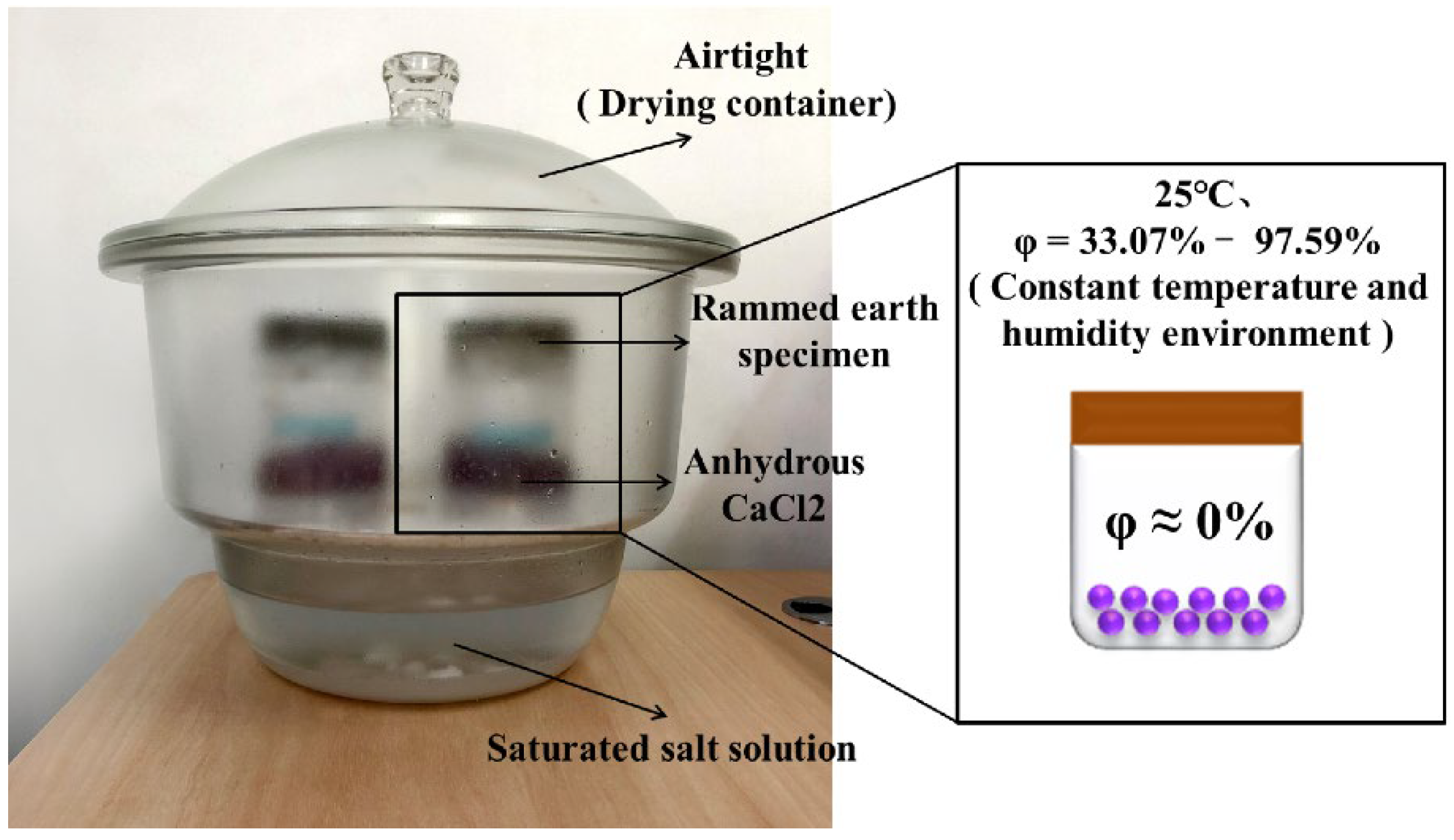
2.2.1. Experimental Principle

The water vapor permeability can be expressed as

$${\delta }_p=\frac{g}{\nabla P_v}L=\frac{g}{P_{sat}\left({\phi }_1-{\phi }_2\right)}L$$

(3)

where $g=\frac{∆m}{A\mathsf{\Delta }t}$ is the density of the moisture flux through the specimen (kg/m²s); $\frac{∆m}{\mathsf{\Delta }t}$ is the moisture flux of water vapor through the specimen (kg/s); $A$ is the superficial area of the specimen (m²); $P_{sat}$ is the partial pressure of the saturated vapor (Pa); ${\phi }_1$ and ${\phi }_2$ are the high and low relative humidity values on both sides of the specimen, respectively (%); and $L$ is the thickness of the specimen (m).

According to standards [27], the desiccant method was used in this experiment, and the test schematic is shown in Figure 3.

2.2.2. Water Vapor Permeability Test

Twelve rammed earth specimens were prepared. Then, 50 g of anhydrous calcium chloride (CaCl₂) was added to each sample cup. The completely dry rammed earth specimen was placed at the mouth of the cup, sealed with beeswax, and weighed. Finally, the sample cups were placed in drying containers with different saturated salt solutions. Relative humidity values corresponding to each saturated salt solution [28] are listed in

Table 3. Relative humidity corresponding to each saturated salt solution at 25 °C.

	1	2	3	4	5	6
Saturated salt solution	MgCl2	K2CO3	NaBr	NaCl	KCl	K2SO4
$\phi$(%)	33.07 ± 0.18	43.16 ± 0.33	59.14 ± 0.44	75.47 ± 0.14	84.11 ± 0.29	97.59 ± 0.53

. Two sample cups were placed in each drying container as a group, and the drying container was placed in an environmental control room (temperature: 25 ± 0.5 °C, relative humidity: 60 ± 2%). The weight of the sample cups was recorded every 24 h and the variation in weight was averaged for each group of sample cups. The recording was stopped if the average variation in weight over five consecutive weights was less than 5%.

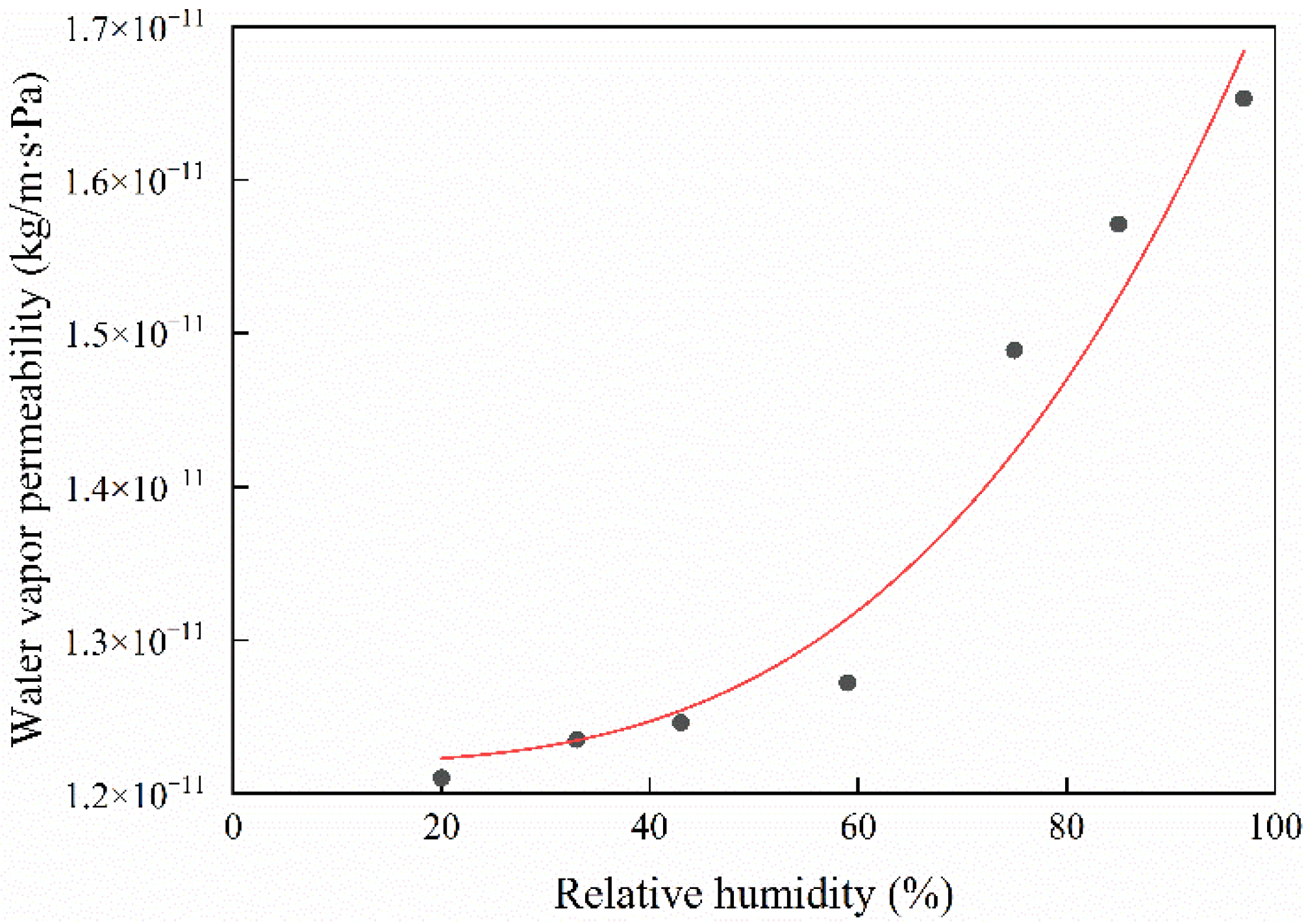
2.2.3. Results

Data were examined through regression analysis [14] based on the curve of variation in the mass of the specimen with time at different relative humidity values obtained from the regression analysis. Equation (3) was used to calculate the water vapor permeability at six relative humidity values, and the data were fitted according to the literature [29]. The results are presented in Figure 4.

Figure 4 shows that the water vapor permeability changes slowly when the relative humidity is less than 60%. Meanwhile, when the relative humidity is greater than 60%, it starts to increase exponentially. From the fitted curve, the equation for water vapor permeability of earth materials was obtained as

$${\delta }_p=1.220\times {10}^{-11}+5.114\times {10}^{-12}{\phi }^{3.21}$$

(4)

where ${\delta }_p$ is the water vapor permeability (kg/m·s·Pa) and $\phi$ is the relative humidity (%).

3. Mathematical Model

The following assumptions are made when the model of heat and moisture transfer of the rammed earth wall was established [30]. The earth material was assumed to be an isotropic continuous homogeneous porous medium; the water vapor was considered as an ideal gas; the influence of gravity on moisture transfer was neglected; the moisture component inside the earth materials was only considered as a gas–liquid two-phase flow and phase change process.

3.1. Heat and Moisture Transfer Equations in the Rammed Earth Wall

3.1.1. Moisture Transfer Equation

According to [31], the total mass in the system remains the same based on Fick’s and Darcy’s laws, which use temperature and relative humidity as driving potentials, ignoring the velocity of airflow inside the wall. The influence of temperature inside the wall on the equilibrium moisture content of the wall material was ignored [32]. The moisture transfer equation was obtained as

$$\xi \frac{\partial \phi }{\partial t}=\nabla \left(\left({\delta }_p\phi \frac{d{P}_{\mathrm{sat}}}{dT}+K_l{\rho }_l{R}_D\ln (\phi )\right)\nabla T+\left({\delta }_p{P}_{sat}+K_l{\rho }_l{R}_D\frac{T}{\phi }\right)\nabla \phi \right)$$

(5)

where $\xi$ is the adsorption capacity (kg/m³); $P_{sat}$ is the partial pressure of the saturated vapor (Pa); $K_l$ is the liquid water permeability (s); ${\rho }_l$ is the density of liquid water (kg/m³), and $R_D$ is the gas constant of water vapor (J/kgK).

3.1.2. Heat Transfer Equation

The sensible heat of water vapor and liquid water and the rate of change of moisture content in the form of water vapor were ignored [33]. According to the law of conservation of energy, the heat transfer equation was obtained as

$$\left({\rho }_m{c}_{p,m}+w{c}_{p,l}\right)\frac{\partial T}{\partial t}=\nabla \left(\left(\lambda +h_{lv}{\delta }_p\phi \frac{d{P}_{sat}}{dT}\right)\nabla T+h_{lv}{\delta }_p{P}_{sat}\nabla \phi \right)$$

(6)

where ${\rho }_m$ is the density of building materials (kg/m³); $c_{p,m}$ is the specific heat capacity of the dry material (J/kgK); $c_{p,l}$ is the specific heat capacity of liquid water (J/kgK), and $h_{lv}$ is the latent heat of the water phase change (J/kg).

3.1.3. Boundary Conditions

It was assumed that the moisture exchange between the wall and the outside environment is only in the form of water vapor. The influence of solar radiation on the heat and moisture transfer on the external surface of the rammed earth wall was considered. The heat and moisture flux through the external surface of the wall can be expressed as

$$q_{n,e}=h_e\left(T_e-T_{\mathit{surfe}}\right)+h_{lv}{g}_{n,e}+\alpha q_{\mathit{solar}}$$

(7)

$$g_{n,e}={\beta }_e\left({\phi }_e{P}_{\mathit{sat},\mathit{e}}-{\phi }_{\mathit{surfe}}{P}_{\mathit{sat},\mathit{surfe}}\right)$$

(8)

The heat and moisture flux through the internal surface of the wall can be expressed as

$$q_{n,i}=h_i\left(T_i-T_{\mathit{surfi}}\right)+h_{lv}{g}_{n,i}$$

(9)

$$g_{n,i}={\beta }_i\left({\phi }_i{P}_{sat,i}-{\phi }_{\mathit{surfi}}{P}_{\mathit{sat},\mathit{surf}i}\right)$$

(10)

where $q_{n,e}$, $q_{n,i}$ are the heat fluxes through the external and internal surfaces (W), respectively; $g_{n,e}$, $g_{n,i}$ are the moisture fluxes through the external and internal surfaces (kg/m²s), respectively; $h_e$, $h_i$ are the convective heat transfer coefficients of the external and internal surfaces (W/m²K), respectively; ${\beta }_e$, ${\beta }_i$ are the moisture exchange transfer coefficients of the external and internal surfaces (m/s), respectively; $T_e$, $T_i$ are outdoor and indoor temperatures (K), respectively; $T_{surfe}$, $T_{surfi}$ are the temperatures on the external and internal surfaces (K), respectively; ${\phi }_e$, ${\phi }_i$ are outdoor and indoor relative humidity values (%), respectively; ${\phi }_{surfe}$, ${\phi }_{surfi}$ are the relative humidity values of the external and internal surfaces (%), respectively; $P_{sat,e}$, $P_{sat,i}$ are the outdoor and indoor partial pressures of saturated vapor (Pa), respectively; $P_{sat,surfe}$, $P_{sat,surfi}$ are the partial pressures of saturated vapor on the external and internal surfaces (Pa), respectively; $\alpha$ is the solar absorptivity of the external surface, and $q_{solar}$ is the solar radiation (W/m²).

The convective heat transfer coefficients of the internal and external surfaces of the rammed earth wall were taken as 8.7 W/m²K and 23 W/m²K, respectively [34]. The literature [35] verified the accuracy of calculating the moisture exchange transfer coefficient of the envelope surface using the Lewis relation, as follows:

$$\beta =\frac{h}{c_{p,m}{\rho }_m}$$

(11)

where $\beta$ is the moisture exchange transfer coefficient (m/s) and $h$ is the convective heat transfer coefficient (W/m²K).

3.2. Heat and Moisture Equilibrium Equation of Indoor Air in a Rammed Earth Building

To analyze the influence of moisture absorption and release on the internal surface of rammed earth walls on the indoor heat and moisture environment [30], this study established the heat and moisture equilibrium equation of indoor air in a rammed earth building.

3.2.1. Heat Equilibrium Equation of Indoor Air

The heat equilibrium equation for indoor air in a rammed-earth building can be written as

$${\rho }_a{c}_{p,a}V\frac{\mathrm{d}{T}_i\left(t\right)}{\mathrm{d}t}=Q_c\left(t\right)+Q_{in}\left(t\right)+Q_v\left(t\right)+Q_s\left(t\right)+Q_L\left(t\right)$$

(12)

where ${\rho }_a$ is the density of air (kg/m³); $c_{p,a}$ is the specific heat capacity of air (J/kgK); $V$ is the volume of the rammed earth building (m³); $T_i\left(t\right)$ is the temperature of the indoor air of the rammed earth building at time t (K); $Q_c\left(t\right)$ is the convective heat exchange between the indoor air and the internal surface of the rammed earth wall at time t (W); $Q_{in}\left(t\right)$ is the heat released from the indoor equipment and personnel at time t (W); $Q_v\left(t\right)$ is the heat entering the room through ventilation at time t (W); $Q_s\left(t\right)$ is the heat obtained through windows and doors at time t (W); and $Q_L\left(t\right)$ is the latent heat owing to the moisture absorption and release from the internal surface of the rammed earth wall at time t (W).

3.2.2. Moisture Equilibrium Equation of Indoor Air

The moisture equilibrium equation for indoor air in a rammed-earth building can be written as

$${\rho }_{a}V\frac{\mathrm{d}{W}_i\left(t\right)}{\mathrm{d}t}=W_V\left(t\right)+W_L\left(t\right)+W_{in}\left(t\right)$$

(13)

where $W_i\left(t\right)$ is the moisture content of the indoor air of the rammed earth building at time t (kg/kg); $W_V\left(t\right)$ is the moisture exchange owing to ventilation at time t (kg/s); $W_L\left(t\right)$ is the moisture exchange between the indoor air and the internal surface of the rammed earth wall at time t (kg/s); and $W_{in}\left(t\right)$ is the moisture release of indoor equipment and personnel at time t (kg/s).

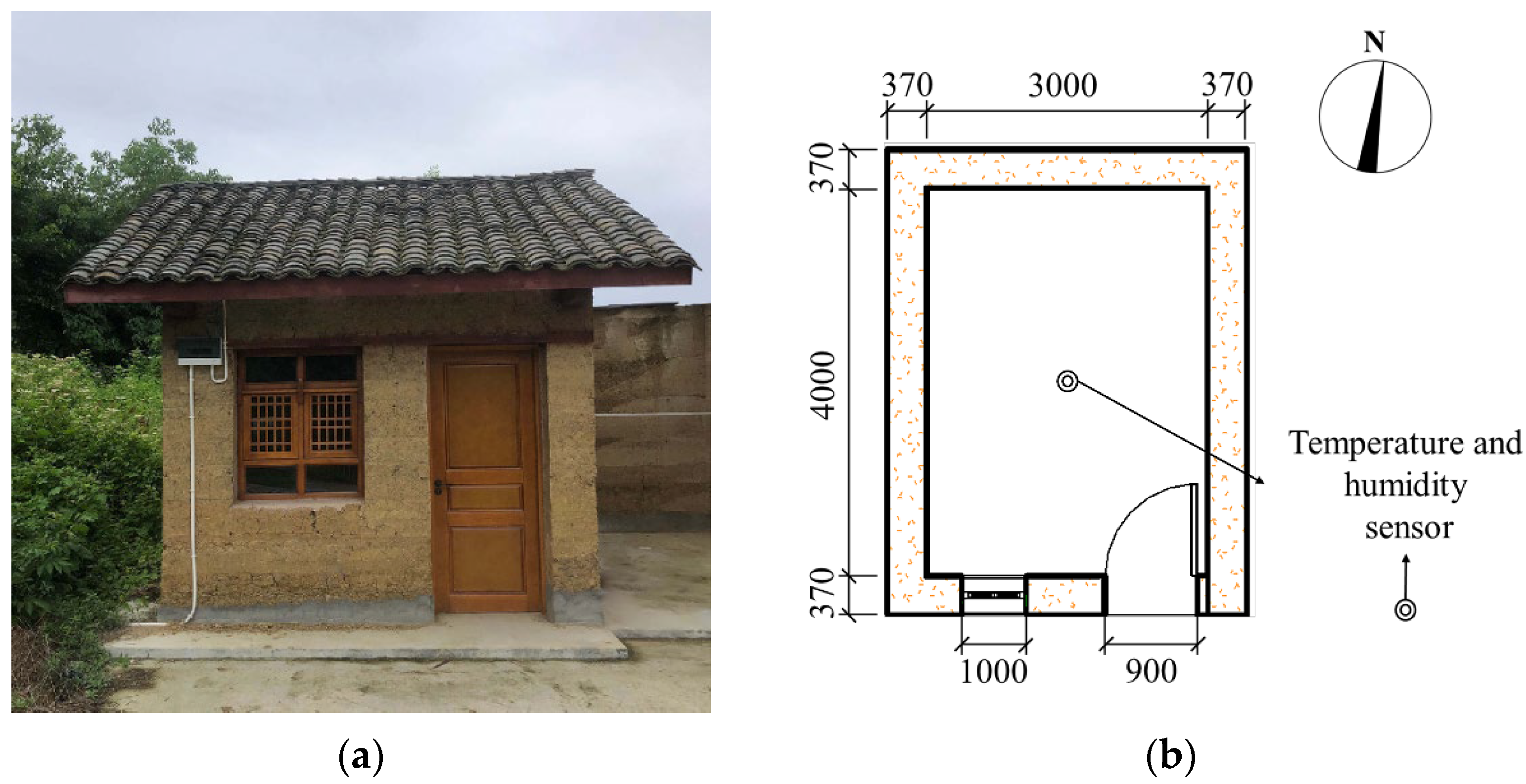
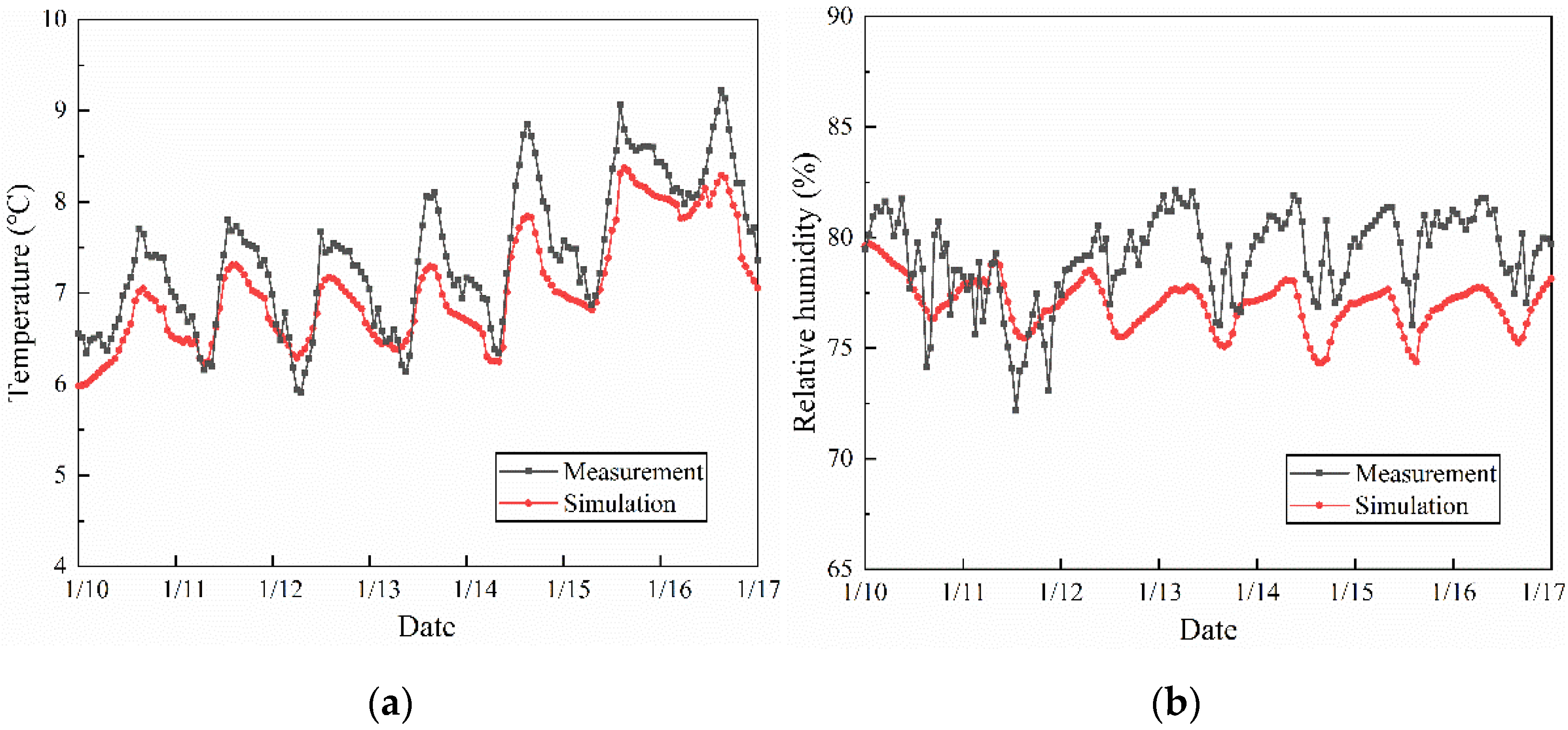
3.3. Model Validation

A newly built half-year-old rammed-earth building was used to measure the change in indoor temperature and humidity. The building size is 4 m × 3 m × 2.7 m, and the wall thickness is 370 mm. There is an outer door with a size of 2.0 m × 0.9 m and a single glass window with a size of 1.2 m × 1.0 m. There is no heat and humidity source in the room. The general situation of the building and the placement of temperature and humidity sensors are shown in Figure 5. The measurement data for one week in January were selected for model validation.

The comparison between the simulation results and measurement data is shown in Figure 6. The maximum relative errors in temperature and relative humidity were 11.43% and 5.33%, respectively, with an average relative error of 7.74% and 3.13%, respectively. It indicates that the numerical model is in good agreement with the measurement results.

4. Simulation of Heat and Moisture Transfer

In this study, a variety of working conditions were simulated and analyzed using the rammed earth wall in Northwest Sichuan as an example. The PDE module of COMSOL software was used to solve the heat and moisture transfer model and the indoor air heat and moisture balance equations. The uniform mesh grid was adopted in the simulation and the size was 0.01 mm. The thermal conductivity and water vapor permeability of earth materials use the functions fitted in the previous section and the constants, respectively. The constant values of the two coefficients are the integral average value of their functions in the range of 0–100% relative humidity. The constant value of thermal conductivity was 0.598 W/mK, and that of water vapor permeability was 1.341 × 10⁻¹¹ kg/s·Pa.

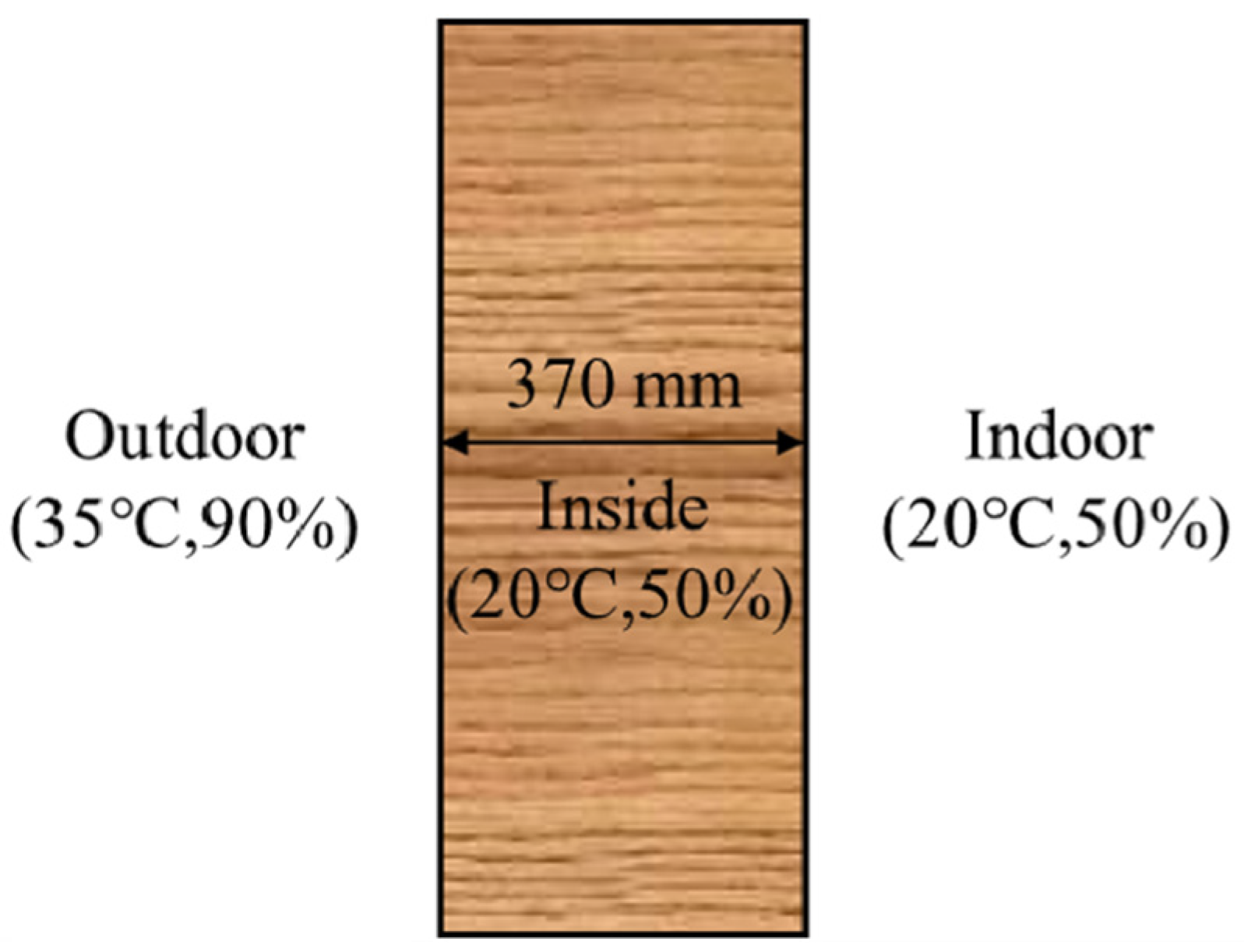
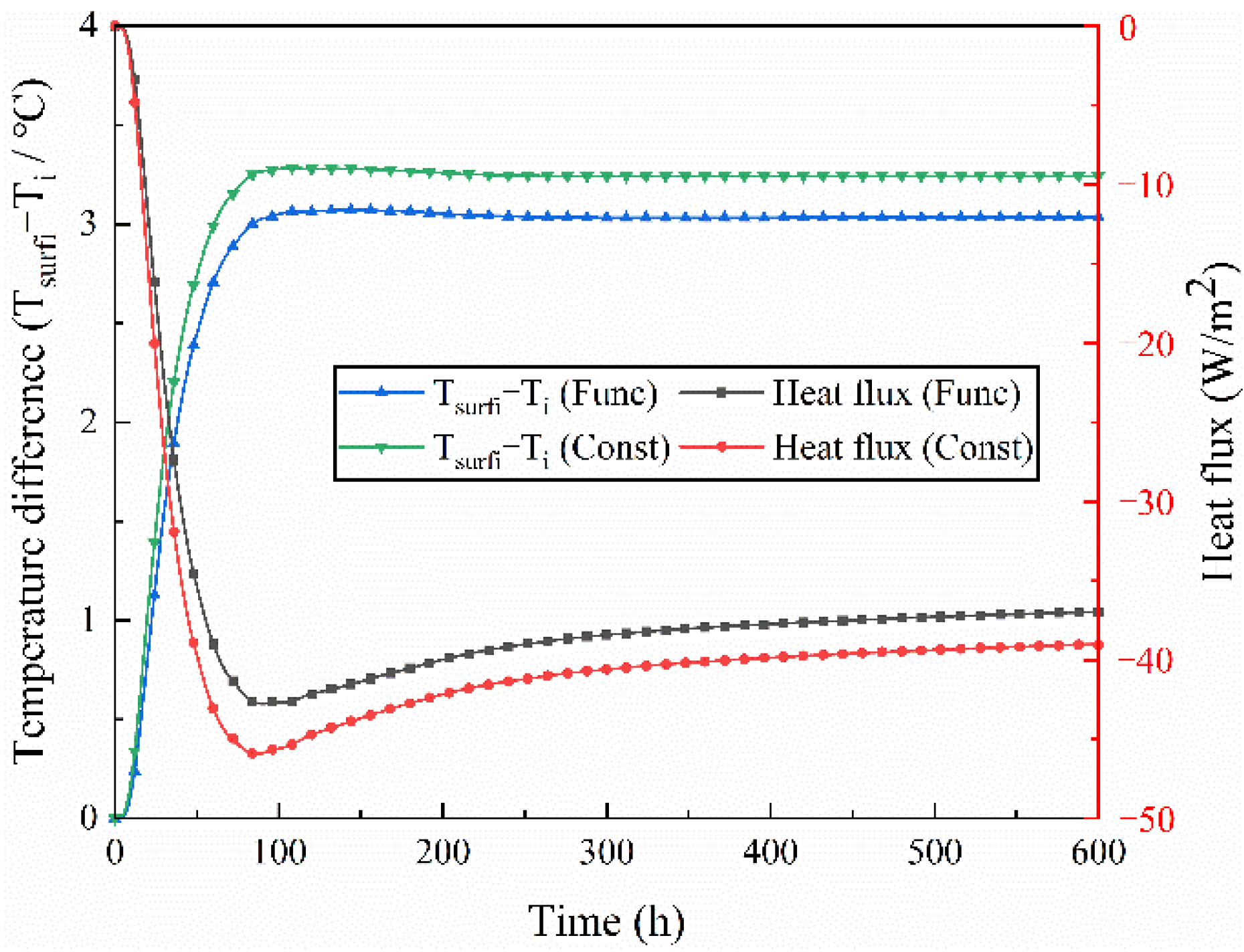
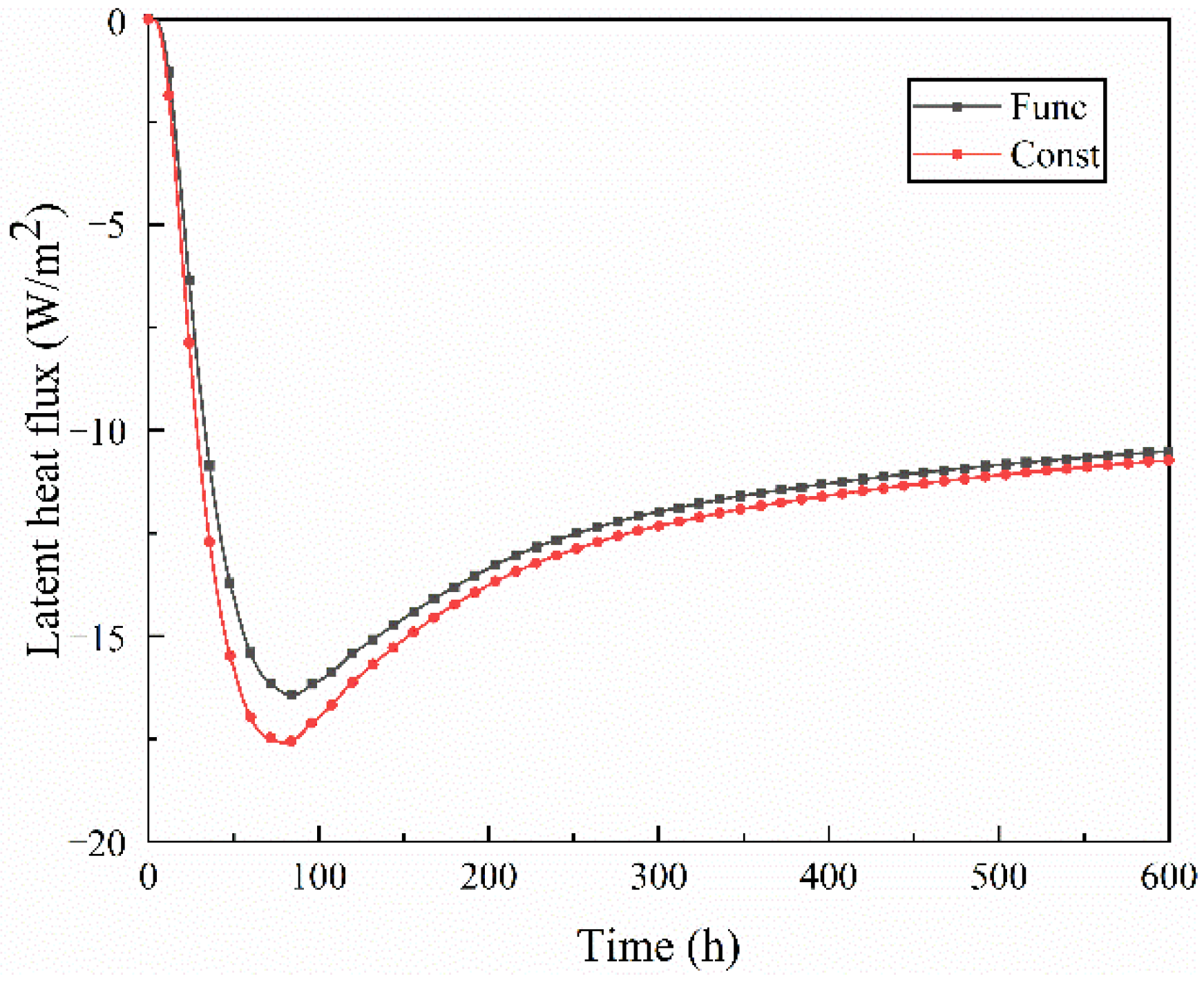
4.1. Steady Boundary

To study the influence of material hygrothermal parameters on the heat and moisture transfer of the rammed earth walls under steady boundary conditions, a 370-mm-thick rammed earth wall (Figure 7) was used as the object of study, and its heat and moisture transfer was simulated and calculated. It was assumed that the outdoor temperature and humidity were 35 °C and 90%, respectively, and the indoor was 20 °C and 50%, respectively. The initial state inside of the wall was the same as the indoors, and the calculated duration was 600 h.

The characteristics of temperature and heat flux variations on the internal surface of the rammed earth wall under the two conditions are shown in Figure 8, Figure 9 and Figure 10.

According to Figure 8 and Figure 9, the negative values of heat flux indicate that the rammed earth wall released heat. T_surfi-T_i indicates the temperature difference between the internal surface of the wall and the indoor air. The internal surface of the wall released heat at a higher rate during the initial 85 h, with the heat flux and temperature rising faster and stabilizing after 85 h. The heat flux and temperature on the internal surface under constant conditions were always higher than those under functional conditions. However, the temperature difference was small, and the difference gradually increased and then began to stabilize. The average heat flux and temperature differences were 2.37 W/m² and 0.21 °C, respectively, with an average relative error of 8.42% and 0.93%. The reasons are as follows: the indoor air temperature and relative humidity were low, and the internal surface of the wall releases moisture and heat. The thermal conductivity of the constant condition was greater than that of the function condition, and the heat release rate under the constant condition was greater. Meanwhile, the moisture transfer under constant conditions was greater than that under functional conditions. The latent heat of phase change under constant conditions was correspondingly greater, and the temperature rise caused by the latent heat of phase change was higher (shown in Figure 10), which causes the difference in heat flux and temperature increase. As the temperature inside the wall increases, the heat release rate begins to decrease and becomes stable. The heat flux and temperature begin to stabilize and the difference between the two conditions is stable.

As shown in Figure 10, the internal surface of the wall released heat at a higher rate during the initial 85 h, with the latent heat flux rising faster and starting to decrease after 85 h. The latent heat flux on the internal surface under constant conditions was always greater than that under functional conditions, and the difference gradually increased and then began to stabilize. The average latent heat flux difference was 0.50 W/m², with an average relative error of 6.07%. The reasons are as follows: the indoor air relative humidity was low, and the internal surface of the wall releases moisture. The water vapor permeability of the constant condition was greater than that of the functional condition, and the moisture release rate under constant conditions was greater. Meanwhile, the thermal conductivity under constant conditions was greater than that under functional conditions, which increases the difference in latent heat flux. As the moisture content inside the wall increases, the moisture release rate begins to decrease, as well as the moisture flux. The latent heat flux begins to decrease and the difference between the two conditions was stable.

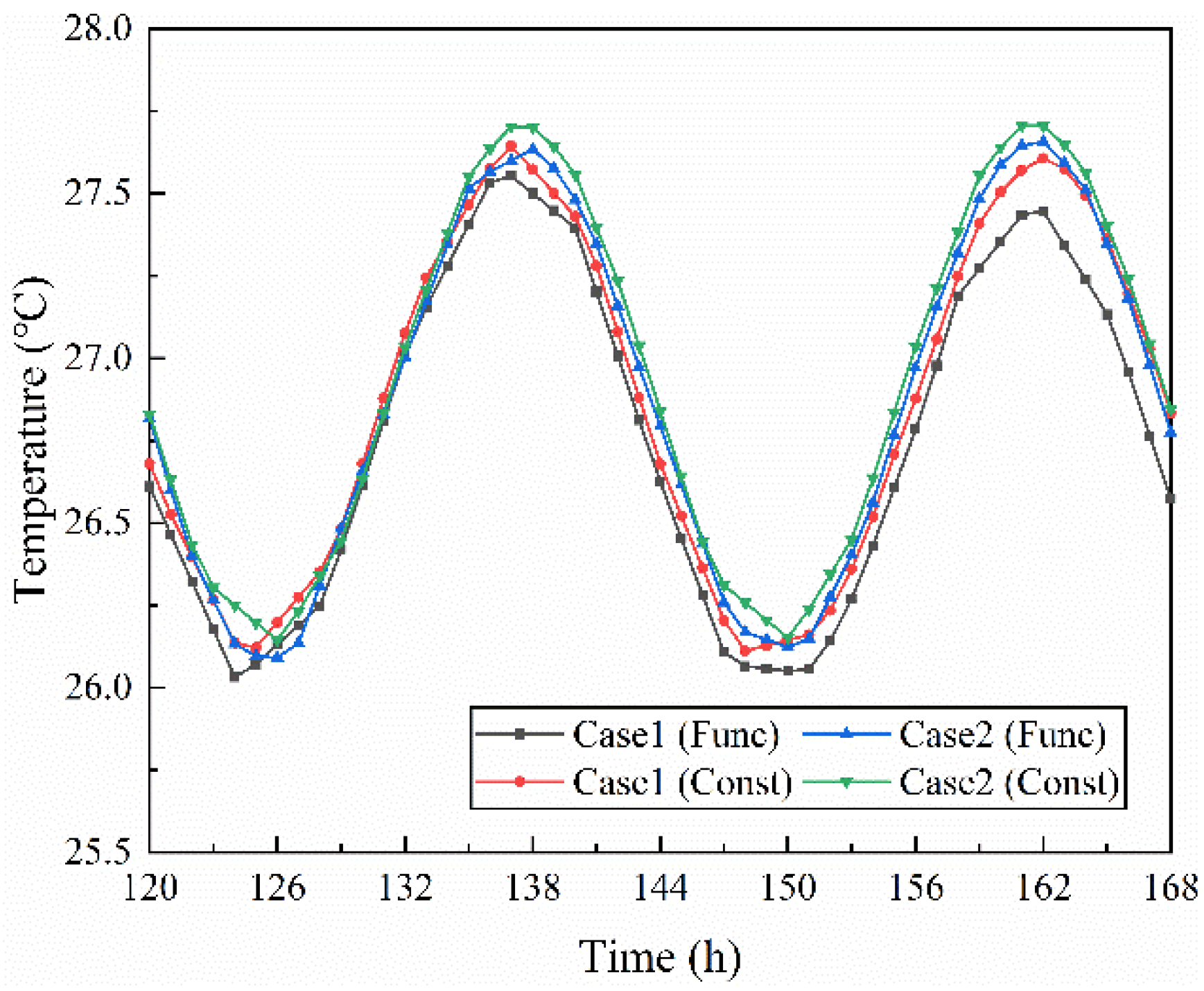
4.2. Period Boundary

To investigate the influence of material hygrothermal parameters on the heat and moisture transfer of rammed earth walls under the diurnal variation in the indoor and outdoor temperatures and humidity, a 370-mm-thick rammed earth wall was used as the object of study. The heat and moisture transfer of the wall were simulated and calculated. The calculation conditions [36] are listed in

Table 4. Indoor and outdoor temperature and humidity during different working conditions.

	Case 1	Case 2
Outdoor temperature	$T_e\left(t\right)=303.15+3\cos \left(\frac{\pi t}{12}-161\right)$	$T_e\left(t\right)=303.15+3\cos \left(\frac{\pi t}{12}-161\right)$
Indoor temperature	$T_i\left(t\right)=299.15+2.5\cos \left(\frac{\pi t}{12}-161\right)$	$T_i\left(t\right)=299.15+2.5\cos \left(\frac{\pi t}{12}-161\right)$
Outdoor relative humidity	${\phi }_e\left(t\right)=0.7-0.1\cos \left(\frac{\pi t}{12}+2.6\right)$	${\phi }_e\left(t\right)=0.4-0.1\cos \left(\frac{\pi t}{12}+2.6\right)$
Indoor relative humidity	${\phi }_i\left(t\right)=0.7-0.05\cos \left(\frac{\pi t}{12}+2.6\right)$	${\phi }_i\left(t\right)=0.4-0.05\cos \left(\frac{\pi t}{12}+2.6\right)$

.

Cases 1 and 2, with different working conditions, represent the periodic variations in temperature and humidity in humid and dry areas in summer, respectively. The initial state inside the wall was the same as that on the internal of the wall, and the calculated duration was 168 h. To eliminate the influence of the initial value on the calculation results, the calculation results of the latter 48 h were analyzed.

As shown in Figure 11, the temperature of the internal surface of the wall varies periodically with the indoor and outdoor temperature and humidity, and the temperature difference between the two conditions is small. In Case 1, the average temperature was 26.76 °C and 26.86 °C under the function and constant conditions, respectively, with a maximum temperature difference of 0.1 °C. In Case 2, the average temperature was 26.88 °C and 26.93 °C under the function and constant conditions, respectively, with a maximum temperature difference of 0.06 °C.

As shown in Figure 12, the negative values of heat flux indicate that the rammed earth wall releases heat, while the positive values indicate that heat is absorbed. In Case 1, the heat flux was 922.15 W/m² under constant conditions, which is 4.65% higher than 881.14 W/m² under functional conditions. In Case 2, the heat flux was 667.10 W/m² under constant conditions, which is 2.02% higher than 653.88 W/m² under functional conditions.

Figure 13 shows the variation of the latent heat flux on the internal surface of the wall. In Case 1, the latent heat flux was 365.87 W/m² under constant conditions, which is 9.93% higher than 332.83 W/m² under functional conditions. In Case 2, the latent heat flux was 216.15 W/m² under constant conditions, which is 0.30% lower than 216.79 W/m² under functional conditions.

The above results indicate that the non-constant hygrothermal parameters have little influence on the internal surface temperature of the rammed walls but have a great influence on the heat transfer. The difference in heat transfer between the two conditions is more obvious in high temperature and high humidity conditions.

4.3. Mianyang Climate Boundary

The results show that whether the hygrothermal parameters are constant or not makes a difference to the heat flux on the internal surfaces of the walls. For ordinary buildings, the indoor temperature and humidity are mainly influenced by the heat and moisture fluxes on the internal surfaces of the walls. Therefore, to investigate the influence of hygrothermal parameters of the wall material on the indoor heat and moisture environment, this section simulates the changes in rammed earth building indoor temperature and humidity, as well as the heat transfer of the internal surfaces of the wall under the climatic conditions in Mianyang City. The hygrothermal parameters of the wall are taken as functions and constants, respectively.

The outdoor meteorological parameters were obtained from typical meteorological year data for Mianyang City, and the initial temperature and humidity conditions inside the walls were consistent with the climate. The size of the room was 4 m × 3 m × 3 m, and the thickness of the wall was 370 mm. The number of air changes in the room was 1 ACH, and there were no sources of heat or humidity in the room. The air penetrating the room through the gaps in the windows and doors was ignored, and the effect of solar radiation on the walls in all orientations was considered. It was assumed that the floor and roof were waterproofed and insulated and the air in the room was well mixed. The calculated duration was 365 d and the results were recorded for one week in January and one week in July to analyze the changes in the indoor temperature and humidity. Finally, the differences in heat transfer throughout the year were analyzed.

As shown in Figure 14 and Figure 15, the difference in temperature and humidity between the two conditions was insignificant. During winter, the indoor average temperature was 6.29 °C and 6.32 °C under the function and constant conditions, respectively, with the maximum temperature difference and maximum relative humidity difference of 0.33 °C and 1.02%. During summer, the indoor average temperature was 26.77 °C and 26.98 °C under the function and constant conditions, respectively, with the maximum temperature difference and maximum relative humidity difference of 0.46 °C and 1.51%.

To analyze the influence of the two conditions on the heat transfer to the wall, the heat transfer for the entire year was calculated, as shown in Figure 16. The heat transfer at a given time can be calculated as

$$Q_i={{\displaystyle \int }}_{t_1}^{t_2}\left[h_i\left(T_i-T_{surfi}\right)+h_{lv}{g}_{n,i}\right]$$

(14)

where $Q_i$ is the heat transfer from the internal surface of the wall (J/m²) and $t$ is the time (s).

As shown in Figure 16, the largest difference in heat transfer was 1.33 MJ/m² in summer, and the heat transfer under constant conditions was 7.52% higher than that under functional conditions. Meanwhile, the largest difference in latent heat transfer was 0.31 MJ/m² in spring, and the latent heat transfer under constant conditions was 6.11% higher than that under functional conditions. In summer, higher outdoor ambient temperature and large temperature difference between indoor and outdoor make a large difference in heat transfer between the two conditions. In spring, higher outdoor ambient humidity and large humidity differences between indoor and outdoor make a large difference in moisture transfer between the two conditions, resulting in large latent heat transfer difference. During the whole year, the heat transfer was 71.03 MJ/m² under constant conditions, which is 4.97% higher than 67.67 MJ/m² under functional conditions. The latent heat transfer was 22.98 MJ/m² under constant conditions, which is 5.03% higher than 21.88 MJ/m² under functional conditions. The above results indicate that there is a significant difference in heat transfer on the internal surface between the two conditions in hot and humid areas.

5. Conclusions

In this study, the functional relationship between the thermal conductivity, water vapor permeability, and humidity of earth materials from Northwestern Sichuan was obtained through experiments. A non-stationary model of the heat and moisture transfer in rammed earth walls and indoor air was developed and validated. The function curves and constants of the two coefficients were substituted into the numerical model and solved using COMSOL Multiphysics software. The differences in the heat and moisture transfer of the wall under different working conditions were analyzed when the material hygrothermal parameters were regarded as the functions and constants. The influence of the material hygrothermal parameters on the heat and moisture transfer of the wall was studied and investigated. The following conclusions were drawn:

• The thermal conductivity of the earth materials from Northwest Sichuan is linearly related to moisture content, with R² being greater than 0.98. The water vapor permeability has a small variation in the 0–60% relative humidity range and increases exponentially above 60%.
• A numerical model with temperature and humidity as driving potential was established. The measured data of the rammed earth building are in good agreement with the simulation results under the same conditions.
• At a steady boundary, when the moisture content of the rammed earth wall was low, the thermal conductivity and water vapor permeability under the constant condition were higher than that under the function condition, making the temperature and the heat flux on the internal surface of the wall under the constant condition greater. Among them, the average relative error of internal surface temperature was 0.93%, which is small. The average relative error of heat flux and latent heat flux was 8.42% and 6.07%, respectively, which shows a large difference.
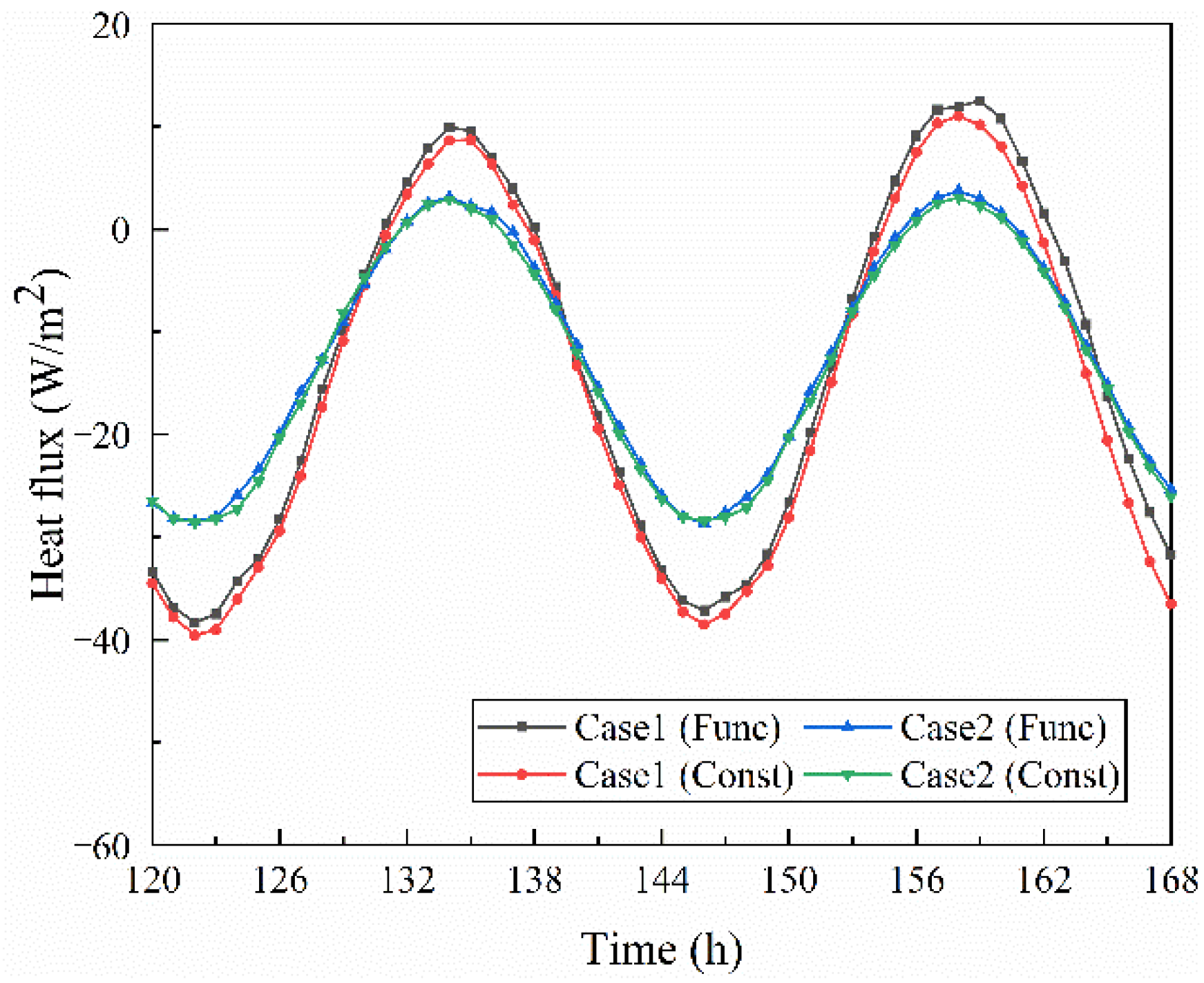
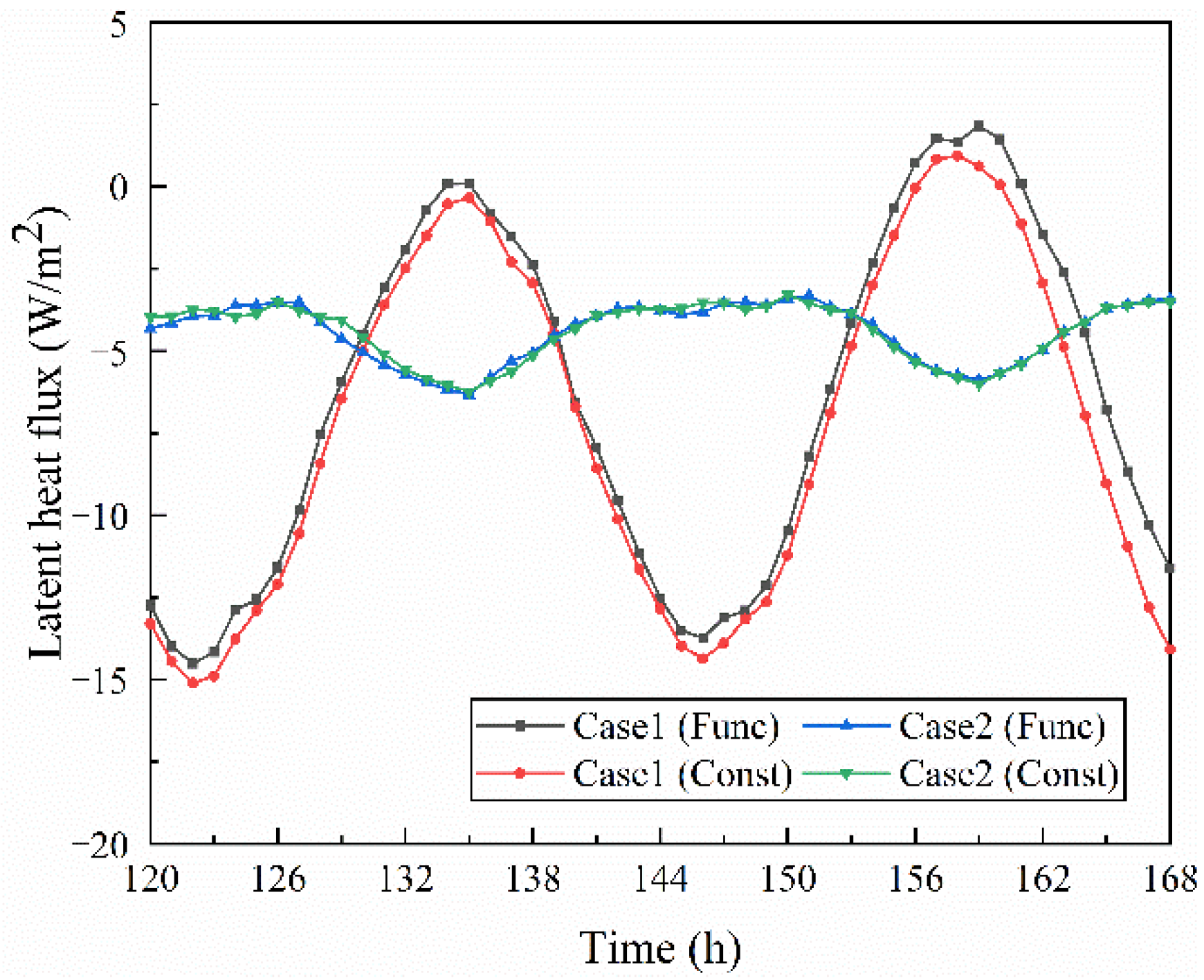
• Under the periodic boundary, the internal surface temperature of the rammed earth wall shows a small difference between the two conditions. The average temperature difference of the internal surface was less than 0.1 °C in wet and dry conditions in summer. The heat flux on the internal surface under constant conditions was 4.65% higher than that under functional conditions, and the latent heat flux on the internal surface under constant conditions was 9.93% higher than that under function conditions in the humid summer condition. In the dry summer conditions, the figures were 2.02% and −0.30%. The heat transfer difference between the two conditions is more obvious in high temperature and high humidity conditions.
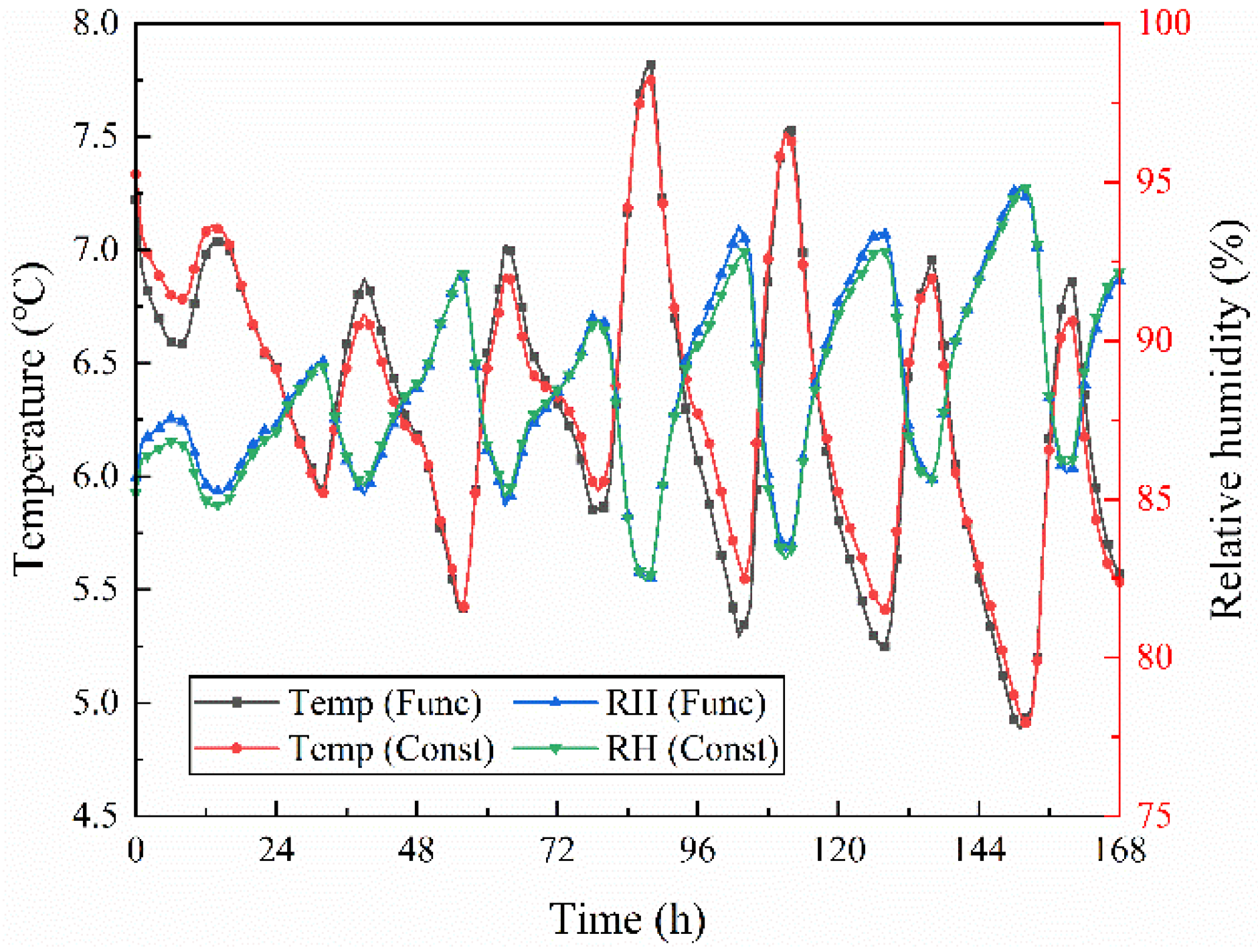
• Under the climate boundary of Mianyang City, the rammed earth building indoor air temperature and humidity in summer and winter were similar under the two conditions. The largest difference in heat transfer on the internal surface was in summer, and under constant conditions was 7.52% higher than that under functional conditions. Meanwhile, the largest difference in latent heat transfer on the internal surface was in spring, and under constant conditions was 6.11% higher than that under functional conditions. Throughout the whole year, the heat flux under constant conditions was 4.97% higher than that under functional conditions, and the latent heat flux under constant conditions was 5.03% higher than that under functional conditions. There is a significant difference in heat transfer between the two conditions in hot and humid areas.