Comparative Analysis of Mechanical Performance of Flat Slabs with Reverse and Conventional Column Caps
Abstract
:1. Introduction
2. FE Modelling
2.1. Selection of Solver
2.2. Element Type and Contact Settings
2.3. Loading Schemes and Boundary Conditions
2.4. Material Constitutive Relations
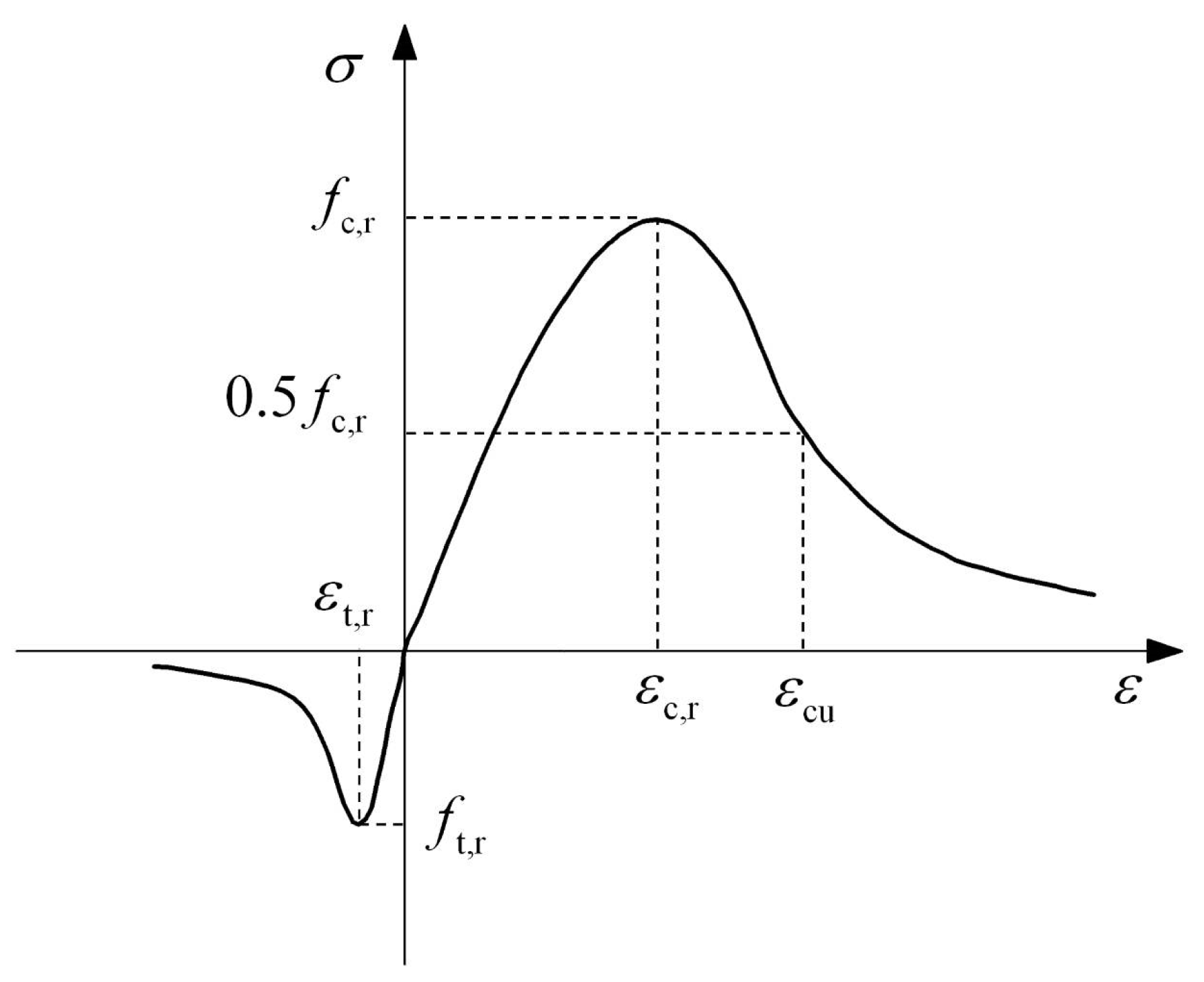
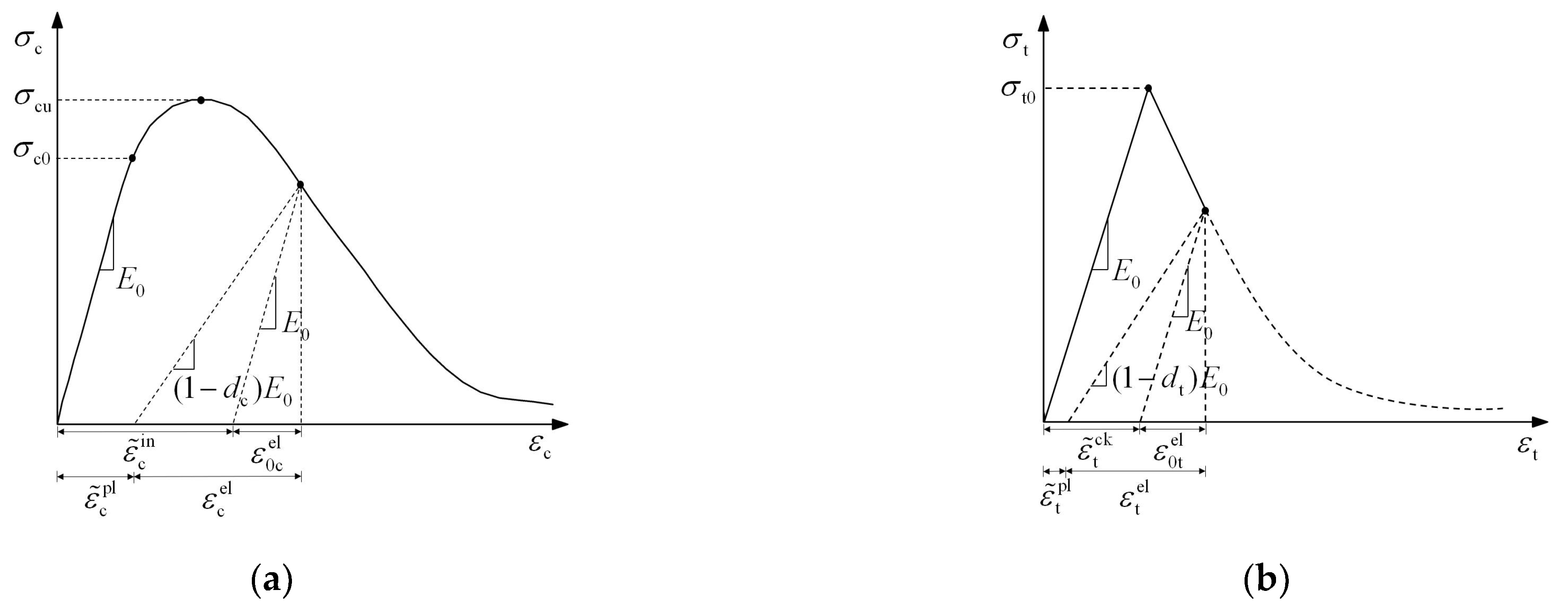
2.4.1. Concrete Constitutive Relations
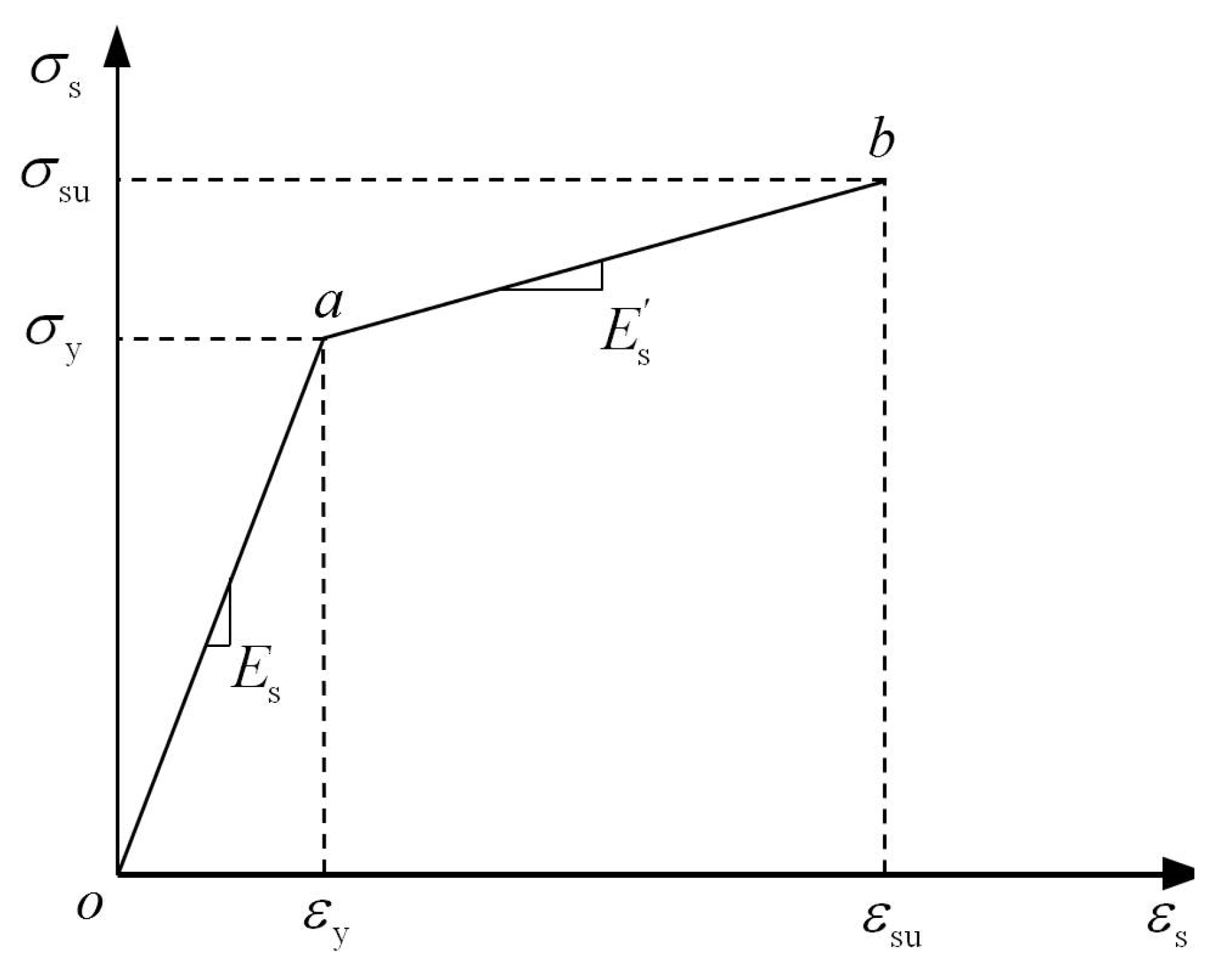
2.4.2. Reinforcement Constitutive Relations
3. Validation of FE Simulation Method
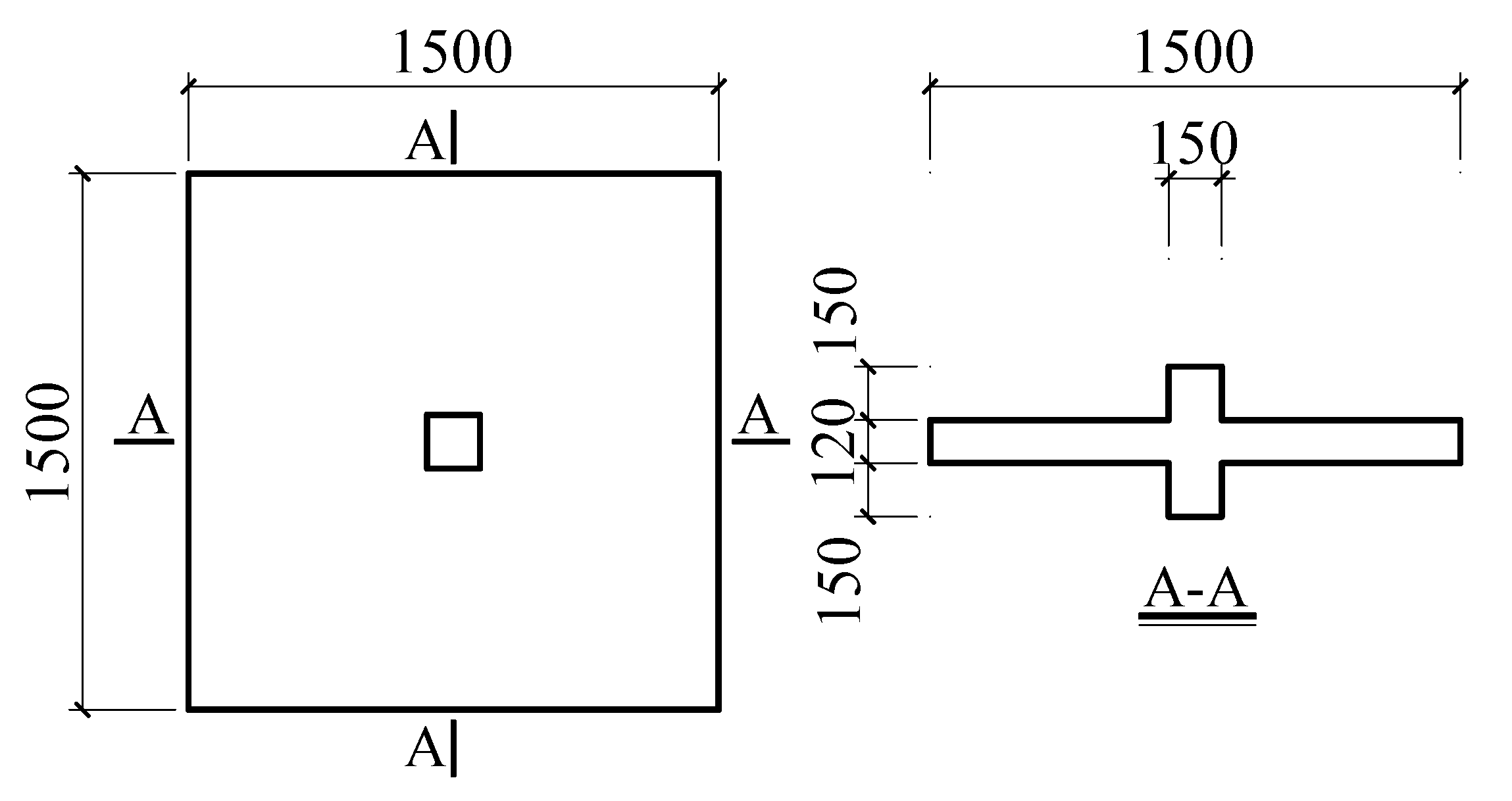
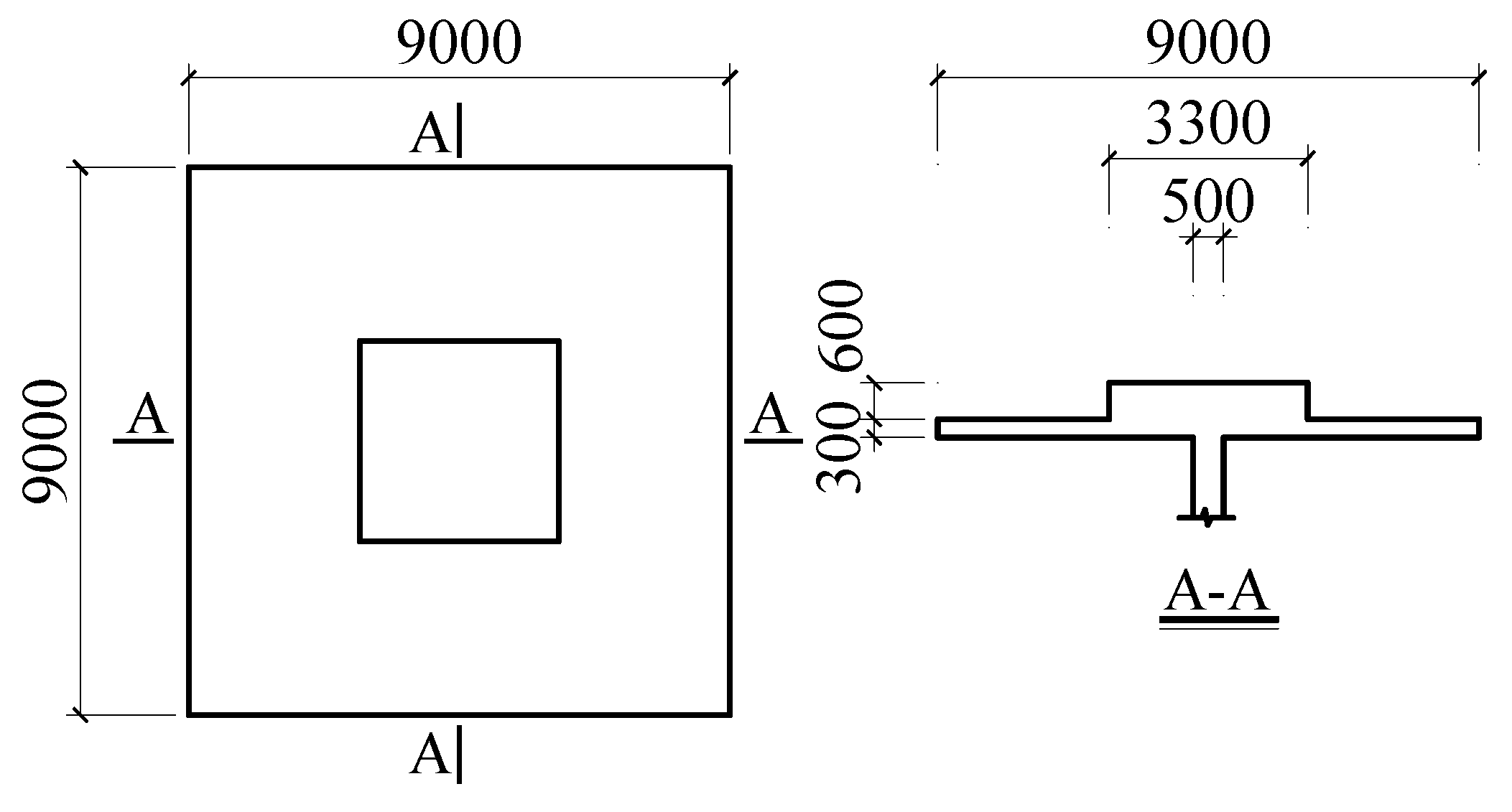
3.1. Overview of Test and Development of FE Models
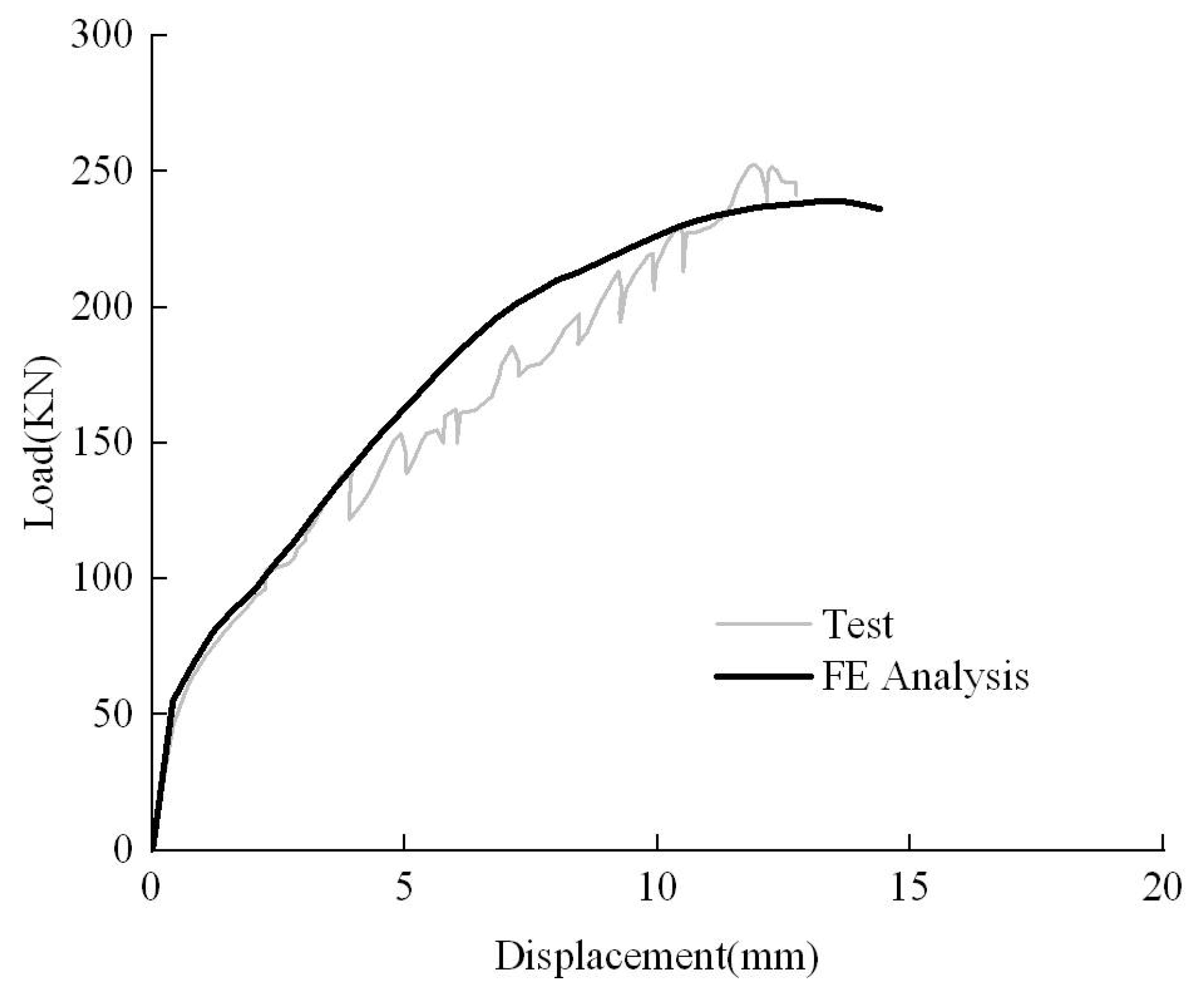
3.2. Comparison of Test and FE Results
4. Mechanical Performance Analysis of Slab-Column Joints
4.1. Analysis of FE Models
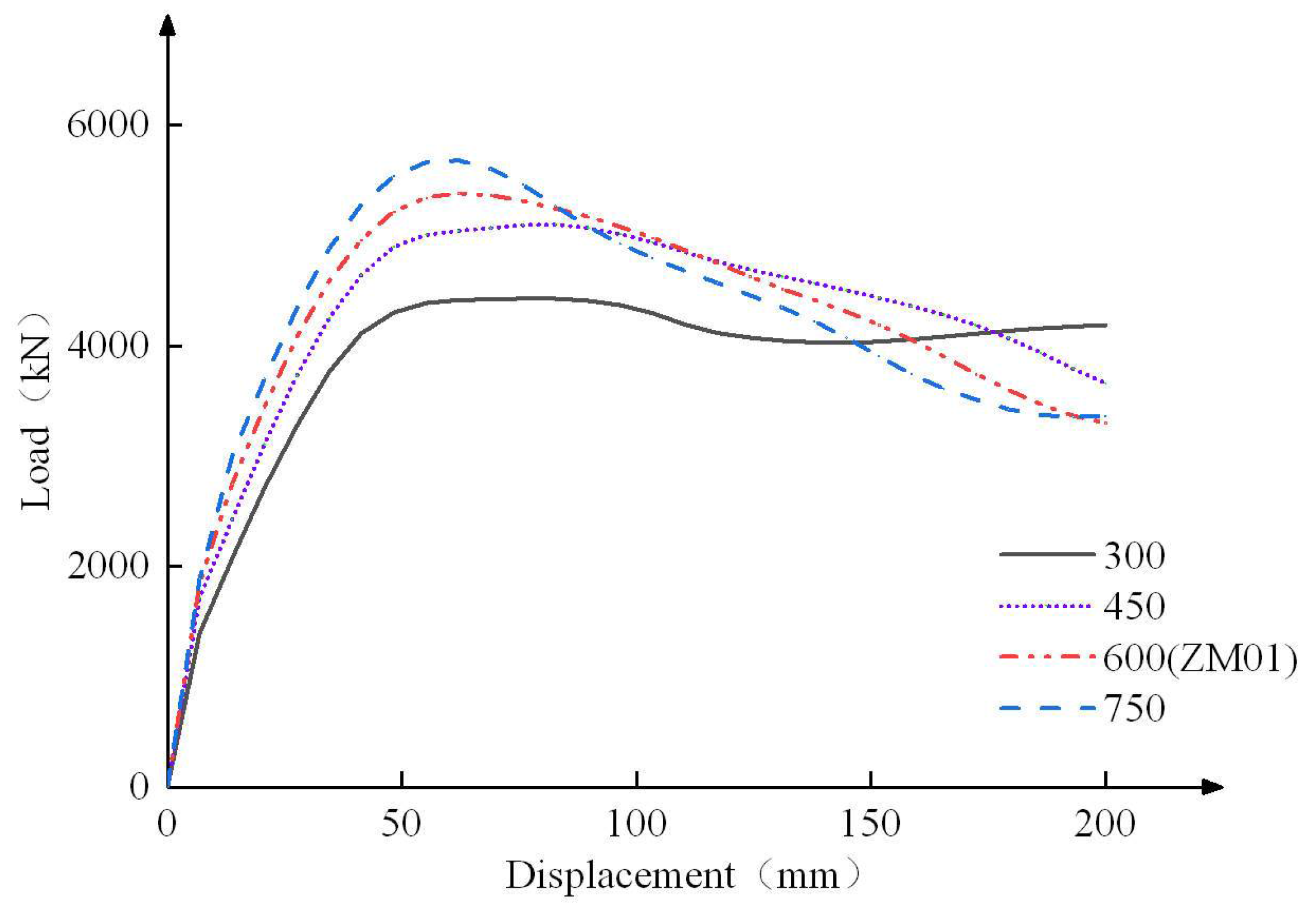
4.2. Comparison of Load–Displacement Curves
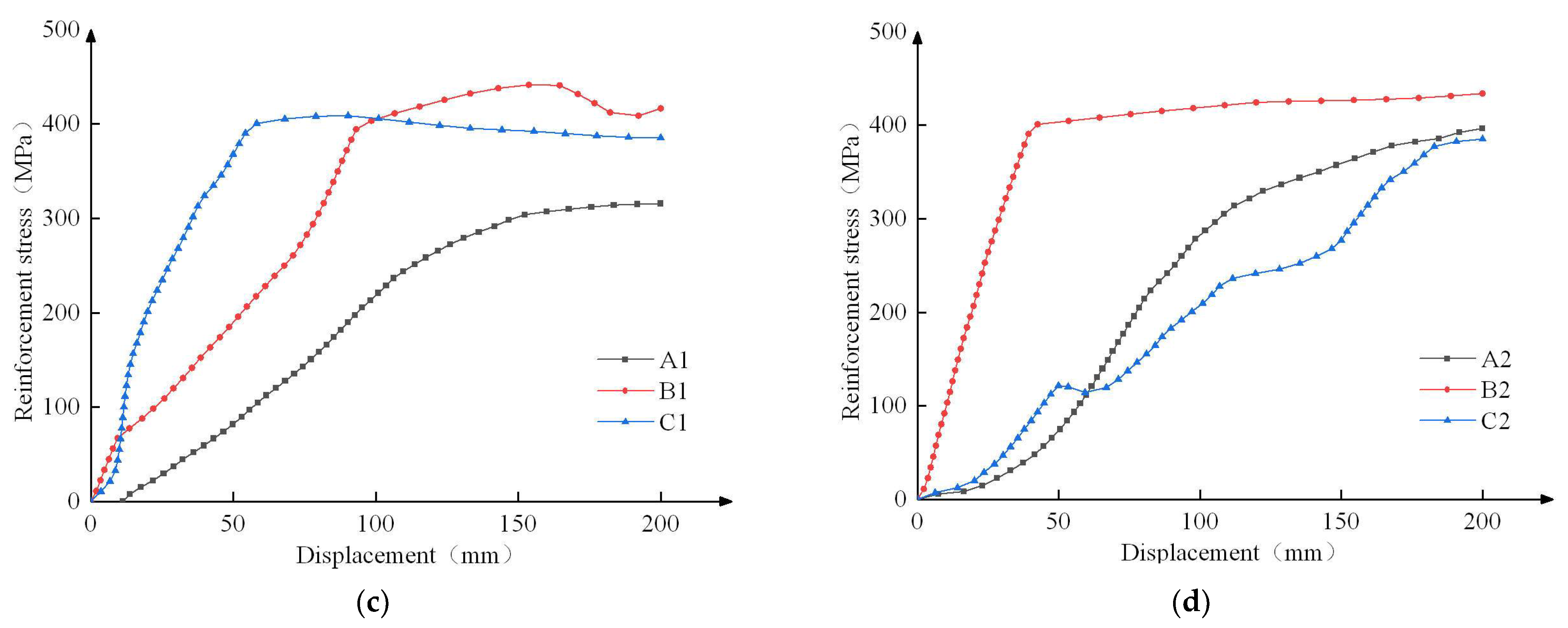
4.3. Comparison of Stress Change in Reinforcement
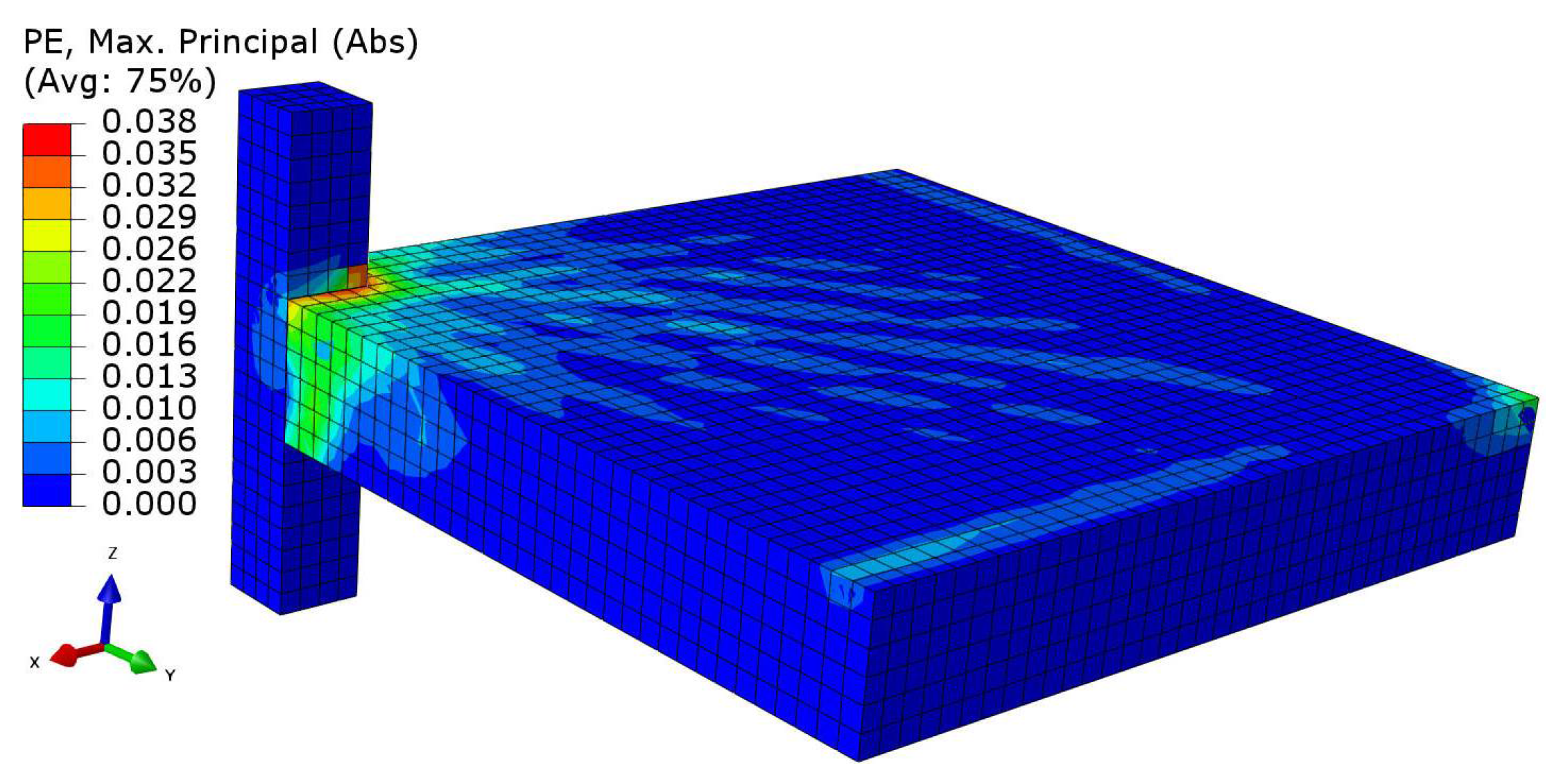
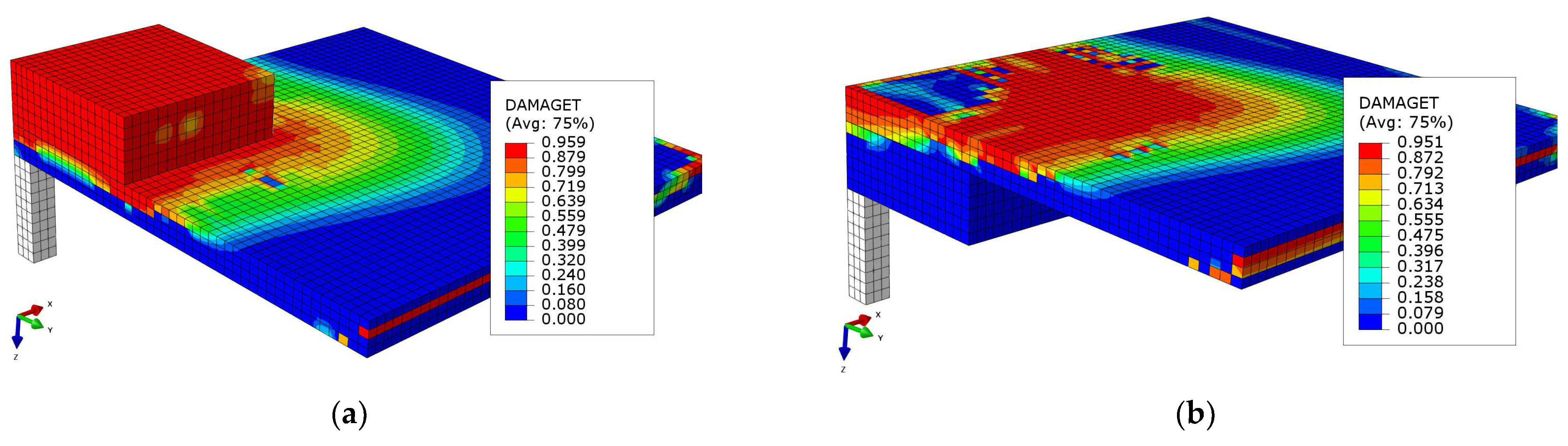
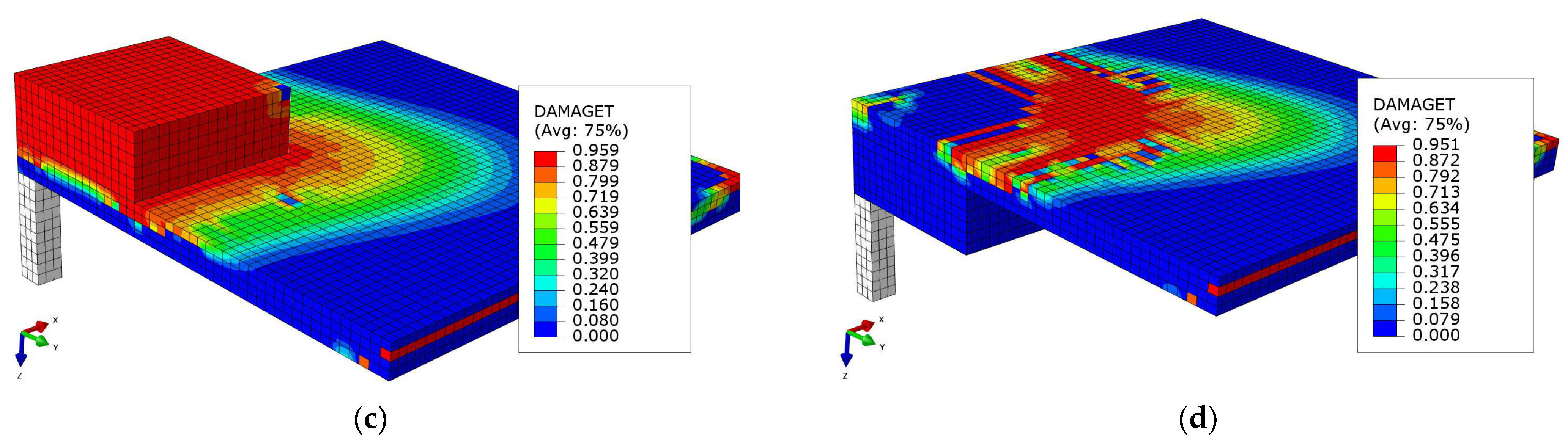
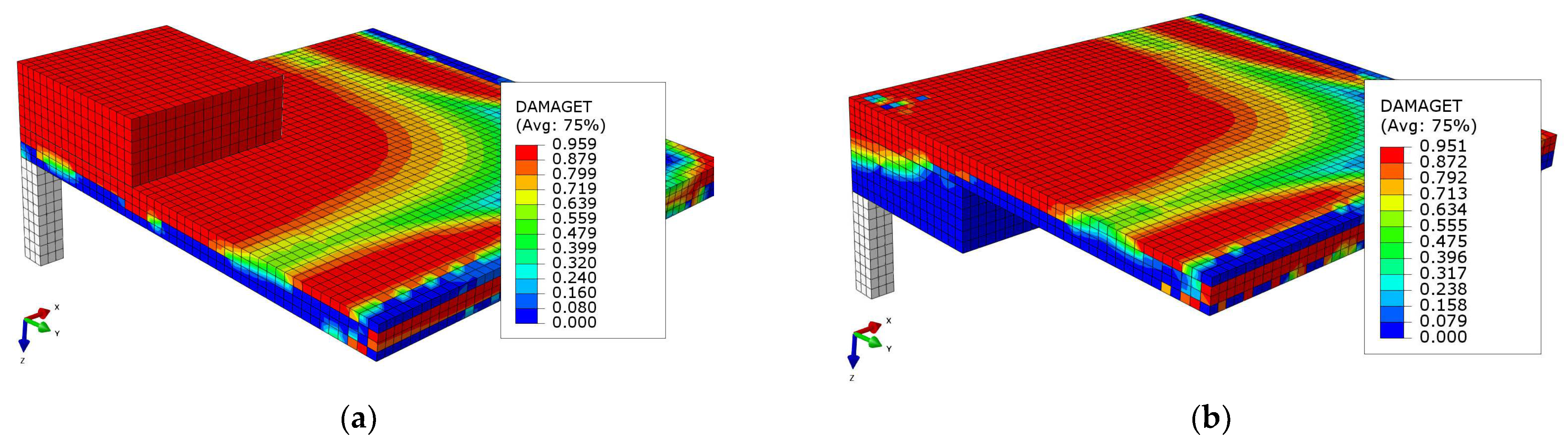
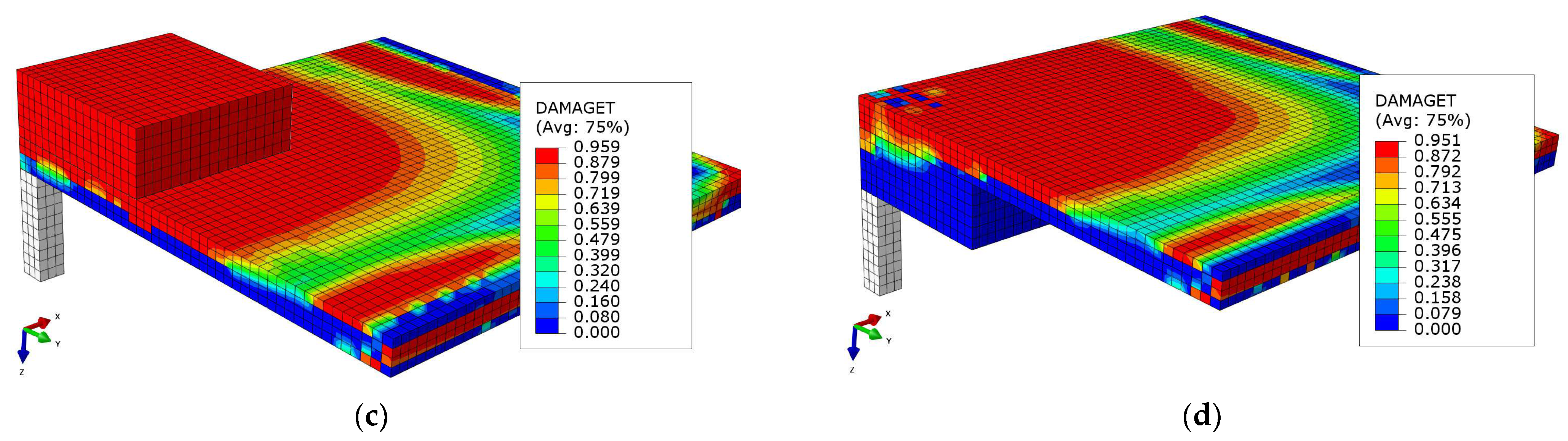
4.4. Development of Concrete Tensile Damage
4.5. Parametric Analysis
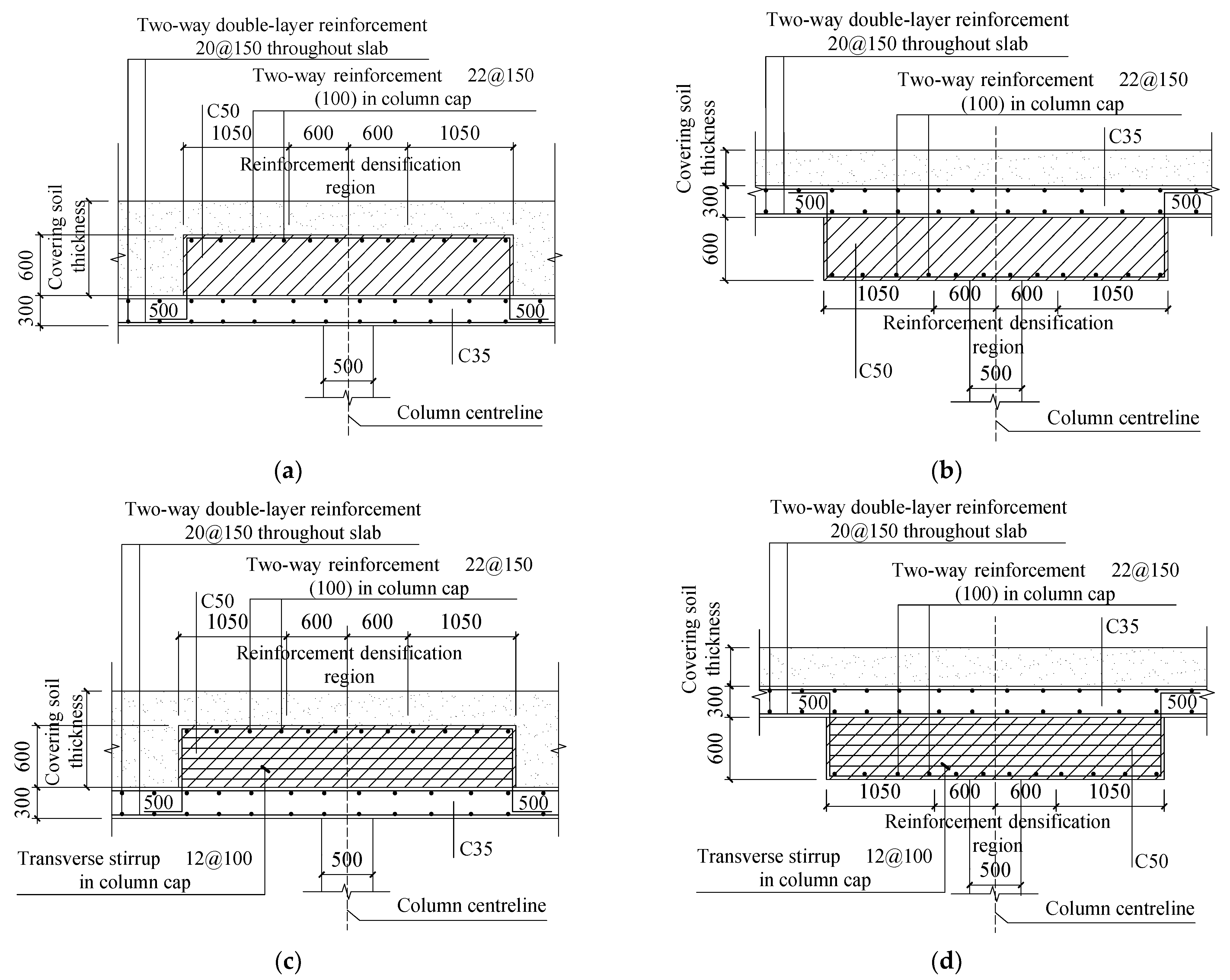
4.5.1. Size of Column Cap
4.5.2. Depth of Column Cap
5. Design
5.1. Punching Shear Design Provisions
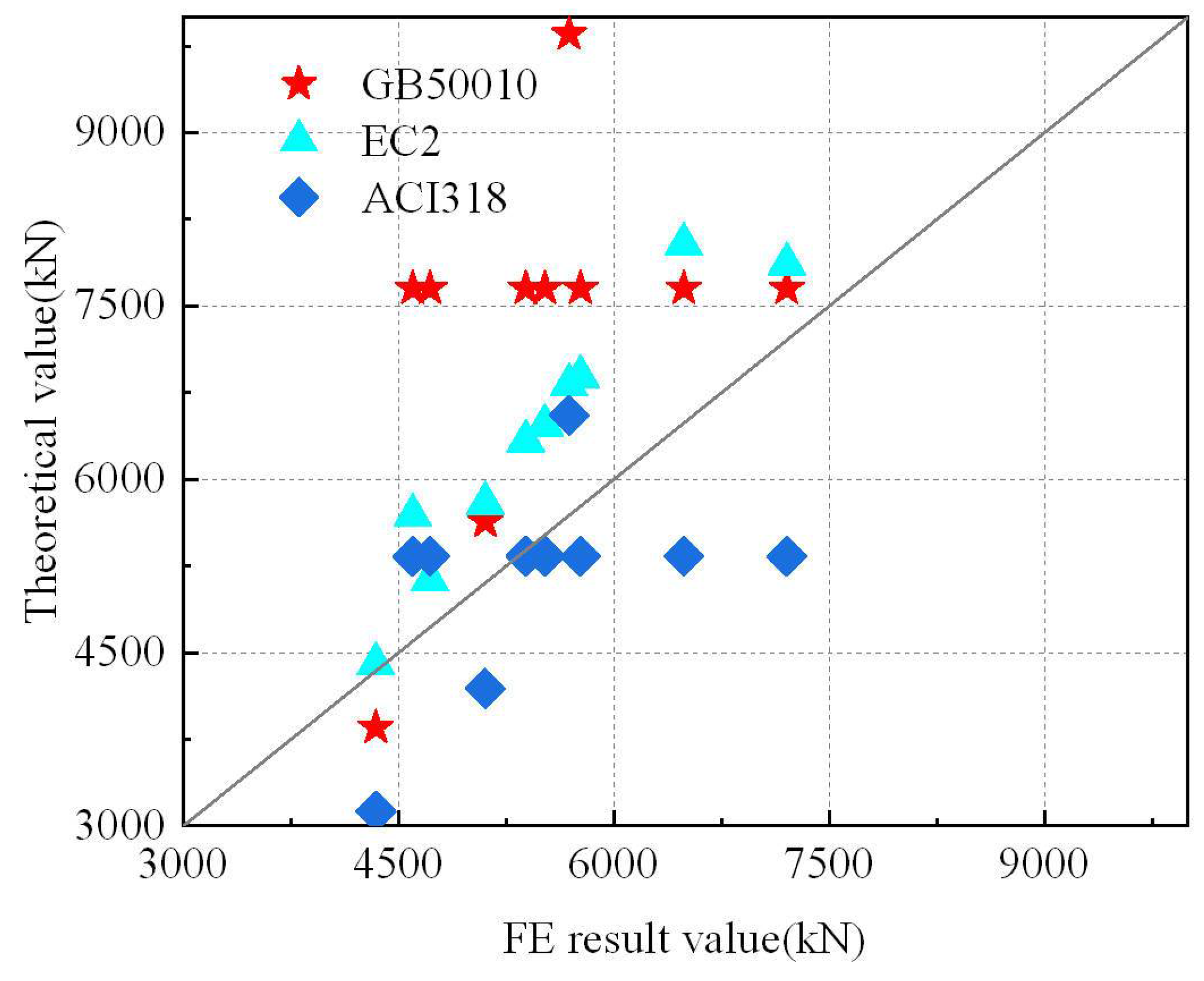
5.2. Evaluation of Design Codes
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- GB50010-2010 (2015); Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Development: Beijing, China, 2015.
- Niehols, T.R. Statistical limitations upon the steel requirement in reinforced concrete flat slab floors. Soc. Civ. Eng. ASCE 1914, 77, 1670. [Google Scholar] [CrossRef]
- Westergaard, H.M.; Slater, W.A. Moments and stresses in slabs. Proc. Am. Concr. Inst. 1921, 17, 415–538. [Google Scholar]
- Elstner, R.C.; Hognestad, E. Shearing strength of reinforced concrete slabs. ACI J. 1956, 53, 29–58. [Google Scholar]
- Regan, P.E. Design for punching shear. J. Struct. Eng. 1974, 52, 197–207. [Google Scholar]
- Luo, Y.H.; Durrani, A.J. Equivalent beam model for flat- slab buildings. ACI Struct. J. 1995, 92, 115–124. [Google Scholar]
- EC2 (2004); EN 1992-1-1:2004: Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. National Standards Authority of Ireland: Dublin, Ireland, 2014.
- ACI-318 (2019); Committee 318—Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary on Building Code Requirements. American Concrete Institute: Farmington Hills, MI, USA, 2019.
- Inácio, M.M.G.; Almeida, A.F.O.; Faria, D.M.V.; Lúcio, V.J.G.; Ramos, A.P. Punching of high strength concrete flat slabs without shear reinforcement. Eng. Struct. 2015, 103, 275–284. [Google Scholar] [CrossRef]
- Majid, M.A.; Abdul, R.S.; Lee, S.C.; Ali, A.S. Numerical investigation of non-shear-reinforced UHPC hybrid flat slabs subject to punching shear. Eng. Struct. 2021, 241, 112444. [Google Scholar]
- Genikomsou, A.S.; Polak, M.A. Finite element analysis of punching shear of concrete slabs using damaged plasticity model in ABAQUS. Eng. Struct. 2015, 98, 38–48. [Google Scholar] [CrossRef]
- Balomenos, G.P.; Genikomsou, A.S.; Polak, M.A.; Pandey, M.D. Efficient method for probabilistic finite element analysis with application to reinforced concrete slabs. Eng. Struct. 2015, 103, 85–101. [Google Scholar] [CrossRef]
- Wosatko, A.; Pamin, J.; Polak, M.A. Application of damage—Plasticity models in finite element analysis of punching shear. Comput. Struct. 2015, 151, 73–85. [Google Scholar] [CrossRef]
- Jahangir, A.; Khan, M.A. FE Analysis on the effect of flexural steel on punching shear of slabs. Int. J. Eng. Res. Technol. 2013, 2, 2878–2901. [Google Scholar]
- Elsamak, G.; Fayed, S. Parametric studies on punching shear behavior of RC flat slabs without shear reinforcement. Computers Concr. 2020, 25, 355–367. [Google Scholar]
- Yooprasertchai, E.; Tiawilai, Y.; Wittayawanitchai, T.; Angsumalee, J.; Joyklad, P.; Hussain, Q. Effect of shape, number, and location of openings on punching shear capacity of flat slabs. Buildings 2021, 11, 484. [Google Scholar] [CrossRef]
- Hussain, H.K.; Abbas, A.M.; Ojaimi, M.F. Fiber-type influence on the flexural behavior of RC two-way slabs with an opening. Buildings 2022, 12, 279. [Google Scholar] [CrossRef]
- Mostofinejad, D.; Jafarian, N.; Naderi, A.; Mostofinejad, A.; Salehi, M. Effects of openings on the punching shear strength of reinforced concrete slabs. Structures 2020, 25, 760–773. [Google Scholar] [CrossRef]
- Wu, L.; Huang, T.; Tong, Y.; Liang, S. A modified compression field theory based analytical model of RC slab-column joint without punching shear reinforcement. Buildings 2022, 12, 226. [Google Scholar] [CrossRef]
- Ma, W. Behavior of Aged Reinforced Concrete Columns under High Sustained Concentric and Eccentric Loads. Ph.D. Dissertation, University of Nevada, Las Vegas, NV, USA, 2021. [Google Scholar]
- Lin, Y.; Lin, F. Discussion on structural analysis and design of flat slab. Build. Struct. 2019, 49, 238–240. [Google Scholar]
- Gong, M.; Lu, J. Design of flat slab with reverse column cap. Ind. Constr. 2011, 41, 233–235. [Google Scholar]
- Simulia, D.S. Abaqus [Computer Software]; SIMULIA: Providence, RI, USA, 2016. [Google Scholar]
- Sidiroff, F. Description of anisotropic damage application to elasticity. In Physical Non-Linearities in Structural Analysis; Springer: Berlin/Heidelberg, Germany, 1981; pp. 237–244. [Google Scholar]
- Zhao, J. Study of Reinforced Concrete Bond-Slip Mechanism and Modelling Techniques under Cyclic Loading. Master’s Thesis, Chang’an University, Xi’an, China, 2016; p. 28. [Google Scholar]
- Adetifa, B.; Polak, M.A. Retrofit of slab column interior connections using shear bolts. ACI Struct. J. 2005, 102, 268–274. [Google Scholar]
- Park, R. State of the art report ductility evaluation from laboratory and analytical testing. In Proceedings of the Ninth World Conference on Earthquake Engineering, Tokyo, Japan, 2–9 August 1991. [Google Scholar]
- JGJ/T 101-2015; Regulations for Seismic Testing of Buildings. Ministry of Housing and Urban-Rural Development: Beijing, China, 2015; p. 15.
- Zhang, C.; Ma, W.; Liu, X.; Tian, Y.; Orton, S.L. Effects of high temperature on residual punching strength of slab-column connections after cooling and enhanced post-punching load resistance. Eng. Struct. 2019, 199, 109580. [Google Scholar] [CrossRef]







| ∈ | σb0/σc0 | ||||
|---|---|---|---|---|---|
| 0.2 | 40 | 0.1 | 1.16 | 0.667 | 0.0005 |
| Concrete | Reinforcement | |||||
|---|---|---|---|---|---|---|
| (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | ||
| 44 | 2.2 | 36880 | 455 | 0.0023 | 650 | 0.25 |
| Specimen | Test | FE Simulation | ||
|---|---|---|---|---|
| Ultimate Load (kN) | Ultimate Displacement (mm) | Ultimate Load (MPa) | Ultimate Displacement (mm) | |
| SB1 | 44 | 2.2 | 455 | 0.0023 |
| Concrete Grade | |||
|---|---|---|---|
| C35 | 23.4 | 2.20 | 31,500 |
| C50 | 32.4 | 2.64 | 34,500 |
| Reinforcement Grade | ||||
|---|---|---|---|---|
| HRB400 | 400 | 0.002 | 540 | 0.02 |
| Specimen | Yield Point | Ultimate Point | Failure Point | Ductility Factor | Failure Mode | |||
|---|---|---|---|---|---|---|---|---|
| Yiled Displacement (mm) | Yield Load (kN) | Ultimate Displacement (mm) | Ultimate Load (kN) | Failure Displacement (mm) | Failure Load (kN) | |||
| ZM01 | 34.12 | 4565.48 | 63.34 | 5385.29 | 127.33 | 4577.19 | 3.73 | Flexure |
| ZM02 | 26.13 | 6308.72 | 39.82 | 7204.04 | 81.33 | 6123.43 | 3.11 | Flexure |
| ZM03 | 35.10 | 4653.22 | 61.02 | 5518.26 | 113.85 | 4690.52 | 3.24 | Flexure |
| ZM04 | 24.51 | 5648.88 | 40.65 | 6486.50 | 74.98 | 5513.53 | 3.06 | Flexure |
| Specimen | Displacements (mm) | ||
|---|---|---|---|
| A1/A2 | B1/B2 | C1/C2 | |
| ZM01 | - | 109.88 | 61.03 |
| ZM02 | - | 44.03 | - |
| ZM03 | - | 93.91 | 57.83 |
| ZM04 | - | 40.65 | - |
| Design Codes | Punching Shear Strength | Note | |
|---|---|---|---|
| GB50010 [1] | The section height influence coefficient βh = 0.9–1.0; η1 is the influence coefficient of the shape of loaded area; η2 is the influence coefficient (um/h0). | um is the critical perimeter, taken at distance 2d for EC2, and taken as distance d/2 for GB50010 and ACI318; h0 is the effective depth; αs is the column position influence coefficient, which is taken as 40, 30 and 20 for the inner, edge and corner columns, respectively; βs is the ratio of long side to short side. | |
| EC2 [7] | |||
| ACI318 [8] | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, M.; Yang, B.; Jiang, Z.; Mo, H. Comparative Analysis of Mechanical Performance of Flat Slabs with Reverse and Conventional Column Caps. Buildings 2022, 12, 1139. https://doi.org/10.3390/buildings12081139
Gong M, Yang B, Jiang Z, Mo H. Comparative Analysis of Mechanical Performance of Flat Slabs with Reverse and Conventional Column Caps. Buildings. 2022; 12(8):1139. https://doi.org/10.3390/buildings12081139
Chicago/Turabian StyleGong, Mosong, Bowen Yang, Zhengrong Jiang, and Huishan Mo. 2022. "Comparative Analysis of Mechanical Performance of Flat Slabs with Reverse and Conventional Column Caps" Buildings 12, no. 8: 1139. https://doi.org/10.3390/buildings12081139
APA StyleGong, M., Yang, B., Jiang, Z., & Mo, H. (2022). Comparative Analysis of Mechanical Performance of Flat Slabs with Reverse and Conventional Column Caps. Buildings, 12(8), 1139. https://doi.org/10.3390/buildings12081139






