Integration Method for Response History Analysis of Single-Degree-of-Freedom Systems with Negative Stiffness
Abstract
:1. Introduction
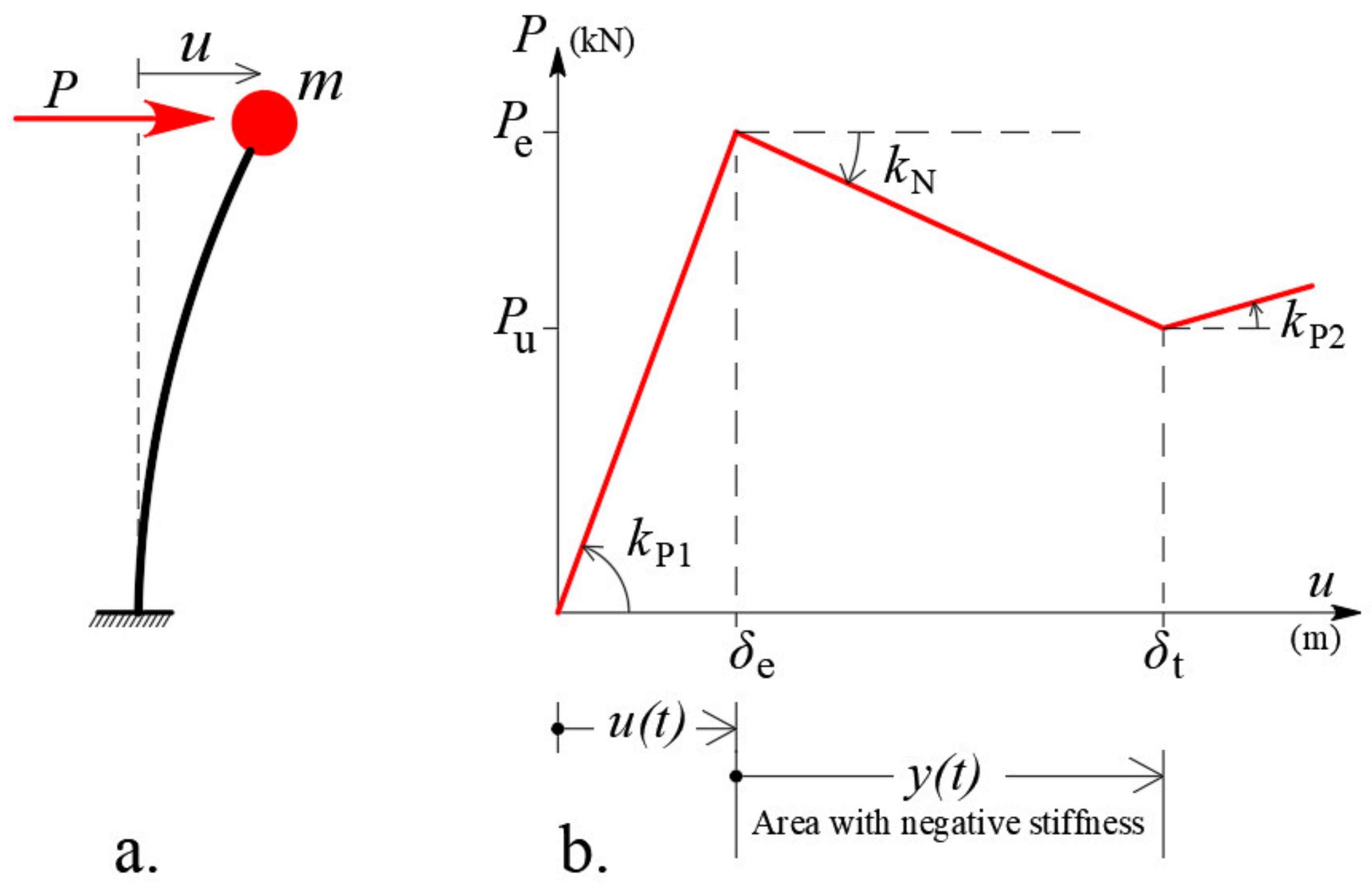
2. Analytical Investigation of a SDoF System with Positive and Negative Stiffness
- -
- Phase A (for response on the first branch, where stiffness is positive, equal to).
- -
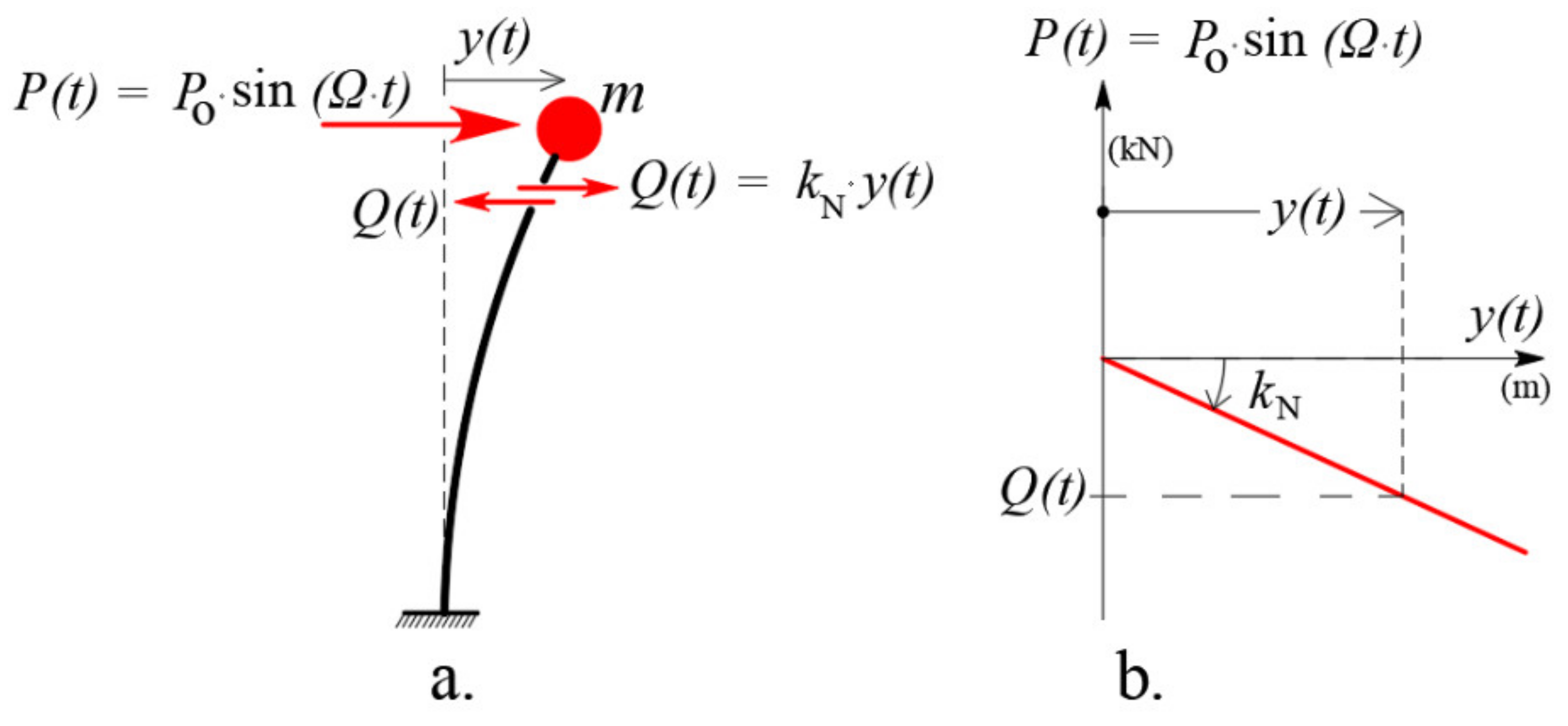
- Phase B (for response on the second branch, where stiffness is negative, equal to ).
- -
- Phase C (for response on the third branch, where stiffness is positive, equal to ).
2.1. Phase A: Mathematical Analysis of the Equation of Motion of the SDOF System for
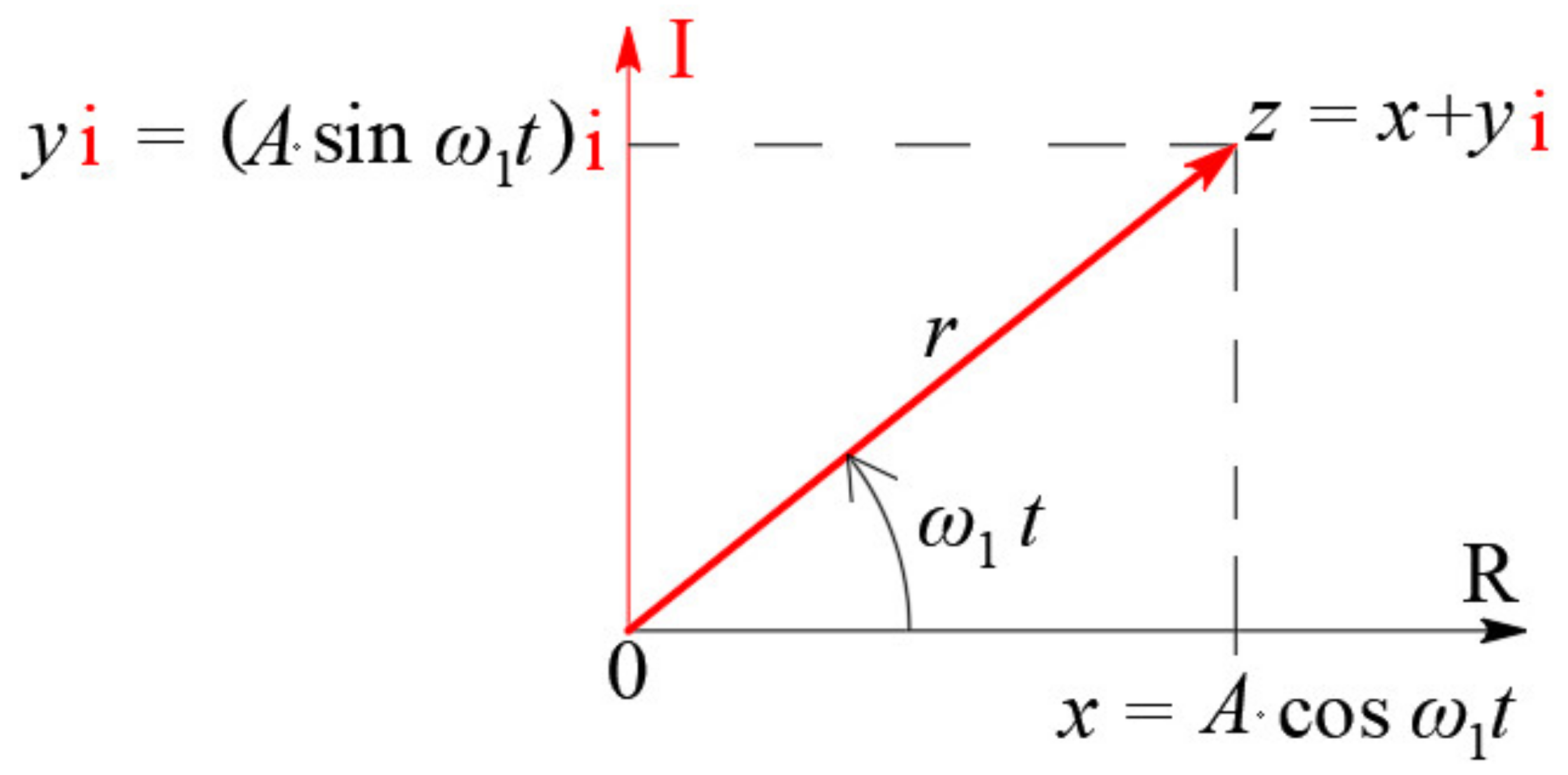
2.2. Phase B: Mathematical Analysis of the SDoF System for
2.3. Phase C: Mathematical Analysis of the Equation of Motion of the SDOF System for
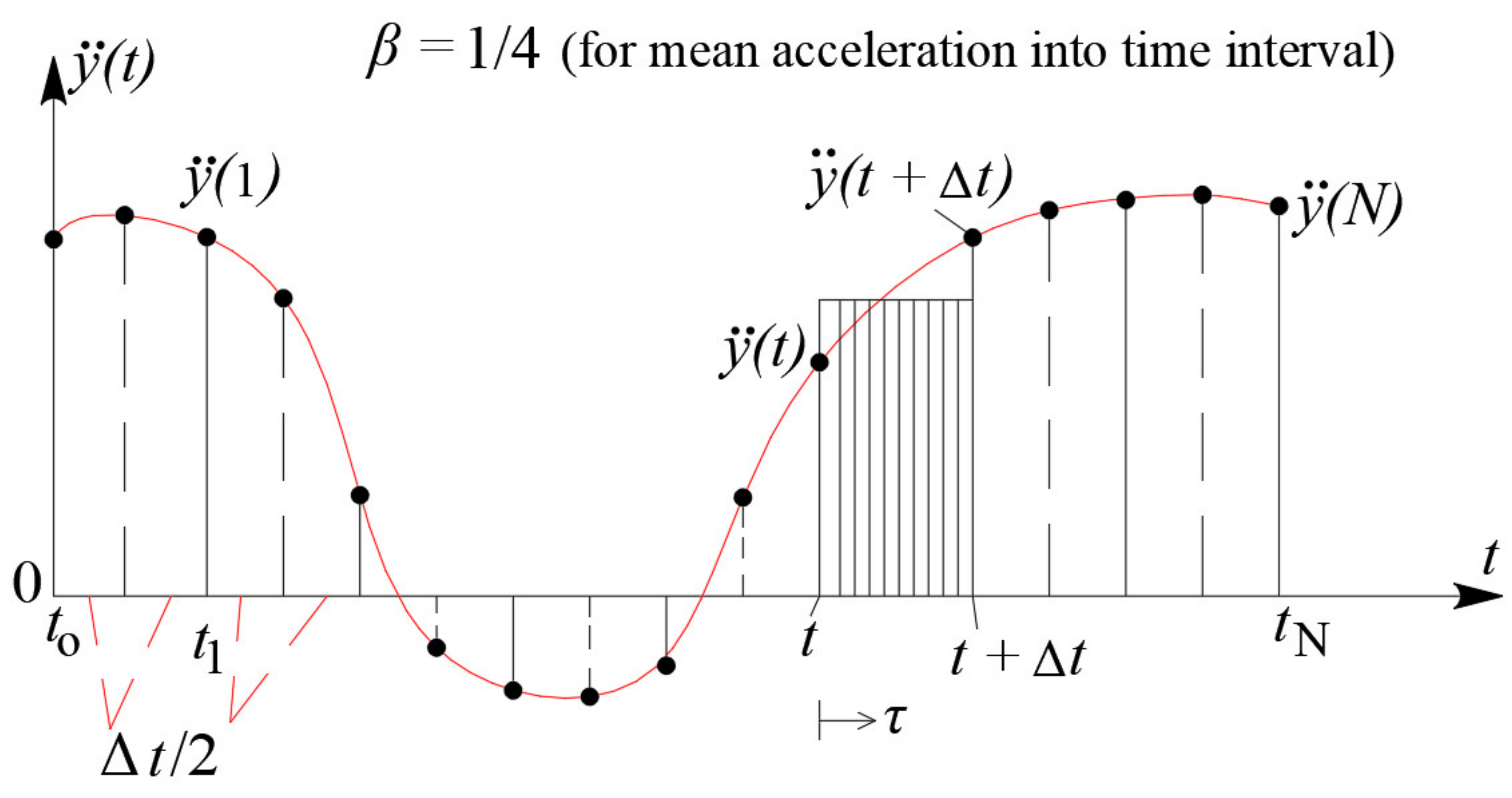
3. Adaptation of the Newmark Numerical Method to Solve the SDoF System with Negative Stiffness
3.1. Analytical Formulation of the Adaptive Newmark Method to Solve SDoF System with Negative Stiffness
3.2. Algorithm of the Modified Newmark Method on a SDoF Negative-Stiffness System
4. Conclusions
- The mathematical investigation of the motion of mas equation has shown that the mathematical equation of response for the theoretical SDoF negative-stiffness system is exponential, which leads to the conclusion that there can be no oscillation of negative-stiffness systems.
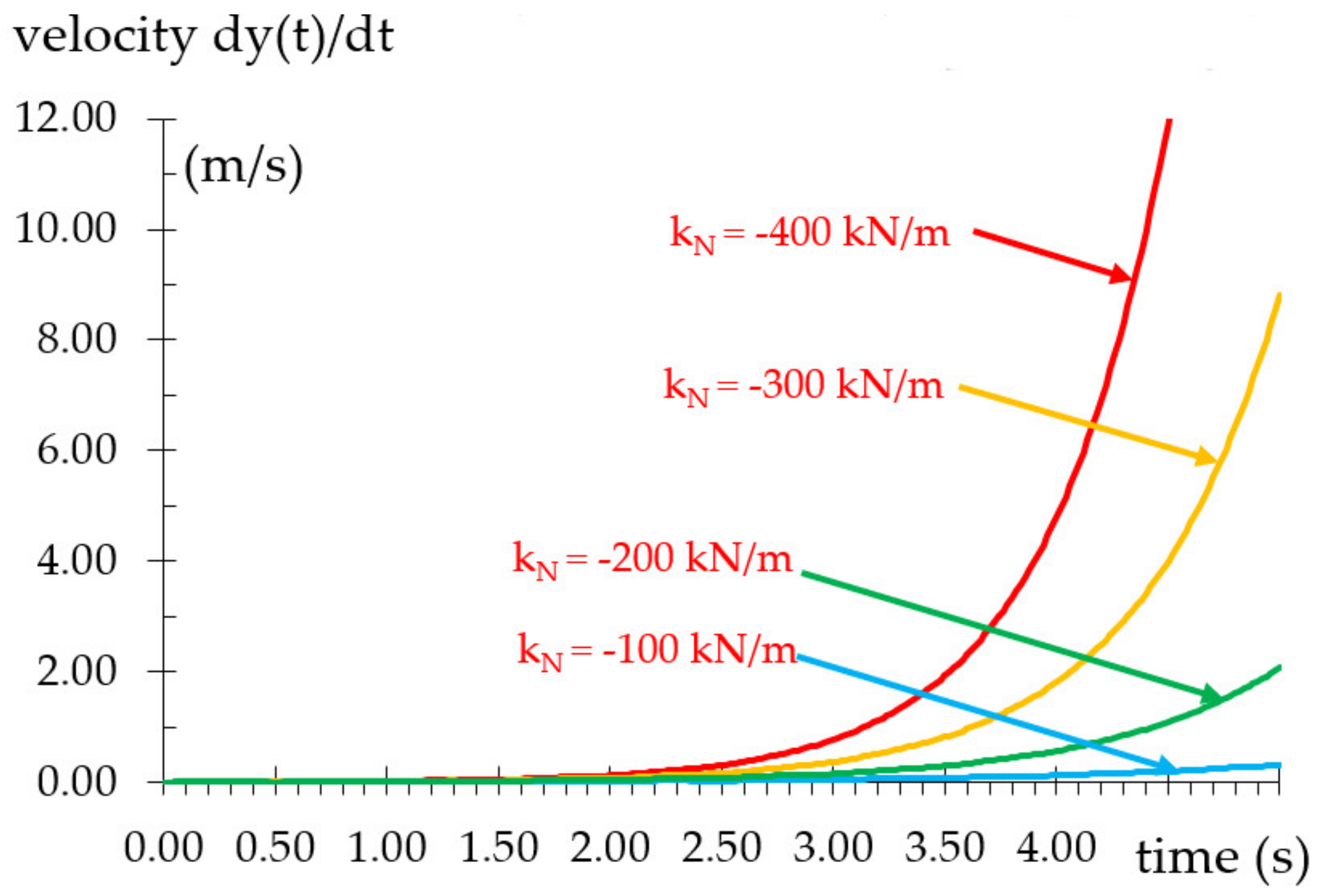
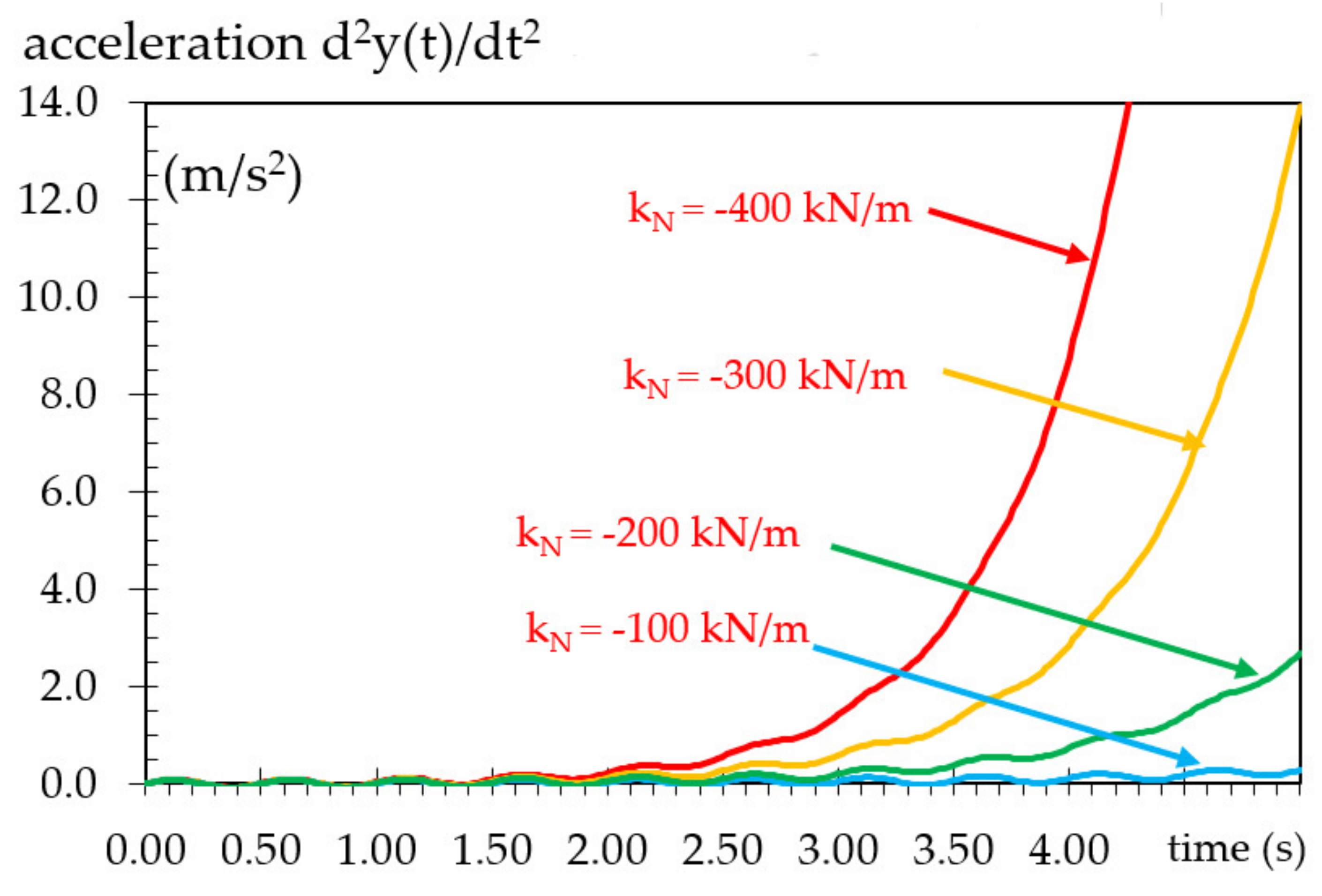
- The Newmark numerical method has been adapted with β = 0.25 and γ = 0.5 to calculate the response of such a system, and the influence of the magnitude of the absolute value of negative stiffness on the response results has been examined. As the absolute value of negative stiffness increases, the more exponential the response type is.
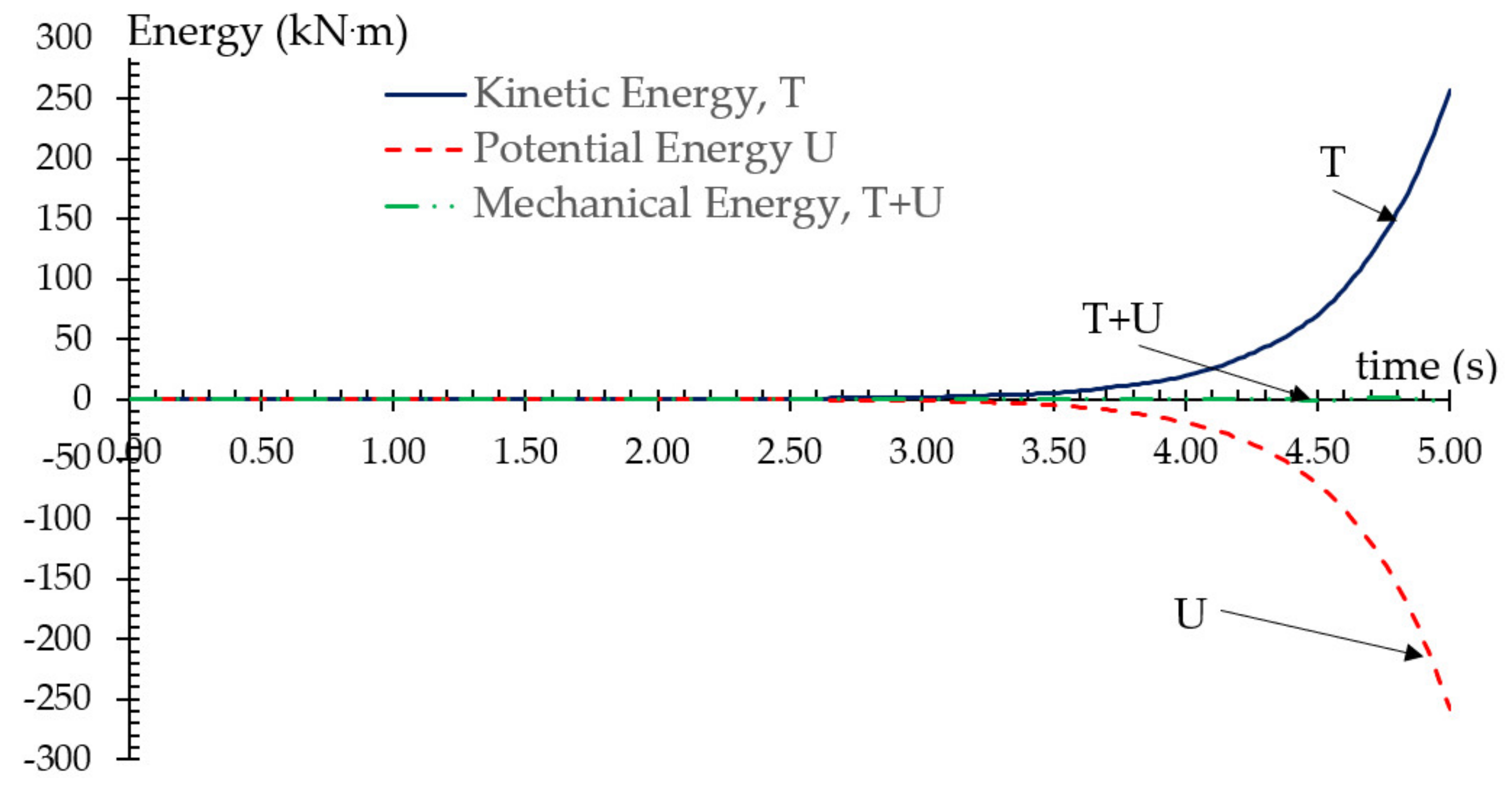
- Finally, it has been shown both analytically and numerically that in negative-stiffness systems, the mechanical energy of the system, which is always defined as the sum of kinetic energy and potential energy, is virtually zero, and this is due to the competitive action between kinetic energy and potential energy. The zeroing of the mechanical energy of a negative-stiffness SDoF shows an absorption of the kinetic energy, even though the examined SDoF oscillator is naturally undamped.
- Further investigation will include the examination of a negative-stiffness SDoF oscillator with viscous and hysteretic damping.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vaiana, N.; Sessa, S.; Rosati, L. A generalized class of uniaxial rate-independent models for simulating asymmetric mechanical hysteresis phenomena. Mech. Syst. Signal Process. 2020, 146, 106984. [Google Scholar] [CrossRef]
- Losanno, D.; Palumbo, F.; Calabrese, A.; Barrasso, T.; Vaiana, N. Preliminary Investigation of Aging Effects on Recycled Rubber Fiber Reinforced Bearings (RR-FRBs). J. Earthq. Eng. 2021, 26, 1–18. [Google Scholar] [CrossRef]
- Vaiana, N.; Sessa, S.; Paradiso, M.; Marmo, F.; Rosati, L. An Efficient Computational Strategy for Nonlinear Time History Analysis of Seismically Base-Isolated Structures. In Lecture Notes in Mechanical Engineering, Proceedings of the XXIV AIMETA Conference, Rome, Italy, 15–19 September 2019; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1340–1353. [Google Scholar] [CrossRef]
- Molyneaux, W. Supports for Vibration Isolation; ARC/CP-322; Aer Res Council, G.: London, UK, 1957. [Google Scholar]
- Alabuzhev, P.; Gritchin, A.; Kim, L.; Migirenko, G.; Chon, V.; Stepanov, P. Vibration Protecting and Measuring Systems with Quasi-Zero Stiffness. Applications of Vibration; Hemisphere Publishing Corp.: New York, NY, USA, 1989. [Google Scholar]
- Platus, D.L. Negative-stiffness-mechanism vibration isolation systems. In Vibration Control in Microelectronics, Optics and Metrology; SPIE: Bellingham, WA, USA, 1991; Volume 1619, p. 44. [Google Scholar]
- Inman, D.J.; Singh, R.C. Engineering Vibration; Prentice-Hall: Hoboken, NJ, USA, 1996; Volume 4. [Google Scholar]
- Carella, A.; Brennan, M.; Waters, T. Static analysis of a passive vibration isolator with quasizero-stiffness characteristic. J. Sound Vib. 2007, 301, 678. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P. Optimization of a quasi-zero-stiffness isolator. J. Mech. Sci. Technol. 2007, 21, 946–949. [Google Scholar] [CrossRef]
- Yang, C.; Yuan, X.; Wu, J.; Yang, B. The research of passive vibration isolation system with broad frequency field. J. Vib. Control 2012, 19, 1348–1356. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, K.; Xu, D.; Ouyang, H.; Fu, Y. Vibration isolation in neonatal transport by using a quasi-zero-stiffness isolator. J. Vib. Control 2017, 24, 3278–3291. [Google Scholar] [CrossRef]
- Yingli, L.; Xu, D. Force transmissibility of floating raft systems with quasi-zero-stiffness isolators. J. Vib. Control. 2017, 24, 3608. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, Y.; Zhou, J.; Lou, J. On the analytical and experimental assessment of the performance of a quasi-zero-stiffness isolator. J. Vib. Control 2013, 20, 2314–2325. [Google Scholar] [CrossRef]
- Zhang, Y.; Mao, Y.; Wang, Z.; Gao, C. Nonlinear Low Frequency Response Research for a Vibration Isolator with Quasi-Zero Stiffness Characteristic. KSCE J. Civ. Eng. 2021, 25, 1849–1856. [Google Scholar] [CrossRef]
- Nagarajaiah, S. Adaptive Negative Stiffness: A new structural modification approach for seismic protection. In Proceedings of the 5th World Conference on Structural Control and Monitoring, Tokyo, Japan, 12–14 July 2010. [Google Scholar]
- Attary, N.; Symans, M.; Nagarajaiah, S. Development of a rotation-based negative stiffness device for seismic protection of structures. J. Vib. Control 2016, 23, 853–867. [Google Scholar] [CrossRef]
- Antoniadis, I.; Kanarachos, S.; Gryllias, K.; Sapountzakis, E. KDamping: A stiffness based vibration absorption concept. J. Vib. Control. 2016, 24, 588. [Google Scholar] [CrossRef]
- Sapountzakis, E.; Syrimi, P.; Pantazis, I.; Antoniadis, I. KDamper concept in seismic isolation of bridges with flexible piers. Eng. Struct. 2017, 153, 525–539. [Google Scholar] [CrossRef]
- Nagarajaiah, S.; Varadarajan, N. Novel semi active variable stiffness tuned mass damper with real time tuning capacity. In Proceedings of the 13th Engineering Mechanics Conference; ASC: Reston, VA, USA, 2000. [Google Scholar]
- Nagarajaiah, S.; Sonmez, E. Structures with semi active Variable Stiffness Single/Multiple Tuned Mass Dampers. J. Struct. Eng. 2007, 133, 67. [Google Scholar] [CrossRef]
- Mofidian, S.; Bardaweel, H. Displacement transmissibility evaluation of vibration isolation system employing nonlinear-damping and nonlinear-stiffness elements. J. Vib. Control. 2017, 24, 4247. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, S.; Xia, D.; He, J.; Zhang, P. The design of negative stiffness spring for precision vibration isolation using axially magnetized permanent magnet rings. J. Vib. Control 2019, 25, 2667–2677. [Google Scholar] [CrossRef]
- Hoque, E.; Mizuno, T.; Ishino, Y.; Takasaki, M. A modified zero-power control and its application to vibration isolation system. J. Vib. Control 2011, 18, 1788–1797. [Google Scholar] [CrossRef]
- Kangkang, L.; Hongzhou, J.; Jingfeng, H.; Hui, Z. Variable-stiffness decoupling of redundant planar rotational parallel mechanisms with crossed legs. J. Vib. Control 2018, 24, 5525–5533. [Google Scholar] [CrossRef]
- Abbasi, A.; Khadem, S.; Bab, S. Vibration control of a continuous rotating shaft employing high-static low-dynamic stiffness isolators. J. Vib. Control 2016, 24, 760–783. [Google Scholar] [CrossRef]
- Li, H.-N.; Sun, T.; Lai, Z.; Nagarajaiah, S. Effectiveness of Negative Stiffness System in the Benchmark Structural-Control Problem for Seismically Excited Highway Bridges. J. Bridg. Eng. 2018, 23, 04018001. [Google Scholar] [CrossRef]
- Adam, C.; Jäger, C. Seismic Induced Global Collapse of Non-deteriorating Frame Structures. In Computational Methods in Earthquake Engineering; Springer: Berlin/Heidelberg, Germany, 2010; pp. 21–40. [Google Scholar] [CrossRef]
- Wang, M.; Sun, F.; Nagarajaiah, S. Simplified optimal design of MDOF structures with negative stiffness amplifying dampers based on effective damping. Struct. Des. Tall Spéc. Build. 2019, 28, e1664. [Google Scholar] [CrossRef]
- Newmark, N.M. A Method of Computation for Structural Dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of structures. In Mathematics and Archaeology; Prentice-hall International Series in Civil Engineering and Engineering Mechanics; Prentice-Hall: Hoboken, NJ, USA, 2007; pp. 164–183. [Google Scholar]
- Vaiana, N.; Sessa, S.; Marmo, F.; Rosati, L. Nonlinear dynamic analysis of hysteretic mechanical systems by combining a novel rate-independent model and an explicit time integration method. Nonlinear Dyn. 2019, 98, 2879–2901. [Google Scholar] [CrossRef]
- Hashamdar, H.; Ibrahim, Z.; Jameel, M. Finite element analysis of nonlinear structures with Newmark method. Int. J. Phys. Sci. 2011, 6, 1395–1403. [Google Scholar]
- Alnahhal, W.; Aref, A. Numerical evaluation of dynamic response by using modified Newmark’s method. Jordan J. Civ. Eng. 2019, 13, 30–43. [Google Scholar]
- Cui, Y.; Liu, A.; Xu, C.; Zheng, J. A Modified Newmark Method for Calculating Permanent Displacement of Seismic Slope considering Dynamic Critical Acceleration. Adv. Civ. Eng. 2019, 2019, 9782515. [Google Scholar] [CrossRef]


|
|---|
| 1.1 |
| 1.2 Time step selection Δt |
| 1.3 c |
|
| 2.1 Determination of equivalent step load of the SDoF oscillator: |
| of the SDoF oscillator: |
| 2.4 |
| 2.5 |
| 2.6 |
| 2.7 |
|
| t | ||||||
|---|---|---|---|---|---|---|
| 0.00 | 0.0000 | 0.000000 | ||||
| 0.02 | 2.486885 | 2.486885 | 0.020727 | 2.486885 | 1,199,800.0 | 0.000002 |
| 0.04 | 4.817512 | 2.330627 | 0.040166 | 12.279826 | 1,199,800.0 | 0.000010 |
| 0.06 | 6.845440 | 2.027928 | 0.057109 | 31.257021 | 1,199,800.0 | 0.000026 |
| 0.08 | 8.443249 | 1.597809 | 0.070505 | 58.239350 | 1,199,800.0 | 0.000049 |
| 0.10 | …. | …. | …. | … | …. | … |
| t | |||||
|---|---|---|---|---|---|
| 0.00 | 0.0000 | 0.00400 | 0.000000 | ||
| 0.02 | 2.486885 | 2.486885 | −0.00012 | 0.00388 | 0.000079 |
| 0.04 | 4.817512 | 2.330627 | −0.00012 | 0.003761 | 0.000155 |
| 0.06 | 6.845440 | 2.027928 | −0.00012 | 0.003641 | 0.000229 |
| 0.08 | 8.443249 | 1.597809 | −0.00012 | 0.003520 | 0.000301 |
| 0.10 | …. | …. | …. | …. | … |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatzikonstantinou, N.; Makarios, T.K.; Athanatopoulou, A. Integration Method for Response History Analysis of Single-Degree-of-Freedom Systems with Negative Stiffness. Buildings 2022, 12, 1214. https://doi.org/10.3390/buildings12081214
Chatzikonstantinou N, Makarios TK, Athanatopoulou A. Integration Method for Response History Analysis of Single-Degree-of-Freedom Systems with Negative Stiffness. Buildings. 2022; 12(8):1214. https://doi.org/10.3390/buildings12081214
Chicago/Turabian StyleChatzikonstantinou, Nikoleta, Triantafyllos K. Makarios, and Asimina Athanatopoulou. 2022. "Integration Method for Response History Analysis of Single-Degree-of-Freedom Systems with Negative Stiffness" Buildings 12, no. 8: 1214. https://doi.org/10.3390/buildings12081214
APA StyleChatzikonstantinou, N., Makarios, T. K., & Athanatopoulou, A. (2022). Integration Method for Response History Analysis of Single-Degree-of-Freedom Systems with Negative Stiffness. Buildings, 12(8), 1214. https://doi.org/10.3390/buildings12081214








