Next Article in Journal
Stability Analysis of the Inclined Capillary Barrier Covers under Rainfall Condition
Next Article in Special Issue
Fragility Functions for Reinforced Concrete Structures Based on Multiscale Approach for Earthquake Damage Criteria
Previous Article in Journal
Numerical Analysis of the Seismic Behavior of a Steel Beam-to-Concrete-Filled Steel Tubular Column Connection Using External Diaphragms
Previous Article in Special Issue
Seismic Performance Target and Fragility of Masonry Infilled RC Frames under In-Plane Loading
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Buildings
Volume 12
Issue 8
10.3390/buildings12081219
buildings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Influence of the Flexural Strength Ratio of Columns to Beams on the Collapse Capacity of RC Frame Structures

by
Maosheng Gong
1,2,
Bo Liu
3,
Zhanxuan Zuo
1,2,*,
Jing Sun
4,* and
Hao Zhang
1,2
1
Key Laboratory of Earthquake Engineering and Engineering Vibration, Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, China
2
Key Laboratory of Earthquake Disaster Mitigation, Ministry of Emergency Management, Harbin 150080, China
3
School of Civil Engineering, Yantai University, Yantai 264005, China
4
School of Civil Engineering, Heilongjiang University, Harbin 150080, China
*
Authors to whom correspondence should be addressed.
Buildings 2022, 12(8), 1219; https://doi.org/10.3390/buildings12081219
Submission received: 25 July 2022 / Revised: 7 August 2022 / Accepted: 8 August 2022 / Published: 12 August 2022
(This article belongs to the Special Issue Earthquake Engineering and Urban Resilience)
Browse Figures
Versions Notes

Abstract

:
Reinforced concrete (RC) frames are designed based on the strong column-weak beam (SCWB) philosophy to reduce structural damage and collapse during earthquakes. The SCWB design philosophy is ensured by the required minimum flexural strength ratio of columns to beams (FSRCB) in the seismic code. Quantifying the relationship between the FSRCB and the collapse capacity of the frames may facilitate the efficient assessment of the seismic performance of the existing or newly designed RC frames. This paper investigates the influence of different FSRCBs on the collapse capacity of three- and nine-story RC frames designed according to Chinese seismic codes. The results show that the collapse capacities of the RC frames can be efficiently improved by increasing the FSRCB, and the collapse capacities of frames with FSRCB = 2.0 are improved by approximately 1.6–2.0 times compared with those of the frames with FSRCB = 1.2. Compared with the middle- or high-rise (nine-story) frames, it is more efficient to improve the collapse capacity for low-rise (three-story) frames by increasing the value of CBFSR. The logarithmic standard deviation of the collapse capacity of the RC frames designed according to the Chinese seismic codes ranges from 0.5–0.9, which is larger than the proposed maximum logarithmic standard deviation (0.4) in FEMA P695.

1. Introduction

The collapse of RC frames during strong earthquakes leads to extensive economic losses and the loss of human lives [1,2]. RC frames are designed to achieve the SCWB failure mechanism based on the minimum required flexural strength ratio of columns to beams (FSRCB) in many seismic codes [3,4,5,6]. The SCWB failure of the RC frames requires that the beams yield earlier than the columns during strong earthquakes. Compared with the strong beam-weak column (SBWC) failure mode, RC frame failure in the SCWB mode provides more energy dissipation and a larger collapse capacity [7].
However, many earthquake field surveys show that a large number of RC frames fail in SBWC mode rather than SCWB mode, which indicates that the current required minimum FSRCB in seismic codes cannot ensure the SCWB failure mode for RC frames [8,9,10,11,12,13,14,15]. The required minimum FSRCB in many building codes to achieve the expected SCWB design concept is based on the assumption that the inflection points are located at the midheight of the columns [16,17,18]. Unexpected SBWC failure may be because the inflection points are not always located at the midheight of the columns, and the inflection points usually move toward the beam-column joints when the structures are in a nonlinear state during earthquakes [17,19,20]. In addition, the required minimum FSRCB to guarantee SCWB failure also depends on the seismic hazard, characteristics of ground motions [21], infill walls [22,23,24,25,26,27], and frame heights [28]. RC frames designed before modern seismic codes sometimes collapse in SBWC failure mode, shear failure mode, soft story failure mode, and other nonductile failure modes [29,30,31]. Some research has been conducted to guarantee the SCWB failure mode by increasing the value FSRCB for steel frames [17,19,20,32] and RC frames [18,21,28,33,34,35,36,37,38,39,40]. Based on the findings above, different FSRCB values ranging from 1.6 to 3.0 have been suggested to ensure the SCWB failure mode [21,28,32,36,37,38].
The FSRCB also has a significant influence on the collapse capacity of structures [40]. However, in the abovementioned research, only Ghorbanzadeh [38] and Sattar [39] investigated the impact of the FSRCB on collapse risk for older type nonductile and modern ductile RC frames in the USA. To the best knowledge of the authors, very little research has been reported about quantifying the influence of the FSRCB on the collapse capacity of RC frames designed according to Chinese seismic codes. Considering the different required seismic measures or details of seismic design between the Chinese seismic codes and codes in other countries may sometimes greatly influence the seismic performance [41]. The conclusions based on the frames in other countries may not necessarily be adopted directly for the frames in China.
Considering the limitation of the above research, the main objective of the present paper is to evaluate the impact of the FSRCB on the collapse capacity of RC frame structures in China. The collapse capacity of RC frames with various FSRCBs is evaluated by incremental dynamic analysis (IDA) [42,43] under the excitation of both far-field non-pulse-like (NPL) and near-field pulse-like (PL) ground motions. The presented results are aimed to provide some insights to improve the collapse capacity by adjusting the FSRCB for RC frame structures in the current Chinese seismic codes.

2. Building Models

Two RC frame structures are designed according to Chinese seismic codes [4]. The elevations of the two frames (3- and 9-story frames) are shown in Figure 1. The design seismic intensity of the frames is 0.1 g according to the Chinese seismic codes (seismic hazard corresponding to a 10% exceedance probability in 50 years). The detailed information on the two frames can be found in reference [21]. To investigate the influence of the FSRCB on the structural collapse capacities, the frames with different FSRCBs are designed by adjusting the reinforcements in the columns. The dimensions of the frames and elastic modulus of the materials are kept constant. Thus, the stiffness of the frames with different FSRCBs is also kept constant, which leads to the periods of the RC frames with different FSRCBs being kept constant. Thus, the periods of the RC frames with different FSRCBs are kept constant. The seismic performance of RC frames with different FSRCBs (1.2, 1.4, 1.6, 1.8, and 2.0) is investigated in this paper. The details of the reinforcement of the 3- and 9-story frames are shown in Table 1 and Table 2, respectively.
All frames are established using the open-source tool OpenSees program (University of California, Berkeley, Berkeley, CA, USA) [44]. The beams and columns are modeled force-based beam-column elements with fiber sections [45]. The Concrete 02 material is used to describe both the confined and unconfined concrete materials. The Kent–Scott–Park constitutive model is adopted to consider the confinement effect of the transverse rebar. The Steel 02 material is adopted to describe the stress-strain model of the reinforcements. Viscous damping is specified using Rayleigh damping (damping ratio = 5%) in the nonlinear dynamic time history analysis. The modeling method referenced above has been verified in previous research [46].

3. Ground Motion Record Selection

This study utilizes two sets of ground motions, namely, non-pulse-like (NPL) and pulse-like (PL) records, to evaluate the effect of the FSRCB on the collapse capacity of RC frames. The first set includes 44 NPL ground motion records recommended by the FEMA P695. To compare the influence of different characteristics of ground motions on the structural collapse capacity, the second set 44 includes PL ground motion records. The PL ground motion records are selected based on the recommendation of Li [47] and Shahi [48]. The selected PL ground motions are caused by forward directivity effects.
Detailed information on the NPL and PL ground motion records can be found in reference [21]. The selected NPL and PL ground motions are mainly recorded during strong earthquakes whose magnitudes range from 5.0 Mw to 8.0 Mw, which usually causes serious structural damage and collapse. For the NPL ground motion records, there are 22 pairs (44 individual components) of horizontal records (two orthogonal horizontal component records in each station). Figure 2 shows the mean spectra of the NPL and PL ground motion records.

4. Collapse Capacity of RC Frames with Different FSRCBs

The definition of collapse in this paper is referred to the loss of lateral load-carrying capacity under earthquake excitation. Vertical collapse is not the focus of this study. Different collapse criterion has been adopted to identify the sideway collapse of buildings [49,50,51]. The criteria proposed by FEMA 351 are adopted in this paper. The collapse criteria in this paper are defined as the tangent stiffness of the IDA curve being smaller than 20% of the initial stiffness of the IDA curve or the maximum inter-story drift ratio being larger than 0.10.

4.1. Incremental Dynamic Analysis

Incremental dynamic analysis (IDA) was proposed by Vamvatsikos and Cornell [42] and has been widely used to assess structural collapse capacity. In IDA, a specific structure is excited by a specific ground motion repeatedly with increasing seismic intensity until the collapse criteria are reached. This study uses two sets of ground motions (44 NPL ground motions and 44 PL ground motions) as input to represent earthquake excitation.
The IDA curves of the frames are obtained by adjusting the seismic intensity of the 88 ground motions one by one until collapse occurs. Figure 3 shows the IDA curves of the three- and nine-story RC frames with an FSRCB equal to 1.2. For illustration, the IDA curves of the frames with other FSRCB values are not presented for the sake of brevity. Figure 4 and Figure 5 show the median IDA curves of the three- and nine-story RC frames with different FSRCBs, respectively. IDRmax is the maximum inter-story ratio (IDR) in the nonlinear dynamic analysis. The median IDA curves of the frames with a larger FSRCB usually have a larger lateral resistance capacity than those of the frames with a smaller FSRCB [21]. As shown in Figure 4 and Figure 5, for a specified value of IDR, the collapse capacity increases as the FSRCB increases.

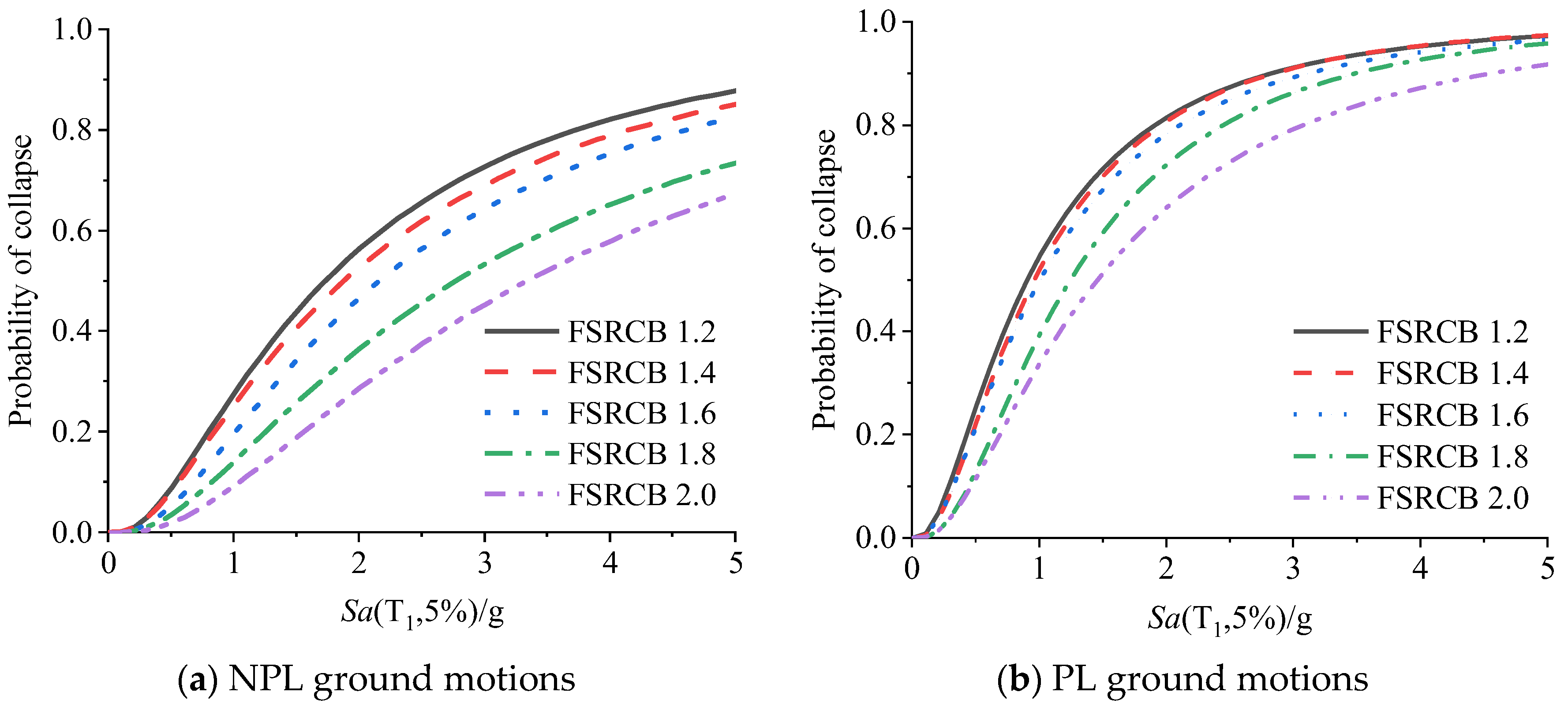
4.2. Collapse Fragility Curves of the RC Frames with Different FSRCBs

Collapse fragility curves are widely adopted to describe the probability of buildings sustaining damage under the excitation of strong earthquakes. Figure 6 shows the fragility curves relating to the collapse probability under the increasing seismic intensity measure of the three-story frames with various FSRCBs. The collapse probability decreases as the FSRCB increases from 1.2 to 2.0 under a specific seismic intensity for both NPL ground motions and PL ground motions for three-story RC frames.
Figure 7a shows the median collapse capacity of the three-story RC frames with various FSRCBs. The median collapse capacity increases as the FSRCB increases for both the NPL record set and the PL record set. The median collapse capacities of the RC frames excited by the PL record set are smaller than those of the frames excited by the NPL record set.
To quantitatively evaluate the effect of the FSRCB on the median collapse capacities of the RC frames, the coefficient ratio is expressed as:
Ratio = Sa FSRCB Collapse / Sa 1 . 2 Collapse ( FSRCB = 1.2 , 1.4 , 1.6 , 1.8 , 2.0 )
where Sa 1 . 2 Collapse is the median collapse capacity of the frame with FSRCB = 1.2 and Sa FSRCB Collapse is the median collapse capacity of the frame with different FSRCBs (1.2, 1.4, 1.6, 1.8, and 2.0). The ratio is used to quantitatively describe the influence of the FSRCB on the collapse capacities.
Figure 7b shows the median collapse capacities of the frames with different FSRCBs compared with those of the frame with FSRCB = 1.2. As shown in Figure 7b, the ratio increases as the FSRCB increases from 1.2 to 2.0. For the NPL ground motions, the collapse capacity of the frame with FSRCB = 2.0 is approximately two times that of the frame with FSRCB = 1.2. For the PL ground motions, the collapse capacity of the frame with FSRCB = 2.0 is approximately 1.5 times that of the frame with FSRCB = 1.2. This means that it is more efficient to improve the collapse capacity of the frames excited by the NPL ground motion records than those excited by the PL ground motion records.
Figure 8 shows the collapse fragility curves of the nine-story frames with different FSRCBs under NPL and PL ground motions. The nine-story frame shows similar trends to those of the three-story frames. For both NPL and PL ground motions, the probability of collapse can be decreased by increasing the value of the FSRCB for the frames under a specific seismic intensity.
Figure 9 shows the effect of the FSRCB on the collapse capacities of the nine-story RC frames with different FSRCBs. As shown in Figure 9a, the median collapse capacities of the frames can be improved by increasing the value of the FSRCB for the frames for both NPL and PL ground motions. The collapse capacities of the frames with different FSRCBs normalized to those of the frames with FSRCB = 1.2 is shown in Figure 9b. As shown in Figure 9b, for the NPL and PL ground motion records, the collapse capacities of the frame with FSRCB = 2.0 are improved to approximately 1.6 times those of the frames with FSRCB = 1.2.
Quantification of the uncertainty of structural collapse capacity is one of the critical aspects of performance-based earthquake engineering (PBEE) [2]. The uncertainty of the collapse capacity consists of record-to-record uncertainty (aleatory uncertainty) and structural modeling uncertainty (epistemic uncertainty) [2,51,52,53,54]. This paper focuses on record-to-record uncertainty. The logarithmic standard deviation (LSD) is a common index used to describe uncertainty. Figure 10 shows the LSD of the structural collapse capacity caused by ground motion uncertainty.
As shown in Figure 10, for the three-story frames, the LSD mainly ranges from 0.8–0.9, which is larger than those of the nine-story frames (mainly ranges from 0.5–0.7). Generally, the LSD of the collapse capacity for the RC frames designed according to the Chinese seismic codes ranges from 0.5–0.9. FEMA P695 also proposes an expression to estimate the LSD of the collapse capacity of structures. The estimated LSD is expressed as:
LSD = 0.1 + 0.1 μ T ≤ 0.40
where μ T is the ductility of the structures. μ T = δ u / δ y , e f f , where is the largest displacement and δ y , e f f is the yield displacement.
The LSD obtained from the results of the three- and nine-story frames, ranging from 0.5–0.9, is larger than the maximum LSD (0.4) estimated by Equation (2). This means that Equation (2) proposed by FEMA P695 may sometimes underestimate the uncertainty of the structural collapse capacity for RC frames designed according to Chinese seismic codes.

5. Conclusions

In the presented paper, the effect of the flexural strength ratio of columns to beams (FSRCB) on the collapse capacity of RC frame structures is studied. The collapse behavior of a series of RC frames with different FSRCBs is investigated by applying incremental dynamic analysis (IDA). The non-pulse-like (NPL) and pulse-like (PL) ground motions are both used as input in the IDA to evaluate the influence of NPL and PL ground motions on the collapse capacity of RC frames. Based on the findings of this paper, the following conclusions are drawn:
(1)
For both NPL and PL ground motions, the collapse capacities of the RC frames can be improved by increasing the FSRCB of the RC frames. The collapse capacities of the three- and nine-story frames with FSRCB = 2.0 are improved to approximately 1.6–2.0 times those of the frames with FSRCB = 1.2. For NPL ground motions, the collapse capacities are improved up to approximately 2 times when the FSRCB of the three-story frames is increased from 1.2 to 2.0, while for the PL ground motions, the collapse capacities are improved up to approximately 1.5 times when the FSRCB of the three-story frames is increased from 1.2 to 2.0. It is more efficient to improve the collapse capacity of the frames under the excitation of NPL ground motions than those under the excitation of PL ground motions.
(2)
It is more efficient to improve the collapse capacity for low-rise (three-story) frames than for middle- or high-rise (nine-story) frames. This difference arises because the deformations of the low-rise frame are mainly dominated by the first mode and the higher mode effects are not significant. However, for the middle or high-rise frame, the higher mode effect is stronger, which may cause the inflection point in the columns to move from near the midheight to the column ends and sometimes will cause the column to undergo a single curvature. Thus, compared with low-rise RC frames, it is less efficient to increase the collapse capacity for the middle- or high-rise frames by increasing the value of the FSRCB.
(3)
The uncertainty (logarithmic standard deviation) of the collapse capacity of the RC frame structures designed according to the Chinese seismic codes ranges from 0.5–0.9, which is larger than the maximum logarithmic standard deviation (0.4) proposed by FEMA P695. This means that FEMA P695 may sometimes underestimate the uncertainty of the collapse capacity of the RC frames in China.
This paper mainly focuses on the influence of FSRCB on the collapse capacity of RC frames. The conclusions of this paper are drawn based on the findings from the three- and nine-story buildings. Whether the conclusions of this paper can be directly adopted in RC frames with other different stories should be investigated in the future.

Author Contributions

Conceptualization, M.G., Z.Z. and J.S.; methodology, M.G., B.L. and H.Z.; software, M.G., B.L. and H.Z.; validation, Z.Z. and J.S.; formal analysis, M.G. and H.Z.; investigation, Z.Z.; writing—original draft preparation, M.G., Z.Z. and B.L.; writing—review and editing, M.G., Z.Z. and J.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research project is supported by the Scientific Research Fund of the Institute of Engineering Mechanics, China Earthquake Administration (Grant No. 2019C11 and 2019A01), National Natural Science Foundation of China (Grant No. 52178514 and 51708523), Natural Science Foundation of Heilongjiang (LH2019E097) and National Key R&D Program of China (2019YFE0112700).

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ger, J.; Cheng, F.Y.; Lu, L. Collapse Behavior of Pino Suarez Building During 1985 Mexico City Earthquake. J. Struct. Eng. 1993, 119, 852–870. [Google Scholar] [CrossRef]
  2. FEMA. Quantification of Building Seismic Performance Factors; Federal Emergency Management Agency: Washington, DC, USA, 2009; Volume 695.
  3. ACI 318-14; Building Code Requirements for Structural Concrete. ACI Committee 318: Indianapolis, IN, USA, 2014.
  4. GB 50011-2010; Code for Seismic Design of Buildings, 2016 ed. Ministry of Housing and Urban-Rural Development of the People’s Republic of China; China Architecture & Building Press: Beijing, China, 2016. (In Chinese)
  5. AISC 2005; Seismic Provisions for Structural Steel Buildings. American Institute of Steel Construction Inc.: Chicago, IL, USA, 2005.
  6. Eurocode 8, N; Design Provisions for Earthquake Resistance of Structures—Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
  7. Gong, M.; Zuo, Z.; Wang, X.; Lu, X.; Xie, L. Comparing seismic performances of pilotis and bare RC frame structures by shaking table tests. Eng. Struct. 2019, 199, 109442. [Google Scholar] [CrossRef]
  8. Ye, L.; Qu, Z.; Ma, Q.; Lin, X.; Lu, X.; Pan, P. Study on ensuring the strong column-weak beam mechanism for RC frames based on the damage analysis in the Wenchuan earthquake. Build. Struct. 2008, 38, 52–53. [Google Scholar]
  9. Sun, B.; Zhang, G. The Wenchuan earthquake creation of a rich database of building performance. Sci. China Technol. Sci. 2010, 53, 2668–2680. [Google Scholar] [CrossRef]
  10. Zhao, B.; Taucer, F.; Rossetto, T. Field investigation on the performance of building structures during the 12 May 2008 Wenchuan earthquake in China. Eng. Struct. 2009, 31, 1707–1723. [Google Scholar] [CrossRef]
  11. Arslan, M.; Korkmaz, H. What is to be learned from damage and failure of reinforced concrete structures during recent earthquakes in Turkey? Eng. Fail. Anal. 2007, 14, 1–22. [Google Scholar] [CrossRef]
  12. Gong, M.; Yang, Y.; Xie, L. Seismic damage to reinforced concrete frame buildings in Lushan M7.0 earthquake. Earthq. Eng. Eng. Vib. 2013, 33, 20–26. [Google Scholar]
  13. Gong, M.; Lin, S.; Sun, J.; Li, S.; Dai, J.; Xie, L. Seismic intensity map and typical structural damage of 2010 Ms 7.1 Yushu earthquake in China. Nat. Hazards 2015, 77, 847–866. [Google Scholar] [CrossRef]
  14. Bondy, K.D. A More Rational Approach to Capacity Design of Seismic Moment Frame Columns. Earthq. Spectra 2019, 12, 395–406. [Google Scholar] [CrossRef]
  15. Lee, H.-S. Revised Rule for Concept of Strong-Column Weak-Girder Design. J. Struct. Eng. 1996, 122, 359–364. [Google Scholar] [CrossRef]
  16. Park, R.; Paulay, T. Reinforced Concrete Structures; John Willey and Sons: New York, NY, USA, 1975. [Google Scholar]
  17. Nakashima, M.; Sawaizumi, S. Column-to-Beam Strength Ratio Required for Ensuring Beam-Collapse Mechanisms in Earthquake Responses of Steel Moment Frames. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zeland, 30 January–4 February 2000. [Google Scholar]
  18. Medina, R.A.; Krawinkler, H. Strength Demand Issues Relevant for the Seismic Design of Moment-Resisting Frames. Earthq. Spectra 2019, 21, 415–439. [Google Scholar] [CrossRef]
  19. Choi, S.W.; Kim, Y.; Lee, J.; Hong, K.; Park, H.S. Minimum column-to-beam strength ratios for beam–hinge mechanisms based on multi-objective seismic design. J. Constr. Steel Res. 2013, 88, 53–62. [Google Scholar] [CrossRef]
  20. Zaghi, A.E.; Soroushian, S.; Itani, A.; Maragakis, E.M.; Pekcan, G.; Mehrraoufi, M. Impact of column-to-beam strength ratio on the seismic response of steel MRFs. Bull. Earthq. Eng. 2014, 13, 635–652. [Google Scholar] [CrossRef]
  21. Zuo, Z.; Gong, M.; Sun, J.; Zhang, H. Seismic performance of RC frames with different column-to-beam flexural strength ratios under the excitation of pulse-like and non-pulse-like ground motion. Bull. Earthq. Eng. 2021, 19, 5139–5159. [Google Scholar] [CrossRef]
  22. Wang, X.; Zhao, W.; Kong, J.; Zhao, T. Numerical Investigation on the Influence of In-Plane Damage on the Out-of-Plane Behavior of Masonry Infill Walls. Adv. Civ. Eng. 2020, 2020, 6276803. [Google Scholar] [CrossRef]
  23. Kong, J.; Su, Y.; Zheng, Z.; Wang, X.; Zhang, Y. The Influence of Vertical Arrangement and Masonry Material of Infill Walls on the Seismic Performance of RC Frames. Buildings 2022, 12, 825. [Google Scholar] [CrossRef]
  24. Zhang, H.; Kuang, J.; Yuen, T.Y. Low-seismic damage strategies for infilled RC frames: Shake-table tests. Earthq. Eng. Struct. Dyn. 2017, 46, 2419–2438. [Google Scholar] [CrossRef]
  25. Zhai, C.; Kong, J.; Wang, X.; Chen, Z. Experimental and Finite Element Analytical Investigation of Seismic Behavior of Full-Scale Masonry Infilled RC Frames. J. Earthq. Eng. 2016, 20, 1171–1198. [Google Scholar] [CrossRef]
  26. Ruggieri, S.; Porco, F.; Uva, G. A practical approach for estimating the floor deformability in existing RC buildings: Evaluation of the effects in the structural response and seismic fragility. Bull. Earthq. Eng. 2020, 18, 2083–2113. [Google Scholar] [CrossRef]
  27. Caprili, S.; Nardini, L.; Salvatore, W. Evaluation of seismic vulnerability of a complex RC existing building by linear and nonlinear modeling approaches. Bull. Earthq. Eng. 2012, 10, 913–954. [Google Scholar] [CrossRef]
  28. Kim, C.-S.; Park, H.-G.; Truong, G.T. Column-to-beam flexural strength ratio for performance-based design of RC moment frames. J. Build. Eng. 2022, 46, 103645. [Google Scholar] [CrossRef]
  29. Liel, A.B.; Haselton, C.B.; Deierlein, G.G. Seismic Collapse Safety of Reinforced Concrete Buildings. II: Comparative Assessment of Nonductile and Ductile Moment Frames. J. Struct. Eng. 2011, 137, 492–502. [Google Scholar] [CrossRef]
  30. Ruggieri, S.; Porco, F.; Uva, G.; Vamvatsikos, D. Two frugal options to assess class fragility and seismic safety for low-rise reinforced concrete school buildings in Southern Italy. Bull. Earthq. Eng. 2021, 19, 1415–1439. [Google Scholar] [CrossRef]
  31. Jalayer, F.; Franchin, P.; Pinto, P.E. A scalar damage measure for seismic reliability analysis of RC frames. Earthq. Eng. Struct. Dyn. 2007, 36, 2059–2079. [Google Scholar] [CrossRef]
  32. Choi, S.W.; Park, H.S. Multi-objective seismic design method for ensuring beam-hinging mechanism in steel frames. J. Constr. Steel Res. 2012, 74, 17–25. [Google Scholar] [CrossRef]
  33. Kara, L.D.; Joseph, M.B. Seismic Evaluation of Column-to-Beam Strength Ratios in Reinforced Concrete Frames. ACI Struct. J. 2002, 98, 843–851. [Google Scholar] [CrossRef]
  34. El-Mandouh, M.A.; Omar, M.S.; Elnaggar, M.A.; El-Maula, A.S.A. Cyclic Behavior of High-Strength Lightweight Concrete Exterior Beam-Column Connections Reinforced with GFRP. Buildings 2022, 12, 179. [Google Scholar] [CrossRef]
  35. Sococol, I.; Mihai, P.; Petrescu, T.-C.; Nedeff, F.; Nedeff, V.; Agop, M. Analytical Study Regarding the Seismic Response of a Moment-Resisting (MR) Reinforced Concrete (RC) Frame System with Reduced Cross Sections of the RC Beams. Buildings 2022, 12, 983. [Google Scholar] [CrossRef]
  36. Ning, N.; Qu, W.; Ma, Z.J. Design recommendations for achieving “strong column-weak beam” in RC frames. Eng. Struct. 2016, 126, 343–352. [Google Scholar] [CrossRef]
  37. Maosheng, G.; Zhanxuan, Z.; Jing, S.; Riteng, H.; Yinan, Z. Influence of the column-to-beam flexural strength ratio on the failure mode of beam-column connections in RC frames. Earthq. Eng. Eng. Vib. 2021, 20, 441–452. [Google Scholar] [CrossRef]
  38. Ghorbanzadeh, M.; Khoshnoudian, F. The Effect of Strong Column-Weak Beam Ratio on the Collapse Behaviour of Reinforced Concrete Moment Frames Subjected to Near-Field Earthquakes. J. Earthq. Eng. 2020, 26, 4030–4053. [Google Scholar] [CrossRef]
  39. Sattar, S.; Liel, A.B. Collapse indicators for existing nonductile concrete frame buildings with varying column and frame characteristics. Eng. Struct. 2017, 152, 188–201. [Google Scholar] [CrossRef]
  40. Goulet, C.A.; Haselton, C.B.; Mitrani-Reiser, J.; Beck, J.L.; Deierlein, G.G.; Porter, K.A.; Stewart, J.P. Evaluation of the seismic performance of a code-conforming reinforced-concrete frame building—from seismic hazard to collapse safety and economic losses. Earthq. Eng. Struct. Dyn. 2007, 36, 1973–1997. [Google Scholar] [CrossRef]
  41. Ye, L.; Song, S. Calculation of design methods for flexure and axial strength of RC columns in Chinese and American codes. J. Archit. Civ. Eng. 2008, 25, 56–63. [Google Scholar]
  42. Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
  43. Vamvatsikos, D.; Cornell, C.A. Applied Incremental Dynamic Analysis. Earthq. Spectra 2004, 20, 523–553. [Google Scholar] [CrossRef]
  44. Open System for Earthquake Engineering Simulation (OpenSees). Available online: https://opensees.berkeley.edu/wiki/index.php/Command_Manual (accessed on 22 June 2022).
  45. Spacone, E.; Filippou, F.C.; Taucer, F.F. Fibre Beam-Column Model for Non-Linear Analysis of R/C Frames: Part I. Formulation. Earthq. Eng. Struct. Dyn. 1996, 25, 711–725. [Google Scholar] [CrossRef]
  46. Li, S.; Zuo, Z.; Zhai, C.; Xie, L. Comparison of static pushover and dynamic analyses using RC building shaking table experiment. Eng. Struct. 2017, 136, 430–440. [Google Scholar] [CrossRef]
  47. Li, C.; Kunnath, S.; Zhai, C. Influence of Early-Arriving Pulse-Like Ground Motions on Ductility Demands of Single-Degree-of-Freedom Systems. J. Earthq. Eng. 2018, 24, 1337–1360. [Google Scholar] [CrossRef]
  48. Shahi, S.K.; Baker, J. An Efficient Algorithm to Identify Strong-Velocity Pulses in Multicomponent Ground Motions. Bull. Seism. Soc. Am. 2014, 104, 2456–2466. [Google Scholar] [CrossRef]
  49. Jäger, C.; Adam, C. Influence of Collapse Definition and Near-Field Effects on Collapse Capacity Spectra. J. Earthq. Eng. 2013, 17, 859–878. [Google Scholar] [CrossRef]
  50. FEMA-351; Recommended Seismic Evaluation and Upgrade Criteria for Existing Welded Steel Moment-Frame Buildings. Federal Emergency Management Agency: Washington, DC, USA, 2000; Volume 351.
  51. Zareian, F.; Krawinkler, H.; Ibarra, L.; Lignos, D. Basic concepts and performance measures in prediction of collapse of buildings under earthquake ground motions. Struct. Des. Tall Spéc. Build. 2009, 19, 167–181. [Google Scholar] [CrossRef]
  52. Liel, A.B.; Haselton, C.B.; Deierlein, G.G.; Baker, J.W. Incorporating modeling uncertainties in the assessment of seismic collapse risk of buildings. Struct. Saf. 2009, 31, 197–211. [Google Scholar] [CrossRef]
  53. Zuo, Z.; Li, S. Discussion of “Experimental Investigation of Seismic Uncertainty Propagation through Shake Table Tests” by Peng Deng, Shiling Pei, John W. van de Lindt, and Chao Zhang. J. Struct. Eng. 2019, 145, 2. [Google Scholar] [CrossRef]
  54. Ibarra, L.; Krawinkler, H. Variance of collapse capacity of SDOF systems under earthquake excitations. Earthq. Eng. Struct. Dyn. 2011, 40, 1299–1314. [Google Scholar] [CrossRef]
Buildings 12 01219 g001 550
Figure 1. Elevations of the 3- and 9-story RC frame structures (unit: mm).
Figure 1. Elevations of the 3- and 9-story RC frame structures (unit: mm).
Buildings 12 01219 g001
Buildings 12 01219 g002 550
Figure 2. Mean spectra of the NPL and PL ground motions (design earthquake). (a) NPL ground motions; (b) PL ground motions.
Figure 2. Mean spectra of the NPL and PL ground motions (design earthquake). (a) NPL ground motions; (b) PL ground motions.
Buildings 12 01219 g002
Buildings 12 01219 g003 550
Figure 3. IDA curves of the RC frames under the excitation of NPL ground motions (FSRCB = 1.2).
Figure 3. IDA curves of the RC frames under the excitation of NPL ground motions (FSRCB = 1.2).
Buildings 12 01219 g003
Buildings 12 01219 g004 550
Figure 4. The median IDA curves of the 3-story RC frames with different FSRCBs.
Figure 4. The median IDA curves of the 3-story RC frames with different FSRCBs.
Buildings 12 01219 g004
Buildings 12 01219 g005 550
Figure 5. The median IDA curves of the 9-story RC frames with different FSRCBs.
Figure 5. The median IDA curves of the 9-story RC frames with different FSRCBs.
Buildings 12 01219 g005
Buildings 12 01219 g006 550
Figure 6. The collapse fragility curves of the 3-story RC frames with different FSRCBs.
Figure 6. The collapse fragility curves of the 3-story RC frames with different FSRCBs.
Buildings 12 01219 g006
Buildings 12 01219 g007 550
Figure 7. The effect of FSRCB on the collapse capacities of the RC frames with different FSRCBs (3-story). (a) The median collapse capacity; (b) Collapse capacities normalized to that of the FSRCB = 1.2.
Figure 7. The effect of FSRCB on the collapse capacities of the RC frames with different FSRCBs (3-story). (a) The median collapse capacity; (b) Collapse capacities normalized to that of the FSRCB = 1.2.
Buildings 12 01219 g007
Buildings 12 01219 g008 550
Figure 8. The collapse fragility curves of the 9-story RC frames with different FSRCBs.
Figure 8. The collapse fragility curves of the 9-story RC frames with different FSRCBs.
Buildings 12 01219 g008
Buildings 12 01219 g009 550
Figure 9. The effect of FSRCB on the collapse capacities of the RC frames with different FSRCBs (9-story). (a) The median collapse capacity; (b) Collapse capacities normalized to that of the FSRCB = 1.2.
Figure 9. The effect of FSRCB on the collapse capacities of the RC frames with different FSRCBs (9-story). (a) The median collapse capacity; (b) Collapse capacities normalized to that of the FSRCB = 1.2.
Buildings 12 01219 g009
Buildings 12 01219 g010 550
Figure 10. The uncertainty of collapse capacity of RC frames with different FSRCB.
Figure 10. The uncertainty of collapse capacity of RC frames with different FSRCB.
Buildings 12 01219 g010
Table
Table 1. The details of the reinforcement of the 3-story frames.
Table 1. The details of the reinforcement of the 3-story frames.
FSRCBAbeam/Transverse RebarAcolumn/Transverse Rebar
1.21206/Φ8@100/150905/Φ8@100/150
1.41206/Φ8@100/1501231/Φ8@100/150
1.61206/Φ8@100/1501608/Φ8@100/150
1.81206/Φ8@100/1502034/Φ8@100/150
2.01206/Φ8@100/1502544/Φ8@100/150
Table
Table 2. The details of the reinforcement of the 9-story frames.
Table 2. The details of the reinforcement of the 9-story frames.
FSRCBAbeam/Transverse RebarAcolumn/Transverse Rebar
1.21885/Φ8@100/1502011/Φ8@100/150
1.41885/Φ8@100/1502512/Φ8@100/150
1.61885/Φ8@100/1502842/Φ8@100/150
1.81885/Φ8@100/1503471/Φ8@100/150
2.01885/Φ8@100/1504163/Φ8@100/150
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Gong, M.; Liu, B.; Zuo, Z.; Sun, J.; Zhang, H. The Influence of the Flexural Strength Ratio of Columns to Beams on the Collapse Capacity of RC Frame Structures. Buildings 2022, 12, 1219. https://doi.org/10.3390/buildings12081219

AMA Style

Gong M, Liu B, Zuo Z, Sun J, Zhang H. The Influence of the Flexural Strength Ratio of Columns to Beams on the Collapse Capacity of RC Frame Structures. Buildings. 2022; 12(8):1219. https://doi.org/10.3390/buildings12081219

Chicago/Turabian Style

Gong, Maosheng, Bo Liu, Zhanxuan Zuo, Jing Sun, and Hao Zhang. 2022. "The Influence of the Flexural Strength Ratio of Columns to Beams on the Collapse Capacity of RC Frame Structures" Buildings 12, no. 8: 1219. https://doi.org/10.3390/buildings12081219

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop