Impact of Temperature and Relative Humidity on Reverberation Time in a Reverberation Room
Abstract
:1. Introduction
2. Methodology
2.1. Theoretical Foundations
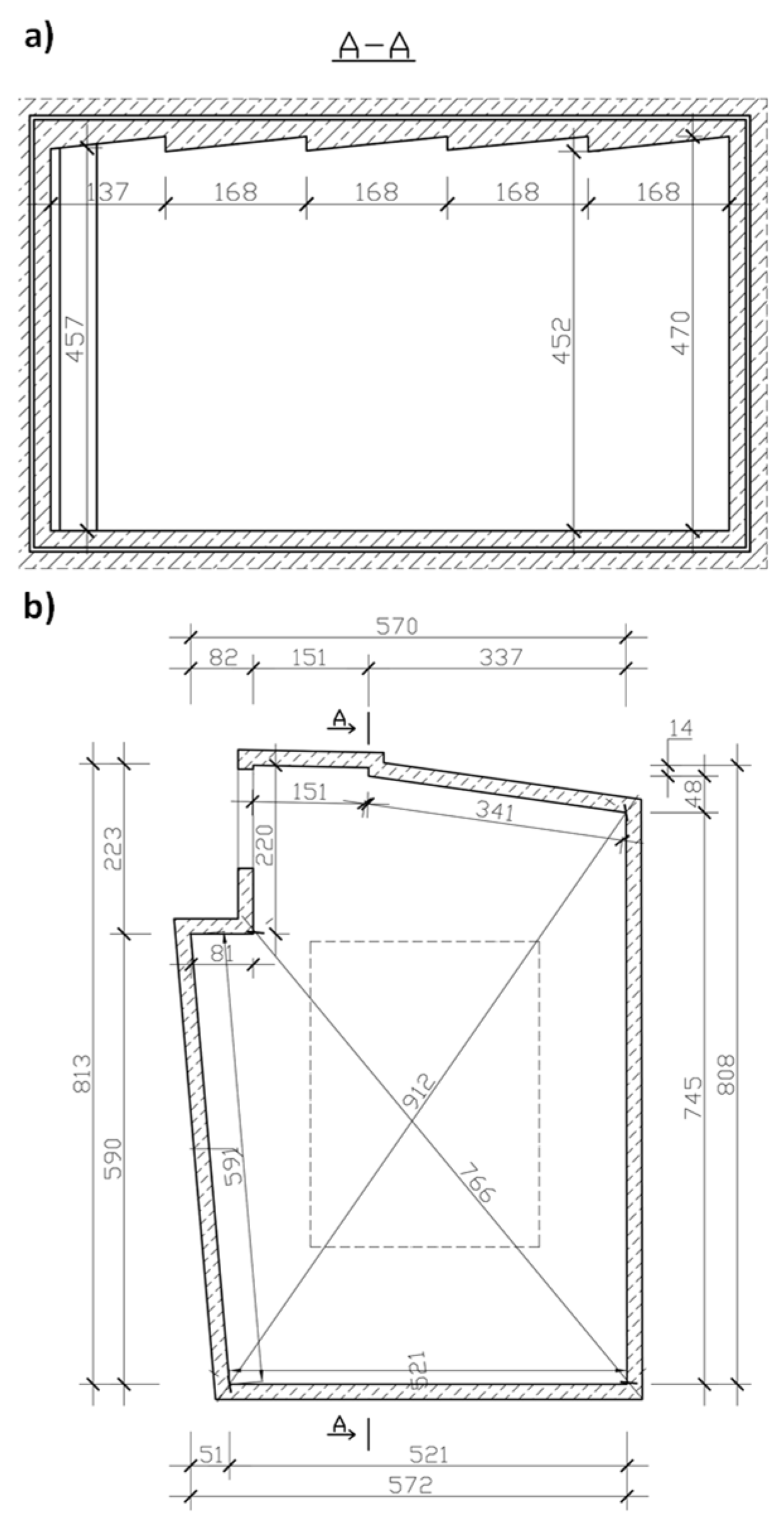
2.2. Measurement in the Reverberation Room
- The transmitting part of the test system consisted of a loudspeaker with a spherical radiation pattern, and an artificial test noise generator with an amplifier manufactured by Svantek.
- The receiving part of the test system consisted of a 4-channel SVAN 958 sound level meter, two 1/2ʺ microphones, an acoustic calibrator SV03A, and a PC computer with the software SvanPC + Software Official 1.0.21 e.
2.3. Simulations
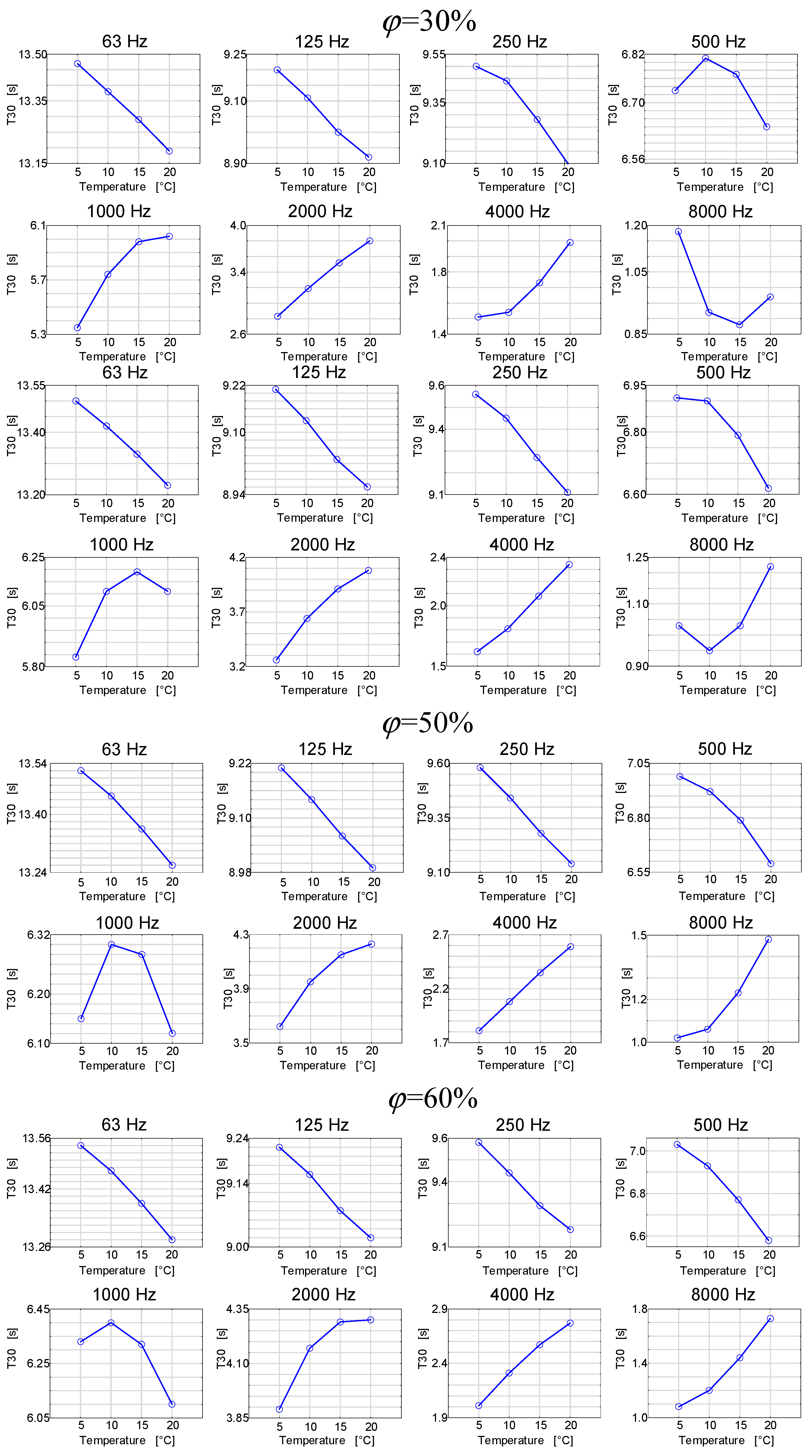
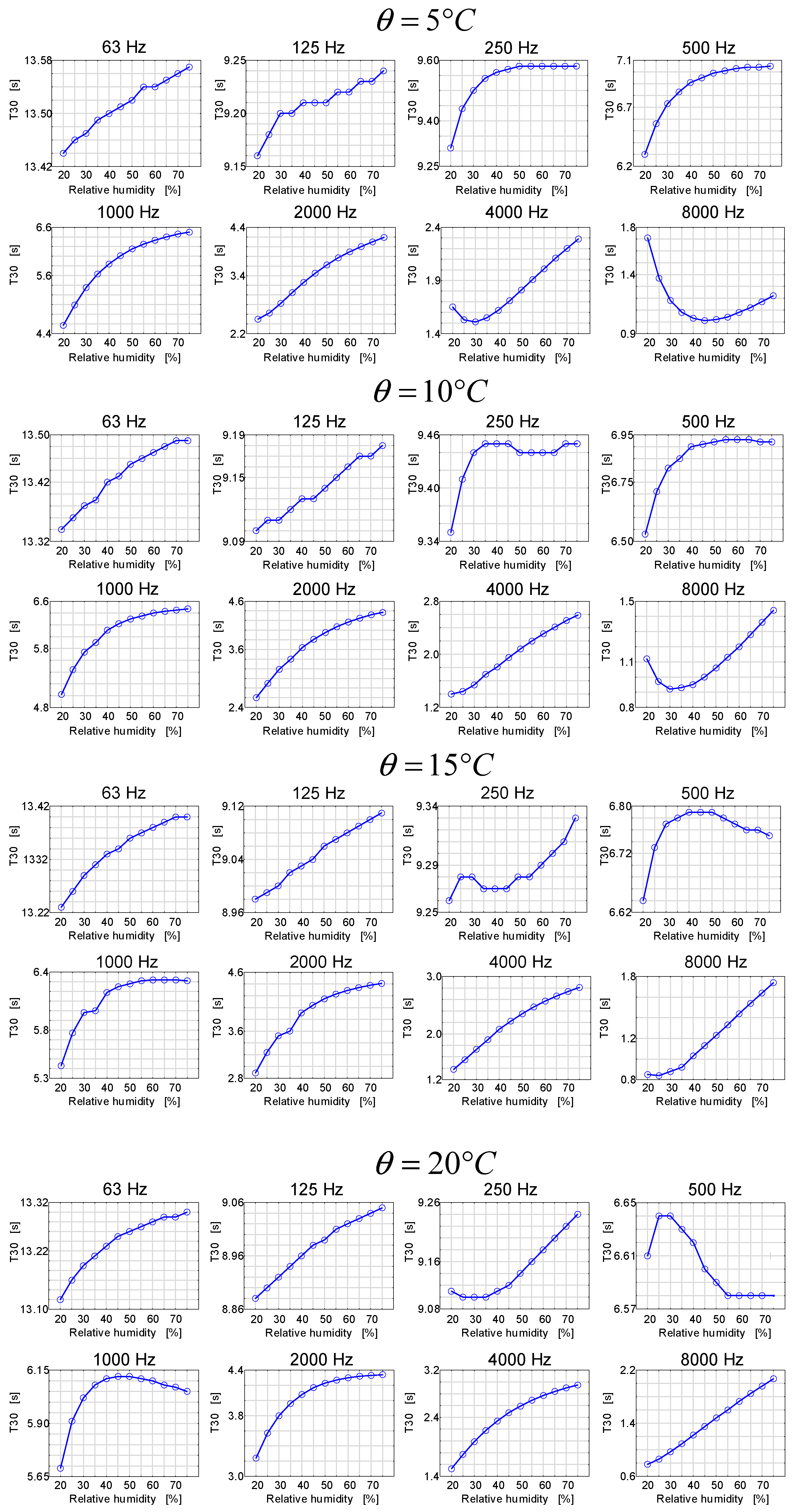
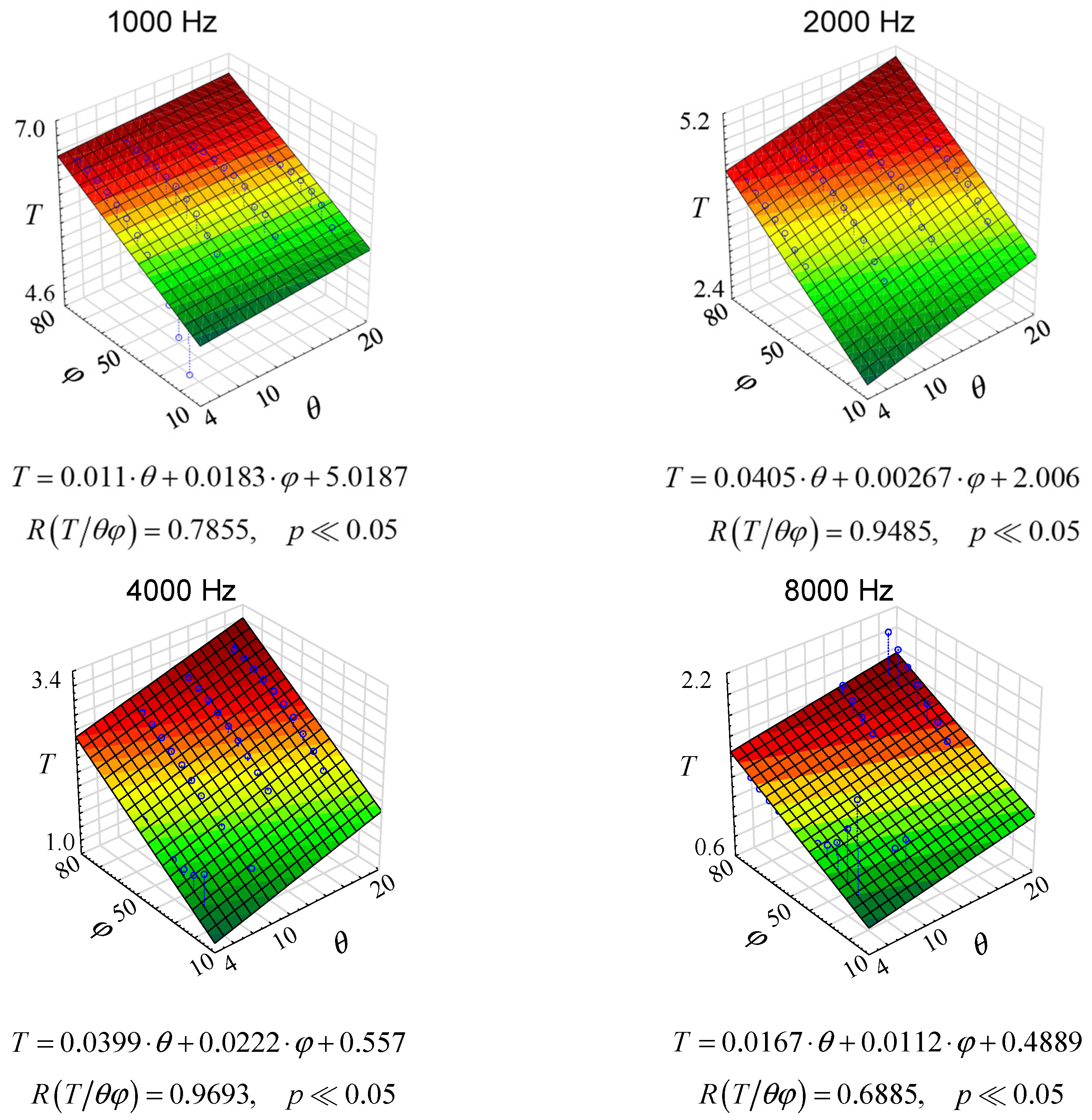
3. Results and Discussion
4. Conclusions
- The nature in the changes of reverberation time depending on temperature and relative air humidity is completely different for different frequency bands.
- The nature of the changes in the reverberation time as a function of relative humidity for the same frequency band is different for the changing air temperatures—see, e.g., the center frequency of 250 Hz for the temperatures of 10 °C and 15 °C.
- The nature of the reverberation time changes as a function of the temperature for the same frequency band and is different for the changing relative air humidity.
- The impact involving the changes in the relative air humidity on the change of the reverberation time characteristics as a function of frequency is much smaller than the impact of temperature change.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Reinten, J.; Braat-Eggen, P.; Horniks, M.; Kort, H.S.M.; Kohlrausch, A. The indoor sound environment and human task performance: A literature review on the role of room acoustics. Build. Environ. 2017, 123, 315–332. [Google Scholar] [CrossRef]
- Aretz, M.; Orlowski, R.I. Sound strength and reverberation time in small concert halls. Appl. Acoust. 2009, 70, 1099–1110. [Google Scholar] [CrossRef]
- Tang, S.K.; Yeung, M.H. Reverberation times and speech transmission index in classrooms. J. Sound Vib. 2006, 294, 596–607. [Google Scholar] [CrossRef]
- Leccese, F.; Rocca, M.; Salvadori, G. Fast estimation of Speech Transmission Index using the Reverberation Time: Comparison between predictive equations for educational rooms of different sizes. Appl. Acoust. 2018, 140, 143–149. [Google Scholar] [CrossRef]
- Nowoświat, A.; Olechowska, M. Fast estimation of Speech Transmission Index using the Reverberation Time. Appl. Acoust. 2016, 102, 55–61. [Google Scholar] [CrossRef]
- Nowoświat, A.; Olechowska, M. Investigation studies on the application of reverberation time. Arch. Acoust. 2016, 41, 15–26. [Google Scholar] [CrossRef] [Green Version]
- Montoya, J.C. Comparison and analysis of the methods defined by ASTM standard E2235-04, ISO 3382-2-2008 and EASY acoustical modeling software to determine reverberation time RT60 in ordinary rooms. J. Acoust. Soc. Am. 2017, 142m, 2508. [Google Scholar] [CrossRef]
- Rosenhouse, G. Reverberation time analysis for nonrectangular rooms using the Monte Carlo method. J. Acoust. Soc. Am. 2017, 141, 3711. [Google Scholar] [CrossRef]
- Meissner, M. Acoustics of small rectangular rooms: Analytical and numerical determination of reverberation parameters. Appl. Acoust. 2017, 120, 111–119. [Google Scholar] [CrossRef]
- Zhou, X.; Späh, M.; Henghst, K.; Zhang, T. Predicting the reverberation time in rectangular rooms with non-uniform absorption distribution. Appl. Acoust. 2021, 171, 107539. [Google Scholar] [CrossRef]
- Brandäo, E.; Santos, E.S.O.; Melo, V.S.G.; Tenenbaum, R.A.; Mereze, P.H. On the performance investigation of distinct algorithms for room acoustics simulation. Appl. Acoust. 2022, 187, 108484. [Google Scholar] [CrossRef]
- Tronchin, L. Variability of room acoustic parameters with thermo-hygrometric conditions. Appl. Acoust. 2021, 177, 107933. [Google Scholar] [CrossRef]
- Winkler-Skalna, A.; Nowoświat, A. Use of n-perturbation interval ray tracing method in predicting acoustic field distribution. Appl. Math. Model. 2021, 93, 426–442. [Google Scholar] [CrossRef]
- ISO 9613-1:1993; Acoustics—Attenuation of Sound during Propagation Outdoors-Part 1: Calculation of the Absorption of Sound by the Atmosphere. International Organization for Standardization, Geneva, Switzerland, 1993.
- ISO 354:2003; Acoustics—Measurement of Sound Absorption in a Reverberation Room. International Organization for Standardization, Geneva, Switzerland, 2003.
- Nowoświat, A.; Olechowska, M.; Marchacz, M. The effect of acoustical remedies changing the reverberation time for different frequencies in a dome used for worship: A case study. Appl. Acoust. 2020, 160, 107143. [Google Scholar] [CrossRef]
- Berardi, U. Simulation of acoustical parameters in rectangular churches. J. Build. Perform. Simul. 2014, 7, 1–16. [Google Scholar] [CrossRef]
- Harris, C. M Absorption of sound in air in the audio-frequency range. J. Acoust. Soc. Am. 1963, 35, 11–17. [Google Scholar] [CrossRef]
- Nowoświat, A.; Bochen, J.; Dulak, L.; Żuchowski, R. Investigation studies involving sound absorbing parameters of roadside screen panels subjected to aging in simulated conditions. Appl. Acoust. 2016, 111, 8–15. [Google Scholar] [CrossRef]
- Nowoświat, A.; Olechowska, M. Experimental validation of the model reverberation time prediction in room. Buildings 2022, 12, 347. [Google Scholar] [CrossRef]
- Lannace, G.; Berardi, U.; De Rossi, F.; Mazza, S.; Trematerra, A.; Ciaburro, G. Acoustic Enhancement of a modern church. Buildings 2019, 9, 83. [Google Scholar]
- Zeng, X.; Christensen, C.L.; Rindel, J.H. Practical methods to define scattering coefficients in a room acoustics computer model. Appl. Acoust. 2006, 67, 771–786. [Google Scholar] [CrossRef]
- Stern, F.; Wilson, R.; Coleman, H.; Paterson, E.G. Comprehensive approach to verification and validation of CFD simulations—Part 1: Methodology and procedures. J. Fluids Eng. 2001, 123, 793–802. [Google Scholar] [CrossRef]
- Marbjerg, G.; Brunskog, J.; Jeong, C. The difficulties of simulating the acoustics of an empty rectangular room with an absorbing ceiling. Appl. Acoust. 2018, 141, 35–45. [Google Scholar] [CrossRef]
- Nowoświat, A. Application of Perturbation Methods in the Acoustic Assessment of Interiors for the Reception of Verbal Sounds; Wyd. Politechniki Śląskiej: Gliwice, Poland, 2019. [Google Scholar]




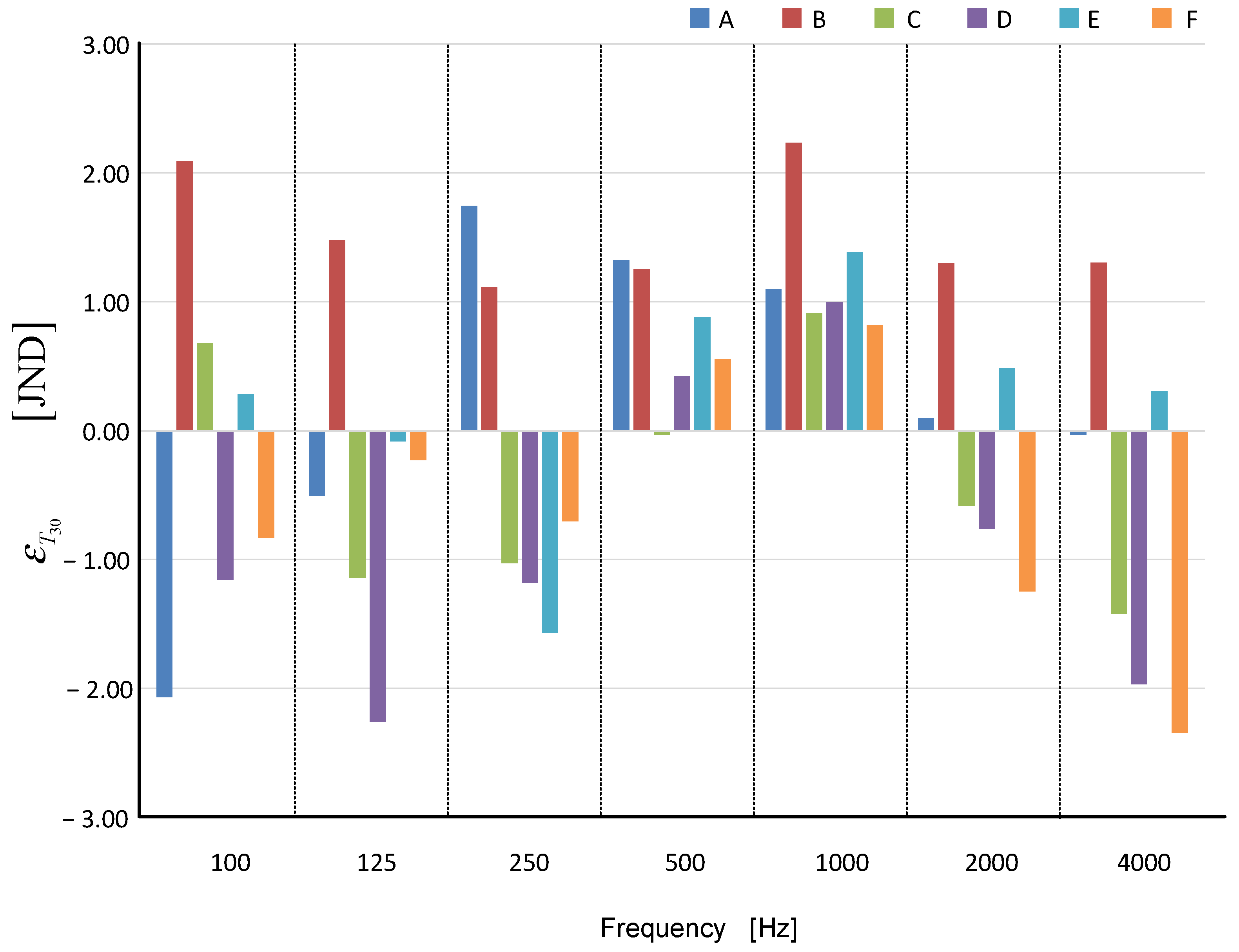


| Relative Humidity | Frequency (kHz) | ||||||
|---|---|---|---|---|---|---|---|
| 0.5 | 1 | 2 | 3 | 4 | 6 | 8 | |
| 40 | 0.60 | 1.07 | 2.58 | 5.03 | 8.40 | 17.71 | 30.00 |
| 50 | 0.63 | 1.08 | 2.28 | 4.20 | 6.84 | 14.26 | 24.29 |
| 60 | 0.64 | 1.11 | 2.14 | 3.72 | 5.91 | 12.08 | 20.52 |
| 70 | 0.64 | 1.15 | 2.08 | 3.45 | 5.32 | 10.62 | 17.91 |
| Frequency [Hz] | Absorption Coefficients |
|---|---|
| 63 | 0.011 |
| 125 | 0.016 |
| 250 | 0.015 |
| 500 | 0.020 |
| 1000 | 0.020 |
| 2000 | 0.026 |
| 4000 | 0.030 |
| Frequency/Climate | 14.6 °C 55.9% | 15.0 °C 42.0% | 15.5 °C 30.0% | 17.8 °C 45.0% | 18.0 °C 33.5% | 19.3 °C 80.0% |
|---|---|---|---|---|---|---|
| 500 Hz | 0.37 | 0.04 | 0.30 | 0.22 | 0.20 | 0.07 |
| 1000 Hz | 0.04 | 0.17 | 0.14 | 0.04 | 0.28 | 0.22 |
| 2000 Hz | 0.08 | 0.07 | 0.06 | 0.11 | 0.07 | 0.11 |
| 5000 Hz | 0.01 | 0.03 | 0.04 | 0.06 | 0.01 | 0.29 |
| Frequency [Hz] | ||
|---|---|---|
| 63 | 2.40 | 11.74 |
| 125 | 2.13 | 5.96 |
| 250 | 0.91 | 4.71 |
| 500 | 0.89 | 3.53 |
| 1000 | 2.3 | 3.80 |
| 2000 | 4.41 | 5.20 |
| 4000 | 8.69 | 9.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nowoświat, A. Impact of Temperature and Relative Humidity on Reverberation Time in a Reverberation Room. Buildings 2022, 12, 1282. https://doi.org/10.3390/buildings12081282
Nowoświat A. Impact of Temperature and Relative Humidity on Reverberation Time in a Reverberation Room. Buildings. 2022; 12(8):1282. https://doi.org/10.3390/buildings12081282
Chicago/Turabian StyleNowoświat, Artur. 2022. "Impact of Temperature and Relative Humidity on Reverberation Time in a Reverberation Room" Buildings 12, no. 8: 1282. https://doi.org/10.3390/buildings12081282
APA StyleNowoświat, A. (2022). Impact of Temperature and Relative Humidity on Reverberation Time in a Reverberation Room. Buildings, 12(8), 1282. https://doi.org/10.3390/buildings12081282






