Effect of Filling Phosphogypsum on the Axial Compression Behavior of Cold-Formed Thin-Walled Steel Walls
Abstract
:Highlights
- The effect of filling phosphogypsum on the axial compression behavior of CFS walls.
- The axial compression performance of CFS walls with different cross-sections.
- The failure mechanism of CFS walls filled with phosphogypsum under axial compression.
- Filling phosphogypsum can effectively improve the axial compression behavior of CFS walls.
- The bearing capacity of the wall filled with phosphogypsum in and between the studs was significantly increased.
- The components affecting the bearing capacity of the wall are steel tubes, phosphogypsum, and wall sheathings.
Abstract
1. Introduction
2. Test Program
2.1. Description of Specimens
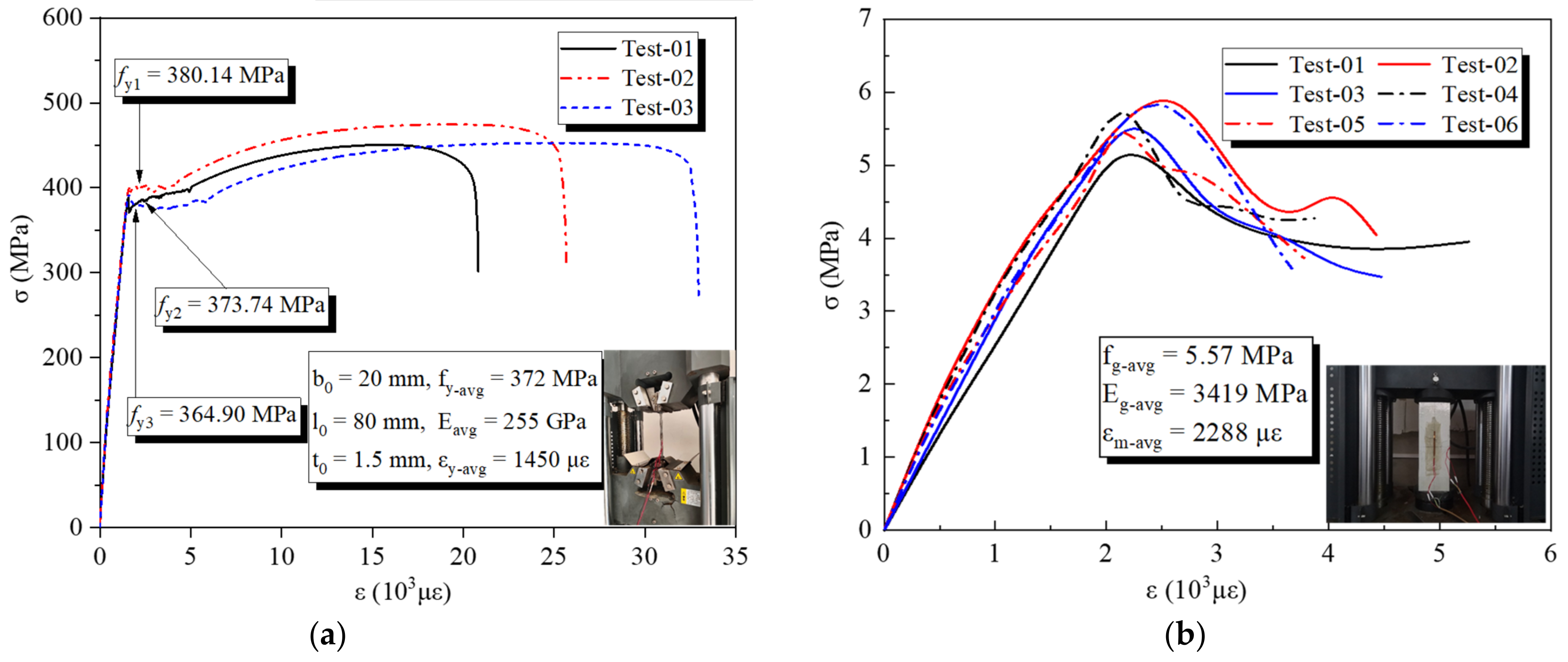
2.2. Material Properties
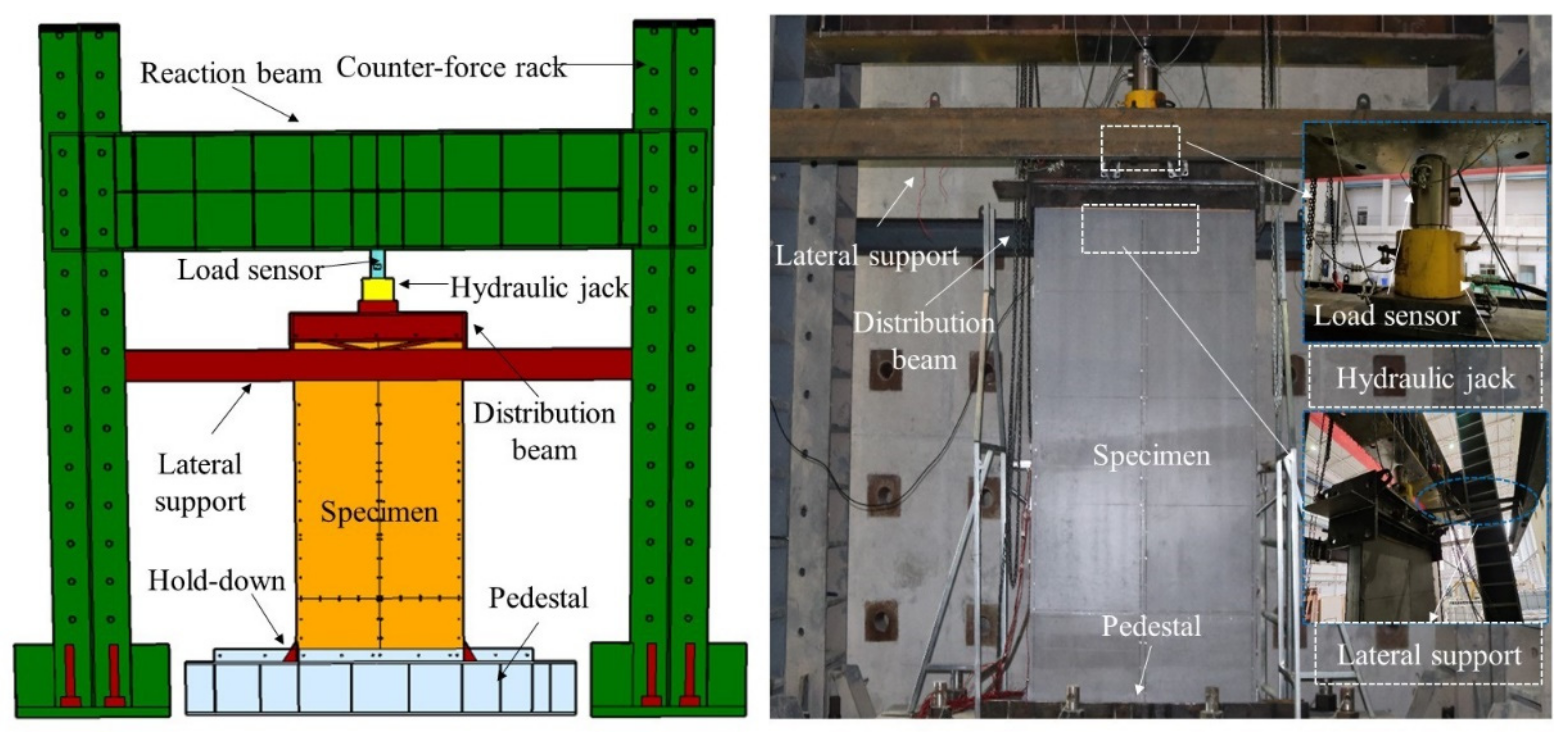
2.3. Test Setup and Loading Scheme
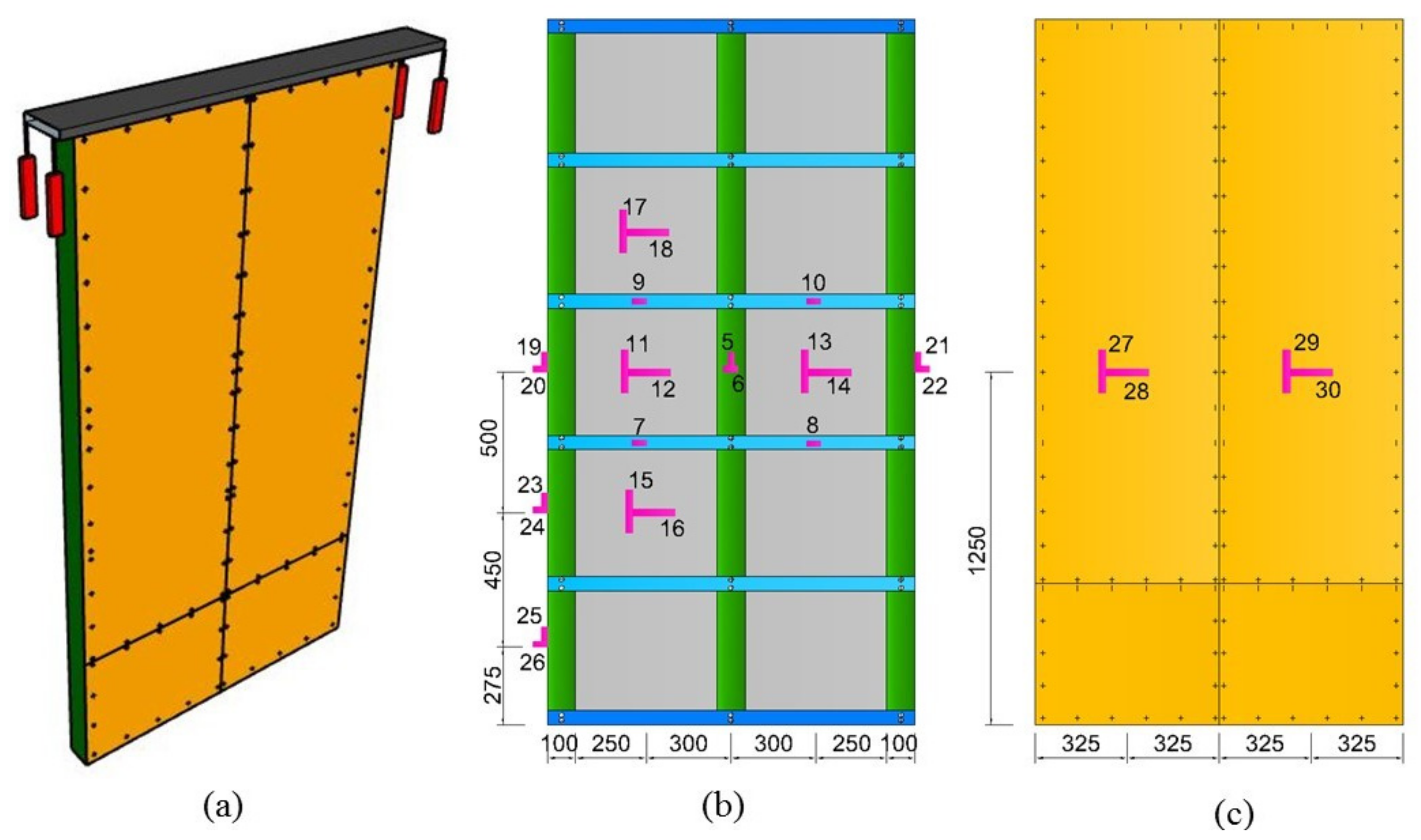
2.4. Arrangement of Measurement Points
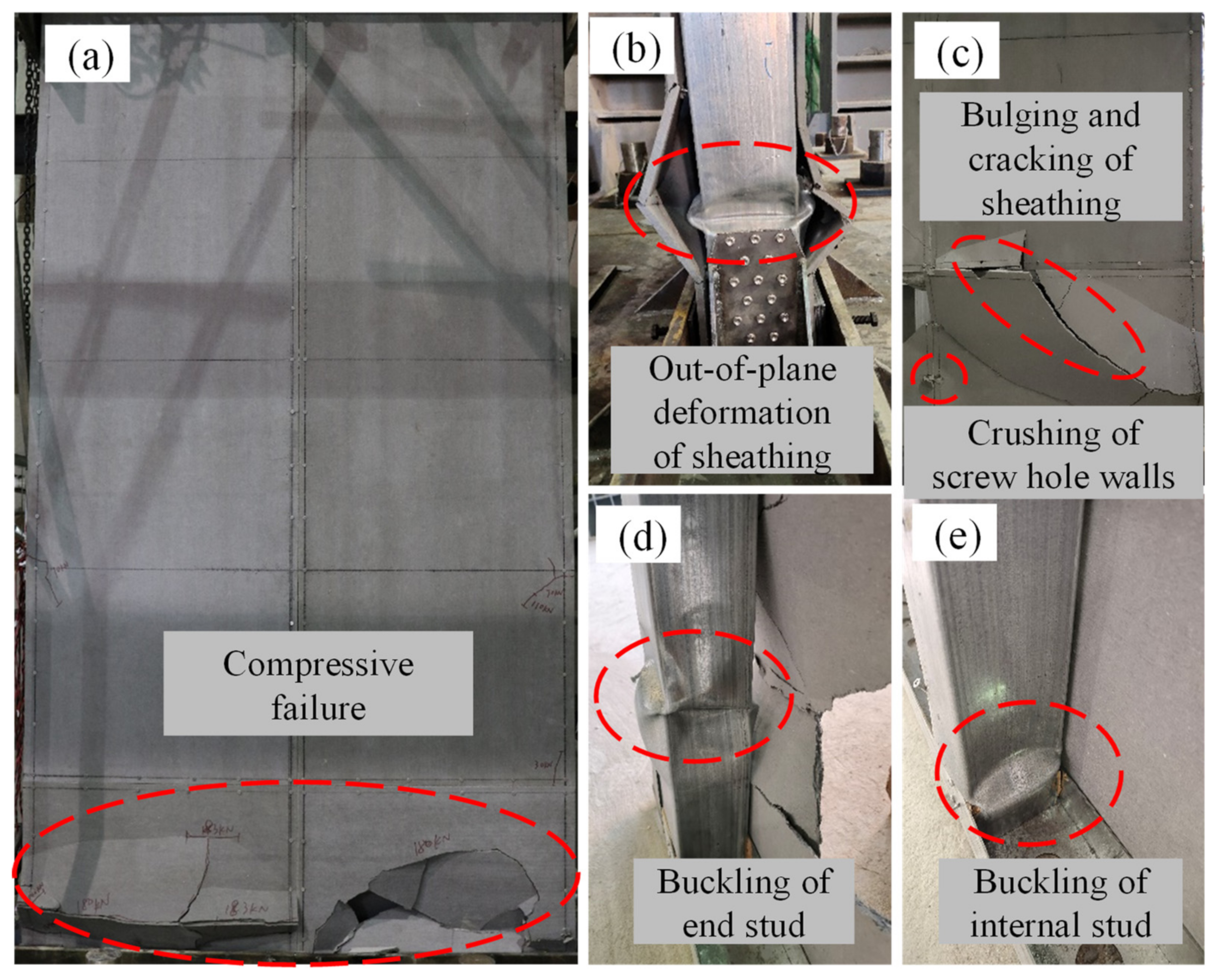
3. General Observation and Failure Modes
3.1. Test Specimen W1
3.2. Test Specimen W2
3.3. Test Specimen W3
3.4. Test Specimen W4
4. Discussion of the Test Results
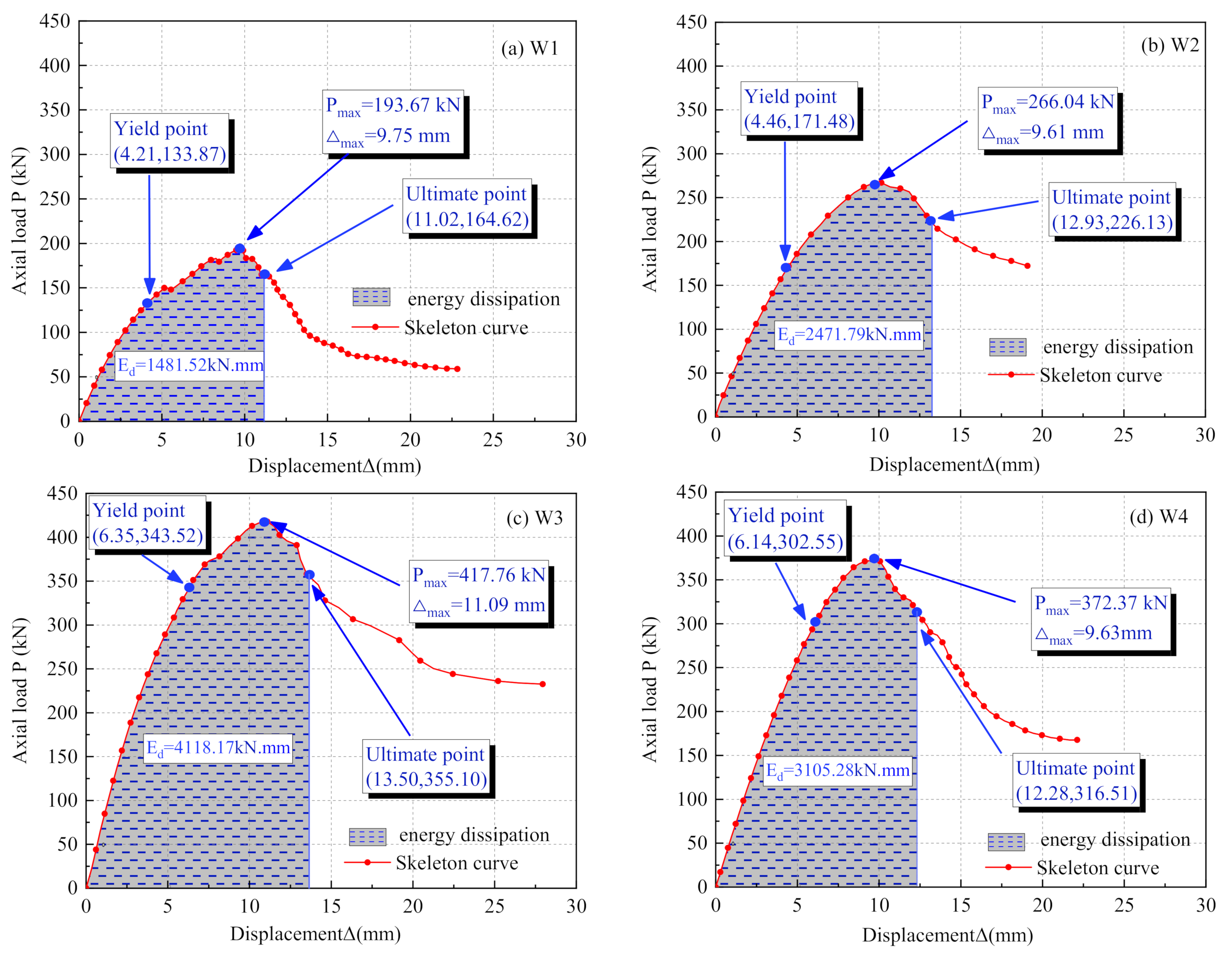
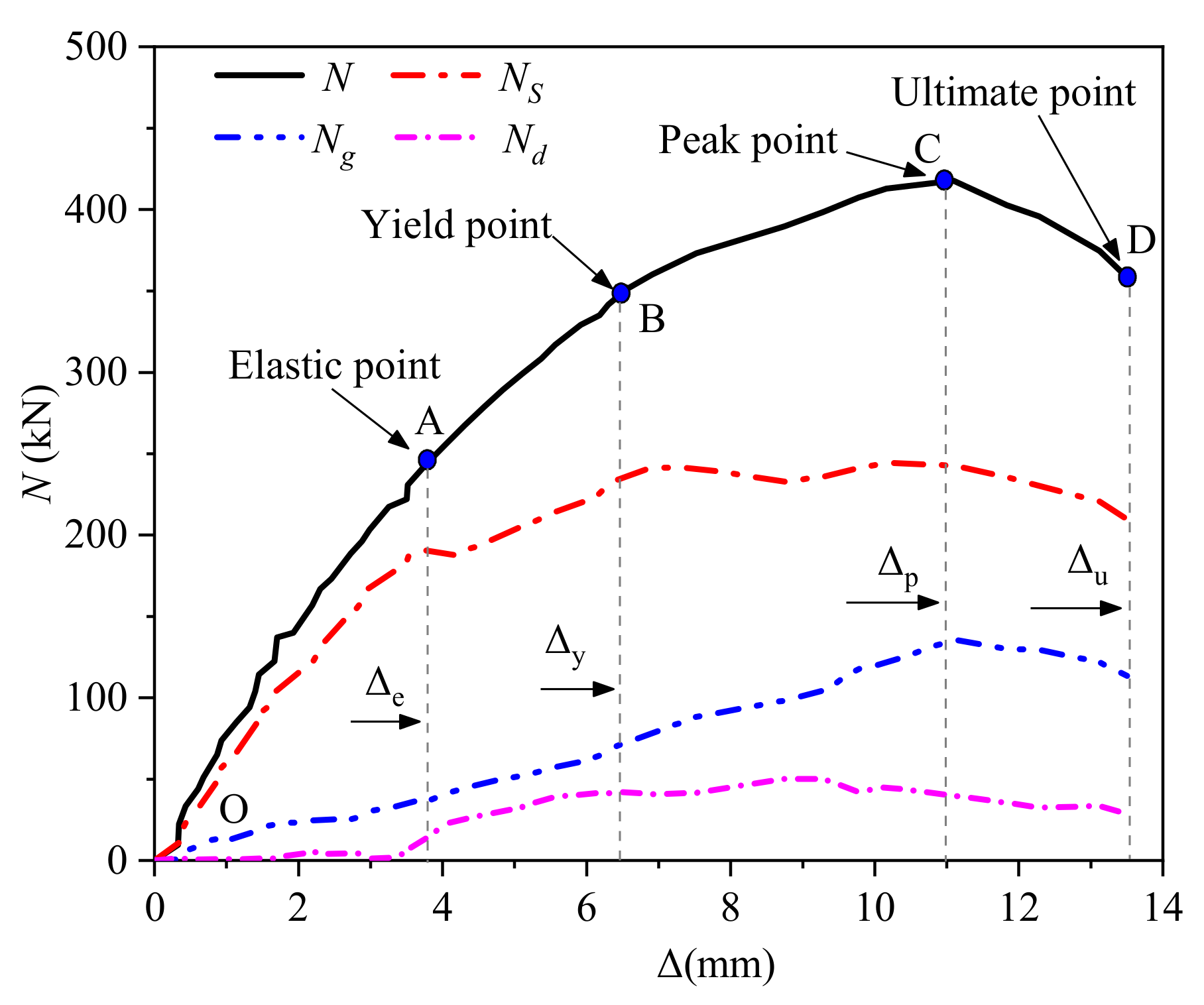
4.1. Vertical Load-Displacement Curve
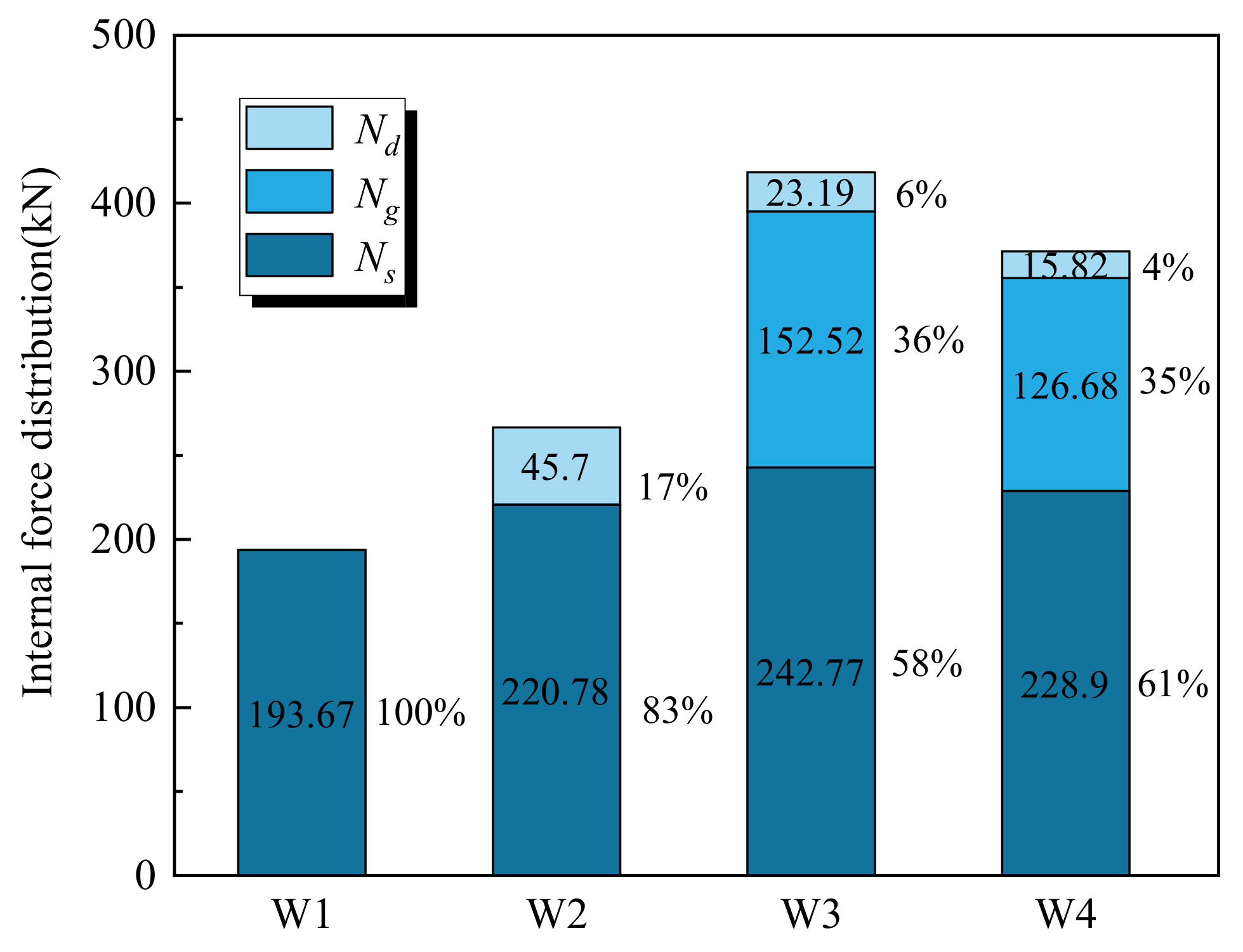
4.2. Analysis of the Axial Bearing Capacity
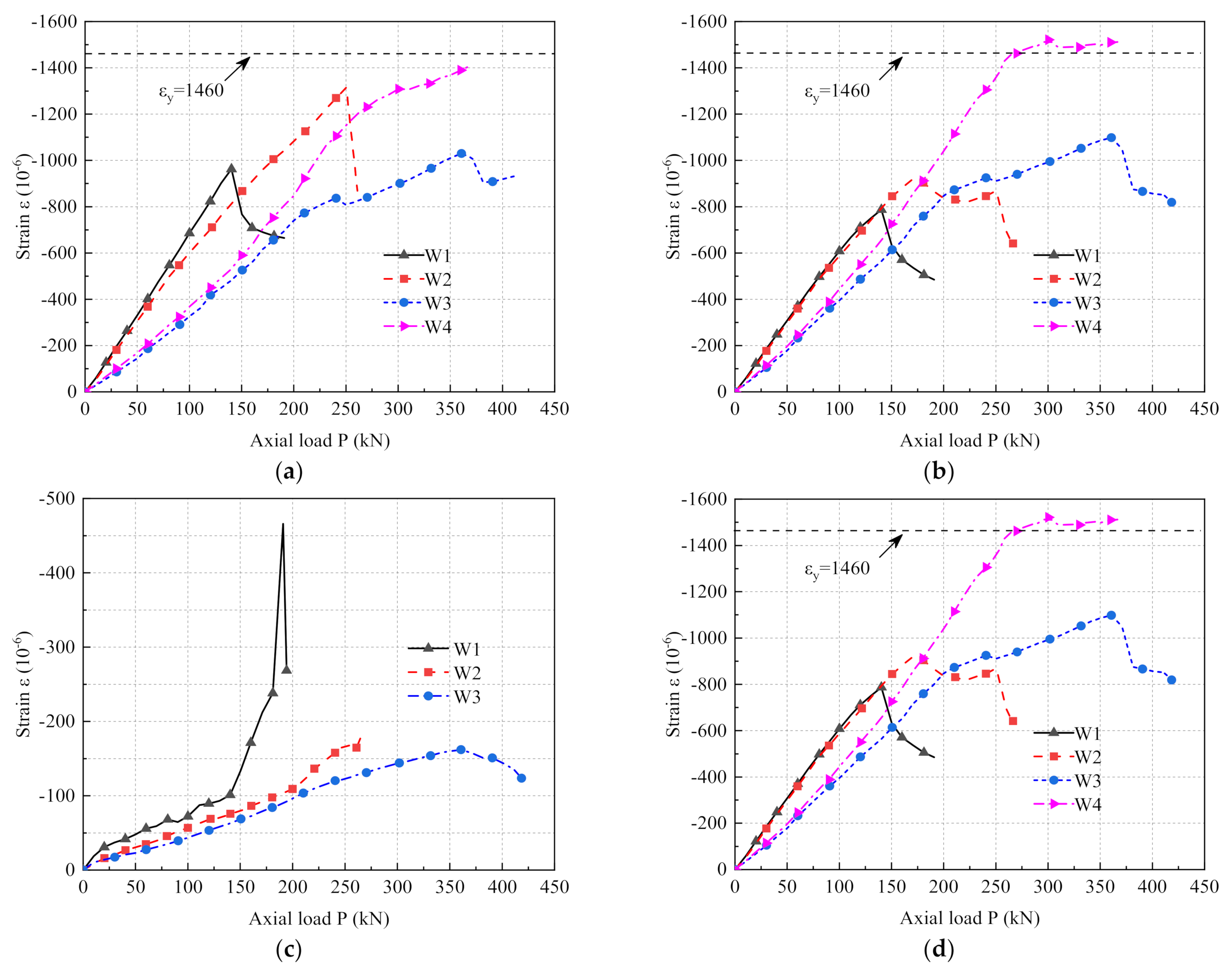
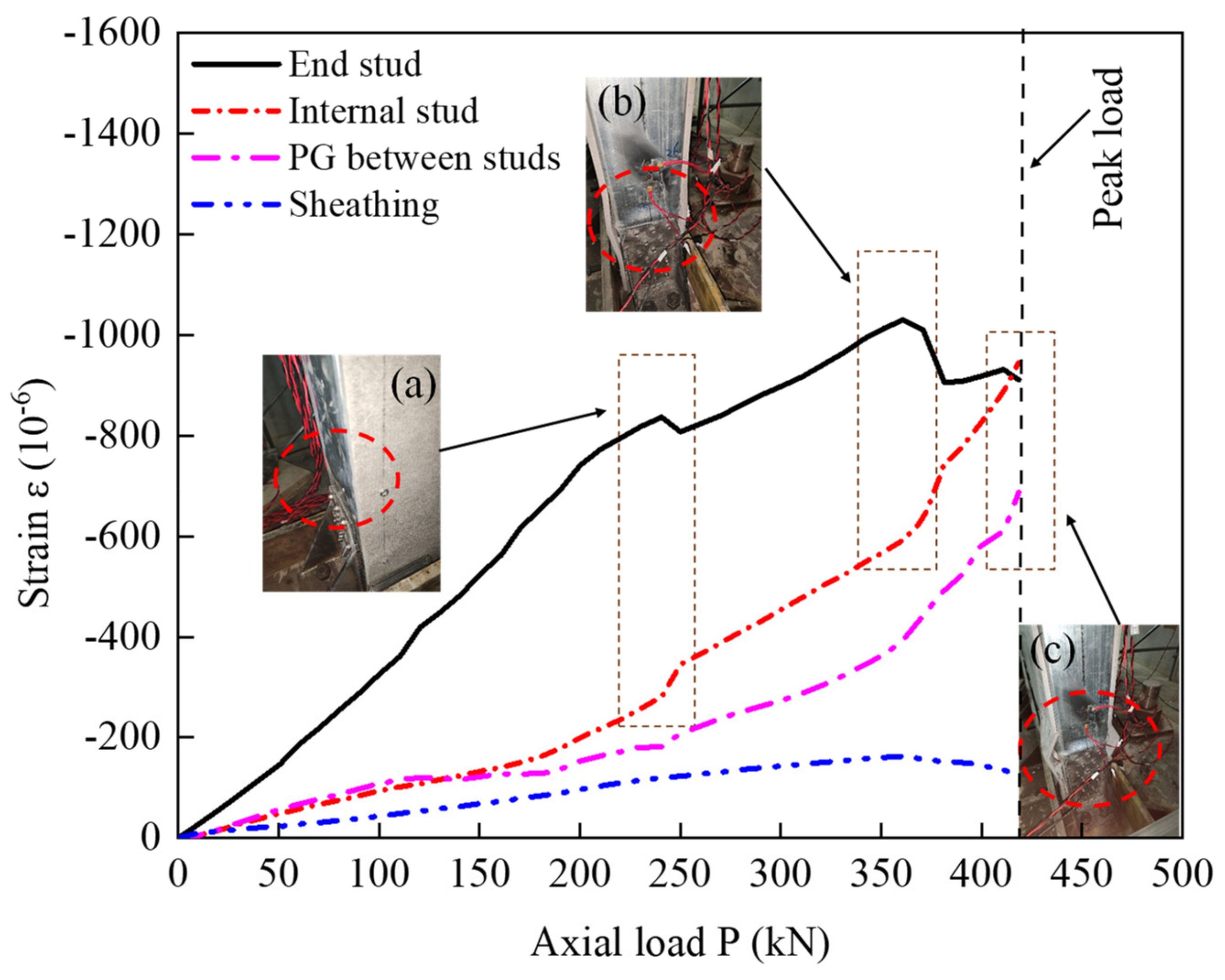
4.3. Strain Analysis
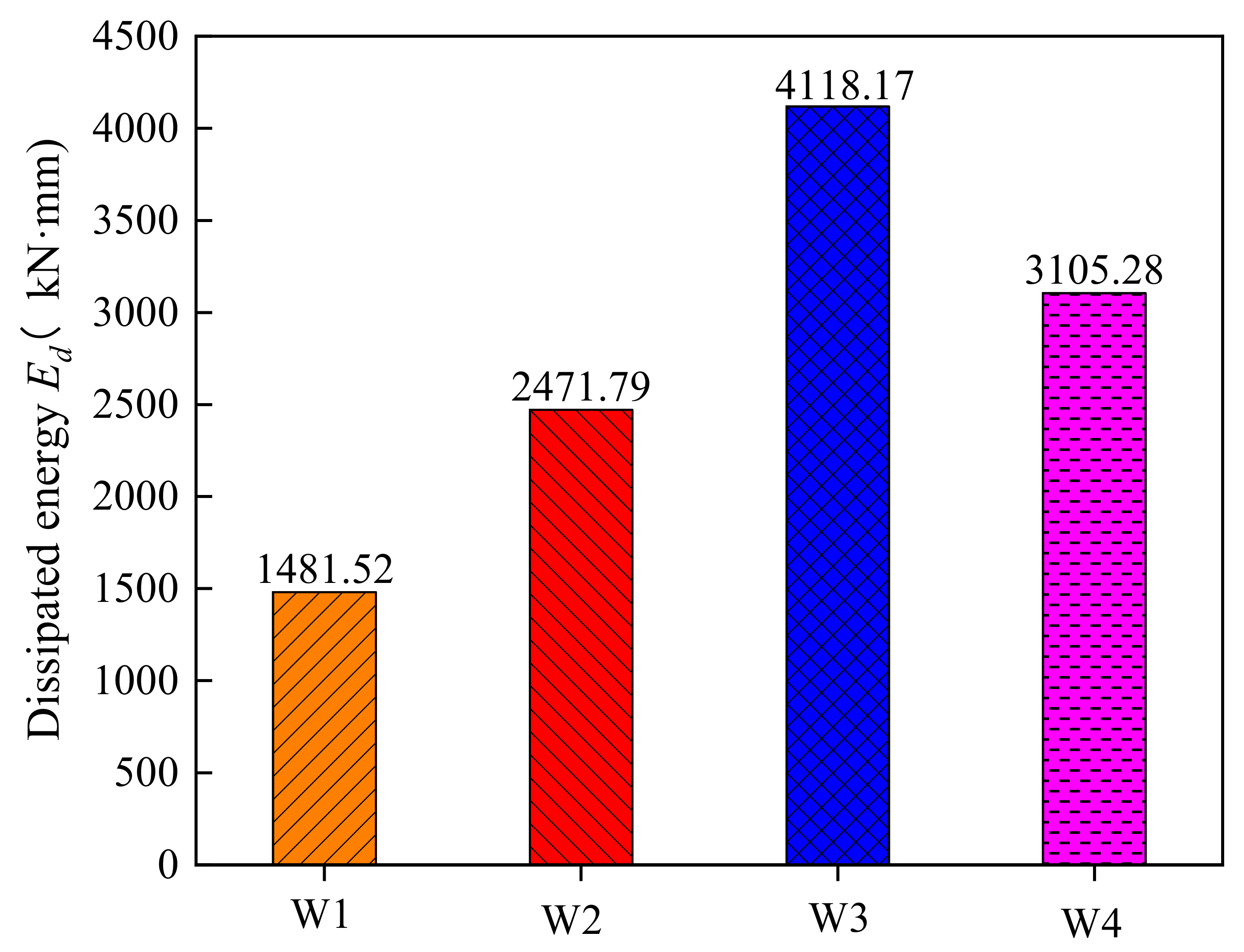
4.4. Energy Dissipation
5. Failure Mechanism
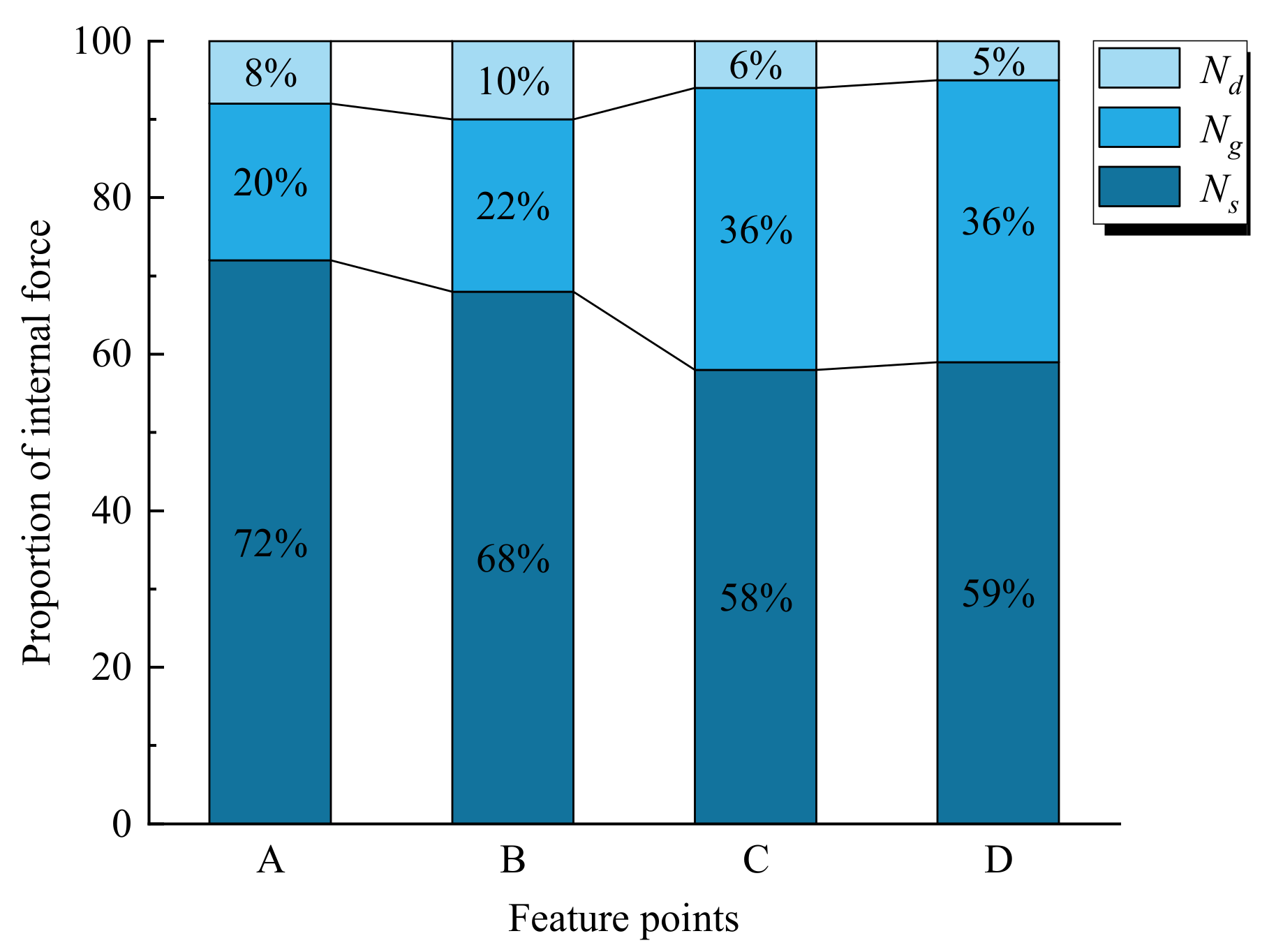
5.1. Analysis of Whole-Process Stress
5.2. Contribution Proportions of Components at Peak Point
5.3. Analysis of Failure Mechanism
6. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Iuorio, O.; Fiorino, L.; Landolfo, R. Testing CFS structures: The new school BFS in Naples. Thin-Walled Struct. 2014, 84, 275–288. [Google Scholar] [CrossRef]
- Kaleeswaran, C.; Saravanakumar, R.; Vivek, D.; Elango, K.S.; Gopi, R.; Balaji, D. A study on cold-formed steel compression member-a review. Mater. Today 2021, 37, 1767–1771. [Google Scholar] [CrossRef]
- Miller, T.H.; Pekoz, T. Behavior of cold-formed steel wall stud assemblies. J. Struct.Eng. 1993, 119, 641–651. [Google Scholar] [CrossRef]
- Miller, T.H.; Pekoz, T. Behavior of gypsum-sheathed cold-formed steel wall studs. J. Struct. Eng. 1994, 120, 1644–1650. [Google Scholar] [CrossRef]
- Telue, Y.; Mahendran, M. Behavior of cold-formed steel wall frames lined with plasterboard. J. Constr. Steel Res. 2001, 57, 435–452. [Google Scholar] [CrossRef]
- Telue, Y.; Mahendran, M. Behavior and design of cold-formed steel wall frames lined with plasterboard on both sides. Eng. Struct. 2004, 26, 567–579. [Google Scholar] [CrossRef]
- Tian, Y.S.; Wang, J.; Lu, T.J. An experimental study on the axial behavior of cold-formed steel wall studs and panels. Thin-Walled Struct. 2004, 42, 557–573. [Google Scholar] [CrossRef]
- Wang, J.; Tian, Y.S.; Lu, T.J. The role of frame members and sheathing in partition wall panels subjected to compression. Thin-Walled Struct. 2005, 43, 983–1002. [Google Scholar] [CrossRef]
- Tian, Y.S.; Wang, J.; Lu, T.J. Axial load capacity of cold-formed steel wall stud with sheathing. Thin-Walled Struct. 2007, 45, 537–551. [Google Scholar] [CrossRef]
- Kashan, K.H.; Chen, Z.H.; Liu, J.D.; Arsalan, K.H.; Khadija, J. Axial compression behaviours of tubular sectioned C-shape continuous-supported steel walls in MSB. J. Constr. Steel Res. 2022, 188, 107009. [Google Scholar]
- Lawson, R. Light steel modular construction high-rise modular building, London three storey modular office building modular residential building four sided modules form of construction. SCI Steel Knowl. 2016, 1, 1–8. [Google Scholar]
- Hou, J.; Wang, X.; Liu, J.; Chen, Z.; Zhong, X. Study on the stability bearing capacity of multi-column wall in modular steel building. Eng. Struct. 2020, 214, 110648. [Google Scholar] [CrossRef]
- Zhang, X.H.; Zhang, E.Y.; Yu, H. Axial compression performance of cold-formed thin-walled square steel stud-straw board composite wall. Sci. Tech. Eng. 2021, 21, 283–289. (In Chinese) [Google Scholar]
- Hegyi, P.; Dunai, L. Experimental study on ultra-lightweight-concrete encased cold-formed steel structures Part I: Stability behaviour of elements subjected to bending. Thin-Walled Struct. 2016, 101, 75–84. [Google Scholar] [CrossRef]
- Hegyi, P.; Dunai, L. Experimental investigations on ultra-lightweight-concrete en-cased cold-formed steel structures Part II: Stability behaviour of elements subjected to compression. Thin-Walled Struct. 2016, 101, 100–108. [Google Scholar] [CrossRef]
- Prabha, P.; Marimuthu, V.; Saravanan, M.; Palani, G.S.; Lakshmanan, N.; Senthil, R. Effect of confinement on steel-concrete composite light-weight load-bearing wall panels under compression. J. Constr. Steel Res. 2013, 81, 11–19. [Google Scholar] [CrossRef]
- Chao, H.W.; Zhou, T. Cold-formed steel framing walls with infilled lightweight FGD gypsum Part II: Axial compression tests. Thin-Walled Struct. 2018, 32, 771–782. [Google Scholar]
- Chen, J.W.; Gao, K.F. Experimental study on axial compression performance of cold-formed steel framing walls with infilled gypsum based material. Build. Sci. 2018, 34, 48–53. (In Chinese) [Google Scholar]
- Wang, J.F.; Wang, R.Z.Q. Experiments and calculation methods on performance of prefabricated clad-formed steel (CFS)composite walls filled with light mortar under axial compression. Indus. Constr. 2021, 51, 99–105. (In Chinese) [Google Scholar]
- Li, H.X.; Liu, D.Z.; Wu, S.Y. Bearing characteristic research of composite foam-concrete wall reinforced with cold-formed thin-wall section steel. Indus. Constr. 2020, 50, 160–169. (In Chinese) [Google Scholar]
- Bianca, R.S.; Calderón, M.; Antonio, G.M.; Paloma, P.; Rafael, G.T. Valorization of phosphogypsum in cement-based materials: Limits and potential in eco-efficient construction. J. Build. Eng. 2021, 44, 102506. [Google Scholar]
- Pereira, M.V.; Geraldo, R.H.; Cruz, A.M.; Gladis, C. Valorization of industrial by-product: Phosphogypsum recycling as green binding material. Cleaner Eng. Tech. 2021, 5, 100310. [Google Scholar] [CrossRef]
- JGJ 227-2011; Technical Specification for Low-Rise Cold-Formed Thin-Walled Steel Buildings. Architecture Industrial Press of China: Beijing, China, 2011.
- GB/T 228.1-2010; Metallic Materials-Tensile Testing-Part 1: Method of Test at Room Temperature. China Standard Press: Beijing, China, 2010.
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. Architecture Industrial Press of China: Beijing, China, 2019.
- GB/T17657-1999; Test Method for Physical and Chemical Properties of Wood-Based Panels and Veneer Panels. Architecture Industrial Press of China: Beijing, China, 1999.
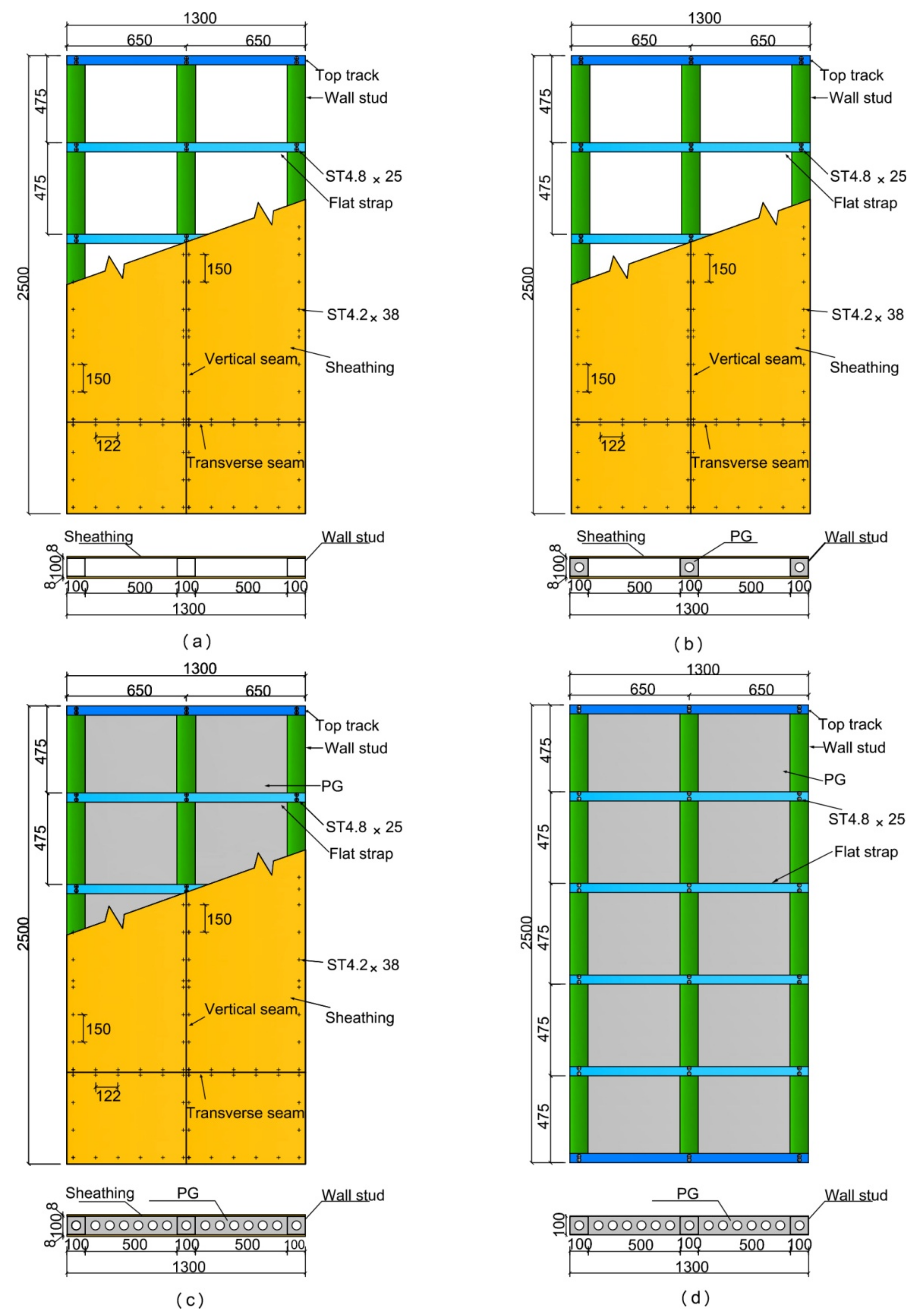




| Specimen | Track Size (mm) | Stud Size (mm) | Stud Spacing (mm) | PG in Studs | PG between Studs | FCB |
|---|---|---|---|---|---|---|
| W1 | U106 × 50 × 1.94 | 100 × 100 × 1.48 | 500 | No | No | Yes |
| W2 | U106 × 50 × 1.94 | 100 × 100 × 1.48 | 500 | Yes | No | Yes |
| W3 | U106 × 50 × 1.94 | 100 × 100 × 1.48 | 500 | Yes | Yes | Yes |
| W4 | U106 × 50 × 1.94 | 100 × 100 × 1.48 | 500 | Yes | Yes | No |
| Thickness (mm) | Yield Stress (MPa) | Ultimate Stress (MPa) | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|---|
| 1.5 | 372.32 | 451.75 | 2.55 × 105 | 0.31 |
| 2.0 | 270.35 | 372.85 | 2.00 × 105 | 0.34 |
| Name | Compressive Strength (MPa) | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|
| PG in studs | 6.01 | 3829 | 0.21 |
| PG between studs | 5.57 | 3419 | 0.21 |
| Name | Compressive Strength (MPa) | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|
| FCB | 23.32 | 1.42 × 104 | 0.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, C.; Zhou, L.; Zou, Q.; Xu, Y. Effect of Filling Phosphogypsum on the Axial Compression Behavior of Cold-Formed Thin-Walled Steel Walls. Buildings 2022, 12, 1325. https://doi.org/10.3390/buildings12091325
Yin C, Zhou L, Zou Q, Xu Y. Effect of Filling Phosphogypsum on the Axial Compression Behavior of Cold-Formed Thin-Walled Steel Walls. Buildings. 2022; 12(9):1325. https://doi.org/10.3390/buildings12091325
Chicago/Turabian StyleYin, Chao, Li Zhou, Qingyu Zou, and Yifeng Xu. 2022. "Effect of Filling Phosphogypsum on the Axial Compression Behavior of Cold-Formed Thin-Walled Steel Walls" Buildings 12, no. 9: 1325. https://doi.org/10.3390/buildings12091325
APA StyleYin, C., Zhou, L., Zou, Q., & Xu, Y. (2022). Effect of Filling Phosphogypsum on the Axial Compression Behavior of Cold-Formed Thin-Walled Steel Walls. Buildings, 12(9), 1325. https://doi.org/10.3390/buildings12091325






