Abstract
Two unique approaches were proposed to strengthen the bond between the glass fiber reinforcement polymer (GFRP) and the RC concrete surfaces. The two bonding materials are epoxy (EP) and geopolymer (GPP) with different ratios of short glass fibers (SGF). The experimental program includes seven reinforced concrete (RC) beams that have the same cross-section (150 mm × 200 mm) and are 1500 mm in length. The first beam is the control beam (B0-Control). The next three beams B1-0-GPP, B2-0.6-GPP, and B3-1.2-GPP have GPP with SGF ratios of 0%, 0.6%, and 1.2%, respectively. The last three beams B4-0-EP, B5-0.6-EP, and B6-1.2-EP have EP with SGF ratios of 0%, 0.6%, and 1.2%, respectively. The results show that the failure loads of beams B1-0-GPP, B2-0.60-GPP, and B3-1.2-GPP are greater than the control beam B0-Control by approximately 20.80%, 25.60%, and 31.40%, respectively, whereas the failure loads of beams B4-0-EP, B5-0.6-EP, and B6-1.2-EP are greater than the B0-Control by approximately 16.90%, 26.90%, and 26.10%, respectively; it is also noted that debonding occurs. In addition to the adhesive material, GPP has a great effect on increasing the beam’s failure load capacity due to the enhanced interfacial bond shear strength. Additionally, a finite-element program ABAQUS is performed to verify the experimental results.
1. Introduction
Among the biggest problems that contemporary civil engineering is currently facing are the strengthening, updating, and retrofitting of old structures. One of the most promising answers to these needs is the use of carbon fiber reinforcement polymer (CFRP) laminates bonded to the tensile face of the member. In addition, the type of adhesive material that is used is important to prevent CFRP debonding.
The need for reinforced concrete (RC) structures strengthening is becoming more important, especially when there is an increase in ultimate load, degradation trouble, and/or design construction shortcomings [1,2,3]. One of the more conventional approaches to strengthening is using epoxy to bond structural elements with steel plates. There are significant drawbacks to using steel plates as a strengthening material [4,5,6], such as corrosion, the heavy weight of the steel plate, the difficulty of forming the steel plate, and the good preparation of the RC beam surface.
A. Jahami et al. [7] studied numerically the effect of using CFRP as a strengthening technique for RC beams subjected to blast loading. Three different configurations of CFRP were considered: bottom CFRP strips for flexural strengthening, diagonal side strips for shear strengthening, and U-shaped strips for both shear and flexural strengthening. Results showed that using CFRP in the bottom tensile face of RC beams helped in absorbing blast energy. In addition, using CFRP has shown a reduction in the tensile strain of the beam reinforcements.
To create a new technique that can replace steels and alloys with one that is dependable, affordable, and easy to use, extensive research has been done in this area [8,9]. Therefore, using externally bonded (EB) fiber-reinforced polymer (FRP) sheets in concrete structures as a means of strengthening and retrofitting has received widespread acceptance in the industries [10,11,12]. This method involves using epoxy to bond the glass fiber reinforcement polymer (GFRP) laminates to the tension surface of RC beams. This EB technique, on the other hand, results in greater ultimate flexural strength and stiffness [13].
According to several studies, FRP has many advantages including high tensile resistance. Furthermore, when FRP is applied to RC members, it improves rehabilitation performance, durability, and cost-effectiveness [14,15]. Glass-fiber-reinforced polymer (GFRP) is the most suited FRP reinforcement for a variety of civil engineering applications because glass fibers offer the highest temperature resistance, the highest strength, and the lowest cost [16]. The process of debonding between GFRP laminates and RC concrete surface due to the weak cohesion of the epoxy as an adhesive material is one of the problems that limit the development of the use of GFRP laminates as an effective system for strengthening concrete structures [17]. Numerous types of FRP debonding failure have been documented in prior studies [18,19,20], including concrete cover separation, intermediate crack debonding, and plate end debonding. The effectiveness of the strengthening mechanism is greatly reduced when FRP debonding fails [21,22].
Current and previous studies have developed various anchorage systems, such as FRP anchors, FRP U-jacket anchors, and mechanical anchors to postpone the debonding process between GFRP laminates and RC concrete surfaces [23,24]. The enhanced concrete beam with anchorage had a bond strength that was eight times greater than the specimen without an anchor, according to the experiment results. Additionally, it was shown that the interfacial bond’s performance was dependent on the site of the anchorage. Anchoring FRP laminates at their ends with anchor bolts can effectively prevent brittle debonding failure while also improving bond shear resistance and ductility of the reinforced structures [25,26]. Such anchorage systems have the potential to significantly improve the interfacial bond between FRP and RC concrete surfaces [27].
On the other hand, the preparation and installation of these anchors greatly increase the difficulty of implementation and the demand for craftsmanship [28,29]. To increase interfacial shear resistance, several indirect anchorage techniques have been created [30,31]. By expanding the adhesive area between the FRP and the concrete, the near-surface mounted (NSM) approach increased the indirect anchoring of FRP composites [32,33]. The American Code Institute (ACI) [34] has suggested the concrete grooving method (GM) as an easy version of the NSM due to its important development in concrete surface roughness [35]. The interfacial bond strength with the adhesive region between FRP and concrete can be greatly enhanced by grooving the concrete before applying epoxy resin [36]. The preparation of concrete surface grooves, on the other hand, would significantly increase construction work [37]. As a result, a variety of substances and techniques have been researched to identify viable alternatives that might be utilized as a partial or full replacement for Portland cement to create ecologically friendly concrete [38].
Geopolymer is typically synthesized by activating aluminosilicate source material with an alkaline solution (such as NaOH or KOH) [39]. Metakaolin (MK) with a lower calcination temperature or industrial waste products such as fly ash (FA), slag, and rice husk ash are frequently employed as an aluminosilicate source material. Because of this, producing geopolymer uses less energy and generates less carbon dioxide. Geopolymer is regarded as a possible substitute for cement due to its exceptional qualities including low shrinkage, fast concretion, high early compressive strength, and superior fire resistance [40]. The bond property of geopolymer has recently piqued the interest of researchers [41,42,43].
Composite materials produce a combination property of two or more materials that neither fiber nor matrix can achieve when acting alone [44]. Short-fiber-reinforced polymer (SFRP) composites are particularly attractive due to their simplicity in manufacture, low cost, and outstanding mechanical properties [45]. High fiber content is generally required to achieve a high-performance SFRP composite. As a result, the effect of fiber content on the mechanical properties of SFRP composites is of particular interest and significance [46]. Glass-fiber-reinforced polymeric composites were the most used materials in the production of composite materials [47]. Finally, adequate bonding between the FRP laminates and the RC concrete surfaces is critical for successful strengthening; failure to do so would result in undesirable premature failure before the ultimate load.
The main objectives of this study are (1) to suggest two adhesive materials to improve the bond between the GFRP laminates and the concrete surface and (2) to study the impact of the adhesive materials on the tested beams’ structural behavior. The adhesive materials used are Sikadur®−330 epoxy (EP) and geopolymer paste (GPP) with different short glass fibers (SGF) ratios. In addition, an analytical examination using the non-linear finite element computer software ABAQUS [48] has been performed to validate the experimental consequences of the tested beams.
2. Experimental Program
2.1. Materials
All the tested beams were constructed using ordinary Portland cement (OPC) 42.5 grade, which has a specific gravity of 3.10 g/cm3 and an average particle size of 20.67 µm. The chemical composition of the OPC is shown in Table 1. In this investigation, natural river sand was used as the fine aggregate. The sand had a specific gravity of 2.42 g/cm3, water absorption of 1.92%, and a fineness modulus of 2.25. As a coarse aggregate, natural crushed stone with a nominal maximum size of 12.5 mm was employed. The coarse aggregate had a specific gravity of 2.78 g/cm3 and water absorption of 1.56%.

Table 1.
Chemical and physical properties: Composition, OPC, and FA.
Concrete was made using tap water, with a water-to-cement ratio of 0.42 in this investigation. It was necessary to utilize a superplasticizer to ensure the required workability. To improve the workability of concrete, this superplasticizer, which complies with ASTM C494 type F [49,50], is made of synthetic resins and added at a dose of 1.5% by weight of cement. The main bottom and top longitudinal deformed bars of all tested beams with a diameter of 12 mm and 10 mm, respectively, and stirrups with diameters of 8 mm. Sika Wrap®-430 G of Sika Egypt, as shown in Figure 1a, was used as unidirectional GFRP laminates, which have a density of 2.56 g/cm3, a thickness of 0.168 mm, a tensile strength of 2500 N/mm2, and modulus of elasticity equal to 72,000 N/mm2, according to the manufacturing sheet.

Figure 1.
(a) Glass fiber sheets; (b) Short glass fiber.
The GFRP installation uses the wet hand-layup system as per ACI [51]. Short glass fibers (SGF), acquired from Sika Egypt, as shown in Figure 1b, have a length of 6 mm, a specific gravity of 0.91, a diameter of 13 microns, and tensile strength of 480 Mpa, according to the manufacturing sheet.
The EP has two components of resin and hardener. The mixing ratio of resin to hardener is 4:1 by weight. The mechanical properties of EP with and without SGF are presented in Table 2. Two percentages of SGF, 0.6% and 1.20%, from the volume of the EP were used. The second bonding material is GPP which includes fly ash (FA) and a mix of sodium silicate (Na2SiO3) solution with sodium hydroxide (NaOH) solution as an alkaline activator. The chemical composition of FA is illustrated in Table 1. The specific surface area and the specific gravity of FA are 379 m2/kg and 2.25, respectively.

Table 2.
The proportion of the beam’s concrete mix.
The utilized sodium hydroxide (NaOH) is available as flakes with a particle size of approximately 3 mm and a specific gravity of 2.13, and a pH of 14. 40 g/mol was utilized as the molar mass. By dissolving sodium hydroxide flakes in water, a sodium hydroxide (NaOH) solution was created. The mass of NaOH solids in a solution disperses according to the solution concentration expressed in terms of the molar. In this research, NaOH solution with 12 M (480 g/L) was used. To provide this molarity, a volume-measured beaker was used. Firstly, NaOH flakes were added, and then water was added until the volume was completed to one liter. After the stirring process was completed, the solution was left to cool down, and then the beaker was refilled to one liter.
From the market, a sodium silicate solution in a ready-to-use form was purchased. The chemical formula for the sodium silicate solution is SiO2 = 29.4%, Na2O = 14.7%, and water of approximately 55.9% by mass. The specific gravity of sodium hydroxide solution was 1.48 g/cc and the viscosity was 400 cp at 20 °C. Inappropriately mixed mortar may cause failures such as not hardening, flash setting, or both, which cause inapplicability. To avoid these drawbacks, the selection of mixture ingredients was made based on the previous research that was summarized in previous works and the results of various trial mixtures in the preliminary study. The selection steps are summarized as follows: FA was used as a base material with 700 kg/m3, and a mixture of sodium hydroxide (NaOH) solution and sodium silicate solution (Na2SiO3) was used as an alkaline liquid by a ratio of 1 to 2.5. The molarity of sodium hydroxide was 12 M, the ratio of alkaline solution to FA was 1:2 by mass, and SGF was added with 0.6 and 1.2% of the total volume of the mixture.
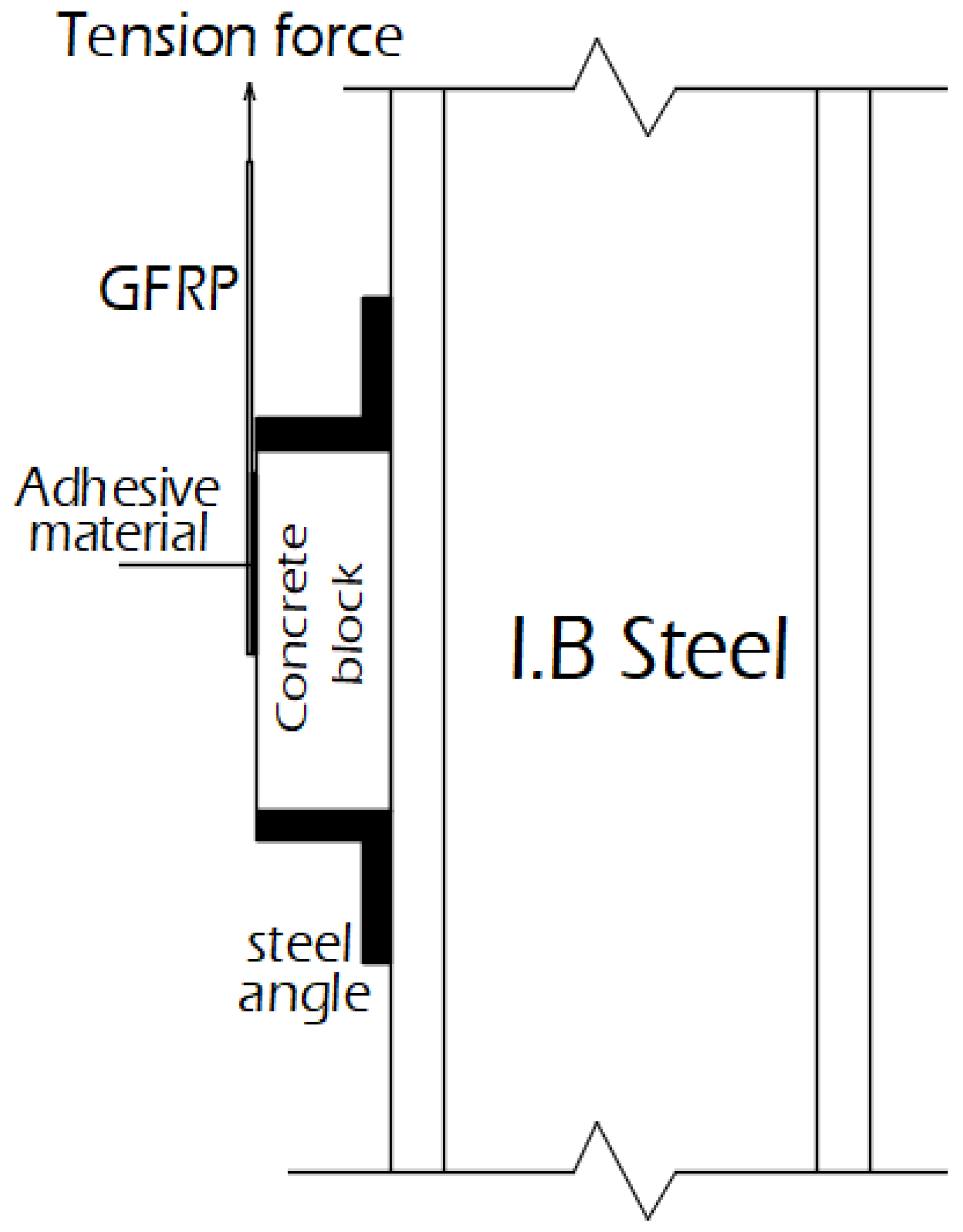
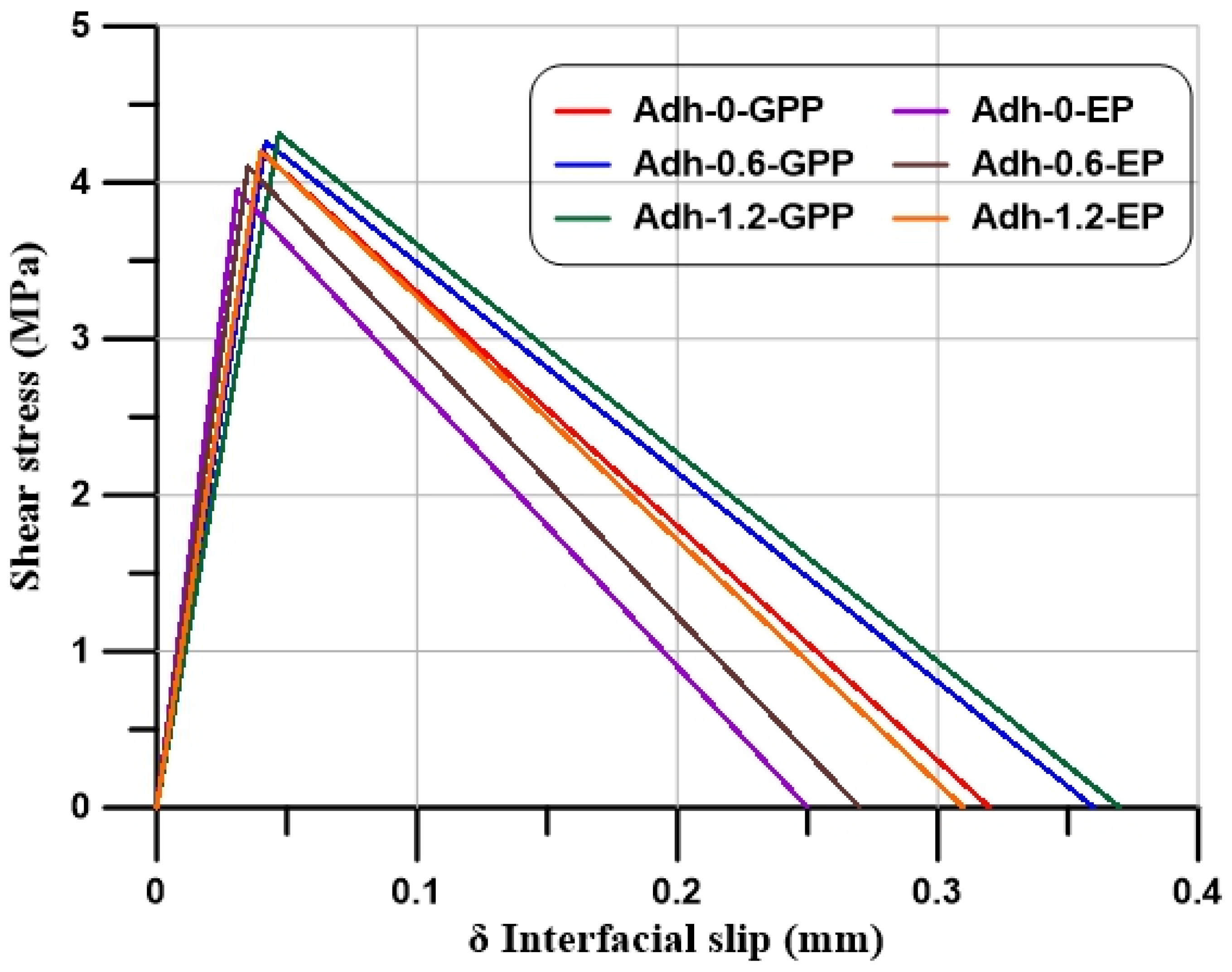
Six direct shear tests were performed under pull static load to calculate the ultimate shear strength between the concrete and examined adhesive materials [GPP without SGF (0-GPP), GPP with 0.60% ratio of SGF (0.6-GPP), GPP with 1.20% ratio of SGF (1.2-GPP), EP without SGF (0-EP), EP with 0.60% ratio of SGF (0.6-EP), and EP with 1.20% ratio of SGF (1.2-EP)]. Six concrete blocks were cast with dimensions (length L = 300 mm, width b = 125 mm, and thickness h = 125 mm). Using an abrasive dry grinder, the concrete block’s surface was prepared by grinding down to a depth of roughly 0.50 mm. Six specimens of GFRP laminates were prepared with dimensions of 152 mm bonded length and 35 mm unbounded length. Each one of the GFRP laminates was pasted to one concrete block along the centerline on one side of the concrete block. The tensile load was applied to the GFRP laminate while the concrete block was restrained from the bottom. Figure 2 shows the test setup. LVDTs that were installed on the concrete surface near the upper corners of the bonded area were used to measure the initial slip and final slip. The typical applied load-slip response is illustrated in Figure 3.
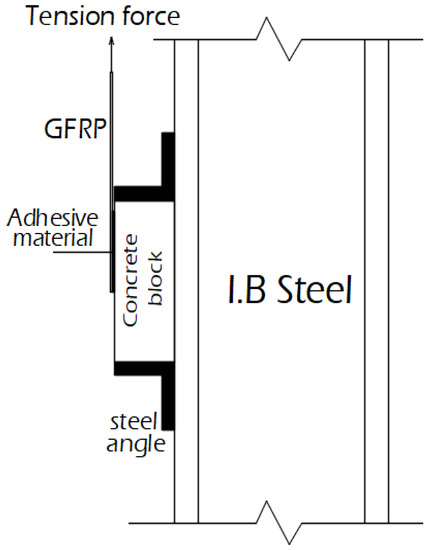
Figure 2.
Pull out static test.
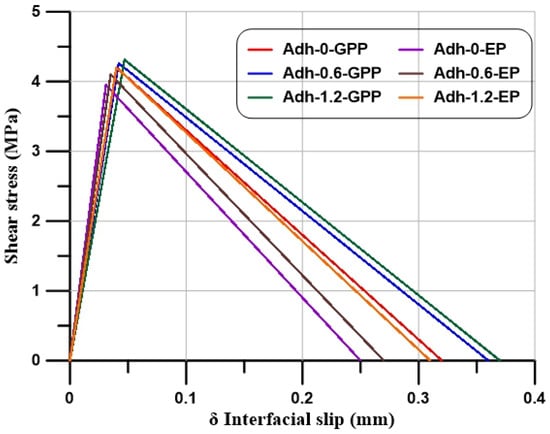
Figure 3.
The interface bond shear stress between the GFRP laminate and concrete surface experimentally.
2.2. Mix Proportioning and Details of Tested Beams
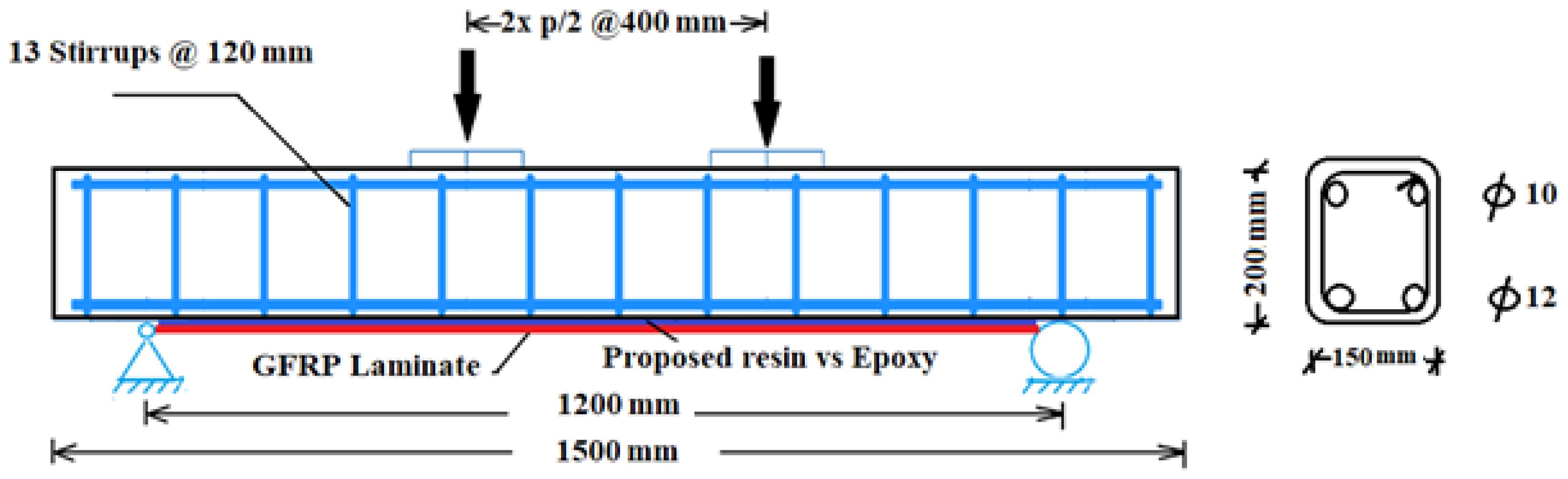
The experimental program included seven simply supported RC beams. All the beams had an equal section of 200 mm depth, 150 mm width, and 1500 mm length. The reinforcement bars, dimensions, and geometry information of the tested beams are illustrated in Figure 4. The main bottom reinforcement was two bars of 12 mm diameter with a design yield stress of 410 MPa, and the top reinforcement bars were two bars of 10 mm diameter with the same yield strength. Vertical stirrups were constructed using 125 mm-spaced, 8 mm-diameter bars with a yield strength of 240 Mpa to ensure that all tested beams failed in the flexural mode according to ACI-19 [52].
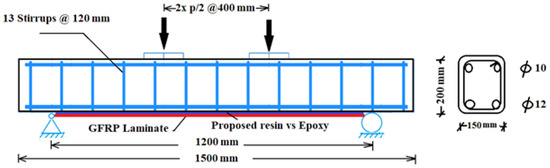
Figure 4.
GFRP externally strengthened RC beam under two-point loads.
The proportioning of the concrete mix of the tested beams is given in Table 2. Table 3 provides a summary of the information and the tested beams’ designation. The beams’ designation is arranged as follows: the beam number, numbers 0, 0.6, and 1.2 referring to the SGF ratio, and GPP and EP referring to the geopolymer and Sikadur®-330 epoxy paste of Sika Egypt, respectively. Three groups of beams were used. The first group included the beam B0-control, which referred to the control beam without strengthening. The second group included three tested beams, which were marked as B1-0-GPP, B2-0.6-GPP, and B3-1.2-GPP, and had bonding material GPP with SGF by the percentages of 0%, 0.6%, and 1.2%, respectively. The third group included three beams, which were marked as B4-0-EP, B5-0.6-EP, and B6-1.2-EP, and had EP with SGF percentages of 0%, 0.6%, and 1.2%, respectively.

Table 3.
The names and specifics of different beams.
2.3. Beam Preparation and GFRP Strengthening
2.3.1. Beam Preparation
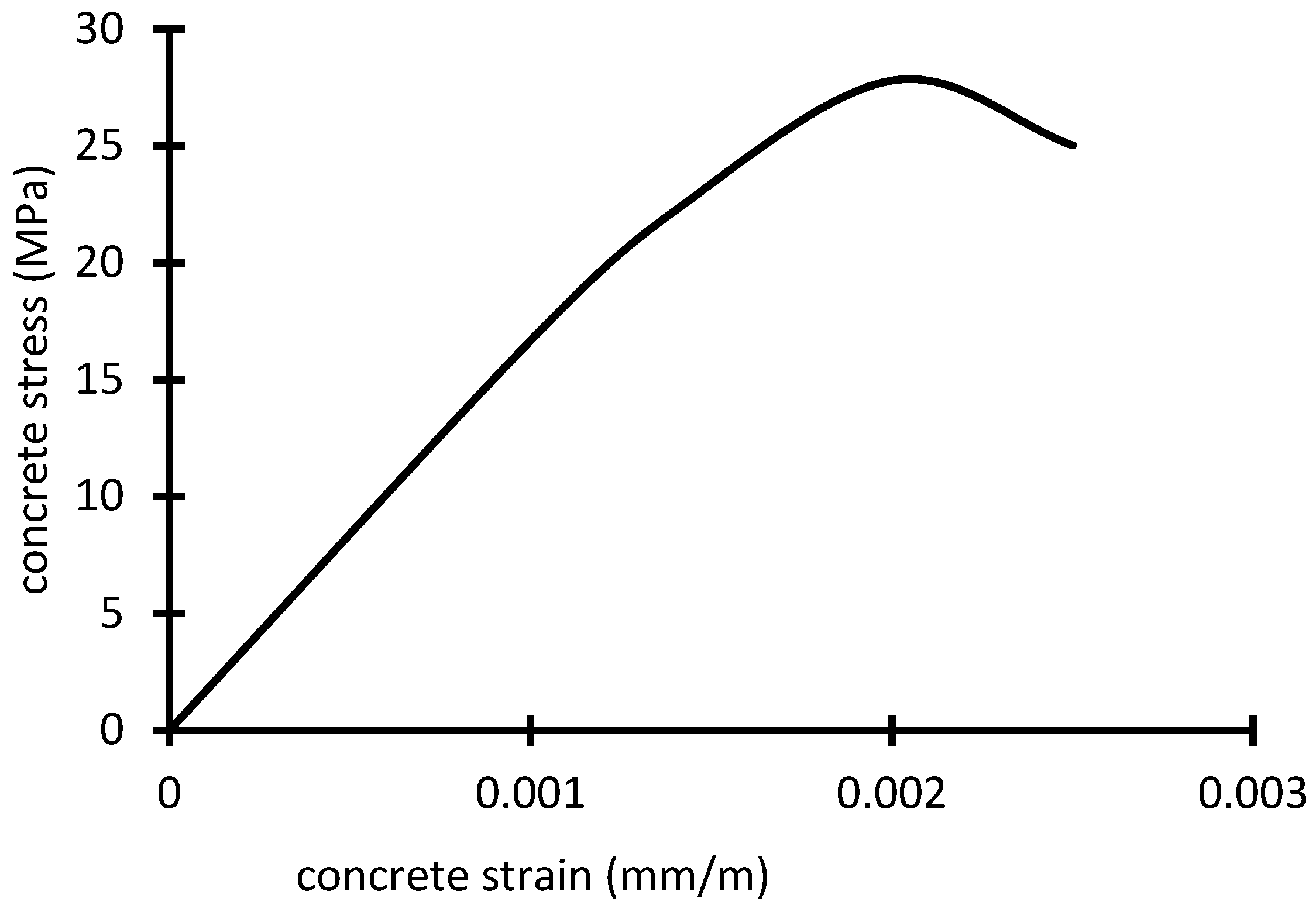
Seven plywood forms were prepared for fabricated RC beams, and then steel reinforcement cages were prepared as shown in Figure 5. The concrete was mixed until the mixture became homogenous, then fresh mixtures were cast in forms at 23 ± 2 °C using an electrical poker vibrator for two minutes; specimens were then covered with polyethylene sheets started immediately after casting and were cured with pure water after 24 h from casting until the test. Three concrete cylinders (ϕ 150 × 300 mm) and three concrete cubes (150 mm × 150 mm ×150 mm) were taken to determine the average cylinder compressive strength (fc’) and the average cube compressive strength (fcu), respectively. The average cylinder compressive strength (fc’) and the cube compressive strength (fcu) were equal to 26.3 Mpa, and 32.60 Mpa, respectively. The average experimental compressive stress–strain curve of the tested beams concrete is shown in Figure 6. The average experimental tensile strength was equal to 2.1 Mpa.

Figure 5.
(a) plywood forms; (b) steel cages; and (c) casting of RC beams.
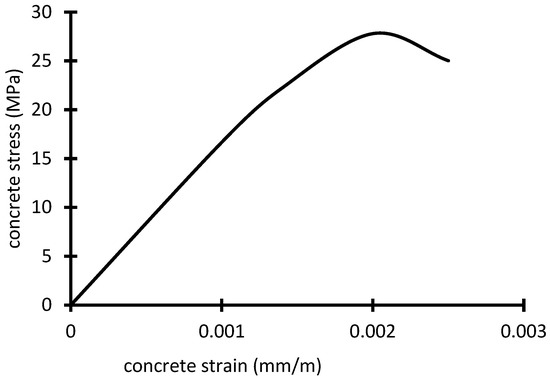
Figure 6.
Stress–strain curve of concrete in compression.
2.3.2. GFRP Strengthening
All the beams were cast and cured for 28 days, and then ACI 440.2R-2017’s “wet layup” technology was used to enhance the tension surface of the RC beams [50]. Before the laminates were bonded, all the beams’ tension surfaces were cleaned, dried, and greased, and contaminates, if any, removed. The International Concrete Repair Institute’s recommended minimum rough profile (CSP3) was used to prepare the tension side of the beams (ICRI 03730) [34]. Any loose cement paste layer was removed using an abrasion wheel so that the exposed aggregate particles could be seen. Figure 7 displays the various surface preparation phases. When using epoxy, the resin and hardener were mixed in the predetermined ratio of 4:1, and the GPP was prepared by the method mentioned in Section 2.1. The GFRP was then cleaned to eliminate contaminants and cut to the required size. The prepared surface was uniformly coated with EP and GPP, and the GFRP was then pressed onto the top surface while employing light pressure and a rubber roller. To ensure that the GFRP adhered well to the surface, released any trapped air, and removed any excess epoxy that might have been present between the GFRP and concrete surface, these steps were taken. Thusly produced laminated beams were cured for a week before being tested. Figure 7a,b illustrate the process for strengthening beams.

Figure 7.
Strengthening RC beams with (a) GFRP and (b) EP.
2.4. Test Setup and Instrumentation
Every RC beam underwent testing with two points of loading. The distance between two-point loads is 400 mm and the distance between two beams supports is 1200 mm. On the right and left ends of the examined beams, roller and hinged supports were employed, respectively. Flexural testing was carried out using load-controlled mode loading at 0.02 KN/s until failure. A steel I-section spreader beam was used to transfer the load from the load cell to the beam. This load from the spreader beam got transferred onto the two loading points on the beam. A linear voltage displacement transducer (LVDT) with an accuracy of 0.01 mm was used to measure the defections at the mid-span of beams. Electrical resistance was used to measure the strains at the midpoint of the bottom longitudinal reinforcing bars. Strain gauges 6 mm long were used. Figure 8 displays an image of the test setup and the associated equipment. Each load interval produced a record of the load and the greatest defection.

Figure 8.
Test setup of RC beams.
3. Results and Discussion
At each loading increment up to failure, deflections and crack pattern propagation were observed. The impact of material paste type on the tested beams’ structural behavior was assessed. Results from beams with stronger ones were compared with those from the control beam. Compared with the control beam, all beams had higher load-carrying capacities.
3.1. Failure Loads
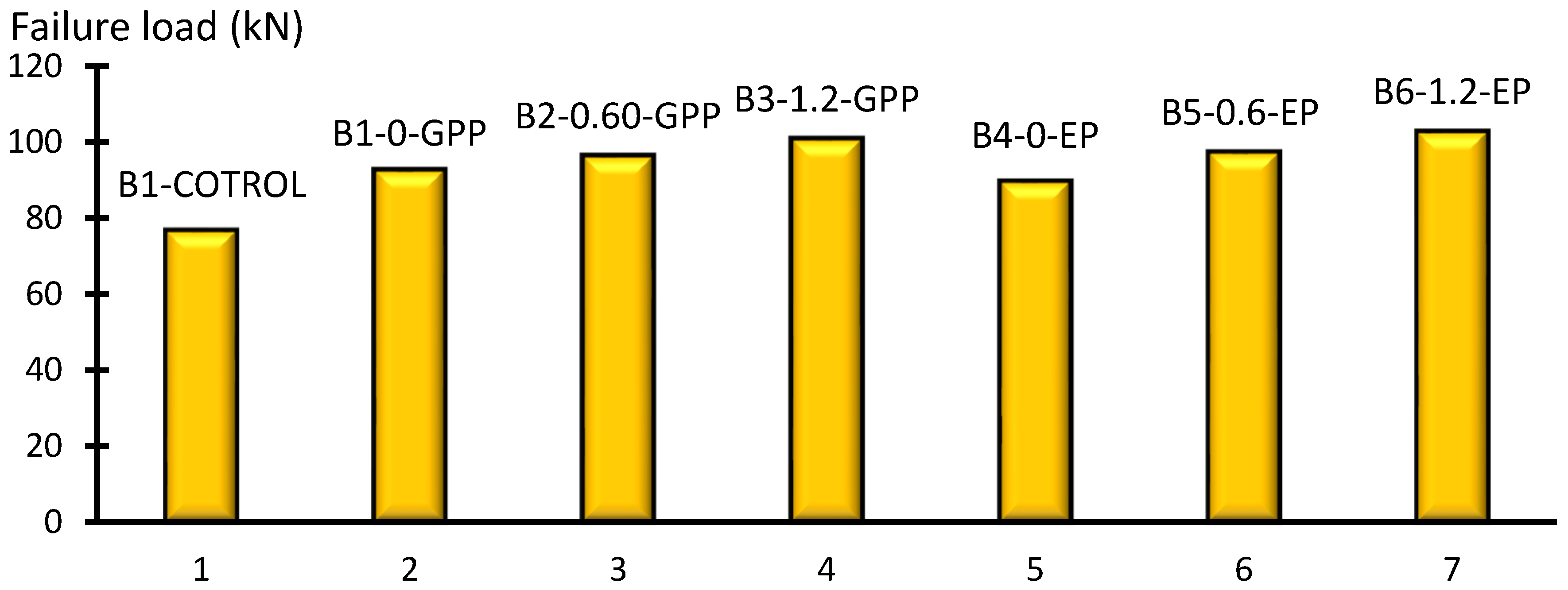
The loads at first crack Pcr, beam longitudinal reinforcement bars yield Py, and the failure load Pu are summarized for all the examined RC beams in Table 4. To assess the effectiveness of the different types of the adhesive material paste, the maximum loads for the tested beams were recorded and compared, as shown in Figure 9. The failure loads of beams B1-0-GPP, B2-0.60-GPP, and B3-1.2-GPP were greater than control beam B0-Control by approximately 20.80%, 25.60%, and 31.40%, respectively. The results showed that increasing the SGF ratio in the GPP had a clear effect on raising the capacity of the beam due to the enhanced interfacial bond shear strength, as illustrated in Figure 3.

Table 4.
Test results synopsis.
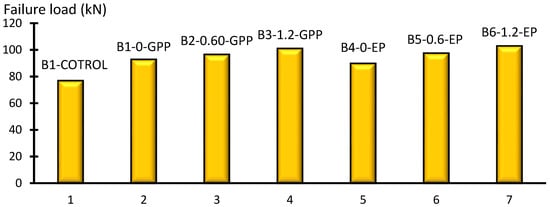
Figure 9.
Load–deflection relationship for tested beams.
The failure loads of beams B4-0-EP, B5-0.6-EP, and B6-1.2-EP were greater than the control beam B0-Control by approximately 16.90%, 26.90%, and 26.10%, respectively. The results showed that the GPP as the adhesive material paste had a great effect on increasing the failure load capacity of the tested beams. Compared with the costs of the bonding materials EP and GPP, we found that bonding material GPP is much less expensive than EP. The GPP is a novel material to increase the bond between the GFRP laminates and the concrete surface. The results showed that the use of GFRP laminates increases the flexural capacity of RC beams [53].
3.2. Failure Behavior and Crack Patterns
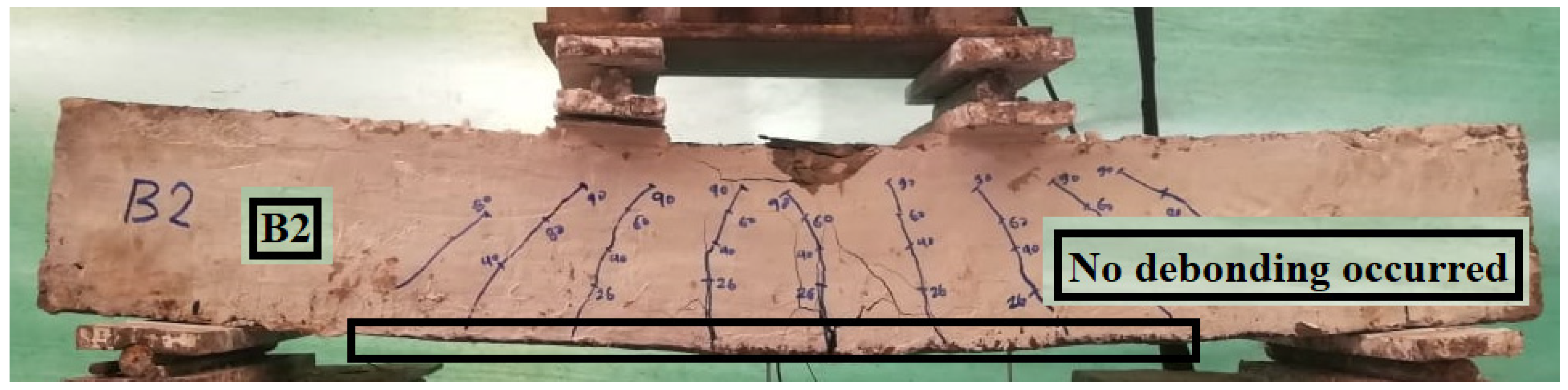
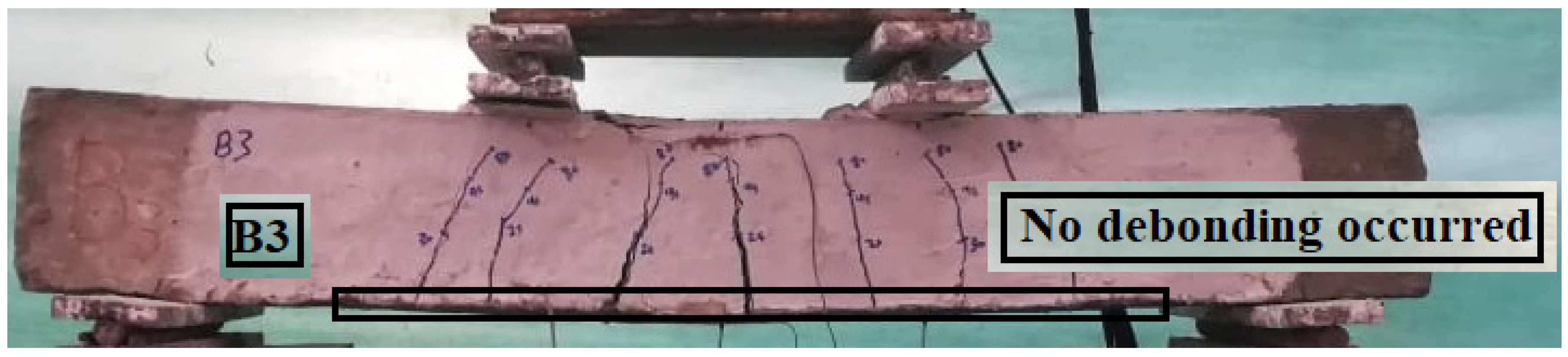
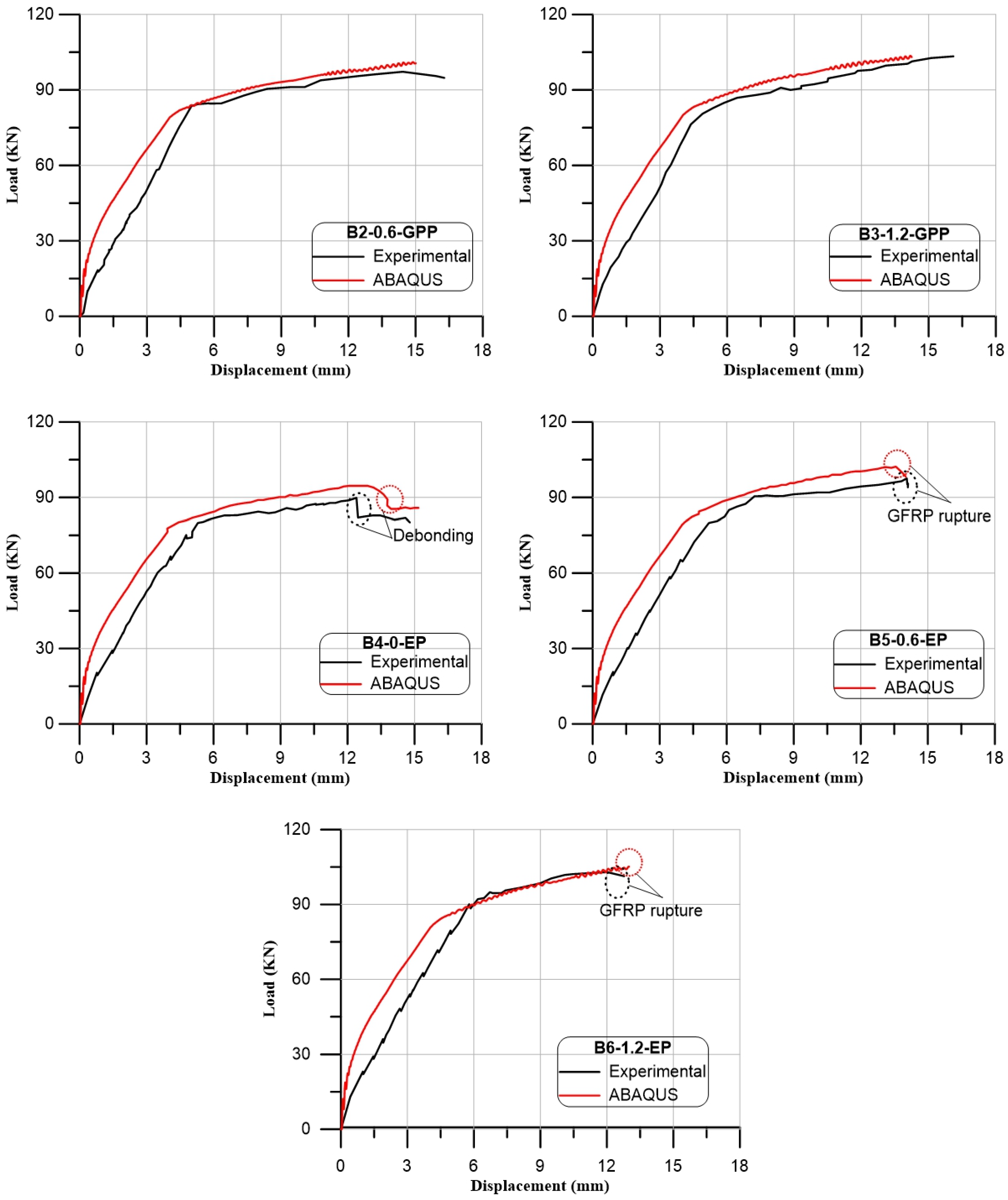
Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 depict the crack patterns of the tested beams that were tested until they failed. For beam B0-Control, the first crack was noticed at a load of approximately 31.20% of the ultimate load. The first crack appeared at a load of approximately 26.90%, 26.90%, 25.70%, 28.90%, 27.70%, and 25.30% of the ultimate load for beams B1-0-GPP, B2-0.60-GPP, B3-1.20-GPP, B4-0-EP, B5-0.6-EP, and B6-1.20-EP, respectively. Most cracks appeared initially under the loads on the bottom surface of all tested beams. Based on the outcomes of the experiment, no debonding occurred for laminates when using GPP with different SGF ratios. On the contrary, there was a debonding when using EP for beams B5-0.6-EP and B6-1.2-EP; however, for the beam B4-0-EP, the failure mode was laminate debonding and concrete cover separation. GFRP reduced the tensile damage that occurred in concrete due to the increase in energy absorption [54,55].

Figure 10.
The final crack of beam B0-Control.

Figure 11.
The final crack of beam B1-0-GPP.
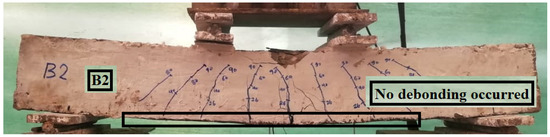
Figure 12.
The final crack of beam B2-0.6-GPP.

Figure 13.
The final crack of beam B3-1.2-GPP.

Figure 14.
The final crack of beam B4-0-EP.

Figure 15.
The final crack of beam B5-0.6-EP.

Figure 16.
The final crack of beam B6-1.2-EP.
3.3. Load–Deflection Curves of Tested Beams
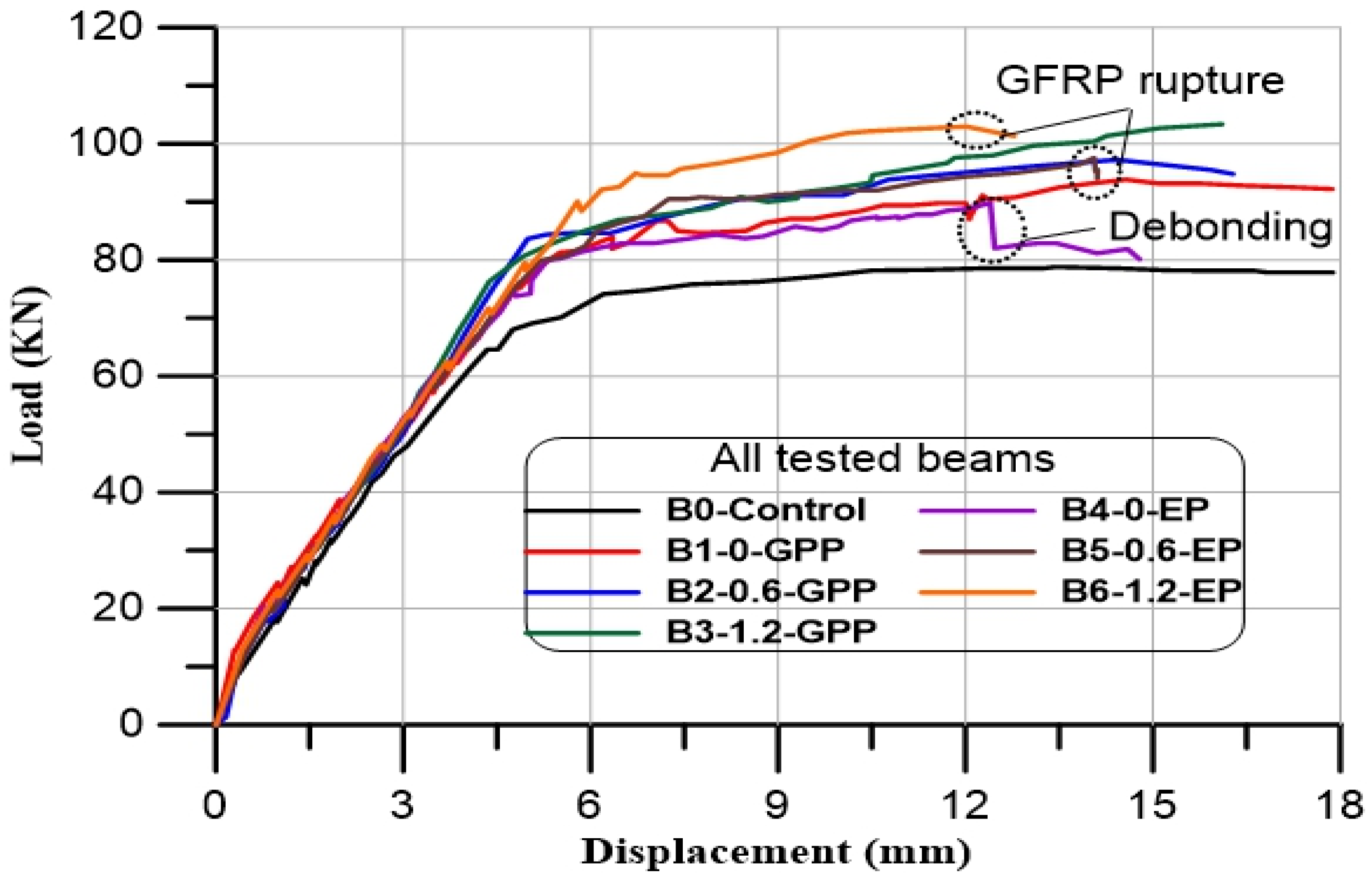
Figure 17 illustrates the load–deflection relationship for tested beams with GPP and EP as adhesive material. All beams displayed linear behavior up to the cracking load. The maximum deflection of tested beams B1-0-GPP, B2-0.6-GPP, B3-1.2-GPP, B4-0-EP, B5-0.6-EP, and B6-1.2-EP was less than the control beam by approximately 14.60%, 6.90%, 6.20%, 19.30%, 5.92%, and 17.10%, respectively. The results showed that GPP as adhesive material paste enhanced the maximum beam’s deflections better than EP. Also, it was found that using GFRP with EP reduced the mid-span displacement of the tested beams [56,57,58].
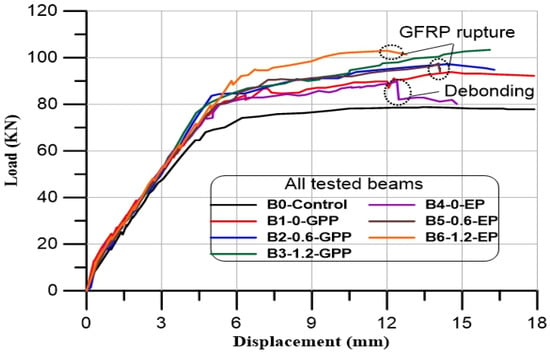
Figure 17.
Load–deflection relationship for tested beams.
3.4. Ductility of Specimens
The ductility factor can be determined as the ratio of the maximum displacement at failure load (Δu) to the maximum displacement at yield load (Δy). The ductility factor of beams B1-0-GPP, B2-0.6-GPP, and B3-1.2-GPP was larger than corresponding beams B4-0-EP, B5-0.6-EP, and B6-1.2-EP by approximately 5.80%, 13.60%, and 21.40%, respectively. Table 4 shows that the beam B3-1.2-GPP had a similar ductility factor to the control beam due to the large ratio of SGF. In addition, the results showed that the ductility factors of beams B2-0.6-GPP and B3-1.2-GPP had a little more ductility than the control beam.
4. Finite Element Analysis
In this section, finite element analysis (FE) was carried out using the ABAQUS software [47]. The FE program can accurately simulate the GFRP/concrete interface, taking into consideration both geometric and material nonlinearity. A series of vertical displacement increments were applied until the maximum experimental deflection value was reached for each beam. The Newton–Raphson technique was utilized in the nonlinear analysis to allow convergence within tolerance limits at the end of each deflection increment. To further prevent a divergent solution, automatic stabilization and short time increments were applied.
4.1. Modeling of Material Properties
4.1.1. Concrete
The concrete was modeled using concrete damage plasticity (CDP). Due to the model’s combination of compressive plasticity and isotropic tensile plasticity, it can simulate the concrete in the inelastic zone. The elastic modulus values, the Poisson’s ratio, characterization of compressive and tensile behavior, and the plastic damage parameters, are necessary for the plastic damage model. In the concrete damage plasticity model (CDP), the plastic damage parameters are the dilation angle, the flow potential eccentricity, the ratio of initial biaxial compressive yield stress to initial uniaxial compressive yield stress, the ratio of the second stress invariant on the tensile meridian to that on the compressive meridian, and the viscosity parameter which defines viscoplastic regularization. The final four parameters for defining concrete material damage are described in Table 5.

Table 5.
Concrete damage parameters (CDP).
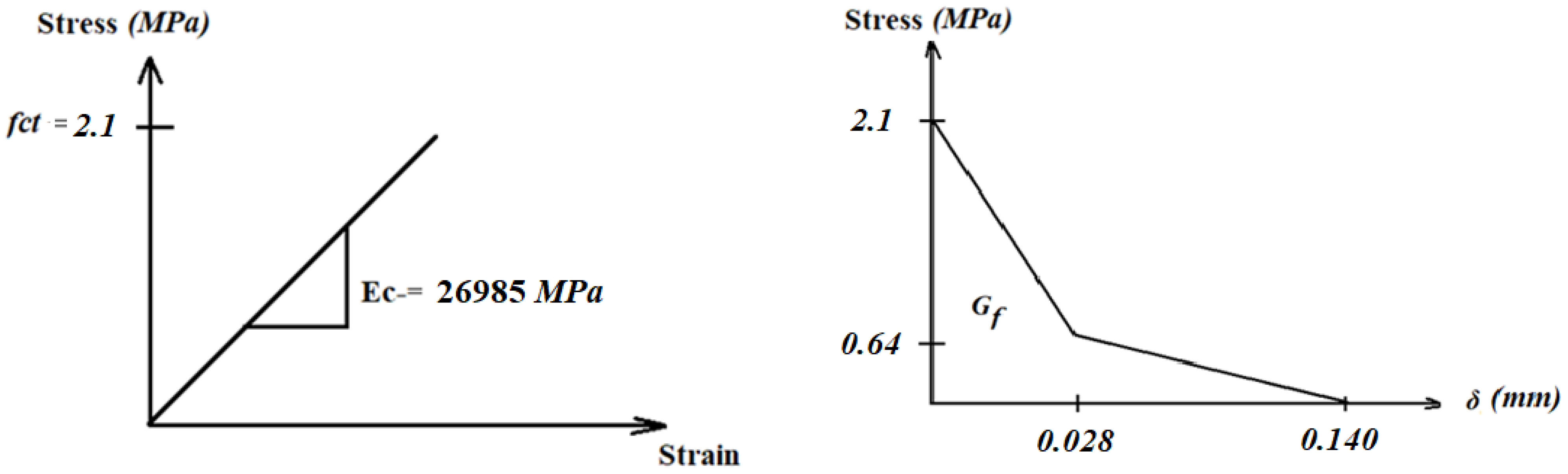
The experimental compressive stress–strain curve for concrete as illustrated in Figure 4 was used in the FE program. The concrete tensile strength was equal to 2.1 MPa. The modulus of elasticity of concrete (Ec) was 26,985 MPa according to the compressive stress–strain curve (See Figure 4, Section 2.3.1). Two primary failure modes are considered for concrete according to (CDP): compressive crushing and tensile cracking. The stress–strain response under uniaxial tension followed a linear elastic relationship up until a value of the failure stress was attained.
The initiation of microcracking in the concrete material is correlated with failure stress. A softening stress–strain response was used to illustrate the propagation of microcracks beyond the failure stress. Therefore, elastic modulus, Ec, and tensile strength, ft, are required to define the first part of the relationship. For descending branch, the fracture energy Gf approach was used to define the post-peak tension failure behavior of concrete, as shown in Figure 18. The area beneath the concrete’s tensile curve following the peak value was the fracture energy Gf.
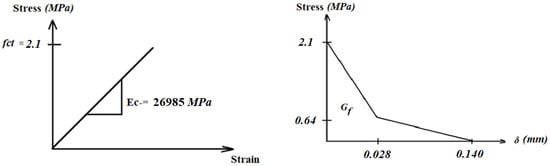
Figure 18.
The tensile curve of the concrete (Simplified curve).
4.1.2. Steel Reinforcement Bars and GFRP Laminate
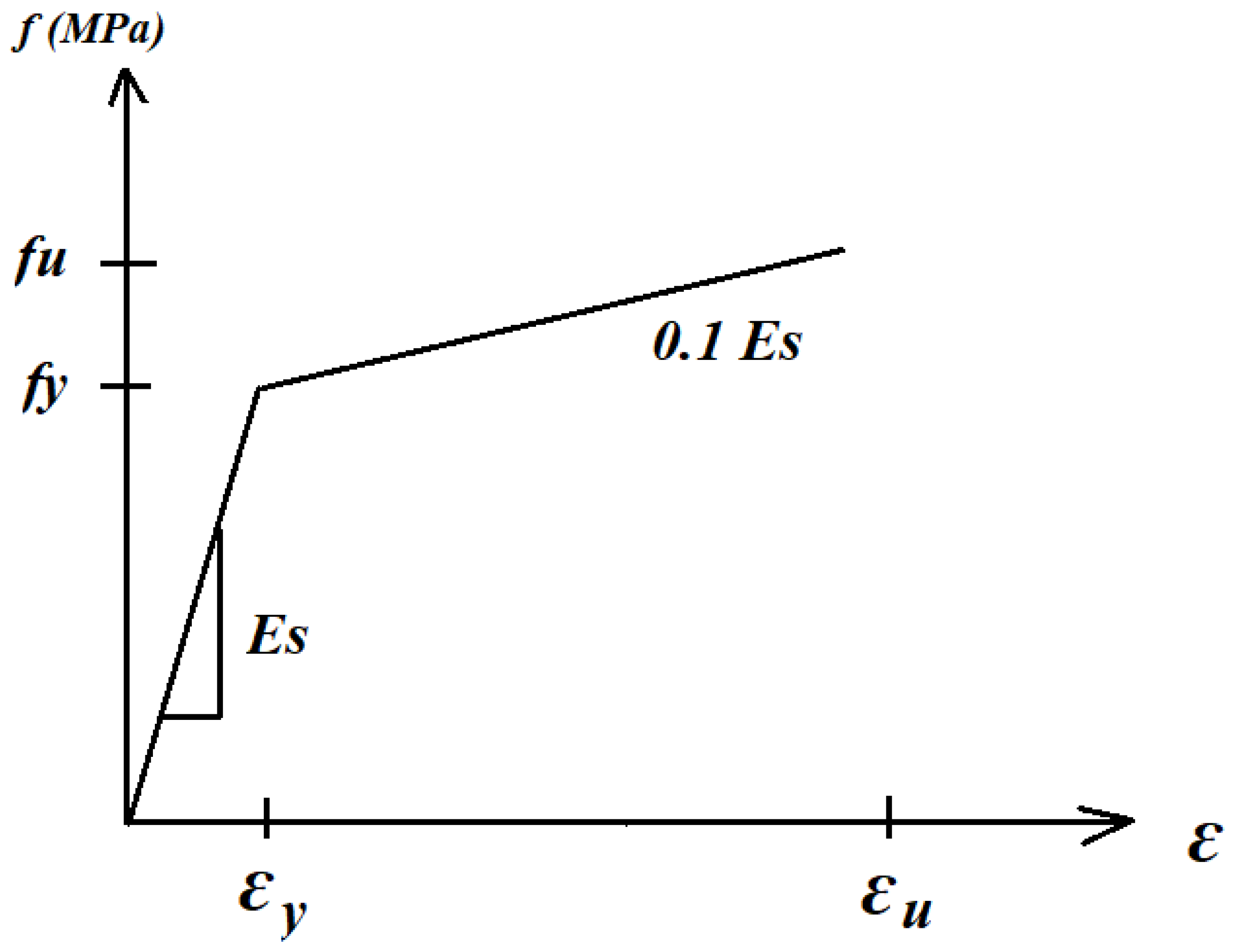
Figure 19 illustrates a bilinear elastic–plastic stress–strain curve for reinforcement bars. The embedded region was modeled for the reinforcement in this investigation. Table 6 illustrates the mechanical properties of reinforcement bars. The interaction surface between reinforcement bars and concrete was assumed to be a perfect bond. In the current study, the GFRP was assumed to be a linear elastic isotropic material. Table 7 illustrates the properties of CFRP laminates as specified by the manufacturer.
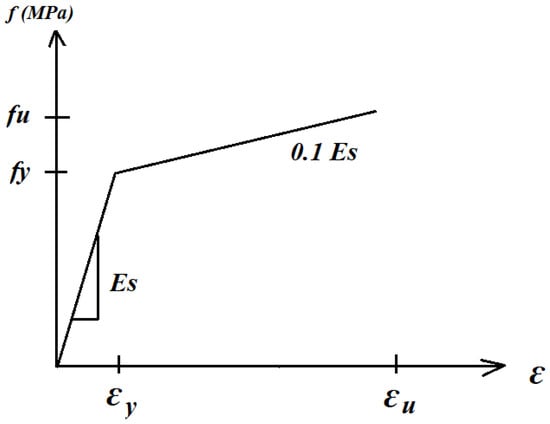
Figure 19.
Stress–strain curve for steel in finite element analysis.

Table 6.
The mechanical properties of reinforcement bars.

Table 7.
The properties of GFRP as specified by the manufacturer.
4.1.3. GFRP Laminate–Concrete Interface
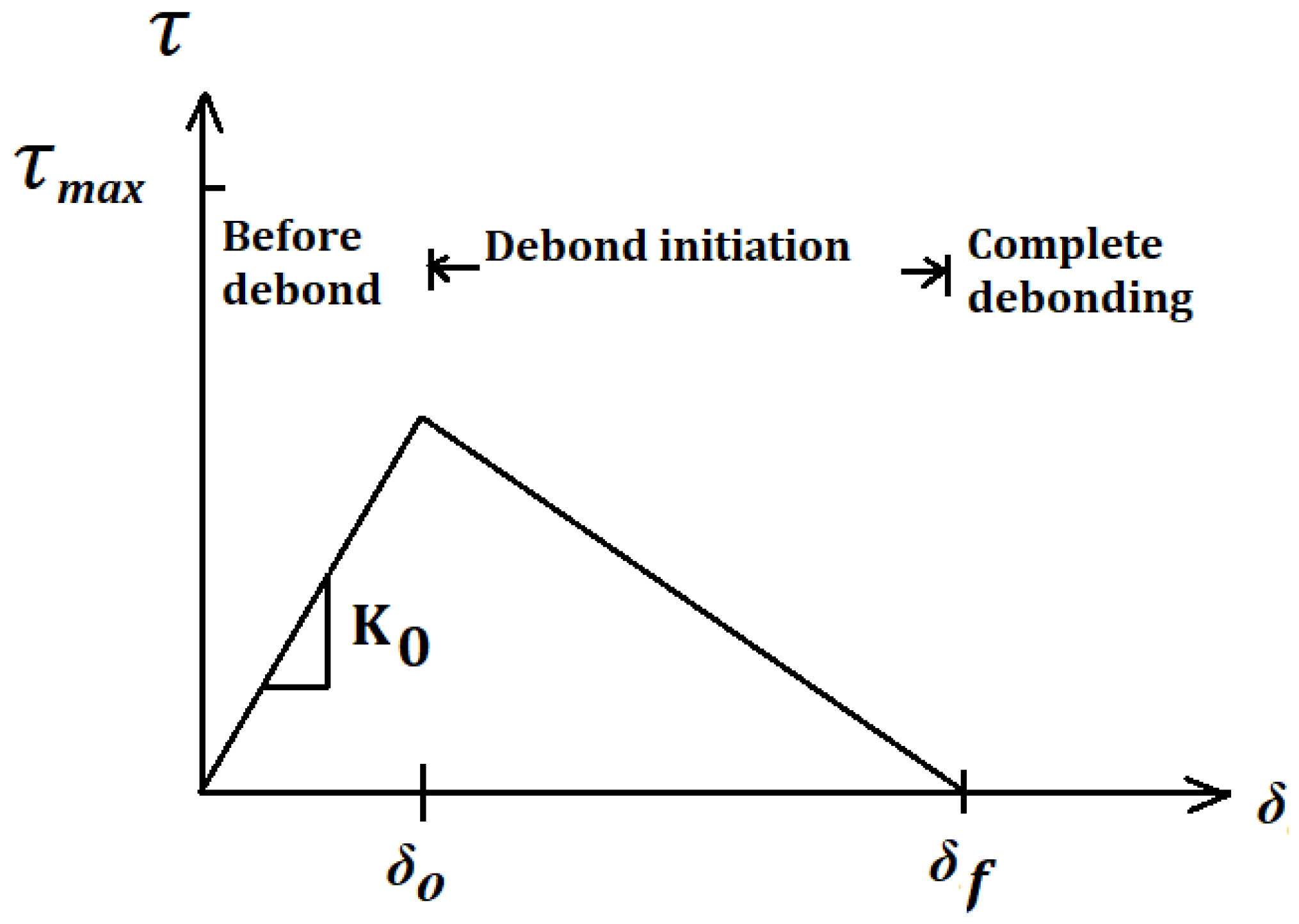
The GFRP laminate–concrete interface can be more effectively modeled using the cohesive model in ABAQUS. When dealing with debonding issues of strengthening materials, cohesive elements and surface-based cohesive behavior are preferable alternatives for this type of modeling. Surface-based cohesive behavior requires a linear elastic traction separation as well as damage initiation and evolution laws, and it has very comparable formulas and constitution laws to cohesive elements. A graphic representation of a standard bilinear traction–separation rule expressed in terms of effective traction τ and effective opening displacement (Interfacial slip) δ is shown in Figure 20. The initial stiffness K0 is specified as [56] and is modeled as a rich zone of small thickness at the interface. The initial stiffness can be expressed as follows:
where ti and tc represent the thickness of adhesive and the concrete thickness, respectively. Gi and Gc are the shear modulus of the adhesive and concrete, respectively. The values of shear stress of each resin τmax according to the experimental results used for B1-0-GPP, B2-0.6-GPP, B3-1.2-GPP, B4-0-EP, B5-0.6-EP, and B6-1.2-EP are 4.2 MPa, 4.26 MPa, 4.31 MPa, 3.95 MPa, 4.1 MPa, and 4.2 MPa, respectively (See Figure 3). The damage initiation criterion was described by using the quadratic nominal stress function:
where is the cohesive tensile, τs and τt are the interface’s shear stresses, and n, s and t denote the direction of the stress component. Damage was considered to initiate when the traction function reached one. The maximum normal stress in comparable studies is equal to 2.1 MPa, while the maximum shear stresses , are taken according to the experimental results (see Figure 3). Energy release was used to assess the development of interface damage. The description of this model can be found in the ABAQUS material library. Previous investigations have found values for the fracture energy, Gcr, ranging from 300 J/m2 to 1500 J/m2 [57]; for this investigation, the values taken were calculated based on experimental results.
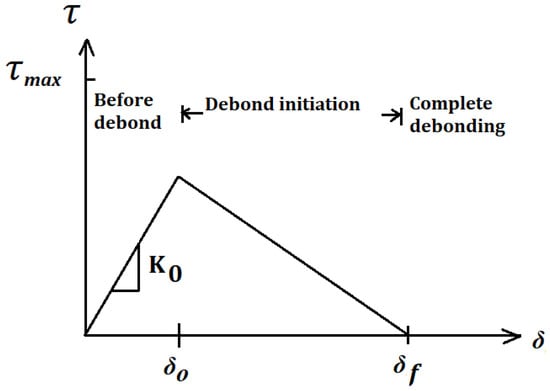
Figure 20.
Bilinear traction–separation constitutive law.
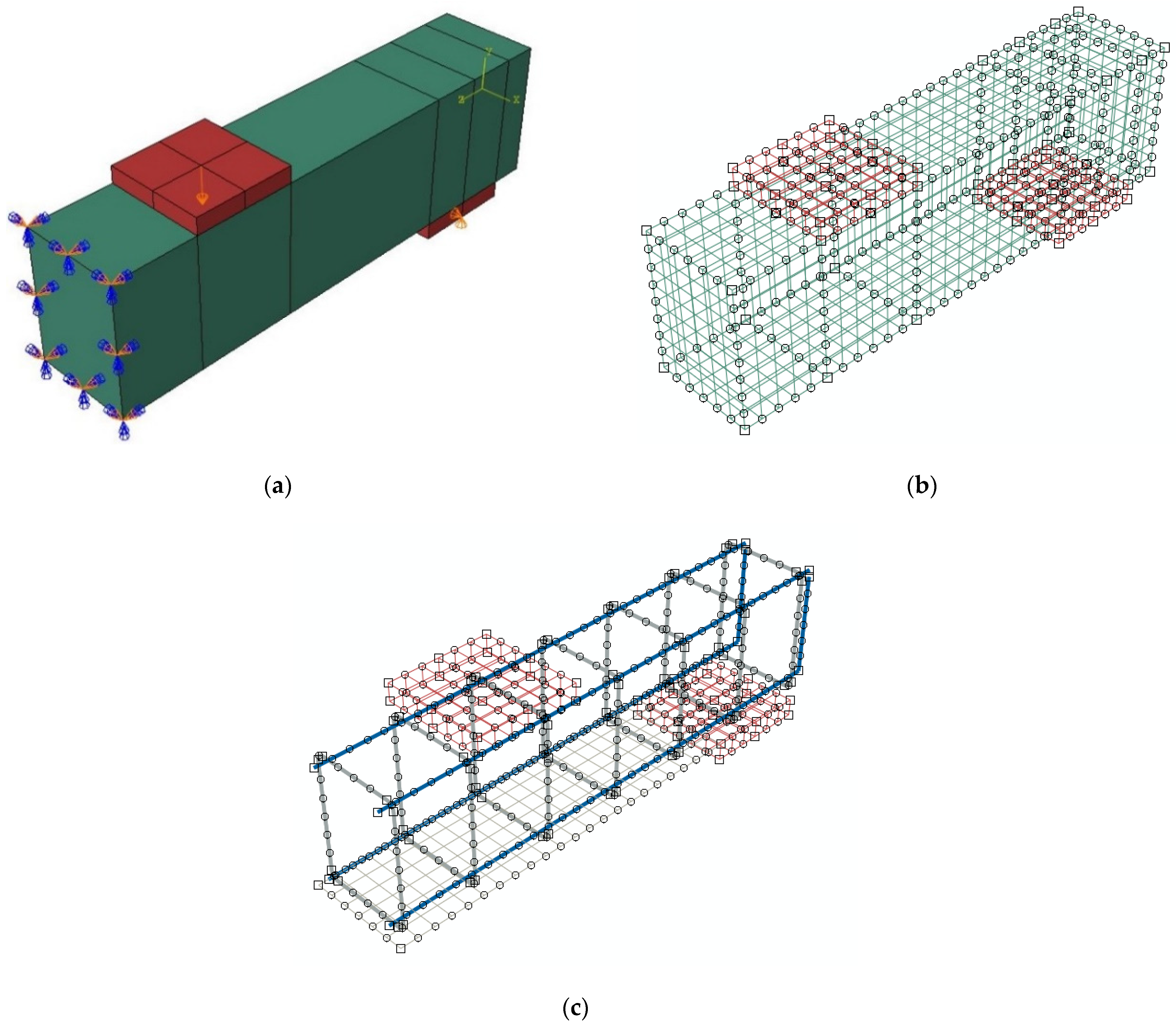
4.2. Boundary Conditions and Meshing
As shown in Figure 21, the geometry of the beams, loads, and boundary conditions were all symmetrical, so just one-half of a beam was modelled using a standard finite element mesh. This approach significantly decreased the amount of computing time and the computer storage space, especially in the case of the GFRP/Concrete interface which is not modeled as a full bond. To choose an appropriate mesh with acceptable accuracy in terms of ultimate load and ultimate deflection, three models with various mesh sizes—fine, medium, and coarse of 15, 25, and 35 mm, respectively—were examined. Figure 21 depicts the concrete volume medium meshes and reinforcing medium meshes for tested beams. The solid three-dimensional eight-node bricks (C3D8R) were adopted in the FE study to model the concrete. The main reinforcement bars were modeled using a bar truss element (T2D3) with the same mesh size as the concrete. GFRP laminate was modeled as a four-nodded doubly thin curved shell, reduced integration, and hourglass control (S4R). The applied load and supports were taken as illustrated in Figure 21a to simulate the experimental program.
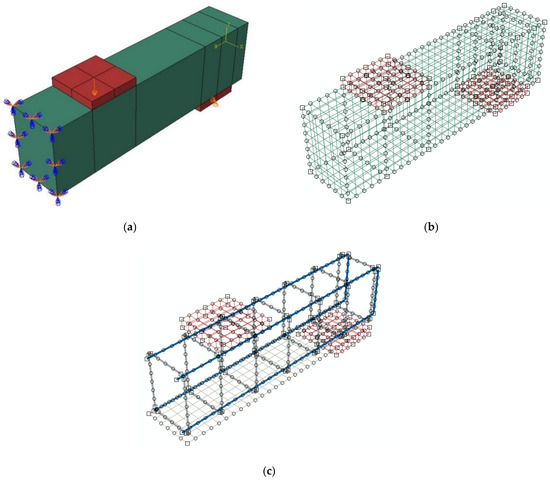
Figure 21.
Geometry and element mesh. (a) Geometry of half of a typical beam; (b) Finite element mesh of half of a typical beam; and (c) Reinforcement bars, stirrups, and GFRP laminate.
5. Comparison of the Experimental and Finite Element Results
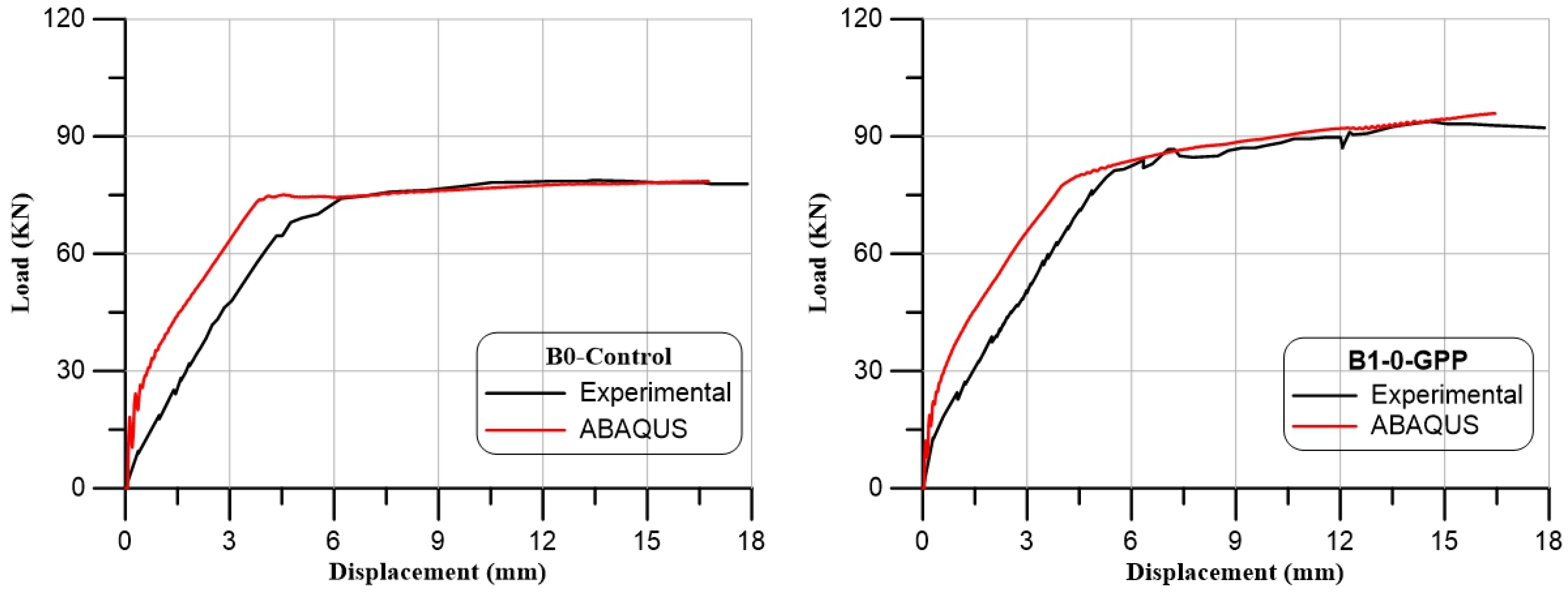
To confirm the experimental findings, the ABAQUS program was used to mimic each tested beam with the same information and the same material characteristics as the experiment. It was found that the medium mesh gives the best results in the ultimate load and deflection values, as shown in Table 8. Additionally, it had an acceptable computational time compared to the other meshes. The load–deflection curves for both experimental and numerical were presented for all tested beams, as illustrated in Figure 22. Compared with the experimental results, the load–deflection curves from numerical simulations behaved more stiffly, which was likely caused by a sizable scatter in the tensile strength of the concrete. The range of 0.95 to 0.98 is the FE forecast for the experimental ultimate load ratio, as illustrated in Table 5. In addition, the range of 0.83 to 1.09 is the FE forecast for the experimental maximum beam displacement ratio.

Table 8.
Comparison of the experimental and finite element findings.
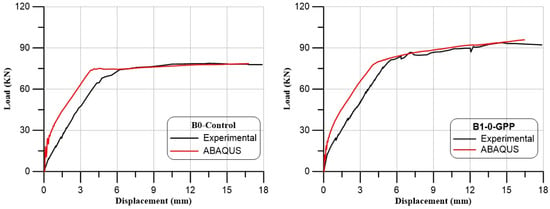
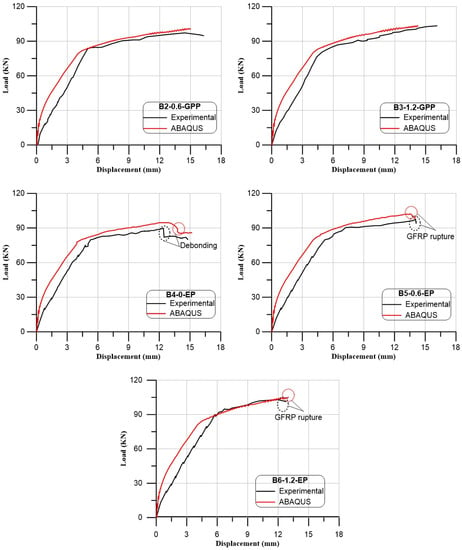
Figure 22.
Load–deflection curves of the tested beams (numerical and experimental results).
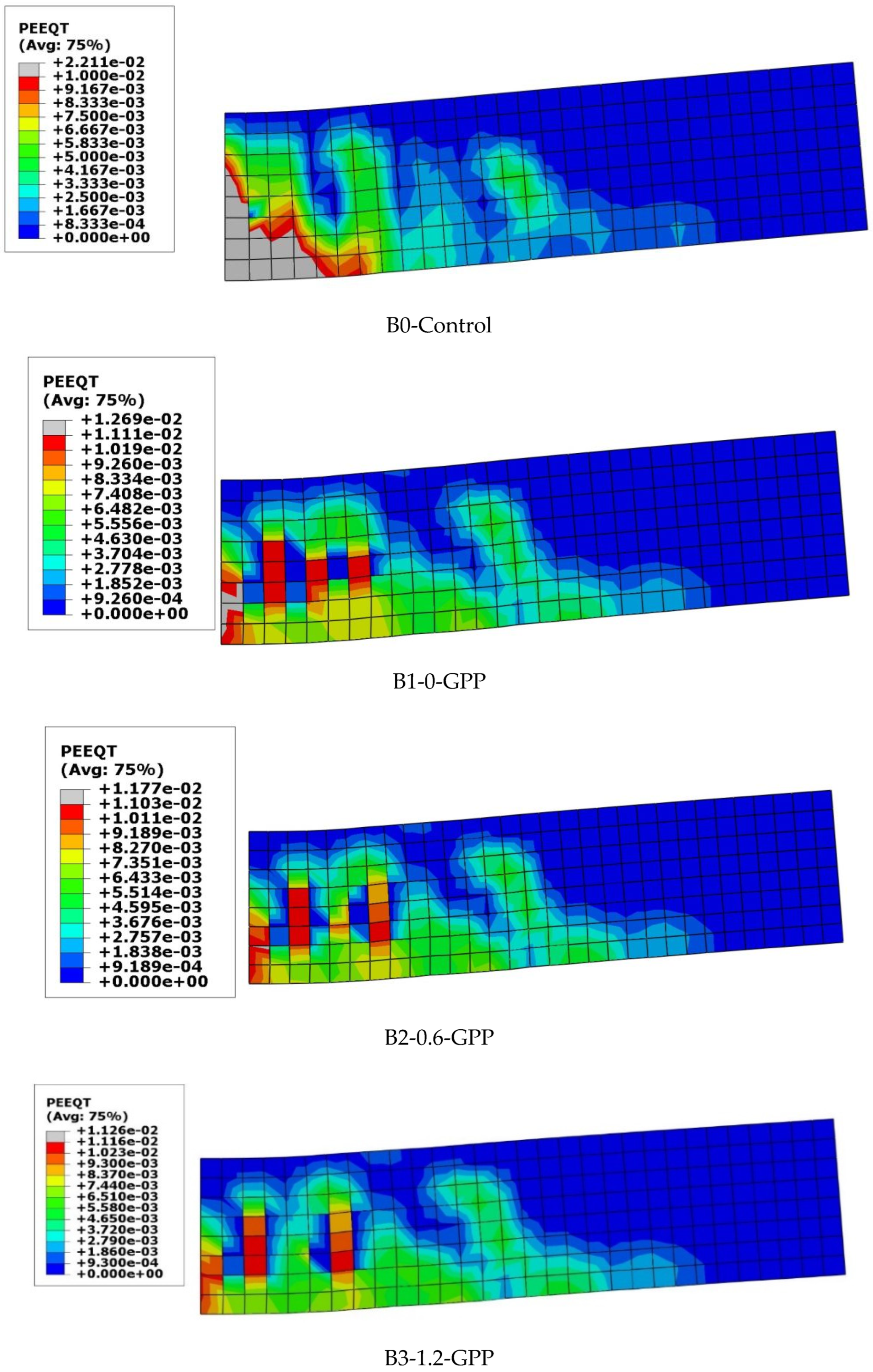
Figure 23 shows the final finite element cracks of the examined beams. All failure modes obtained numerically were tension failures at the flexural zone. All cracks formed in the middle third of the beams verified the experimental results. The experimental findings and FE predictions can be seen to be in good agreement. Due to the complexity of using the cohesive model in modeling the GFRP laminate–concrete interface, there was a slight variation in the results.
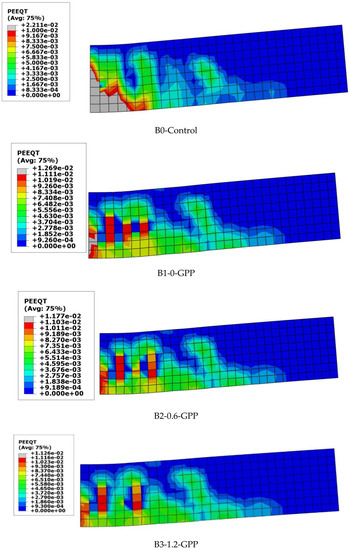
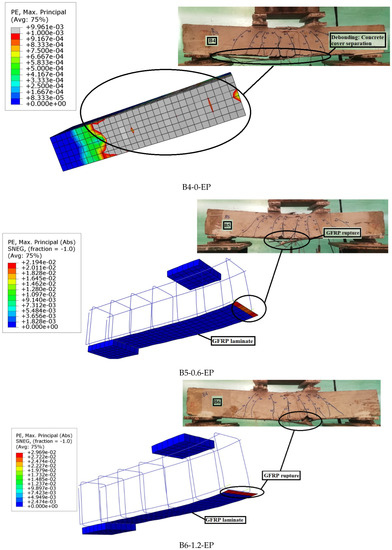
Figure 23.
Finite element final cracks of studied beams.
6. Conclusions
The subsequent conclusions may be taken from the findings of the experimental and analytical investigations to suggest two novel ways to enhance the bond between the GFRP laminates and the concrete’s surface.
- The geopolymer paste with and without short glass fibers outperformed epoxy in the strengthened beams. No debonding was observed between the GFRP laminate and the concrete surface, which is the most significant issue that frequently limits the strengthening of structures using GFRP laminate. On the other hand, compared with epoxy, geopolymer paste with and without short glass fibers reduced adhesive materials costs by more than 90%.
- The failure loads of beams B1-0-GPP, B2-0.60-GPP, and B3-1.2-GPP were greater than control beam B0-Control by approximately 20.80%, 25.60%, and 31.40%, respectively, whereas the failure loads of beams B4-0-EP, B5-0.6-EP, and B6-1.2-EP were greater than the control beam B0-Control by approximately 16.90%, 26.90%, and 26.10%, respectively. The results showed that increasing the SGF ratio in the GPP had a clear effect on raising the capacity of the beam due to the enhanced interfacial bond shear strength. In addition, the GPP had a great effect on increasing the failure load capacity of the tested beams.
- Based on the experimental results, no debonding occurred for laminates when using GPP as adhesive material with different SGF ratios. On the contrary, there was a debonding when using EP as adhesive material.
- The maximum deflection of the tested beams B1-0-GPP, B2-0.6-GPP, and B3-1.2-GPP was less than the control beam by approximately 14.60%, 6.90%, and 6.20%, respectively, whereas the maximum deflection of the tested beams B4-0-EP, B5-0.6-EP, and B6-1.2-EP was less than the control beam by approximately 19.30%, 5.92%, and 17.10%, respectively. This showed that the GPP as adhesive material pastes enhanced the maximum beam’s deflections better than EP.
- The ductility factor of beams B1-0-GPP, B2-0.6-GPP, and B3-1.2-GPP was larger than corresponding beams B4-0-EP, B5-0.6-EP, and B6-1.2-EP by approximately 5.80%, 13.60%, and 21.40%, respectively. This showed that the GPP as adhesive material pastes enhanced the beam’s ductility factor more than EP.
- The experimental findings and FE predictions are shown to be in good agreement. Due to the complexity of using the cohesive model in modeling the GFRP laminate–concrete interface, there was a slight variation in the results.
7. Recommendations for Future Research
The study will be continued to examine the efficiency of using the GPP as an adhesive material in strengthening beams in shear using GFRP and CFRP laminates.
Author Contributions
Conceptualization and methodology, M.M.A.; software, validation, formal analysis, data curation, writing—original draft preparation, writing—review and editing, and visualization, B.O.R., M.A.E.-M., A.H.E. and M.M.A.; investigation, B.O.R., M.A.E.-M. and M.M.A.; resources, supervision, and project administration, B.O.R., M.A.E.-M. and M.M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Attia, M.M.; El-Shaer, M.A.A.; Shawky, S.M.M.; Samaan, M.F. Replacement efficiency of steel reinforcement with FRB bars in RC beams under flexure load: Experimental and FE study. Innov. Infrastruct. Solut. 2022, 7, 281. [Google Scholar] [CrossRef]
- El Ghadioui, R.; Wagner, J.; Klein, J.; Proske, T.; Curbach, M.; Graubner, C. RC members with a flexural-strengthening layer of CFRP textile-reinforced concrete under monotonic and cyclic long-term loading. Struct. Concr. 2022, 23, 939–953. [Google Scholar] [CrossRef]
- Barros, J.; Figueiredo, F.P.; Costa, I.G.; Dourado, F. New type of CFRP reinforcement and technique for the flexural strengthening of RC balconies. Compos. Struct. 2022, 280, 114899. [Google Scholar] [CrossRef]
- Prasertsri, T.; Lenwari, A.; Thepchatri, T. Flexural Response of CFRP-Strengthened Steel Beams with Initial Bond Defects. Eng. J. 2020, 24, 115–127. [Google Scholar] [CrossRef]
- Yuan, P.; Xiao, L.; Wang, X.; Xu, G. Failure mechanism of corroded RC beams strengthened at shear and bending positions. Eng. Struct. 2021, 240, 112382. [Google Scholar] [CrossRef]
- Song, L.; Li, L.G.; Fan, C. Analysis on bending resistance of RC beams reinforced with steel bonding plates under secondary stress. Shenyang Gongye Daxue Xuebao/J. Shenyang Univ. Technol. 2021, 43, 470–475. [Google Scholar] [CrossRef]
- Jahami, A.; Temsah, Y.; Khatib, J.; Baalbaki, O.; Kenai, S. The behavior of CFRP strengthened RC beams subjected to blast loading. Mag. Civ. Eng. 2021, 103, 10309. [Google Scholar] [CrossRef]
- Abuodeh, O.R.; Abdalla, J.A.; Hawileh, R.A. Flexural strengthening of RC beams using aluminum alloy plates with mechanically-fastened anchorage systems: An experimental investigation. Eng. Struct. 2021, 234, 111969. [Google Scholar] [CrossRef]
- Abuodeh, O.R.; Hawileh, R.A.; Abdalla, J.A. Nonlinear finite element models of reinforced concrete beams strengthened in bending with mechanically fastened aluminum alloy plates. Comput. Struct. 2021, 253, 106573. [Google Scholar] [CrossRef]
- Kumar, M.V.; Muthukannan, M. Investigation of HFRC beams retrofitted using GFRP for enhancement in flexural capacity. Int. J. Manuf. Technol. Manag. 2020, 34, 1–24. [Google Scholar] [CrossRef]
- Yang, Y.; Fahmy, M.F.; Cui, J.; Pan, Z.; Shi, J. Nonlinear behavior analysis of flexural strengthening of RC beams with NSM FRP laminates. Structures 2019, 20, 374–384. [Google Scholar] [CrossRef]
- Patil, S.; Dhongade, A.V. Literature review for use of FRP in Civil Engineering. Int. Res. J. Eng. Technol. 2021, 8, 446–449. [Google Scholar]
- Ibrahim, S.S.; Kandasamy, S.; Pradeepkumar, S.; Bose, R.S.C. Effect of discrete steel fibres on strength and ductility of FRP laminated RC beams. Ain Shams Eng. J. 2021, 12, 1329–1337. [Google Scholar] [CrossRef]
- Tahmouresi, B.; Momeninejad, K.; Mohseni, E. Flexural response of FRP-strengthened lightweight RC beams: Hybrid bond efficiency of L-shape ribbed bars and NSM technique. Arch. Civ. Mech. Eng. 2022, 22, 95. [Google Scholar] [CrossRef]
- Attia, M.M.; Ahmed, O.; Kobesy, O.; Malek, A.S. Behavior of FRP rods under uniaxial tensile strength with multiple materials as an alternative to steel rebar. Case Stud. Constr. Mater. 2022, 17, e01241. [Google Scholar] [CrossRef]
- Aravind, N.; Samanta, A.K.; Thanikal, J.V.; Roy, D.K.S. An experimental study on the effectiveness of externally bonded corrugated GFRP laminates for flexural cracks of RC beams. Constr. Build. Mater. 2017, 136, 348–360. [Google Scholar] [CrossRef]
- Alam, A.; Onik, S.A.; Bin Mustapha, K.N. Crack based bond strength model of externally bonded steel plate and CFRP laminate to predict debonding failure of shear strengthened RC beams. J. Build. Eng. 2020, 27, 100943. [Google Scholar] [CrossRef]
- Radfar, S.; Foret, G.; Saeedi, N.; Sab, K. Simulation of concrete cover separation failure in FRP plated RC beams. Constr. Build. Mater. 2012, 37, 791–800. [Google Scholar] [CrossRef]
- De Maio, U.; Fabbrocino, F.; Greco, F.; Leonetti, L.; Lonetti, P. A study of concrete cover separation failure in FRP-plated RC beams via an inter-element fracture approach. Compos. Struct. 2019, 212, 625–636. [Google Scholar] [CrossRef]
- Fu, B.; Teng, J.G.; Chen, J.F.; Chen, G.M.; Guo, Y.C. Concrete Cover Separation in FRP-Plated RC Beams: Mitigation Using FRP U-Jackets. J. Compos. Constr. 2017, 21, 04016077. [Google Scholar] [CrossRef]
- Zhang, W.; Tang, Z.; Yang, Y.; Wei, J. Assessment of FRP–Concrete Interfacial Debonding with Coupled Mixed-Mode Cohesive Zone Model. J. Compos. Constr. 2021, 25, 04021002. [Google Scholar] [CrossRef]
- Zhang, F.; Gao, L.; Wu, Y.-F.; Liu, J. Flexural design of reinforced concrete structures strengthened with hybrid bonded FRP. Compos. Struct. 2021, 269, 113996. [Google Scholar] [CrossRef]
- Yazdani, N.; Aljaafreh, T.; Beneberu, E. Concrete beam flexural strengthening with anchored pre-saturated CFRP laminates. Compos. Struct. 2020, 235, 111733. [Google Scholar] [CrossRef]
- Mostofinejad, D.; Hosseini, S.M.; Tehrani, B.N.; Eftekhar, M.R.; Dyari, M. Innovative warp and woof strap (WWS) method to anchor the FRP sheets in strengthened concrete beams. Constr. Build. Mater. 2019, 218, 351–364. [Google Scholar] [CrossRef]
- Ababneh, A.N.; Al-Rousan, R.Z.; Ghaith, I.M. Experimental study on anchoring of FRP-strengthened concrete beams. Structures 2020, 23, 26–33. [Google Scholar] [CrossRef]
- Sun, W.; Liu, S.; Zhang, C. An effective improvement for enhancing the strength and feasibility of FRP spike anchors. Compos. Struct. 2020, 247, 112449. [Google Scholar] [CrossRef]
- Grelle, S.V.; Sneed, L.H. Review of Anchorage Systems for Externally Bonded FRP Laminates. Int. J. Concr. Struct. Mater. 2013, 7, 17–33. [Google Scholar] [CrossRef]
- Ibrahim, W.; Ali, W. Comparison of Anchorage Systems for Externally Bonded FRP Laminates. Int. J. Eng. Technol. 2019, 11, 1128–1135. [Google Scholar] [CrossRef]
- Al-Saoudi, A.; Kalfat, R.; Al-Mahaidi, R.; Cervenka, J.; Pryl, D. Numerical and experimental investigation into the fatigue life of FRP bonded to concrete and anchored with bidirectional fabric patches. Eng. Struct. 2021, 239, 112335. [Google Scholar] [CrossRef]
- Godat, A.; Hammad, F.; Chaallal, O. State-of-the-art review of anchored FRP shear-strengthened RC beams: A study of influencing factors. Compos. Struct. 2020, 254, 112767. [Google Scholar] [CrossRef]
- Eslami, A.; Moghavem, A.; Shayegh, H.R.; Ronagh, H.R. Effect of FRP stitching anchors on ductile performance of shear-deficient RC beams retrofitted using FRP U-wraps. Structures 2020, 23, 407–414. [Google Scholar] [CrossRef]
- Zhang, S.; Ke, Y.; Smith, S.; Zhu, H.; Wang, Z. Effect of FRP U-jackets on the behaviour of RC beams strengthened in flexure with NSM CFRP strips. Compos. Struct. 2021, 256, 113095. [Google Scholar] [CrossRef]
- Abdallah, M.; Al Mahmoud, F.; Khelil, A.; Mercier, J.; Almassri, B. Assessment of the flexural behavior of continuous RC beams strengthened with NSM-FRP bars, experimental and analytical study. Compos. Struct. 2020, 242, 112127. [Google Scholar] [CrossRef]
- ACI. ACI SP 275. In Fiber-Reinforced Polymer Reinforcement for Concrete Structures 10th International Symposium, Tampa, FL, USA, 2–4 April 2011; ACI: Farmington Hills, MI, USA, 2011. [Google Scholar]
- Yuan, C.; Chen, W.; Pham, T.M.; Hao, H.; Chen, L.; Zhang, M. New epoxy anchor for better bonding between FRP sheets and concrete. Constr. Build. Mater. 2020, 248, 118628. [Google Scholar] [CrossRef]
- Mostofinejad, D.; Mofrad, M.H.; Hosseini, A.; Mofrad, H.H. Investigating the effects of concrete compressive strength, CFRP thickness and groove depth on CFRP-concrete bond strength of EBROG joints. Constr. Build. Mater. 2018, 189, 323–337. [Google Scholar] [CrossRef]
- Jiang, C.; Wan, B.; Wu, Y.F.; Omboko, J. Epoxy interlocking: A novel approach to enhance FRP-to-concrete bond behavior. Constr. Build. Mater. 2018, 193, 643–653. [Google Scholar] [CrossRef]
- Almutairi, A.L.; Tayeh, B.A.; Adesina, A.; Isleem, H.F.; Zeyad, A.M. Potential applications of geopolymer concrete in construction: A review. Case Stud. Constr. Mater. 2021, 15, e00733. [Google Scholar] [CrossRef]
- Mackenzie, K.; Welter, M. Geopolymer (aluminosilicate) composites: Synthesis, properties and applications. In Advances in Ceramic Matrix Composites; Victoria University of Wellington: Wellington, New Zealand, 2014; pp. 445–470. [Google Scholar] [CrossRef]
- Singh, N.; Middendorf, B. Geopolymers as an alternative to Portland cement: An overview. Constr. Build. Mater. 2020, 237, 117455. [Google Scholar] [CrossRef]
- Dong, M.; Feng, W.; Elchalakani, M.; Li, G.; Karrech, A.; Sheikh, N.M. Material and glass-fibre-reinforced polymer bond properties of geopolymer concrete. Mag. Concr. Res. 2020, 72, 509–525. [Google Scholar] [CrossRef]
- Abdulrahman, H.; Muhamad, R.; Visintin, P.; Shukri, A.A. Mechanical properties and bond stress-slip behaviour of fly ash geopolymer concrete. Constr. Build. Mater. 2022, 327, 126909. [Google Scholar] [CrossRef]
- Saranya, P.; Nagarajan, P.; Shashikala, A.P. Experimental Investigation on Bond Strength Properties of Geopolymer Concrete. In Advances in Civil Engineering; Lecture Notes in Civil Engineering; Singh, R.M., Sudheer, K.P., Kurian, B., Eds.; Springer: Singapore, 2021; Volume 83. [Google Scholar] [CrossRef]
- Rajak, D.K.; Pagar, D.D.; Kumar, R.; Pruncu, C.I. Recent progress of reinforcement materials: A comprehensive overview of composite materials. J. Mater. Res. Technol. 2019, 8, 6354–6374. [Google Scholar] [CrossRef]
- Mohamedou, M.; Zulueta, K.; Chung, C.N.; Rappel, H.; Beex, L.; Adam, L.; Arriaga, A.; Major, Z.; Wu, L.; Noels, L. Bayesian identification of Mean-Field Homogenization model parameters and uncertain matrix behavior in non-aligned short fiber composites. Compos. Struct. 2019, 220, 64–80. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Z.; Lei, Z.; Zhu, P. An innovative computational framework for the analysis of complex mechanical behaviors of short fiber reinforced polymer composites. Compos. Struct. 2021, 277, 114594. [Google Scholar] [CrossRef]
- Sharma, K.K.; Kushwaha, J.; Kumar, K.; Singh, H.; Shrivastava, Y. Fabrication and testing of hybrid fibre reinforced composite: A comprehensive review. Aust. J. Mech. Eng. 2022, 1–17. [Google Scholar] [CrossRef]
- Abaqus, S. CAE 6.14 User’s Manual Dassault; Systémes Inc. Provid.: Johnston, RI, USA, 2014; Volume IV. [Google Scholar]
- ASTM C494; Standard Specification for Chemical Admixtures for Concrete. ASTM Int.: West Conshohocken, PA, USA, 2019; Volume 04.
- Attia, M.M.; Abdelsalam, B.A.; Amin, M.; Agwa, I.S.; Abdelmagied, M.F. Metal-Nails Waste and Steel Slag Aggregate as Alternative and Eco-Friendly Radiation Shielding Composites. Buildings 2022, 12, 1120. [Google Scholar] [CrossRef]
- ACI Committee 440. ACI440.2R-17 Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures Reported by ACI Committee 440. Am. Concr. Inst. 2017, 5, 45. [Google Scholar]
- American Concrete Institute. ACI 318 Building Code Requirements for Structure Concrete and Commentary; American Concrete Institute ACI Committee: Farmington Hills, MI, USA, 2019. [Google Scholar]
- Hamrat, M.; Bouziadi, F.; Boulekbache, B.; Daouadji, T.H.; Chergui, S.; Labed, A.; Amziane, S. Experimental and numerical investigation on the deflection behavior of pre-cracked and repaired reinforced concrete beams with fiber-reinforced polymer. Constr. Build. Mater. 2020, 249, 118745. [Google Scholar] [CrossRef]
- Almusallam, T.; Al-Salloum, Y.; Alsayed, S.; Iqbal, R.; Abbas, H. Effect of CFRP strengthening on the response of RC slabs to hard projectile impact. Nucl. Eng. Des. 2015, 286, 211–226. [Google Scholar] [CrossRef]
- Radnić, J.; Matešan, D.; Grgić, N.; Baloević, G. Impact testing of RC slabs strengthened with CFRP strips. Compos. Struct. 2015, 121, 90–103. [Google Scholar] [CrossRef]
- Guo, Z.; Cao, S.; Sun, W.; Lin, X. Experimental study on bond stress-slip behaviour between FRP sheets and concrete. In Proceedings of the International Symposium on Bond Behaviour of FRP in Structures, Hong Kong, China, 7–9 December 2005. [Google Scholar]
- Obaidat, Y.T.; Heyden, S.; Dahlblom, O. The effect of CFRP and CFRP/concrete interface models when modelling retrofitted RC beams with FEM. Compos. Struct. 2010, 92, 1391–1398. [Google Scholar] [CrossRef]
- Jahami, A.; Temsah, Y.; Khatib, J.; Sonebi, M.; Ali, J. Numerical study for the effect of carbon fiber reinforced polymers (CFRP) sheets on structural behavior of posttensioned slab subjected to impact loading. In Proceedings of the Symposium on Concrete Modelling–CONMOD2018, Delft, The Netherlands, 27–30 August 2018; pp. 259–267. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).