Laws and Numerical Analysis of Surface Deformation Caused by Excavation of Large Diameter Slurry Shield in Upper-Soft and Lower-Hard Composite Stratum
Abstract
:1. Introduction
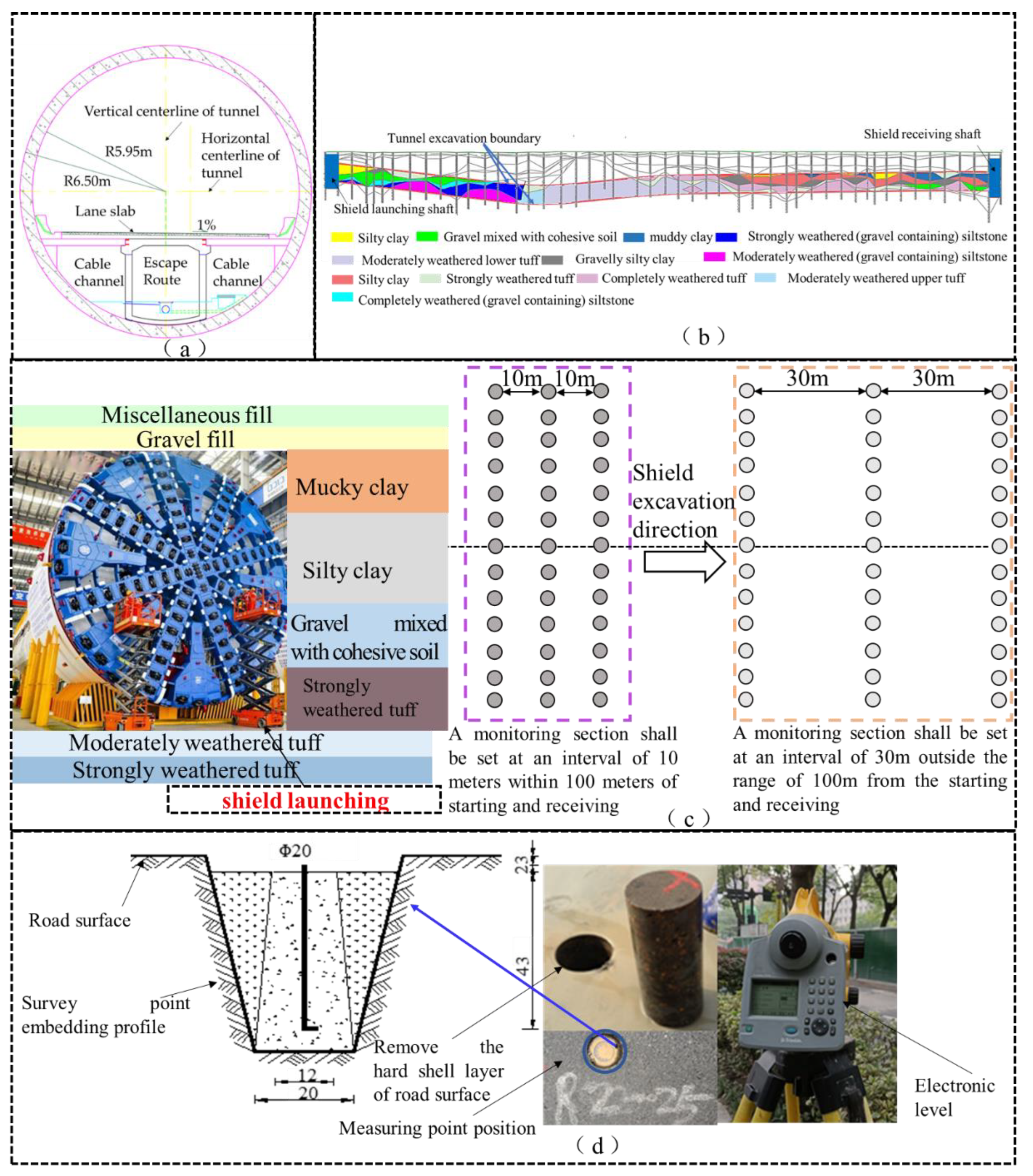
2. Overview of the Test Section
3. Monitoring and Analysis of Surface Deformation of Large Diameter Shield Tunnel
3.1. Monitoring Scheme
3.2. Diachronic Analysis of Surface Settlement at Axis during Construction Period
3.2.1. The Stage before the Shield Machine Reaches the Working Face
3.2.2. Shield Passing Stage
3.2.3. Shield Tail Grouting Stage
3.2.4. Shield Away Stage
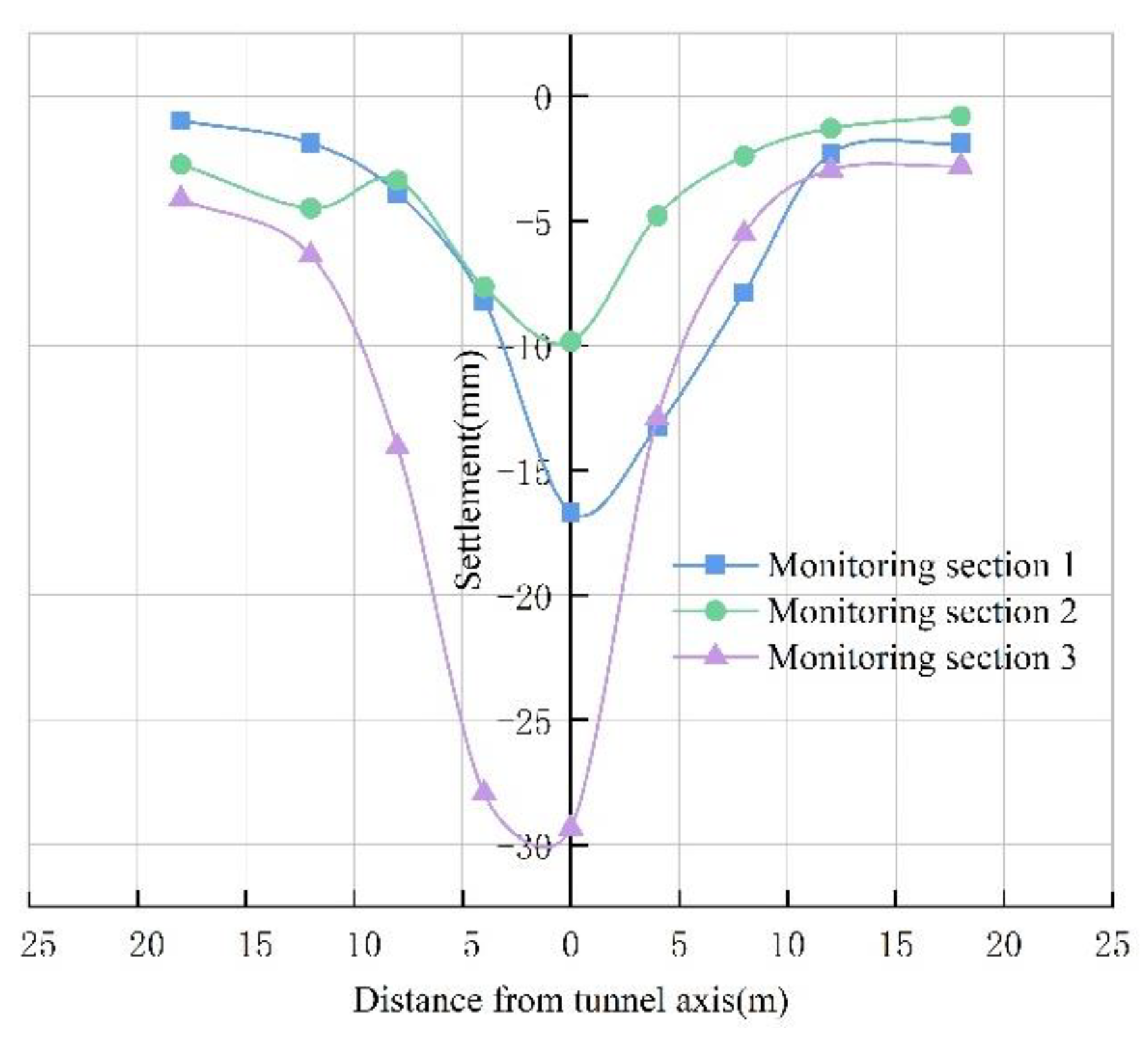
3.3. Variation Law of Surface Transverse
4. Numerical Analysis of Stratum Deformation Caused by Large Diameter Slurry Shield Tunneling
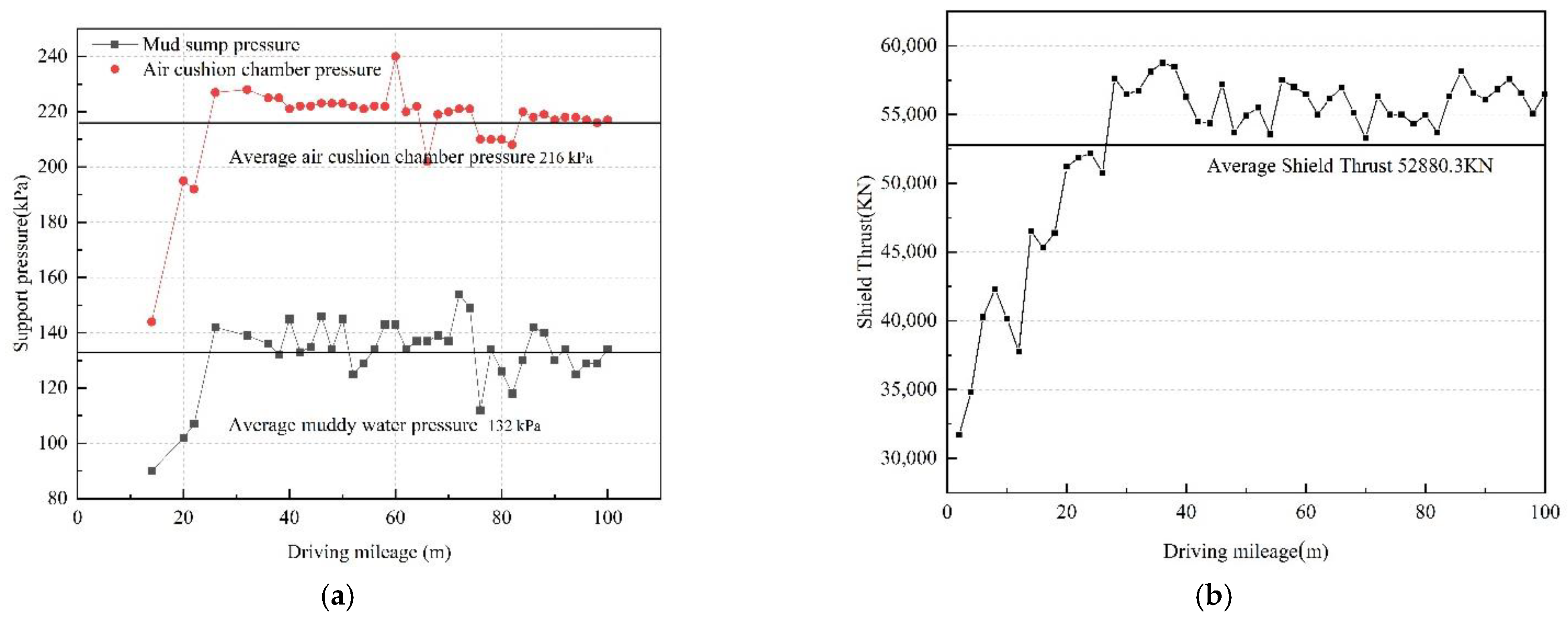
4.1. Model Excavation Condition Setting and Parameter Selection
4.2. The Basic Assumption of Model Calculation
- (1)
- The horizontal layered distribution of each soil layer, the shield thrust is evenly distributed on the excavation surface, and the buried depth of the tunnel axis remains unchanged during the simulation process;
- (2)
- Before construction, the self-weight stress of soil and the stress and strain caused by surrounding loads have been completed;
- (3)
- The influence of groundwater is not considered in the simulation process;
- (4)
- In the calculation model, the concrete structures such as tunnel segments adopt the elastic model.
- (5)
- In order to reduce the computational complexity, it is assumed that the soil deformation does not depend on time, and the creep and deformation of the soil are not considered.
- (6)
- The influence of tectonic stress on soil deformation is ignored, and the initial ground stress only considers the self-weight of the soil.
4.3. Three-Dimensional Finite Element Analysis Model of Shield Tunnel
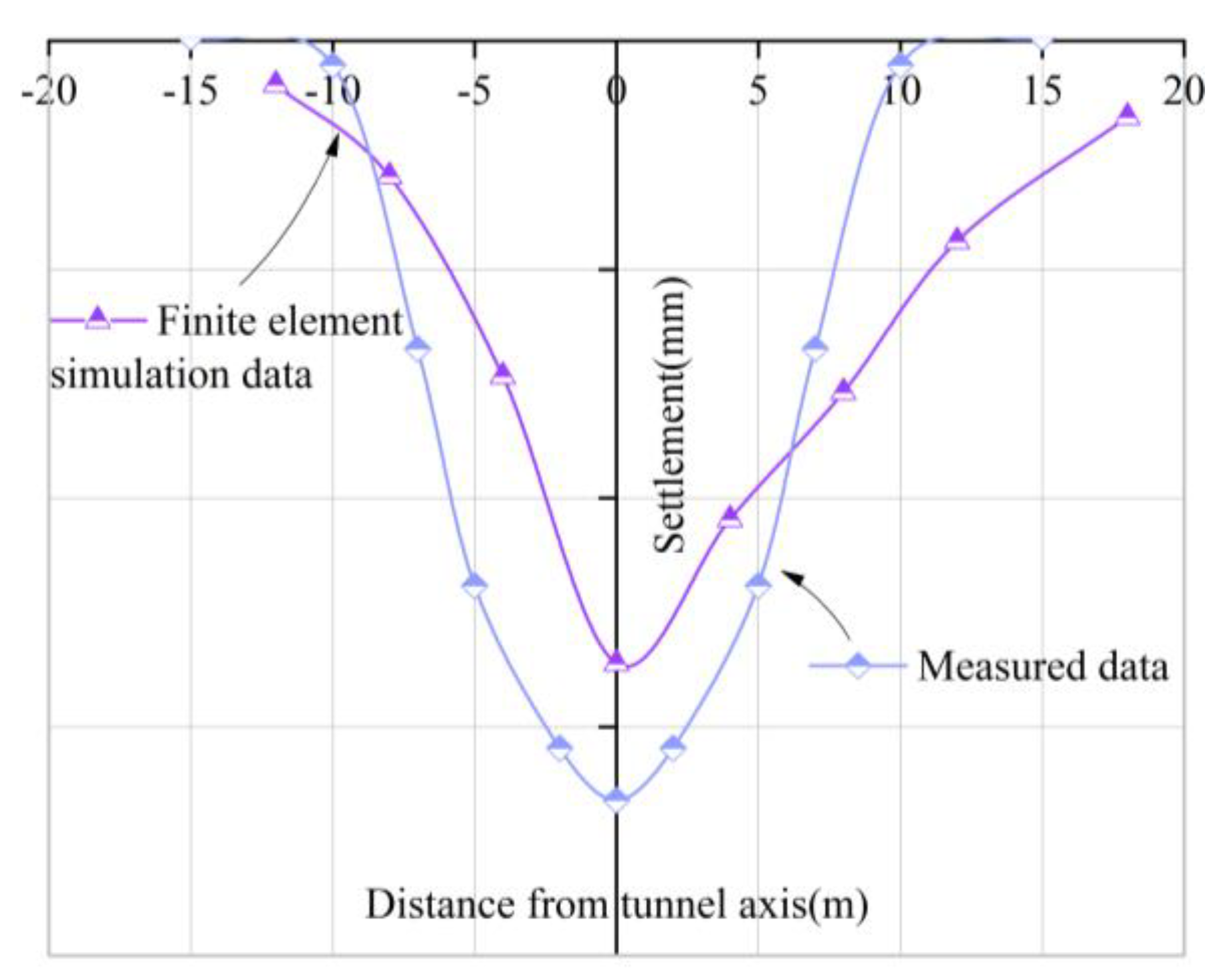
4.4. Test of Model Rationality
4.5. Sensitivity Analysis of Key Parameters in Shield Tunneling
4.5.1. Sensitivity Analysis of Surface Lateral Deformation Parameters
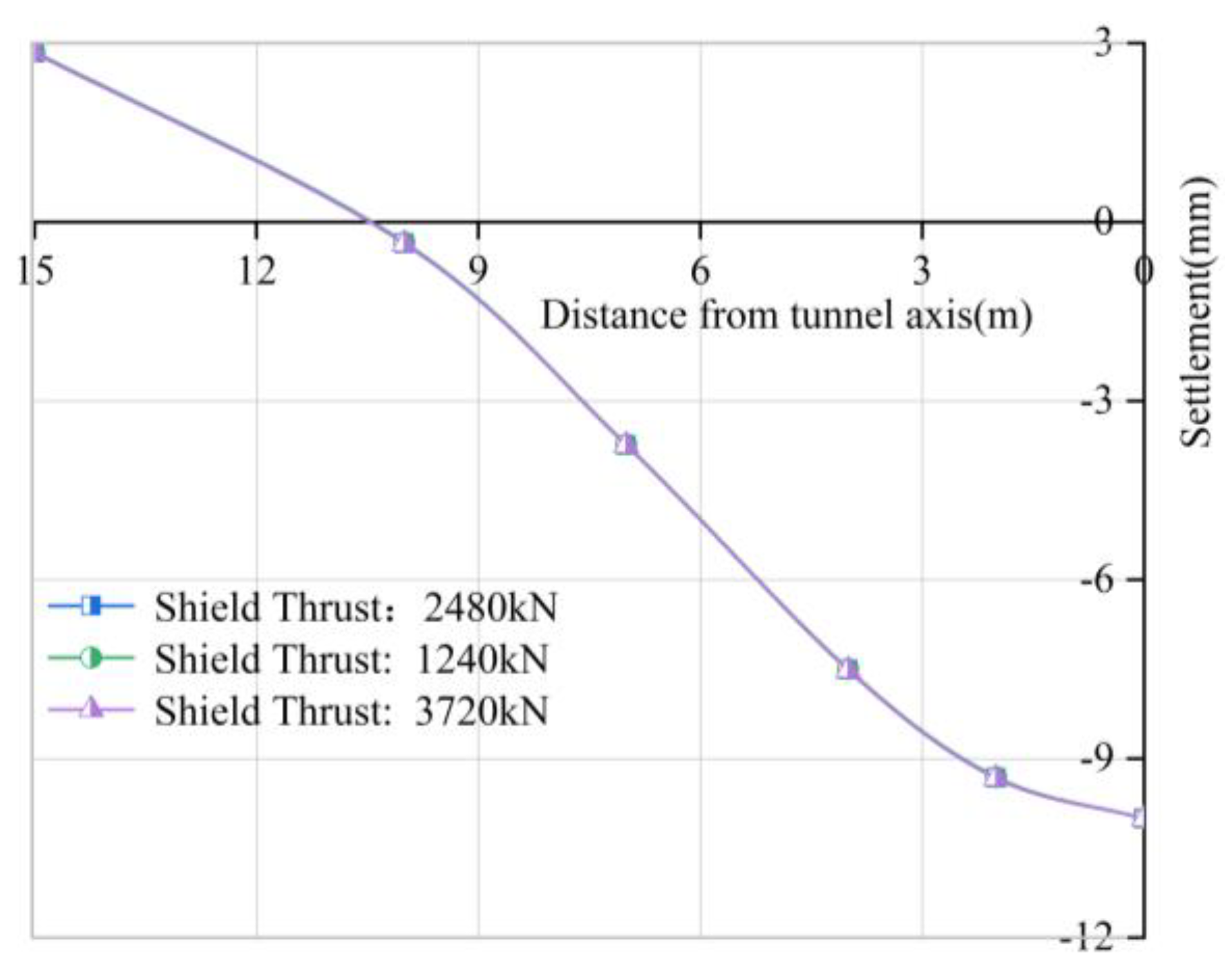
Influence of Shield Thrust on the Lateral Deformation of Ground Surface
Influence of Support Pressure on the Lateral Deformation of Ground Surface
Influence of Grouting Pressure on the Lateral Deformation of Ground Surface
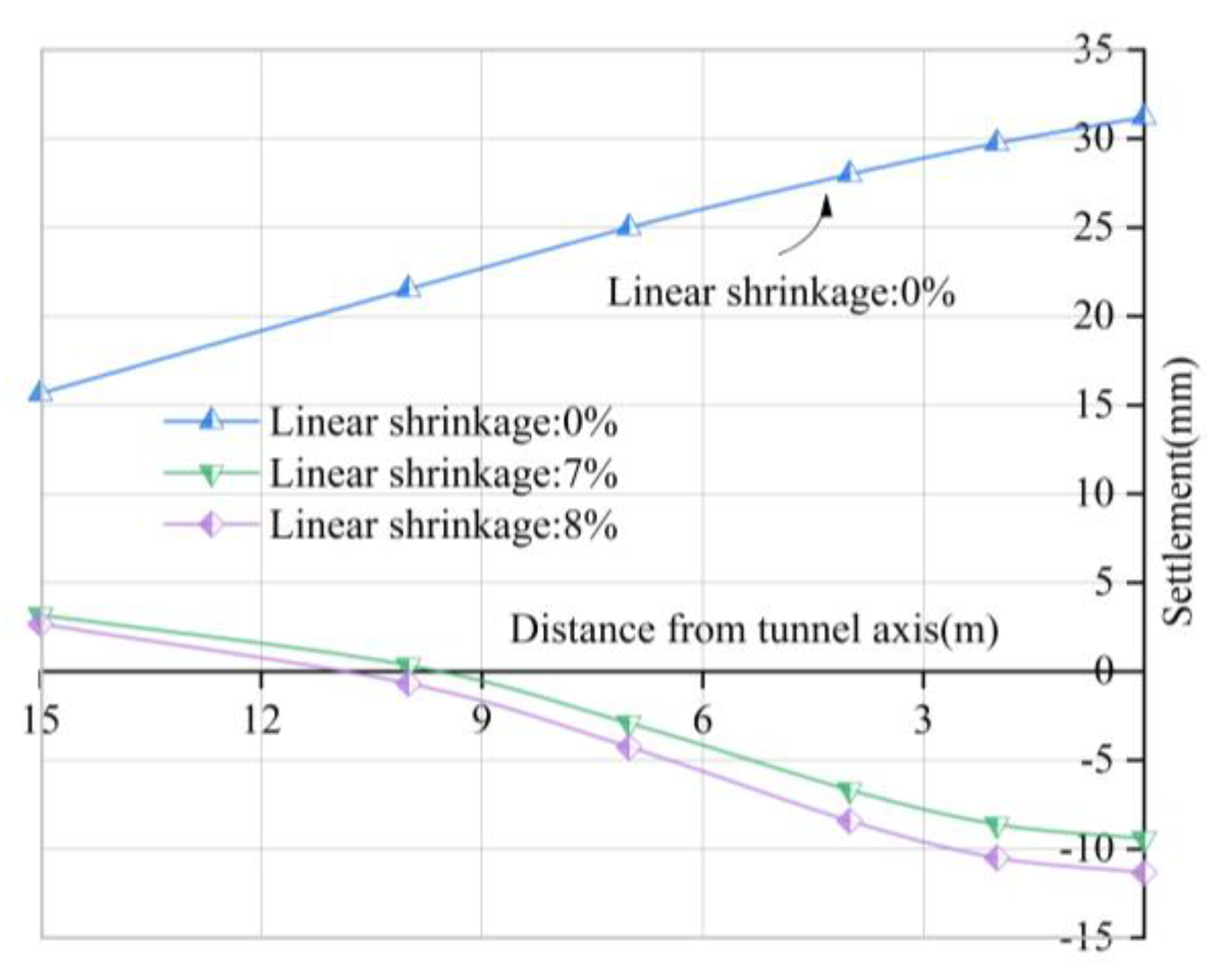
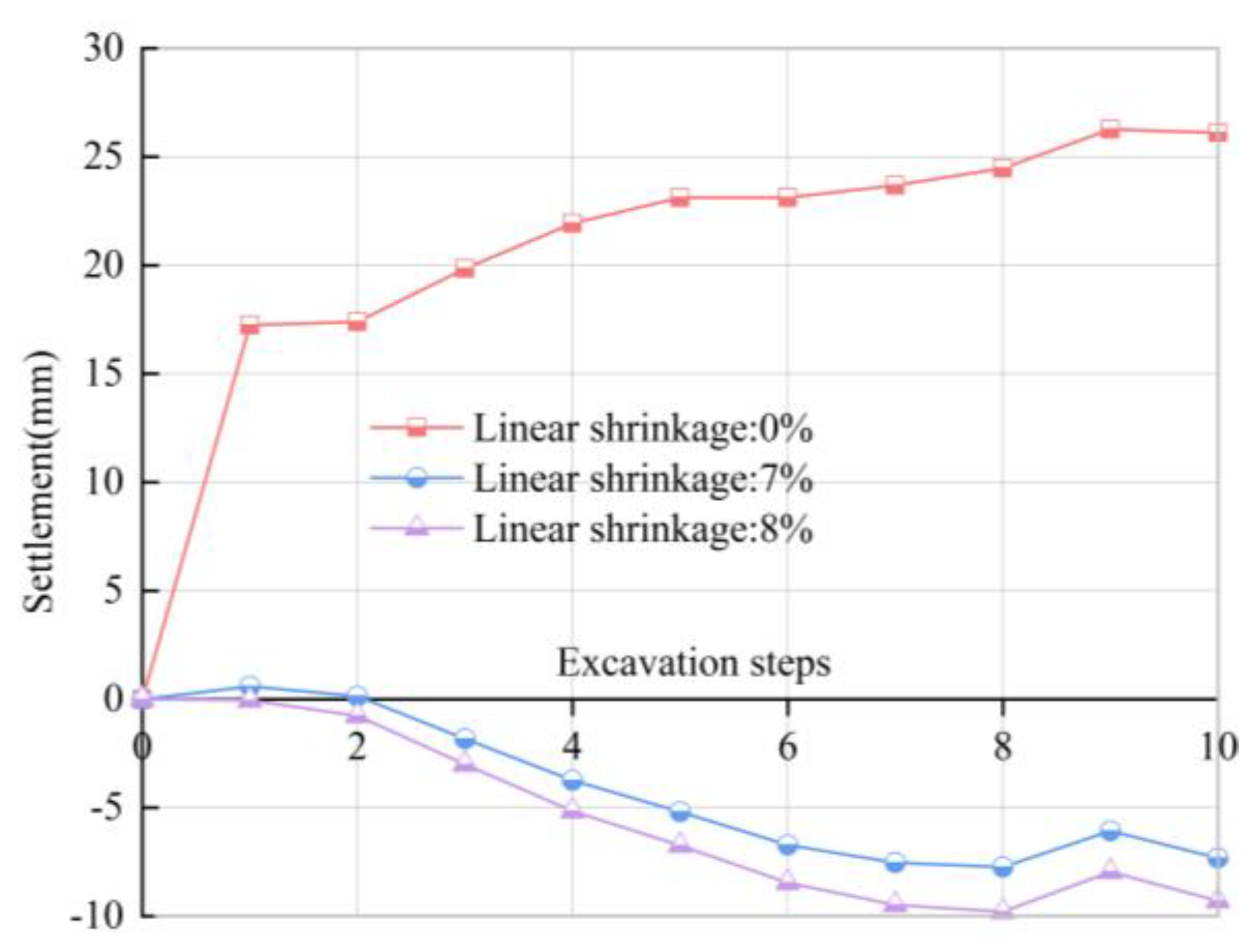
Influence of Linear Shrinkage Rate on the Lateral Deformation of Ground Surface
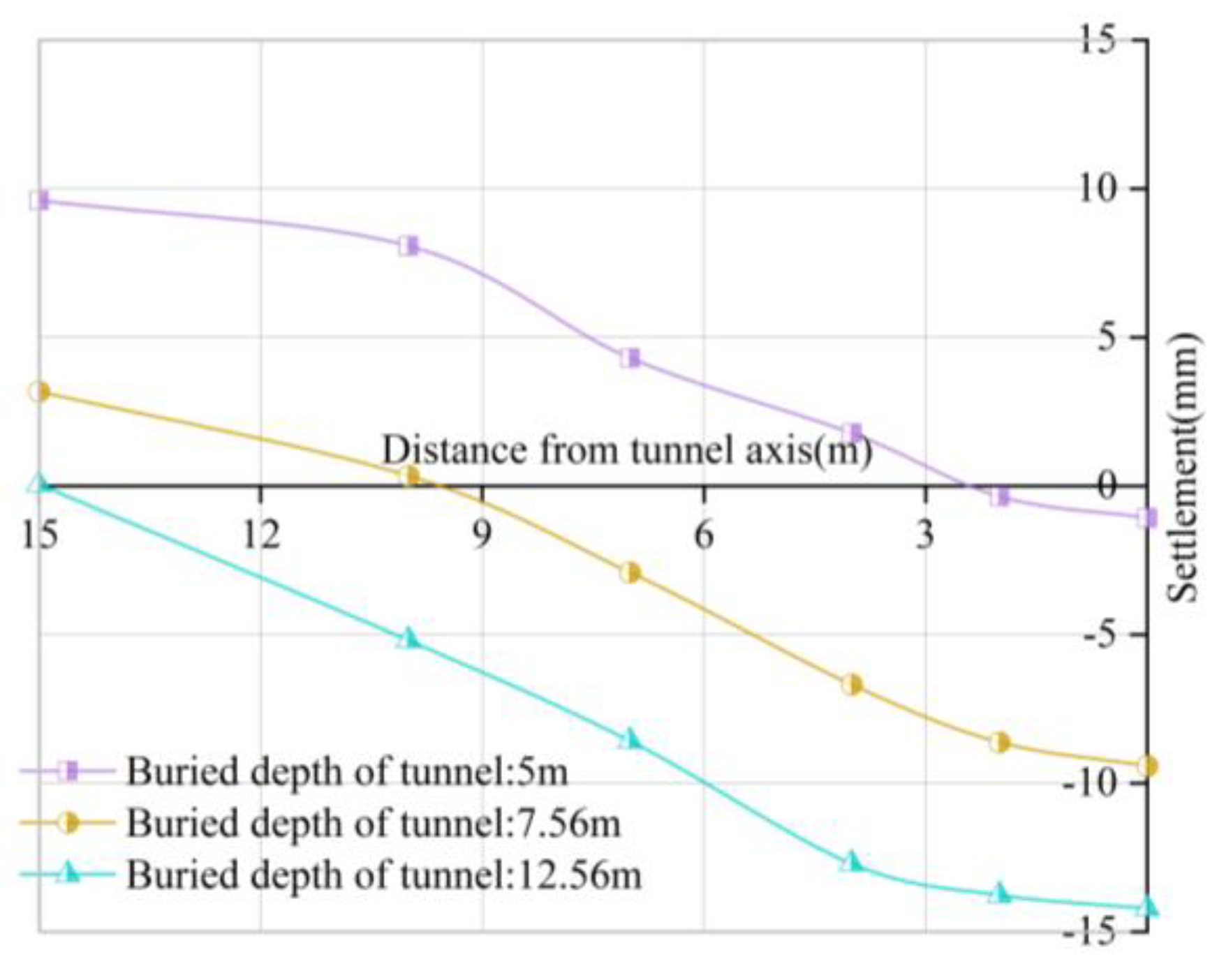
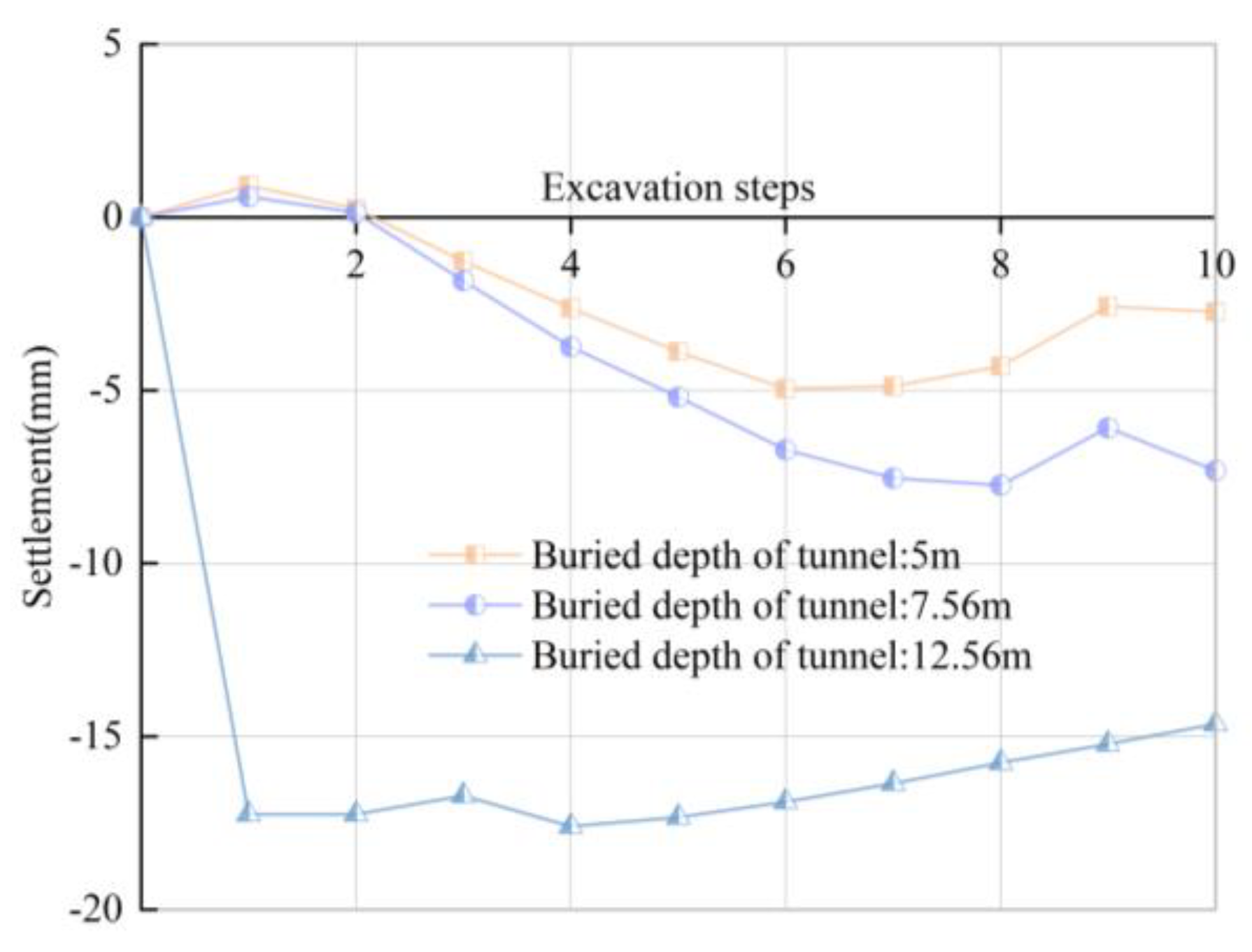
Influence of Buried Depth of Tunnel on the Lateral Deformation of Ground Surface
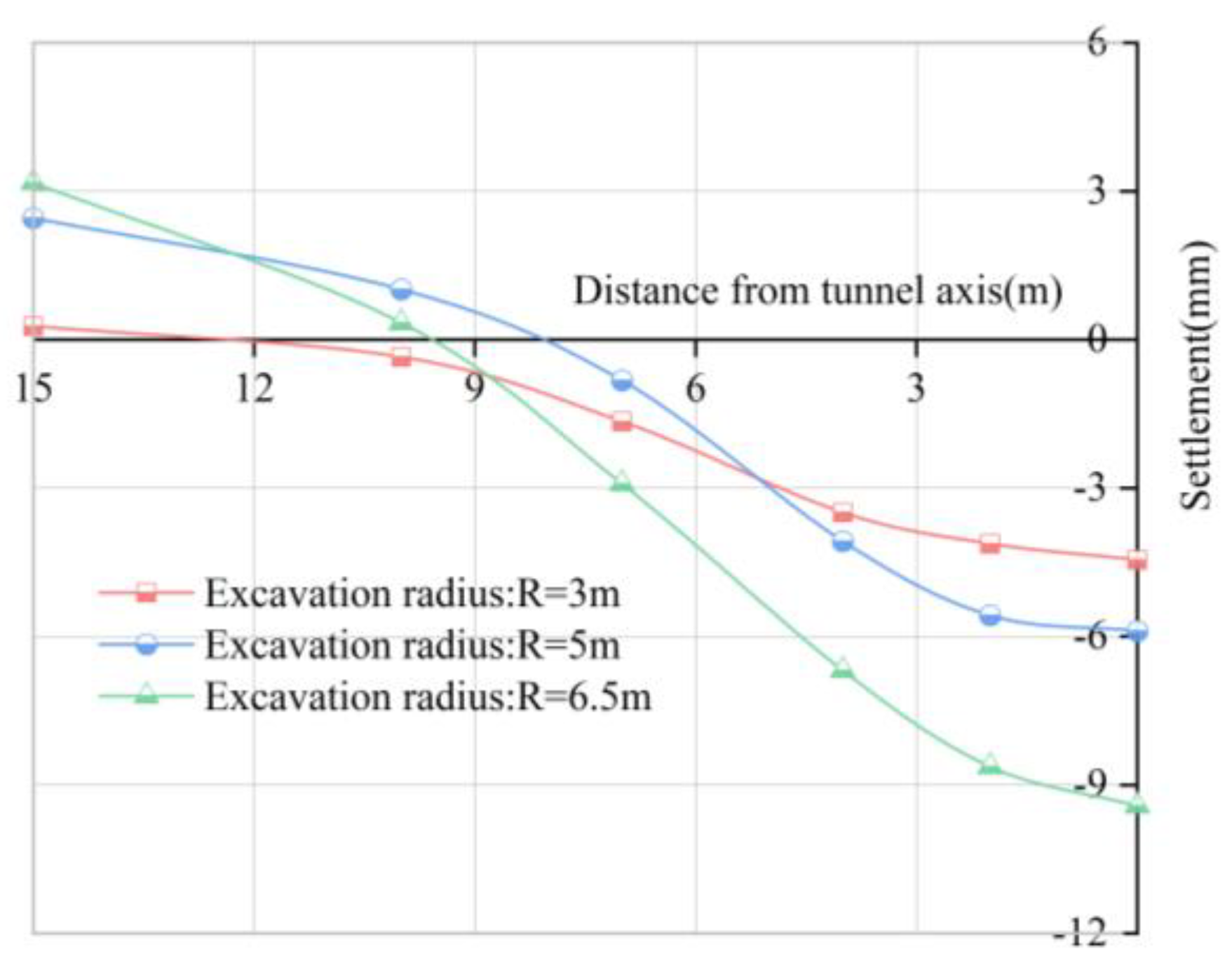
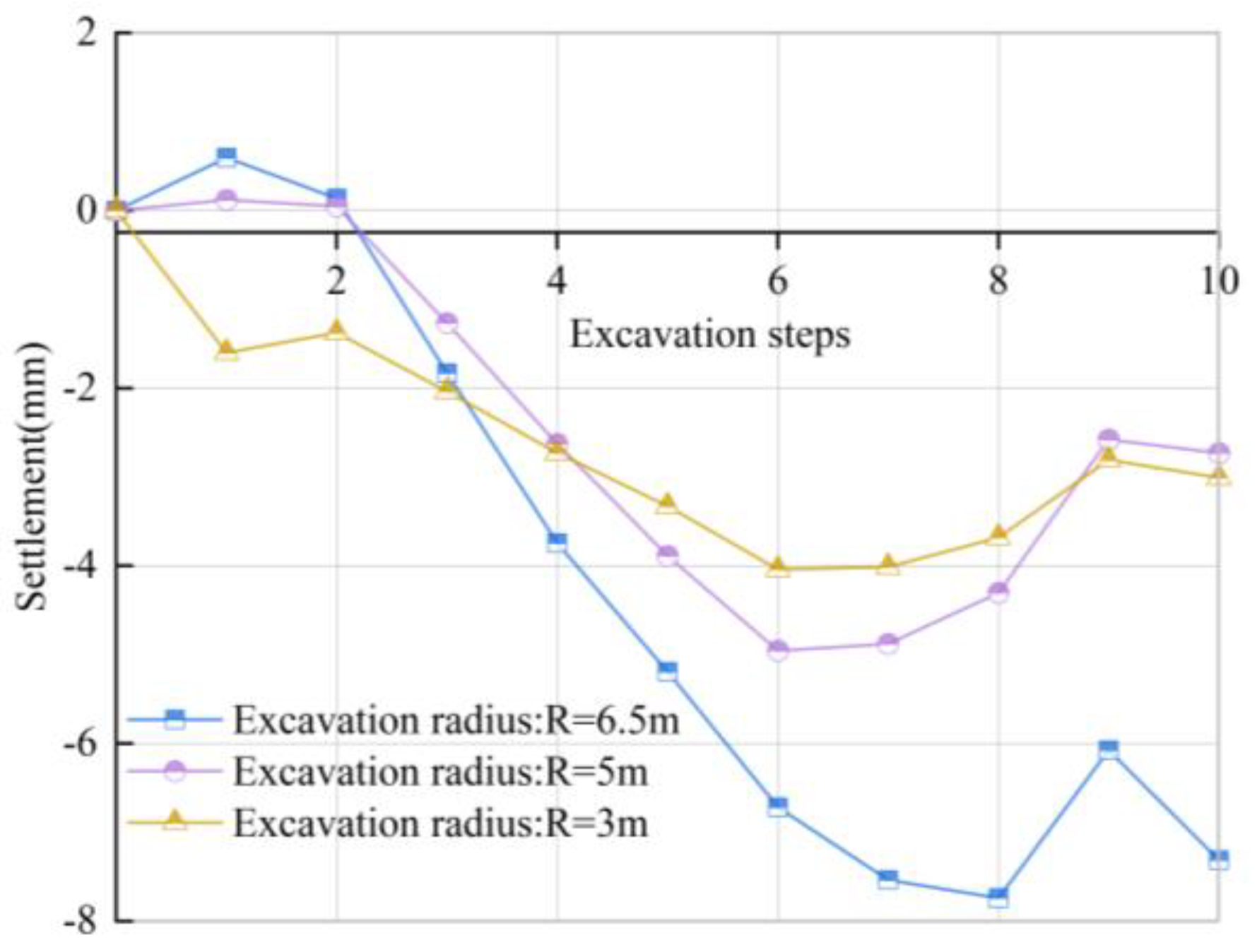
Influence of Excavation Radius on the Lateral Deformation of Ground Surface
4.5.2. Sensitivity Analysis of Surface Longitudinal Deformation Parameters
Influence of Grouting Pressure on the Longitudinal Deformation of Ground Surface
Influence of Linear Shrinkage Rate on the Longitudinal Deformation of Ground Surface
Influence of Excavation Radius on the Longitudinal Deformation of Ground Surface
Influence of the Buried Depth of the Tunnel on the Longitudinal Deformation of Ground Surface
5. Conclusions
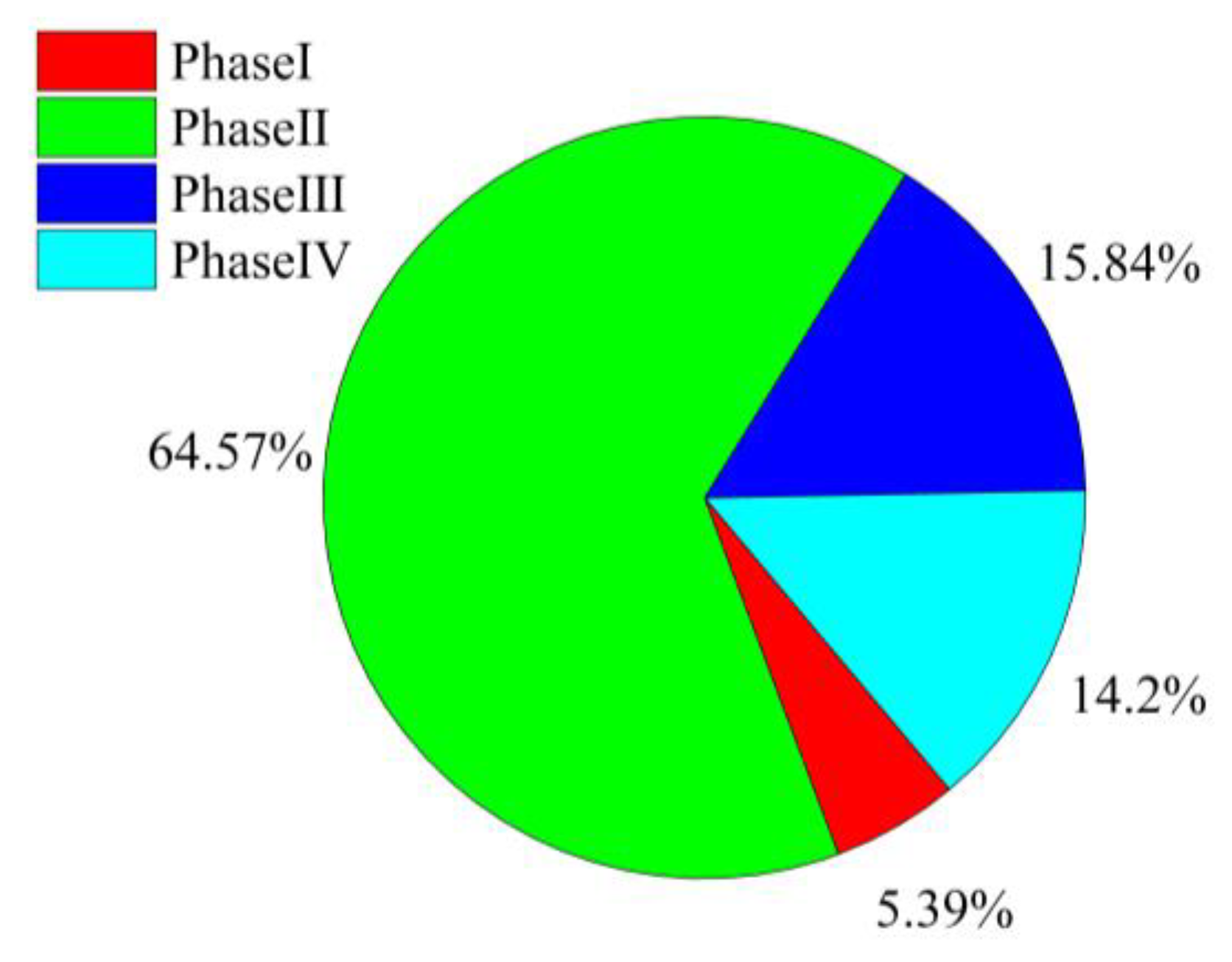
- According to the on-site monitoring data, the surface settlement curve at the shield axis during the construction period can be divided into four stages: pre-deformation, shield passing, shield tail exit, and shield moving away. The proportion of soil settlement in each stage to total settlement is 5.39%, 64.58%, 15.84%, and 14.2% respectively.
- Statistical values of on-site construction parameters can be used as an effective method for parameter setting of numerical simulation models, as the main factor affecting soil deformation during shield excavation, linear shrinkage rate should be considered in numerical analysis.
- Support pressure and grouting pressure as important construction parameters of shield tunneling. The maximum settlement value of the ground surface at the center of the tunnel increases with the increase of the support pressure, when the support pressure exceeds 300 kPa, the surface uplift and the settlement caused by stratum loss are offset, and the surface settlement is reduced instead, the maximum settlement value of the surface is inversely proportional to the grouting pressure, but with the increase of the grouting pressure, the maximum surface uplift continues to increase.
- With the numerical simulation of excavation step construction, the surface uplift increases with the increase of grouting pressure and shield radius, and decreases with the increase of shield buried depth.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mei, Y.; Zhou, D.; Wang, X.; Zhao, L.; Shen, J.; Zhang, S.; Liu, Y. Deformation Law of the Diaphragm Wall during Deep Foundation Pit Construction on Lake and Sea Soft Soil in the Yangtze River Delta. Adv. Civ. Eng. 2021, 2021, 6682921. [Google Scholar] [CrossRef]
- Wang, X.Y.; Ma, Z.; Zhang, Y.T. Research on Safety Early Warning Standard of Large-Scale Underground Utility Tunnel in Ground Fissure Active Period. Front. Earth Sci. 2022, 10, 828477. [Google Scholar] [CrossRef]
- Wang, X.; Gong, H.; Song, Q.; Yan, X.; Luo, Z. Risk Assessment of EPB Shield Construction Based on the Nonlinear FAHP Method. Adv. Civ. Eng. 2022, 2022, 9233833. [Google Scholar] [CrossRef]
- Yuan, B.; Li, Z.; Chen, W.; Zhao, J.; Lv, J.; Song, J.; Cao, X. Influence of Groundwater Depth on Pile—Soil Mechanical Properties and Fractal Characteristics under Cyclic Loading. Fractal Fract. 2022, 6, 198. [Google Scholar] [CrossRef]
- Jin, H.; Yu, K.; Gong, Q.; Zhou, S. Load-carrying capability of shield tunnel damaged by shield shell squeezing action during construction. Thin-Walled Struct. 2018, 132, 69–78. [Google Scholar] [CrossRef]
- Wang, X.; Song, Q.; Gong, H. Research on Deformation Law of Deep Foundation Pit of Station in Core Region of Saturated Soft Loess Based on Monitoring. Adv. Civ. Eng. 2022, 2022, 7848152. [Google Scholar] [CrossRef]
- Zheng, G.; Fan, Q.; Zhang, T.; Zhang, Q. Numerical study of the Soil-Tunnel and Tunnel-Tunnel interactions of EPBM overlapping tunnels constructed in soft ground. Tunn. Undergr. Space Technol. 2022, 124, 104490. [Google Scholar] [CrossRef]
- Xie, X.; Yang, Y.; Ji, M. Analysis of ground surface settlement induced by the construction of a large-diameter shield-driven tunnel in Shanghai, China. Tunn. Undergr. Space Technol. 2016, 51, 120–132. [Google Scholar] [CrossRef]
- Shi, C.; Cao, C.; Lei, M. An analysis of the ground deformation caused by shield tunnel construction combining an elastic half-space model and stochastic medium theory. KSCE J. Civ. Eng. 2016, 21, 1933–1944. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, J.; Chen, G. Analysis of ground surface settlement induced by a large EPB shield tunnelling: A case study in Beijing, China. Environ. Earth Sci. 2019, 78, 605. [Google Scholar] [CrossRef]
- Wang, P.; Kong, X.; Guo, Z.; Hu, L. Prediction of Axis Attitude Deviation and Deviation Correction Method Based on Data Driven during Shield Tunneling. IEEE Access 2019, 7, 163487–163501. [Google Scholar] [CrossRef]
- Yuan, B.; Chen, M.; Chen, W.; Luo, Q.; Li, H. Effect of Pile-Soil Relative Stiffness on Deformation Characteristics of the Laterally Loaded Pile. Adv. Mater. Sci. Eng. 2022, 2022, 4913887. [Google Scholar] [CrossRef]
- Peck, R.B. Deep excavation sand tunneling in soft ground. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, Mexico, 25 August 1969; Volume 10, pp. 225–290. [Google Scholar]
- Attewell, P.B. Engineering Contract, Site investigation and Surface Movements in Tunnelling Works. In Soft-Ground Tunneling, Failures and Displacement. Panamerican Conference on Soil Mechanics and Foundation Engineering; A.A. Balkema: Rotterdam, The Netherlands, 1981; Volume 1, pp. 5–12. [Google Scholar]
- Mair, R.J.; Taylor, R.N.; Bracegirdle, A. Subsurface settlement profiles above tunnels in clays. Géotechnique 1993, 43, 315–320. [Google Scholar] [CrossRef]
- Mei, Y.; Song, Q. Analytical Solution for Settlement of Homogeneous Structure where the Tunnel Passes Underneath and Its Application. KSCE J. Civ. Eng. 2021, 25, 3556–3567. [Google Scholar] [CrossRef]
- Sagaseta, C. Analysis of undrained soil deformation due to ground loss. Geotechnique 1987, 37, 301–320. [Google Scholar] [CrossRef]
- Sagaseta, C. Discussion: Analysis of undrained soil deformation due to ground loss. Geotechnique 1988, 38, 647–649. [Google Scholar] [CrossRef]
- Loganathan, N.; Poulos, H.G. Analytical Prediction for Tunneling-Induced Ground Movements in Clays. J. Geotech. Geoenviron. Eng. 1998, 124, 846–856. [Google Scholar] [CrossRef]
- Lin, Q.; Lu, D.; Lei, C.; Tian, Y.; Gong, Q.; Du, X. Model test study on the stability of cobble strata during shield under-crossing. Tunn. Undergr. Space Technol. 2021, 110, 103807. [Google Scholar] [CrossRef]
- Cheng, Q.X.; Lu, A.Z.; Yin, C.L. Analytical Stress Solutions for a Deep Buried Circular Tunnel under an Unsteady Temperature Field. Rock Mech. Rock Eng. 2021, 54, 1355–1368. [Google Scholar] [CrossRef]
- Zheng, G.; Yang, X.; Zhou, H.; Du, Y.; Sun, J.; Yu, X. A simplified prediction method for evaluating tunnel displacement induced by laterally adjacent excavation. Comput. Geotech. 2018, 95, 119–128. [Google Scholar] [CrossRef]
- Lu, P.; Yuan, D.; Chen, J.; Jin, D.; Wu, J.; Luo, W. Face Stability Analysis of Slurry Shield Tunnels in Rock-Soil Interface Mixed Ground. KSCE J. Civ. Eng. 2021, 25, 2250–2260. [Google Scholar] [CrossRef]
- Pan, H.; Tong, L.; Wang, Z.; Yang, T. Effects of Soil—Cement Mixing Wall Construction on Adjacent Shield Tunnel Linings in Soft Soil. Arab. J. Sci. Eng. 2022, 1–15. [Google Scholar] [CrossRef]
- Zhang, D.-M.; Liu, Z.-S.; Wang, R.-L. Influence of grouting on rehabilitation of an over-deformed operating shield tunnel lining in soft clay. Acta Geotech. 2018, 14, 1227–1247. [Google Scholar] [CrossRef]
- Qi, W.; Yang, Z.; Jiang, Y.; Shao, X.; Yang, X.; He, Q. Structural Deformation of Existing Horseshoe-Shaped Tunnels by Shield Overcrossing. KSCE J. Civ. Eng. 2020, 25, 735–749. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, L.; Peng, T.; Wang, H.; Zhang, Y.; Guo, L. Model Testing on Failure Mechanism of Tunnel Face in Sandy Cobble Stratum. Arab. J. Sci. Eng. 2020, 45, 4077–4089. [Google Scholar] [CrossRef]
- Dai, X.; Cai, J.; Diao, Y.; Huo, H.; Xu, G. Influence of tunnelling on the deformation of the overlying excavation bracing system and analysis of countermeasures. Comput. Geotech. 2021, 134, 104089. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Y.; Cao, M.; Wang, Z. Study on Excavation Sequence of Pilot Tunnels for a Rectangular Tunnel Using Numerical Simulation and Field Monitoring Method. Rock Mech. Rock Eng. 2022, 55, 3507–3523. [Google Scholar] [CrossRef]
- Yuan, B.; Chen, W.; Zhao, J.; Yang, F.; Luo, Q.; Chen, T. The Effect of Organic and Inorganic Modifiers on the Physical Properties of Granite Residual Soil. Adv. Mater. Sci. Eng. 2022, 2022, 9542258. [Google Scholar] [CrossRef]
- Lee, H.; Choi, H.; Choi, S.-W.; Chang, S.-H.; Kang, T.-H.; Lee, C. Numerical Simulation of EPB Shield Tunnelling with TBM Operational Condition Control Using Coupled DEM-FDM. Appl. Sci. 2021, 11, 2551. [Google Scholar] [CrossRef]
- Qian, J.-G.; Li, W.-Y.; Yin, Z.-Y.; Yang, Y. Influences of buried depth and grain size distribution on seepage erosion in granular soils around tunnel by coupled CFD-DEM approach. Transp. Geotech. 2021, 29, 100574. [Google Scholar] [CrossRef]
- Wu, C.S. Study on the Ground Deformation Induced by Large Diameter Shield Tunnelling Construction. Ph.D. Thesis, School of Transportation Southeast University, Nanjing, China, October 2018. (In Chinese). [Google Scholar]
- Zhang, Z.M.; Lin, C.G.; Wu, S.M.; Liu, G.S.; Wang, C.S.; Xie, W.B. Analysis and control of ground settlement of embankments in construction of cross-river shield tunnels. Chin. J. Geotech. 2011, 33, 977–984. (In Chinese) [Google Scholar]

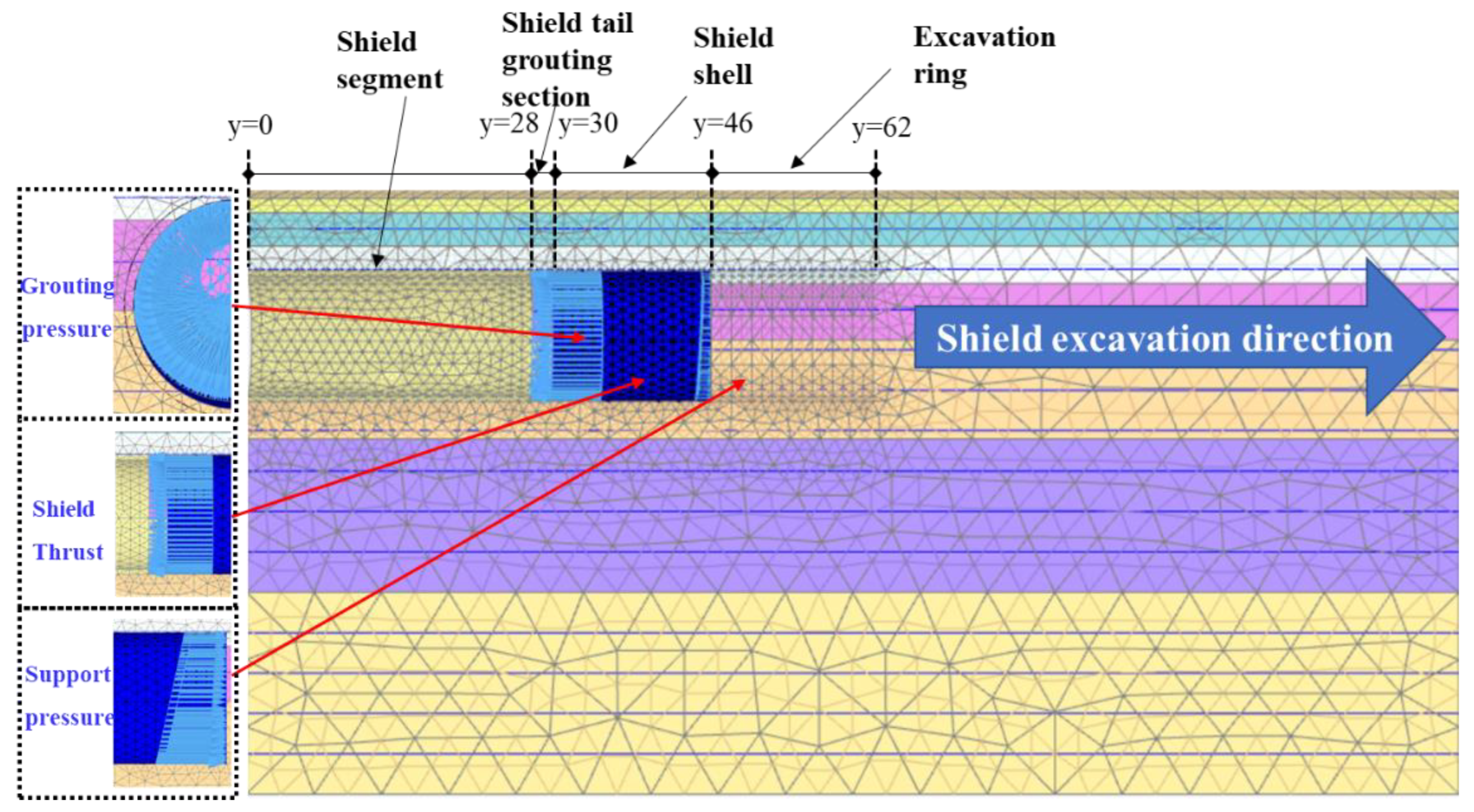



| Phase | Shield Position | Main Simulation Content |
|---|---|---|
| 0 | initial step | geo-stress balance, generated stress field |
| 1 | the shield machine is located at y = 46 m | stratum loss in an initial state; grouting pressure at shield tail; excavation face support pressure |
| 2 | the shield machine is located at y = 48 m | stratum loss; grouting pressure at shield tail; excavation face support pressure; shield forward thrust |
| … | … | … |
| 10 | the shield machine is located at y = 62 m | stratum loss; grouting pressure at shield tail; excavation face support pressure; shield forward thrust |
| Soil Horizon | Thickness/m | γ/(kN/m3) | c’ (kPa) | φ’/° | E/MPa | K0 | v |
|---|---|---|---|---|---|---|---|
| crushed stone fill | 1.0 | 17.0 | 10 | 30 | 40 | autonomous | 0.30 |
| miscellaneous fill | 1.4 | 18.0 | 20 | 35 | 25 | autonomous | 0.30 |
| silt clay | 3.3 | 18.5 | 20 | 30 | 35 | autonomous | 0.25 |
| silty clay | 3.7 | 17.5 | 20 | 35 | 35 | autonomous | 0.25 |
| crushed stone with cohesive soil | 5.6 | 19.0 | 20 | 30 | 30 | autonomous | 0.20 |
| fully weathered siltstone | 9.8 | 18.0 | 40 | 50 | 35 | autonomous | 0.20 |
| strongly weathered siltstone | 15.2 | 19.0 | 40 | 50 | 40 | autonomous | 0.25 |
| moderately weathered siltstone | 20.0 | 21.5 | 200 | 40 | 500 | autonomous | 0.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, Y.; Zhou, D.; Shi, W.; Zhang, Y.; Zhang, Y. Laws and Numerical Analysis of Surface Deformation Caused by Excavation of Large Diameter Slurry Shield in Upper-Soft and Lower-Hard Composite Stratum. Buildings 2022, 12, 1470. https://doi.org/10.3390/buildings12091470
Mei Y, Zhou D, Shi W, Zhang Y, Zhang Y. Laws and Numerical Analysis of Surface Deformation Caused by Excavation of Large Diameter Slurry Shield in Upper-Soft and Lower-Hard Composite Stratum. Buildings. 2022; 12(9):1470. https://doi.org/10.3390/buildings12091470
Chicago/Turabian StyleMei, Yuan, Dongbo Zhou, Wenyan Shi, Yuhang Zhang, and Yu Zhang. 2022. "Laws and Numerical Analysis of Surface Deformation Caused by Excavation of Large Diameter Slurry Shield in Upper-Soft and Lower-Hard Composite Stratum" Buildings 12, no. 9: 1470. https://doi.org/10.3390/buildings12091470
APA StyleMei, Y., Zhou, D., Shi, W., Zhang, Y., & Zhang, Y. (2022). Laws and Numerical Analysis of Surface Deformation Caused by Excavation of Large Diameter Slurry Shield in Upper-Soft and Lower-Hard Composite Stratum. Buildings, 12(9), 1470. https://doi.org/10.3390/buildings12091470





