Location Optimization of Tower Cranes on High-Rise Modular Housing Projects
Abstract
:1. Introduction
2. Related Research Studies
2.1. Layout Planning of Tower Cranes in Traditional Buildings
2.2. Tower Crane Layout Planning in Modular Buildings
2.3. Relevant Algorithms in Tower Crane Layout Planning
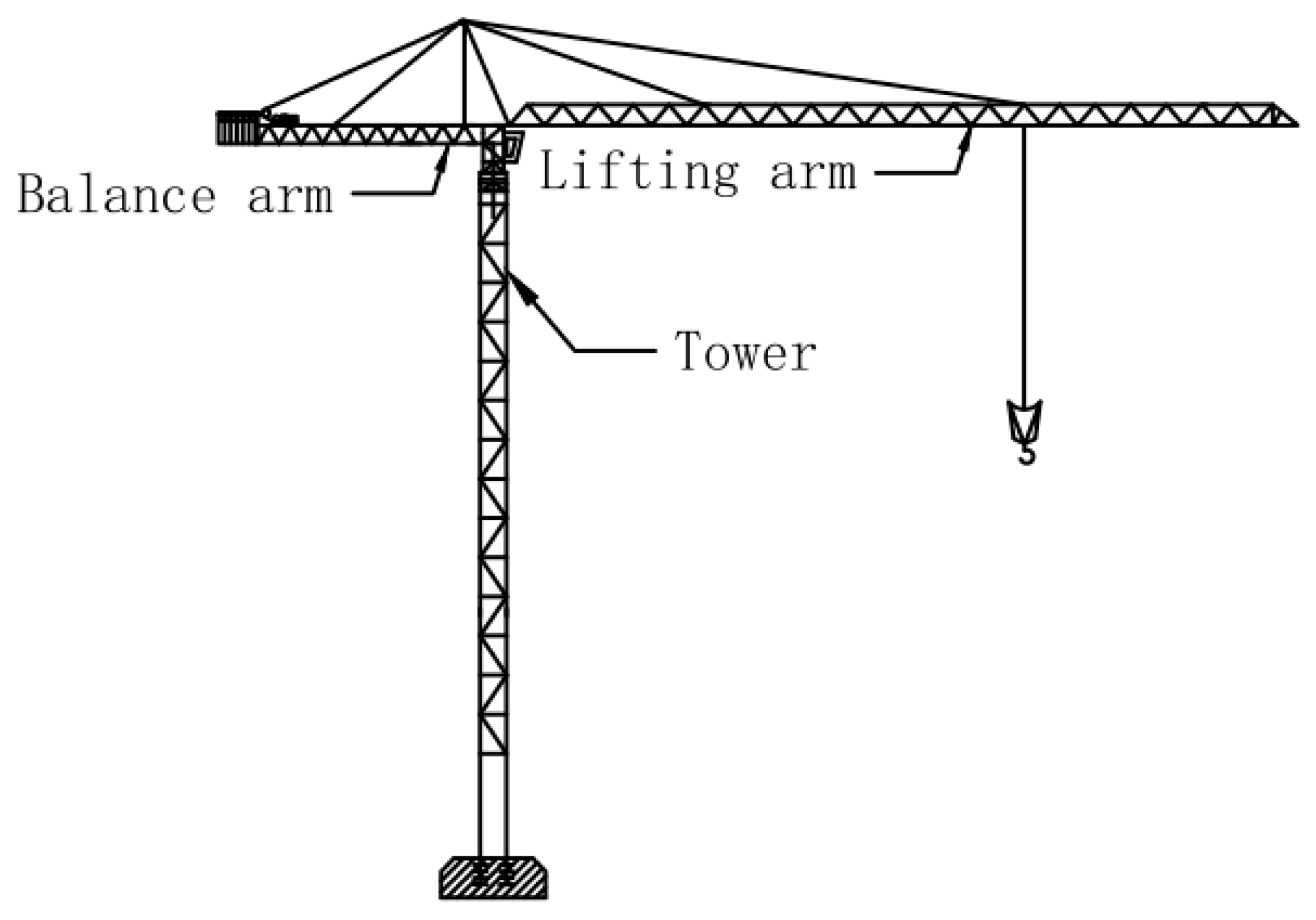
3. Information and Mathematical Models
3.1. Problem Statement and Hypothesis
- For each lifting task, the tower crane operates at the same rate under full-load and no-load conditions;
- The maximum lifting height of the tower crane meets the requirements of the building height;
- There is no collision between tower cranes in operation;
- The effect of component installation time on tower crane running time is excluded;
- Multiple components can be provided for a particular trailer dock.
3.2. Symbol Definition
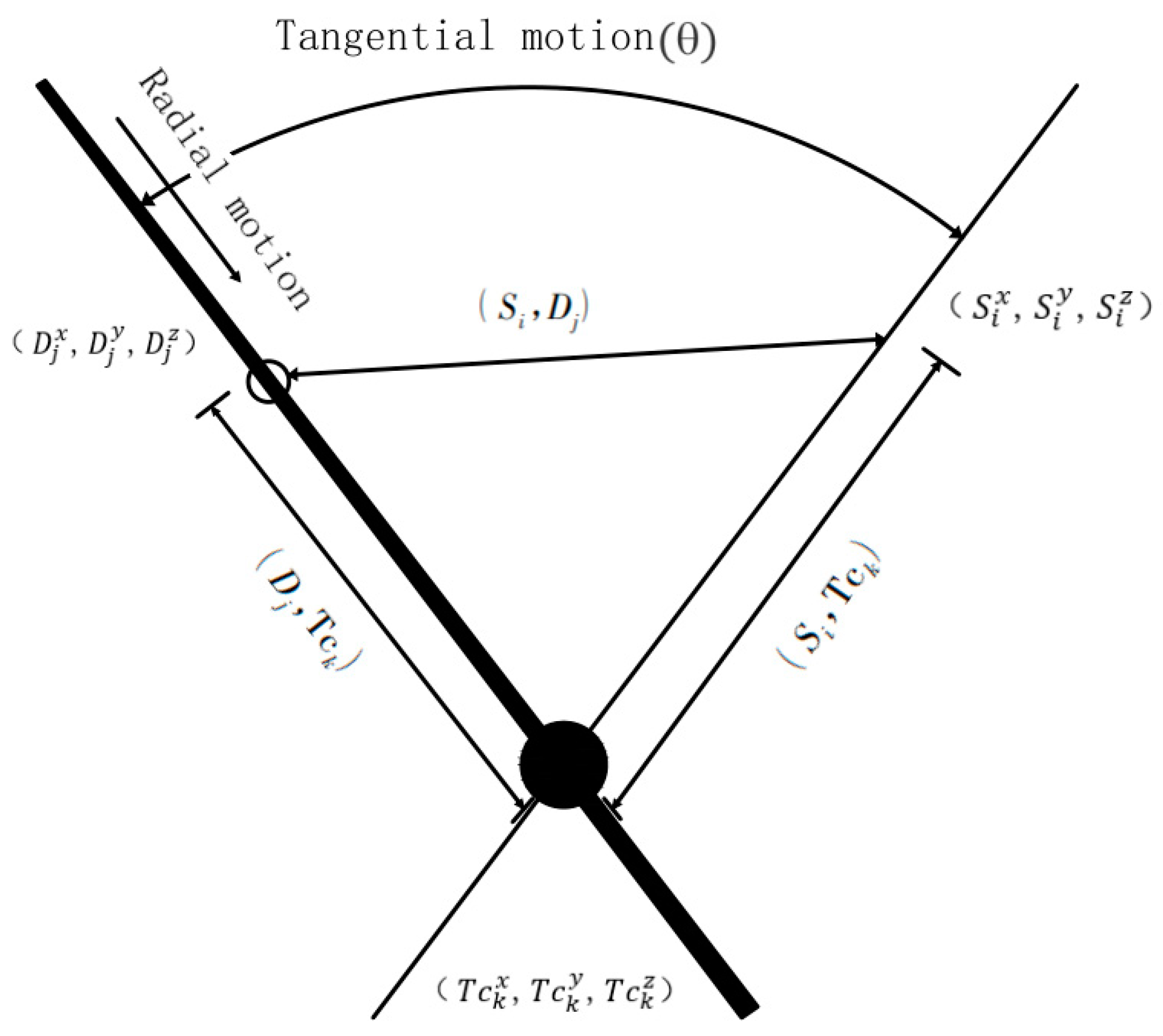
3.3. Horizontal Motion Model of Tower Crane
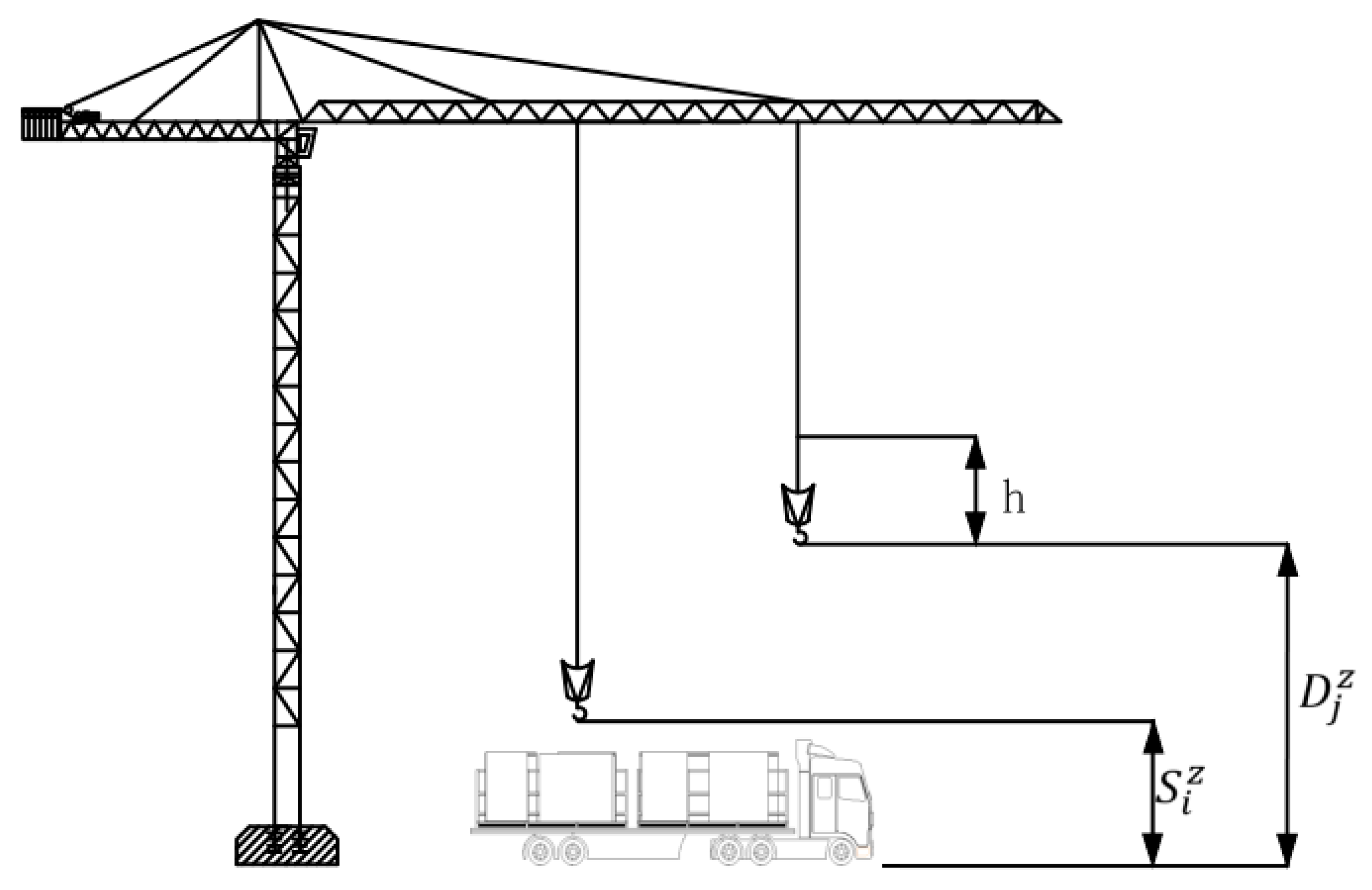
3.4. Model of Vertical Motion of Tower Crane
3.5. Decision Variables
3.6. Demand Identification and Supply of Components
3.7. Constraints on Trailer Stopping Points
3.8. Constraints on Tower Crane Position
3.9. Constraints on the Type of Tower Crane
3.10. Capacity Constraints on the Selected Tower Crane Configuration
3.11. Objective Function
4. Case Study
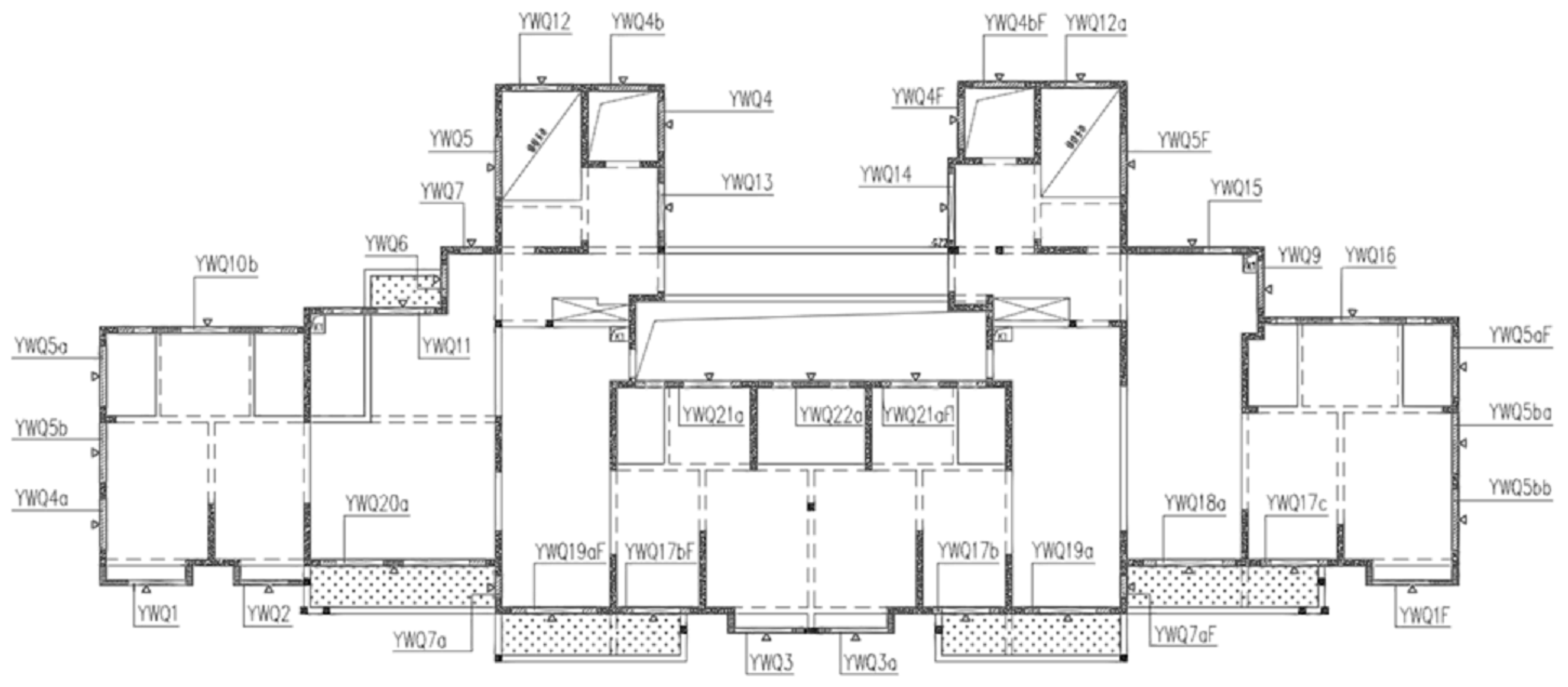
4.1. Project Overview
4.2. Data Information
4.3. Optimization Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lawson, R.M.; Ogden, R.G. Application of modular construction in high-rise buildings. J. Archit. Eng. 2012, 18, 148–154. [Google Scholar] [CrossRef]
- Shan, S.; Looi, D.; Cai, Y.; Ma, P.; Chen, M.T.; Su, R.; Pan, W. Engineering modular integrated construction for high-rise building: A case study in Hong Kong. Proc. Inst. Civ. Eng.-Civ. Eng. 2019, 172, 51–57. [Google Scholar] [CrossRef]
- Zhang, Z.; Pan, W. Multi-criteria decision analysis for tower crane layout planning in high-rise modular integrated construction. Autom. Constr. 2021, 127, 103709. [Google Scholar] [CrossRef]
- Masood, R.; Lim, J.B.; González, V.A. Performance of the supply chains for New Zealand prefabricated house-building. Sustain. Cities Soc. 2021, 64, 102537. [Google Scholar] [CrossRef]
- Kaveh, A.; Vazirinia, Y. Optimization of tower crane location and material quantity between supply and demand points: A comparative study. Period. Polytech. Civ. Eng. 2018, 62, 732–745. [Google Scholar] [CrossRef] [Green Version]
- Olearczyk, J.; Al-Hussein, M.; Bouferguène, A. Evolution of the crane selection and on-site utilization process for modular construction multilifts. Autom. Constr. 2014, 43, 59–72. [Google Scholar] [CrossRef]
- Moussavi Nadoushani, Z.S.; Hammad, A.W.; Akbarnezhad, A. Location optimization of tower crane and allocation of material supply points in a construction site considering operating and rental costs. J. Constr. Eng. Manag. 2017, 143, 04016089. [Google Scholar] [CrossRef]
- Lu, Y.; Zhu, Y. Integrating hoisting efficiency into construction site layout plan model for prefabricated construction. J. Constr. Eng. Manag. 2021, 147, 04021130. [Google Scholar] [CrossRef]
- Hyun, H.; Park, M.; Lee, D.; Lee, J. Tower crane location optimization for heavy unit lifting in high-rise modular construction. Buildings 2021, 11, 121. [Google Scholar] [CrossRef]
- Ji, Y.; Leite, F. Optimized planning approach for multiple tower cranes and material supply points using mixed-integer programming. J. Constr. Eng. Manag. 2020, 146, 04020007. [Google Scholar] [CrossRef]
- Jaillon, L.; Poon, C.S. The evolution of prefabricated residential building systems in Hong Kong: A review of the public and the private sector. Autom. Constr. 2009, 18, 239–248. [Google Scholar] [CrossRef]
- Smith, R.E. Prefab Architecture: A Guide to Modular Design and Construction; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 3–20. [Google Scholar]
- Riga, K.; Jahr, K.; Thielen, C.; Borrmann, A. Mixed integer programming for dynamic tower crane and storage area optimization on construction sites. Autom. Constr. 2020, 120, 103259. [Google Scholar] [CrossRef]
- Thomas, H.R.; Ellis, R.D., Jr. Construction site management and labor productivity improvement: How to improve the bottom line and shorten the project schedule. Am. Soc. Civ. Eng. 2017. [Google Scholar] [CrossRef]
- Rodriguez-Ramos, W.E.; Francis, R.L. Single crane location optimization. J. Constr. Eng. Manag. 1983, 109, 387–397. [Google Scholar] [CrossRef]
- Zhang, P.; Harris, F.C.; Olomolaiye, P.O.; Holt, G.D. Location optimization for a group of tower cranes. J. Constr. Eng. Manag. 1999, 125, 115–122. [Google Scholar] [CrossRef]
- Huang, C.; Wong, C.K.; Tam, C.M. Optimization of tower crane and material supply locations in a high-rise building site by mixed-integer linear programming. Autom. Constr. 2011, 20, 571–580. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X.; Shou, W.; Wang, X.; Xu, B.; Kim, M.J.; Wu, P. A BIM-based approach for automated tower crane layout planning. Autom. Constr. 2015, 59, 168–178. [Google Scholar] [CrossRef]
- Marzouk, M.; Abubakr, A. Decision support for tower crane selection with building information models and genetic algorithms. Autom. Constr. 2016, 61, 1–15. [Google Scholar] [CrossRef]
- Younes, A.; Marzouk, M. Tower cranes layout planning using agent-based simulation considering activity conflicts. Autom. Constr. 2018, 93, 348–360. [Google Scholar] [CrossRef]
- Han, S.; Bouferguene, A.; Al-Hussein, M.; Hermann, U. 3D-based crane evaluation system for mobile crane operation selection on modular-based heavy construction sites. J. Constr. Eng. Manag. 2017, 143, 04017060. [Google Scholar] [CrossRef]
- Ji, Y.; Leite, F. Automated tower crane planning: Leveraging 4-dimensional BIM and rule-based checking. Autom. Constr. 2018, 93, 78–90. [Google Scholar] [CrossRef]
- Lei, Z.; Taghaddos, H.; Olearczyk, J.; Al-Hussein, M.; Hermann, U. Automated method for checking crane paths for heavy lifts in industrial projects. J. Constr. Eng. Manag. 2013, 139, 04013011. [Google Scholar] [CrossRef]
- Han, S.H.; Hasan, S.; Bouferguène, A.; Al-Hussein, M.; Kosa, J. Utilization of 3D visualization of mobile crane operations for modular construction on-site assembly. J. Manag. Eng. 2015, 31, 04014080. [Google Scholar] [CrossRef]
- Dutta, S.; Cai, Y.; Huang, L.; Zheng, J. Automatic replanning of lifting paths for robotized tower cranes in dynamic BIM environments. Autom. Constr. 2020, 110, 102998. [Google Scholar] [CrossRef]
- Zhang, Z.; Pan, W. Virtual reality supported interactive tower crane layout planning for high-rise modular integrated construction. Autom. Constr. 2021, 130, 103854. [Google Scholar] [CrossRef]
- Hussein, M.; Zayed, T. Crane operations and planning in modular integrated construction: Mixed review of literature. Autom. Constr. 2021, 122, 103466. [Google Scholar] [CrossRef]
- Thomas, H.R.; Riley, D.R.; Sanvido, V.E. Loss of labor productivity due to delivery methods and weather. J. Constr. Eng. Manag. 1999, 125, 39–46. [Google Scholar] [CrossRef]
- Loiola, E.M.; Boaventura-Netto, P.O.; Hahn, P.; Querido, Y. A survey for the quadratic assignment problem. Eur. J. Oper. Res. 2007, 176, 657–690. [Google Scholar] [CrossRef]
- Chau, K.W. A two-stage dynamic model on allocation of construction facilities with genetic algorithm. Autom. Constr. 2004, 13, 481–490. [Google Scholar] [CrossRef]
- Trevino, C.; Abdel-Raheem, M. Single tower crane allocation using ant colony optimization. In Proceedings of the ASCE International Workshop on Computing in Civil Engineering 2017, Seattle, WA, USA, 25–27 June 2017; pp. 132–140. [Google Scholar] [CrossRef]
- Easa, S.M.; Hossain, K.M. New mathematical optimization model for construction site layout. J. Constr. Eng. Manag. 2008, 134, 653–662. [Google Scholar] [CrossRef]
- Kaveh, A.; Ghazaan, M.I. A new meta-heuristic algorithm: Vibrating particles system. Sci. Iranica. Trans. A Civ. Eng. 2017, 24, 551. [Google Scholar] [CrossRef] [Green Version]
- Kaveh, A.; Vazirinia, Y. An upgraded sine cosine algorithm for tower crane selection and layout problem. Period. Polytech. Civ. Eng. 2020, 64, 325–343. [Google Scholar] [CrossRef]
- Briskorn, D.; Dienstknecht, M. Covering polygons with discs: The problem of crane selection and location on construction sites. Omega 2020, 97, 102114. [Google Scholar] [CrossRef]
- Dasović, B.; Galić, M.; Klanšek, U. Active BIM approach to optimize work facilities and tower crane locations on construction sites with repetitive operations. Buildings 2019, 9, 21. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Wong, C.K. Optimization of crane setup location and servicing schedule for urgent material requests with non-homogeneous and non-fixed material supply. Autom. Constr. 2018, 89, 183–198. [Google Scholar] [CrossRef]

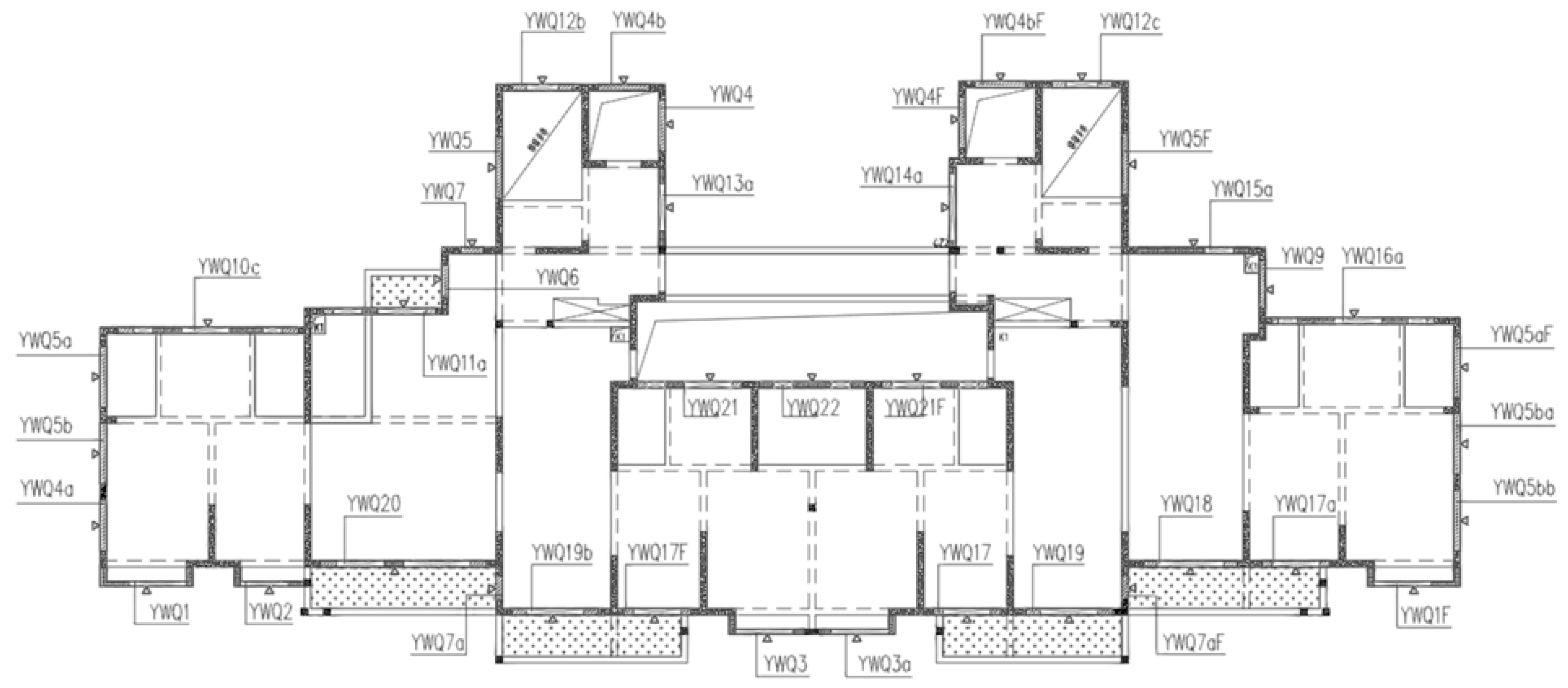
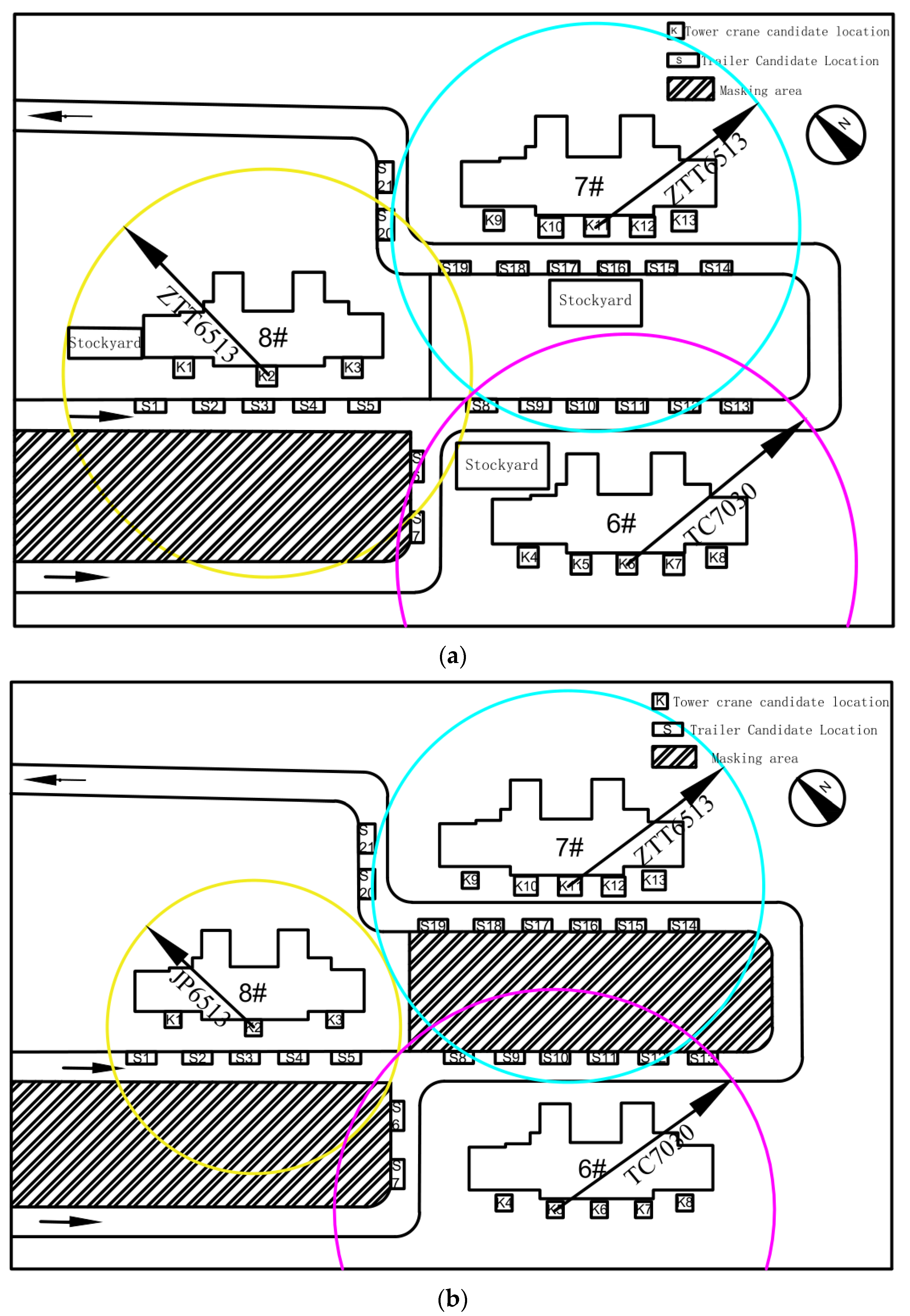
| Demand Point Serial Number | Required Component Number | Number of Components (Pcs) | Weight of Individual Components (T) | Demand Point Coordinates (x, y, z) |
|---|---|---|---|---|
| D81 | YWQ1 | 1 | 4.348 | (27.9, 53.5, 34.8) |
| D82 | YWQ1F | 1 | 4.348 | (68.7, 53.5, 34.8) |
| D83 | YWQ2 | 1 | 2.403 | (30.9, 53.5, 34.8) |
| D84 | YWQ3 | 1 | 2.461 | (48.9, 52, 34.8) |
| D85 | YWQ3a | 1 | 2.461 | (51.6, 52, 34.8) |
| D86 | YWQ4 | 1 | 2.304 | (45.3, 66, 34.8) |
| D87 | YWQ4F | 1 | 2.304 | (54.3, 66, 34.8) |
| D88 | YWQ4a | 1 | 2.248 | (27.6, 55.2, 34.8) |
| D89 | YWQ4b | 1 | 2.304 | (43.5, 68.1, 34.8) |
| D90 | YWQ4bF | 1 | 2.304 | (55.5, 68.1, 34.8) |
| D91 | YWQ5 | 1 | 2.736 | (39.9, 66, 34.8) |
| D92 | YWQ5F | 1 | 2.736 | (59.7, 66, 34.8) |
| D93 | YWQ5a | 1 | 2.736 | (27.6, 60, 34.8) |
| D94 | YWQ5aF | 1 | 2.736 | (69.9, 60, 34.8) |
| D95 | YWQ5b | 1 | 2.67 | (27.6, 55.8, 34.8) |
| D96 | YWQ5ba | 1 | 2.67 | (69.9, 57, 34.8) |
| D97 | YWQ5bb | 1 | 2.67 | (69.9, 54, 34.8) |
| D98 | YWQ6 | 1 | 1.347 | (38.1, 61.2, 34.8) |
| D99 | YWQ7 | 1 | 0.98 | (39, 63, 34.8) |
| D100 | YWQ7a | 1 | 0.958 | (39.9, 51.6, 34.8) |
| D101 | YWQ7aF | 1 | 0.958 | (59.7, 52.5, 34.8) |
| D102 | YWQ9 | 1 | 2.11 | (63.9, 61.8, 34.8) |
| D103 | YWQ10c | 1 | 4.961 | (30, 60.6, 34.8) |
| D104 | YWQ11a | 1 | 1.82 | (37.5, 61, 34.8) |
| D105 | YWQ12b | 1 | 2.046 | (40.5, 68.1, 34.8) |
| D106 | YWQ12c | 1 | 2.046 | (58.5, 68.1, 34.8) |
| D107 | YWQ13a | 1 | 2.445 | (45.3, 63, 34.8) |
| D108 | YWQ14a | 1 | 1.71 | (54, 63, 34.8) |
| D109 | YWQ15a | 1 | 4.257 | (63, 63, 34.8) |
| D110 | YWQ16a | 1 | 5.254 | (66.6, 60.6, 34.8) |
| D111 | YWQ17 | 1 | 1.82 | (54.9, 51.6, 34.8) |
| D112 | YWQ17a | 1 | 1.82 | (65.4, 52.8, 34.8) |
| D113 | YWQ17F | 1 | 1.82 | (44.7, 51.6, 34.8) |
| D114 | YWQ18 | 1 | 1.52 | (61.5, 52.8, 34.8) |
| D115 | YWQ19 | 1 | 1.59 | (58.8, 51.6, 34.8) |
| D116 | YWQ19b | 1 | 1.59 | (41.1, 51.6, 34.8) |
| D117 | YWQ20 | 1 | 3.61 | (36, 53.1, 34.8) |
| D118 | YWQ21 | 1 | 3.118 | (45, 57.5, 34.8) |
| D119 | YWQ21F | 1 | 3.118 | (57, 57.5, 34.8) |
| D120 | YWQ22 | 1 | 3.83 | (51, 57.5, 34.8) |
| Type | Model | Arm Length (m) | Lifting Weight at the End of the Jib (t) | Maximum Lifting Weight (t) | Operating Cost (Yuan/min) |
|---|---|---|---|---|---|
| KC1 | JP6513 | 30 | 5.1 | 6 | 1.48 |
| KC2 | ZTT6513 | 40 | 3.21 | 6 | 1.87 |
| KC3 | TC6513 | 50 | 2.14 | 6 | 2.16 |
| KC4 | TC7030 | 45 | 6 | 12 | 2.23 |
| Type | Model | 10 m | 20 m | 30 m | 40 m | 50 m |
|---|---|---|---|---|---|---|
| KC1 | JP6513 | 6.0 | 6.0 | 5.1 | — | — |
| KC2 | ZTT6513 | 6.0 | 6.0 | 4.8 | 3.21 | — |
| KC3 | TC6513 | 6.0 | 6.0 | 3.77 | 2.86 | 2.14 |
| KC4 | TC7030 | 12.0 | 12.0 | 9.76 | 6.93 | — |
| Type | Model | Hook Lifting Speed (m/min) | Rotation Speed of the Boom (r/min) | Radial Velocity of the Trolley (m/min) | Difficulty of Operation | |
|---|---|---|---|---|---|---|
| α | β | |||||
| KC1 | JP6513 | 36 | 0.7 | 30 | 0.2 | 0.7 |
| KC2 | ZTT6513 | 45 | 0.7 | 35 | 0.2 | 0.7 |
| KC3 | TC6513 | 40 | 0.7 | 50 | 0.2 | 0.7 |
| KC4 | TC7030 | 50 | 0.6 | 60 | 0.2 | 0.7 |
| Location | x | y | z | Location | x | y | z |
|---|---|---|---|---|---|---|---|
| K1 | 33 | 51 | 0 | K8 | 138 | 13.5 | 0 |
| K2 | 49.5 | 49.5 | 0 | K9 | 93 | 79.5 | 0 |
| K3 | 66 | 51 | 0 | K10 | 105 | 78 | 0 |
| K4 | 95 | 13.5 | 0 | K11 | 114 | 78 | 0 |
| K5 | 111 | 12 | 0 | K12 | 123 | 78 | 0 |
| K6 | 120 | 12 | 0 | K13 | 132 | 79.5 | 0 |
| K7 | 129 | 12 | 0 |
| Location | x | y | z | Location | x | y | z |
|---|---|---|---|---|---|---|---|
| S1 | 27 | 43.5 | 2 | S12 | 129.9 | 43.5 | 2 |
| S2 | 37.5 | 43.5 | 2 | S13 | 141.6 | 43.5 | 2 |
| S3 | 48 | 43.5 | 2 | S14 | 138 | 70.5 | 2 |
| S4 | 57.6 | 43.5 | 2 | S15 | 126.9 | 70.5 | 2 |
| S5 | 67.2 | 43.5 | 2 | S16 | 120.6 | 70.5 | 2 |
| S6 | 78.9 | 31.5 | 2 | S17 | 111 | 70.5 | 2 |
| S7 | 78.9 | 19.5 | 2 | S18 | 102 | 70.5 | 2 |
| S8 | 91.5 | 43.5 | 2 | S19 | 91.5 | 70.5 | 2 |
| S9 | 102 | 43.5 | 2 | S20 | 72.6 | 78.6 | 2 |
| S10 | 111 | 43.5 | 2 | S21 | 72.6 | 87.6 | 2 |
| S11 | 120.9 | 43.5 | 2 |
| Selected Tower Crane Location | Selected Tower Crane Model | Selected Trailer Stopping Points and Supply Components | Tower Crane Operation Time (min) | Tower Crane Operation Cost (Yuan) |
|---|---|---|---|---|
| KC2 | JP6513 | S1(YWQ1, YWQ2, YWQ4, YWQ4a YWQ4b, YWQ5, YWQ5a, YWQ5b YWQ7, YWQ10c, YWQ12b) S2(YWQ3, YWQ6, YWQ7a, YWQ11a YWQ13a, YWQ17F, YWQ19b, YWQ20 YWQ21) S4(YWQ3a, YWQ7aF, YWQ17, YWQ18 YWQ19, YWQ21F, YWQ22) S5(YWQ1F, YWQ4F, YWQ4bF, YWQ5F YWQ5aF, YWQ5ba, YWQ5bb, YWQ9 YWQ12c, YWQ14a, YWQ15a, YWQ16a YWQ17a) | 1699.74 | 2515.68 |
| KC6 | TC7030 | S7(YWQ1, YWQ2, YWQ20a, YWQ7a YWQ10b, YWQ5a, YWQ5b, YWQ4a) S10(YWQ19aF, YWQ17F, YWQ21aF, YWQ22a, YWQ13, YWQ4, YWQ4b, YWQ12, YWQ5, YWQ7, YWQ6, YWQ11) S11(YWQ3, YWQ3a, YWQ4bF, YWQ4F YWQ14, YWQ21a) S12(YWQ17, YWQ19a, YWQ7aF, YWQ18a YWQ17c, YWQ1F, YWQ5bb, YWQ5ba YWQ5aF, YWQ16, YWQ9, YWQ15 YWQ5F, YWQ12a) | 2854.98 | 6366.6 |
| KC11 | ZTT6513 | S14(YWQ17c, YWQ5bb, YWQ5ba, YWQ5aF, YWQ16, YWQ9, YWQ15, YWQ5F, YWQ12a, YWQ4bF YWQ4F, YWQ14) S15(YWQ3a, YWQ17, YWQ19a, YWQ7aF YWQ18a, YWQ1F, YWQ21a) S18(YWQ20a, YWQ7a, YWQ19aF, YWQ17F, YWQ3, YWQ21aF) S19(YWQ1, YWQ2, YWQ22a, YWQ13 YWQ4, YWQ4b, YWQ12, YWQ5 YWQ7, YWQ6, YWQ11, YWQ10b YWQ5a, YWQ5b, YWQ4a) | 3129.63 | 5852.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, C.; Dai, F.; Xiao, Z.; Liu, W. Location Optimization of Tower Cranes on High-Rise Modular Housing Projects. Buildings 2023, 13, 115. https://doi.org/10.3390/buildings13010115
Zhou C, Dai F, Xiao Z, Liu W. Location Optimization of Tower Cranes on High-Rise Modular Housing Projects. Buildings. 2023; 13(1):115. https://doi.org/10.3390/buildings13010115
Chicago/Turabian StyleZhou, Cong, Fu Dai, Zerui Xiao, and Wei Liu. 2023. "Location Optimization of Tower Cranes on High-Rise Modular Housing Projects" Buildings 13, no. 1: 115. https://doi.org/10.3390/buildings13010115
APA StyleZhou, C., Dai, F., Xiao, Z., & Liu, W. (2023). Location Optimization of Tower Cranes on High-Rise Modular Housing Projects. Buildings, 13(1), 115. https://doi.org/10.3390/buildings13010115





