Comparative Analysis of Data-Driven Techniques to Predict Heating and Cooling Energy Requirements of Poultry Buildings
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Characteristics of the Broiler Buildings and Physical Modeling
3.2. EnergyPlus Model
3.3. Artificial Neural Networks (ANN)
3.4. Support Vector Regressions (SVR)
3.5. Random Forest (RF)
| Algorithm 1 |
| In case A is the number of trees For a = 1 to A:
|
3.6. Model Performance Evaluation
3.6.1. Statistical Evaluation
3.6.2. Graphic Evaluation
4. Results and Discussion
4.1. EnergyPlus Model
4.2. Exploratory Factor Analysis
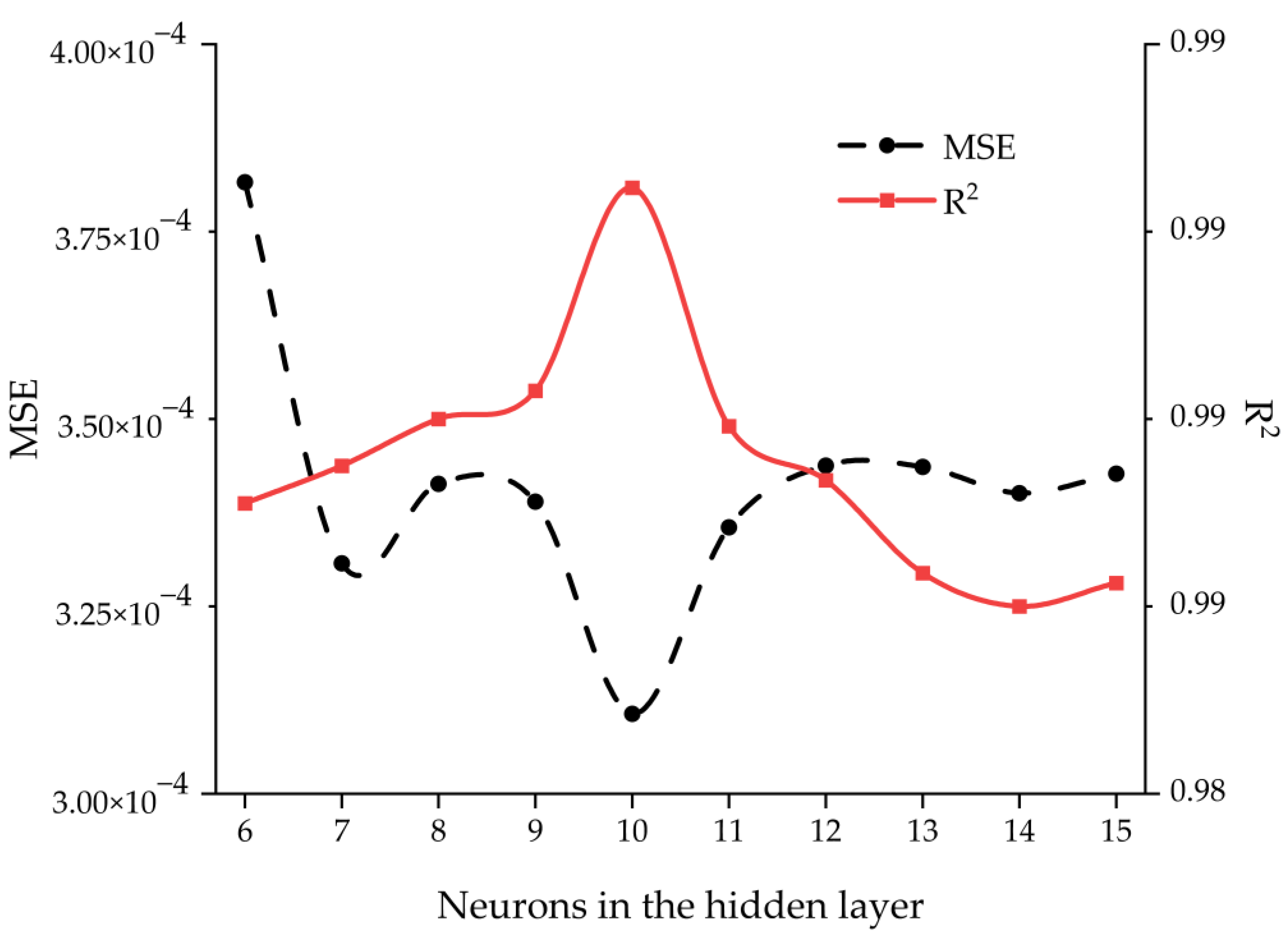
4.3. Hyper-Parametric Tuning
4.4. Comparison of the Models
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Küçüktopcu, E.; Cemek, B. The use of artificial neural networks to estimate optimum insulation thickness, energy savings, and carbon dioxide emissions. Environ. Prog. Sustain. 2021, 40, e13478. [Google Scholar] [CrossRef]
- Roy, S.S.; Roy, R.; Balas, V.E. Estimating heating load in buildings using multivariate adaptive regression splines, extreme learning machine, a hybrid model of MARS and ELM. Renew. Sustain. Energy Rev. 2018, 82, 4256–4268. [Google Scholar]
- Meng, X.; Yan, B.; Gao, Y.; Wang, J.; Zhang, W.; Long, E. Factors affecting the in situ measurement accuracy of the wall heat transfer coefficient using the heat flow meter method. Energy Build. 2015, 86, 754–765. [Google Scholar] [CrossRef]
- Huang, H.; Zhou, Y.; Huang, R.; Wu, H.; Sun, Y.; Huang, G.; Xu, T. Optimum insulation thicknesses and energy conservation of building thermal insulation materials in Chinese zone of humid subtropical climate. Sustain. Cities Soc. 2020, 52, 101840. [Google Scholar] [CrossRef]
- Açıkkalp, E.; Kandemir, S.Y. A method for determining optimum insulation thickness: Combined economic and environmental method. Therm. Sci. Eng. Prog. 2019, 11, 249–253. [Google Scholar] [CrossRef]
- Küçüktopcu, E.; Cemek, B. A study on environmental impact of insulation thickness of poultry building walls. Energy 2018, 150, 583–590. [Google Scholar] [CrossRef]
- Verichev, K.; Zamorano, M.; Carpio, M. Effects of climate change on variations in climatic zones and heating energy consumption of residential buildings in the southern Chile. Energy Build. 2020, 215, 109874. [Google Scholar] [CrossRef]
- Huo, T.; Ren, H.; Cai, W. Estimating urban residential building-related energy consumption and energy intensity in China based on improved building stock turnover model. Sci. Total Environ. 2019, 650, 427–437. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, L. Data-driven estimation of building energy consumption with multi-source heterogeneous data. Appl. Energy 2020, 268, 114965. [Google Scholar] [CrossRef]
- Balaras, C.; Droutsa, K.; Argiriou, A.; Asimakopoulos, D. Potential for energy conservation in apartment buildings. Energy Build. 2000, 31, 143–154. [Google Scholar] [CrossRef]
- Zhao, H.-x.; Magoulès, F. A review on the prediction of building energy consumption. Renew. Sustain. Energy Rev. 2012, 16, 3586–3592. [Google Scholar] [CrossRef]
- Paudel, S.; Elmitri, M.; Couturier, S.; Nguyen, P.H.; Kamphuis, R.; Lacarrière, B.; Le Corre, O. A relevant data selection method for energy consumption prediction of low energy building based on support vector machine. Energy Build. 2017, 138, 240–256. [Google Scholar] [CrossRef]
- Fumo, N.; Mago, P.; Luck, R. Methodology to estimate building energy consumption using EnergyPlus benchmark models. Energy Build. 2010, 42, 2331–2337. [Google Scholar] [CrossRef]
- Yang, J.; Fu, H.; Qin, M. Evaluation of different thermal models in EnergyPlus for calculating moisture effects on building energy consumption in different climate conditions. Procedia Eng. 2015, 121, 1635–1641. [Google Scholar] [CrossRef] [Green Version]
- Boyano, A.; Hernandez, P.; Wolf, O. Energy demands and potential savings in European office buildings: Case studies based on EnergyPlus simulations. Energy Build. 2013, 65, 19–28. [Google Scholar] [CrossRef]
- Ciancio, V.; Falasca, S.; Golasi, I.; Curci, G.; Coppi, M.; Salata, F. Influence of input climatic data on simulations of annual energy needs of a building: EnergyPlus and WRF modeling for a case study in Rome (Italy). Energies 2018, 11, 2835. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.-B.; Kim, D.D.; Kim, T. Energy performance assessment of HVAC commissioning using long-term monitoring data: A case study of the newly built office building in South Korea. Energy Build. 2019, 204, 109465. [Google Scholar] [CrossRef]
- Mathews Roy, A.; Prasanna Venkatesan, R.; Shanmugapriya, T. Simulation and analysis of a factory building’s energy consumption using eQuest software. Chem. Eng. Technol. 2021, 44, 928–933. [Google Scholar] [CrossRef]
- Farzan, H. The study of thermostat impact on energy consumption in a residential building by using TRNSYS. J. Renew. Energy Environ. 2019, 6, 15–20. [Google Scholar]
- Tsanas, A.; Xifara, A. Accurate quantitative estimation of energy performance of residential buildings using statistical machine learning tools. Energy Build. 2012, 49, 560–567. [Google Scholar] [CrossRef]
- Tang, W.; Wang, H.; Lee, X.-L.; Yang, H.-T. Machine learning approach to uncovering residential energy consumption patterns based on socioeconomic and smart meter data. Energy 2022, 240, 122500. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N. Machine learning for occupant-behavior-sensitive cooling energy consumption prediction in office buildings. Renew. Sustain. Energy Rev. 2021, 142, 110714. [Google Scholar] [CrossRef]
- Anand, P.; Deb, C.; Yan, K.; Yang, J.; Cheong, D.; Sekhar, C. Occupancy-based energy consumption modelling using machine learning algorithms for institutional buildings. Energy Build. 2021, 252, 111478. [Google Scholar] [CrossRef]
- Robinson, C.; Dilkina, B.; Hubbs, J.; Zhang, W.; Guhathakurta, S.; Brown, M.A.; Pendyala, R.M. Machine learning approaches for estimating commercial building energy consumption. Appl. Energy 2017, 208, 889–904. [Google Scholar] [CrossRef]
- Kharseh, M.; Nordell, B. Sustainable heating and cooling systems for agriculture. Int. J. Energy Res. 2011, 35, 415–422. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N.M. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Moon, J.; Kim, J. ANN-based thermal control methods for residential buildings. Build. Environ. 2010, 45, 1612–1625. [Google Scholar] [CrossRef]
- Moon, J.W.; Jung, S.K.; Lee, Y.O.; Choi, S. Prediction performance of an artificial neural network model for the amount of cooling energy consumption in hotel rooms. Energies 2015, 8, 8226–8243. [Google Scholar] [CrossRef] [Green Version]
- Deb, C.; Eang, L.S.; Yang, J.; Santamouris, M. Forecasting diurnal cooling energy load for institutional buildings using Artificial Neural Networks. Energy Build. 2016, 121, 284–297. [Google Scholar] [CrossRef]
- Melo, A.; Fossati, M.; Versage, R.; Sorgato, M.; Scalco, V.; Lamberts, R. Development and analysis of a metamodel to represent the thermal behavior of naturally ventilated and artificially air-conditioned residential buildings. Energy Build. 2016, 112, 209–221. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Mourshed, M.; Rezgui, Y. Trees vs Neurons: Comparison between random forest and ANN for high-resolution prediction of building energy consumption. Energy Build. 2017, 147, 77–89. [Google Scholar] [CrossRef]
- Li, Z.; Dai, J.; Chen, H.; Lin, B. An ANN-based fast building energy consumption prediction method for complex architectural form at the early design stage. Build. Simul. 2019, 12, 665–681. [Google Scholar] [CrossRef]
- Kalogirou, S.A.; Bojic, M. Artificial neural networks for the prediction of the energy consumption of a passive solar building. Energy 2000, 25, 479–491. [Google Scholar] [CrossRef]
- Kavaklioglu, K. Modeling and prediction of Turkey’s electricity consumption using support vector regression. Appl. Energy 2011, 88, 368–375. [Google Scholar] [CrossRef]
- Oğcu, G.; Demirel, O.F.; Zaim, S. Forecasting electricity consumption with neural networks and support vector regression. Procedia Soc. Behav. Sci. 2012, 58, 1576–1585. [Google Scholar] [CrossRef] [Green Version]
- Jain, R.K.; Smith, K.M.; Culligan, P.J.; Taylor, J.E. Forecasting energy consumption of multi-family residential buildings using support vector regression: Investigating the impact of temporal and spatial monitoring granularity on performance accuracy. Appl. Energy 2014, 123, 168–178. [Google Scholar] [CrossRef]
- Chou, J.-S.; Bui, D.-K. Modeling heating and cooling loads by artificial intelligence for energy-efficient building design. Energy Build. 2014, 82, 437–446. [Google Scholar] [CrossRef]
- Zhong, H.; Wang, J.; Jia, H.; Mu, Y.; Lv, S. Vector field-based support vector regression for building energy consumption prediction. Appl. Energy 2019, 242, 403–414. [Google Scholar] [CrossRef]
- Li, X.; Yao, R. A machine-learning-based approach to predict residential annual space heating and cooling loads considering occupant behaviour. Energy 2020, 212, 118676. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Mansour-Saatloo, A.; Mohammadi-Ivatloo, B.; Anvari-Moghaddam, A. Performance evaluation of two machine learning techniques in heating and cooling loads forecasting of residential buildings. Appl. Sci. 2020, 10, 3829. [Google Scholar] [CrossRef]
- Hansen, L.; Salamon, P. Neural network ensembles. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 993–1001. [Google Scholar] [CrossRef] [Green Version]
- Dietterich, T.G. Ensemble methods in machine learning. In Multiple Classifier Systems; Kittler, J., Roli, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1857, pp. 1–15. [Google Scholar]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar]
- Statnikov, A.; Wang, L.; Aliferis, C.F. A comprehensive comparison of random forests and support vector machines for microarray-based cancer classification. BMC Bioinform. 2008, 9, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Lahouar, A.; Slama, J.B.H. Day-ahead load forecast using random forest and expert input selection. Energy Convers. Manag. 2015, 103, 1040–1051. [Google Scholar]
- Yan, L.; Hu, P.; Li, C.; Yao, Y.; Xing, L.; Lei, F.; Zhu, N. The performance prediction of ground source heat pump system based on monitoring data and data mining technology. Energy Build. 2016, 127, 1085–1095. [Google Scholar] [CrossRef]
- National Chicken Council Animal Welfare Guidelines and Audit Checklist for Broilers. Available online: https://www.nationalchickencouncil.org/policy/animal-welfare/ (accessed on 15 November 2022).
- CIGR. Heat and moisture production at animal and house level. In 4th Report of Working Group on Climatization of Animal Houses; Pedersen, S., Sallvik, K., Eds.; Danish Institute of Agricultural Sciences: Horsens, Denmark, 2002. [Google Scholar]
- Ross 308 Performance Objectives. 2019. Available online: http://eu.aviagen.com/tech-center/download/1339/Ross308-308FF-BroilerPO2019-EN.pdf (accessed on 15 November 2022).
- Wang, Y.; Li, B.; Liang, C.; Zheng, W. Dynamic simulation of thermal load and energy efficiency in poultry buildings in the cold zone of China. Comput. Electron. Agric. 2020, 168, 105127. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar]
- Jalili Ghazi Zade, M.; Noori, R. Prediction of municipal solid waste generation by use of artificial neural network: A case study of Mashhad. Int. J. Environ. Res. 2008, 2, 13–22. [Google Scholar]
- Atkinson, P.M.; Tatnall, A.R. Introduction neural networks in remote sensing. Int. J. Remote Sens. 1997, 18, 699–709. [Google Scholar] [CrossRef]
- Haykin, S.S. Neural Networks and Learning Machines, 3rd ed.; Pearson Education: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Yadav, N.; Yadav, A.; Kumar, M. An Introduction to Neural Network Methods for Differential Equations, 1st ed.; Springer: Dordrecht, The Netherlands, 2015. [Google Scholar]
- Gholami, R.; Fakhari, N. Support Vector Machine: Principles, Parameters, and Applications. In Handbook of Neural Computation; Samui, P., Sekhar, S., Balas, V.E., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 515–535. [Google Scholar]
- Hosseinzadeh, A.; Moeinaddini, A.; Ghasemzadeh, A. Investigating factors affecting severity of large truck-involved crashes: Comparison of the SVM and random parameter logit model. J. Saf. Res. 2021, 77, 151–160. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Vapnik, V.; Golowich, S.E.; Smola, A.J. Support vector method for function approximation, regression estimation and signal processing. In Proceedings of the 9th International Conference on Neural Information Processing Systems, Denver, CO, USA, 3–5 December 1996; Mozer, M.C., Jordan, M., Petsche, T., Eds.; MIT Press: Cambridge, UK, 1996; pp. 281–287. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Cengel, Y.A.; Boles, M.A.; Kanoğlu, M. Thermodynamics: An Engineering Approach, 5th ed.; McGraw Hill: New York, NY, USA, 2006. [Google Scholar]
- Williams, B.; Onsman, A.; Brown, T. Exploratory factor analysis: A five-step guide for novices. Australas. J. Paramed. 2010, 8, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Henson, R.K.; Roberts, J.K. Use of exploratory factor analysis in published research: Common errors and some comment on improved practice. Educ. Psychol. Meas. 2006, 66, 393–416. [Google Scholar] [CrossRef] [Green Version]
- Tabachnick, B.G.; Fidell, L.S. Using Multivariate Statistics, 5th ed.; Allyn & Bacon/Pearson Education: Boston, MA, USA, 2007. [Google Scholar]
- Hecht-Nielsen, R. Theory of the backpropagation neural network. In Neural Networks for Perception; Wechsler, H., Ed.; Academic Press: Cambridge, MA, USA, 1992; pp. 65–93. [Google Scholar]
- Rafiq, M.; Bugmann, G.; Easterbrook, D. Neural network design for engineering applications. Comput. Struct. 2001, 79, 1541–1552. [Google Scholar] [CrossRef]
- Li, Q.; Meng, Q.; Cai, J.; Yoshino, H.; Mochida, A. Predicting hourly cooling load in the building: A comparison of support vector machine and different artificial neural networks. Energy Convers. Manag. 2009, 50, 90–96. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Yu, P.-S.; Chen, S.-T.; Chang, I.F. Support vector regression for real-time flood stage forecasting. J. Hydrol. 2006, 328, 704–716. [Google Scholar] [CrossRef]
- Daviran, M.; Maghsoudi, A.; Ghezelbash, R.; Pradhan, B. A new strategy for spatial predictive mapping of mineral prospectivity: Automated hyperparameter tuning of random forest approach. Comput. Geosci. 2021, 148, 104688. [Google Scholar] [CrossRef]
- Tien Bui, D.; Moayedi, H.; Anastasios, D.; Kok Foong, L. Predicting heating and cooling loads in energy-efficient buildings using two hybrid intelligent models. Appl. Sci. 2019, 9, 3543. [Google Scholar] [CrossRef] [Green Version]
- Irshad, K.; Zahir, M.H.; Shaik, M.S.; Ali, A. Buildings’ Heating and Cooling Load Prediction for Hot Arid Climates: A Novel Intelligent Data-Driven Approach. Buildings 2022, 12, 1677. [Google Scholar] [CrossRef]
- Sholahudin, S.; Han, H. Simplified dynamic neural network model to predict heating load of a building using Taguchi method. Energy 2016, 115, 1672–1678. [Google Scholar] [CrossRef]
- Kwok, S.S.; Lee, E.W. A study of the importance of occupancy to building cooling load in prediction by intelligent approach. Energy Convers. Manag. 2011, 52, 2555–2564. [Google Scholar] [CrossRef]
- Jihad, A.S.; Tahiri, M. Forecasting the heating and cooling load of residential buildings by using a learning algorithm “gradient descent”, Morocco. Case Stud. Therm. Eng. 2018, 12, 85–93. [Google Scholar] [CrossRef]
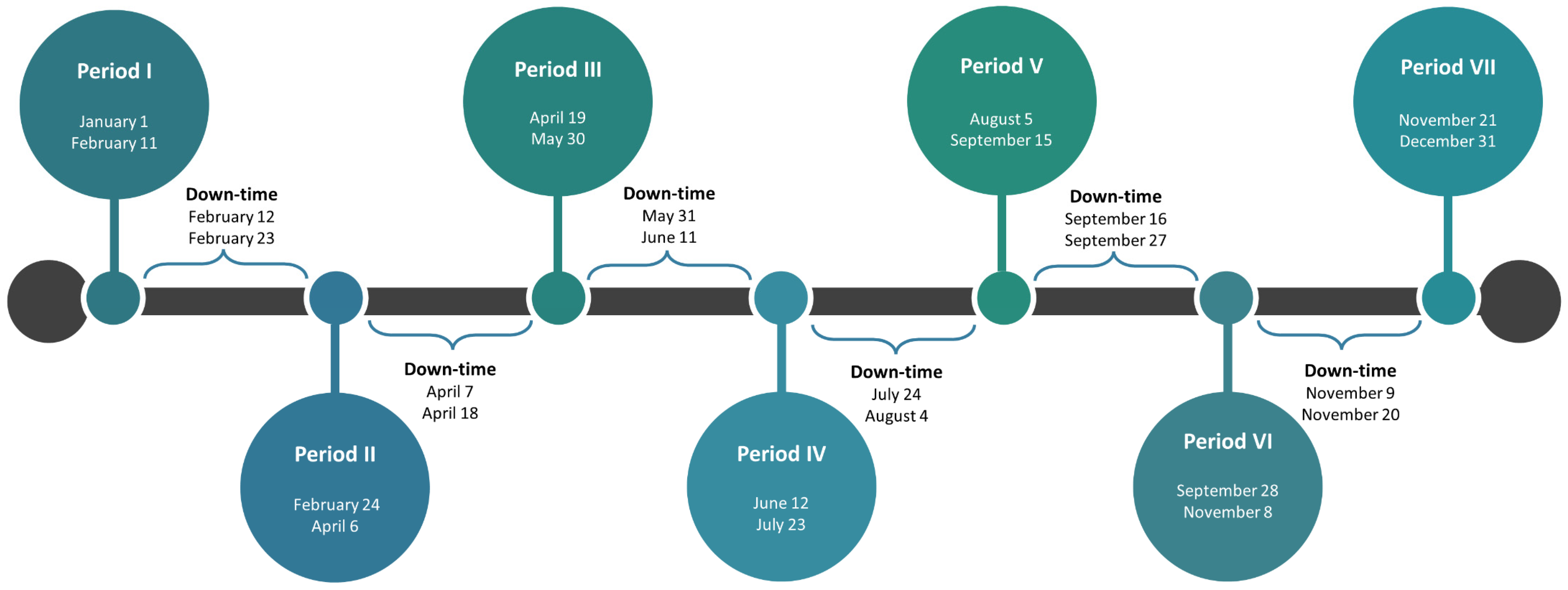









| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | |
|---|---|---|---|---|---|
| Capacity (birds) | 12,000 | 15,000 | 20,000 | 23,000 | 30,000 |
| Ground area (m2) | 750 | 960 | 1260 | 1400 | 1920 |
| Wall area (m2) | 360.5 | 383.6 | 419.2 | 467.2 | 546.8 |
| Roof area (m2) | 768 | 976 | 1274.4 | 1416 | 1936.8 |
| Inlet area (m2) | 37.5 | 48 | 63 | 70 | 96 |
| Door area (m2) | 10 | 10 | 10 | 10 | 10 |
| Weeks | Base Temperatures (°C) |
|---|---|
| Week 1 | 32–34 |
| Week 2 | 28–32 |
| Week 3 | 26–28 |
| Week 4 | 24–26 |
| Week 5 | 18–24 |
| Week 6 | 18–24 |
| Wall Type | Wall Component | Thickness (m) | Conductivity (W/mK) | Specific Heat (J/KgK) | Density (Kg/m3) |
|---|---|---|---|---|---|
| Wall 1 | Lightweight Metallic Cladding | 0.006 | 0.290 | 1000 | 1250 |
| Insulation | Various | Various | 1400 | 35 | |
| Lightweight Metallic Cladding | 0.006 | 0.290 | 1000 | 1250 | |
| Wall 2 | Brickwork outer | 0.006 | 0.290 | 1000 | 1250 |
| Insulation | Various | Various | 1400 | 35 | |
| Concrete block | 0.100 | 0.510 | 1000 | 1400 | |
| Gypsum plastering | 0.015 | 0.400 | 1000 | 1000 | |
| Wall 3 | Cement plaster | 0.020 | 0.720 | 840 | 1760 |
| Insulation | Various | Various | 1400 | 35 | |
| Brick-aerated | 0.200 | 0.300 | 840 | 1000 | |
| Gypsum plastering | 0.020 | 0.400 | 1000 | 1000 |
| TSE825 | Köppen-Geiger | Province | Altitude (m) | Longitude | Latitude |
|---|---|---|---|---|---|
| Zone1 | Csa | Antalya | 47 | 30°42′ | 36°53′ |
| Zone 2 | Cfa | Samsun | 04 | 36°20′ | 41°17′ |
| Zone 3 | Csb | Ankara | 891 | 35°52′ | 39°56′ |
| Zone4 | Dsb | Erzurum | 1860 | 41°17′ | 39°55′ |
| Models | Training | Validation | Testing | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (kWh) | MAPE (%) | R2 | RMSE (kWh) | MAPE (%) | R2 | RMSE (kWh) | MAPE(%) | ||
| Heating loads | ANN | 0.987 | 0.795 | 4.147 | 0.987 | 0.802 | 4.148 | 0.986 | 0.806 | 4.152 |
| SVR | 0.988 | 0.732 | 3.655 | 0.988 | 0.737 | 3.730 | 0.988 | 0.741 | 3.729 | |
| RF | 0.990 | 0.692 | 3.245 | 0.990 | 0.697 | 3.334 | 0.990 | 0.695 | 3.328 | |
| Cooling loads | ANN | 0.995 | 7.116 | 3.383 | 0.994 | 7.131 | 3.415 | 0.994 | 7.149 | 3.466 |
| SVR | 0.995 | 6.923 | 3.171 | 0.995 | 6.956 | 3.198 | 0.995 | 6.979 | 3.209 | |
| RF | 0.997 | 6.476 | 2.603 | 0.996 | 6.442 | 2.612 | 0.996 | 6.514 | 2.624 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Küçüktopcu, E. Comparative Analysis of Data-Driven Techniques to Predict Heating and Cooling Energy Requirements of Poultry Buildings. Buildings 2023, 13, 142. https://doi.org/10.3390/buildings13010142
Küçüktopcu E. Comparative Analysis of Data-Driven Techniques to Predict Heating and Cooling Energy Requirements of Poultry Buildings. Buildings. 2023; 13(1):142. https://doi.org/10.3390/buildings13010142
Chicago/Turabian StyleKüçüktopcu, Erdem. 2023. "Comparative Analysis of Data-Driven Techniques to Predict Heating and Cooling Energy Requirements of Poultry Buildings" Buildings 13, no. 1: 142. https://doi.org/10.3390/buildings13010142





