Influence of the Vertical Component of Yangbi Ground Motion on the Dynamic Response of RC Frame and Brick-Concrete Structure
Abstract
:1. Introduction
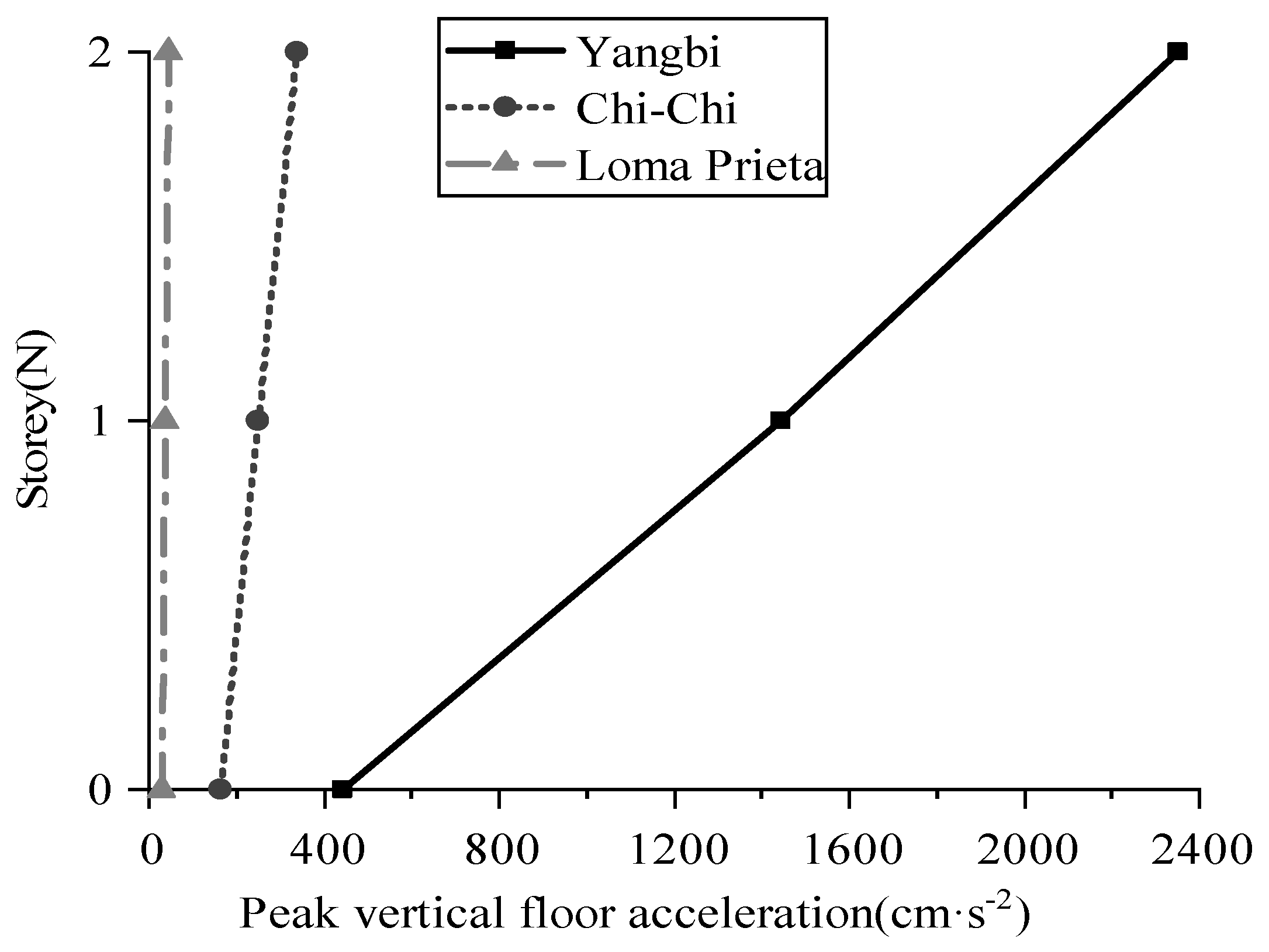
2. Ground Motion Waveform Information
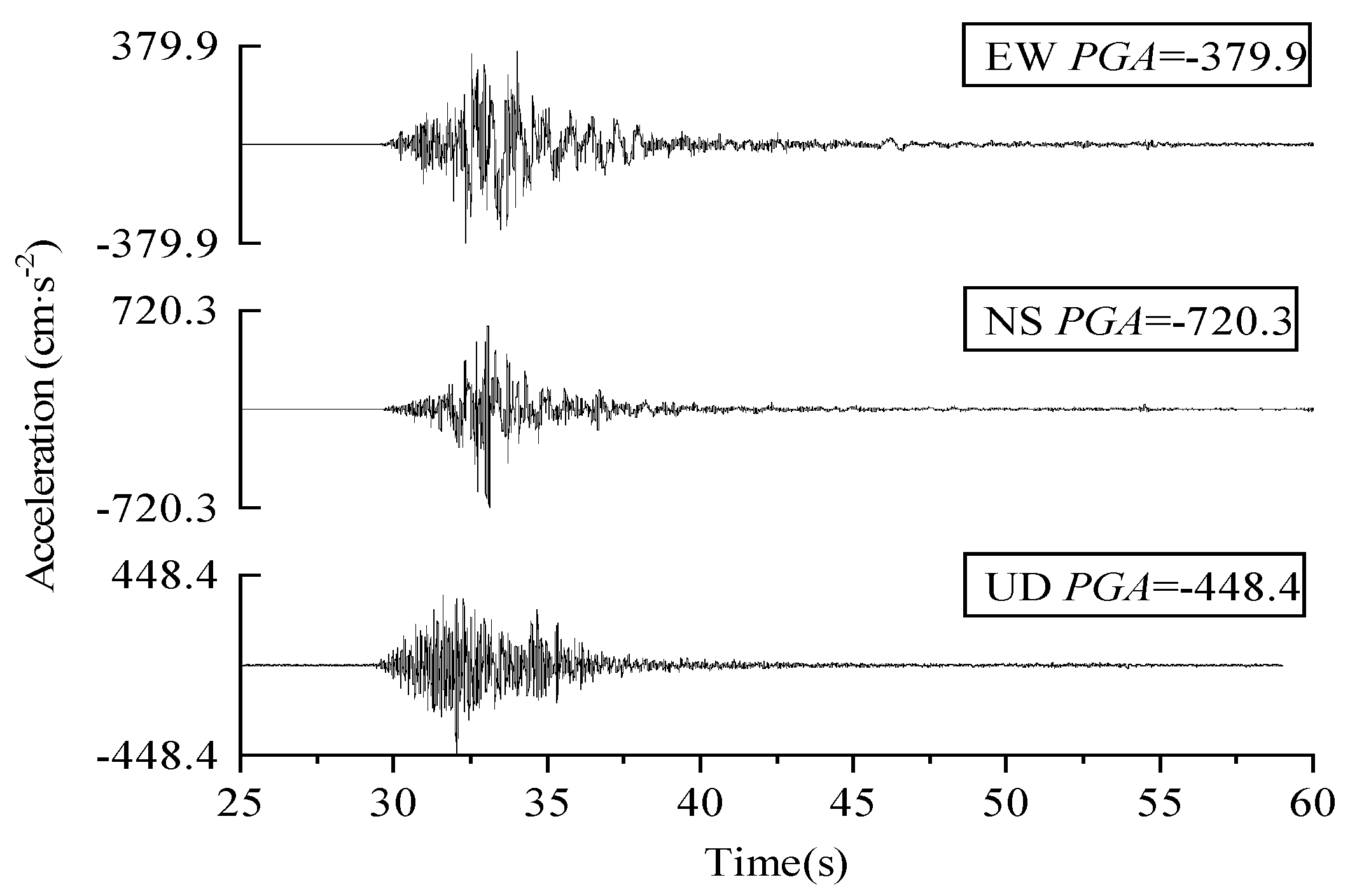
2.1. Yangbi Ground Motion
2.2. Chi-Chi and Loma Prieta Ground Motion
3. Dynamic Time History Analysis of RC Frame Structure
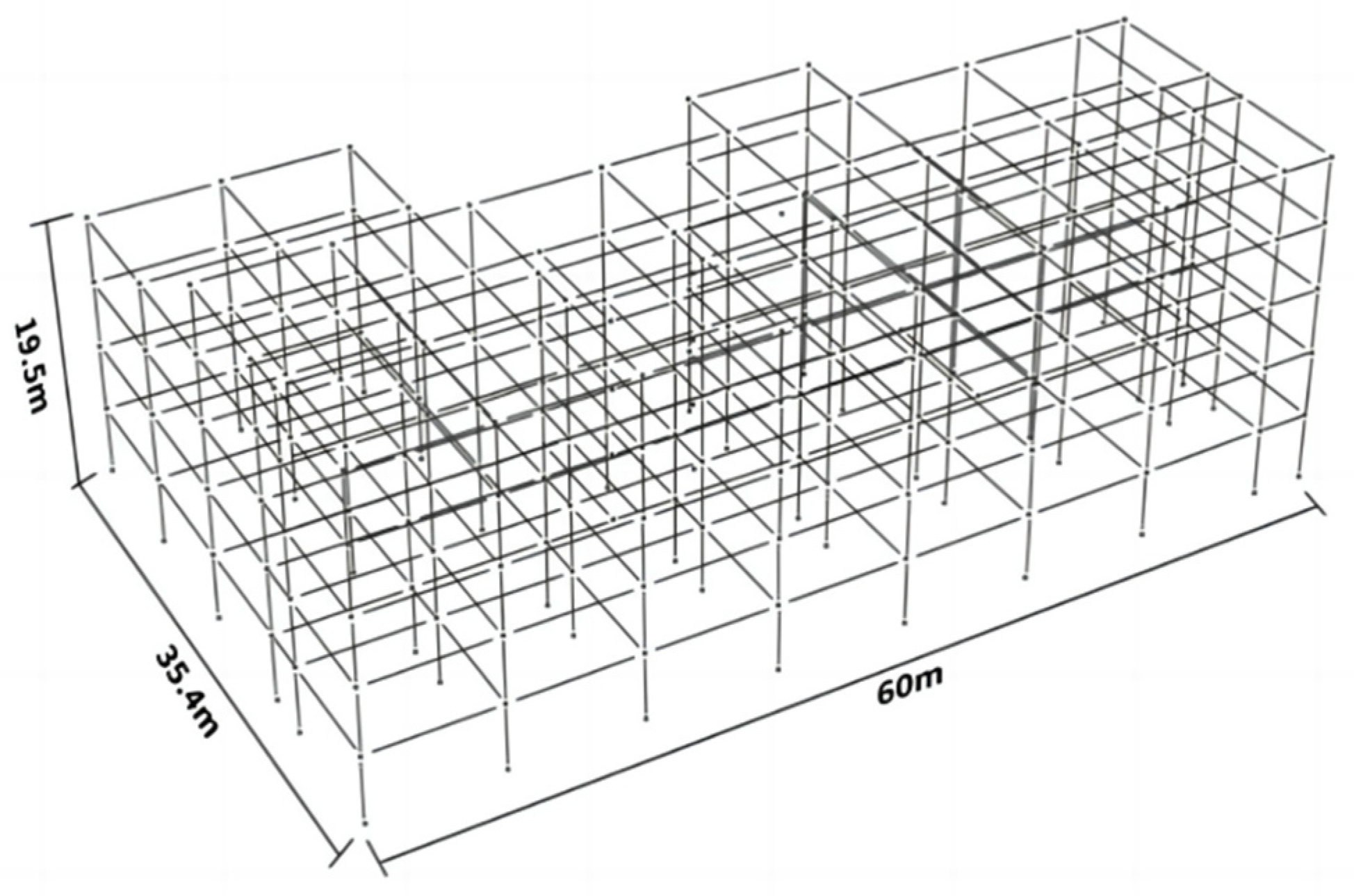
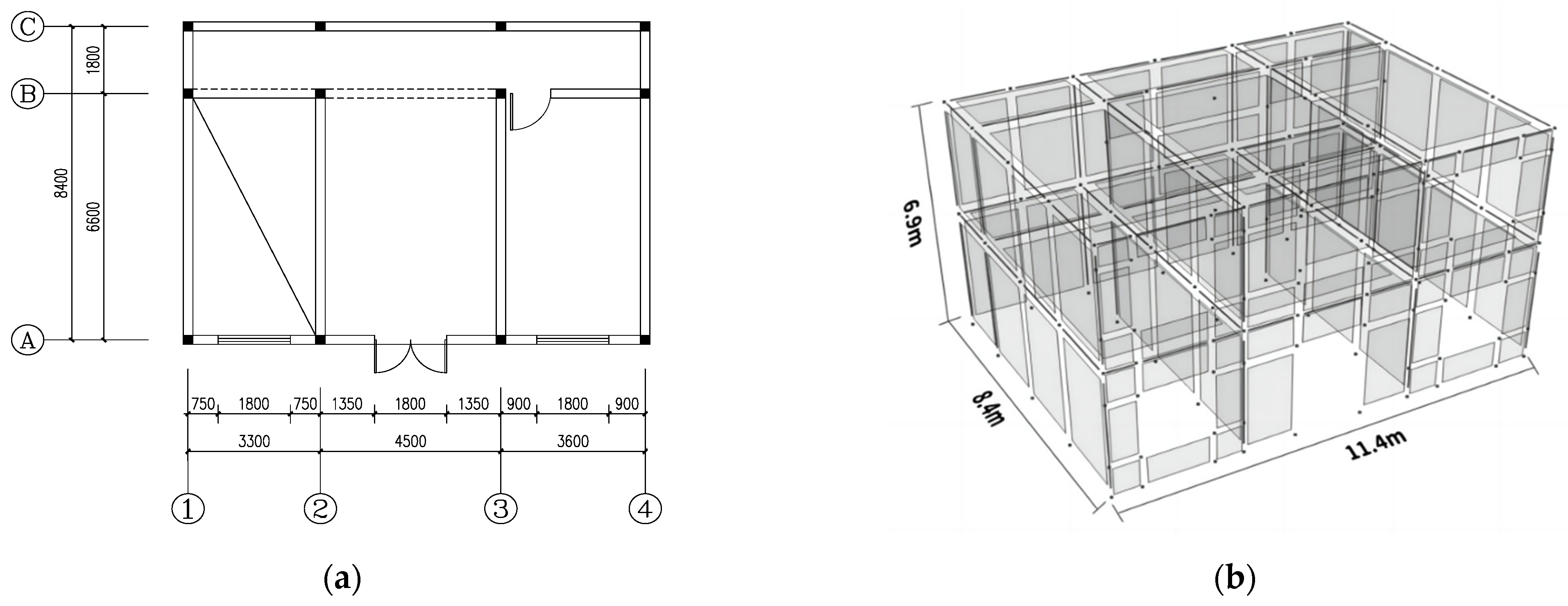
3.1. The Information on the RC Frame Structure
3.2. Comparison of Top-Floor Displacement
3.3. Comparison of Top-Floor Acceleration
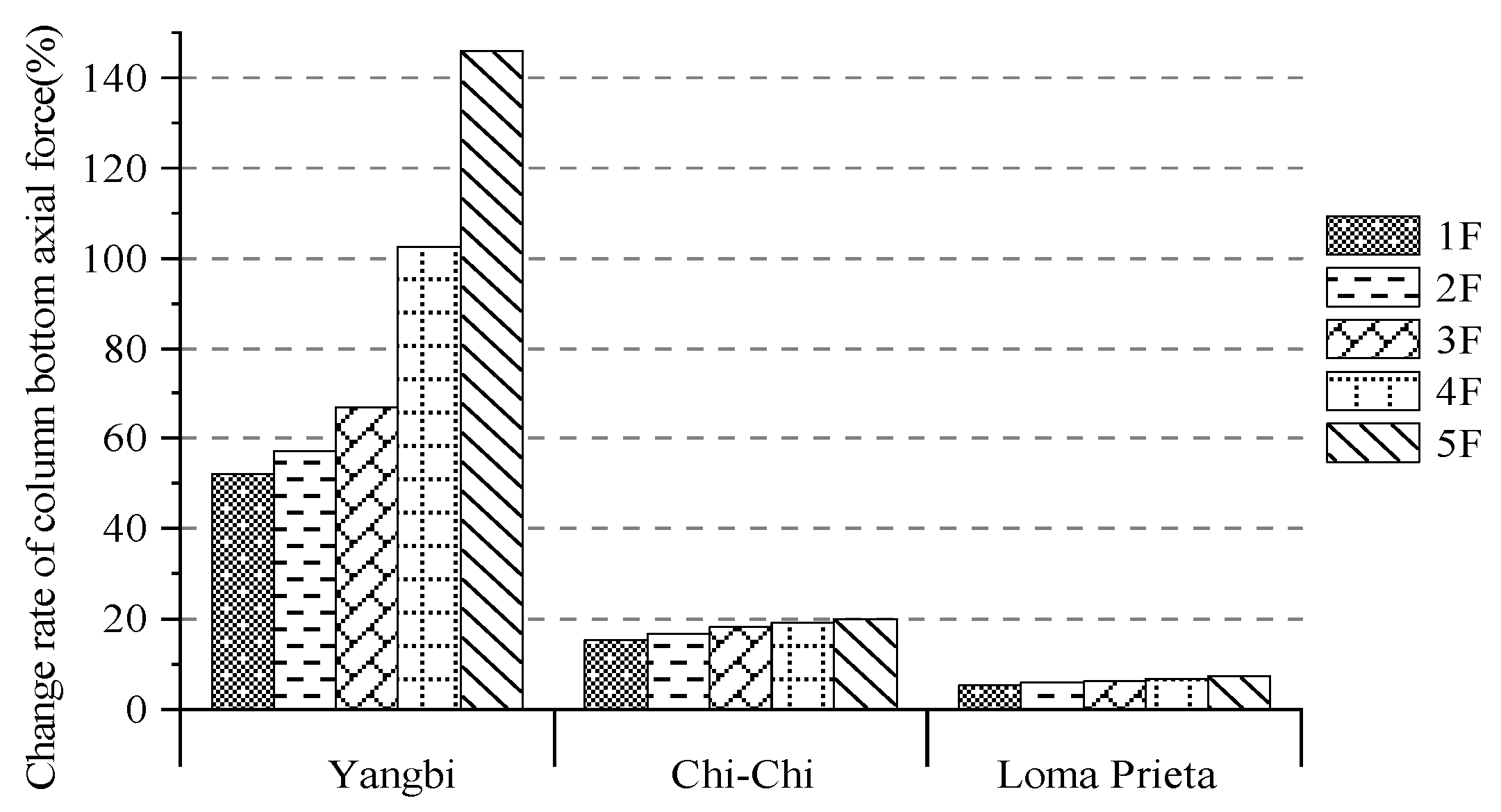
3.4. Comparison of Axial Force at Column Bottom of Each Floor
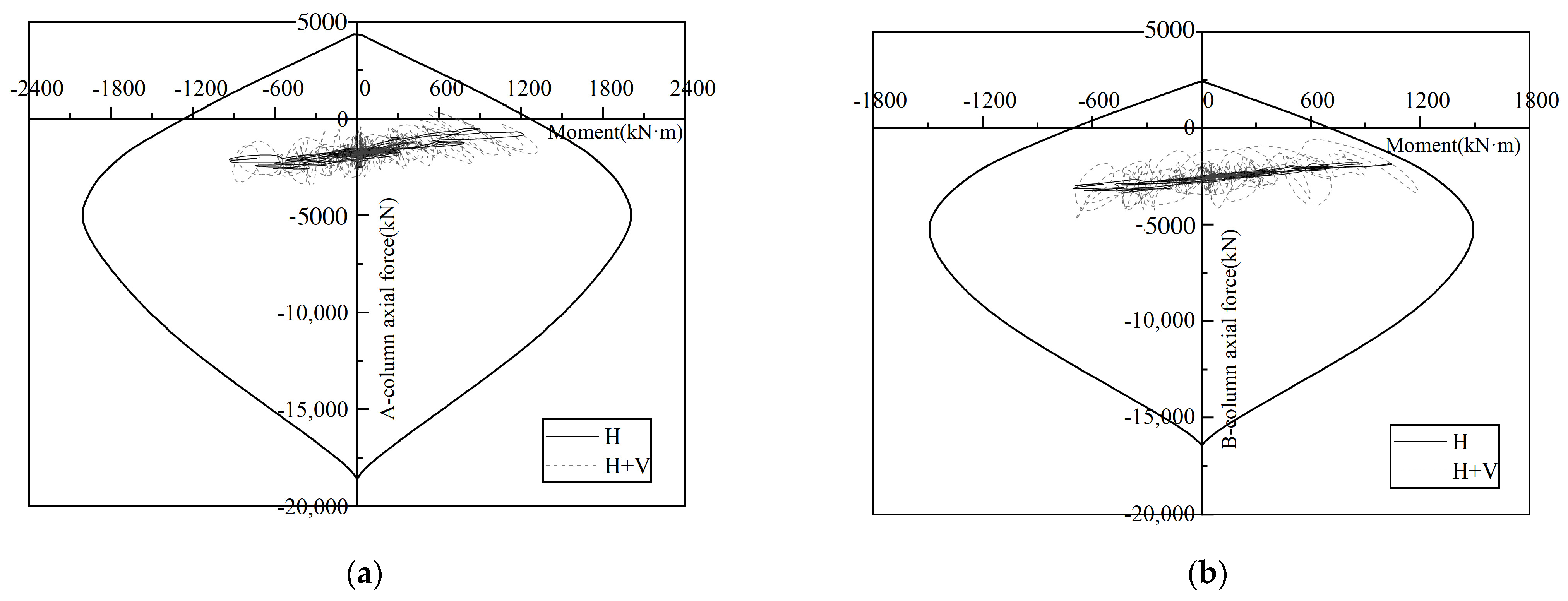
3.5. Analysis of the Axial Force and Moment of a Single Column under Yangbi Ground Motion
4. Dynamic Time History Analysis of Brick-Concrete Structure
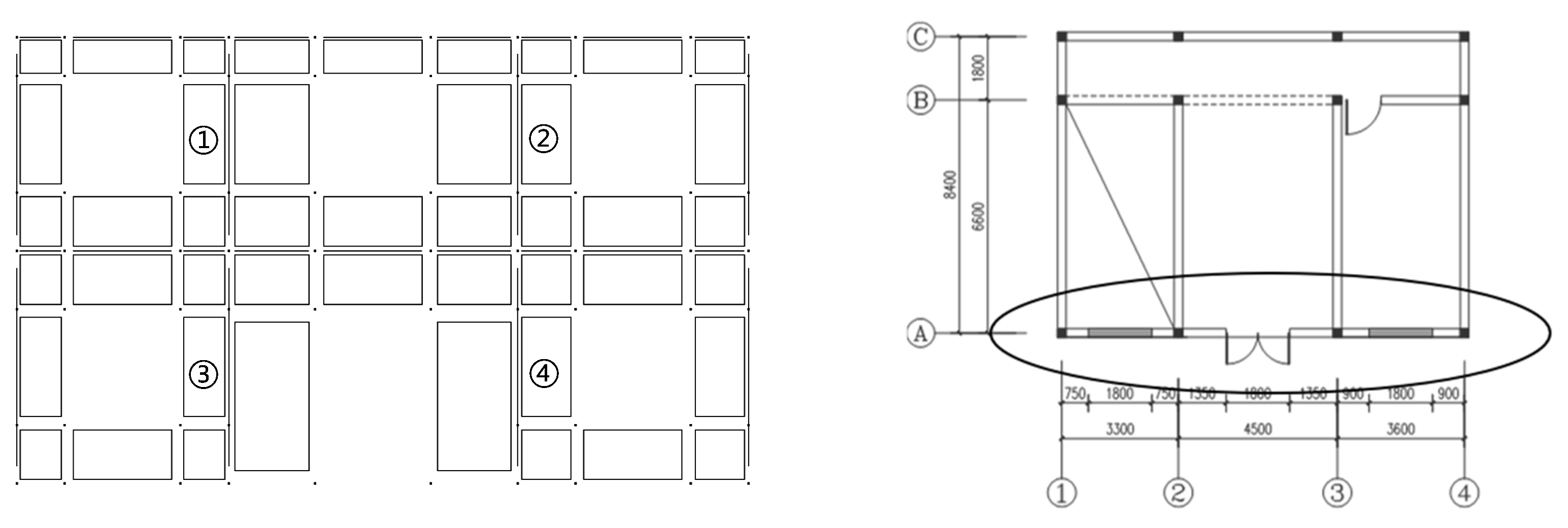
4.1. The Information on the Brick-Concrete Structure
4.2. Comparison of Top-Floor Displacement
4.3. Comparison of Top-Floor Acceleration
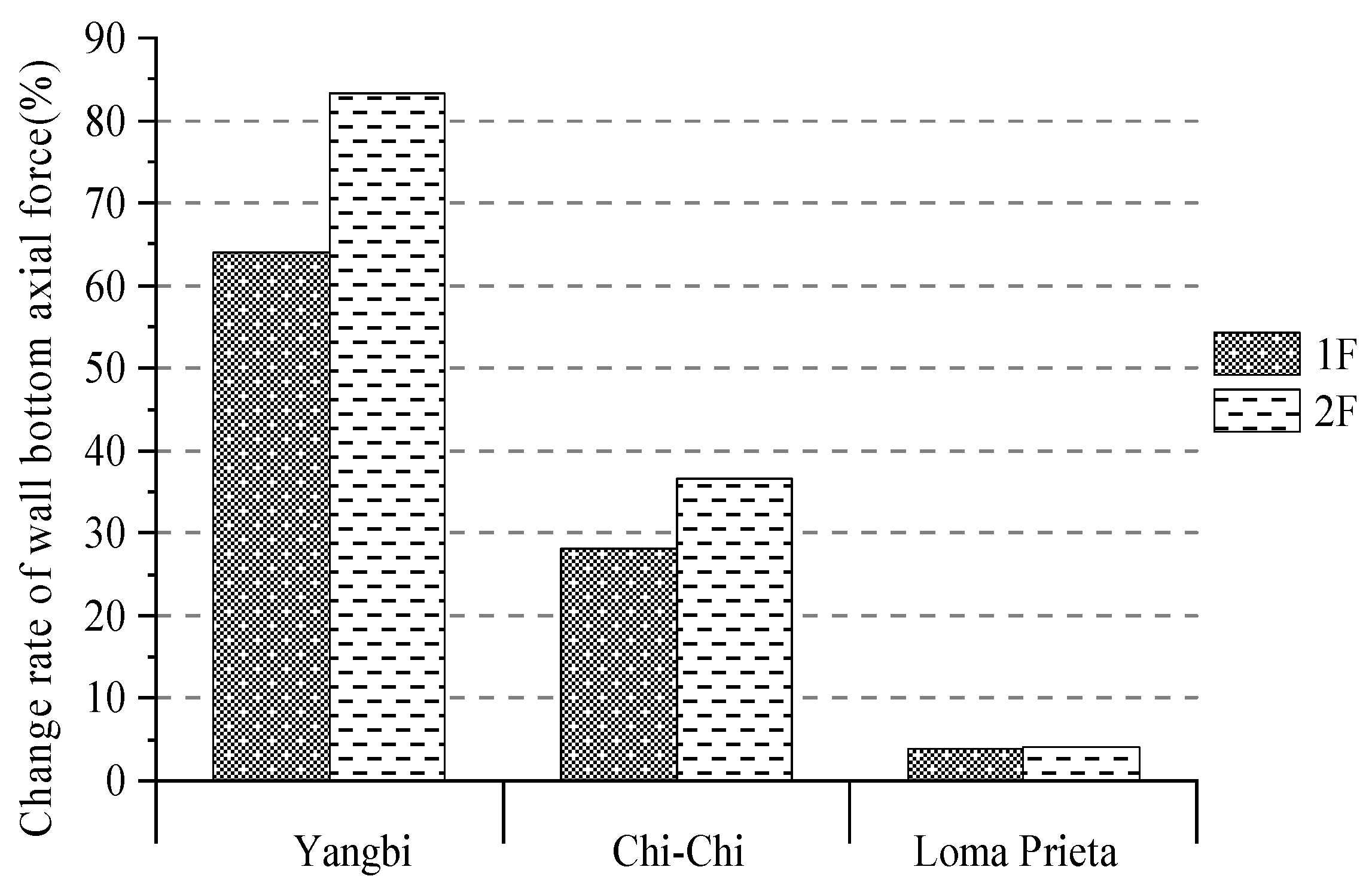
4.4. Comparison of Axial Force at the Bottom of Brick Masonry Walls of Each Floor
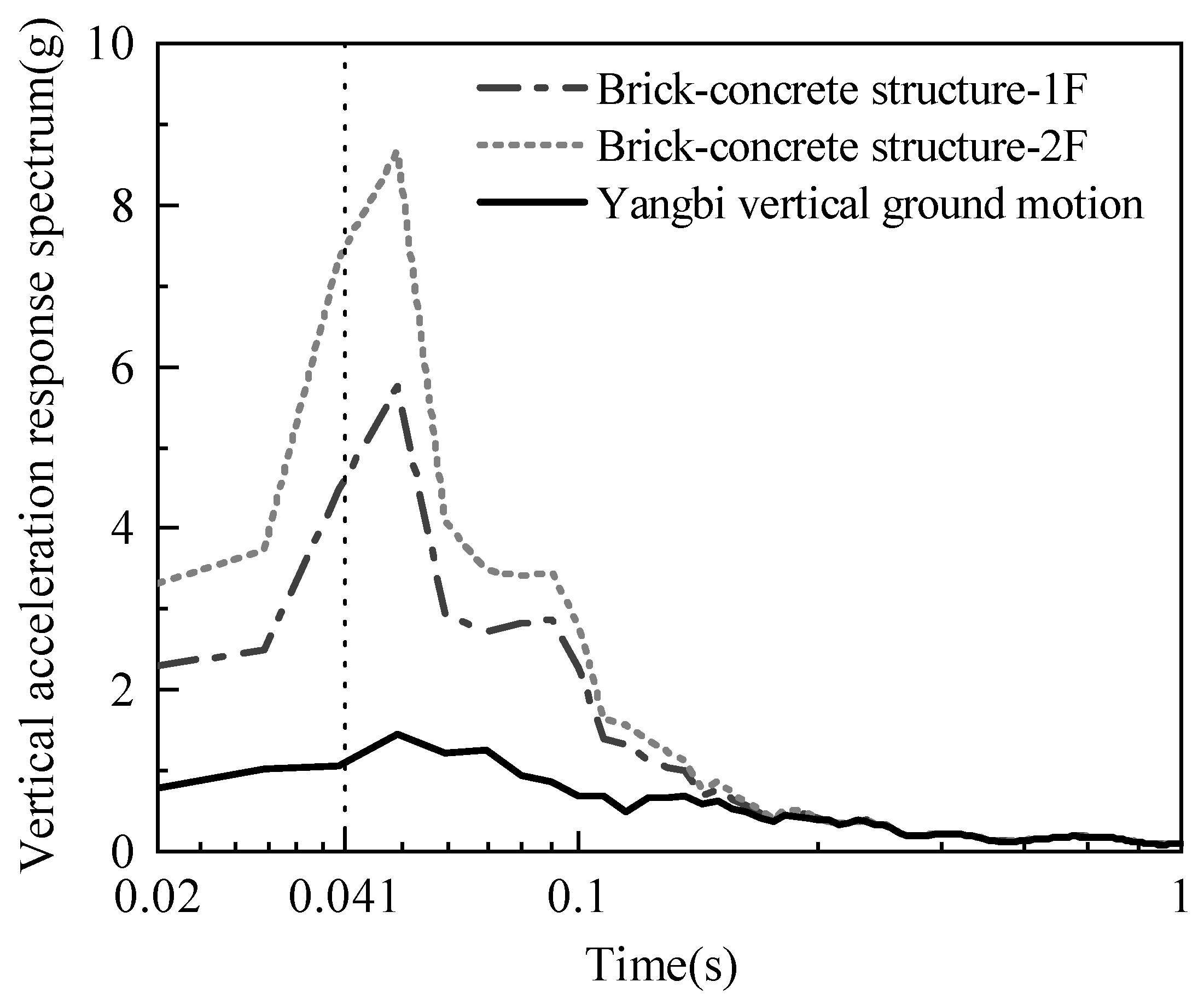
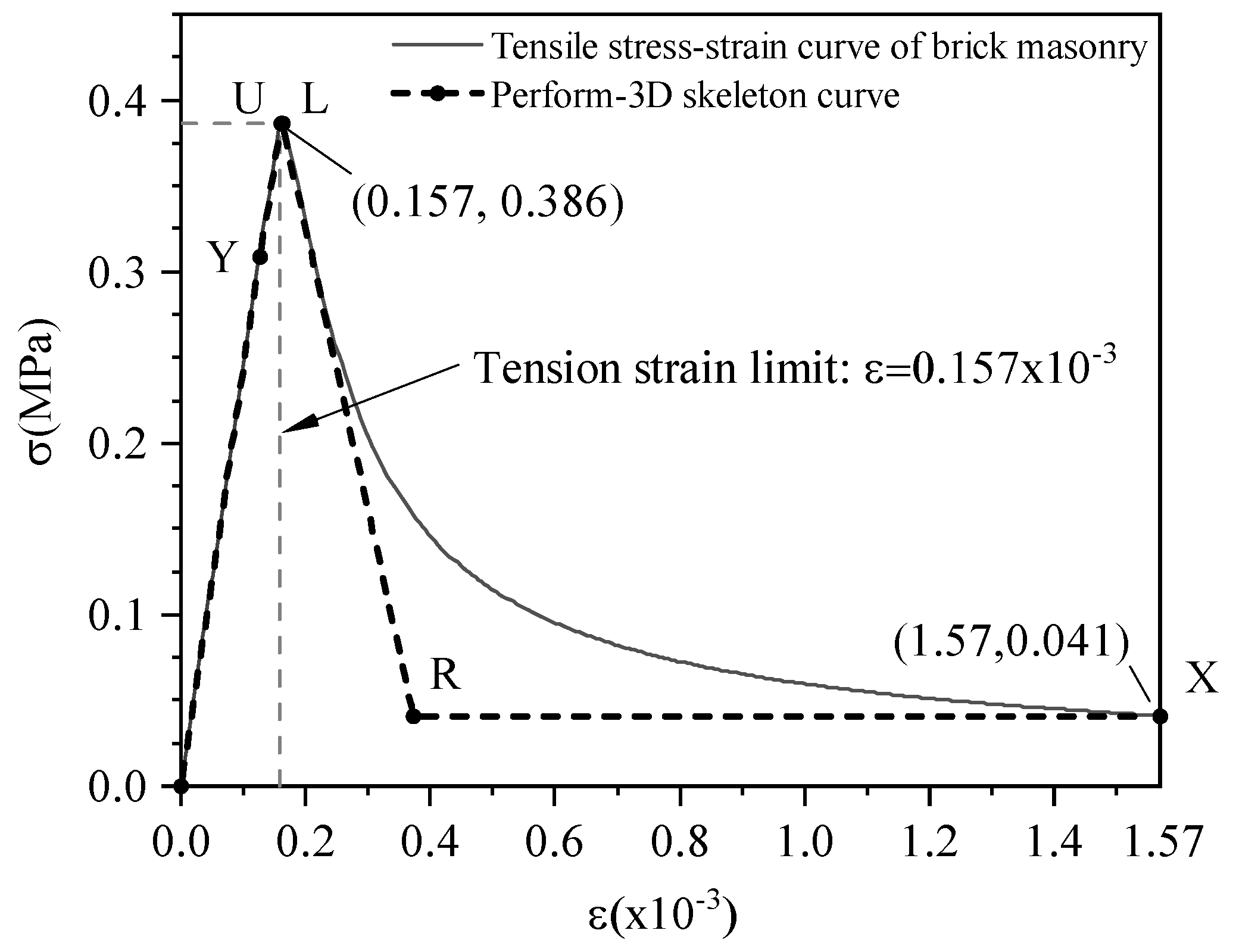
4.5. Analysis of the Tensile State of Brick Masonry Wall under Yangbi Ground Motion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zucconi, M.; Bovo, M.; Ferracuti, B. Fragility Curves of Existing RC Buildings Accounting for Bidirectional Ground Motion. Buildings 2022, 12, 872. [Google Scholar] [CrossRef]
- Yi, W.; Wang, W. Effect of vertical ground motion on seismic behavior of RC frame in near-fault region. Tumu Gongcheng Xuebao China Civ. Eng. J. 2012, 45, 81–88. [Google Scholar]
- Huang, L.; Han, J.; Wen, H.; Li, C.; He, H.; Luo, Y.; Qian, Z. The Seismic Performance and Global Collapse Resistance Capacity of Infilled Reinforced Concrete Frames Considering the Axial-Shear-Bending Interaction of Columns. Buildings 2022, 12, 2030. [Google Scholar] [CrossRef]
- Gallardo, J.A.; de la Llera, J.C.; Santa María, H.; Chacón, M.F. Damage and sensitivity analysis of a reinforced concrete wall building during the 2010, Chile earthquake. Eng. Struct. 2021, 240, 112093. [Google Scholar] [CrossRef]
- Trifunac, M.D.; Todorovska, M.I. A note on energy of strong ground motion during Northridge, California, earthquake of January 17, 1994. Soil Dyn. Earthq. Eng. 2013, 47, 175–184. [Google Scholar] [CrossRef]
- Nguyen, V.Q.; Nizamani, Z.A.; Park, D.; Kwon, O.-S. Numerical simulation of damage evolution of Daikai station during the 1995 Kobe earthquake. Eng. Struct. 2020, 206, 110180. [Google Scholar] [CrossRef]
- Lin, M.L.; Lin, C.H.; Li, C.H.; Liu, C.Y.; Hung, C.-H. 3D modeling of the ground deformation along the fault rupture and its impact on engineering structures: Insights from the 1999 Chi-Chi earthquake, Shigang District, Taiwan. Eng. Geol. 2021, 281, 105993. [Google Scholar] [CrossRef]
- Jia, J.F.; Ou, J.P. Vertical-to-horizontal acceleration response spectrum ratio of near-fault ground motion. Acta Seismol. Sin. 2010, 32, 41–50. (In Chinese) [Google Scholar]
- Chen, L.K.; Zhang, N.; He, X. Effects of directivity pulse and vertical earthquake on seismic response of high-speed railway bridge. J. Vib. Eng. 2016, 29, 704–713. [Google Scholar] [CrossRef]
- Quaranta, G.; Angelucci, G.; Mollaioli, F. Near-fault earthquakes with pulse-like horizontal and vertical seismic ground motion components: Analysis and effects on elastomeric bearings. Soil Dyn. Earthq. Eng. 2022, 160, 107361. [Google Scholar] [CrossRef]
- Kim, S.J. Seismic Assessment of RC Structures Considering Vertical Ground Motion; Mid-America Earthquake Center: Champaign, IL, USA, 2008. [Google Scholar]
- He, Z.; Zhang, H. Spectrum elements for simulating responses of ultra high-rise building structures excited by vertical component of impulse-type strong earthquakes. Harbin Gongye Daxue Xuebao J. Harbin Inst. Technol. 2014, 46, 72–77. [Google Scholar]
- Li, C.; Ji, D.; Zhai, C.; Ma, Y.; Xie, L. Vertical ground motion model for the NGA-West2 database using deep learning method. Soil Dyn. Earthq. Eng. 2023, 165, 107713. [Google Scholar] [CrossRef]
- Diotallevi, P.; Landi, L. Effect of the axial force and of the vertical ground motion component on the seismic response of R/C frames. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Jara, J.M.; Hernández, E.J.; Olmos, B.A. Effect of epicentral distance on the applicability of base isolation and energy dissipation systems to improve seismic behavior of RC buildings. Eng. Struct. 2021, 230, 111727. [Google Scholar] [CrossRef]
- Poreddy, L.; Pathapadu, M.; Navyatha, C.; Vemuri, J.; Chenna, R. Correlation analysis between ground motion parameters and seismic damage of buildings for near-field ground motions. Nat. Hazards Res. 2022, 2, 202–209. [Google Scholar] [CrossRef]
- Işık, E.; Peker, F.; Buyuksarac, A. The Effect of Vertical Earthquake Motion on Structural Behaviour in Steel Structures in Different Seismic Zones. J. Adv. Res. Nat. Appl. Sci. 2022, 8, 527–542. [Google Scholar] [CrossRef]
- Bas, S.; Kalkan, I.; Lee, J.H. Structural behavior of a high-rise RC structure under vertical earthquake motion. In Proceedings of the 2016 Structures Congress (Structures16), Jeju Island, Republic of Korea, 28 August–1 September 2016. [Google Scholar]
- Rinaldin, G.; Fasan, M.; Noé, S.; Amadio, C. The influence of earthquake vertical component on the seismic response of masonry structures. Eng. Struct. 2019, 185, 184–1937. [Google Scholar] [CrossRef]
- Wang, X.; Su, Y.; Kong, J.; Gong, M.; Liu, C. The Over-Strength Coefficient of Masonry-Infilled RC Frame Structures under Bidirectional Ground Motions. Buildings 2022, 12, 1290. [Google Scholar] [CrossRef]
- Li, X.; Dou, H.; Zhu, X. Engineering characteristics of near-fault vertical ground motions and their effect on the seismic response of bridges. Earthq. Eng. Eng. Vib. 2007, 6, 345–350. [Google Scholar] [CrossRef]
- Khan, M.; Ali, M. Optimization of concrete stiffeners for confined brick masonry structures. J. Build. Eng. 2020, 32, 101689. [Google Scholar] [CrossRef]
- Cao, M.; Khan, M. Effectiveness of multiscale hybrid fiber reinforced cementitious composites under single degree of freedom hydraulic shaking table. Struct. Concr. 2021, 22, 535–549. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, Y.; Lu, X.; Lin, K. A simplified method for quantifying the progressive collapse fragility of multi-story RC frames in China. Eng. Fail. Anal. 2023, 143, 106924. [Google Scholar] [CrossRef]
- Yong, M.; Hai-Jiang, Z.; Lei, G.; Jin-Meng, B. Three-dimensional high-resolution velocity structure imaging and seismicity study of Yangbi Ms6.4 earthquake. Appl. Geophys. 2021, 18, 579–591. [Google Scholar] [CrossRef]
- Lu, D.W.; Yang, Z.B. Strong Motion Observation from Recent Destructive Earthquakes in China Mainland. Appl. Mech. Mater. 2015, 724, 358–361. (In Chinese) [Google Scholar] [CrossRef]
- Tian, W.T.; Dong, J.H.; Yang, B.; Zhao, L.H. Basic characteristics of the three elements of strong ground motion of the Yangbi M6.4 earthquake in Yunnan Province. China Earthq. Eng. J. 2021, 43, 760–766. (In Chinese) [Google Scholar]
- Wang, H.D.; Liu, B.C.; Chang, F. The selection principle of near-field horizontal ground motions and characteristics of elastic response spectra for pulse-type horizontal ground motion. Earthq. Eng. Eng. Dyn. 2019, 39, 222–230. (In Chinese) [Google Scholar]
- Sriwastav, R.K.; Basu, D. Vertical spectra consistent with horizontal seismic hazard. Soil Dyn. Earthq. Eng. 2022, 157, 107242. [Google Scholar] [CrossRef]
- Kasai, K.; Maison, B.F. Building pounding damage during the 1989 Loma Prieta earthquake. Eng. Struct. 1997, 19, 195–207. [Google Scholar] [CrossRef]
- Computers and Structures, Inc. Nonlinear Analysis and Performance Assessment for 3d Structures User Guide; Computers and Structures, Inc.: Berkeley, CA, USA, 2006. [Google Scholar]
- Kent, D.C.; Park, R. Flexural Members with Confined Concrete. J. Struct. Div. 1971, 97, 1969–1990. [Google Scholar] [CrossRef]
- Scott, B.; Park, R.; Priestley, M.J.N. Stress-Strain Behavior of Concrete Confined by Overlapping Hoops at Low and High Strain Rates. ACI J. 1982, 79, 13–27. [Google Scholar]
- Guo, Z.M.; Fang, Y.P.; Yu, L.G.; Li, Y.C.; Guo, M. Dynamic elastic-plastic comparative analysis of high-rise structure based on PERFORM-3D and STRAT. Build. Struct. 2020, 50, 257–265. (In Chinese) [Google Scholar]
- Papazoglou, A.J.; Elnashai, A.S. Analytical and field evidence of the damaging effect of vertical earthquake ground motion. Earthq. Eng. Struct. Dyn. 1996, 25, 1109–1137. [Google Scholar] [CrossRef]
- Wang, X.L.; Lu, X.Z.; Ye, L.P. Analysis of earthquake-resistant behaviors of RC columns under variable axial loads. Ind. Constr. 2007, 71–75. (In Chinese) [Google Scholar]
- Cheng, X.; Ji, X.; Henry, R.S.; Xu, M. Coupled axial tension-flexure behavior of slender reinforced concrete walls. Eng. Struct. 2019, 188, 261–276. [Google Scholar] [CrossRef]
- Wu, Z.B.; Zhou, X.X.; Xie, W.; An, X.J. Statistics of wenchuan earthquake investigation and some ideas on seismic design of buildings. Build. Struct. 2010, 40 (Suppl. S2), 144–148. (In Chinese) [Google Scholar]
- Liu, G.Q. The Research on the Basic Mechanical Behavior of Masonry Structure. PhD Thesis, Hunan University, Hunan, China, 2005. (In Chinese). [Google Scholar]
- GB 50003-2011; Code for Design of Masonry Structure. Standards Press of China: Beijing, China, 2011.
- Zheng, N. Research on Seismic Behavior of Masonry Structures with Fabricated Tie-Columns. PhD Thesis, Chongqing University, Chongqing, China, 2010. (In Chinese). [Google Scholar]
- Liu, L. Study on Failure Mode of Masonry Structures under Strong Ground Motion. Master’s Thesis, Chongqing University, Chongqing, China, 2012. (In Chinese). [Google Scholar]
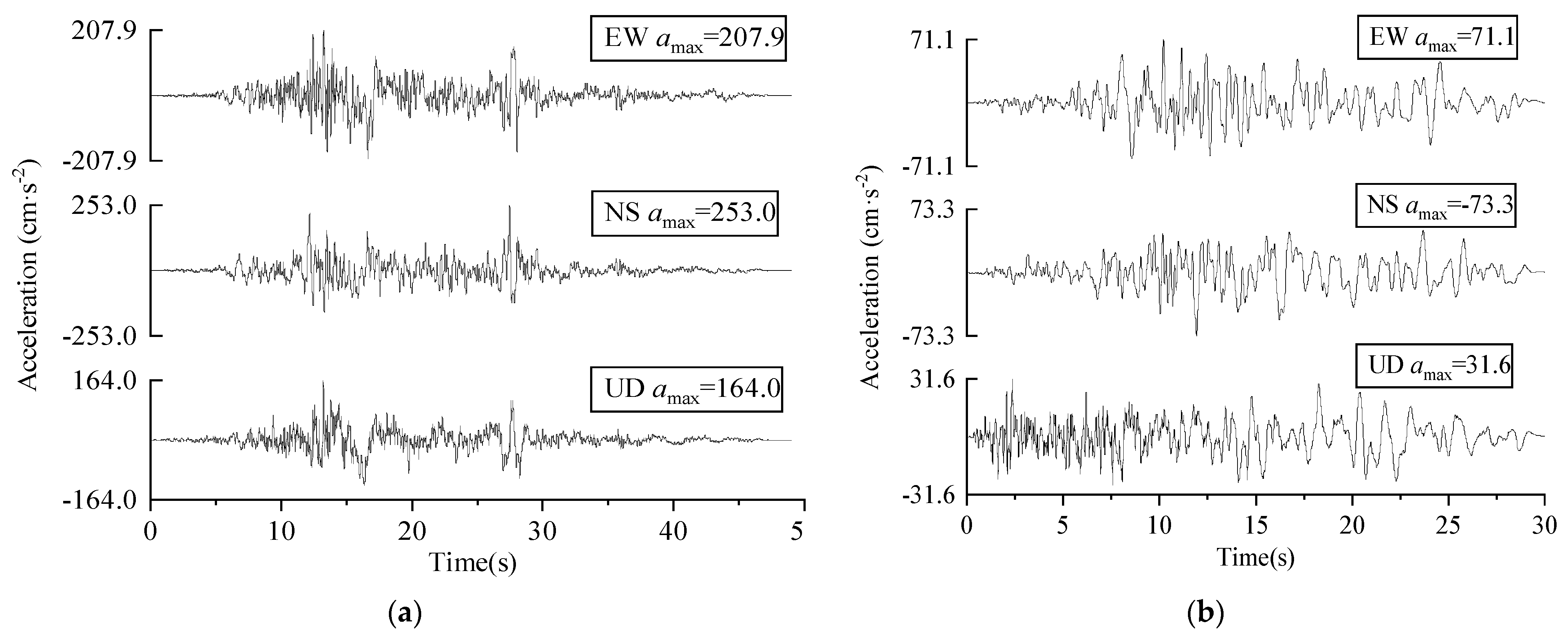



| Earthquake Name | Time of Occurrence | Magnitude | Station | Mechanism | Rrup (km) | Site Category | PGA (cm·s−2) | PGV (cm·s−1) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EW | NS | UD | EW | NS | UD | |||||||
| Chi-Chi | 1999 | 7.62 | TCU101 | Reverse Oblique | 2.11 | II | 207.9 | 253.0 | 164.0 | −76.8 | −50.9 | 46.7 |
| Loma Prieta | 1989 | 6.93 | Dublin-Fire | 58.8 | II | 71.1 | −73.3 | 31.6 | −12.4 | −15.2 | 7.9 | |
| Working Condition | Yangbi | Chi-Chi | Loma Prieta | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Node 1 | Node 2 | Node 1 | Node 2 | Node 1 | Node 2 | |||||||
| EW | NS | EW | NS | EW | NS | EW | NS | EW | NS | EW | NS | |
| H | 101.05 | 72.02 | 101.05 | 69.10 | 93.57 | 81.83 | 93.57 | 79.94 | 30.83 | 32.69 | 30.83 | 33.85 |
| H + V | 101.03 | 72.81 | 101.03 | 69.80 | 93.69 | 81.86 | 93.69 | 79.96 | 30.82 | 32.68 | 30.82 | 33.83 |
| The change rate of displacement (%) | −0.02 | 1.10 | −0.02 | 1.01 | 0.13 | 0.04 | 0.13 | 0.03 | −0.03 | −0.03 | −0.03 | −0.06 |
| Working Condition | Yangbi | Chi-Chi | Loma Prieta | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Node 1 | Node 2 | Node 1 | Node 2 | Node 1 | Node 2 | |||||||
| Max | Min | Max | Min | Max | Min | Max | Min | Max | Min | Max | Min | |
| H | 0.53 | −1.64 | −1.02 | −2.27 | 0.95 | −1.42 | −0.40 | −2.38 | −0.36 | −1.44 | −1.54 | −2.24 |
| H + V | 2.24 | −2.39 | 0.41 | −3.51 | 1.14 | −1.57 | −0.01 | −2.58 | −0.37 | −1.44 | −1.55 | −2.26 |
| The change rate of vertical displacement amplitude (%) | 113.36 | 213.60 | 14.35 | 29.80 | −0.93 | 1.43 | ||||||
| Working Condition | Yangbi | Chi-Chi | Loma Prieta | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Node 1 | Node 2 | Node 1 | Node 2 | Node 1 | Node 2 | |||||||||||||
| EW | NS | UD | EW | NS | UD | EW | NS | UD | EW | NS | UD | EW | NS | UD | EW | NS | UD | |
| H | 248.8 | 271.4 | 93.5 | 248.8 | 249.6 | 76.2 | 191.3 | 245.1 | 43.2 | 191.3 | 230.6 | 36.9 | 133.1 | 134.9 | 10.7 | 133.1 | 139.1 | 5.0 |
| H + V | 258.2 | 296.1 | 3199.5 | 258.2 | 260.8 | 1501.9 | 190.3 | 246.0 | 258.9 | 190.3 | 232.3 | 250.8 | 133.7 | 134.9 | 65.0 | 133.7 | 138.9 | 98.3 |
| H + V/H | 1.04 | 1.09 | 34.22 | 1.04 | 1.04 | 19.71 | 0.99 | 1.00 | 5.99 | 0.99 | 1.01 | 6.80 | 1.00 | 1.00 | 6.07 | 1.00 | 1.00 | 19.66 |
| Floor Number | Initial Value under the Gravity Load | Yangbi | Chi-Chi | Loma Prieta | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H | H + V | H | H + V | H | H + V | ||||||||
| Max | Min | Max | Min | Max | Min | Max | Min | Max | Min | Max | Min | ||
| 1 | 87,985 | 90,614 | 85,050 | 137,920 | 45,369 | 88,939 | 86,886 | 102,530 | 75,118 | 88,120 | 87,804 | 92,673 | 83,699 |
| 2 | 69,381 | 71,821 | 66,743 | 112,970 | 30,828 | 70,259 | 68,440 | 82,061 | 57,861 | 69,505 | 69,230 | 73,513 | 65,588 |
| 3 | 51,313 | 53,337 | 49,160 | 89,018 | 18,298 | 52,075 | 50,558 | 61,536 | 41,706 | 51,415 | 51,186 | 54,640 | 48,210 |
| 4 | 33,246 | 34,673 | 31,738 | 70,216 | 6894.6 | 33,863 | 32,633 | 40,394 | 26,328 | 33,318 | 33,151 | 35,553 | 31,041 |
| 5 | 15,178 | 16,001 | 14,392 | 39,319 | 2042.5 | 15,532 | 14,864 | 18,665 | 11,553 | 15,222 | 15,127 | 16,324 | 14,076 |
| Working Condition | Yangbi | Chi-Chi | Loma Prieta | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Node 3 | Node 4 | Node 3 | Node 4 | Node 3 | Node 4 | |||||||
| EW | NS | EW | NS | EW | NS | EW | NS | EW | NS | EW | NS | |
| H | 5.13 | 6.99 | 3.58 | 6.99 | 1.99 | 0.95 | 1.46 | 0.95 | 0.59 | 0.24 | 0.45 | 0.24 |
| H + V | 5.11 | 7.47 | 3.54 | 7.47 | 2.00 | 0.99 | 1.47 | 0.99 | 0.59 | 0.24 | 0.45 | 0.24 |
| The change rate of displacement (%) | −0.39 | 6.87 | −1.12 | 6.87 | 0.50 | 4.21 | 0.68 | 4.21 | 0 | 0 | 0 | 0 |
| Working Condition | Yangbi | Chi-Chi | Loma Prieta | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Node 3 | Node 4 | Node 3 | Node 4 | Node 3 | Node 4 | |||||||
| Max | Min | Max | Min | Max | Min | Max | Min | Max | Min | Max | Min | |
| H | 0.34 | −1.11 | 0.28 | −1.74 | −0.38 | −0.62 | −0.34 | −0.80 | −0.43 | −0.50 | −0.51 | −0.62 |
| H + V | 0.71 | −1.71 | 0.41 | −1.76 | −0.32 | −0.63 | −0.31 | −0.84 | −0.43 | −0.50 | −0.51 | −0.63 |
| The change rate of displacement amplitude (%) | 66.90 | 7.43 | 29.17 | 15.22 | 0 | 9.09 | ||||||
| Working Condition | Yangbi | Chi-Chi | Loma Prieta | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Node 3 | Node 4 | Node 3 | Node 4 | Node 3 | Node 4 | |||||||||||||
| EW | NS | UD | EW | NS | UD | EW | NS | UD | EW | NS | UD | EW | NS | UD | EW | NS | UD | |
| H | 829.8 | 1341.1 | 685.7 | 818.8 | 1341.1 | 815.0 | 438.7 | 322.6 | 102.1 | 328.3 | 322.6 | 102.9 | 118.4 | 85.0 | 4.9 | 100.5 | 85.0 | 9.6 |
| H + V | 807.7 | 1389.5 | 2143.5 | 753.9 | 1389.5 | 2352.1 | 433.2 | 481.4 | 382.3 | 332.6 | 481.4 | 339.6 | 118.5 | 84.2 | 46.2 | 99.7 | 84.2 | 44.3 |
| H + V/H | 0.97 | 1.04 | 3.13 | 0.92 | 1.04 | 2.89 | 0.99 | 1.49 | 3.74 | 1.01 | 1.49 | 3.30 | 1.00 | 0.99 | 9.43 | 0.99 | 0.99 | 4.61 |
| Floor Number | Initial Value under the Gravity Load | Yangbi | Chi-Chi | Loma Prieta | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H | H + V | H | H + V | H | H + V | ||||||||
| Max | Min | Max | Min | Max | Min | Max | Min | Max | Min | Max | Min | ||
| 1 | 3352.2 | 4082.5 | 2564.1 | 6696.2 | −635.0 | 3428.0 | 3274.2 | 4392.3 | 2328.0 | 3353.5 | 3350.9 | 3484.4 | 3224.1 |
| 2 | 1623.8 | 2047.9 | 1205.1 | 3753.5 | −566.9 | 1676.0 | −1571.4 | 2289.2 | 1010.4 | 1624.9 | 1622.7 | 1690.4 | 1555.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Jia, M.; Yao, Y.; Chen, X.; Zhang, Z. Influence of the Vertical Component of Yangbi Ground Motion on the Dynamic Response of RC Frame and Brick-Concrete Structure. Buildings 2023, 13, 147. https://doi.org/10.3390/buildings13010147
Wang H, Jia M, Yao Y, Chen X, Zhang Z. Influence of the Vertical Component of Yangbi Ground Motion on the Dynamic Response of RC Frame and Brick-Concrete Structure. Buildings. 2023; 13(1):147. https://doi.org/10.3390/buildings13010147
Chicago/Turabian StyleWang, Hongwei, Mingming Jia, Yanwu Yao, Xueliang Chen, and Zirong Zhang. 2023. "Influence of the Vertical Component of Yangbi Ground Motion on the Dynamic Response of RC Frame and Brick-Concrete Structure" Buildings 13, no. 1: 147. https://doi.org/10.3390/buildings13010147
APA StyleWang, H., Jia, M., Yao, Y., Chen, X., & Zhang, Z. (2023). Influence of the Vertical Component of Yangbi Ground Motion on the Dynamic Response of RC Frame and Brick-Concrete Structure. Buildings, 13(1), 147. https://doi.org/10.3390/buildings13010147







