Optimal Design Formula for Tuned Mass Damper Based on an Analytical Solution of Interaction between Soil and Structure with Rigid Foundation Subjected to Plane SH-Waves
Abstract
:1. Introduction
2. Methodology
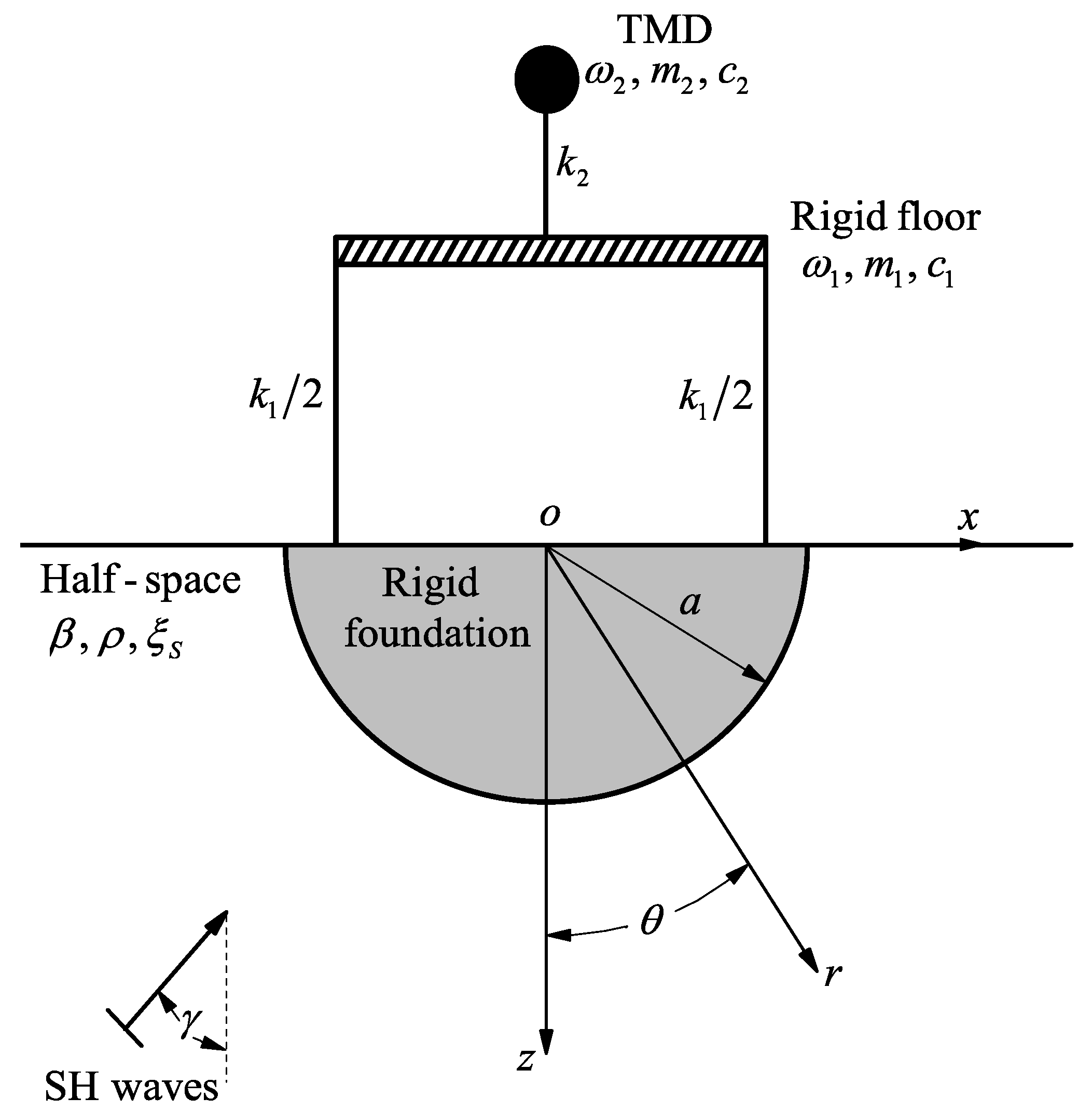
2.1. The Model
2.2. Analytical Solutions for Soil-Structure-TMD Seismic Interaction
2.3. Performance Evaluation Index
2.4. Dimensionless Calculation Parameters
3. The Proposed Design Framework
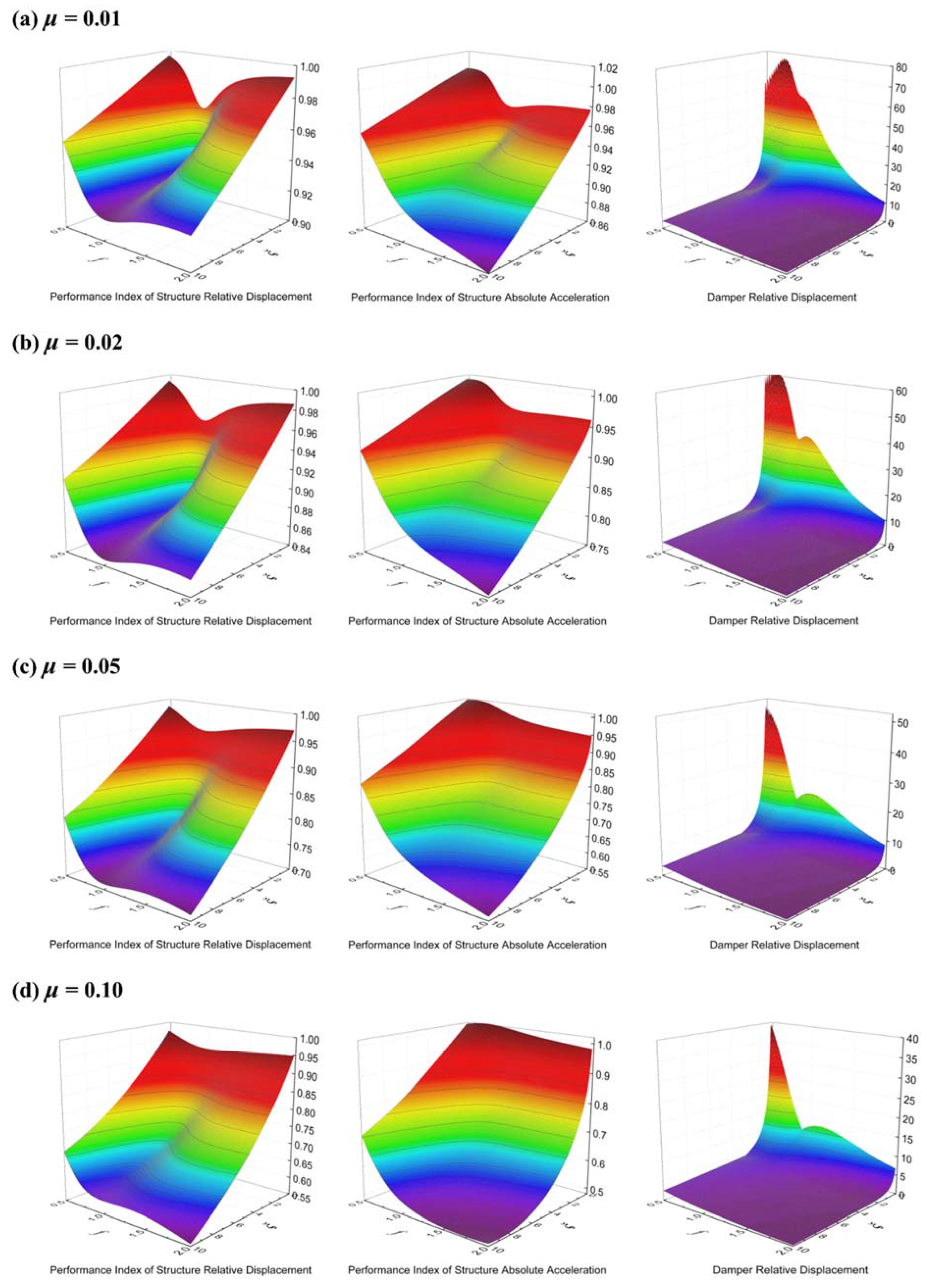
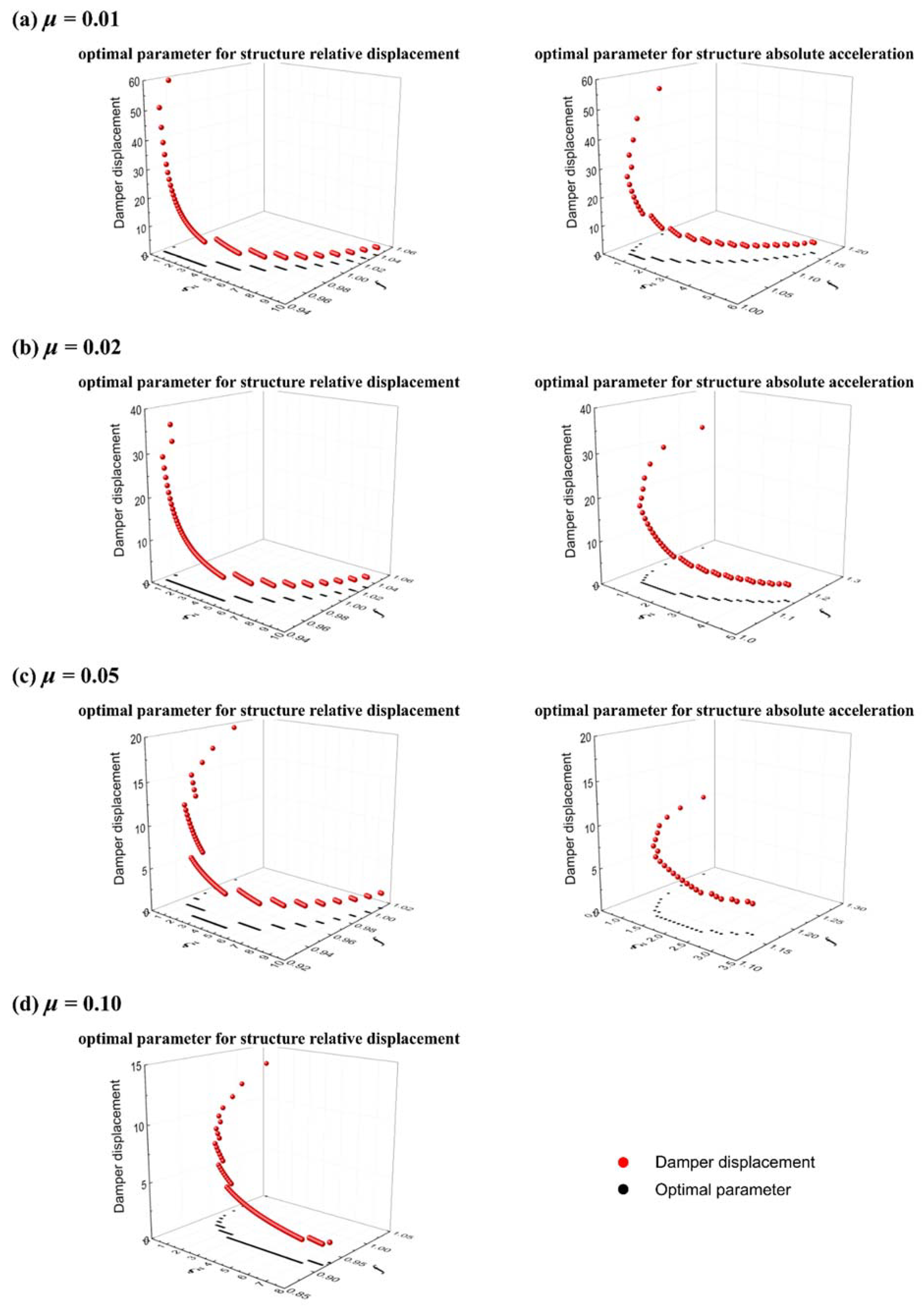
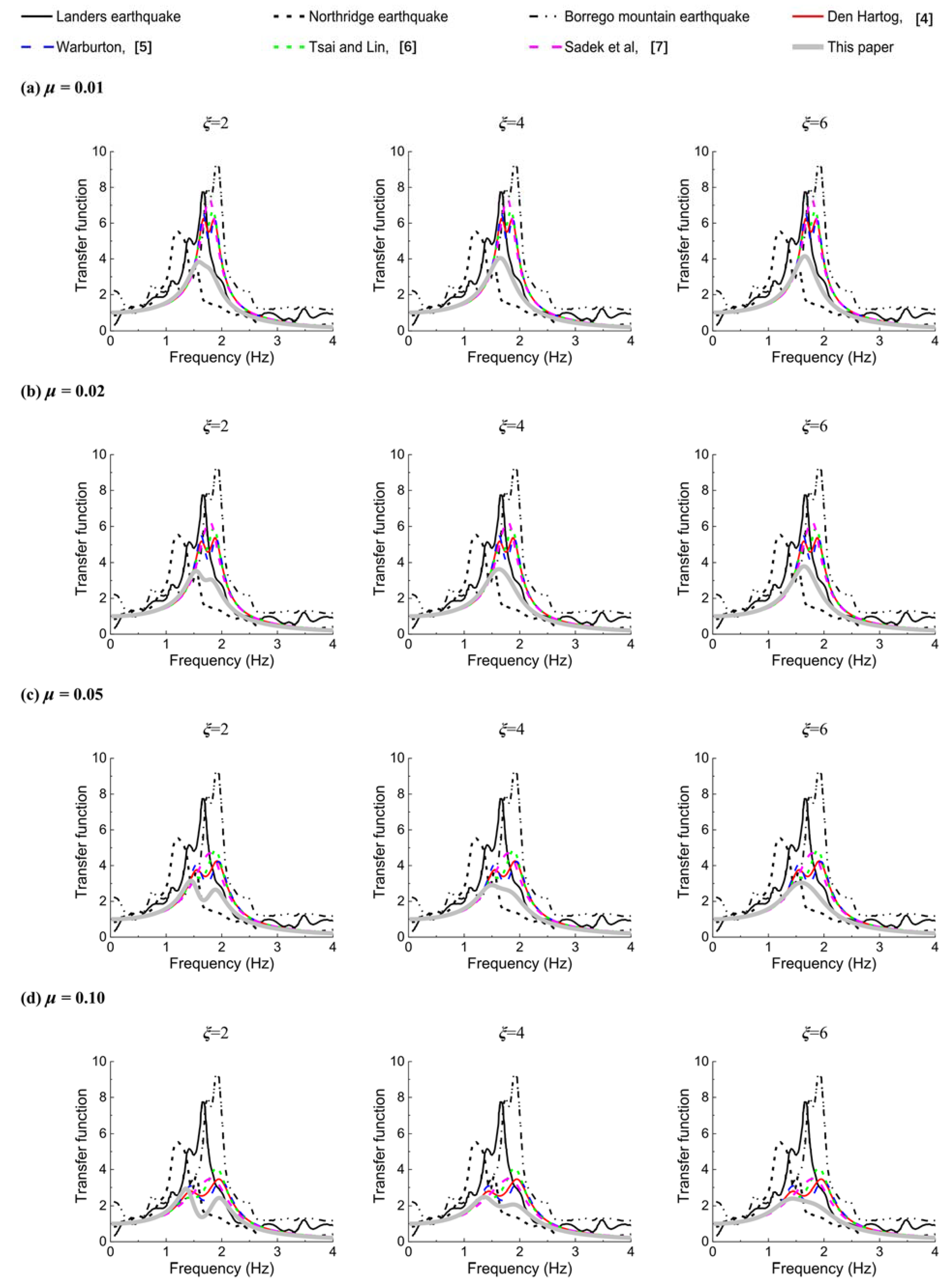
3.1. Dynamic Behaviors of the TMD System
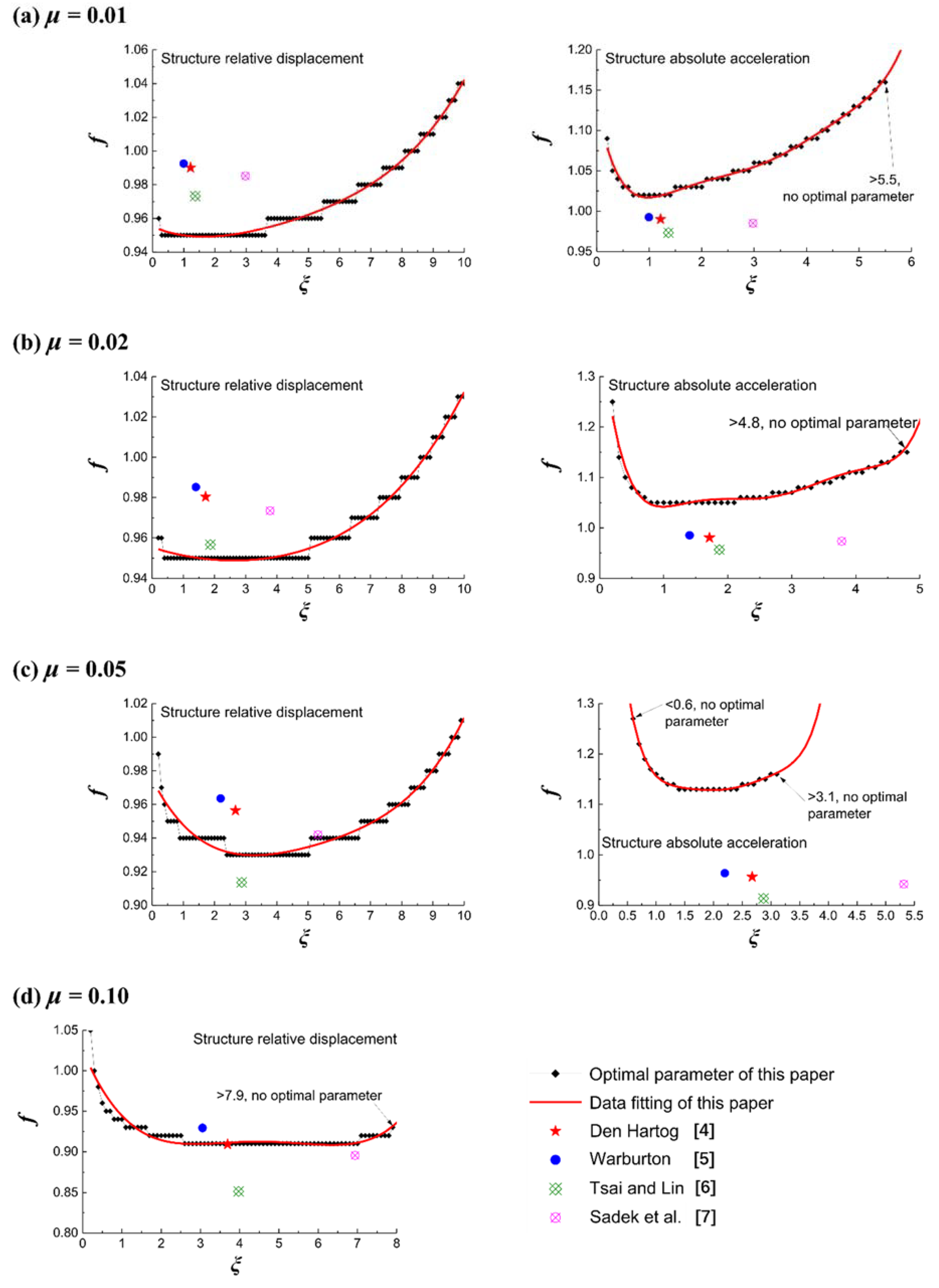
3.2. Design Formulae
- (1)
- Based on stroke and installation budget limits, design the damping system for the .
- (2)
- Estimate the of the damping system and obtain .
- (3)
- Check the mitigation performance as well as practicability of the system.
4. Case Study
5. Conclusions
- (1)
- The proposed design formulae are easy-to-use while being highly effective and robust to loads of various frequency contents, compared with the traditional design formulae.
- (2)
- For the problem setup in this research, with the consideration of SSI, a global optimal design may not exist. Therefore, for the related optimization problems, extra constraints, e.g., selected damping ratios, are suggested to be considered.
- (3)
- Similar to those observed in cases without SSI, TMD systems with larger mass ratios are more robust to the changes in damping ratio and frequency ratio, while larger TMD damping would lead to a lower TMD stroke.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sladek, J.R.; Klingner, R.E. Effect of tuned-mass dampers on seismic response. J. Struct. Eng. 1983, 109, 2004–2009. [Google Scholar] [CrossRef]
- Soto, M.G.; Adeli, H. Tuned mass dampers. Arch. Comput. Methods Eng. 2013, 20, 419–431. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, Q.; Weng, D.; Zhou, Z.; Wang, S.; Mahin, S.A.; Ding, S.; Qian, F. Improving performance of a super tall building using a new eddy-current tuned mass damper. Struct. Control. Health Monit. 2017, 24, e1882. [Google Scholar] [CrossRef]
- Den Hartog, J.P. Mechanical Vibrations; Courier Corporation: Chelmsford, MA, USA, 1985. [Google Scholar]
- Warburton, G.B. Optimum absorber parameters for various combinations of response and excitation parameters. Earthq. Eng. Struct. Dyn. 1982, 10, 381–401. [Google Scholar] [CrossRef]
- Tsai, H.C.; Lin, G.C. Optimum tuned-mass dampers for minimizing steady-state response of support-excited and damped systems. Earthq. Eng. Struct. Dyn. 1993, 22, 957–973. [Google Scholar] [CrossRef]
- Sadek, F.; Mohraz, B.; Taylor, A.W.; Chung, R.M. A method of estimating the parameters of tuned mass dampers for seismic applications. Earthq. Eng. Struct. Dyn. 1997, 26, 617–635. [Google Scholar] [CrossRef]
- Veletsos, A.S. Dynamics of structure-foundation systems. In Structural and Geotechnical Mechanics; Hall, W.J., Ed.; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1977; pp. 333–361. [Google Scholar]
- Wolf, J.P. Dynamic Soil–Structure Interaction; Prentice-Hall: Englewood Cliffs, NJ, USA, 1985. [Google Scholar]
- Domenico, D.; Impollonia, N.; Ricciardi, G. Soil-dependent optimum design of a new passive vibration control system combining seismic base isolation with tuned inerter damper. Soil Dyn. Earthq. Eng. 2018, 105, 37–53. [Google Scholar] [CrossRef]
- Abd-Elhamed, A.; Mahmoud, S. Simulation analysis of TMD controlled building subjected to far- and near-fault records considering soil-structure interaction. J. Build. Eng. 2019, 26, 100930. [Google Scholar] [CrossRef]
- Boksmati, J.I.; Madabhushi, G.S.; Thusyanthan, I.N. Dynamic soil-structure interaction of a shallow founded shear frame and a frame equipped with viscous dampers under seismic loading. Eng. Struct. 2021, 227, 111388. [Google Scholar] [CrossRef]
- Wu, J.; Chen, G.; Lou, M. Seismic effectiveness of tuned mass dampers considering soil–structure interaction. Earthq. Eng. Struct. Dyn. 1999, 28, 1219–1233. [Google Scholar] [CrossRef]
- Ghosh, A.; Basu, B. Effect of soil interaction on the performance of tuned mass dampers for seismic applications. J. Sound Vib. 2004, 3, 1079–1090. [Google Scholar] [CrossRef]
- Jabary, R.N.; Madabhushi, S.P. Tuned mass damper effects on the response of multi-storied structures observed in geotechnical centrifuge tests. Soil Dyn. Earthq. Eng. 2015, 77, 373–380. [Google Scholar] [CrossRef]
- Khatibinia, M.; Gholami, H.; Labbafi, S.F. Multi-objective optimization of tuned mass dampers considering soil-structure interaction. Int. J. Optim. Civ. Eng. 2016, 6, 595–610. [Google Scholar]
- Khoshnoudian, F.; Ziaei, R.; Ayyobi, P. Effects of nonlinear soil-structure interaction on the seismic response of structure-TMD systems subjected to near-field earthquakes. Bull. Earthq. Eng. 2017, 15, 199–226. [Google Scholar] [CrossRef]
- Ding, H.; Kaup, A.; Wang, J.; Lu, L.; Altay, O. Real-time hybrid simulation framework for the investigation of soil-structure interaction effects on the vibration control performance of shape memory alloys. Eng. Struct. 2021, 243, 112621. [Google Scholar] [CrossRef]
- Mortezaie, H.; Rezaie, F. Effect of soil in controlling the seismic response of three-dimensional PBPD high-rise concrete structures. Struct. Eng. Mech. 2018, 66, 217–227. [Google Scholar]
- Zhou, Z.; Wei, X.; Lu, Z.; Jeremic, B. Influence of soil-structure interaction on performance of a super tall building using a new eddy-current tuned mass damper. Struct. Des. Tall Spec. Build. 2018, 27, e1501. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.F.; Lin, C.C. Seismic performance of multiple tuned mass dampers for soil-irregular building interaction systems. Int. J. Solids Struct. 2005, 42, 5536–5554. [Google Scholar] [CrossRef]
- Salvi, J.; Pioldi, F.; Rizzi, E. Optimum tuned mass dampers under seismic soil-structure interaction. Soil Dyn. Earthq. Eng. 2018, 114, 576–597. [Google Scholar] [CrossRef]
- Dai, K.; Li, B.; Wang, J.; Li, A.; Li, H.; Li, J.; Tesfamariam, S. Optimal probability-based partial mass isolation of elevated coal scuttle in thermal power plant building. Struct. Des. Tall Spec. Build. 2018, 27, e1477. [Google Scholar] [CrossRef]
- Tavakolinia, M.; Ch Basim, M. Performance-based optimum tuning of tuned mass dampers on steel moment frames for seismic applications using the endurance time method. Earthq. Eng. Struct. Dyn. 2021, 50, 3646–3669. [Google Scholar] [CrossRef]
- Farshidianfar, A.; Soheili, S. Ant colony optimization of tuned mass dampers for earthquake oscillations of high-rise structures including soil–structure interaction. Soil Dyn. Earthq. Eng. 2013, 51, 14–22. [Google Scholar] [CrossRef]
- Bekdaş, G.; Nigdeli, S.M. Metaheuristic based optimization of tuned mass dampers under earthquake excitation by considering soil-structure interaction. Soil Dyn. Earthq. Eng. 2017, 92, 443–461. [Google Scholar] [CrossRef]
- Bekdaş, G.; Kayabekir, A.E.; Nigdeli, S.M.; Toklu, Y.C. Tranfer function amplitude minimization for structures with tuned mass dampers considering soil-structure interaction. Soil Dyn. Earthq. Eng. 2019, 116, 552–562. [Google Scholar] [CrossRef]
- Fu, J.; Liang, J. Performance degradation of tuned-mass-dampers arising from ignoring soil-structure interaction effects. Soil Dyn. Earthq. Eng. 2019, 125, 105701. [Google Scholar]
- Liu, S.; Lu, Z.; Li, P.; Ding, S.; Wan, F. Shaking table test and numerical simulation of eddy-current tuned mass damper for structural seismic control considering soil-structure interaction. Eng. Struct. 2020, 212, 110531. [Google Scholar]
- Nigdeli, S.M.; Bekdaş, G. Optimum design of multiple positioned tuned mass dampers for structures constrained with axial force capacity. Struct. Des. Tall Spec. Build. 2019, 28, e1593. [Google Scholar] [CrossRef]
- Jin, L.; Liang, J. Dynamic soil-structure interaction with a flexible foundation embedded in a half-space: Closed-form analytical solution for incident plane SH-waves. J. Earthq. Eng. 2021, 25, 1565–1589. [Google Scholar] [CrossRef]
- Trifunac, M.D. Dynamic interaction of a shear wall with the soil for incident plane SH Waves. Bull. Seismol. Soc. Am. 1972, 62, 62–83. [Google Scholar] [CrossRef]
- ASCE/SEI 7-16; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers (ASCE): Reston, VA, USA, 2017.
- Zuo, L.; Nayfeh, S.A. Optimization of the individual stiffness and damping parameters in multiple-tuned-mass-damper systems. J. Vib. Acoust. 2005, 127, 77–83. [Google Scholar] [CrossRef]
- Todorovska, M.I.; Trifunac, M.D. The system damping, the system frequency and the system response peak amplitudes during in-plane building-soil interaction. Earthq. Eng. Struct. Dyn. 1992, 21, 127–144. [Google Scholar] [CrossRef]
- Trifunac, M.D.; Hao, T.Y.; Todorovska, M.I. Response of a 14-Story Reinforced Concrete Structure to Nine Earthquakes: 61 Years of Observation in the Hollywood Storage Building; Report CE01-02; Department of Civil Engineering, University of Southern California: Los Angeles, CA, USA, 2001. [Google Scholar]
- Todorovska, M.I. Full-scale experimental studies of soil-structure interaction. ISET J. Earthq. Technol. 2002, 39, 139–165. [Google Scholar]
- Duke, C.M.; Luco, J.E.; Carriveau, A.R.; Hradilex, P.J.; Lastrico, R.; Ostrom, D. Strong earthquake motion and site conditions: Hollywood. Bull. Seismol. Soc. Am. 1970, 60, 1271–1289. [Google Scholar] [CrossRef]
- Crouse, C.B.; Jennings, P.C. Soil-structure interaction during the San Fernando earthquake. Bull. Seismol. Soc. Am. 1975, 65, 13–36. [Google Scholar] [CrossRef]
- Liang, J.; Fu, J.; Todorovska, M.I.; Trifunac, M.D. Effects of the site dynamic characteristics on soil-structure interaction (I): Incident SH-waves. Soil Dyn. Earthq. Eng. 2013, 44, 27–37. [Google Scholar] [CrossRef]
- Liang, J.; Fu, J.; Todorovska, M.I.; Trifunac, M.D. Effects of the site dynamic characteristics on soil-structure interaction (II): Incident P and SV waves. Soil Dyn. Earthq. Eng. 2013, 51, 58–76. [Google Scholar] [CrossRef]

| Optimal Minimizing | ||||||||
|---|---|---|---|---|---|---|---|---|
| Displacement | 0.01 | 0 | 0 | 2.39 × 10−5 | −4.02 × 10−4 | 3.31 × 10−3 | −8.08 × 10−3 | 0.9551 |
| 0.02 | 0 | 0 | 8.23 × 10−6 | −6.73 × 10−5 | 1.14 × 10−3 | −5.16 × 10−3 | 0.9554 | |
| 0.05 | 0 | 0 | 5.58 × 10−5 | −1.17 × 10−3 | 0.0101 | −0.0363 | 0.9751 | |
| 0.10 | 0 | 0 | 3.64 × 10−4 | −6.65 × 10−3 | 0.0434 | −0.1188 | 1.0260 | |
| Acceleration | 0.01 | 3.21 × 10−4 | −6.19 × 10−3 | 0.0472 | −0.1800 | 0.3599 | −0.3372 | 1.1330 |
| 0.02 | 2.39 × 10−3 | −0.0392 | 0.2543 | −0.8227 | 1.3895 | −1.1436 | 1.4011 | |
| 0.05 | 0.0102 | −0.1378 | 0.7580 | −2.1706 | 3.4322 | −2.8714 | 2.1358 | |
| 0.10 | - | - | - | - | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, L.; Li, B.; Lin, S.; Li, G. Optimal Design Formula for Tuned Mass Damper Based on an Analytical Solution of Interaction between Soil and Structure with Rigid Foundation Subjected to Plane SH-Waves. Buildings 2023, 13, 17. https://doi.org/10.3390/buildings13010017
Jin L, Li B, Lin S, Li G. Optimal Design Formula for Tuned Mass Damper Based on an Analytical Solution of Interaction between Soil and Structure with Rigid Foundation Subjected to Plane SH-Waves. Buildings. 2023; 13(1):17. https://doi.org/10.3390/buildings13010017
Chicago/Turabian StyleJin, Liguo, Bowei Li, Siqi Lin, and Guangning Li. 2023. "Optimal Design Formula for Tuned Mass Damper Based on an Analytical Solution of Interaction between Soil and Structure with Rigid Foundation Subjected to Plane SH-Waves" Buildings 13, no. 1: 17. https://doi.org/10.3390/buildings13010017
APA StyleJin, L., Li, B., Lin, S., & Li, G. (2023). Optimal Design Formula for Tuned Mass Damper Based on an Analytical Solution of Interaction between Soil and Structure with Rigid Foundation Subjected to Plane SH-Waves. Buildings, 13(1), 17. https://doi.org/10.3390/buildings13010017







