Effect of Precompression and Material Uncertainty on the In-Plane Behavior of URM Pier–Spandrel Systems
Abstract
1. Introduction
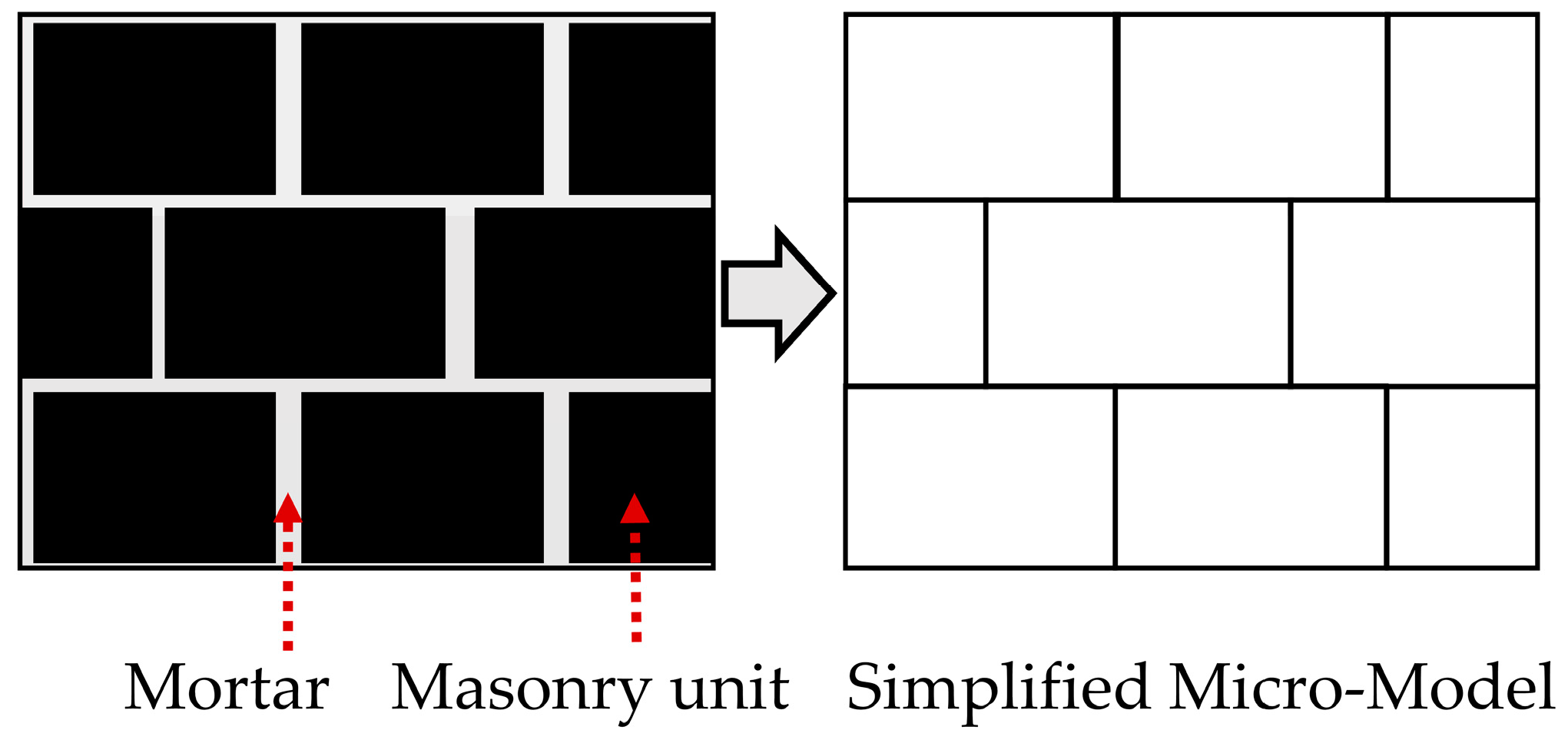
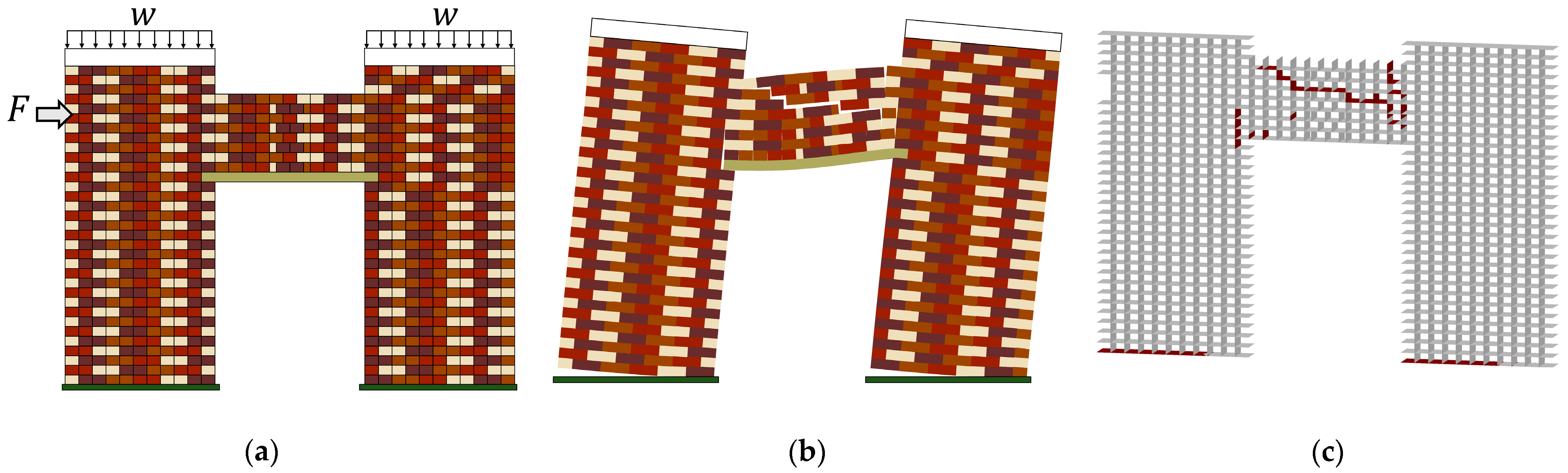
2. Computational Modeling: Discrete Rigid Block Analysis (D-RBA)
3. Brief Overview of Data Preparation and Material Uncertainty
3.1. Benchmark Study and Validation
3.2. Data Preparation
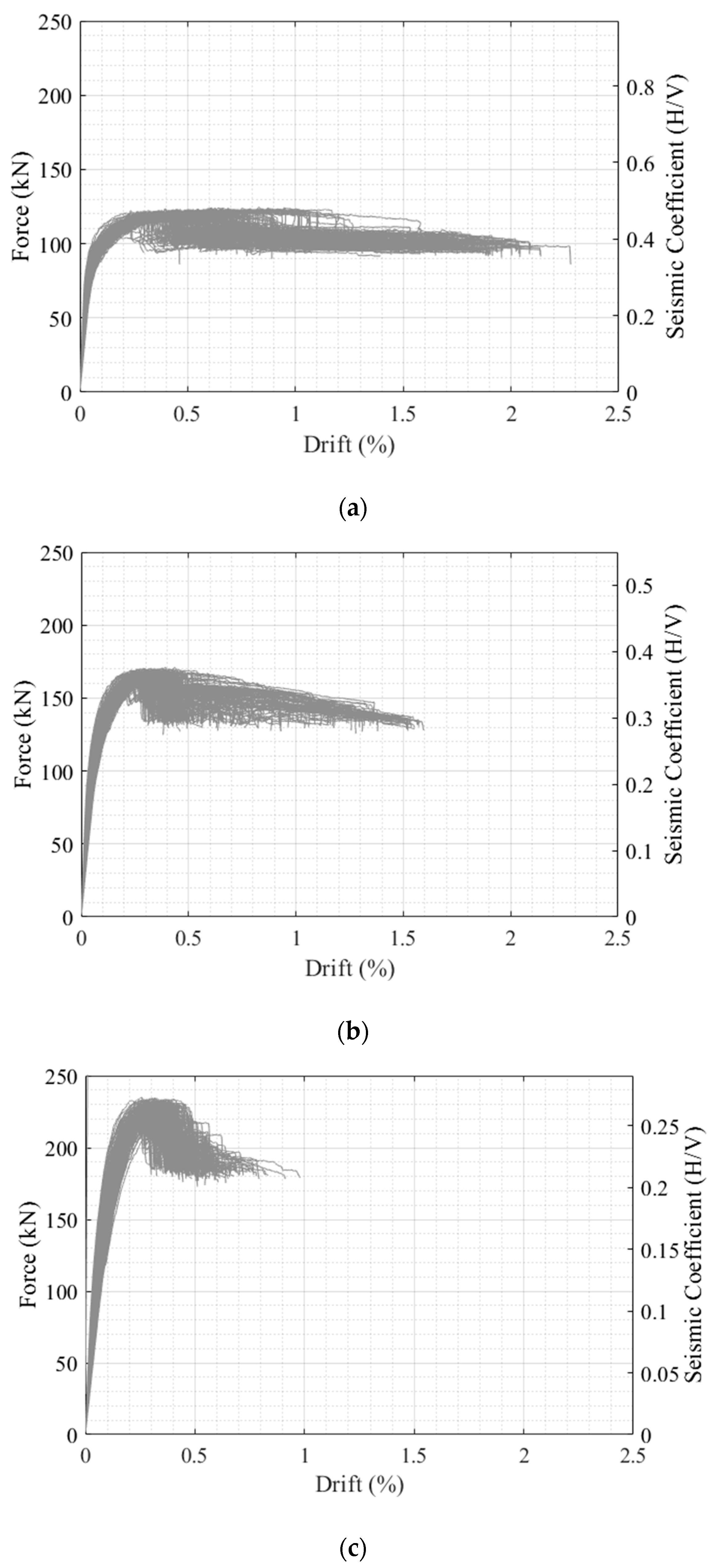
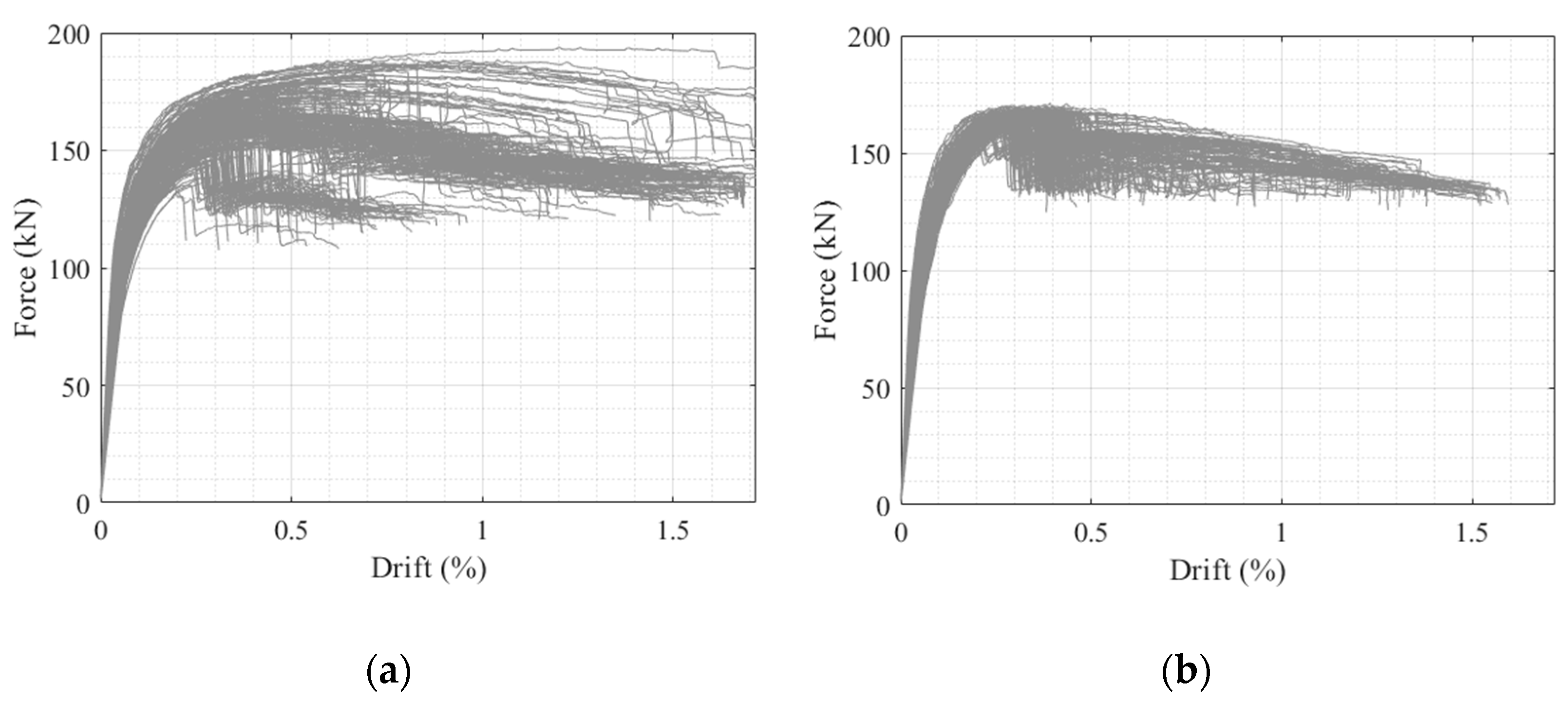
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gonen, S.; Soyoz, S. Investigations on the Elasticity Modulus of Stone Masonry. Structures 2021, 30, 378–389. [Google Scholar] [CrossRef]
- Bosiljkov, V.; D’Ayala, D.; Novelli, V. Evaluation of Uncertainties in Determining the Seismic Vulnerability of Historic Masonry Buildings in Slovenia: Use of Macro-Element and Structural Element Modelling. Bull. Earthq. Eng. 2015, 13, 311–329. [Google Scholar] [CrossRef]
- Isfeld, A.C.; Stewart, M.G.; Masia, M.J. Stochastic Finite Element Model Assessing Length Effect for Unreinforced Masonry Walls Subjected to One-Way Vertical Bending under out-of-Plane Loading. Eng. Struct. 2021, 236, 112115. [Google Scholar] [CrossRef]
- Tondelli, M.; Rota, M.; Penna, A.; Magenes, G. Evaluation of Uncertainties in the Seismic Assessment of Existing Masonry Buildings. J. Earthq. Eng. 2012, 16, 36–64. [Google Scholar] [CrossRef]
- Gonen, S.; Soyoz, S. Reliability-Based Seismic Performance of Masonry Arch Bridges. Struct. Infrastruct. Eng. 2022, 18, 1658–1673. [Google Scholar] [CrossRef]
- Gonen, S.; Pulatsu, B.; Soyoz, S.; Erdogmus, E. Stochastic Discontinuum Analysis of Unreinforced Masonry Walls: Lateral Capacity and Performance Assessments. Eng. Struct. 2021, 238, 112175. [Google Scholar] [CrossRef]
- Parisi, F.; Augenti, N. Uncertainty in Seismic Capacity of Masonry Buildings. Buildings 2012, 2, 218–230. [Google Scholar] [CrossRef]
- Müller, D.; Graubner, C.-A. Assessment of Masonry Compressive Strength in Existing Structures Using a Bayesian Method. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7, 04020057. [Google Scholar] [CrossRef]
- Gooch, L.J.; Masia, M.J.; Stewart, M.G. Application of Stochastic Numerical Analyses in the Assessment of Spatially Variable Unreinforced Masonry Walls Subjected to In-Plane Shear Loading. Eng. Struct. 2021, 235, 112095. [Google Scholar] [CrossRef]
- Pulatsu, B.; Gonen, S.; Parisi, F.; Erdogmus, E.; Tuncay, K.; Funari, M.F.; Lourenço, P.B. Probabilistic Approach to Assess URM Walls with Openings Using Discrete Rigid Block Analysis (D-RBA). J. Build. Eng. 2022, 61, 105269. [Google Scholar] [CrossRef]
- Gonen, S.; Pulatsu, B.; Lourenço, P.B.; Lemos, V.; Tuncay, K.; Erduran, E. Analysis and Prediction of Masonry Wallette Strength under Combined Compression-Bending via Stochastic Computational Modeling. Eng. Struct. 2023, 278, 115492. [Google Scholar] [CrossRef]
- Li, J.; Masia, M.J.; Stewart, M.G. Stochastic Spatial Modelling of Material Properties and Structural Strength of Unreinforced Masonry in Two-Way Bending. Struct. Infrastruct. Eng. 2017, 13, 683–695. [Google Scholar] [CrossRef]
- Müller, D.; Förster, V.; Graubner, C.-A. Influence of Material Spatial Variability on Required Safety Factors for Masonry Walls in Compression. Mauerwerk 2017, 21, 209–222. [Google Scholar] [CrossRef]
- Tabbakhha, M.; Deodatis, G. Effect of Uncertainty of Tensile Strength of Mortar Joints on the Behavior of Masonry Walls under Lateral Loads. J. Struct. Eng. 2017, 143, 04016166. [Google Scholar] [CrossRef]
- Backes, H.P. Tensile Strength of Masonry. In Proceedings of the 7th International Brick Masonry Conference, Melbourne, Australia, 17–20 February 1985; pp. 779–790. [Google Scholar]
- Pulatsu, B.; Gonen, S.; Erdogmus, E.; Lourenço, P.B.; Lemos, J.V.; Hazzard, J. Tensile Fracture Mechanism of Masonry Wallettes Parallel to Bed Joints: A Stochastic Discontinuum Analysis. Modelling 2020, 1, 78–93. [Google Scholar] [CrossRef]
- Pulatsu, B.; Erdogmus, E.; Lourenço, P.B.; Lemos, J.V.; Hazzard, J. Discontinuum Analysis of the Fracture Mechanism in Masonry Prisms and Wallettes via Discrete Element Method. Meccanica 2020, 55, 505–523. [Google Scholar] [CrossRef]
- Augenti, N.; Parisi, F. Learning from Construction Failures Due to the 2009 L’Aquila, Italy, Earthquake. J. Perform. Constr. Facil. 2010, 24, 536–555. [Google Scholar] [CrossRef]
- Vlachakis, G.; Vlachaki, E.; Lourenço, P.B. Learning from Failure: Damage and Failure of Masonry Structures, after the 2017 Lesvos Earthquake (Greece). Eng. Fail. Anal. 2020, 117, 104803. [Google Scholar] [CrossRef]
- Borri, A.; Corradi, M.; De Maria, A. The Failure of Masonry Walls by Disaggregation and the Masonry Quality Index. Heritage 2020, 3, 1162–1198. [Google Scholar] [CrossRef]
- Lourenço, P.B. Computational Strategies for Masonry Structures; Faculdade de Engenharia da Universidade do Porto: Porto, Portugal, 1996. [Google Scholar]
- Lourenço, P.B.; Rots, J.G.; Blaauwendraad, J. Continuum Model for Masonry: Parameter Estimation and Validation. J. Struct. Eng. 1998, 124, 642–652. [Google Scholar] [CrossRef]
- Saloustros, S.; Pelà, L.; Cervera, M.; Roca, P. An Enhanced Finite Element Macro-Model for the Realistic Simulation of Localized Cracks in Masonry Structures: A Large-Scale Application. Int. J. Archit. Herit. 2018, 12, 432–447. [Google Scholar] [CrossRef]
- Roca, P.; Cervera, M.; Gariup, G.; Pela’, L. Structural Analysis of Masonry Historical Constructions. Classical and Advanced Approaches. Arch. Comput. Methods Eng. 2010, 17, 299–325. [Google Scholar] [CrossRef]
- Pelà, L.; Cervera, M.; Roca, P. An Orthotropic Damage Model for the Analysis of Masonry Structures. Constr. Build. Mater. 2013, 41, 957–967. [Google Scholar] [CrossRef]
- Pelà, L.; Cervera, M.; Oller, S.; Chiumenti, M. A Localized Mapped Damage Model for Orthotropic Materials. Eng. Fract. Mech. 2014, 124–125, 196–216. [Google Scholar] [CrossRef]
- Gonen, S.; Soyoz, S. Seismic Analysis of a Masonry Arch Bridge Using Multiple Methodologies. Eng. Struct. 2021, 226, 111354. [Google Scholar] [CrossRef]
- Petracca, M.; Camata, G.; Spacone, E.; Pelà, L. Efficient Constitutive Model for Continuous Micro-Modeling of Masonry Structures. Int. J. Archit. Herit. 2022, 1–13. [Google Scholar] [CrossRef]
- Massart, T.J.; Peerlings, R.H.J.; Geers, M.G.D. Mesoscopic Modeling of Failure and Damage-Induced Anisotropy in Brick Masonry. Eur. J. Mech. A/Solids 2004, 23, 719–735. [Google Scholar] [CrossRef]
- Massart, T.J.; Peerlings, R.H.J.; Geers, M.G.D. Structural Damage Analysis of Masonry Walls Using Computational Homogenization. Int. J. Damage Mech. 2007, 16, 199–226. [Google Scholar] [CrossRef]
- Calderini, C.; Lagomarsino, S. Continuum Model for In-Plane Anisotropic Inelastic Behavior of Masonry. J. Struct. Eng. 2008, 134, 209–220. [Google Scholar] [CrossRef]
- Pascuzzo, A.; Greco, F.; Leonetti, L.; Lonetti, P.; Ronchei, C.; Gaetano, D. An Interface-Based Detailed Micro-Model for the Failure Simulation of Masonry Structures. Eng. Fail. Anal. 2022, 142, 106753. [Google Scholar] [CrossRef]
- Pulatsu, B.; Erdogmus, E.; Lourenço, P.B.; Quey, R. Simulation of Uniaxial Tensile Behavior of Quasi-Brittle Materials Using Softening Contact Models in DEM. Int. J. Fract. 2019, 217, 105–125. [Google Scholar] [CrossRef]
- Zhang, S.; Taheri Mousavi, S.M.; Richart, N.; Molinari, J.F.; Beyer, K. Micro-Mechanical Finite Element Modeling of Diagonal Compression Test for Historical Stone Masonry Structure. Int. J. Solids Struct. 2017, 112, 122–132. [Google Scholar] [CrossRef]
- Cross, T.; De Luca, F.; De Risi, R.; Camata, G.; Petracca, M. Micro-Modelling of Stone Masonry Template Buildings as a Strategy for Seismic Risk Assessment in Developing Countries. Eng. Struct. 2023, 274, 114910. [Google Scholar] [CrossRef]
- Guo, Y.T.; Bompa, D.V.; Elghazouli, A.Y. Nonlinear Numerical Assessments for the In-Plane Response of Historic Masonry Walls. Eng. Struct. 2022, 268, 114734. [Google Scholar] [CrossRef]
- Nie, Y.; Sheikh, A.; Visintin, P.; Griffith, M. An Interfacial Damage-Plastic Model for the Simulation of Masonry Structures under Monotonic and Cyclic Loadings. Eng. Fract. Mech. 2022, 271, 108645. [Google Scholar] [CrossRef]
- Chang, L.-Z.; Rots, J.G.; Esposito, R. Influence of Aspect Ratio and Pre-Compression on Force Capacity of Unreinforced Masonry Walls in out-of-Plane Two-Way Bending. Eng. Struct. 2021, 249, 113350. [Google Scholar] [CrossRef]
- Noor-E-Khuda, S.; Dhanasekar, M.; Thambiratnam, D.P. An Explicit Finite Element Modelling Method for Masonry Walls under Out-of-Plane Loading. Eng. Struct. 2016, 113, 103–120. [Google Scholar] [CrossRef]
- Abdulla, K.F.; Cunningham, L.S.; Gillie, M. Simulating Masonry Wall Behaviour Using a Simplified Micro-Model Approach. Eng. Struct. 2017, 151, 349–365. [Google Scholar] [CrossRef]
- Gonen, S.; Pulatsu, B.; Erdogmus, E.; Lourenço, P.B.; Soyoz, S. Effects of Spatial Variability and Correlation in Stochastic Discontinuum Analysis of Unreinforced Masonry Walls. Constr. Build. Mater. 2022, 337, 127511. [Google Scholar] [CrossRef]
- Patel, K.P.; Dubey, R.N. Effect of Flanges on the In-Plane Behavior of the Masonry Walls. Eng. Struct. 2022, 273, 115059. [Google Scholar] [CrossRef]
- Kesavan, P.; Menon, A. Investigation of In-Plane and out-of-Plane Interaction in Unreinforced Masonry Piers by Block-Based Micro-Modeling. Structures 2022, 46, 1327–1344. [Google Scholar] [CrossRef]
- Gonen, S.; Pulatsu, B.; Erdogmus, E.; Karaesmen, E.; Karaesmen, E. Quasi-Static Nonlinear Seismic Assessment of a Fourth Century A.D. Roman Aqueduct in Istanbul, Turkey. Heritage 2021, 4, 401–421. [Google Scholar] [CrossRef]
- Celano, T.; Argiento, L.U.; Ceroni, F.; Casapulla, C. Literature Review of the In-Plane Behavior of Masonry Walls: Theoretical vs. Experimental Results. Materials 2021, 14, 3063. [Google Scholar] [CrossRef] [PubMed]
- Lourenço, P.B.; Oliveira, D.V.; Roca, P.; Orduña, A. Dry Joint Stone Masonry Walls Subjected to In-Plane Combined Loading. J. Struct. Eng. 2005, 131, 1665–1673. [Google Scholar] [CrossRef]
- Malomo, D.; DeJong, M.J.; Penna, A. Influence of Bond Pattern on the In-Plane Behavior of URM Piers. Int. J. Archit. Herit. 2021, 15, 1492–1511. [Google Scholar] [CrossRef]
- Pulatsu, B.; Bretas, E.M.; Lourenço, P.B. Discrete Element Modeling of Masonry Structures: Validation and Application. Earthquakes Struct. 2016, 11, 563–582. [Google Scholar] [CrossRef]
- Beyer, K. Peak and Residual Strengths of Brick Masonry Spandrels. Eng. Struct. 2012, 41, 533–547. [Google Scholar] [CrossRef]
- Beyer, K.; Mangalathu, S. Numerical Study on the Peak Strength of Masonry Spandrels with Arches. J. Earthq. Eng. 2014, 18, 169–186. [Google Scholar] [CrossRef]
- Foraboschi, P. Coupling Effect between Masonry Spandrels and Piers. Mater. Struct. Constr. 2009, 42, 279–300. [Google Scholar] [CrossRef]
- Liu, Z.; Crewe, A. Effects of Size and Position of Openings on In-Plane Capacity of Unreinforced Masonry Walls. Bull. Earthq. Eng. 2020, 18, 4783–4812. [Google Scholar] [CrossRef]
- Parisi, F.; Lignola, G.P.; Augenti, N.; Prota, A.; Manfredi, G. Rocking Response Assessment of In-Plane Laterally-Loaded Masonry Walls with Openings. Eng. Struct. 2013, 56, 1234–1248. [Google Scholar] [CrossRef]
- Nowak, R.; Orłowicz, R. Testing of Chosen Masonry Arched Lintels. Int. J. Archit. Herit. 2021, 15, 1895–1909. [Google Scholar] [CrossRef]
- Cundall, P.A. A Computer Model for Simulating Progressive, Large-Scale Movements in Blocky Rock Systems. In Proceedings of the The International Symposium on Rock Mechanics, Nancy, France, 4–6 October 1971; Volume 2, pp. 47–65. [Google Scholar]
- Lemos, J.V. Discrete Element Modeling of the Seismic Behavior of Stone Masonry Arches. In Proceedings of the Computer Methods in Structural Masonry, Florence, Italy, 3–5 September 1997; pp. 220–227. [Google Scholar]
- Foti, D.; Vacca, V.; Facchini, I. DEM Modeling and Experimental Analysis of the Static Behavior of a Dry-Joints Masonry Cross Vaults. Constr. Build. Mater. 2018, 170, 111–120. [Google Scholar] [CrossRef]
- Hamp, E.; Gerber, R.; Pulatsu, B.; Quintero, M.S.; Erochko, J. Nonlinear Seismic Assessment of a Historic Rubble Masonry Building via Simplified and Advanced Computational Approaches. Buildings 2022, 12, 1130. [Google Scholar] [CrossRef]
- Pulatsu, B.; Sarhosis, V.; Bretas, E.M.; Nikitas, N.; Lourenço, P.B. Non-Linear Static Behaviour of Ancient Free-Standing Stone Columns. Struct. Build. 2017, 170, 406–418. [Google Scholar] [CrossRef]
- Tavafi, E.; Mohebkhah, A.; Sarhosis, V. Seismic Behavior of the Cube of Zoroaster Tower Using the Discrete Element Method. Int. J. Archit. Herit. 2019, 15, 1097–1112. [Google Scholar] [CrossRef]
- Sarhosis, V.; Forgács, T.; Lemos, J. Stochastic Strength Prediction of Masonry Structures: A Methodological Approach or a Way Forward? RILEM Tech. Lett. 2020, 4, 122–129. [Google Scholar] [CrossRef]
- Malomo, D.; DeJong, M.J. A Macro-Distinct Element Model (M-DEM) for out-of-Plane Analysis of Unreinforced Masonry Structures. Eng. Struct. 2021, 244, 112754. [Google Scholar] [CrossRef]
- Malomo, D.; DeJong, M.J. A Macro-Distinct Element Model (M-DEM) for Simulating the in-Plane Cyclic Behavior of URM Structures. Eng. Struct. 2021, 227, 111428. [Google Scholar] [CrossRef]
- Erdogmus, E.; Pulatsu, B.; Gaggioli, A.; Hoff, M. Reverse Engineering a Fully Collapsed Ancient Roman Temple through Geoarchaeology and DEM. Int. J. Archit. Herit. 2021, 15, 1795–1815. [Google Scholar] [CrossRef]
- Mendes, N.; Zanotti, S.; Lemos, J.V. Seismic Performance of Historical Buildings Based on Discrete Element Method: An Adobe Church. J. Earthq. Eng. 2020, 24, 1270–1289. [Google Scholar] [CrossRef]
- Bretas, E.M.; Léger, P.; Lemos, J.V. 3D Stability Analysis of Gravity Dams on Sloped Rock Foundations Using the Limit Equilibrium Method. Comput. Geotech. 2012, 44, 147–156. [Google Scholar] [CrossRef]
- Lourenço, P.B.; Rots, J.G. Multisurface Interface Model for Analysis of Masonry Structures. J. Eng. Mech. 1997, 123, 660–668. [Google Scholar] [CrossRef]
- Cundall, P.A. Formulation of a Three-Dimensional Disctinct Element Model—Part I. A Scheme to Detect and Represent Contacts in a System Composed of Many Polyhedral Blocks. Int. J. Rock Mech. Min. Sci. Geomech. 1988, 25, 107–116. [Google Scholar] [CrossRef]
- Pulatsu, B.; Erdogmus, E.; Lourenço, P.B.; Lemos, J.V.; Tuncay, K. Simulation of the In-Plane Structural Behavior of Unreinforced Masonry Walls and Buildings Using DEM. Structures 2020, 27, 2274–2287. [Google Scholar] [CrossRef]
- Pulatsu, B.; Gonen, S.; Erdogmus, E.; Lourenço, P.B.; Lemos, J.V.; Prakash, R. In-Plane Structural Performance of Dry-Joint Stone Masonry Walls: A Spatial and Non-Spatial Stochastic Discontinuum Analysis. Eng. Struct. 2021, 242, 112620. [Google Scholar] [CrossRef]
- Cundall, P.; Detournay, C. Dynamic Relaxation Applied to Continuum and Discontinuum Numerical Models in Geomechanics. In Rock Mechanics and Engineering; CRC Press: Boca Raton, FL, USA, 2017; Volume 3, pp. 45–90. [Google Scholar] [CrossRef]
- Itasca Consulting Group Inc. 3DEC Three Dimensional Distinct Element Code 2013.
- Parisi, F.; Augenti, N.; Prota, A. Implications of the Spandrel Type on the Lateral Behavior of Unreinforced Masonry Walls. Earthq. Eng. Struct. Dyn. 2014, 43, 1867–1887. [Google Scholar] [CrossRef]
- Augenti, N.; Parisi, F. Constitutive Models for Tuff Masonry under Uniaxial Compression. J. Mater. Civ. Eng. 2010, 22, 1102–1111. [Google Scholar] [CrossRef]
- Augenti, N.; Parisi, F. Constitutive Modelling of Tuff Masonry in Direct Shear. Constr. Build. Mater. 2011, 25, 1612–1620. [Google Scholar] [CrossRef]
- Lourenço, P.B. Recent Advances in Masonry Structures: Micromodelling and Homogenisation. In Multiscale Modeling in Solid Mechanics: Computational Approaches; Imperial College Press: London, UK, 2009; pp. 251–294. [Google Scholar]
- Pina-Henriques, J.; Lourenço, P.B. Masonry Compression: A Numerical Investigation at the Meso-Level. Eng. Comput. 2006, 23, 382–407. [Google Scholar] [CrossRef]
- Li, J.; Stewart, M.G.; Masia, M.J.; Lawrence, S.J. Spatial Correlation of Material Properties and Structural Strength of Masonry in Horizontal Bending. J. Struct. Eng. 2016, 142, 04016112. [Google Scholar] [CrossRef]
- Stein, M. Large Sample Properties of Simulations Using Latin Hypercube Sampling. Technometrics 1987, 29, 143–151. [Google Scholar] [CrossRef]

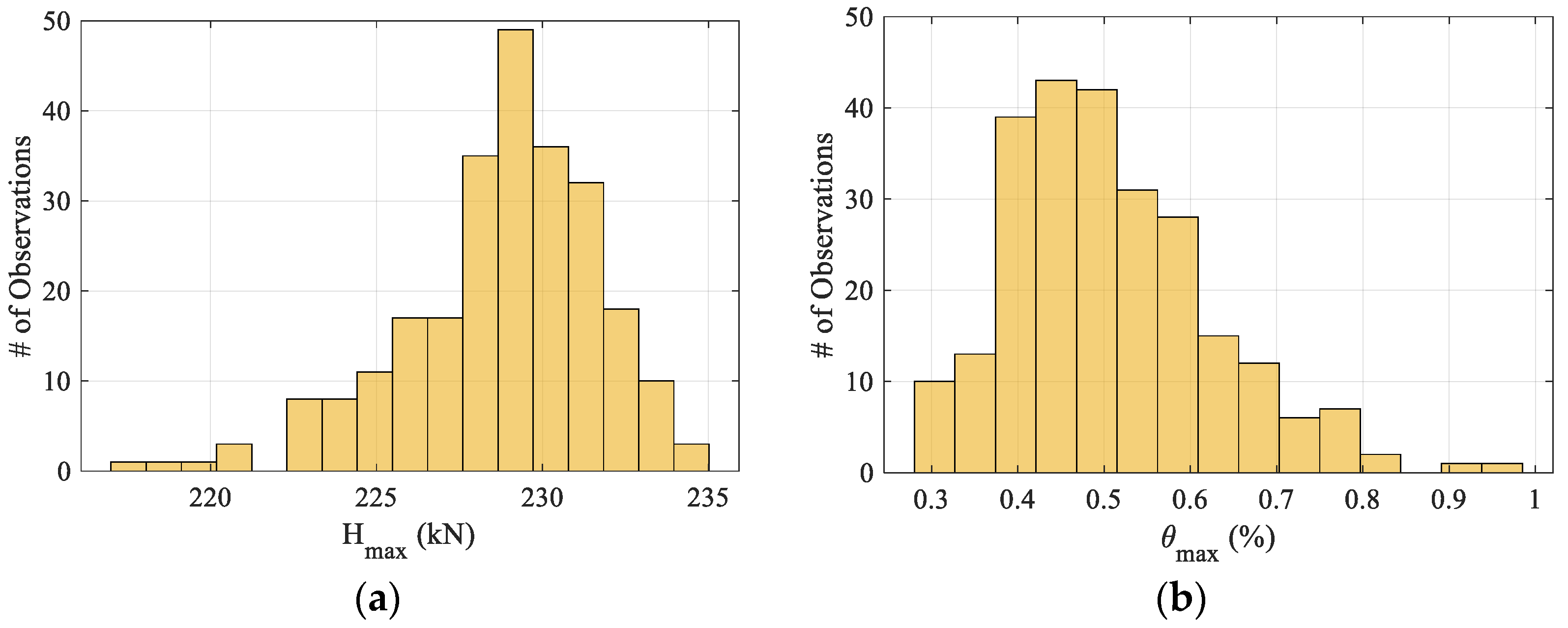
| Random Variable | Probability Distribution | Mean (μ) | Coefficient of Variation (CoV) |
|---|---|---|---|
| Normal | 3.96 | 0.125 | |
| Lognormal | 0.15 | 0.30 | |
| Lognormal | 0.23 | 0.22 | |
| Normal | 16 | 0.20 | |
| Dependent Variable | Relationship | ||
| 1.5 | |||
| 0.029 | |||
| 3.2 | |||
| Low Pressure (0.20 MPa) | Medium Pressure (0.38 MPa) | High Pressure (0.75 MPa) | |||
|---|---|---|---|---|---|
| Spatial | Mean (kN) | 120.3 | 166.3 | 228.8 | |
| CoV | 0.02 | 0.01 | 0.01 | ||
| Mean (%) | 1.23 | 0.73 | 0.51 | ||
| CoV | 0.40 | 0.54 | 0.23 | ||
| Nonspatial [10] | Mean (kN) | N/A | 163.3 | N/A | |
| CoV | 0.07 | ||||
| Mean (%) | N/A | 1.10 | N/A | ||
| CoV | 0.43 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pulatsu, B.; Gonen, S.; Parisi, F. Effect of Precompression and Material Uncertainty on the In-Plane Behavior of URM Pier–Spandrel Systems. Buildings 2023, 13, 203. https://doi.org/10.3390/buildings13010203
Pulatsu B, Gonen S, Parisi F. Effect of Precompression and Material Uncertainty on the In-Plane Behavior of URM Pier–Spandrel Systems. Buildings. 2023; 13(1):203. https://doi.org/10.3390/buildings13010203
Chicago/Turabian StylePulatsu, Bora, Semih Gonen, and Fulvio Parisi. 2023. "Effect of Precompression and Material Uncertainty on the In-Plane Behavior of URM Pier–Spandrel Systems" Buildings 13, no. 1: 203. https://doi.org/10.3390/buildings13010203
APA StylePulatsu, B., Gonen, S., & Parisi, F. (2023). Effect of Precompression and Material Uncertainty on the In-Plane Behavior of URM Pier–Spandrel Systems. Buildings, 13(1), 203. https://doi.org/10.3390/buildings13010203








